Topología de filtro electrónico

Este artículo incluye una lista de referencias generales , pero carece de suficientes citas en línea correspondientes . Por favor, ayude a mejorar este artículo introduciendo citas más precisas. ( Noviembre de 2014 ) ( Aprenda cómo y cuándo eliminar este mensaje )

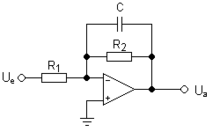
La topología de filtro electrónico define circuitos de filtro electrónico sin tener en cuenta los valores de los componentes utilizados sino únicamente la forma en que dichos componentes están conectados.

El diseño de filtros caracteriza los circuitos de filtro principalmente por su función de transferencia en lugar de su topología . Las funciones de transferencia pueden ser lineales o no lineales . Los tipos comunes de función de transferencia de filtro lineal son; paso alto , paso bajo , paso de banda , rechazo de banda o muesca y paso todo . Una vez que se elige la función de transferencia para un filtro, se puede seleccionar la topología particular para implementar dicho filtro prototipo de modo que, por ejemplo, se podría elegir diseñar un filtro Butterworth utilizando la topología Sallen–Key .

Las topologías de filtros se pueden dividir en tipos pasivos y activos . Las topologías pasivas se componen exclusivamente de componentes pasivos : resistencias, condensadores e inductores. Las topologías activas también incluyen componentes activos (como transistores, amplificadores operacionales y otros circuitos integrados) que requieren energía. Además, las topologías se pueden implementar en forma no balanceada o en forma balanceada cuando se emplean en circuitos balanceados . Las implementaciones como mezcladores electrónicos y sonido estéreo pueden requerir conjuntos de circuitos idénticos.

Los filtros pasivos se han desarrollado y utilizado durante mucho tiempo . La mayoría se construyen a partir de redes simples de dos puertos llamadas "secciones". No existe una definición formal de una sección, excepto que debe tener al menos un componente en serie y un componente en derivación. Las secciones están invariablemente conectadas en una topología de "cascada" o "en cadena" , que consiste en copias adicionales de la misma sección o de secciones completamente diferentes. Las reglas de impedancia en serie y en paralelo combinarían dos secciones que constan solo de componentes en serie o componentes en derivación en una sola sección.

Algunos filtros pasivos, que constan de una o dos secciones de filtro, reciben nombres especiales, como la sección en L, la sección en T y la sección en P, que son filtros no balanceados, y la sección en C, la sección en H y la sección en caja, que son balanceados. Todos están construidos sobre una topología de "escalera" muy simple (ver a continuación). El gráfico en la parte inferior de la página muestra estas diversas topologías en términos de filtros generales de k constante .

Los filtros diseñados mediante síntesis de red suelen repetir la forma más simple de topología de sección en L, aunque los valores de los componentes pueden cambiar en cada sección. Por otro lado, los filtros diseñados con imágenes mantienen los mismos valores básicos de los componentes de una sección a otra, aunque la topología puede variar, y tienden a utilizar secciones más complejas.

Las secciones en L nunca son simétricas, pero dos secciones en L consecutivas forman una topología simétrica y muchas otras secciones tienen una forma simétrica.

La topología en escalera, a menudo llamada topología de Cauer en honor a Wilhelm Cauer (inventor del filtro elíptico ), fue utilizada por primera vez por George Campbell (inventor del filtro k constante ). Campbell publicó la topología en 1922, pero claramente ya la había utilizado durante algún tiempo antes. Cauer fue el primero en utilizar la topología en escalera (publicada en 1926) inspirado por el trabajo de Foster (1924). Existen dos formas de topologías en escalera básicas: desequilibrada y equilibrada. La topología de Cauer suele considerarse una topología en escalera desequilibrada.

Una red en escalera consta de secciones en L asimétricas en cascada (no balanceadas) o secciones en C (balanceadas). En forma de paso bajo, la topología constaría de inductores en serie y condensadores en derivación. Otras formas de banda tendrían una topología igualmente simple transformada a partir de la topología de paso bajo. La red transformada tendrá admitancias en derivación que son redes duales de las impedancias en serie si fueran duales en la red inicial, lo que es el caso de los inductores en serie y los condensadores en derivación.

Secciones de filtros de imagen
	Desequilibrado L Media sección Sección T Sección Π Red de escalera
	Equilibrado C Media sección Sección H Sección de caja Red de escalera Sección X (derivada de T media) Sección X (derivada de la mitad de la línea Π)
NÓTESE BIEN Los libros de texto y los dibujos de diseño generalmente muestran las implementaciones no balanceadas, pero en telecomunicaciones a menudo es necesario convertir el diseño a la implementación balanceada cuando se utiliza con líneas balanceadas . editar

El diseño de filtros de imagen comúnmente utiliza modificaciones de la topología básica de escalera. Estas topologías, inventadas por Otto Zobel , ^[1] tienen las mismas bandas de paso que la escalera en la que se basan, pero sus funciones de transferencia se modifican para mejorar algún parámetro como la adaptación de impedancia , el rechazo de banda de rechazo o la inclinación de la transición de banda de paso a banda de rechazo. Por lo general, el diseño aplica alguna transformación a una topología de escalera simple: la topología resultante es similar a una escalera, pero ya no obedece la regla de que las admitancias en derivación son la red dual de impedancias en serie: invariablemente se vuelve más compleja con un mayor número de componentes. Tales topologías incluyen;

• filtro derivado de m
• Filtro tipo mm
• Filtro general tipo m _n

El filtro de tipo m (derivado de m) es, con diferencia, la topología de escalera de imagen modificada más utilizada. Hay dos topologías de tipo m para cada una de las topologías de escalera básicas: la derivada en serie y la derivada en derivación. Estas tienen funciones de transferencia idénticas entre sí, pero diferentes impedancias de imagen. Cuando se diseña un filtro con más de una banda de paso, la topología de tipo m dará como resultado un filtro en el que cada banda de paso tiene una respuesta análoga en el dominio de la frecuencia. Es posible generalizar la topología de tipo m para filtros con más de una banda de paso utilizando parámetros m ₁ , m ₂ , m ₃ etc., que no son iguales entre sí, lo que da como resultado filtros generales de tipo m _n ^[2] que tienen formas de banda que pueden diferir en diferentes partes del espectro de frecuencia.

La topología de tipo mm' puede considerarse como un diseño de tipo m doble. Al igual que el tipo m, tiene la misma forma de banda pero ofrece características de transferencia mejoradas. Sin embargo, es un diseño que rara vez se utiliza debido al mayor número de componentes y la complejidad, así como a que normalmente requiere secciones de tipo m y de escalera básicas en el mismo filtro por razones de adaptación de impedancia. Normalmente solo se encuentra en un filtro compuesto .

Los filtros de resistencia constante Zobel ^[3] utilizan una topología algo diferente a otros tipos de filtros, que se distinguen por tener una resistencia de entrada constante en todas las frecuencias y por utilizar componentes resistivos en el diseño de sus secciones. El mayor número de componentes y secciones de estos diseños suele limitar su uso a aplicaciones de ecualización. Las topologías que suelen asociarse a los filtros de resistencia constante son la T puenteada y sus variantes, todas descritas en el artículo sobre redes Zobel ;

• Topología en T con puente
• Topología de puente en T balanceado
• Topología de sección en L de circuito abierto
• Topología de sección en L de cortocircuito
• Topología de sección en C de circuito abierto balanceado
• Topología de sección en C de cortocircuito equilibrado

La topología en T puente también se utiliza en secciones destinadas a producir un retardo de señal, pero en este caso no se utilizan componentes resistivos en el diseño.

Tanto la sección en T (de la topología en escalera) como la sección en T de puente (de la topología Zobel) se pueden transformar en una sección de filtro de topología de red, pero en ambos casos esto da como resultado un alto número de componentes y una gran complejidad. La aplicación más común de los filtros de red (secciones en X) es en los filtros de paso total utilizados para la ecualización de fase . ^[4]

Aunque las secciones en T y en T puente siempre se pueden transformar en secciones en X, lo inverso no siempre es posible debido a la posibilidad de que surjan valores negativos de inductancia y capacitancia en la transformación.

La topología en red es idéntica a la topología de puente más conocida ; la diferencia es simplemente la representación dibujada en la página en lugar de cualquier diferencia real en topología, circuitos o función.

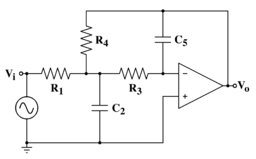
La topología de retroalimentación múltiple es una topología de filtro electrónico que se utiliza para implementar un filtro electrónico agregando dos polos a la función de transferencia . En la figura de la derecha se muestra un diagrama de la topología del circuito para un filtro de paso bajo de segundo orden.

La función de transferencia del circuito de topología de retroalimentación múltiple, como todos los filtros lineales de segundo orden , es:

${\displaystyle H(s)={\frac {V_{o}}{V_{i}}}=-{\frac {1}{As^{2}+Bs+C}}={\frac {K{\omega _{0}}^{2}}{s^{2}+{\frac {\omega _{0}}{Q}}s+{\omega _{0}}^{2}}}}$.

En un filtro MF,

${\displaystyle A=(R_{1}R_{3}C_{2}C_{5})\,}$

${\displaystyle B=R_{3}C_{5}+R_{1}C_{5}+R_{1}R_{3}C_{5}/R_{4}\,}$

${\displaystyle C=R_{1}/R_{4}\,}$

${\displaystyle Q={\frac {\sqrt {R_{3}R_{4}C_{2}C_{5}}}{(R_{4}+R_{3}+|K|R_{3})C_{5}}}}$es el factor Q.

${\displaystyle K=-R_{4}/R_{1}\,}$es la ganancia de voltaje de CC

${\displaystyle \omega _{0}=2\pi f_{0}=1/{\sqrt {R_{3}R_{4}C_{2}C_{5}}}}$es la frecuencia de esquina

Para encontrar valores de componentes adecuados para lograr las propiedades de filtro deseadas, se puede seguir un enfoque similar al de la sección Opciones de diseño de la topología alternativa de Sallen–Key.

Para la implementación digital de un filtro biquad, consulte Filtro biquad digital .

Un filtro biquad es un tipo de filtro lineal que implementa una función de transferencia que es la relación de dos funciones cuadráticas . El nombre biquad es la abreviatura de biquadratic . Cualquier topología de filtro de segundo orden puede denominarse biquad , como el MFB o el Sallen-Key. ^{[5] [6]} Sin embargo, también existe una topología "biquad" específica. A veces también se la denomina circuito de "anillo de 3". ^{[ cita requerida ]}

Los filtros biquad suelen ser activos y se implementan con una topología de amplificador único biquad (SAB) o de bucle de dos integradores .

• La topología SAB utiliza retroalimentación para generar polos complejos y posiblemente ceros complejos . En particular, la retroalimentación mueve los polos reales de un circuito RC para generar las características de filtro adecuadas.
• La topología de dos bucles integradores se deriva de la reorganización de una función de transferencia bicuadrática. La reorganización equiparará una señal con la suma de otra señal, su integral y la integral de la integral. En otras palabras, la reorganización revela una estructura de filtro de variable de estado . Al utilizar diferentes estados como salidas, se puede implementar cualquier tipo de filtro de segundo orden.

La topología SAB es sensible a la elección de componentes y puede ser más difícil de ajustar. Por lo tanto, normalmente el término biquad se refiere a la topología de filtro variable de estado de dos bucles integradores.

Por ejemplo, la configuración básica de la Figura 1 se puede utilizar como filtro de paso bajo o de paso de banda dependiendo de dónde se tome la señal de salida.

La función de transferencia de paso bajo de segundo orden está dada por

${\displaystyle H(s)={\frac {G_{\mathrm {lpf}}}{\omega _{0}}^{2}}{s^{2}+{\frac {\omega _{0}}{Q}}s+{\omega _{0}}^{2}}}}$

donde la ganancia de paso bajo es . La función de transferencia de paso de banda de segundo orden está dada por${\displaystyle G_{\mathrm {lpf} }=-R_{2}/R_{1}}$

${\displaystyle H(s)={\frac {G_{\mathrm {bpf}}}{\frac {\omega _{0}}{Q}}s}{s^{2}+{\frac {\omega _{0}}{Q}}s+{\omega _{0}}^{2}}}}$.

con ganancia de paso de banda . En ambos casos, la${\ Displaystyle G _ {\ mathrm {bpf}} = -R_ {3}/R_ {1}}$

• La frecuencia natural es .${\displaystyle \omega _{0}=1/{\sqrt {R_{2}R_{4}C_{1}C_{2}}}}$
• El factor de calidad es .${\displaystyle Q={\sqrt {\frac {{R_{3}}^{2}C_{1}}{R_{2}R_{4}C_{2}}}}}$

El ancho de banda se aproxima mediante , y Q a veces se expresa como una constante de amortiguamiento . Si se requiere un filtro de paso bajo no inversor, la salida se puede tomar en la salida del segundo amplificador operacional , después de que se haya cambiado el orden del segundo integrador y el inversor. Si se requiere un filtro de paso de banda no inversor, se puede cambiar el orden del segundo integrador y el inversor, y la salida se puede tomar en la salida del amplificador operacional del inversor.${\displaystyle B=\omega _{0}/Q}$ ${\displaystyle \zeta = 1/2Q}$

La figura 2 muestra una variante de la topología Tow-Thomas, conocida como topología Akerberg-Mossberg, que utiliza un integrador Miller compensado activamente, que mejora el rendimiento del filtro.

El diseño de Sallen-Key es un filtro de segundo orden no inversor con la opción de alta Q y ganancia de banda de paso.

• Filtro prototipo
• Topología (electrónica)
• Filtro lineal
• Filtro de variable de estado

• Medios relacionados con Topología de filtros electrónicos en Wikimedia Commons