Deriva genética
| Parte de una serie sobre |
| Biología evolutiva |
|---|
 |
La deriva genética , también conocida como deriva genética aleatoria , deriva alélica o efecto Wright , [1] es el cambio en la frecuencia de una variante genética existente ( alelo ) en una población debido al azar. [2]
La deriva genética puede provocar que las variantes genéticas desaparezcan por completo y, por lo tanto, reducir la variación genética . [3] También puede provocar que alelos inicialmente raros se vuelvan mucho más frecuentes e incluso fijos.
Cuando existen pocas copias de un alelo, el efecto de la deriva genética es más notable, y cuando existen muchas copias, el efecto es menos notable (debido a la ley de los grandes números ). A mediados del siglo XX, se produjeron intensos debates sobre la importancia relativa de la selección natural frente a los procesos neutrales, incluida la deriva genética. Ronald Fisher , que explicó la selección natural utilizando la genética mendeliana , [4] sostuvo la opinión de que la deriva genética desempeña como mucho un papel menor en la evolución , y esta siguió siendo la opinión dominante durante varias décadas. En 1968, el genetista de poblaciones Motoo Kimura reavivó el debate con su teoría neutral de la evolución molecular , que afirma que la mayoría de los casos en los que un cambio genético se propaga por una población (aunque no necesariamente cambios en los fenotipos ) son causados por la deriva genética que actúa sobre mutaciones neutrales . [5] [6] En la década de 1990, se propuso la evolución neutral constructiva que busca explicar cómo surgen los sistemas complejos a través de transiciones neutrales. [7] [8]
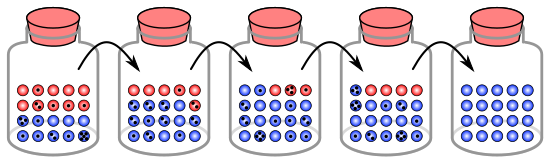
Analogía con canicas en un frasco
El proceso de deriva genética se puede ilustrar utilizando 20 canicas en un frasco para representar 20 organismos en una población. [9] Considere este frasco de canicas como la población inicial. La mitad de las canicas en el frasco son rojas y la otra mitad son azules, y cada color corresponde a un alelo diferente de un gen en la población. En cada nueva generación, los organismos se reproducen al azar. Para representar esta reproducción, seleccione aleatoriamente una canica del frasco original y deposite una nueva canica del mismo color en un nuevo frasco. Esta es la "descendencia" de la canica original, lo que significa que la canica original permanece en su frasco. Repita este proceso hasta que haya 20 nuevas canicas en el segundo frasco. El segundo frasco ahora contendrá 20 "descendencias", o canicas de varios colores. A menos que el segundo frasco contenga exactamente 10 canicas rojas y 10 canicas azules, se ha producido un cambio aleatorio en las frecuencias de los alelos.
Si este proceso se repite varias veces, la cantidad de canicas rojas y azules que se extraen en cada generación fluctúa. A veces, un frasco tiene más canicas rojas que su frasco "padre" y, a veces, más azules. Esta fluctuación es análoga a la deriva genética: un cambio en la frecuencia de alelos de la población que resulta de una variación aleatoria en la distribución de alelos de una generación a la siguiente.
En cualquier generación, no se pueden elegir canicas de un color en particular, lo que significa que no tienen descendencia. En este ejemplo, si no se selecciona ninguna canica roja, el frasco que representa a la nueva generación solo contiene descendencia azul. Si esto sucede, el alelo rojo se ha perdido de forma permanente en la población, mientras que el alelo azul restante se ha fijado: todas las generaciones futuras son completamente azules. En poblaciones pequeñas, la fijación puede ocurrir en solo unas pocas generaciones.
Probabilidad y frecuencia de alelos
Los mecanismos de la deriva genética se pueden ilustrar con un ejemplo muy simple. Consideremos una colonia muy grande de bacterias aisladas en una gota de solución. Las bacterias son genéticamente idénticas excepto por un único gen con dos alelos denominados A y B , que son alelos neutros, lo que significa que no afectan la capacidad de las bacterias para sobrevivir y reproducirse; todas las bacterias de esta colonia tienen la misma probabilidad de sobrevivir y reproducirse. Supongamos que la mitad de las bacterias tienen el alelo A y la otra mitad el alelo B. Por lo tanto, A y B tienen cada uno una frecuencia alélica de 1/2.
Luego, la gota de solución se encoge hasta que solo tiene suficiente alimento para sustentar cuatro bacterias. Todas las demás bacterias mueren sin reproducirse. Entre los cuatro que sobreviven, existen 16 combinaciones posibles para los alelos A y B
: (AAAA), (BAAA), (ABAA), (BBAA),
(AABA), (BABA), (ABBA), (BBBA),
( AAAB), (BAAB), (ABAB), (BBAB),
(AABB), (BABB), (ABBB), (BBBB).
Dado que todas las bacterias de la solución original tienen la misma probabilidad de sobrevivir cuando la solución se encoge, los cuatro supervivientes son una muestra aleatoria de la colonia original. La probabilidad de que cada uno de los cuatro supervivientes tenga un alelo determinado es 1/2, por lo que la probabilidad de que se produzca cualquier combinación de alelos en particular cuando la solución se encoge es
(El tamaño original de la población es tan grande que el muestreo se realiza efectivamente con reemplazo). En otras palabras, cada una de las 16 combinaciones de alelos posibles tiene la misma probabilidad de ocurrir, con una probabilidad de 1/16.
Contando las combinaciones con el mismo número de A y B se obtiene la siguiente tabla:
| A | B | Combinaciones | Probabilidad |
| 4 | 0 | 1 | 1/16 |
| 3 | 1 | 4 | 4/16 |
| 2 | 2 | 6 | 6/16 |
| 1 | 3 | 4 | 4/16 |
| 0 | 4 | 1 | 1/16 |
Como se muestra en la tabla, el número total de combinaciones que tienen el mismo número de alelos A que de alelos B es seis, y la probabilidad de esta combinación es 6/16. El número total de otras combinaciones es diez, por lo que la probabilidad de un número desigual de alelos A y B es 10/16. Por lo tanto, aunque la colonia original comenzó con un número igual de alelos A y B , es muy posible que el número de alelos en la población restante de cuatro miembros no sea igual. La situación de números iguales es en realidad menos probable que la de números desiguales. En este último caso, se ha producido una deriva genética porque las frecuencias de alelos de la población han cambiado debido al muestreo aleatorio. En este ejemplo, la población se contrajo a solo cuatro supervivientes aleatorios, un fenómeno conocido como cuello de botella poblacional .
Las probabilidades de que sobrevivan el número de copias del alelo A (o B ) (dadas en la última columna de la tabla anterior) se pueden calcular directamente a partir de la distribución binomial , donde la probabilidad de "éxito" (probabilidad de que esté presente un alelo dado) es 1/2 (es decir, la probabilidad de que haya k copias de los alelos A (o B ) en la combinación) viene dada por:
donde n=4 es el número de bacterias supervivientes.
Modelos matemáticos
Se pueden diseñar modelos matemáticos de deriva genética utilizando procesos de ramificación o una ecuación de difusión que describa los cambios en la frecuencia de los alelos en una población idealizada . [10]
Modelo de Wright-Fisher
Consideremos un gen con dos alelos, A o B. En la diploidía , las poblaciones formadas por N individuos tienen 2 N copias de cada gen. Un individuo puede tener dos copias del mismo alelo o dos alelos diferentes. La frecuencia de un alelo se asigna p y la del otro q . El modelo de Wright-Fisher (nombrado así por Sewall Wright y Ronald Fisher ) supone que las generaciones no se superponen (por ejemplo, las plantas anuales tienen exactamente una generación por año) y que cada copia del gen que se encuentra en la nueva generación se extrae de forma independiente al azar de todas las copias del gen en la generación anterior. La fórmula para calcular la probabilidad de obtener k copias de un alelo que tuvo frecuencia p en la última generación es entonces [11] [12]
donde el símbolo " ! " significa la función factorial . Esta expresión también se puede formular utilizando el coeficiente binomial ,
Modelo Moran
El modelo de Moran supone que hay generaciones superpuestas. En cada paso temporal, se elige un individuo para reproducirse y otro para morir. Por lo tanto, en cada paso temporal, el número de copias de un alelo determinado puede aumentar en uno, disminuir en uno o permanecer igual. Esto significa que la matriz de transición es tridiagonal , lo que significa que las soluciones matemáticas son más fáciles para el modelo de Moran que para el modelo de Wright-Fisher. Por otro lado, las simulaciones por ordenador suelen ser más fáciles de realizar utilizando el modelo de Wright-Fisher, porque se necesitan calcular menos pasos temporales. En el modelo de Moran, se necesitan N pasos temporales para atravesar una generación, donde N es el tamaño efectivo de la población . En el modelo de Wright-Fisher, se necesita solo uno. [13]
En la práctica, los modelos de Moran y Wright-Fisher dan resultados cualitativamente similares, pero la deriva genética se produce dos veces más rápido en el modelo de Moran.
Otros modelos de deriva
Si la varianza en el número de descendientes es mucho mayor que la dada por la distribución binomial asumida por el modelo de Wright-Fisher, entonces, dada la misma velocidad general de deriva genética (el tamaño efectivo de la población de la varianza), la deriva genética es una fuerza menos poderosa en comparación con la selección. [14] Incluso para la misma varianza, si los momentos más altos de la distribución del número de descendientes exceden los de la distribución binomial, entonces nuevamente la fuerza de la deriva genética se debilita sustancialmente. [15]
Efectos aleatorios distintos del error de muestreo
Los cambios aleatorios en las frecuencias de los alelos también pueden ser causados por efectos distintos al error de muestreo , por ejemplo, cambios aleatorios en la presión de selección. [16]
Una fuente alternativa importante de estocasticidad , quizás más importante que la deriva genética, es el reclutamiento genético . [17] El reclutamiento genético es el efecto que la selección de loci vinculados tiene sobre un locus . Las propiedades matemáticas del reclutamiento genético son diferentes a las de la deriva genética. [18] La dirección del cambio aleatorio en la frecuencia de los alelos está autocorrelacionada a lo largo de las generaciones. [2]
Deriva y fijación
El principio de Hardy-Weinberg establece que, dentro de poblaciones suficientemente grandes, las frecuencias de los alelos permanecen constantes de una generación a la siguiente a menos que el equilibrio se altere por la migración , las mutaciones genéticas o la selección . [19]
Sin embargo, en poblaciones finitas, no se obtienen nuevos alelos del muestreo aleatorio de alelos pasados a la siguiente generación, pero el muestreo puede hacer que desaparezca un alelo existente. Debido a que el muestreo aleatorio puede eliminar, pero no reemplazar, un alelo, y debido a que las disminuciones o aumentos aleatorios en la frecuencia de los alelos influyen en las distribuciones alélicas esperadas para la siguiente generación, la deriva genética conduce a una población hacia la uniformidad genética con el tiempo. Cuando un alelo alcanza una frecuencia de 1 (100%) se dice que está "fijo" en la población y cuando un alelo alcanza una frecuencia de 0 (0%) se pierde. Las poblaciones más pequeñas logran la fijación más rápido, mientras que en el límite de una población infinita, la fijación no se logra. Una vez que un alelo se vuelve fijo, la deriva genética se detiene y la frecuencia del alelo no puede cambiar a menos que se introduzca un nuevo alelo en la población a través de una mutación o flujo genético . Por lo tanto, incluso si bien la deriva genética es un proceso aleatorio y sin dirección, actúa para eliminar la variación genética con el tiempo. [20]
Tasa de cambio de frecuencia de alelos debido a la deriva

Suponiendo que la deriva genética es la única fuerza evolutiva que actúa sobre un alelo, después de t generaciones en muchas poblaciones replicadas, comenzando con frecuencias alélicas de p y q , la varianza en la frecuencia alélica en esas poblaciones es
- [21]
Tiempo de fijación o pérdida
Suponiendo que la deriva genética es la única fuerza evolutiva que actúa sobre un alelo, en cualquier momento dado la probabilidad de que un alelo finalmente se fije en la población es simplemente su frecuencia en la población en ese momento. [22] Por ejemplo, si la frecuencia p para el alelo A es del 75% y la frecuencia q para el alelo B es del 25%, entonces, dado un tiempo ilimitado, la probabilidad de que A finalmente se fije en la población es del 75% y la probabilidad de que B se fije es del 25%.
El número esperado de generaciones para que ocurra la fijación es proporcional al tamaño de la población, de modo que se predice que la fijación ocurrirá mucho más rápidamente en poblaciones más pequeñas. [23] Normalmente, el tamaño efectivo de la población, que es menor que la población total, se utiliza para determinar estas probabilidades. La población efectiva ( N e ) tiene en cuenta factores como el nivel de endogamia , la etapa del ciclo de vida en la que la población es la más pequeña y el hecho de que algunos genes neutrales están genéticamente vinculados a otros que están bajo selección. [14] El tamaño efectivo de la población puede no ser el mismo para cada gen en la misma población. [24]
Una fórmula prospectiva utilizada para aproximar el tiempo esperado antes de que un alelo neutral se fije a través de la deriva genética, según el modelo de Wright-Fisher, es
donde T es el número de generaciones, N e es el tamaño efectivo de la población y p es la frecuencia inicial del alelo dado. El resultado es el número de generaciones que se espera que transcurran antes de que se produzca la fijación de un alelo dado en una población con un tamaño ( N e ) y una frecuencia alélica ( p ) dados. [25]
El tiempo esperado para que el alelo neutral se pierda a través de la deriva genética se puede calcular como [11]
Cuando una mutación aparece sólo una vez en una población lo suficientemente grande como para que la frecuencia inicial sea insignificante, las fórmulas se pueden simplificar a [26]
para el número promedio de generaciones esperadas antes de la fijación de una mutación neutral, y
para el número promedio de generaciones esperadas antes de la pérdida de una mutación neutral en una población de tamaño real N. [27]
Es hora de perder tanto la deriva como la mutación
Las fórmulas anteriores se aplican a un alelo que ya está presente en una población y que no está sujeto ni a mutación ni a selección natural. Si un alelo se pierde por mutación con mucha más frecuencia de la que se gana por mutación, entonces la mutación, así como la deriva, pueden influir en el tiempo hasta la pérdida. Si el alelo propenso a la pérdida por mutación comienza como fijo en la población y se pierde por mutación a una tasa m por replicación, entonces el tiempo esperado en generaciones hasta su pérdida en una población haploide está dado por
donde es la constante de Euler . [28] La primera aproximación representa el tiempo de espera hasta que el primer mutante está destinado a la pérdida, y la pérdida ocurre entonces relativamente rápido por deriva genética, tomando tiempo .1/metro ≫ N e . La segunda aproximación representa el tiempo necesario para la pérdida determinista por acumulación de mutaciones. En ambos casos, el tiempo hasta la fijación está dominado por la mutación a través del término 1/metro , y se ve menos afectado por el tamaño efectivo de la población .
Contra la selección natural
En las poblaciones naturales, la deriva genética y la selección natural no actúan de manera aislada; ambos fenómenos están siempre en juego, junto con la mutación y la migración. La evolución neutral es el producto tanto de la mutación como de la deriva, no sólo de la deriva. De manera similar, incluso cuando la selección supera a la deriva genética, sólo puede actuar sobre la variación que proporciona la mutación.
Mientras que la selección natural tiene una dirección, guiando la evolución hacia adaptaciones hereditarias al entorno actual, la deriva genética no tiene dirección y está guiada únicamente por las matemáticas del azar . [29] Como resultado, la deriva actúa sobre las frecuencias genotípicas dentro de una población sin tener en cuenta sus efectos fenotípicos. En contraste, la selección favorece la propagación de alelos cuyos efectos fenotípicos aumentan la supervivencia y/o reproducción de sus portadores, reduce las frecuencias de alelos que causan rasgos desfavorables e ignora aquellos que son neutrales. [30]
La ley de los grandes números predice que cuando el número absoluto de copias del alelo es pequeño (por ejemplo, en poblaciones pequeñas ), la magnitud de la deriva en las frecuencias alélicas por generación es mayor. La magnitud de la deriva es lo suficientemente grande como para abrumar la selección en cualquier frecuencia alélica cuando el coeficiente de selección es menor que 1 dividido por el tamaño efectivo de la población. Por lo tanto, se considera que la evolución no adaptativa resultante del producto de la mutación y la deriva genética es un mecanismo consecuente de cambio evolutivo principalmente dentro de poblaciones pequeñas y aisladas. [31] Las matemáticas de la deriva genética dependen del tamaño efectivo de la población, pero no está claro cómo esto se relaciona con el número real de individuos en una población. [17] El ligamiento genético con otros genes que están bajo selección puede reducir el tamaño efectivo de la población experimentado por un alelo neutral. Con una tasa de recombinación más alta , el ligamiento disminuye y con él este efecto local en el tamaño efectivo de la población. [32] [33] Este efecto es visible en los datos moleculares como una correlación entre la tasa de recombinación local y la diversidad genética , [34] y una correlación negativa entre la densidad genética y la diversidad en regiones de ADN no codificantes . [35] La estocasticidad asociada con el ligamiento a otros genes que están bajo selección no es lo mismo que el error de muestreo, y a veces se conoce como borrador genético para distinguirlo de la deriva genética. [17]
Una frecuencia alélica baja hace que los alelos sean más vulnerables a ser eliminados por el azar, incluso anulando la influencia de la selección natural. Por ejemplo, mientras que las mutaciones desventajosas suelen eliminarse rápidamente dentro de la población, las nuevas mutaciones ventajosas son casi tan vulnerables a la pérdida por deriva genética como las mutaciones neutrales. La deriva genética no tendrá efecto hasta que la frecuencia alélica de la mutación ventajosa alcance un cierto umbral. [30]
Cuello de botella poblacional

Un cuello de botella poblacional se produce cuando una población se contrae hasta un tamaño significativamente menor en un corto período de tiempo debido a algún evento ambiental aleatorio. En un verdadero cuello de botella poblacional, las probabilidades de supervivencia de cualquier miembro de la población son puramente aleatorias y no mejoran por ninguna ventaja genética inherente particular. El cuello de botella puede dar lugar a cambios radicales en las frecuencias de los alelos, completamente independientes de la selección. [36]
El impacto de un cuello de botella poblacional puede ser sostenido, incluso cuando el cuello de botella es causado por un evento único como una catástrofe natural. Un ejemplo interesante de un cuello de botella que causa una distribución genética inusual es la proporción relativamente alta de individuos con daltonismo total de células bastón ( acromatopsia ) en el atolón Pingelap en Micronesia . [37] Después de un cuello de botella, la endogamia aumenta. Esto aumenta el daño causado por mutaciones deletéreas recesivas, en un proceso conocido como depresión endogámica . Las peores de estas mutaciones son seleccionadas en contra, lo que lleva a la pérdida de otros alelos que están genéticamente vinculados a ellas, en un proceso de selección de fondo . [2] Para las mutaciones dañinas recesivas, esta selección puede ser mejorada como consecuencia del cuello de botella, debido a la purga genética . Esto conduce a una mayor pérdida de diversidad genética. Además, una reducción sostenida en el tamaño de la población aumenta la probabilidad de más fluctuaciones de alelos por deriva en las generaciones venideras.
La variación genética de una población puede verse muy reducida por un cuello de botella, e incluso las adaptaciones beneficiosas pueden eliminarse de forma permanente. [38] La pérdida de variación deja a la población superviviente vulnerable a cualquier nueva presión selectiva, como enfermedades, cambios climáticos o cambios en la fuente de alimentos disponibles, porque la adaptación en respuesta a los cambios ambientales requiere una variación genética suficiente en la población para que se produzca la selección natural. [39] [40]
En el pasado reciente se han conocido muchos casos de cuello de botella de población. Antes de la llegada de los europeos , las praderas de América del Norte eran hábitat de millones de gallos de pradera mayores . Solo en Illinois , su número se desplomó de unos 100 millones de aves en 1900 a unas 50 aves en la década de 1990. Las disminuciones de la población resultaron de la caza y la destrucción del hábitat , pero una consecuencia ha sido la pérdida de la mayor parte de la diversidad genética de la especie. El análisis de ADN que compara aves de mediados de siglo con aves de la década de 1990 documenta una pronunciada disminución de la variación genética en solo las últimas décadas. Actualmente, el gallo de pradera mayor está experimentando un bajo éxito reproductivo . [41]
Sin embargo, la pérdida genética causada por el cuello de botella y la deriva genética puede aumentar la aptitud, como en Ehrlichia . [42]
La caza excesiva también provocó un grave cuello de botella en la población de elefantes marinos del norte en el siglo XIX. La disminución resultante de su variación genética se puede deducir comparándola con la de los elefantes marinos del sur , que no fueron cazados tan agresivamente. [43]
Efecto fundador

El efecto fundador es un caso especial de cuello de botella poblacional, que ocurre cuando un pequeño grupo de una población se separa de la población original y forma una nueva. Se espera que la muestra aleatoria de alelos en la nueva colonia recién formada tergiverse enormemente la población original en al menos algunos aspectos. [44] Incluso es posible que el número de alelos para algunos genes en la población original sea mayor que el número de copias de genes en los fundadores, lo que hace imposible una representación completa. Cuando una colonia recién formada es pequeña, sus fundadores pueden afectar fuertemente la composición genética de la población a largo plazo.
Un ejemplo bien documentado se encuentra en la migración Amish a Pensilvania en 1744. Dos miembros de la nueva colonia compartían el alelo recesivo del síndrome de Ellis-Van Creveld . Los miembros de la colonia y sus descendientes tienden a ser religiosos aislados y permanecen relativamente insulares. Como resultado de muchas generaciones de endogamia, el síndrome de Ellis-Van Creveld es ahora mucho más frecuente entre los Amish que en la población general. [30] [45]
La diferencia en las frecuencias genéticas entre la población original y la colonia también puede provocar que los dos grupos diverjan significativamente en el transcurso de muchas generaciones. A medida que aumenta la diferencia, o distancia genética , las dos poblaciones separadas pueden volverse distintas, tanto genética como fenéticamente , aunque no solo la deriva genética sino también la selección natural, el flujo genético y la mutación contribuyen a esta divergencia. Este potencial de cambios relativamente rápidos en la frecuencia genética de la colonia llevó a la mayoría de los científicos a considerar el efecto fundador (y por extensión, la deriva genética) como una fuerza impulsora significativa en la evolución de nuevas especies . Sewall Wright fue el primero en atribuir esta importancia a la deriva aleatoria y a las poblaciones pequeñas y recientemente aisladas con su teoría del equilibrio cambiante de la especiación. [46] Siguiendo a Wright, Ernst Mayr creó muchos modelos persuasivos para demostrar que la disminución de la variación genética y el pequeño tamaño de la población después del efecto fundador fueron de importancia crítica para el desarrollo de nuevas especies. [47] Sin embargo, hoy en día hay mucho menos apoyo para esta visión, ya que la hipótesis se ha probado repetidamente a través de la investigación experimental y los resultados han sido equívocos en el mejor de los casos. [48]
Historia
El papel del azar en la evolución fue descrito por primera vez por Arend L. Hagedoorn y Anna Cornelia Hagedoorn-Vorstheuvel La Brand en 1921. [49] Destacaron que la supervivencia aleatoria juega un papel clave en la pérdida de variación de las poblaciones. Fisher (1922) respondió a esto con el primer tratamiento matemático, aunque marginalmente incorrecto, del "efecto Hagedoorn". [50] En particular, esperaba que muchas poblaciones naturales fueran demasiado grandes (un N ~10.000) para que los efectos de la deriva fueran sustanciales y pensó que la deriva tendría un efecto insignificante en el proceso evolutivo. El tratamiento matemático corregido y el término "deriva genética" fueron acuñados más tarde por un fundador de la genética de poblaciones , Sewall Wright . Su primer uso del término "deriva" fue en 1929, [51] aunque en ese momento lo estaba usando en el sentido de un proceso dirigido de cambio o selección natural. La deriva aleatoria por medio de un error de muestreo llegó a conocerse como el "efecto Sewall-Wright", aunque nunca se sintió del todo cómodo al ver que se le daba su nombre. Wright se refirió a todos los cambios en la frecuencia de los alelos como "deriva constante" (por ejemplo, selección) o "deriva aleatoria" (por ejemplo, error de muestreo). [52] "Deriva" llegó a ser adoptado como un término técnico en el sentido estocástico exclusivamente. [53] Hoy en día se suele definir aún más estrictamente, en términos de error de muestreo, [54] aunque esta definición estrecha no es universal. [55] [56] Wright escribió que la "restricción de la "deriva aleatoria" o incluso "deriva" a un solo componente, los efectos de los accidentes del muestreo, tiende a llevar a confusión". [52] Sewall Wright consideró que el proceso de deriva genética aleatoria por medio de un error de muestreo era equivalente al que se produce por medio de la endogamia, pero trabajos posteriores han demostrado que son distintos. [57]
En los primeros días de la síntesis evolutiva moderna , los científicos estaban empezando a mezclar la nueva ciencia de la genética de poblaciones con la teoría de la selección natural de Charles Darwin . Dentro de este marco, Wright se centró en los efectos de la endogamia en poblaciones pequeñas relativamente aisladas. Introdujo el concepto de un paisaje adaptativo en el que fenómenos como el cruzamiento y la deriva genética en poblaciones pequeñas podrían alejarlas de los picos adaptativos, lo que a su vez permitiría que la selección natural las empujara hacia nuevos picos adaptativos. [58] Wright pensaba que las poblaciones más pequeñas eran más adecuadas para la selección natural porque "la endogamia era lo suficientemente intensa como para crear nuevos sistemas de interacción a través de la deriva aleatoria, pero no lo suficientemente intensa como para causar una fijación aleatoria no adaptativa de genes". [59]
Las opiniones de Wright sobre el papel de la deriva genética en el esquema evolutivo fueron controvertidas casi desde el principio. Uno de los críticos más enérgicos e influyentes fue su colega Ronald Fisher, quien admitió que la deriva genética desempeñó algún papel en la evolución, pero fue un papel insignificante. Fisher ha sido acusado de no entender las opiniones de Wright porque en sus críticas Fisher parecía argumentar que Wright había rechazado la selección casi por completo. Para Fisher, considerar el proceso de evolución como una progresión larga, constante y adaptativa era la única manera de explicar la creciente complejidad a partir de formas más simples. Pero los debates han continuado entre los "gradualistas" y aquellos que se inclinan más hacia el modelo de evolución de Wright, donde la selección y la deriva juntas desempeñan un papel importante. [60]
En 1968, Motoo Kimura reavivó el debate con su teoría neutral de la evolución molecular , que afirma que la mayoría de los cambios genéticos son causados por la deriva genética que actúa sobre mutaciones neutrales. [5] [6]
El papel de la deriva genética mediante el error de muestreo en la evolución ha sido criticado por John H. Gillespie [61] y William B. Provine , quienes sostienen que la selección en sitios vinculados es una fuerza estocástica más importante.
Véase también
- Especiación peripátrica
- Deriva antigénica
- Teoría coalescente
- Evolución neutral constructiva
- Acervo genético
- Impulso meiótico
Notas y referencias
- ^ Gould SJ (2002). "Capítulo 7, sección "Síntesis como endurecimiento"". La estructura de la teoría evolutiva .
- ^ abc Masel J (octubre de 2011). "Deriva genética". Current Biology . 21 (20). Cell Press : R837-8. Bibcode :2011CBio...21.R837M. doi : 10.1016/j.cub.2011.08.007 . PMID 22032182.
- ^ Star B, Spencer HG (mayo de 2013). "Efectos de la deriva genética y el flujo genético en el mantenimiento selectivo de la variación genética". Genética . 194 (1): 235–44. doi :10.1534/genetics.113.149781. PMC 3632471 . PMID 23457235.
- ^ Miller 2000, pág. 54
- ^ ab Kimura M (febrero de 1968). "Tasa evolutiva a nivel molecular". Nature . 217 (5129). Nature Publishing Group: 624–6. Código Bibliográfico :1968Natur.217..624K. doi :10.1038/217624a0. PMID 5637732. S2CID 4161261.
- ^Ab Futuyma 1998, pág. 320
- ^ Stoltzfus A (1999). "Sobre la posibilidad de una evolución neutral constructiva". Journal of Molecular Evolution . 49 (2): 169–181. Bibcode :1999JMolE..49..169S. doi :10.1007/PL00006540. ISSN 0022-2844. PMID 10441669. S2CID 1743092. Archivado desde el original el 30 de julio de 2022 . Consultado el 20 de enero de 2022 .
- ^ Muñoz-Gómez SA, Bilolikar G, Wideman JG, Geiler-Samerotte K (abril de 2021). "Evolución neutral constructiva 20 años después". Journal of Molecular Evolution . 89 (3): 172–182. Bibcode :2021JMolE..89..172M. doi :10.1007/s00239-021-09996-y. PMC 7982386 . PMID 33604782.
- ^ "Error de muestreo y evolución". Entendiendo la evolución . Universidad de California, Berkeley . Archivado desde el original el 8 de diciembre de 2015. Consultado el 1 de diciembre de 2015 .
- ^ Wahl LM (agosto de 2011). "Fijación cuando N y s varían: los enfoques clásicos dan nuevos resultados elegantes". Genética . 188 (4). Sociedad de Genética de América : 783–5. doi :10.1534/genetics.111.131748. PMC 3176088 . PMID 21828279.
- ^ ab Hartl y Clark 2007, pág. 112
- ^ Tian 2008, pág. 11
- ^ Moran PA (1958). "Procesos aleatorios en genética". Actas matemáticas de la Sociedad filosófica de Cambridge . 54 (1): 60–71. Bibcode :1958PCPS...54...60M. doi :10.1017/S0305004100033193. S2CID 85823386.
- ^ ab Charlesworth B (marzo de 2009). "Conceptos fundamentales en genética: tamaño efectivo de la población y patrones de evolución y variación molecular". Nature Reviews. Genética . 10 (3). Nature Publishing Group : 195–205. doi :10.1038/nrg2526. PMID 19204717. S2CID 205484393.
- ^ Der R, Epstein CL , Plotkin JB (septiembre de 2011). "Modelos de población generalizados y la naturaleza de la deriva genética". Biología de poblaciones teórica . 80 (2). Elsevier : 80–99. Bibcode :2011TPBio..80...80D. doi :10.1016/j.tpb.2011.06.004. PMID 21718713.
- ^ Li y Graur 1991, pág. 28
- ^ abc Gillespie JH (noviembre de 2001). "¿El tamaño de la población de una especie es relevante para su evolución?". Evolución; Revista internacional de evolución orgánica . 55 (11). John Wiley & Sons para la Sociedad para el Estudio de la Evolución : 2161–9. doi : 10.1111/j.0014-3820.2001.tb00732.x . PMID 11794777. S2CID 221735887.
- ^ Neher RA, Shraiman BI (agosto de 2011). "Proyecto genético y cuasi-neutralidad en grandes poblaciones facultativamente sexuales". Genética . 188 (4). Sociedad de Genética de América: 975–96. arXiv : 1108.1635 . doi :10.1534/genetics.111.128876. PMC 3176096 . PMID 21625002.
- ^ Ewens 2004
- ^ Li y Graur 1991, pág. 29
- ^ Barton y otros, 2007, pág. 417
- ^ Futuyma 1998, pág. 300
- ^ Otto SP , Whitlock MC (junio de 1997). "La probabilidad de fijación en poblaciones de tamaño cambiante" (PDF) . Genética . 146 (2). Sociedad de Genética de América: 723–33. doi :10.1093/genetics/146.2.723. PMC 1208011. PMID 9178020. Archivado (PDF) desde el original el 19 de marzo de 2015 .
- ^ Cutter AD, Choi JY (agosto de 2010). "La selección natural moldea el polimorfismo de nucleótidos en todo el genoma del nematodo Caenorhabditis briggsae". Genome Research . 20 (8). Cold Spring Harbor Laboratory Press : 1103–11. doi :10.1101/gr.104331.109. PMC 2909573 . PMID 20508143.
- ^ Hedrick 2005, pág. 315
- ^ Li y Graur 1991, pág. 33
- ^ Kimura y Ohta 1971
- ^ Masel J , King OD, Maughan H (enero de 2007). "La pérdida de plasticidad adaptativa durante largos períodos de estasis ambiental". The American Naturalist . 169 (1). University of Chicago Press en nombre de la American Society of Naturalists : 38–46. doi :10.1086/510212. PMC 1766558. PMID 17206583 .
- ^ "Selección natural: cómo funciona la evolución". Actionbioscience . Washington, DC: Instituto Americano de Ciencias Biológicas . Archivado desde el original el 6 de enero de 2010 . Consultado el 24 de noviembre de 2009 .Entrevista a Douglas J. Futuyma . Ver respuesta a la pregunta: ¿Es la selección natural el único mecanismo de la evolución?
- ^ a b C Cavalli-Sforza, Menozzi y Piazza 1996
- ^ Zimmer 2001
- ^ Golding 1994, pág. 46
- ^ Charlesworth B, Morgan MT, Charlesworth D (agosto de 1993). "El efecto de las mutaciones deletéreas en la variación molecular neutra" (PDF) . Genética . 134 (4). Sociedad de Genética de América: 1289–303. doi :10.1093/genetics/134.4.1289. PMC 1205596 . PMID 8375663. Archivado (PDF) del original el 12 de marzo de 2020 . Consultado el 9 de diciembre de 2015 .
- ^ Presgraves DC (septiembre de 2005). "La recombinación mejora la adaptación de proteínas en Drosophila melanogaster". Current Biology . 15 (18). Cell Press: 1651–6. Bibcode :2005CBio...15.1651P. doi : 10.1016/j.cub.2005.07.065 . PMID 16169487. S2CID 15120927.
- ^ Nordborg M, Hu TT, Ishino Y, Jhaveri J, Toomajian C, Zheng H, Bakker E, Calabrese P, Gladstone J, Goyal R, Jakobsson M, Kim S, Morozov Y, Padhukasahasram B, Plagnol V, Rosenberg NA, Shah C, Wall JD, Wang J, Zhao K, Kalbfleisch T, Schulz V, Kreitman M, Bergelson J (julio de 2005). "El patrón de polimorfismo en Arabidopsis thaliana". Más biología . 3 (7). Biblioteca Pública de Ciencias : e196. doi : 10.1371/journal.pbio.0030196 . PMC 1135296 . PMID 15907155.

- ^ Robinson R, ed. (2003). "Cuello de botella poblacional" . Genética . Vol. 3. Nueva York: Macmillan Reference USA . ISBN. 0-02-865609-1. LCCN 2002003560. OCLC 614996575. Consultado el 14 de diciembre de 2015 .
- ^ Hussels IE, Morton NE (mayo de 1972). "Atolones Pingelap y Mokil: acromatopsia". Revista estadounidense de genética humana . 24 (3): 304–309. PMC 1762260 . PMID 4555088.
- ^ Futuyma 1998, págs. 303-304
- ^ O'Corry-Crowe G (marzo de 2008). "Cambio climático y ecología molecular de los mamíferos marinos del Ártico". Aplicaciones ecológicas . 18 (2 Suppl). Sociedad Ecológica de América : S56-76. Bibcode :2008EcoAp..18S..56O. doi : 10.1890/06-0795.1 . PMID 18494363.
- ^ Cornuet JM, Luikart G (diciembre de 1996). "Descripción y análisis de potencia de dos pruebas para detectar cuellos de botella poblacionales recientes a partir de datos de frecuencia de alelos". Genética . 144 (4). Sociedad de Genética de América: 2001–14. doi :10.1093/genetics/144.4.2001. PMC 1207747 . PMID 8978083.
- ^ Sadava et al. 2008, capítulos 1, 21–33, 52–57
- ^ Dale C, Moran NA (agosto de 2006). "Interacciones moleculares entre simbiontes bacterianos y sus anfitriones". Cell . 126 (3): 453–65. doi : 10.1016/j.cell.2006.07.014 . PMID 16901780. S2CID 15985536.
- ^ "Cuellos de botella y efectos fundadores". Entendiendo la evolución . Universidad de California, Berkeley. Archivado desde el original el 4 de diciembre de 2015 . Consultado el 14 de diciembre de 2015 .
- ^ Campbell 1996, pág. 423
- ^ "Deriva genética y el efecto fundador". Evolution Library (recurso web). Evolution. Boston, MA: WGBH Educational Foundation ; Clear Blue Sky Productions, Inc. 2001. OCLC 48165595. Archivado desde el original el 14 de marzo de 2009. Consultado el 7 de abril de 2009 .
- ^ Wolf, Brodie y Wade 2000
- ^ Hola, Fitch y Ayala 2005
- ^ Howard y Berlocher 1998
- ^ Hagedoorn AL, Hagedoorn-Vorstheuvel La Brand AC (1921). El valor relativo de los procesos que causan la evolución. La Haya: Martinus Nijhoff. Archivado desde el original el 28 de marzo de 2019. Consultado el 28 de marzo de 2019 .
- ^ Fisher RA (1922). "Sobre la proporción de dominancia". Actas de la Royal Society de Edimburgo . 42 : 321–341. doi :10.1017/s0370164600023993.
- ^ Wright S (noviembre-diciembre de 1929). "La evolución de la dominancia". The American Naturalist . 63 (689). Chicago, IL: University of Chicago Press en representación de la American Society of Naturalists: 556–561. doi :10.1086/280290. ISSN 0003-0147. JSTOR 2456825. S2CID 85301374.
- ^ ab Wright S (1955). "Clasificación de los factores de la evolución". Simposios de Cold Spring Harbor sobre biología cuantitativa . 20. Cold Spring Harbor Laboratory Press: 16–24D. doi :10.1101/SQB.1955.020.01.004. PMID 13433551.Simposio: "Genética de Poblaciones: Naturaleza y Causas de la Variabilidad Genética en las Poblaciones".
- ^ Stevenson 1991
- ^ Freeman y Herron 2007
- ^ Masel J (agosto de 2012). "Replanteamiento de Hardy-Weinberg y la deriva genética en la biología de pregrado". BioEssays . 34 (8). John Wiley & Sons: 701–710. doi :10.1002/bies.201100178. PMID 22576789. S2CID 28513167.
- ^ Linch 2007
- ^ Crow JF (marzo de 2010). "Wright y Fisher sobre la endogamia y la deriva aleatoria". Genética . 184 (3). Sociedad de Genética de América: 609–611. doi :10.1534/genetics.109.110023. PMC 2845331 . PMID 20332416.
- ^ Larson 2004, págs. 221–243
- ^ Stevenson 1991: Cita atribuida a William B. Provine en The Origins of Theoretical Population Genetics (1971), pág. 162; Chicago: University of Chicago Press.
- ^ Avers 1989
- ^ Gillespie JH (junio de 2000). "Deriva genética en una población infinita. El modelo de pseudoautostop". Genética . 155 (2). Sociedad de Genética de América: 909–919. doi :10.1093/genetics/155.2.909. PMC 1461093 . PMID 10835409.
Bibliografía
- Avers CJ (1989). Proceso y patrón en la evolución. Nueva York: Oxford University Press . ISBN 0-19-505275-7. Código LCCN: 88005368. Código OCLC : 17677554.
- Barton NH , Briggs DE , Eisen JA , Goldstein DB , Patel NH (2007). Evolución . Cold Spring Harbor, Nueva York: Cold Spring Harbor Laboratory Press . ISBN 978-0-87969-684-9. OCLC 86090399 .
- Campbell NA (1996). Biología . Serie Benjamin/Cummings en las ciencias de la vida (4.ª ed.). Menlo Park, CA: Benjamin/Cummings Pub. Co. ISBN 0-8053-1940-9. LCCN 95045572. OCLC 33333455.
- Cavalli-Sforza LL , Menozzi P, Piazza A (1996). Historia y geografía de los genes humanos (edición de bolsillo abreviada). Princeton, NJ: Princeton University Press . ISBN 0-691-02905-9.OCLC 35527063 .
- Ewens WJ (2004). Genética de poblaciones matemática I. Introducción teórica . Matemáticas aplicadas interdisciplinarias. Vol. 27 (2.ª ed.). Nueva York: Springer-Verlag . ISBN. 0-387-20191-2. OCLC 53231891 .
- Freeman S, Herron JC (2007). Análisis evolutivo (4.ª ed.). Upper Saddle River, Nueva Jersey: Pearson Prentice Hall . ISBN 978-0-13-227584-2. OCLC 73502978 .
- Futuyma D (1998). Biología evolutiva (3.ª ed.). Sunderland, MA: Sinauer Associates . ISBN 0-87893-189-9. Código LCCN 97037947. Código OCLC 37560100.
- Golding B, ed. (1994). Evolución no neutral: teorías y datos moleculares . Nueva York: Chapman & Hall . ISBN 0-412-05391-8. Código LCCN 93047006. Código OCLC 29638235."Artículos de un taller patrocinado por el Instituto Canadiense de Investigación Avanzada ".
- Hartl DL, Clark AG (2007). Principios de genética de poblaciones (4.ª ed.). Sunderland, MA: Sinauer Associates. ISBN 978-0-87893-308-2. OCLC 75087956 .
- Hedrick PW (2005). Genética de poblaciones (3.ª ed.). Boston, MA: Jones and Bartlett Publishers . ISBN 0-7637-4772-6. OCLC 56194719 .
- Hey J , Fitch WM , Ayala FJ , eds. (2005). Sistemática y el origen de las especies: en el centenario de Ernst Mayr . Washington, DC: National Academies Press . ISBN 978-0-309-09536-5. OCLC 70745851 .
- Howard DJ, Berlocher SH, eds. (1998). Formas infinitas: especies y especiación . Nueva York: Oxford University Press. ISBN 978-0-19-510901-6. Código LCCN 97031461. Código OCLC 37545522.
- Kimura M , Ohta T (1971). Aspectos teóricos de la genética de poblaciones . Monografías en biología de poblaciones. Vol. 4. Princeton, NJ: Princeton University Press . Págs. 1–219. ISBN. 0-691-08096-8. LCCN 75155963. OCLC 299867647. PMID 5162676.
- Larson EJ (2004). Evolución: La notable historia de una teoría científica. Modern Library Chronicles. Vol. 17. Nueva York: Modern Library . ISBN 0-679-64288-9. OCLC 53483597 .
- Li WH , Graur D (1991). Fundamentos de la evolución molecular. Sunderland, MA: Sinauer Associates. ISBN 0-87893-452-9. Código LCCN 90043581. Código OCLC 22113526.
- Lynch M (2007). Los orígenes de la arquitectura del genoma . Sunderland, MA: Sinauer Associates. ISBN 978-0-87893-484-3. OCLC 77574049 .
- Miller G (2000). La mente de apareamiento: cómo la elección sexual moldeó la evolución de la naturaleza humana. Nueva York: Doubleday . ISBN 0-385-49516-1. Código LCCN 00022673. Código OCLC 43648482.
- Sadava D, Heller HC , Orians GH , Purves WK, Hillis DM (2008). La vida: la ciencia de la biología . Vol. II: Evolución, diversidad y ecología (8.ª ed.). Sunderland, MA; Gordonsville, VA: Sinauer Associates; WH Freeman and Company . ISBN 978-0-7167-7674-1. OCLC 71632224 .
- Stevenson JC (1991). Diccionario de conceptos en antropología física . Fuentes de referencia para las ciencias sociales y las humanidades. Vol. 10. Westport, CT: Greenwood Press . ISBN 0-313-24756-0. LCCN 90022815. OCLC 22732327.
- Tian JP (2008). Álgebras evolutivas y sus aplicaciones . Apuntes de clase sobre matemáticas. Vol. 1921. Berlín; Nueva York: Springer. doi :10.1007/978-3-540-74284-5. ISBN 978-3-540-74283-8. LCCN 2007933498. OCLC 173807298. Zbl 1136.17001.
- Wolf JB, Brodie ED, Wade MJ , eds. (2000). Epistasis y el proceso evolutivo . Oxford, Reino Unido; Nueva York: Oxford University Press. ISBN 0-19-512806-0. Código LCCN 99046515. Código OCLC 42603105.
- Zimmer C (2001). Evolución: el triunfo de una idea. Introducción de Stephen Jay Gould ; prólogo de Richard Hutton (1.ª ed.). Nueva York: HarperCollins . ISBN 0-06-019906-7. OCLC 46359440 .
Enlaces externos
- Sheehy, Bob. "Programa de simulación de genética de poblaciones". Radford, VA: Radford University . Consultado el 21 de diciembre de 2015 .
- Grimes, Bill. "Simulación de deriva genética". Tucson, Arizona: The University of Arizona . Consultado el 25 de agosto de 2016 .











![{\displaystyle {\bar {T}}_{\text{perdido}}\approx {\begin{cases}{\dfrac {1}{m}},{\text{ si }}mN_{e}\ll 1\\[8pt]{\dfrac {\ln {(mN_{e})}+\gamma }{m}}{\text{ si }}mN_{e}\gg 1\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0dca9b7dc746a7b2a8d8a63770ac53782d1639e3)



