Historia de la notación matemática
Es posible que este artículo requiera una corrección de estilo, gramática, coherencia, tono u ortografía . ( Agosto de 2024 ) |
La historia de la notación matemática [1] incluye el comienzo, el progreso y la difusión cultural de los símbolos matemáticos y el conflicto de los métodos de notación que se enfrentan en el movimiento de una notación hacia la popularidad o la invisibilidad. La notación matemática [2] comprende los símbolos utilizados para escribir ecuaciones y fórmulas matemáticas . La notación generalmente implica un conjunto de representaciones bien definidas de cantidades y operadores de símbolos. [3] La historia incluye números hindúes y árabes , letras de los alfabetos romano , griego , hebreo y alemán , y una gran cantidad de símbolos inventados por matemáticos durante los últimos siglos.
El desarrollo de la notación matemática se puede dividir en etapas: [4] [5]
- La etapa " retórica " es donde los cálculos se realizan con palabras y no se utilizan símbolos. [6]
- La etapa " sincopada " es aquella en la que las operaciones y cantidades de uso frecuente se representan mediante abreviaturas sintácticas simbólicas . Durante la Antigüedad y la Edad Media, a menudo los estallidos de creatividad matemática iban seguidos de siglos de estancamiento. A medida que se iniciaba la Edad Moderna y comenzaba la difusión mundial del conocimiento, aparecieron ejemplos escritos de desarrollos matemáticos.
- La etapa " simbólica " es donde los sistemas integrales de notación reemplazan a la retórica. A partir del siglo XVI, en Italia, se produjeron nuevos avances matemáticos que interactuaban con nuevos descubrimientos científicos a un ritmo cada vez mayor que continúa hasta nuestros días. Este sistema simbólico fue utilizado por los matemáticos indios medievales y en Europa desde mediados del siglo XVII, [7] y ha seguido desarrollándose en la era contemporánea .
El área de estudio conocida como historia de las matemáticas es principalmente una investigación sobre el origen de los descubrimientos en matemáticas y el enfoque aquí es la investigación de los métodos matemáticos y la notación del pasado.
Etapa retórica
Aunque la historia comienza con la de las escuelas jónicas, no hay duda de que los antiguos griegos que le prestaron atención estaban en gran parte en deuda con las investigaciones previas de los antiguos egipcios y fenicios . La característica distintiva de la notación numérica, es decir, los símbolos que tienen valores locales e intrínsecos ( aritmética ), implica un estado de civilización en el período de su invención. Nuestro conocimiento de los logros matemáticos de estos pueblos primitivos, a los que está dedicada esta sección, es imperfecto y las siguientes breves notas deben considerarse como un resumen de las conclusiones que parecen más probables, y la historia de las matemáticas comienza con las secciones simbólicas.
Muchas áreas de las matemáticas comenzaron con el estudio de problemas del mundo real , antes de que se identificaran y definieran las reglas y los conceptos subyacentes como estructuras abstractas . Por ejemplo, la geometría tiene su origen en el cálculo de distancias y áreas en el mundo real; el álgebra comenzó con métodos de resolución de problemas aritméticos .
No cabe duda de que la mayoría de los pueblos primitivos que han dejado registros sabían algo de numeración y mecánica y que algunos también estaban familiarizados con los elementos de la agrimensura . En particular, los egipcios prestaban atención a la geometría y los números, y los fenicios a la aritmética práctica, la contabilidad , la navegación y la agrimensura. Los resultados obtenidos por estos pueblos parecen haber sido accesibles , bajo ciertas condiciones, a los viajeros. Es probable que el conocimiento de los egipcios y los fenicios fuera en gran parte el resultado de la observación y la medición , y representara la experiencia acumulada de muchas épocas.
Comienzo de la notación

Las matemáticas escritas comenzaron con números expresados como marcas de conteo , cada una de las cuales representaba una unidad. Los símbolos numéricos probablemente consistían en trazos o muescas cortadas en madera o piedra, y eran inteligibles por igual para todas las naciones. Por ejemplo, una muesca en un hueso representaba un animal, una persona o cualquier otra cosa. Los pueblos con los que los griegos de Asia Menor (entre los que comienza la notación en la historia occidental) probablemente entraron en contacto frecuente fueron los que habitaban el litoral oriental del Mediterráneo: y la tradición griega asignó uniformemente el desarrollo especial de la geometría a los egipcios, y el de la ciencia de los números a los egipcios o a los fenicios.
Los antiguos egipcios tenían una notación simbólica que era la numeración por jeroglíficos . [8] [9] Las matemáticas egipcias tenían un símbolo para uno, diez, cien, mil, diez mil, cien mil y un millón. Los dígitos más pequeños se colocaban a la izquierda del número, como en los numerales hindúes y árabes. Más tarde, los egipcios utilizaron la escritura hierática en lugar de la jeroglífica para mostrar números. La hierática era más como la cursiva y reemplazó varios grupos de símbolos con símbolos individuales. Por ejemplo, las cuatro líneas verticales utilizadas para representar cuatro fueron reemplazadas por una sola línea horizontal. Esto se encuentra en el Papiro matemático Rhind (c. 2000-1800 a. C.) y el Papiro matemático de Moscú (c. 1890 a. C.). El sistema que usaban los egipcios fue descubierto y modificado por muchas otras civilizaciones en el Mediterráneo. Los egipcios también tenían símbolos para operaciones básicas: las piernas que avanzaban representaban la suma y las piernas que caminaban hacia atrás para representar la resta.
Los mesopotámicos tenían símbolos para cada potencia de diez. [10] Más tarde, escribieron sus números de casi exactamente la misma manera en que se hace en los tiempos modernos. En lugar de tener símbolos para cada potencia de diez, simplemente ponían el coeficiente de ese número. Cada dígito estaba separado solo por un espacio, pero en la época de Alejandro Magno , habían creado un símbolo que representaba el cero y era un marcador de posición. Los mesopotámicos también usaban un sistema sexagesimal , es decir, de base sesenta. Es este sistema el que se usa en los tiempos modernos para medir el tiempo y los ángulos. Las matemáticas babilónicas se derivan de más de 400 tablillas de arcilla desenterradas desde la década de 1850. [11] Escritas en escritura cuneiforme , las tablillas se inscribían mientras la arcilla estaba húmeda y se horneaban en un horno o al calor del sol. Algunas de estas parecen ser tareas calificadas. La evidencia más temprana de matemáticas escritas se remonta a los antiguos sumerios y al sistema de metrología del 3000 a. C. A partir del año 2500 a. C., los sumerios escribieron tablas de multiplicar en tablillas de arcilla y resolvieron ejercicios geométricos y problemas de división . Los primeros rastros de los numerales babilónicos también datan de este período. [12]
La mayoría de las tablillas de arcilla mesopotámicas datan de 1800 a 1600 a. C. y cubren temas que incluyen fracciones, álgebra, ecuaciones cuadráticas y cúbicas, y el cálculo de ecuaciones regulares , recíprocas y pares . [13] Las tablillas también incluyen tablas de multiplicar y métodos para resolver ecuaciones lineales y cuadráticas . La tablilla babilónica YBC 7289 da una aproximación de √ 2 que es precisa a un equivalente de seis decimales. Las matemáticas babilónicas se escribieron utilizando un sistema numérico sexagesimal (base 60) . De esto se deriva el uso moderno de 60 segundos en un minuto, 60 minutos en una hora y 360 (60 × 6) grados en un círculo, así como el uso de minutos y segundos de arco para denotar fracciones de un grado. Los avances babilónicos en matemáticas se vieron facilitados por el hecho de que 60 tiene muchos divisores: el recíproco de cualquier número entero que sea múltiplo de divisores de 60 tiene una expansión decimal finita en base 60. (En aritmética decimal, solo los recíprocos de múltiplos de 2 y 5 tienen expansiones decimales finitas). Además, a diferencia de los egipcios, griegos y romanos, los babilonios tenían un verdadero sistema de valor posicional, en el que los dígitos escritos en la columna de la izquierda representaban valores mayores, de forma muy similar al sistema decimal . Sin embargo, carecían de un equivalente del punto decimal, por lo que el valor posicional de un símbolo a menudo tenía que inferirse del contexto.
El álgebra retórica fue desarrollada por primera vez por los antiguos babilonios y se mantuvo dominante hasta el siglo XVI. En este sistema, las ecuaciones se escriben en oraciones completas. Por ejemplo, la forma retórica de es "La cosa más uno es igual a dos" o posiblemente "La cosa más 1 es igual a 2".
Etapa sincopada

La historia de las matemáticas no puede remontarse con certeza a ninguna escuela o período anterior al de los griegos jonios. Aun así, la historia posterior puede dividirse en períodos, cuyas distinciones están bastante bien marcadas. Las matemáticas griegas, que se originaron con el estudio de la geometría, tendieron a ser deductivas y científicas desde sus inicios. Desde el siglo IV d. C., a Pitágoras se le ha dado comúnmente crédito por descubrir el teorema de Pitágoras , un teorema de geometría que establece que en un triángulo rectángulo el área del cuadrado de la hipotenusa (el lado opuesto al ángulo recto) es igual a la suma de las áreas de los cuadrados de los otros dos lados. [14] Los textos matemáticos antiguos están disponibles con la notación de los Antiguos Egipcios mencionada anteriormente y con Plimpton 322 , una matemática babilónica alrededor de 1900 a. C. El estudio de las matemáticas como materia en sí misma comienza en el siglo VI a. C. con los pitagóricos , quienes acuñaron el término «matemáticas» del griego antiguo μάθημα ( mathema ), que significa «materia de instrucción». [15]
La influencia de Platón ha sido especialmente fuerte en las matemáticas y las ciencias. Ayudó a distinguir entre las matemáticas puras y las aplicadas al ampliar la brecha entre la «aritmética», ahora llamada teoría de números y la «logística», ahora llamada aritmética . Las matemáticas griegas refinaron enormemente los métodos (especialmente mediante la introducción del razonamiento deductivo y el rigor matemático en las demostraciones ) y ampliaron el contenido de las matemáticas. [16] A Aristóteles se le atribuye lo que más tarde se llamaría la ley del tercio excluido .
Las matemáticas abstractas o puras [17] tratan conceptos como magnitud y cantidad sin tener en cuenta ninguna aplicación o situación práctica, e incluyen la aritmética y la geometría . Por el contrario, en las matemáticas mixtas o aplicadas , las propiedades y relaciones matemáticas se aplican a objetos del mundo real para modelar leyes de la física, por ejemplo en hidrostática , óptica y navegación . [17]
Arquímedes es considerado generalmente como el mayor matemático de la antigüedad y uno de los más grandes de todos los tiempos. [18] [19] Utilizó el método de agotamiento para calcular el área bajo el arco de una parábola con la suma de una serie infinita , y dio una aproximación notablemente precisa de pi . [20] También definió la espiral que lleva su nombre, fórmulas para los volúmenes de superficies de revolución y un ingenioso sistema para expresar números muy grandes.

En el desarrollo histórico de la geometría, los pasos en la abstracción de la geometría fueron dados por los antiguos griegos. Los Elementos de Euclides son la documentación existente más antigua de los axiomas de la geometría plana, aunque Proclo habla de una axiomatización anterior por Hipócrates de Quíos . [21] Los Elementos de Euclides (c. 300 a. C.) es uno de los tratados matemáticos griegos más antiguos existentes y consta de 13 libros escritos en Alejandría; recopilando teoremas probados por otros matemáticos, complementados con algún trabajo original. El documento es una colección exitosa de definiciones, postulados (axiomas), proposiciones (teoremas y construcciones) y pruebas matemáticas de las proposiciones. El primer teorema de Euclides es un lema que posee propiedades de los números primos . Los trece libros influyentes cubren la geometría euclidiana, el álgebra geométrica y la versión griega antigua de los sistemas algebraicos y la teoría elemental de números. Fue omnipresente en el Quadrivium y es fundamental para el desarrollo de la lógica, las matemáticas y la ciencia. El libro De la esfera en movimiento de Autólico es otro manuscrito matemático antiguo de la época. [ cita requerida ]
La siguiente fase de la notación para el álgebra fue el álgebra sincopada, en la que se utiliza algún simbolismo, pero que no contiene todas las características del álgebra simbólica. Por ejemplo, puede haber una restricción de que la resta se pueda utilizar solo una vez dentro de un lado de una ecuación, lo que no es el caso del álgebra simbólica. La expresión algebraica sincopada apareció por primera vez en una serie de libros llamada Arithmetica , de Diofanto de Alejandría (siglo III d. C., muchos de los cuales se han perdido), seguida por Brahma Sphuta Siddhanta de Brahmagupta (siglo VII).
Numeración acrofónica y milesia
Los griegos empleaban la numeración ática , [22] que se basaba en el sistema de los egipcios y que más tarde fue adaptado y utilizado por los romanos . Los números griegos del uno al cuatro eran líneas verticales, como en los jeroglíficos. El símbolo del cinco era la letra griega Π (pi), que es la letra de la palabra griega para cinco, pente . Los números del seis al nueve eran pente con líneas verticales al lado. El diez se representaba con la letra (Δ) de la palabra para diez, deka , el cien con la letra de la palabra para cien, etc.
El sistema de numeración jónico utilizaba todo su alfabeto, incluidas tres letras arcaicas. La notación numérica de los griegos, aunque mucho menos conveniente que la que se utiliza actualmente, se formaba según un plan perfectamente regular y científico, [23] y podía utilizarse con un efecto tolerable como instrumento de cálculo, para cuyo propósito el sistema romano era totalmente inaplicable. Los griegos dividían las veinticuatro letras de su alfabeto en tres clases y, añadiendo otro símbolo a cada clase, tenían caracteres para representar las unidades, las decenas y las centenas. ( Astronomie Ancienne de Jean Baptiste Joseph Delambre , t. ii.)
| Una (α) | B (β) | G (γ) | Δ (δ) | E (ε) | Ϝ (ϝ) | O (O) | Η (η) | θ (θ) | Yo (yo) | K (k) | La (La) | mi (μ) | N (ν) | Ξ (ξ) | O (o) | P (π) | Ϟ (ϟ) | P (ρ) | Σ (σ) | T (τ) | Υ (υ) | Φ (φ) | Χ (χ) | Ψ (ψ) | Ω (ω) | Ϡ (ϡ) |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 |
Este sistema apareció en el siglo III a. C., antes de que las letras digamma (Ϝ), koppa (Ϟ) y sampi (Ϡ) quedaran obsoletas. Cuando las letras minúsculas se diferenciaron de las mayúsculas, se utilizaron las letras minúsculas como símbolos de notación. Los múltiplos de mil se escribían como los nueve números con un trazo delante: así, mil era ",α", dos mil era ",β", etc. M (por μύριοι, como en "miríada") se utilizaba para multiplicar números por diez mil. Por ejemplo, el número 88.888.888 se escribiría como M,ηωπη*ηωπη. [24]
El razonamiento matemático griego era casi enteramente geométrico (aunque a menudo se utilizaba para razonar sobre temas no geométricos como la teoría de números ), y por lo tanto los griegos no tenían interés en los símbolos algebraicos . La gran excepción fue Diofanto de Alejandría , el gran algebrista. [25] Su Arithmetica fue uno de los textos que utilizó símbolos en ecuaciones. No era completamente simbólico, pero lo era mucho más que los libros anteriores. Un número desconocido se llamaba s. [26] El cuadrado de s era ; el cubo era ; la cuarta potencia era ; y la quinta potencia era . [27] Así, por ejemplo, la expresión:
se escribiría como: [ cita requerida ]
- SS2 C3 x5 M S4 u6
Notación matemática china
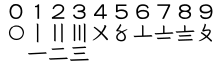
Los chinos utilizaban números que se parecían mucho al sistema de conteo. [28] Los números del uno al cuatro eran líneas horizontales. El cinco era una X entre dos líneas horizontales; parecía casi exactamente igual al número romano para diez. Hoy en día, el sistema huama solo se utiliza para mostrar precios en los mercados chinos o en las facturas tradicionales escritas a mano.
En la historia de los chinos, hubo quienes estaban familiarizados con las ciencias de la aritmética, la geometría, la mecánica, la óptica, la navegación y la astronomía. Las matemáticas en China surgieron de forma independiente en el siglo XI a. C. [29] Los chinos estaban familiarizados con los ciclos astronómicos, los instrumentos geométricos como la regla , el compás y la plomada , y las máquinas como la rueda y el eje . Los chinos desarrollaron de forma independiente números muy grandes y negativos , decimales , un sistema decimal de valor posicional, un sistema binario , álgebra, geometría y trigonometría.

Las matemáticas chinas hicieron contribuciones tempranas, incluyendo un sistema de valor posicional . [30] [31] El teorema geométrico conocido por los antiguos chinos era aplicable en ciertos casos, a saber, la proporción de lados . Es que los teoremas geométricos que pueden demostrarse en la forma cuasi experimental de superposición también eran conocidos por ellos. En aritmética, su conocimiento parece haber estado confinado al arte del cálculo por medio del suanpan y al poder de expresar los resultados por escrito. Nuestro conocimiento de los primeros logros de los chinos, aunque es escaso, es más completo que en el caso de la mayoría de sus contemporáneos. Por lo tanto, es instructivo y sirve para ilustrar el hecho de que se puede saber que una nación puede poseer una habilidad considerable en las artes aplicadas, pero nuestro conocimiento de las matemáticas posteriores en las que se basan esas artes puede ser escaso. El conocimiento de las matemáticas chinas antes del 254 a. C. es algo fragmentario, e incluso después de esta fecha las tradiciones manuscritas son oscuras. Los eruditos chinos generalmente consideran que las fechas de siglos anteriores al período clásico son conjeturas, a menos que estén acompañadas de evidencia arqueológica verificada.
Como en otras sociedades primitivas, el enfoque se centró en la astronomía con el fin de perfeccionar el calendario agrícola y otras tareas prácticas, y no en establecer sistemas formales . Las funciones de la Junta China de Matemáticas se limitaban a la preparación anual de un almanaque, cuyas fechas y predicciones regulaban. Los matemáticos chinos antiguos no desarrollaron un enfoque axiomático, pero sí hicieron avances en el desarrollo de algoritmos y en el álgebra. El logro del álgebra china alcanzó su cenit en el siglo XIII, cuando Zhu Shijie inventó el método de las cuatro incógnitas.
Como resultado de las obvias barreras lingüísticas y geográficas, así como del contenido, se presume que las matemáticas chinas y las matemáticas del mundo mediterráneo antiguo se desarrollaron más o menos independientemente hasta el momento en que Los nueve capítulos sobre el arte matemático alcanzaron su forma final, mientras que el Libro sobre números y computación y Huainanzi son aproximadamente contemporáneos con las matemáticas griegas clásicas. Es probable que haya algún intercambio de ideas en Asia a través de intercambios culturales conocidos al menos desde la época romana. Con frecuencia, los elementos de las matemáticas de las sociedades tempranas corresponden a resultados rudimentarios encontrados más tarde en ramas de las matemáticas modernas como la geometría o la teoría de números . Por ejemplo, el teorema de Pitágoras ha sido atestiguado en el Zhoubi Suanjing . También se ha demostrado que el conocimiento del triángulo de Pascal existía en China siglos antes de Blaise Pascal , [32] articulado por matemáticos como el polímata Shen Kuo (1031-1095).
El estado de la trigonometría avanzó durante la dinastía Song (960-1279), donde los matemáticos chinos comenzaron a expresar un mayor énfasis en la necesidad de la trigonometría esférica en la ciencia del calendario y los cálculos astronómicos. [33] Shen Kuo utilizó funciones trigonométricas para resolver problemas matemáticos de cuerdas y arcos. [33] Sal Restivo escribe que el trabajo de Shen en las longitudes de arcos de círculos proporcionó la base para la trigonometría esférica desarrollada en el siglo XIII por el matemático y astrónomo Guo Shoujing (1231-1316). [34] Como afirman los historiadores L. Gauchet y Joseph Needham, Guo Shoujing utilizó la trigonometría esférica en sus cálculos para mejorar el sistema de calendario y la astronomía china . [33] [35] La ciencia matemática de los chinos incorporaría el trabajo y la enseñanza de los misioneros árabes con conocimientos de trigonometría esférica que habían llegado a China a lo largo del siglo XIII.
Números y notación indios y árabes
Aunque el origen de nuestro actual sistema de notación numérica es antiguo, no hay duda de que ya se utilizaba entre los hindúes hace más de dos mil años. La notación algebraica del matemático indio Brahmagupta era sincopada . La adición se indicaba colocando los números uno al lado del otro, la resta colocando un punto sobre el sustraendo (el número a restar) y la división colocando el divisor debajo del dividendo, de forma similar a nuestra notación pero sin la barra. La multiplicación, la evolución y las cantidades desconocidas se representaban mediante abreviaturas de los términos apropiados. [36] El sistema de numeración hindú-arábigo y las reglas para el uso de sus operaciones, que se utilizan en todo el mundo hoy en día, probablemente evolucionaron a lo largo del primer milenio d. C. en la India y se transmitieron a Occidente a través de las matemáticas islámicas. [37] [38]

A pesar de su nombre, los números arábigos tienen raíces en la India. La razón de este nombre erróneo es que los europeos vieron los números utilizados en un libro árabe, Sobre el arte hindú del cálculo , de Muhammed ibn-Musa al-Khwarizmi . Al-Khwārizmī escribió varios libros importantes sobre los números hindúes-arábigos y sobre métodos para resolver ecuaciones. Su libro Sobre el cálculo con números hindúes , escrito alrededor de 825, junto con el trabajo de Al-Kindi , fueron fundamentales para difundir las matemáticas indias y los números indios en Occidente. Al-Khwarizmi no afirmó que los números fueran árabes, pero a lo largo de varias traducciones latinas, se perdió el hecho de que los números eran de origen indio. La palabra algoritmo se deriva de la latinización del nombre de Al-Khwārizmī, Algoritmi, y la palabra álgebra del título de una de sus obras, Al-Kitāb al-mukhtaṣar fī hīsāb al-ğabr wa'l-muqābala ( El libro compendioso sobre cálculo por compleción y balanceo ).
Las matemáticas islámicas desarrollaron y ampliaron las matemáticas conocidas en las civilizaciones de Asia Central , [39] incluida la adición de la notación del punto decimal a los números arábigos . [ contradictorio ]
Los símbolos de numeración arábiga modernos que se utilizan en todo el mundo aparecieron por primera vez en el norte de África islámico en el siglo X. Una variante árabe occidental distintiva de los números arábigos orientales comenzó a surgir alrededor del siglo X en el Magreb y Al-Ándalus (a veces llamados números ghubar , aunque el término no siempre se acepta), que son el antecesor directo de los números arábigos modernos que se utilizan en todo el mundo. [40]
Muchos textos griegos y árabes sobre matemáticas fueron luego traducidos al latín , lo que condujo a un mayor desarrollo de las matemáticas en la Europa medieval. En el siglo XII, los eruditos viajaron a España y Sicilia en busca de textos científicos árabes, incluidos el de al-Khwārizmī (traducido al latín por Roberto de Chester ) y el texto completo de los Elementos de Euclides (traducido en varias versiones por Adelardo de Bath , Herman de Carintia y Gerardo de Cremona ). [41] [42] Uno de los libros europeos que abogaba por el uso de los numerales fue el Liber Abaci , de Leonardo de Pisa, más conocido como Fibonacci . El Liber Abaci es más conocido por el problema matemático que Fibonacci escribió en él sobre una población de conejos. El crecimiento de la población terminó siendo una secuencia de Fibonacci , donde un término es la suma de los dos términos precedentes.
Escenario simbólico
- Símbolos por fecha de introducción popular

Aritmética temprana y multiplicación
La transición al álgebra simbólica, donde solo se utilizan símbolos, se puede ver por primera vez en el trabajo de Ibn al-Banna' al-Marrakushi (1256-1321) y Abū al-Ḥasan ibn ʿAlī al-Qalaṣādī (1412-1482). [43] [44] Al-Qalasādī fue el último gran algebrista árabe medieval , que mejoró la notación algebraica utilizada anteriormente en el Magreb por Ibn al-Banna. [45] En contraste con las notaciones sincopadas de sus predecesores, Diofanto y Brahmagupta , que carecían de símbolos para operaciones matemáticas , [46] la notación algebraica de al-Qalasadi fue la primera en tener símbolos para estas funciones y fue, por lo tanto, "los primeros pasos hacia la introducción del simbolismo algebraico". Representó símbolos matemáticos utilizando caracteres del alfabeto árabe . [45]

El siglo XIV fue testigo del desarrollo de nuevos conceptos matemáticos para investigar una amplia gama de problemas. [47] Los dos símbolos aritméticos ampliamente utilizados son la suma y la resta, + y −. El signo más fue utilizado a partir de 1351 por Nicole Oresme [48] y se hizo público en 1360 en su obra Algorismus percentageum . [49] Se cree que es una abreviatura de "et", que significa "y" en latín, de la misma manera que el signo & también comenzaba como "et". Oresme en la Universidad de París y el italiano Giovanni di Casali proporcionaron de forma independiente demostraciones gráficas de la distancia recorrida por un cuerpo sometido a un movimiento uniformemente acelerado, afirmando que el área bajo la línea que representa la aceleración constante representaba la distancia total recorrida. [50] El signo menos fue utilizado en 1489 por Johannes Widmann en Aritmética mercantil o Behende und hüpsche Rechenung auff allen Kauffmanschafft, . [51] Widmann utilizó el símbolo menos junto con el símbolo más para indicar déficit y superávit, respectivamente. [52] En Summa de arithmetica, geometria, percentagei e percentageità , [53] Luca Pacioli utilizó símbolos para los símbolos más y menos y contenía álgebra , aunque gran parte del trabajo se originó en Piero della Francesca, de quien se apropió y robó. [ cita requerida ]
El símbolo radical (√), para la raíz cuadrada, fue introducido por Christoph Rudolff a principios del siglo XVI. La importante obra de Michael Stifel , Arithmetica integra [54], contenía importantes innovaciones en la notación matemática. En 1556, Niccolò Tartaglia utilizó paréntesis para agrupar por precedencia. En 1557, Robert Recorde publicó The Whetstone of Witte , que introdujo el signo igual (=), así como los signos más y menos para el lector inglés. En 1564, Gerolamo Cardano analizó los juegos de azar iniciando las primeras etapas de la teoría de la probabilidad . En 1572, Rafael Bombelli publicó su L'Algebra en el que mostraba cómo tratar las cantidades imaginarias que podían aparecer en la fórmula de Cardano para resolver ecuaciones cúbicas. El libro de Simon Stevin De Thiende ('el arte de las décimas'), publicado en holandés en 1585, contenía un tratamiento sistemático de la notación decimal , que influyó en todo el trabajo posterior sobre el sistema de números reales . La nueva álgebra (1591) de François Viète introdujo la moderna manipulación notacional de expresiones algebraicas.
John Napier es mejor conocido como el inventor de los logaritmos (publicado en Descripción del maravilloso canon de los logaritmos ) [55] e hizo común el uso del punto decimal en aritmética y matemáticas. [56] [57] Después de Napier, Edmund Gunter creó las escalas logarítmicas (líneas o reglas) en las que se basan las reglas de cálculo , fue William Oughtred quien utilizó dos de esas escalas deslizándose una sobre la otra para realizar la multiplicación y división directas ; y se le atribuye la invención de la regla de cálculo en 1622. En 1631 Oughtred introdujo el signo de multiplicación (×), su signo de proporcionalidad (∷) y las abreviaturas sen y cos para las funciones seno y coseno . [58] Albert Girard también utilizó las abreviaturas 'sin', 'cos' y 'tan' para las funciones trigonométricas en su tratado.
A René Descartes se le atribuye el mérito de ser el padre de la geometría analítica , el puente entre el álgebra y la geometría, crucial para el descubrimiento del cálculo infinitesimal y el análisis . En el siglo XVII, Descartes introdujo las coordenadas cartesianas que permitieron el desarrollo de la geometría analítica, llevando la notación de ecuaciones a la geometría. Blaise Pascal influyó en las matemáticas a lo largo de su vida. Su Traité du triangle arithmétique ("Tratado sobre el triángulo aritmético") de 1653 describió una presentación tabular conveniente para los coeficientes binomiales , ahora llamado triángulo de Pascal . John Wallis introdujo el símbolo de infinito (∞) y también utilizó esta notación para los infinitesimales , por ejemplo ,1/∞ .
Johann Rahn introdujo el signo de división (÷, una variante del óbelo reutilizada) y el signo por tanto en 1659. William Jones utilizó π en Synopsis palmariorum mathesios [59] en 1706 porque es la letra inicial de la palabra griega Perimetron (περιμετρον), que significa perímetro en griego. Este uso fue popularizado en 1737 por Euler. En 1734, Pierre Bouguer utilizó una doble barra horizontal debajo del signo de desigualdad . [60]
Notación de derivadas: Leibniz y Newton
El estudio del álgebra lineal surgió del estudio de los determinantes , que se utilizaban para resolver sistemas de ecuaciones lineales . El cálculo tenía dos sistemas principales de notación, cada uno creado por uno de los creadores: el desarrollado por Isaac Newton y la notación desarrollada por Gottfried Leibniz . La notación de Leibniz es la que se utiliza con más frecuencia en la actualidad. La de Newton era simplemente un punto o raya colocado encima de la función. Por ejemplo, la derivada de la función x se escribiría como . La segunda derivada de x se escribiría como . En el uso moderno, esta notación generalmente denota derivadas de cantidades físicas con respecto al tiempo, y se utiliza con frecuencia en la ciencia de la mecánica . Leibniz, por otro lado, utilizó la letra d como prefijo para indicar diferenciación, e introdujo la notación que representa las derivadas como si fueran un tipo especial de fracción. Por ejemplo, la derivada de la función x con respecto a la variable t en la notación de Leibniz se escribiría como . Esta notación hace explícita la variable con respecto a la cual se toma la derivada de la función. Leibniz también creó el símbolo de la integral ( ∫ ). Por ejemplo: . Al hallar áreas bajo curvas, la integración se suele ilustrar dividiendo el área en infinitos rectángulos altos y delgados, cuyas áreas se suman. Por lo tanto, el símbolo de la integral es una S alargada , que representa la palabra latina summa , que significa "suma".
Operadores y funciones de alta división
En esta época, las letras del alfabeto debían utilizarse como símbolos de cantidad y, aunque existía mucha diversidad con respecto a la elección de las letras, en la historia posterior se aplicaron varias reglas universalmente reconocidas . [23] Así, en la historia de las ecuaciones, las primeras letras del alfabeto se conocían de manera indicativa como coeficientes y las últimas letras como términos desconocidos (an incerti ordinis ). En geometría algebraica , de nuevo, se debía observar una regla similar, pues las últimas letras del alfabeto denotaban las coordenadas variables o actuales . Ciertas letras, como , , etc. , fueron aceptadas por consenso universal como símbolos de los números de aparición frecuente 3,14159 ... y 2,7182818 ... , y se debían evitar otros usos tanto como fuera posible. [23] También se debían emplear letras como símbolos de operaciones, y con ellas otros caracteres de operaciones arbitrarias mencionados anteriormente. Las letras , alargadas, se usaron como símbolos operativos en el cálculo diferencial y el cálculo integral , y Σ en el cálculo de diferencias . [23] En la notación funcional , una letra, como símbolo de operación, se combina con otra que se considera como símbolo de cantidad . [23]
Así, denota el resultado matemático de la realización de la operación sobre el sujeto . Si sobre este resultado se repitiera la misma operación, el nuevo resultado se expresaría por , o más concisamente por , y así sucesivamente. La cantidad misma considerada como el resultado de la misma operación sobre alguna otra función; el símbolo apropiado para el cual es, por analogía, . Así , y son símbolos de operaciones inversas , la primera cancela el efecto de la segunda sobre el sujeto . y de manera similar se denominan funciones inversas .
A partir de 1718, Thomas Twinin utilizó la barra de división ( solidus ), derivándola de la barra de fracción horizontal árabe anterior . Pierre-Simon, marqués de Laplace, desarrolló el operador diferencial laplaciano (eg ). En 1750, Gabriel Cramer desarrolló la " Regla de Cramer " para resolver sistemas lineales .
Euler y notaciones primos

Leonhard Euler fue uno de los matemáticos más prolíficos de la historia, y también un prolífico inventor de la notación canónica. Sus contribuciones incluyen su uso de e para representar la base de los logaritmos naturales . No se sabe exactamente por qué fue elegido, pero probablemente fue porque las cuatro letras del alfabeto ya se usaban comúnmente para representar variables y otras constantes. Euler solía representar pi de manera consistente. El uso de fue sugerido por William Jones , quien lo usó como abreviatura de perímetro . Euler solía representar la raíz cuadrada de menos uno ( ) aunque antes lo usó como un número infinito. Hoy, el símbolo creado por John Wallis , , se usa para el infinito, como en p. ej . Para la suma , Euler usó una forma ampliada de la letra griega mayúscula vertical Sigma (Σ), conocida como notación sigma-capital . Esta se define como:
donde i representa el índice de suma ; a i es una variable indexada que representa cada término sucesivo de la serie; m es el límite inferior de la suma y n es el límite superior de la suma . El "i = m" debajo del símbolo de suma significa que el índice i comienza igual a m . El índice, i , se incrementa en 1 para cada término sucesivo, deteniéndose cuando i = n .
Para las funciones , Euler utilizó la notación para representar una función de .
El matemático William Emerson [61] desarrollaría el signo de proporcionalidad (∝). La proporcionalidad es la relación de una cantidad con otra, y el signo se utiliza para indicar que la relación entre dos variables es constante. [62] [63] Mucho más tarde, en las expresiones abstractas del valor de varios fenómenos proporcionales, la notación de partes por se volvería útil como un conjunto de pseudounidades para describir valores pequeños de diversas cantidades adimensionales . Marqués de Condorcet , en 1768, propuso el signo diferencial parcial , conocido como d rizada o delta de Jacobi . El símbolo primo para las derivadas también fue creado por Joseph-Louis Lagrange .
Pero en nuestra opinión, verdades de este tipo deberían extraerse de nociones más que de notaciones.
— Carl Friedrich Gauss, escribiendo sobre la prueba del teorema de Wilson [64]
Notaciones de Gauss, Hamilton y Matrix
A principios del siglo XIX, Carl Friedrich Gauss desarrolló el signo de identidad para la relación de congruencia y, en la reciprocidad cuadrática , la parte integral . Gauss contribuyó con funciones de variables complejas , en geometría y en la convergencia de series . Dio las pruebas satisfactorias del teorema fundamental del álgebra y de la ley de reciprocidad cuadrática . Gauss desarrolló la teoría de resolución de sistemas lineales mediante el uso de la eliminación gaussiana , que inicialmente se consideró un avance en geodesia . [65] También desarrollaría el signo del producto .
Después de 1800, Christian Kramp promovería la notación factorial durante su investigación en función factorial generalizada que se aplicaba a números no enteros. [66] Joseph Diaz Gergonne introdujo los signos de inclusión de conjuntos (⊆, ⊇), posteriormente desarrollados por Ernst Schröder . Peter Gustav Lejeune Dirichlet desarrolló las L -funciones de Dirichlet para dar la prueba del teorema de Dirichlet sobre progresiones aritméticas y comenzó la teoría analítica de números . En 1829, Carl Gustav Jacob Jacobi publicó Fundamenta nova theoriae functionum ellipticarum con sus funciones theta elípticas .
La notación matricial sería desarrollada más completamente por Arthur Cayley en sus tres artículos, sobre temas que habían sido sugeridos al leer la Mécanique analytique [67] de Lagrange y algunas de las obras de Laplace. Cayley definió la multiplicación de matrices y las matrices inversas . Cayley utilizó una sola letra para denotar una matriz, [68] tratando así a una matriz como un objeto agregado. También se dio cuenta de la conexión entre matrices y determinantes, [69] y escribió " Habría muchas cosas que decir sobre esta teoría de matrices que, me parece, deberían preceder a la teoría de determinantes ". [70]
William Rowan Hamilton introduciría el símbolo nabla ( o, posteriormente llamado del , ∇) para diferenciales vectoriales . [71] [72] Hamilton lo utilizó previamente como un signo de operador de propósito general . [73] , , y se utilizan para el operador hamiltoniano en mecánica cuántica y ℋ para la función hamiltoniana en mecánica hamiltoniana clásica .
En matemáticas, Hamilton es quizás más conocido como el inventor de la notación de cuaterniones y bicuaterniones .
Notaciones de Maxwell, Clifford y Ricci

El logro más destacado de Maxwell fue formular un conjunto de ecuaciones que unieron observaciones, experimentos y ecuaciones de electricidad , magnetismo y óptica que antes no estaban relacionados en una teoría consistente. [74]
En 1864, James Clerk Maxwell redujo todo el conocimiento entonces vigente sobre el electromagnetismo a un conjunto enlazado de ecuaciones diferenciales con 20 ecuaciones en 20 variables, contenidas en A Dynamical Theory of the Electromagnetic Field . [75] (Véase Ecuaciones de Maxwell ). El método de cálculo que es necesario emplear fue dado por Lagrange, y desarrollado posteriormente, con algunas modificaciones, por las ecuaciones de Hamilton . Generalmente se hace referencia a él como principio de Hamilton ; cuando se utilizan las ecuaciones en la forma original se conocen como ecuaciones de Lagrange . En 1871, Richard Dedekind llamó cuerpo a un conjunto de números reales o complejos que está cerrado bajo las cuatro operaciones aritméticas . En 1873 Maxwell presentó A Treatise on Electricity and Magnetism .
En 1878, William Kingdon Clifford publicó su obra Elements of Dynamic . [76] Clifford desarrolló biquaternions divididos (por ejemplo , ) a los que llamó motores algebraicos . Clifford eliminó el estudio de los cuaterniones al separar el producto escalar y el producto vectorial de dos vectores de la notación de cuaterniones completa.
Las notaciones vectoriales comunes se utilizan cuando se trabaja con vectores que son miembros espaciales o más abstractos de espacios vectoriales , mientras que la notación angular (o notación fasorial ) es una notación utilizada en electrónica .
La teoría del átomo etérico de Lord Kelvin (década de 1860) llevó a Peter Guthrie Tait , en 1885, a publicar una tabla topológica de nudos con hasta diez cruces conocida como las conjeturas de Tait . El cálculo tensorial fue desarrollado por Gregorio Ricci-Curbastro entre 1887 y 1896, presentado en 1892 bajo el título de cálculo diferencial absoluto , [77] y el uso contemporáneo de "tensor" fue establecido por Woldemar Voigt en 1898. [78] En 1895, Henri Poincaré publicó Analysis Situs . [79] En 1897, Charles Proteus Steinmetz publicaría Theory and Calculation of Alternating Current Phenomena, con la ayuda de Ernst J. Berg. [80]
De las matemáticas de fórmulas a los tensores
En 1895, Giuseppe Peano publicó su Formulario Mathematico , [81] un esfuerzo por digerir las matemáticas en un texto conciso basado en símbolos especiales. Proporcionaría una definición de un espacio vectorial y un mapa lineal . También introduciría el signo de intersección , el signo de unión , el signo de pertenencia (es un elemento de) y el cuantificador existencial (existe). Peano le pasaría su trabajo a Bertrand Russell en 1900 en una conferencia en París; impresionó tanto a Russell que Russell también se sintió atraído por el impulso de presentar las matemáticas de manera más concisa. El resultado fue Principia Mathematica escrito con Alfred North Whitehead . Este tratado marca un hito en la literatura moderna donde el símbolo se volvió dominante. El Formulario Mathematico de Peano , aunque menos popular que el trabajo de Russell, continuó a través de cinco ediciones. La quinta apareció en 1908 e incluía 4200 fórmulas y teoremas.
Ricci-Curbastro y Tullio Levi-Civita popularizaron la notación del índice tensorial alrededor de 1900. [82]
Lógica matemática y abstracción
| Abstracción | |
|---|---|
| |
Georg Cantor , inventor de la teoría de conjuntos , introdujo los números Aleph , llamados así porque utilizan el símbolo aleph (א) con subíndices de números naturales para indicar la cardinalidad en conjuntos infinitos . Para los ordinales empleó la letra griega ω ( omega ). Esta notación todavía se utiliza hoy en día en la notación ordinal de una secuencia finita de símbolos de un alfabeto finito que nombra un número ordinal según algún esquema que da significado al lenguaje.
Después del cambio de siglo, Josiah Willard Gibbs introduciría en la química física el punto medio para el producto escalar y el signo de multiplicación para los productos vectoriales . También proporcionaría la notación para los productos escalares y vectoriales, que se introdujo en el análisis vectorial . Bertrand Russell introduciría poco después la disyunción lógica ( OR ) en 1906. Gerhard Kowalewski y Cuthbert Edmund Cullis [83] [84] [85] introducirían sucesivamente la notación matricial, la matriz parentética y la notación matricial de caja respectivamente.

Albert Einstein , en 1916, introdujo la notación de Einstein , que sumaba un conjunto de términos indexados en una fórmula, lo que permitía una notación breve. Por ejemplo, los índices abarcan el conjunto {1, 2, 3 }:
se reduce por convención a:
Los índices superiores no son exponentes sino índices de coordenadas, coeficientes o vectores base .
Arnold Sommerfeld crearía el signo integral de contorno en 1917. También en 1917, Dimitry Mirimanoff propone el axioma de regularidad . En 1919, Theodor Kaluza resolvería ecuaciones de relatividad general utilizando cinco dimensiones , los resultados habrían surgido ecuaciones electromagnéticas. [86] Esto se publicaría en 1921 en "Zum Unitätsproblem der Physik". [87] En 1922, Abraham Fraenkel y Thoralf Skolem propusieron independientemente reemplazar el esquema axiomático de especificación con el esquema axiomático de reemplazo . También en 1922, se desarrolló la teoría de conjuntos de Zermelo-Fraenkel . En 1923, Steinmetz publicaría Cuatro conferencias sobre relatividad y espacio. Alrededor de 1924, Jan Arnoldus Schouten desarrollaría la notación y el formalismo modernos para el marco del cálculo de Ricci durante las aplicaciones del cálculo diferencial absoluto a la relatividad general y la geometría diferencial a principios del siglo XX. El cálculo de Ricci constituye las reglas de notación de índices y manipulación para tensores y campos tensoriales . [88] [89] [90] [91] En 1925, Enrico Fermi describiría un sistema que comprende muchas partículas idénticas que obedecen al principio de exclusión de Pauli , desarrollando después una ecuación de difusión ( ecuación de la edad de Fermi ). En 1926, Oskar Klein desarrollaría la teoría de Kaluza-Klein . En 1928, Emil Artin abstrajo la teoría de anillos con anillos artinianos . En 1933, Andrey Kolmogorov introduce los axiomas de Kolmogorov . En 1937, Bruno de Finetti dedujo el concepto de " subjetivo operacional " .
Simbolismo matemático
La abstracción matemática comenzó como un proceso de extracción de la esencia subyacente de un concepto matemático, [92] [93] eliminando cualquier dependencia de objetos del mundo real con los que originalmente podría haber estado conectado, [94] y generalizándolo para que tenga aplicaciones más amplias o coincida con otras descripciones abstractas de fenómenos equivalentes . Dos áreas abstractas de las matemáticas modernas son la teoría de categorías y la teoría de modelos . Bertrand Russell, [95] dijo: " El lenguaje ordinario es totalmente inadecuado para expresar lo que la física realmente afirma, ya que las palabras de la vida cotidiana no son lo suficientemente abstractas. Sólo las matemáticas y la lógica matemática pueden decir tan poco como el físico quiere decir ". Sin embargo, uno puede sustituir las matemáticas por objetos del mundo real y divagar a través de ecuación tras ecuación, y puede construir una estructura de concepto que no tiene relación con la realidad. [96]
Algunas de las notaciones de lógica matemática introducidas durante este tiempo incluyeron el conjunto de símbolos utilizados en el álgebra de Boole . Este fue creado por George Boole en 1854. Boole mismo no veía la lógica como una rama de las matemáticas, pero ha llegado a ser abarcada de todos modos. Los símbolos que se encuentran en el álgebra de Boole incluyen (AND), (OR) y ( not ). Con estos símbolos y letras para representar diferentes valores de verdad , uno puede hacer declaraciones lógicas como , es decir "( a es verdadero O a no es verdadero) es verdadero", lo que significa que es cierto que a es verdadero o no es verdadero (es decir, falso). El álgebra de Boole tiene muchos usos prácticos tal como es, pero también fue el comienzo de lo que sería un gran conjunto de símbolos para ser utilizados en lógica. La mayoría de estos símbolos se pueden encontrar en el cálculo proposicional , un sistema formal descrito como . es el conjunto de elementos, como a en el ejemplo con álgebra de Boole anterior. es el conjunto que contiene los subconjuntos que contienen operaciones, como o . contiene las reglas de inferencia , que son las reglas que dictan cómo se pueden hacer inferencias lógicamente, y contiene los axiomas . La lógica de predicados, originalmente llamada cálculo de predicados , amplía la lógica proposicional mediante la introducción de variables , generalmente denotadas por x , y , z u otras letras minúsculas, y por oraciones que contienen variables, llamadas predicados . Estos generalmente se denotan por una letra mayúscula seguida de una lista de variables, como P( x ) o Q( y , z ). La lógica de predicados usa símbolos especiales para cuantificadores : ∃ para "existe" y ∀ para "para todos".
Notación de incompletitud de Gödel
A cada clase recursiva ω-consistente κ de fórmulas corresponden signos de clase recursiva r , tales que ni v Gen r ni Neg ( v Gen r ) pertenecen a Flg (κ) (donde v es la variable libre de r ).
— Kurt Gödel [97]
Al probar sus teoremas de incompletitud , Kurt Gödel creó una alternativa a los símbolos que se usan normalmente en lógica. Utilizó los números de Gödel , que eran números que representaban operaciones con números de conjuntos y variables con números primos mayores que 10. Con los números de Gödel, las proposiciones lógicas se pueden descomponer en una secuencia numérica. Gödel luego llevó esto un paso más allá, tomando los n números primos y elevándolos a la potencia de los números en la secuencia. Luego, estos números se multiplicaron entre sí para obtener el producto final, dando a cada proposición lógica su propio número. [98]
Por ejemplo, tomemos la afirmación "Existe un número x tal que no es y ". Utilizando los símbolos del cálculo proposicional, esto se convertiría en
- .
Si los números de Gödel sustituyen a los símbolos, se convierte en:
- .
Hay diez números, entonces se encuentran los diez números primos y estos son:
- .
Luego, los números de Gödel se convierten en potencias de los respectivos primos y se multiplican, dando:
- .
El número resultante es aproximadamente .
Notación contemporánea y temas
Notación de principios del siglo XX
La abstracción de la notación es un proceso continuo y el desarrollo histórico de muchos temas matemáticos muestra una progresión desde lo concreto a lo abstracto. Se desarrollarían varias notaciones de conjuntos para conjuntos de objetos fundamentales . Alrededor de 1924, David Hilbert y Richard Courant publicaron " Métodos de física matemática. Ecuaciones diferenciales parciales ". [99] En 1926, Oskar Klein y Walter Gordon propusieron la ecuación de Klein-Gordon para describir partículas relativistas:
La primera formulación de una teoría cuántica que describe la interacción entre la radiación y la materia se debe a Paul Adrien Maurice Dirac , quien, durante 1920, fue capaz de calcular por primera vez el coeficiente de emisión espontánea de un átomo . [100] En 1928, Dirac formuló la ecuación relativista de Dirac para explicar el comportamiento del electrón en movimiento relativista . La ecuación de Dirac en la forma propuesta originalmente por Dirac es:
donde, ψ = ψ( x , t ) es la función de onda para el electrón , x y t son las coordenadas de espacio y tiempo, m es la masa en reposo del electrón, p es el momento , entendido como el operador de momento en la teoría de Schrödinger , c es la velocidad de la luz , y ħ = h /2 π es la constante de Planck reducida . Dirac describió la cuantificación del campo electromagnético como un conjunto de osciladores armónicos con la introducción del concepto de operadores de creación y aniquilación de partículas. En los años siguientes, con contribuciones de Wolfgang Pauli , Eugene Wigner , Pascual Jordan y Werner Heisenberg , y una elegante formulación de la electrodinámica cuántica debido a Enrico Fermi , [101] los físicos llegaron a creer que, en principio, sería posible realizar cualquier cálculo para cualquier proceso físico que involucrara fotones y partículas cargadas.
En 1931, Alexandru Proca desarrolló la ecuación de Proca ( ecuación de Euler-Lagrange ) para la teoría de mesones vectoriales de fuerzas nucleares y las ecuaciones de campo cuánticas relativistas . John Archibald Wheeler en 1937 desarrolla la matriz S. Los estudios de Felix Bloch con Arnold Nordsieck , [102] y Victor Weisskopf , [103] en 1937 y 1939, revelaron que tales cálculos eran confiables solo en un primer orden de teoría de perturbación , un problema ya señalado por Robert Oppenheimer . [104] En órdenes superiores en la serie surgieron infinitos, haciendo que tales cálculos carecieran de sentido y arrojando serias dudas sobre la consistencia interna de la teoría misma. Sin una solución para este problema conocida en ese momento, parecía que existía una incompatibilidad fundamental entre la relatividad especial y la mecánica cuántica .
En la década de 1930, Edmund Landau creó la letra Z mayúscula de doble tachado para los conjuntos de números enteros . Nicolas Bourbaki creó la letra Q mayúscula de doble tachado para los conjuntos de números racionales. En 1935, Gerhard Gentzen creó cuantificadores universales . André Weil y Nicolas Bourbaki desarrollarían el signo de conjunto vacío en 1939. Ese mismo año, Nathan Jacobson acuñaría la letra C mayúscula de doble tachado para los conjuntos de números complejos .
Alrededor de la década de 1930, se desarrollaría la notación de Voigt (llamada así en honor al trabajo de Voigt de 1898) para el álgebra multilineal como una forma de representar un tensor simétrico reduciendo su orden. La notación de Schönflies se convirtió en una de las dos convenciones utilizadas para describir grupos de puntos (la otra es la notación de Hermann-Mauguin ). También en esta época, la notación de van der Waerden [105] [106] se hizo popular para el uso de espinores de dos componentes ( espinores de Weyl ) en cuatro dimensiones del espacio-tiempo. Arend Heyting introduciría el álgebra de Heyting y la aritmética de Heyting .
La flecha, p. ej., →, fue desarrollada para la notación de funciones en 1936 por Øystein Ore para denotar imágenes de elementos específicos y para denotar conexiones de Galois . Más tarde, en 1940, tomó su forma actual, p. ej., f: X → Y , a través del trabajo de Witold Hurewicz . Werner Heisenberg , en 1941, propuso la teoría de la matriz S de interacciones de partículas.

La notación bra-ket ( notación de Dirac ) es una notación estándar para describir estados cuánticos , compuesta por corchetes angulares y barras verticales . También se puede utilizar para denotar vectores abstractos y funcionales lineales . Se llama así porque el producto interno (o producto escalar en un espacio vectorial complejo) de dos estados se denota por un ⟨bra|ket⟩: . La notación fue introducida en 1939 por Paul Dirac , [107] aunque la notación tiene precursores en el uso de Grassmann de la notación [ φ | ψ ] para sus productos internos casi 100 años antes. [108]
La notación Bra-ket está muy extendida en la mecánica cuántica : casi todos los fenómenos que se explican utilizando la mecánica cuántica (incluida una gran parte de la física moderna ) suelen explicarse con la ayuda de la notación Bra-ket. La notación establece una independencia de representación abstracta codificada, produciendo una representación específica versátil (por ejemplo, x o p , o base de función propia ) sin mucho ruido o dependencia excesiva de la naturaleza de los espacios lineales involucrados. La expresión de superposición ⟨ φ | ψ ⟩ se interpreta típicamente como la amplitud de probabilidad para que el estado ψ colapse en el estado ϕ . La notación de barra de Feynman (notación de barra de Dirac [109] ) fue desarrollada por Richard Feynman para el estudio de los campos de Dirac en la teoría cuántica de campos .
Geoffrey Chew , junto con otros, promovería la notación matricial para la interacción fuerte en física de partículas, y el principio de bootstrap asociado , en 1960. En la década de 1960, se desarrolló la notación constructora de conjuntos para describir un conjunto al indicar las propiedades que sus miembros deben satisfacer. También en la década de 1960, los tensores se abstraen dentro de la teoría de categorías por medio del concepto de categoría monoidal . Más tarde, la notación de múltiples índices elimina las nociones convencionales utilizadas en el cálculo multivariable , las ecuaciones diferenciales parciales y la teoría de distribuciones , al abstraer el concepto de un índice entero a una tupla ordenada de índices.
Notación matemática moderna
En las matemáticas modernas de la relatividad especial , el electromagnetismo y la teoría ondulatoria , el operador de d'Alembert ( ) es el operador de Laplace del espacio de Minkowski . El símbolo de Levi-Civita , también conocido como símbolo de permutación , se utiliza en el cálculo tensorial .
Los diagramas de Feynman se utilizan en física de partículas, equivalentes al enfoque basado en operadores de Sin-Itiro Tomonaga y Julian Schwinger . El sistema de notación orbifold , inventado por William Thurston , se ha desarrollado para representar tipos de grupos de simetría en espacios bidimensionales de curvatura constante.
El formalismo de tétrada ( notación de índice de tétrada ) se introduciría como un enfoque de la relatividad general que reemplaza la elección de una base de coordenadas por la elección menos restrictiva de una base local para el fibrado tangente (un conjunto definido localmente de cuatro campos vectoriales linealmente independientes llamado tétrada ). [110]
En la década de 1990, Roger Penrose propondría la notación gráfica de Penrose ( notación de diagrama tensorial ) como una representación visual, generalmente manuscrita, de funciones multilineales o tensores . [111] Penrose también introduciría la notación de índice abstracto . Su uso de la suma de Einstein fue para compensar el inconveniente de describir contracciones y diferenciación covariante en la notación tensorial abstracta moderna, manteniendo al mismo tiempo la covarianza explícita de las expresiones involucradas. [ cita requerida ]
.jpg/440px-John_H_Conway_2005_(cropped).jpg)
John Conway desarrollaría diversas notaciones, entre ellas la notación de flecha encadenada de Conway , la notación de teoría de nudos de Conway y la notación de poliedro de Conway . El sistema de notación de Coxeter clasifica los grupos de simetría, describiendo los ángulos entre ellos con reflexiones fundamentales de un grupo de Coxeter . Utiliza una notación entre corchetes, con modificadores para indicar ciertos subgrupos. La notación recibe su nombre de HSM Coxeter y Norman Johnson, quienes la definieron de forma más completa.
La notación combinatoria MCF , ideada por Joshua Lederberg y ampliada por Harold Scott MacDonald Coxeter y Robert Frucht , fue desarrollada para la representación de grafos cúbicos que son hamiltonianos . [112] [113] La notación cíclica es la convención para escribir una permutación en términos de sus ciclos constituyentes . [114] Esto también se denomina notación circular y la permutación se denomina permutación cíclica o circular . [115]
Computadoras y notación de marcado
En 1931, IBM produce el IBM 601 Multiplying Punch ; es una máquina electromecánica que podía leer dos números, de hasta 8 dígitos de longitud, de una tarjeta y perforar su producto en la misma tarjeta. [116] En 1934, Wallace Eckert utilizó un IBM 601 Multiplying Punch manipulado para automatizar la integración de ecuaciones diferenciales. [117]
En 1962, Kenneth E. Iverson desarrolló una notación de partes integrales, que se conoció como notación de Iverson, que se convirtió en APL . [118] En la década de 1970, dentro de la arquitectura informática , se desarrolló la notación Quote para un sistema numérico de representación de números racionales . También en esta década, la notación Z (al igual que el lenguaje APL , mucho antes) utiliza muchos símbolos que no son ASCII , la especificación incluye sugerencias para representar los símbolos de notación Z en ASCII y en LaTeX . Actualmente existen varias funciones matemáticas de C (Math.h) y bibliotecas numéricas. Son bibliotecas utilizadas en el desarrollo de software para realizar cálculos numéricos . Estos cálculos pueden manejarse mediante ejecuciones simbólicas ; analizando un programa para determinar qué entradas hacen que se ejecute cada parte de un programa. Mathematica y SymPy son ejemplos de programas de software computacionales basados en matemáticas simbólicas .
Referencias y citas
- General
- Florian Cajori (1929) Una historia de las notaciones matemáticas , 2 vols. Reimpresión de Dover en 1 vol., 1993. ISBN 0-486-67766-4 .
- Citas
- ^ Florian Cajori . Una historia de las notaciones matemáticas: dos volúmenes en uno. Cosimo, Inc., 1 de diciembre de 2011
- ^ Diccionario de ciencia, literatura y arte, volumen 2. Editado por William Thomas Brande y George William Cox . Pág. 683
- ^ "Notación - de Wolfram MathWorld". Mathworld.wolfram.com . Consultado el 24 de junio de 2014 .
- ^ Diofanto de Alejandría: Un estudio sobre la historia del álgebra griega. Por Sir Thomas Little Heath. Pág. 77.
- ^ Matemáticas: su poder y utilidad. Por Karl J. Smith. Pág. 86.
- ^ La revolución comercial y los comienzos de las matemáticas occidentales en la Florencia renacentista, 1300-1500. Warren Van Egmond. 1976. Página 233.
- ^ Solomon Gandz . "Las fuentes del álgebra de Al-Khowarizmi"
- ^ Enciclopedia americana. Por Thomas Gamaliel Bradford. Pág. 314
- ^ Excursión matemática, edición mejorada: Edición mejorada de Webassign Por Richard N. Aufmann, Joanne Lockwood, Richard D. Nation, Daniel K. Cleg. Pág. 186
- ^ "Matemáticas en Egipto y Mesopotamia" (PDF) . Archivado desde el original (PDF) el 28 de diciembre de 2022. Consultado el 25 de julio de 2013 .
- ^ Boyer, CB Una historia de las matemáticas , 2ª ed. Rdo. por Uta C. Merzbach . Nueva York: Wiley, 1989 ISBN 0-471-09763-2 (edición pbk de 1991 ISBN 0-471-54397-7 ). "Mesopotamia" pág. 25.
- ^ Duncan J. Melville (2003). Cronología del tercer milenio, Matemáticas del tercer milenio . Universidad de St. Lawrence .
- ^ Aaboe, Asger (1998). Episodios de la historia temprana de las matemáticas . Nueva York: Random House. págs. 30-31.
- ^ Es decir, .
- ^ Heath (1931). "Un manual de matemáticas griegas". Nature . 128 (3235): 5. Bibcode :1931Natur.128..739T. doi :10.1038/128739a0. S2CID 3994109.
- ^ Sir Thomas L. Heath, A Manual of Greek Mathematics , Dover, 1963, pág. 1: "En el caso de las matemáticas, lo más esencial es conocer la contribución griega, pues fueron los griegos quienes hicieron de las matemáticas una ciencia".
- ^ ab La nueva enciclopedia; o, Diccionario universal de artes y ciencias. Por Encyclopaedia Perthensi. Pg 49
- ^ Calinger, Ronald (1999). Una historia contextual de las matemáticas . Prentice-Hall. pág. 150. ISBN 0-02-318285-7Poco después de
Euclides, compilador del libro de texto definitivo, llegó Arquímedes de Siracusa (ca. 287-212 a. C.), el matemático más original y profundo de la antigüedad.
- ^ "Arquímedes de Siracusa". Archivo de Historia de las Matemáticas de MacTutor. Enero de 1999. Consultado el 9 de junio de 2008 .
- ^ O'Connor, JJ; Robertson, EF (febrero de 1996). "Una historia del cálculo". Universidad de St Andrews . Archivado desde el original el 15 de julio de 2007. Consultado el 7 de agosto de 2007 .
- ^ "Resumen de Proclo". Gap.dcs.st-and.ac.uk. Archivado desde el original el 23 de septiembre de 2015. Consultado el 24 de junio de 2014 .
- ^ Matemáticas y medición Por Oswald Ashton Wentworth Dilk. Pág. 14
- ^ abcde Diccionario de ciencia, literatura y arte, editado por WT Brande. Pág. 683
- ^ Boyer, Carl B. Una historia de las matemáticas , 2.ª edición, John Wiley & Sons, Inc., 1991.
- ^ Ecuaciones diofánticas. Presentado por: Aaron Zerhusen, Chris Rakes y Shasta Meece. MA 330-002. Dr. Carl Eberhart. 16 de febrero de 1999.
- ^ Historia de las matemáticas griegas: desde Aristarco hasta Diofanto. Por Sir Thomas Little Heath. Pág. 456
- ^ Historia de las matemáticas griegas: desde Aristarco hasta Diofanto. Por Sir Thomas Little Heath. Pág. 458
- ^ The American Mathematical Monthly, volumen 16, pág. 131
- ^ "Resumen de las matemáticas chinas". Groups.dcs.st-and.ac.uk . Consultado el 24 de junio de 2014 .
- ^ George Gheverghese Joseph, La cresta del pavo real: raíces no europeas de las matemáticas , Penguin Books, Londres, 1991, págs. 140-148
- ^ Georges Ifrah, Universalgeschichte der Zahlen , Campus, Frankfurt/Nueva York, 1986, págs. 428—437
- ^ "Frank J. Swetz y TI Kao: ¿Pitágoras era chino?". Psupress.psu.edu . Consultado el 24 de junio de 2014 .
- ^ abc Needham, Joseph (1986). Ciencia y civilización en China: Volumen 3, Matemáticas y ciencias de los cielos y la tierra. Taipei: Caves Books, Ltd.
- ^ Sal Restivo
- ^ Marcel Gauchet , 151.
- ^ Boyer, CB A History of Mathematics, 2.ª ed. rev. por Uta C. Merzbach. Nueva York: Wiley, 1989 ISBN 0-471-09763-2 (edición de 1991 ISBN 0-471-54397-7 ). "China e India", pág. 221. (cf., "fue el primero en dar una solución general de la ecuación diofántica lineal ax + by = c, donde a, b y c son números enteros. [...] Es un gran mérito de Brahmagupta que diera todas las soluciones integrales de la ecuación diofántica lineal, mientras que el propio Diofanto se había contentado con dar una solución particular de una ecuación indeterminada. En la medida en que Brahmagupta utilizó algunos de los mismos ejemplos que Diofanto, vemos de nuevo la probabilidad de influencia griega en la India - o la posibilidad de que ambos hicieran uso de una fuente común, posiblemente de Babilonia. Es interesante notar también que el álgebra de Brahmagupta, como la de Diofanto, era sincopada. La adición se indicaba por yuxtaposición, la resta colocando un punto sobre el sustraendo y la división colocando el divisor debajo del dividendo, como en nuestra notación fraccionaria pero sin la barra. Las operaciones de multiplicación y evolución (la toma de raíces), así como las cantidades desconocidas, se representaban mediante abreviaturas. de palabras apropiadas."")
- ^ Robert Kaplan, "La nada que es: una historia natural del cero", Allen Lane/The Penguin Press, Londres, 1999
- ^ ""El ingenioso método de expresar cada número posible utilizando un conjunto de diez símbolos (cada símbolo con un valor posicional y un valor absoluto) surgió en la India. La idea parece tan simple hoy en día que su significado y profunda importancia ya no se aprecian. Su simplicidad radica en la forma en que facilitó el cálculo y colocó a la aritmética en primer lugar entre las invenciones útiles. La importancia de esta invención se aprecia más fácilmente cuando se considera que estaba más allá de los dos grandes hombres de la Antigüedad, Arquímedes y Apolonio." – Pierre-Simon Laplace". History.mcs.st-and.ac.uk . Consultado el 24 de junio de 2014 .
- ^ AP Juschkewitsch , "Geschichte der Mathematik im Mittelalter", Teubner, Leipzig, 1964
- ^ Kunitzsch, Paul (2003), "Reconsideración de la transmisión de numerales hindúes y árabes", en JP Hogendijk; AI Sabra (eds.), La empresa científica en el Islam: nuevas perspectivas , MIT Press, págs. 3-22 (12-13), ISBN 978-0-262-19482-2
- ↑ Marie-Thérèse d'Alverny , "Traducciones y traductores", págs. 421–62 en Robert L. Benson y Giles Constable, Renacimiento y renovación en el siglo XII , (Cambridge: Harvard University Press, 1982).
- ^ Guy Beaujouan, "La transformación del Quadrivium", págs. 463–87 en Robert L. Benson y Giles Constable, Renacimiento y renovación en el siglo XII , (Cambridge: Harvard University Press, 1982).
- ^ O'Connor, John J.; Robertson, Edmund F. , "al-Marrakushi ibn Al-Banna", Archivo de Historia de las Matemáticas MacTutor , Universidad de St Andrews
- ^ Gullberg, Jan (1997). Matemáticas: desde el nacimiento de los números . WW Norton. pág. 298. ISBN 0-393-04002-X.
- ^ ab O'Connor, John J.; Robertson, Edmund F. , "Abu'l Hasan ibn Ali al Qalasadi", Archivo MacTutor de Historia de las Matemáticas , Universidad de St Andrews
- ^ Boyer, CB A History of Mathematics, 2.ª ed. rev. por Uta C. Merzbach. Nueva York: Wiley, 1989 ISBN 0-471-09763-2 (edición de 1991 en papel ISBN 0-471-54397-7 ). "Renacimiento y decadencia de las matemáticas griegas", pág. 178 (cf., "La principal diferencia entre la síncopa diofántica y la notación algebraica moderna es la falta de símbolos especiales para operaciones y relaciones, así como de la notación exponencial").
- ^ Grant, Edward y John E. Murdoch (1987), eds., Matemáticas y sus aplicaciones a la ciencia y la filosofía natural en la Edad Media , (Cambridge: Cambridge University Press) ISBN 0-521-32260-X .
- ^ Revista Matemática, Volumen 1. Artemas Martin, 1887. Pág. 124
- ^ Der Algorismus proporcionalum des Nicolaus Oresme: Zum ersten Male nach der Lesart der Handschrift R.40.2. der Königlichen Gymnasial-bibliothek zu Thorn. Nicole Oresme . S. Calvario y Compañía, 1868.
- ^ Clagett, Marshall (1961) La ciencia de la mecánica en la Edad Media , (Madison: University of Wisconsin Press), págs. 332–45, 382–91.
- ^ Versión moderna temprana posterior : Un nuevo sistema de aritmética mercantil: adaptado al comercio de los Estados Unidos, en sus relaciones internas y externas con formas de contabilidad y otros escritos que suelen aparecer en el comercio. Por Michael Walsh. Edmund M. Blunt (propietario), 1801.
- ^ Miller, Jeff (4 de junio de 2006). "Usos más antiguos de los símbolos de operación". Gulf High School . Consultado el 24 de septiembre de 2006 .
- ^ Libros de aritmética desde la invención de la imprenta hasta la actualidad. Por Augustus De Morgan . pág. 2.
- ^ Aritmética integra. Por Michael Stifel y Philipp Melanchton . Norimbergæ : Apud Iohan Petreium, 1544.
- ^ La historia de las matemáticas, por Anne Roone. Pág. 40
- ^ Memorias de John Napier de Merchiston. Por Mark Napier
- ^ Relato de la vida, los escritos y las invenciones de John Napier, de Merchiston. Por David Stewart Erskine, conde de Buchan, Walter Minto
- ^ Cajori, Florian (1919). Una historia de las matemáticas. Macmillan. pág. 157.
- ^ Sinopsis Palmariorum Matheseos. Por William Jones . 1706. (Alt: Sinopsis Palmariorum Matheseos: o una nueva introducción a las matemáticas. archive.org.)
- ^ Cuando menos es más: Visualización de desigualdades básicas. Por Claudi Alsina y Roger B. Nelse. Pág. 18.
- ^ Los elementos de la geometría. Por William Emerson
- ^ La doctrina de la proporción, aritmética y geométrica, junto con un método general de cálculo por cantidades proporcionales. Por William Emerson.
- ^ El corresponsal matemático. Por George Baron. 83
- ^ Disquisitiones Arithmeticae (1801) Artículo 76
- ^ Vitulli, Marie . "Una breve historia del álgebra lineal y la teoría de matrices". Departamento de Matemáticas . Universidad de Oregon. Archivado desde el original el 10 de septiembre de 2012. Consultado el 24 de enero de 2012 .
- ^ "Biografía de Kramp". History.mcs.st-and.ac.uk . Consultado el 24 de junio de 2014 .
- ^ Mécanique analytique: Volumen 1, Volumen 2. Por Joseph Louis Lagrange . Sra. Ve Courcier, 1811.
- ^ Los artículos matemáticos recopilados de Arthur Cayley. Volumen 11. Página 243.
- ^ Enciclopedia histórica de ciencias naturales y matemáticas, volumen 1. Por Ari Ben-Menahem. Pág. 2070.
- ^ Vitulli, Marie . "Una breve historia del álgebra lineal y la teoría de matrices". Departamento de Matemáticas. Universidad de Oregon. Originalmente en: darkwing.uoregon.edu/~vitulli/441.sp04/LinAlgHistory.html
- ^ Las palabras de las matemáticas. Por Steven Schwartzman. 6.
- ^ Electromagnetismo: teoría y aplicaciones. Por A. Pramanik. 38
- ^ Historia de Nabla y otros símbolos matemáticos. homepages.math.uic.edu/~hanson.
- ^ "James Clerk Maxwell". IEEE Global History Network . Consultado el 25 de marzo de 2013 .
- ^ Maxwell, James Clerk (1865). "Una teoría dinámica del campo electromagnético" (PDF) . Philosophical Transactions of the Royal Society of London . 155 : 459–512. Bibcode :1865RSPT..155..459M. doi :10.1098/rstl.1865.0008. S2CID 186207827.(Este artículo acompañó una presentación realizada por Maxwell el 8 de diciembre de 1864 ante la Royal Society.)
- ^ Libros I, II, III (1878) en Internet Archive ; Libro IV (1887) en Internet Archive
- ^ Ricci Curbastro, G. (1892). "Resumé de los trabajos en los sistemas variables de funciones asociadas a una forma diferente cuadrada". Boletín de Ciencias Matemáticas . 2 (16): 167–189.
- ^ Voigt, Woldemar (1898). Die fundamentalen physikalischen Eigenschaften der Krystalle in elementarer Darstellung. Leipzig: von Veit.
- ^ Poincaré, Henri, "Analysis situs", Journal de l'École Polytechnique ser 2, 1 (1895) págs.
- ^ Whitehead, John B. Jr. (1901). "Revisión: fenómenos de corriente alterna, por CP Steinmetz" (PDF) . Bull. Amer. Math. Soc . 7 (9): 399–408. doi : 10.1090/s0002-9904-1901-00825-7 .
- ^
Existen muchas ediciones. Aquí se mencionan dos:
- (Francés) Publicado en 1901 por Gauthier-Villars, París. 230 págs. OpenLibrary OL15255022W, PDF.
- (Italiano) Publicado en 1960 por Edizione cremonese, Roma. 463p. Biblioteca abierta OL16587658M.
- ^ Ricci, Gregorio ; Levi-Civita, Tullio (marzo de 1900), "Méthodes de calcul différentiel absolu et leurs apps", Mathematische Annalen , 54 (1–2), Springer: 125–201, doi :10.1007/BF01454201, S2CID 120009332
- ^ Cullis, Cuthbert Edmund (marzo de 2013). Matrices y determinoides . Vol. 2. Cambridge University Press. ISBN 978-1-107-62083-4.
- ^ Se puede asignar una matriz determinada: Acerca de una clase de matrices. (Gr. Ueber eine Klasse von Matrizen: die sich einer gegebenen Matrix zuordnen lassen.) de Isay Schur
- ^ Introducción a la teoría moderna de ecuaciones. Por Florian Cajori.
- ^ Actas de la Academia Prusiana de Ciencias (1918). Pág. 966.
- ^ Sitzungsberichte der Preussischen Akademie der Wissenschaften (1918) (Tr. Actas de la Academia de Ciencias de Prusia (1918)). archivo.org; Véase también: Teoría de Kaluza-Klein .
- ^ Synge JL; Schild A. (1949). Cálculo tensorial . Primera edición de Dover Publications de 1978. Págs. 6-108.
- ^ JA Wheeler; C. Misner; KS Thorne (1973). Gravitación . WH Freeman & Co., págs. 85-86, §3.5. ISBN 0-7167-0344-0.
- ^ R. Penrose (2007). El camino hacia la realidad . Libros antiguos. ISBN 978-0-679-77631-4.
- ^ Schouten, enero A. (1924). R. Courant (ed.). Der Ricci-Kalkül - Eine Einführung in die neueren Methoden und Probleme der mehrdimensionalen Differentialgeometrie (Ricci Calculus - Una introducción a los últimos métodos y problemas en geometría diferencial multidimensional). Grundlehren der mathematischen Wissenschaften (en alemán). vol. 10. Berlín: Springer Verlag.
- ^ Robert B. Ash. Introducción a las matemáticas abstractas. Cambridge University Press, 1 de enero de 1998
- ^ El Nuevo Diccionario Enciclopédico Americano. Editado por Edward Thomas Roe, Le Roy Hooker, Thomas W. Handford. Pág. 34
- ^ Los principios matemáticos de la filosofía natural, volumen 1. Por Sir Isaac Newton, John Machin. Pág. 12.
- ^ En La perspectiva científica (1931)
- ^ Las matemáticas simplificadas y hechas atractivas: o, Las leyes del movimiento explicadas. Por Thomas Fisher. Pg 15. (Cf. Pero una abstracción que no se fundamente en la Naturaleza y la Verdad ( lógica ) y que no esté en consonancia con ellas sería una falsedad , una locura . )
- ^ Proposición VI, Sobre proposiciones formalmente indecidibles en Principia Mathematica y sistemas relacionados I (1931)
- ^ Casti, John L. Cinco reglas de oro . Nueva York: MJF Books, 1996.
- ^ Gr. Método de la física matemática
- ^ PAM Dirac (1927). "La teoría cuántica de la emisión y absorción de la radiación". Actas de la Royal Society of London A . 114 (767): 243–265. Bibcode :1927RSPSA.114..243D. doi : 10.1098/rspa.1927.0039 .
- ^ E. Fermi (1932). "Teoría cuántica de la radiación". Reseñas de física moderna . 4 (1): 87–132. Código Bibliográfico :1932RvMP....4...87F. doi :10.1103/RevModPhys.4.87.
- ^ F. Bloch ; A. Nordsieck (1937). "Nota sobre el campo de radiación del electrón". Physical Review . 52 (2): 54–59. Bibcode :1937PhRv...52...54B. doi :10.1103/PhysRev.52.54.
- ^ VF Weisskopf (1939). "Sobre la autoenergía y el campo electromagnético del electrón". Physical Review . 56 (1): 72–85. Bibcode :1939PhRv...56...72W. doi :10.1103/PhysRev.56.72.
- ^ R. Oppenheimer (1930). "Nota sobre la teoría de la interacción del campo y la materia". Physical Review . 35 (5): 461–477. Bibcode :1930PhRv...35..461O. doi :10.1103/PhysRev.35.461.
- ^ Van der Waerden BL (1929). "Espinoranálisis". Nachr. Ges. Wiss. Göttingen Matemáticas-Física . 1929 : 100–109.
- ^ Veblen O. (1933). "Geometría de espinores de dos componentes". Proc. Natl. Sci. USA . 19 (4): 462–474. Bibcode :1933PNAS...19..462V. doi : 10.1073/pnas.19.4.462 . PMC 1086023 . PMID 16577541.
- ^ Dirac, PAM (1939). "Una nueva notación para la mecánica cuántica". Actas matemáticas de la Sociedad filosófica de Cambridge . 35 (3): 416–418. Bibcode :1939PCPS...35..416D. doi :10.1017/S0305004100021162. S2CID 121466183.
- ^ H. Grassmann (1862). Teoría de la extensión . Historia de las fuentes matemáticas. American Mathematical Society, London Mathematical Society, 2000, traducción de Lloyd C. Kannenberg.
- ^ Weinberg, Steven (1964), La teoría cuántica de campos, Volumen 2, Cambridge University Press, 1995, pág. 358, ISBN 0-521-55001-7
- ^ De Felice, F.; Clarke, CJS (1990), Relatividad en variedades curvas , pág. 133
- ^ "Invariantes cuánticos de nudos y variedades tridimensionales" de VG Turaev (1994), página 71
- ^ Pisanski, Tomaž ; Servatius, Brigitte (2013), "2.3.2 Gráficos cúbicos y notación LCF", Configuraciones desde un punto de vista gráfico, Springer, p. 32, ISBN 978-0-8176-8364-1
- ^ Frucht, R. (1976), "Una representación canónica de grafos hamiltonianos trivalentes", Journal of Graph Theory , 1 (1): 45–60, doi :10.1002/jgt.3190010111
- ^ Fraleigh 2002:89; Hungerford 1997:230
- ^ Dehn, Edgar. Ecuaciones algebraicas, Dover. 1930:19
- ^ "El punzón multiplicador IBM 601". Columbia.edu . Consultado el 24 de junio de 2014 .
- ^ "Equipo de tarjetas perforadas interconectadas". Columbia.edu. 24 de octubre de 1935. Consultado el 24 de junio de 2014 .
- ^ McDonnell, Eugene , ed. (1981), A Source Book in APL, Introducción, APL Press , consultado el 19 de abril de 2016
Lectura adicional
- General
- Breve relato de la historia de las matemáticas. Por Walter William Rouse Ball .
- Una introducción a la historia de las matemáticas. Por Walter William Rouse Ball.
- Historia de las matemáticas elementales: con sugerencias sobre métodos de enseñanza. Por Florian Cajori.
- Historia de las matemáticas elementales. Por Florian Cajori.
- Una historia de las matemáticas. Por Florian Cajori.
- Breve historia de las matemáticas griegas. Por James Gow .
- Sobre el desarrollo del pensamiento matemático durante el siglo XIX. Por John Theodore Merz .
- Un nuevo diccionario matemático y filosófico. Por Peter Barlow.
- Introducción histórica a la literatura matemática. Por George Abram Miller
- Breve historia de las matemáticas. Por Karl Fink, Wooster Woodruff Beman y David Eugene Smith
- Historia de las matemáticas modernas. Por David Eugene Smith.
- Historia de las matemáticas modernas. Por David Eugene Smith, Mansfield Merriman .
- Otro
- Principia Mathematica, Volumen 1 y Volumen 2. Por Alfred North Whitehead, Bertrand Russell.
- Los principios matemáticos de la filosofía natural, volumen 1, número 1. Por Sir Isaac Newton, Andrew Motte, William Davis, John Machin, William Emerson.
- Investigaciones generales de superficies curvas de 1827 y 1825. Por Carl Friedrich Gaus.
Enlaces externos
- Notación matemática: pasado y futuro
- Historia de la notación matemática
- Los primeros usos de la notación matemática
- Conteo de dedos. files.chem.vt.edu.
- Algunos símbolos y abreviaturas matemáticas comunes (con su historia). Isaiah Lankham, Bruno Nachtergaele, Anne Schilling.



















![{\displaystyle f[f(x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f54da4ffd78a97e0493340583f3157015327436)




































