Trigonometría esférica

La trigonometría esférica es la rama de la geometría esférica que estudia las relaciones métricas entre los lados y los ángulos de los triángulos esféricos , tradicionalmente expresados ​​mediante funciones trigonométricas . En la esfera , las geodésicas son círculos máximos . La trigonometría esférica es de gran importancia para los cálculos en astronomía , geodesia y navegación .

Los orígenes de la trigonometría esférica en las matemáticas griegas y los principales avances en las matemáticas islámicas se analizan en profundidad en History of trigonometry and Mathematics in medieval Islam . El tema llegó a su plenitud en la época moderna temprana con importantes avances de John Napier , Delambre y otros, y alcanzó una forma esencialmente completa a fines del siglo XIX con la publicación del libro de texto de Todhunter Spherical trigonometry for the use of colleges and Schools . ^[1] Desde entonces, los avances significativos han sido la aplicación de métodos vectoriales, métodos de cuaterniones y el uso de métodos numéricos.

Un polígono esférico es un polígono en la superficie de la esfera. Sus lados son arcos de círculos máximos , el equivalente geométrico esférico de los segmentos de línea en la geometría plana .

Estos polígonos pueden tener cualquier número de lados mayor que 1. Los polígonos esféricos de dos lados —lunes , también llamados digones o biángulos— están delimitados por dos arcos de círculo máximo: un ejemplo conocido es la superficie curvada que mira hacia afuera de un segmento de una naranja. Tres arcos sirven para definir un triángulo esférico, el tema principal de este artículo. Los polígonos con un mayor número de lados (cuadriláteros esféricos de 4 lados, pentágonos esféricos de 5 lados, etc.) se definen de manera similar. Análogamente a sus contrapartes planas, los polígonos esféricos con más de 3 lados siempre pueden tratarse como la composición de triángulos esféricos.

Un polígono esférico con propiedades interesantes es el pentagramma mirificum , un polígono estrellado esférico de cinco lados con un ángulo recto en cada vértice.

A partir de este punto del artículo, la discusión se limitará a los triángulos esféricos, denominados simplemente triángulos .

• Tanto los vértices como los ángulos en los vértices de un triángulo se denotan con las mismas letras mayúsculas A , B y C.
• Los lados se indican con letras minúsculas: a , b y c . La esfera tiene un radio de 1, por lo que las longitudes de los lados y los ángulos en minúsculas son equivalentes (ver longitud del arco).
• El ángulo A (respectivamente, B y C ) puede considerarse como el ángulo entre los dos planos que intersecan la esfera en el vértice A o, equivalentemente, como el ángulo entre las tangentes de los arcos del círculo máximo donde se encuentran en el vértice.
• Los ángulos se expresan en radianes . Los ángulos de los triángulos esféricos propios son (por convención) menores que π , de modo que (Todhunter, ^[1] Art.22,32).$${\displaystyle \pi <A+B+C<3\pi }$$

En particular, la suma de los ángulos de un triángulo esférico es estrictamente mayor que la suma de los ángulos de un triángulo definido en el plano euclidiano, que es siempre exactamente π radianes.

• Los lados también se expresan en radianes. Un lado (considerado como un arco de círculo máximo) se mide por el ángulo que subtiende en el centro. En la esfera unitaria, esta medida en radianes es numéricamente igual a la longitud del arco. Por convención, los lados de los triángulos esféricos propios son menores que π , de modo que (Todhunter, ^[1] Art.22,32).$${\displaystyle 0<a+b+c<2\pi}$$
• El radio de la esfera se toma como unidad. Para problemas prácticos específicos en una esfera de radio R, las longitudes medidas de los lados deben dividirse por R antes de utilizar las identidades que se dan a continuación. Del mismo modo, después de un cálculo en la esfera unitaria, los lados a , b y c deben multiplicarse por  R.

El triángulo polar asociado a un triángulo △ ABC se define de la siguiente manera. Considere el círculo máximo que contiene el lado  BC . Este círculo máximo se define por la intersección de un plano diametral con la superficie. Dibuje la normal a ese plano en el centro: interseca la superficie en dos puntos y el punto que está en el mismo lado del plano que A se denomina (convencionalmente) polo de A y se denota por A' . Los puntos B' y C' se definen de manera similar.

El triángulo △ A'B'C' es el triángulo polar correspondiente al triángulo  △ ABC . Un teorema muy importante (Todhunter, ^[1] Art.27) demuestra que los ángulos y lados del triángulo polar están dados por Por lo tanto, si se demuestra alguna identidad para △ ABC entonces podemos derivar inmediatamente una segunda identidad aplicando la primera identidad al triángulo polar haciendo las sustituciones anteriores. Así es como las ecuaciones de coseno suplementarias se derivan de las ecuaciones de coseno. De manera similar, las identidades para un triángulo cuadrantal se pueden derivar de aquellas para un triángulo rectángulo. El triángulo polar de un triángulo polar es el triángulo original.$${\displaystyle {\begin{alignedat}{3}A'&=\pi -a,&\qquad B'&=\pi -b,&\qquad C'&=\pi -c,\\a'&=\pi -A,&b'&=\pi -B,&c'&=\pi -C.\end{alignedat}}}$$

La regla del coseno es la identidad fundamental de la trigonometría esférica: todas las demás identidades, incluida la regla del seno, pueden derivarse de la regla del coseno:$${\displaystyle {\begin{aligned}\cos a&=\cos b\cos c+\sin b\sin c\cos A,\\[2pt]\cos b&=\cos c\cos a+\sin c\sin a\cos B,\\[2pt]\cos c&=\cos a\cos b+\sin a\sin b\cos C.\end{aligned}}}$$

Estas identidades generalizan la regla del coseno de la trigonometría plana , a la que son asintóticamente equivalentes en el límite de ángulos interiores pequeños. (En la esfera unitaria, si se establece , etc.; véase Ley esférica de los cosenos ).${\displaystyle a,b,c\rightarrow 0}$${\displaystyle \sin a\approx a}$${\displaystyle (\cos a-\cos b)^{2}\approx 0}$

La ley esférica de los senos está dada por la fórmula Estas identidades aproximan la regla del seno de la trigonometría plana cuando los lados son mucho más pequeños que el radio de la esfera.$${\displaystyle {\frac {\sin A}{\sin a}}={\frac {\sin B}{\sin b}}={\frac {\sin C}{\sin c}}.}$$

Las fórmulas del coseno esférico se demostraron originalmente mediante geometría elemental y la regla del coseno plano (Todhunter, ^[1] Art.37). También proporciona una derivación utilizando geometría de coordenadas simple y la regla del coseno plano (Art.60). El enfoque descrito aquí utiliza métodos vectoriales más simples . (Estos métodos también se analizan en Ley esférica de los cosenos ).

Considérese tres vectores unitarios OA → , OB → , OC → dibujados desde el origen hasta los vértices del triángulo (en la esfera unitaria). El arco BC subtiende un ángulo de magnitud a en el centro y, por lo tanto, OB → · OC → = cos a . Introduzca una base cartesiana con OA → a lo largo del eje z y OB → en el plano xz formando un ángulo c con el eje z . El vector OC → se proyecta hacia ON en el plano xy y el ángulo entre ON y el eje x es A . Por lo tanto, los tres vectores tienen componentes:

$${\displaystyle {\begin{aligned}{\vec {OA}}:&\quad (0,\,0,\,1)\\{\vec {OB}}:&\quad (\sin c,\,0,\,\cos c)\\{\vec {OC}}:&\quad (\sin b\cos A,\,\sin b\sin A,\,\cos b).\end{aligned}}}$$

El producto escalar OB → · OC → en términos de los componentes es Igualando las dos expresiones para el producto escalar se obtiene Esta ecuación se puede reorganizar para dar expresiones explícitas para el ángulo en términos de los lados:$${\displaystyle {\vec {OB}}\cdot {\vec {OC}}=\sin c\sin b\cos A+\cos c\cos b.}$$$${\displaystyle \cos a=\cos b\cos c+\sin b\sin c\cos A.}$$$${\displaystyle \cos A={\frac {\cos a-\cos b\cos c}{\sin b\sin c}}.}$$

Las demás reglas del coseno se obtienen mediante permutaciones cíclicas.

Esta derivación se da en Todhunter, ^[1] (Art.40). A partir de la identidad y la expresión explícita para cos A dadas inmediatamente arriba, dado que el lado derecho es invariante bajo una permutación cíclica de a , b y c , la regla del seno esférico se deduce inmediatamente.${\displaystyle \sin ^{2}A=1-\cos ^{2}A}$$${\displaystyle {\begin{aligned}\sin ^{2}A&=1-\left({\frac {\cos a-\cos b\cos c}{\sin b\sin c}}\right)^{2}\\[5pt]&={\frac {(1-\cos ^{2}b)(1-\cos ^{2}c)-(\cos a-\cos b\cos c)^{2}}{\sin ^{2}\!b\,\sin ^{2}\!c}}\\[5pt]{\frac {\sin A}{\sin a}}&={\frac {\sqrt {1-\cos ^{2}\!a-\cos ^{2}\!b-\cos ^{2}\!c+2\cos a\cos b\cos c}}{\sin a\sin b\sin c}}.\end{aligned}}}$$

Existen muchas maneras de derivar las reglas fundamentales del coseno y del seno, así como las demás reglas que se desarrollan en las secciones siguientes. Por ejemplo, Todhunter ^[1] ofrece dos demostraciones de la regla del coseno (artículos 37 y 60) y dos demostraciones de la regla del seno (artículos 40 y 42). La página sobre la ley esférica de los cosenos ofrece cuatro demostraciones diferentes de la regla del coseno. Los libros de texto sobre geodesia ^[2] y astronomía esférica ^[3] ofrecen diferentes demostraciones y los recursos en línea de MathWorld ofrecen aún más. ^[4] Existen incluso derivaciones más exóticas, como la de Banerjee ^[5], que deriva las fórmulas utilizando el álgebra lineal de matrices de proyección y también cita métodos de geometría diferencial y la teoría de rotaciones de grupos.

La derivación de la regla del coseno presentada anteriormente tiene los méritos de la simplicidad y la franqueza y la derivación de la regla del seno enfatiza el hecho de que no se requiere una prueba separada además de la regla del coseno. Sin embargo, la geometría anterior se puede utilizar para dar una prueba independiente de la regla del seno. El producto triple escalar , OA → · ( OB → × OC → ) evalúa a sen b sen c sen A en la base mostrada. De manera similar, en una base orientada con el eje z a lo largo de OB → , el producto triple OB → · ( OC → × OA → ) , evalúa a sen c sen a sen B . Por lo tanto, la invariancia del producto triple bajo permutaciones cíclicas da sen b sen A = sen a sen B que es la primera de las reglas del seno. Vea las variaciones curvas de la ley de los senos para ver los detalles de esta derivación.

Aplicando las reglas del coseno al triángulo polar se obtiene (Todhunter, ^[1] Art.47), es decir , reemplazando A por π – a , a por π – A etc.,$${\displaystyle {\begin{aligned}\cos A&=-\cos B\,\cos C+\sin B\,\sin C\,\cos a,\\\cos B&=-\cos C\,\cos A+\sin C\,\sin A\,\cos b,\\\cos C&=-\cos A\,\cos B+\sin A\,\sin B\,\cos c.\end{aligned}}}$$

Las seis partes de un triángulo pueden escribirse en orden cíclico como ( aCbAcB ). Las fórmulas de la cotangente, o de cuatro partes, relacionan dos lados y dos ángulos que forman cuatro partes consecutivas alrededor del triángulo, por ejemplo ( aCbA ) o BaCb ). En un conjunto de este tipo hay partes internas y externas: por ejemplo, en el conjunto ( BaCb ) el ángulo interno es C , el lado interno es a , el ángulo externo es B , el lado externo es b . La regla de la cotangente puede escribirse como (Todhunter, ^[1] Art.44) y las seis ecuaciones posibles son (con el conjunto relevante mostrado a la derecha): Para demostrar la primera fórmula, comience con la primera regla del coseno y en el lado derecho sustituya cos c de la tercera regla del coseno: El resultado se obtiene al dividir por sen a sen b . Técnicas similares con las otras dos reglas del coseno dan CT3 y CT5. Las otras tres ecuaciones se obtienen aplicando las reglas 1, 3 y 5 al triángulo polar.$${\displaystyle \cos \!{\Bigl (}{\begin{smallmatrix}{\text{inner}}\\{\text{side}}\end{smallmatrix}}{\Bigr )}\cos \!{\Bigl (}{\begin{smallmatrix}{\text{inner}}\\{\text{angle}}\end{smallmatrix}}{\Bigr )}=\cot \!{\Bigl (}{\begin{smallmatrix}{\text{outer}}\\{\text{side}}\end{smallmatrix}}{\Bigr )}\sin \!{\Bigl (}{\begin{smallmatrix}{\text{inner}}\\{\text{side}}\end{smallmatrix}}{\Bigr )}-\cot \!{\Bigl (}{\begin{smallmatrix}{\text{outer}}\\{\text{angle}}\end{smallmatrix}}{\Bigr )}\sin \!{\Bigl (}{\begin{smallmatrix}{\text{inner}}\\{\text{angle}}\end{smallmatrix}}{\Bigr )},}$$$${\displaystyle {\begin{alignedat}{5}{\text{(CT1)}}&&\qquad \cos b\,\cos C&=\cot a\,\sin b-\cot A\,\sin C\qquad &&(aCbA)\\[0ex]{\text{(CT2)}}&&\cos b\,\cos A&=\cot c\,\sin b-\cot C\,\sin A&&(CbAc)\\[0ex]{\text{(CT3)}}&&\cos c\,\cos A&=\cot b\,\sin c-\cot B\,\sin A&&(bAcB)\\[0ex]{\text{(CT4)}}&&\cos c\,\cos B&=\cot a\,\sin c-\cot A\,\sin B&&(AcBa)\\[0ex]{\text{(CT5)}}&&\cos a\,\cos B&=\cot c\,\sin a-\cot C\,\sin B&&(cBaC)\\[0ex]{\text{(CT6)}}&&\cos a\,\cos C&=\cot b\,\sin a-\cot B\,\sin C&&(BaCb)\end{alignedat}}}$$$${\displaystyle {\begin{aligned}\cos a&=\cos b\cos c+\sin b\sin c\cos A\\&=\cos b\ (\cos a\cos b+\sin a\sin b\cos C)+\sin b\sin C\sin a\cot A\\\cos a\sin ^{2}b&=\cos b\sin a\sin b\cos C+\sin b\sin C\sin a\cot A.\end{aligned}}}$$

Con y${\displaystyle 2s=(a+b+c)}$${\displaystyle 2S=(A+B+C),}$$${\displaystyle {\begin{alignedat}{5}\sin {\tfrac {1}{2}}A&={\sqrt {\frac {\sin(s-b)\sin(s-c)}{\sin b\sin c}}}&\qquad \qquad \sin {\tfrac {1}{2}}a&={\sqrt {\frac {-\cos S\cos(S-A)}{\sin B\sin C}}}\\[2ex]\cos {\tfrac {1}{2}}A&={\sqrt {\frac {\sin s\sin(s-a)}{\sin b\sin c}}}&\cos {\tfrac {1}{2}}a&={\sqrt {\frac {\cos(S-B)\cos(S-C)}{\sin B\sin C}}}\\[2ex]\tan {\tfrac {1}{2}}A&={\sqrt {\frac {\sin(s-b)\sin(s-c)}{\sin s\sin(s-a)}}}&\tan {\tfrac {1}{2}}a&={\sqrt {\frac {-\cos S\cos(S-A)}{\cos(S-B)\cos(S-C)}}}\end{alignedat}}}$$

Otras doce identidades siguen por permutación cíclica.

La demostración (Todhunter, ^[1] Art.49) de la primera fórmula parte de la identidad utilizando la regla del coseno para expresar A en términos de los lados y reemplazando la suma de dos cosenos por un producto. (Ver identidades de suma a producto .) La segunda fórmula parte de la identidad la tercera es un cociente y el resto se obtiene aplicando los resultados al triángulo polar.${\displaystyle 2\sin ^{2}\!{\tfrac {A}{2}}=1-\cos A,}$${\displaystyle 2\cos ^{2}\!{\tfrac {A}{2}}=1+\cos A,}$

Las analogías de Delambre (también llamadas analogías de Gauss) fueron publicadas independientemente por Delambre, Gauss y Mollweide entre 1807 y 1809. ^[6]

$${\displaystyle {\begin{aligned}{\frac {\sin {\tfrac {1}{2}}(A+B)}{\cos {\tfrac {1}{2}}C}}={\frac {\cos {\tfrac {1}{2}}(a-b)}{\cos {\tfrac {1}{2}}c}}&\qquad \qquad &{\frac {\sin {\tfrac {1}{2}}(A-B)}{\cos {\tfrac {1}{2}}C}}={\frac {\sin {\tfrac {1}{2}}(a-b)}{\sin {\tfrac {1}{2}}c}}\\[2ex]{\frac {\cos {\tfrac {1}{2}}(A+B)}{\sin {\tfrac {1}{2}}C}}={\frac {\cos {\tfrac {1}{2}}(a+b)}{\cos {\tfrac {1}{2}}c}}&\qquad &{\frac {\cos {\tfrac {1}{2}}(A-B)}{\sin {\tfrac {1}{2}}C}}={\frac {\sin {\tfrac {1}{2}}(a+b)}{\sin {\tfrac {1}{2}}c}}\end{aligned}}}$$Otras ocho identidades siguen por permutación cíclica.

Se demuestra desarrollando los numeradores y utilizando las fórmulas de los ángulos medios. (Todhunter, ^[1] Art.54 y Delambre ^[7] )

$${\displaystyle {\begin{aligned}\tan {\tfrac {1}{2}}(A+B)={\frac {\cos {\tfrac {1}{2}}(a-b)}{\cos {\tfrac {1}{2}}(a+b)}}\cot {\tfrac {1}{2}}C&\qquad &\tan {\tfrac {1}{2}}(a+b)={\frac {\cos {\tfrac {1}{2}}(A-B)}{\cos {\tfrac {1}{2}}(A+B)}}\tan {\tfrac {1}{2}}c\\[2ex]\tan {\tfrac {1}{2}}(A-B)={\frac {\sin {\tfrac {1}{2}}(a-b)}{\sin {\tfrac {1}{2}}(a+b)}}\cot {\tfrac {1}{2}}C&\qquad &\tan {\tfrac {1}{2}}(a-b)={\frac {\sin {\tfrac {1}{2}}(A-B)}{\sin {\tfrac {1}{2}}(A+B)}}\tan {\tfrac {1}{2}}c\end{aligned}}}$$

Otras ocho identidades siguen por permutación cíclica.

Estas identidades se deducen de la división de las fórmulas de Delambre. (Todhunter, ^[1] Art.52)

Tomando cocientes de estos se obtiene la ley de las tangentes , enunciada por primera vez por el matemático persa Nasir al-Din al-Tusi (1201-1274),

$${\displaystyle {\frac {\tan {\tfrac {1}{2}}(A-B)}{\tan {\tfrac {1}{2}}(A+B)}}={\frac {\tan {\tfrac {1}{2}}(a-b)}{\tan {\tfrac {1}{2}}(a+b)}}}$$

Cuando uno de los ángulos, digamos C , de un triángulo esférico es igual a π /2 las distintas identidades dadas anteriormente se simplifican considerablemente. Hay diez identidades que relacionan tres elementos elegidos del conjunto a , b , c , A y B.

Napier ^[8] proporcionó una elegante ayuda mnemotécnica para las diez ecuaciones independientes: la mnemotecnia se llama círculo de Napier o pentágono de Napier (cuando el círculo en la figura anterior, a la derecha, se reemplaza por un pentágono).

Primero, escribe las seis partes del triángulo (tres ángulos de vértice, tres ángulos de arco para los lados) en el orden en que ocurren alrededor de cualquier circuito del triángulo: para el triángulo que se muestra arriba a la izquierda, yendo en el sentido de las agujas del reloj comenzando con a se obtiene aCbAcB . Luego reemplaza las partes que no son adyacentes a C (es decir, A , c y B ) por sus complementos y luego elimina el ángulo C de la lista. Las partes restantes se pueden dibujar como cinco rebanadas iguales y ordenadas de un pentagrama o círculo, como se muestra en la figura anterior (derecha). Para cualquier elección de tres partes contiguas, una (la parte del medio ) será adyacente a dos partes y opuesta a las otras dos partes. Las diez reglas de Napier están dadas por

• seno de la parte media = el producto de las tangentes de las partes adyacentes
• seno de la parte media = el producto de los cosenos de las partes opuestas

La clave para recordar qué función trigonométrica corresponde a cada parte es observar la primera vocal del tipo de parte: las partes del medio toman el seno, las partes adyacentes toman la tangente y las partes opuestas toman el coseno. Por ejemplo, comenzando con el sector que contiene a tenemos: El conjunto completo de reglas para el triángulo esférico rectángulo es (Todhunter, ^[1] Art.62)$${\displaystyle {\begin{aligned}\sin a&=\tan({\tfrac {\pi }{2}}-B)\,\tan b\\[2pt]&=\cos({\tfrac {\pi }{2}}-c)\,\cos({\tfrac {\pi }{2}}-A)\\[2pt]&=\cot B\,\tan b\\[4pt]&=\sin c\,\sin A.\end{aligned}}}$$$${\displaystyle {\begin{alignedat}{4}&{\text{(R1)}}&\qquad \cos c&=\cos a\,\cos b,&\qquad \qquad &{\text{(R6)}}&\qquad \tan b&=\cos A\,\tan c,\\&{\text{(R2)}}&\sin a&=\sin A\,\sin c,&&{\text{(R7)}}&\tan a&=\cos B\,\tan c,\\&{\text{(R3)}}&\sin b&=\sin B\,\sin c,&&{\text{(R8)}}&\cos A&=\sin B\,\cos a,\\&{\text{(R4)}}&\tan a&=\tan A\,\sin b,&&{\text{(R9)}}&\cos B&=\sin A\,\cos b,\\&{\text{(R5)}}&\tan b&=\tan B\,\sin a,&&{\text{(R10)}}&\cos c&=\cot A\,\cot B.\end{alignedat}}}$$

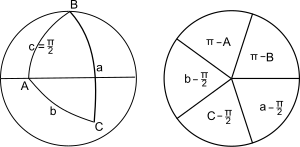
Un triángulo esférico cuadrantal se define como un triángulo esférico en el que uno de los lados subtiende un ángulo de π /2 radianes en el centro de la esfera: en la esfera unitaria el lado tiene una longitud de π /2. En el caso de que el lado c tenga una longitud de π /2 en la esfera unitaria, las ecuaciones que rigen los lados y ángulos restantes se pueden obtener aplicando las reglas para el triángulo esférico rectángulo de la sección anterior al triángulo polar △ A'B'C' con lados a', b', c' tales que A' = π − a , a' = π − A etc. Los resultados son:$${\displaystyle {\begin{alignedat}{4}&{\text{(Q1)}}&\qquad \cos C&=-\cos A\,\cos B,&\qquad \qquad &{\text{(Q6)}}&\qquad \tan B&=-\cos a\,\tan C,\\&{\text{(Q2)}}&\sin A&=\sin a\,\sin C,&&{\text{(Q7)}}&\tan A&=-\cos b\,\tan C,\\&{\text{(Q3)}}&\sin B&=\sin b\,\sin C,&&{\text{(Q8)}}&\cos a&=\sin b\,\cos A,\\&{\text{(Q4)}}&\tan A&=\tan a\,\sin B,&&{\text{(Q9)}}&\cos b&=\sin a\,\cos B,\\&{\text{(Q5)}}&\tan B&=\tan b\,\sin A,&&{\text{(Q10)}}&\cos C&=-\cot a\,\cot b.\end{alignedat}}}$$

Sustituyendo la segunda regla del coseno en la primera y simplificando obtenemos: Cancelando el factor de sen c obtenemos$${\displaystyle {\begin{aligned}\cos a&=(\cos a\,\cos c+\sin a\,\sin c\,\cos B)\cos c+\sin b\,\sin c\,\cos A\\[4pt]\cos a\,\sin ^{2}c&=\sin a\,\cos c\,\sin c\,\cos B+\sin b\,\sin c\,\cos A\end{aligned}}}$$$${\displaystyle \cos a\sin c=\sin a\,\cos c\,\cos B+\sin b\,\cos A}$$

Sustituciones similares en otras fórmulas de coseno y coseno suplementario dan lugar a una gran variedad de reglas de cinco partes. Se utilizan raramente.

Al multiplicar la primera regla del coseno por cos A se obtiene De manera similar, al multiplicar la primera regla suplementaria del coseno por cos a se obtiene Restando los dos y notando que se sigue de las reglas del seno que produce la ecuación de Cagnoli , que es una relación entre las seis partes del triángulo esférico. ^[9]$${\displaystyle \cos a\cos A=\cos b\,\cos c\,\cos A+\sin b\,\sin c-\sin b\,\sin c\,\sin ^{2}A.}$$$${\displaystyle \cos a\cos A=-\cos B\,\cos C\,\cos a+\sin B\,\sin C-\sin B\,\sin C\,\sin ^{2}a.}$$${\displaystyle \sin b\,\sin c\,\sin ^{2}A=\sin B\,\sin C\,\sin ^{2}a}$$${\displaystyle \sin b\,\sin c+\cos b\,\cos c\,\cos A=\sin B\,\sin C-\cos B\,\cos C\,\cos a}$$

La solución de triángulos es el objetivo principal de la trigonometría esférica: dados tres, cuatro o cinco elementos del triángulo, determinar los demás. El caso de cinco elementos dados es trivial, y requiere sólo una única aplicación de la regla del seno. Para cuatro elementos dados hay un caso no trivial, que se analiza a continuación. Para tres elementos dados hay seis casos: tres lados, dos lados y un ángulo incluido u opuesto, dos ángulos y un lado incluido u opuesto, o tres ángulos. (El último caso no tiene análogo en la trigonometría plana). Ningún método único resuelve todos los casos. La figura siguiente muestra los siete casos no triviales: en cada caso, los lados dados están marcados con una barra transversal y los ángulos dados con un arco. (Los elementos dados también se enumeran debajo del triángulo). En la notación resumida aquí, como ALA, A se refiere a un ángulo dado y S se refiere a un lado dado, y la secuencia de A y S en la notación se refiere a la secuencia correspondiente en el triángulo.

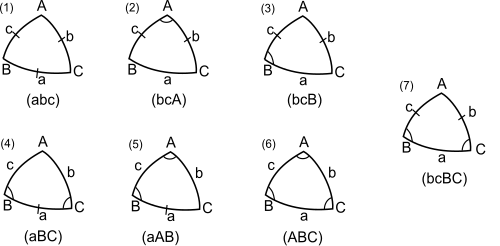
• Caso 1: se dan tres lados (SSS). Se puede utilizar la regla del coseno para obtener los ángulos A , B y C , pero, para evitar ambigüedades, se prefieren las fórmulas de los ángulos medios.
• Caso 2: se dan dos lados y un ángulo incluido (LSC). La regla del coseno da un y entonces volvemos al caso 1.
• Caso 3: se dan dos lados y un ángulo opuesto (SSA). La regla del seno da C y entonces tenemos el caso 7. Hay una o dos soluciones.
• Caso 4: se dan dos ángulos y un lado incluido (ALA). Las fórmulas de cotangente de cuatro partes para los conjuntos ( cBaC ) y ( BaCb ) dan c y b , luego A se deduce de la regla del seno.
• Caso 5: se dan dos ángulos y un lado opuesto (AAL). La regla del seno da b y entonces tenemos el caso 7 (rotado). Hay una o dos soluciones.
• Caso 6: se dan tres ángulos (AAA). Se puede utilizar la regla suplementaria del coseno para obtener los lados a , b y c , pero, para evitar ambigüedades, se prefieren las fórmulas de los medios lados.
• Caso 7: se dan dos ángulos y dos lados opuestos (SSAA). Utilice las analogías de Napier para a y A ; o utilice el caso 3 (SSA) o el caso 5 (AAS).

Los métodos de solución que se enumeran aquí no son las únicas opciones posibles: existen muchas otras. En general, es mejor elegir métodos que eviten tomar un seno inverso debido a la posible ambigüedad entre un ángulo y su suplemento. El uso de fórmulas de semiángulos suele ser aconsejable porque los semiángulos serán menores que π /2 y, por lo tanto, estarán libres de ambigüedad. Hay una discusión completa en Todhunter. El artículo Solución de triángulos#Resolución de triángulos esféricos presenta variantes de estos métodos con una notación ligeramente diferente.

Hay una discusión completa de la solución de triángulos oblicuos en Todhunter. ^{[1] : Cap. VI} Véase también la discusión en Ross. ^[10] Nasir al-Din al-Tusi fue el primero en enumerar los seis casos distintos (2-7 en el diagrama) de un triángulo rectángulo en trigonometría esférica. ^[11]

Otro enfoque es dividir el triángulo en dos triángulos rectángulos. Por ejemplo, tomemos el ejemplo del Caso 3 donde se dan b , c y B . Construya el círculo máximo desde A que sea normal al lado BC en el punto D . Use las reglas de Napier para resolver el triángulo △ ABD : use c y B para encontrar los lados AD y BD y el ángulo ∠ BAD . Luego use las reglas de Napier para resolver el triángulo △ ACD : es decir, use AD y b para encontrar el lado DC y los ángulos C y ∠ DAC . El ángulo A y el lado a se obtienen por adición.

No todas las reglas obtenidas son numéricamente robustas en ejemplos extremos, por ejemplo, cuando un ángulo se acerca a cero o  a π . Es posible que haya que examinar los problemas y las soluciones con cuidado, en particular cuando se escribe código para resolver un triángulo arbitrario.

Consideremos un polígono esférico de N lados y sea A _n el n -ésimo ángulo interior. El área de dicho polígono está dada por (Todhunter, ^[1] Art.99)$${\displaystyle {{\text{Area of polygon}} \atop {\text{(on the unit sphere)}}}\equiv E_{N}=\left(\sum _{n=1}^{N}A_{n}\right)-(N-2)\pi .}$$

Para el caso de un triángulo esférico con ángulos A , B y C, esto se reduce al teorema de Girard , donde E es la cantidad en la que la suma de los ángulos excede π radianes, llamado exceso esférico del triángulo. Este teorema recibe su nombre de su autor, Albert Girard . ^[12] Una prueba anterior fue derivada, pero no publicada, por el matemático inglés Thomas Harriot . En una esfera de radio R, ambas expresiones de área anteriores se multiplican por R ^2. La definición del exceso es independiente del radio de la esfera.$${\displaystyle {{\text{Area of triangle}} \atop {\text{(on the unit sphere)}}}\equiv E=E_{3}=A+B+C-\pi ,}$$

El resultado inverso puede escribirse como

$${\displaystyle A+B+C=\pi +{\frac {4\pi \times {\text{Area of triangle}}}{\text{Area of the sphere}}}.}$$

Como el área de un triángulo no puede ser negativa, el exceso esférico siempre es positivo. No es necesariamente pequeño, porque la suma de los ángulos puede alcanzar 5 π (3 π para ángulos propios ). Por ejemplo, un octante de una esfera es un triángulo esférico con tres ángulos rectos, de modo que el exceso es π /2. En aplicaciones prácticas, a menudo es pequeño: por ejemplo, los triángulos de los estudios geodésicos suelen tener un exceso esférico mucho menor que 1' de arco. ^[13] En la Tierra, el exceso de un triángulo equilátero con lados de 21,3 km (y área de 393 km ² ) es aproximadamente 1 segundo de arco.

Existen muchas fórmulas para el exceso. Por ejemplo, Todhunter, ^[1] (Art.101—103) da diez ejemplos incluyendo el de L'Huilier : donde$${\displaystyle \tan {\tfrac {1}{4}}E={\sqrt {\tan {\tfrac {1}{2}}s\,\tan {\tfrac {1}{2}}(s-a)\,\tan {\tfrac {1}{2}}(s-b)\,\tan {\tfrac {1}{2}}(s-c)}}}$$${\displaystyle s={\tfrac {1}{2}}(a+b+c)}$

Debido a que algunos triángulos están mal caracterizados por sus aristas (por ejemplo, si ), a menudo es mejor utilizar la fórmula para el exceso en términos de dos aristas y su ángulo incluido.${\textstyle a=b\approx {\frac {1}{2}}c}$$${\displaystyle \tan {\tfrac {1}{2}}E={\frac {\tan {\frac {1}{2}}a\tan {\frac {1}{2}}b\sin C}{1+\tan {\frac {1}{2}}a\tan {\frac {1}{2}}b\cos C}}.}$$

Cuando el triángulo △ ABC es un triángulo rectángulo con ángulo recto en C , entonces cos C = 0 y sen C = 1 , por lo que esto se reduce a$${\displaystyle \tan {\tfrac {1}{2}}E=\tan {\tfrac {1}{2}}a\tan {\tfrac {1}{2}}b.}$$

El déficit de ángulo se define de manera similar para la geometría hiperbólica .

El exceso esférico de un cuadrángulo esférico limitado por el ecuador, los dos meridianos de longitudes y y el arco de círculo máximo entre dos puntos con longitud y latitud y es${\displaystyle \lambda _{1}}$${\displaystyle \lambda _{2},}$${\displaystyle (\lambda _{1},\varphi _{1})}$${\displaystyle (\lambda _{2},\varphi _{2})}$$${\displaystyle \tan {\tfrac {1}{2}}E_{4}={\frac {\sin {\tfrac {1}{2}}(\varphi _{2}+\varphi _{1})}{\cos {\tfrac {1}{2}}(\varphi _{2}-\varphi _{1})}}\tan {\tfrac {1}{2}}(\lambda _{2}-\lambda _{1}).}$$

Este resultado se obtiene a partir de una de las analogías de Napier. En el límite donde son todos pequeños, esto se reduce al área trapezoidal conocida, .${\displaystyle \varphi _{1},\varphi _{2},\lambda _{2}-\lambda _{1}}$${\textstyle E_{4}\approx {\frac {1}{2}}(\varphi _{2}+\varphi _{1})(\lambda _{2}-\lambda _{1})}$

El área de un polígono se puede calcular a partir de cuadrángulos individuales del tipo mencionado anteriormente, a partir de (análogamente) un triángulo individual delimitado por un segmento del polígono y dos meridianos, ^[14] mediante una línea integral con el teorema de Green , ^[15] o mediante una proyección de áreas iguales como se hace comúnmente en SIG. Los otros algoritmos también se pueden utilizar con las longitudes de los lados calculadas utilizando una fórmula de distancia de círculo máximo .

• Navegación aérea
• Navegación celestial
• Trigonometría elipsoidal
• Distancia del círculo máximo o distancia esférica
• Esfera de Lenart
• Triángulo de Schwarz
• Geometría esférica
• Poliedro esférico
• Triangulación (topografía)

• Weisstein, Eric W. "Trigonometría esférica". MathWorld .una lista más completa de identidades, con algunas derivaciones
• Weisstein, Eric W. "Triángulo esférico". MathWorld .una lista más completa de identidades, con algunas derivaciones
• TriSph Un software libre para resolver los triángulos esféricos, configurable para diferentes aplicaciones prácticas y configurado para gnomónicos.
• "Revisiting Spherical Trigonometry with Orthogonal Projectors" (Revisitando la trigonometría esférica con proyectores ortogonales) de Sudipto Banerjee. El artículo deriva la ley esférica de los cosenos y la ley de los senos utilizando álgebra lineal elemental y matrices de proyección.
• "Una prueba visual del teorema de Girard". Proyecto de demostraciones Wolfram .Por Okay Arik
• "El libro de instrucción sobre planos desviados y planos simples", un manuscrito en árabe que data de 1740 y habla sobre trigonometría esférica, con diagramas
• Algunos algoritmos para polígonos en una esfera Robert G. Chamberlain, William H. Duquette, Laboratorio de Propulsión a Chorro. El artículo desarrolla y explica muchas fórmulas útiles, quizás con un enfoque en la navegación y la cartografía.
• Cálculo en línea de triángulos esféricos