Tunelaje cuántico

Parte de una serie de artículos sobre
Mecánica cuántica
${\displaystyle i\hbar {\frac {d}{dt}}|\Psi \rangle ={\hat {H}}|\Psi \rangle }$ Ecuación de Schrödinger
Introducción Glosario Historia
Fondo Mecánica clásica Antigua teoría cuántica Notación de corchetes Hamiltoniano Interferencia
Fundamentos Complementariedad Decoherencia Enredo Nivel de energía Medición No localidad Quantum number State Superposition Symmetry Tunnelling Uncertainty Wave function Collapse
Experiments Bell's inequality CHSH inequality Davisson–Germer Double-slit Elitzur–Vaidman Franck–Hertz Leggett inequality Leggett–Garg inequality Mach–Zehnder Popper Quantum eraser Delayed-choice Schrödinger's cat Stern–Gerlach Wheeler's delayed-choice
Formulations Overview Heisenberg Interaction Matrix Phase-space Schrödinger Sum-over-histories (path integral)
Equations Dirac Klein–Gordon Pauli Rydberg Schrödinger
Interpretations Bayesian Consistent histories Copenhagen de Broglie–Bohm Ensemble Hidden-variable Local Superdeterminism Many-worlds Objective-collapse Quantum logic Relational Transactional Von Neumann–Wigner
Advanced topics Relativistic quantum mechanics Quantum field theory Quantum information science Quantum computing Quantum chaos EPR paradox Density matrix Scattering theory Quantum statistical mechanics Quantum machine learning
Scientists Aharonov Bell Bethe Blackett Bloch Bohm Bohr Born Bose de Broglie Compton Dirac Davisson Debye Ehrenfest Einstein Everett Fock Fermi Feynman Glauber Gutzwiller Heisenberg Hilbert Jordan Kramers Lamb Landau Laue Moseley Millikan Onnes Pauli Planck Rabi Raman Rydberg Schrödinger Simmons Sommerfeld von Neumann Weyl Wien Wigner Zeeman Zeilinger
v t e

En física, el efecto túnel cuántico , penetración de barrera o simplemente tunelización es un fenómeno mecánico cuántico en el que un objeto, como un electrón o un átomo, pasa a través de una barrera de energía potencial que, según la mecánica clásica , no debería ser transitable debido a que el objeto no tiene suficiente energía para pasar o superar la barrera.

El efecto túnel es una consecuencia de la naturaleza ondulatoria de la materia , donde la función de onda cuántica describe el estado de una partícula u otro sistema físico , y las ecuaciones de onda como la ecuación de Schrödinger describen su comportamiento. La probabilidad de transmisión de un paquete de ondas a través de una barrera disminuye exponencialmente con la altura de la barrera, el ancho de la barrera y la masa de la partícula que realiza el efecto túnel, por lo que el efecto túnel se observa más prominentemente en partículas de baja masa, como electrones o protones, que atraviesan barreras microscópicamente estrechas. El efecto túnel es fácilmente detectable con barreras de espesor de aproximadamente 1 a 3 nm o más pequeñas para electrones, y aproximadamente 0,1 nm o más pequeñas para partículas más pesadas, como protones o átomos de hidrógeno. ^[1] Algunas fuentes describen la mera penetración de una función de onda en la barrera, sin transmisión al otro lado, como un efecto túnel, como en el caso del efecto túnel en las paredes de un pozo de potencial finito . ^{[2] [3]}

La tunelización desempeña un papel esencial en fenómenos físicos como la fusión nuclear ^[4] y la desintegración radiactiva alfa de los núcleos atómicos. Las aplicaciones de la tunelización incluyen el diodo túnel , ^[5] la computación cuántica , la memoria flash y el microscopio de efecto túnel de barrido . La tunelización limita el tamaño mínimo de los dispositivos utilizados en microelectrónica porque los electrones atraviesan fácilmente capas aislantes y transistores que son más delgados que aproximadamente 1 nm. ^[6]

El efecto fue predicho a principios del siglo XX y su aceptación como fenómeno físico general llegó a mediados de siglo. ^[7]

El efecto túnel cuántico se enmarca en el campo de la mecánica cuántica . Para comprender el fenómeno , las partículas que intentan atravesar una barrera de potencial pueden compararse con una pelota que intenta rodar por una colina. La mecánica cuántica y la mecánica clásica difieren en su tratamiento de este escenario.

La mecánica clásica predice que las partículas que no tienen suficiente energía para superar una barrera de manera clásica no pueden llegar al otro lado. Por lo tanto, una pelota sin suficiente energía para superar la colina rodaría hacia abajo. En mecánica cuántica, una partícula puede, con una pequeña probabilidad, atravesar la barrera a través de un túnel. La razón de esta diferencia proviene de tratar la materia como si tuviera propiedades de ondas y partículas .

La función de onda de un sistema físico de partículas especifica todo lo que se puede saber sobre el sistema. ^[8] Por lo tanto, los problemas de mecánica cuántica analizan la función de onda del sistema. Utilizando formulaciones matemáticas, como la ecuación de Schrödinger , se puede deducir la evolución temporal de una función de onda conocida. El cuadrado del valor absoluto de esta función de onda está directamente relacionado con la distribución de probabilidad de las posiciones de las partículas, que describe la probabilidad de que las partículas se midan en esas posiciones.

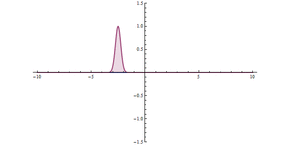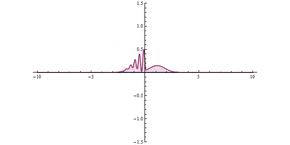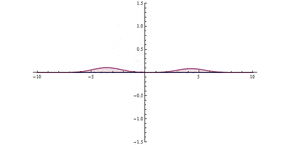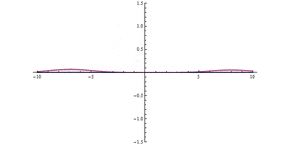
Como se muestra en la animación, un paquete de ondas choca contra la barrera, la mayor parte se refleja y una parte se transmite a través de ella. El paquete de ondas se deslocaliza más: ahora está a ambos lados de la barrera y tiene una amplitud máxima menor, pero es igual en magnitud cuadrada integrada, lo que significa que la probabilidad de que la partícula esté en algún lugar sigue siendo la unidad. Cuanto más ancha sea la barrera y mayor sea su energía, menor será la probabilidad de que se produzca un efecto túnel.

Algunos modelos de una barrera de tunelaje, como las barreras rectangulares mostradas, pueden analizarse y resolverse algebraicamente. ^{[9] : 96} La mayoría de los problemas no tienen una solución algebraica, por lo que se utilizan soluciones numéricas. Los " métodos semiclásicos " ofrecen soluciones aproximadas que son más fáciles de calcular, como la aproximación WKB .

La ecuación de Schrödinger se publicó en 1926. La primera persona en aplicar la ecuación de Schrödinger a un problema que implicaba la tunelización entre dos regiones clásicamente permitidas a través de una barrera de potencial fue Friedrich Hund en una serie de artículos publicados en 1927. Estudió las soluciones de un potencial de doble pozo y analizó los espectros moleculares . ^[10] Leonid Mandelstam y Mikhail Leontovich descubrieron la tunelización de forma independiente y publicaron sus resultados en 1928. ^[11]

En 1927, Lothar Nordheim , asistido por Ralph Fowler , publicó un artículo que analizaba la emisión termoiónica y la reflexión de electrones de los metales. Supuso una barrera de potencial de superficie que confina los electrones dentro del metal y demostró que los electrones tienen una probabilidad finita de atravesar o reflejarse en la barrera de superficie cuando sus energías están cerca de la energía de la barrera. Clásicamente, el electrón transmitiría o reflejaría con un 100% de certeza, dependiendo de su energía. En 1928, J. Robert Oppenheimer publicó dos artículos sobre la emisión de campo , es decir, la emisión de electrones inducida por campos eléctricos fuertes. Nordheim y Fowler simplificaron la derivación de Oppenheimer y encontraron valores para las corrientes emitidas y las funciones de trabajo que concordaban con los experimentos. ^[10]

Un gran éxito de la teoría del efecto túnel fue la explicación matemática de la desintegración alfa , que fue desarrollada en 1928 por George Gamow e independientemente por Ronald Gurney y Edward Condon . ^{[12] [13] [14] [15]} Estos últimos investigadores resolvieron simultáneamente la ecuación de Schrödinger para un potencial nuclear modelo y derivaron una relación entre la vida media de la partícula y la energía de emisión que dependía directamente de la probabilidad matemática del efecto túnel. Los tres investigadores estaban familiarizados con los trabajos sobre emisión de campo, ^[10] y Gamow estaba al tanto de los hallazgos de Mandelstam y Leontovich. ^[16]

En los primeros tiempos de la teoría cuántica, no se utilizaba el término efecto túnel , sino que se hacía referencia al efecto como penetración o fuga a través de una barrera. El término alemán wellenmechanische Tunneleffekt fue utilizado en 1931 por Walter Schottky. ^[10] El término inglés efecto túnel entró en el lenguaje en 1932 cuando fue utilizado por Yakov Frenkel en su libro de texto. ^[10]

En 1957, Leo Esaki demostró el efecto túnel de los electrones sobre una barrera de unos pocos nanómetros de ancho en una estructura semiconductora y desarrolló un diodo basado en el efecto túnel. ^[17] En 1960, siguiendo el trabajo de Esaki, Ivar Giaever demostró experimentalmente que el efecto túnel también tenía lugar en superconductores . El espectro de efecto túnel proporcionó evidencia directa de la brecha de energía superconductora . En 1962, Brian Josephson predijo el efecto túnel de los pares de Cooper superconductores. Esaki, Giaever y Josephson compartieron el Premio Nobel de Física de 1973 por sus trabajos sobre el efecto túnel cuántico en sólidos. ^{[18] [7]}

En 1981, Gerd Binnig y Heinrich Rohrer desarrollaron un nuevo tipo de microscopio, llamado microscopio de efecto túnel , que se basa en el efecto túnel y se utiliza para obtener imágenes de superficies a nivel atómico . Binnig y Rohrer recibieron el Premio Nobel de Física en 1986 por su descubrimiento. ^[19]

La tunelización es la causa de algunos fenómenos físicos macroscópicos importantes.

La tunelización es una fuente de fuga de corriente en la electrónica de integración a muy gran escala (VLSI) y da como resultado un consumo de energía sustancial y efectos de calentamiento que afectan a dichos dispositivos. Se considera el límite inferior en cuanto a cómo se pueden fabricar los elementos de los dispositivos microelectrónicos. ^[20] La tunelización es una técnica fundamental que se utiliza para programar las puertas flotantes de la memoria flash .

La emisión fría de electrones es relevante para la física de semiconductores y superconductores . Es similar a la emisión termoiónica , donde los electrones saltan aleatoriamente de la superficie de un metal para seguir un sesgo de voltaje porque estadísticamente terminan con más energía que la barrera, a través de colisiones aleatorias con otras partículas. Cuando el campo eléctrico es muy grande, la barrera se vuelve lo suficientemente delgada como para que los electrones salgan del estado atómico por efecto túnel, lo que genera una corriente que varía aproximadamente exponencialmente con el campo eléctrico. ^[21] Estos materiales son importantes para la memoria flash, los tubos de vacío y algunos microscopios electrónicos.

Se puede crear una barrera sencilla separando dos conductores con un aislante muy fino . Se trata de uniones túnel, cuyo estudio requiere comprender el efecto túnel cuántico. ^[22] Las uniones Josephson aprovechan el efecto túnel cuántico y la superconductividad para crear el efecto Josephson . Esto tiene aplicaciones en mediciones de precisión de voltajes y campos magnéticos , ^[21] así como en la célula solar multiunión .

Los diodos son dispositivos semiconductores eléctricos que permiten que la corriente eléctrica fluya en una dirección más que en la otra. El dispositivo depende de una capa de agotamiento entre los semiconductores de tipo N y tipo P para cumplir su propósito. Cuando estos están muy dopados, la capa de agotamiento puede ser lo suficientemente delgada para la tunelización. Cuando se aplica una pequeña polarización directa, la corriente debido a la tunelización es significativa. Esto tiene un máximo en el punto donde la polarización de voltaje es tal que el nivel de energía de las bandas de conducción p y n son iguales. A medida que aumenta la polarización de voltaje, las dos bandas de conducción ya no se alinean y el diodo actúa de manera típica. ^[23]

Debido a que la corriente de tunelización disminuye rápidamente, se pueden crear diodos de tunelización que tienen un rango de voltajes para los cuales la corriente disminuye a medida que el voltaje aumenta. Esta propiedad peculiar se utiliza en algunas aplicaciones, como dispositivos de alta velocidad donde la probabilidad de tunelización característica cambia tan rápidamente como el voltaje de polarización. ^[23]

El diodo de efecto túnel resonante utiliza el efecto túnel cuántico de una manera muy diferente para lograr un resultado similar. Este diodo tiene un voltaje resonante para el cual una corriente favorece un voltaje particular, que se logra colocando dos capas delgadas con una banda de conductancia de alta energía cerca una de la otra. Esto crea un pozo de potencial cuántico que tiene un nivel de energía más bajo discreto . Cuando este nivel de energía es más alto que el de los electrones, no se produce efecto túnel y el diodo está en polarización inversa. Una vez que las dos energías de voltaje se alinean, los electrones fluyen como un cable abierto. A medida que el voltaje aumenta aún más, el efecto túnel se vuelve improbable y el diodo actúa como un diodo normal nuevamente antes de que se note un segundo nivel de energía. ^[24]

Un proyecto de investigación europeo demostró transistores de efecto de campo en los que la compuerta (canal) se controla mediante tunelización cuántica en lugar de inyección térmica, lo que reduce el voltaje de la compuerta de aproximadamente 1 voltio a 0,2 voltios y reduce el consumo de energía hasta en 100 veces. Si estos transistores se pueden ampliar a chips VLSI , mejorarían el rendimiento por potencia de los circuitos integrados . ^{[25] [26]}

Si bien el modelo de conductividad eléctrica de Drude-Lorentz hace excelentes predicciones sobre la naturaleza de los electrones que conducen en los metales, se puede profundizar utilizando el efecto túnel cuántico para explicar la naturaleza de las colisiones de los electrones. ^[21] Cuando un paquete de ondas de electrones libres encuentra una larga matriz de barreras espaciadas uniformemente , la parte reflejada del paquete de ondas interfiere uniformemente con la transmitida entre todas las barreras de modo que se hace posible la transmisión del 100%. La teoría predice que si los núcleos cargados positivamente forman una matriz perfectamente rectangular, los electrones atravesarán el metal como electrones libres, lo que dará lugar a una conductancia extremadamente alta , y que las impurezas en el metal la interrumpirán. ^[21]

El microscopio de efecto túnel de barrido (STM), inventado por Gerd Binnig y Heinrich Rohrer , puede permitir la obtención de imágenes de átomos individuales en la superficie de un material. ^[21] Funciona aprovechando la relación entre el efecto túnel cuántico y la distancia. Cuando la punta de la aguja del STM se acerca a una superficie de conducción que tiene un sesgo de voltaje, la medición de la corriente de electrones que están haciendo efecto túnel entre la aguja y la superficie revela la distancia entre la aguja y la superficie. Al utilizar varillas piezoeléctricas que cambian de tamaño cuando se aplica voltaje, la altura de la punta se puede ajustar para mantener constante la corriente de efecto túnel. Los voltajes variables en el tiempo que se aplican a estas varillas se pueden registrar y utilizar para obtener imágenes de la superficie del conductor. ^[21] Los STM tienen una precisión de 0,001 nm, o aproximadamente el 1 % del diámetro atómico. ^[24]

El efecto túnel cuántico es un fenómeno esencial para la fusión nuclear. La temperatura en los núcleos estelares es generalmente insuficiente para permitir que los núcleos atómicos superen la barrera de Coulomb y logren la fusión termonuclear . El efecto túnel cuántico aumenta la probabilidad de atravesar esta barrera. Aunque esta probabilidad todavía es baja, la cantidad extremadamente grande de núcleos en el núcleo de una estrella es suficiente para mantener una reacción de fusión constante. ^[27]

La desintegración radiactiva es el proceso de emisión de partículas y energía desde el núcleo inestable de un átomo para formar un producto estable. Esto se hace mediante la tunelización de una partícula fuera del núcleo (la tunelización de un electrón hacia el núcleo se denomina captura de electrones ). Esta fue la primera aplicación de la tunelización cuántica. La desintegración radiactiva es un tema relevante para la astrobiología , ya que esta consecuencia de la tunelización cuántica crea una fuente de energía constante durante un gran intervalo de tiempo para entornos fuera de la zona habitable circunestelar donde la insolación no sería posible ( océanos subterráneos ) o efectiva. ^[27]

La tunelización cuántica puede ser uno de los mecanismos de la hipotética desintegración de protones . ^{[28] [29]}

Las reacciones químicas en el medio interestelar ocurren a energías extremadamente bajas. Probablemente la reacción ion-molécula más fundamental involucra iones de hidrógeno con moléculas de hidrógeno. La tasa de tunelización mecánica cuántica para la misma reacción usando el isótopo de hidrógeno deuterio , D ^- + H ₂ → H ^- + HD, se ha medido experimentalmente en una trampa de iones. El deuterio se colocó en una trampa de iones y se enfrió. Luego, la trampa se llenó con hidrógeno. A las temperaturas utilizadas en el experimento, la barrera de energía para la reacción no permitiría que la reacción tuviera éxito con la dinámica clásica únicamente. La tunelización cuántica permitió que las reacciones ocurrieran en raras colisiones. Se calculó a partir de los datos experimentales que las colisiones ocurrieron una en cien mil millones. ^[30]

En cinética química , la sustitución de un isótopo ligero de un elemento por uno más pesado suele dar como resultado una velocidad de reacción más lenta. Esto se atribuye generalmente a las diferencias en las energías vibracionales del punto cero para los enlaces químicos que contienen los isótopos más ligeros y más pesados ​​y generalmente se modela utilizando la teoría del estado de transición . Sin embargo, en ciertos casos, se observan grandes efectos isotópicos que no se pueden explicar con un tratamiento semiclásico y se requiere un efecto túnel cuántico. RP Bell desarrolló un tratamiento modificado de la cinética de Arrhenius que se utiliza comúnmente para modelar este fenómeno. ^[31]

Al incluir la tunelización cuántica, se pueden explicar las síntesis astroquímicas de varias moléculas en las nubes interestelares , como la síntesis de hidrógeno molecular , agua ( hielo ) y el importante prebiótico formaldehído . ^[27] La ​​tunelización del hidrógeno molecular se ha observado en el laboratorio. ^[32]

La tunelización cuántica es uno de los efectos cuánticos no triviales centrales en la biología cuántica . ^[33] Aquí es importante tanto como tunelización de electrones como de protones . La tunelización de electrones es un factor clave en muchas reacciones redox bioquímicas ( fotosíntesis , respiración celular ), así como en la catálisis enzimática. La tunelización de protones es un factor clave en la mutación espontánea del ADN . ^[27]

La mutación espontánea ocurre cuando la replicación normal del ADN tiene lugar después de que un protón particularmente significativo haya realizado un túnel. ^[34] Un enlace de hidrógeno une pares de bases de ADN. Un potencial de doble pozo a lo largo de un enlace de hidrógeno separa una barrera de energía potencial. Se cree que el potencial de doble pozo es asimétrico, con un pozo más profundo que el otro, de modo que el protón normalmente descansa en el pozo más profundo. Para que ocurra una mutación, el protón debe haber realizado un túnel hacia el pozo más superficial. El movimiento del protón desde su posición normal se denomina transición tautomérica . Si la replicación del ADN tiene lugar en este estado, la regla de apareamiento de bases para el ADN puede verse comprometida, lo que provoca una mutación. ^[35] Per-Olov Lowdin fue el primero en desarrollar esta teoría de mutación espontánea dentro de la doble hélice . Se cree que otros casos de mutaciones inducidas por túneles cuánticos en biología son una causa del envejecimiento y el cáncer. ^[36]

La ecuación de Schrödinger independiente del tiempo para una partícula en una dimensión se puede escribir como o donde$${\displaystyle -{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}}{dx^{2}}}\Psi (x)+V(x)\Psi (x)=E\Psi (x)}$$$${\displaystyle {\frac {d^{2}}{dx^{2}}}\Psi (x)={\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right)\Psi (x)\equiv {\frac {2m}{\hbar ^{2}}}M(x)\Psi (x),}$$

• ${\displaystyle \hbar }$es la constante de Planck reducida ,
• m es la masa de la partícula,
• x representa la distancia medida en la dirección del movimiento de la partícula,
• Ψ es la función de onda de Schrödinger,
• V es la energía potencial de la partícula (medida en relación con cualquier nivel de referencia conveniente),
• E es la energía de la partícula que está asociada con el movimiento en el eje x (medida en relación con V ),
• M ( x ) es una cantidad definida por V ( x ) − E , que no tiene un nombre aceptado en física.

Las soluciones de la ecuación de Schrödinger toman formas diferentes para diferentes valores de x , dependiendo de si M ( x ) es positivo o negativo. Cuando M ( x ) es constante y negativo, entonces la ecuación de Schrödinger puede escribirse en la forma$${\displaystyle {\frac {d^{2}}{dx^{2}}}\Psi (x)={\frac {2m}{\hbar ^{2}}}M(x)\Psi (x)=-k^{2}\Psi (x),\qquad {\text{where}}\quad k^{2}=-{\frac {2m}{\hbar ^{2}}}M.}$$

Las soluciones de esta ecuación representan ondas viajeras, con constante de fase + k o − k . Alternativamente, si M ( x ) es constante y positiva, entonces la ecuación de Schrödinger puede escribirse en la forma$${\displaystyle {\frac {d^{2}}{dx^{2}}}\Psi (x)={\frac {2m}{\hbar ^{2}}}M(x)\Psi (x)={\kappa }^{2}\Psi (x),\qquad {\text{where}}\quad {\kappa }^{2}={\frac {2m}{\hbar ^{2}}}M.}$$

Las soluciones de esta ecuación son exponenciales ascendentes y descendentes en forma de ondas evanescentes . Cuando M ( x ) varía con la posición, se produce la misma diferencia de comportamiento, dependiendo de si M ( x ) es negativo o positivo. De ello se deduce que el signo de M ( x ) determina la naturaleza del medio, correspondiendo M ( x ) negativo al medio A y M ( x ) positivo al medio B. Por tanto, se deduce que puede producirse un acoplamiento de ondas evanescentes si una región de M ( x ) positivo está intercalada entre dos regiones de M ( x ) negativo , creando así una barrera de potencial.

El tratamiento matemático de la situación en la que M ( x ) varía con x es difícil, excepto en casos especiales que normalmente no corresponden a la realidad física. Un tratamiento matemático completo aparece en la monografía de 1965 de Fröman y Fröman. Sus ideas no se han incorporado a los libros de texto de física, pero sus correcciones tienen poco efecto cuantitativo.

La función de onda se expresa como la exponencial de una función: donde luego se separa en partes reales e imaginarias: donde A ( x ) y B ( x ) son funciones de valor real.$${\displaystyle \Psi (x)=e^{\Phi (x)},}$$$${\displaystyle \Phi ''(x)+\Phi '(x)^{2}={\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right).}$$${\displaystyle \Phi '(x)}$$${\displaystyle \Phi '(x)=A(x)+iB(x),}$$

Sustituyendo la segunda ecuación en la primera y utilizando el hecho de que la parte imaginaria debe ser 0, obtenemos:

$${\displaystyle A'(x)+A(x)^{2}-B(x)^{2}={\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right).}$$

Para resolver esta ecuación utilizando la aproximación semiclásica, cada función debe expandirse como una serie de potencias en . A partir de las ecuaciones, la serie de potencias debe comenzar con al menos un orden de para satisfacer la parte real de la ecuación; para un buen límite clásico es preferible comenzar con la potencia más alta posible de la constante de Planck , lo que conduce a y con las siguientes restricciones en los términos de orden más bajo, y${\displaystyle \hbar }$${\displaystyle \hbar ^{-1}}$$${\displaystyle A(x)={\frac {1}{\hbar }}\sum _{k=0}^{\infty }\hbar ^{k}A_{k}(x)}$$$${\displaystyle B(x)={\frac {1}{\hbar }}\sum _{k=0}^{\infty }\hbar ^{k}B_{k}(x),}$$$${\displaystyle A_{0}(x)^{2}-B_{0}(x)^{2}=2m\left(V(x)-E\right)}$$$${\displaystyle A_{0}(x)B_{0}(x)=0.}$$

En este punto se pueden considerar dos casos extremos.

Caso 1

Si la amplitud varía lentamente en comparación con la fase y corresponde al movimiento clásico, al resolver el siguiente orden de expansión se obtiene${\displaystyle A_{0}(x)=0}$$${\displaystyle B_{0}(x)=\pm {\sqrt {2m\left(E-V(x)\right)}}}$$$${\displaystyle \Psi (x)\approx C{\frac {e^{i\int dx{\sqrt {{\frac {2m}{\hbar ^{2}}}\left(E-V(x)\right)}}+\theta }}{\sqrt[{4}]{{\frac {2m}{\hbar ^{2}}}\left(E-V(x)\right)}}}}$$

Caso 2

Si la fase varía lentamente en comparación con la amplitud, lo que corresponde a la tunelización, al resolver el siguiente orden de expansión se obtiene${\displaystyle B_{0}(x)=0}$$${\displaystyle A_{0}(x)=\pm {\sqrt {2m\left(V(x)-E\right)}}}$$$${\displaystyle \Psi (x)\approx {\frac {C_{+}e^{+\int dx{\sqrt {{\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right)}}}+C_{-}e^{-\int dx{\sqrt {{\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right)}}}}{\sqrt[{4}]{{\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right)}}}}$$

En ambos casos, el denominador muestra que ambas soluciones aproximadas son malas cerca de los puntos de inflexión clásicos . Lejos de la colina de potencial, la partícula actúa de manera similar a una onda libre y oscilante; por debajo de la colina de potencial, la partícula experimenta cambios exponenciales en amplitud. Al considerar el comportamiento en estos límites y puntos de inflexión clásicos, se puede llegar a una solución global.${\displaystyle E=V(x)}$

Para empezar, se elige un punto de inflexión clásico y se expande en una serie de potencias sobre :${\displaystyle x_{1}}$${\displaystyle {\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right)}$${\displaystyle x_{1}}$$${\displaystyle {\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right)=v_{1}(x-x_{1})+v_{2}(x-x_{1})^{2}+\cdots }$$

Mantener sólo el término de primer orden garantiza la linealidad:$${\displaystyle {\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right)=v_{1}(x-x_{1}).}$$

Usando esta aproximación, la ecuación se convierte casi en una ecuación diferencial :${\displaystyle x_{1}}$$${\displaystyle {\frac {d^{2}}{dx^{2}}}\Psi (x)=v_{1}(x-x_{1})\Psi (x).}$$

Esto se puede resolver utilizando funciones de Airy como soluciones.$${\displaystyle \Psi (x)=C_{A}Ai\left({\sqrt[{3}]{v_{1}}}(x-x_{1})\right)+C_{B}Bi\left({\sqrt[{3}]{v_{1}}}(x-x_{1})\right)}$$

Tomando estas soluciones para todos los puntos de inflexión clásicos, se puede formar una solución global que vincule las soluciones límite. Dados los dos coeficientes de un lado de un punto de inflexión clásico, los dos coeficientes del otro lado de un punto de inflexión clásico se pueden determinar utilizando esta solución local para conectarlos.

Por lo tanto, las soluciones de la función Airy se transformarán asintóticamente en funciones seno, coseno y exponencial en los límites adecuados. Las relaciones entre y son y${\displaystyle C,\theta }$${\displaystyle C_{+},C_{-}}$$${\displaystyle C_{+}={\frac {1}{2}}C\cos {\left(\theta -{\frac {\pi }{4}}\right)}}$$

${\displaystyle C_{-}=-C\sin {\left(\theta -{\frac {\pi }{4}}\right)}}$

Con los coeficientes encontrados, se puede hallar la solución global. Por lo tanto, el coeficiente de transmisión para una partícula que atraviesa una única barrera de potencial es donde están los dos puntos de inflexión clásicos de la barrera de potencial.$${\displaystyle T(E)=e^{-2\int _{x_{1}}^{x_{2}}dx{\sqrt {{\frac {2m}{\hbar ^{2}}}\left[V(x)-E\right]}}},}$$${\displaystyle x_{1},x_{2}}$

Para una barrera rectangular, esta expresión se simplifica a:$${\displaystyle T(E)=e^{-2{\sqrt {{\frac {2m}{\hbar ^{2}}}(V_{0}-E)}}(x_{2}-x_{1})}.}$$

Algunos físicos han afirmado que es posible que las partículas de espín cero viajen más rápido que la velocidad de la luz cuando se produce el efecto túnel. ^[7] Esto parece violar el principio de causalidad , ya que existe un marco de referencia en el que la partícula llega antes de haber salido. En 1998, Francis E. Low revisó brevemente el fenómeno del efecto túnel de tiempo cero. ^{[37] Más recientemente,} Günter Nimtz publicó datos experimentales del tiempo de efecto túnel de fonones , fotones y electrones . ^[38] Otro experimento supervisado por AM Steinberg parece indicar que las partículas podrían producir un efecto túnel a velocidades aparentes más rápidas que la luz. ^{[39] [40]}

Otros físicos, como Herbert Winful ^[41] , cuestionaron estas afirmaciones. Winful argumentó que el paquete de ondas de una partícula que produce un efecto túnel se propaga localmente, por lo que una partícula no puede atravesar la barrera mediante un efecto túnel de manera no local. Winful también argumentó que los experimentos que supuestamente demuestran la propagación no local han sido malinterpretados. En particular, la velocidad de grupo de un paquete de ondas no mide su velocidad, sino que está relacionada con la cantidad de tiempo que el paquete de ondas se almacena en la barrera. Además, si el efecto túnel cuántico se modela con la ecuación relativista de Dirac , teoremas matemáticos bien establecidos implican que el proceso es completamente subluminal. ^{[42] [43]}

El concepto de tunelización cuántica se puede extender a situaciones en las que existe un transporte cuántico entre regiones que clásicamente no están conectadas, incluso si no hay una barrera de potencial asociada. Este fenómeno se conoce como tunelización dinámica. ^{[44] [45]}

El concepto de tunelización dinámica es particularmente adecuado para abordar el problema de la tunelización cuántica en dimensiones altas (d>1). En el caso de un sistema integrable , donde las trayectorias clásicas acotadas están confinadas en toros en el espacio de fases , la tunelización puede entenderse como el transporte cuántico entre estados semiclásicos construidos sobre dos toros distintos pero simétricos. ^[46]

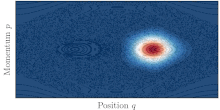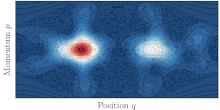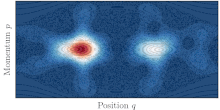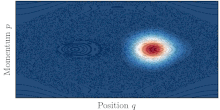
En la vida real, la mayoría de los sistemas no son integrables y muestran diversos grados de caos. Se dice entonces que la dinámica clásica es mixta y el espacio de fases del sistema está compuesto típicamente de islas de órbitas regulares rodeadas por un gran mar de órbitas caóticas. La existencia del mar caótico, donde clásicamente se permite el transporte, entre los dos toros simétricos ayuda entonces al efecto túnel cuántico entre ellos. Este fenómeno se conoce como efecto túnel asistido por el caos. ^[47] y se caracteriza por resonancias agudas de la tasa de efecto túnel al variar cualquier parámetro del sistema.

Cuando es pequeño en comparación con el tamaño de las islas regulares, la estructura fina del espacio de fase clásico desempeña un papel clave en la tunelización. En particular, los dos toros simétricos están acoplados "a través de una sucesión de transiciones prohibidas clásicamente a través de resonancias no lineales" que rodean las dos islas. ^[48]${\displaystyle \hbar }$

Varios fenómenos tienen el mismo comportamiento que el efecto túnel cuántico. Dos ejemplos son el acoplamiento de ondas evanescentes ^[49] (la aplicación de la ecuación de onda de Maxwell a la luz ) y la aplicación de la ecuación de onda no dispersiva de la acústica aplicada a las "ondas en cuerdas" . ^{[ cita requerida ]}

Estos efectos se modelan de manera similar a la barrera de potencial rectangular . En estos casos, un medio de transmisión a través del cual se propaga la onda es el mismo o casi el mismo en todo su recorrido, y un segundo medio a través del cual la onda viaja de manera diferente. Esto puede describirse como una región delgada del medio B entre dos regiones del medio A. El análisis de una barrera rectangular mediante la ecuación de Schrödinger puede adaptarse a estos otros efectos siempre que la ecuación de onda tenga soluciones de ondas viajeras en el medio A pero soluciones exponenciales reales en el medio B.

En óptica , el medio A es el vacío, mientras que el medio B es el vidrio. En acústica, el medio A puede ser un líquido o un gas y el medio B un sólido. En ambos casos, el medio A es una región del espacio donde la energía total de la partícula es mayor que su energía potencial y el medio B es la barrera de potencial. Estos tienen una onda entrante y ondas resultantes en ambas direcciones. Puede haber más medios y barreras, y las barreras no necesitan ser discretas. Las aproximaciones son útiles en este caso.

Una asociación onda-partícula clásica fue analizada originalmente como análoga al efecto túnel cuántico, ^[50] pero un análisis posterior encontró una causa de dinámica de fluidos relacionada con el momento vertical impartido a las partículas cerca de la barrera. ^[51]

• Descarga de barrera dieléctrica
• Emisión de electrones de campo
• Método Holstein-Herring
• Tunelización de protones
• Clonación cuántica
• Unión túnel superconductora
• Diodo túnel
• Cruce de túneles
• Agujero blanco

• Binney, James; Skinner, David (2010). La física de la mecánica cuántica (3.ª ed.). Great Malvern: Cappella Archive. ISBN 978-1-902918-51-8.
• Fröman, Nanny; Fröman, Per Olof (1965). Aproximación JWKB: contribuciones a la teoría . Ámsterdam: Holanda Septentrional. ISBN 978-0-7204-0085-4.
• Griffiths, David J. (2004). Introducción a la electrodinámica (3.ª ed.). Upper Saddle River, NJ: Prentice Hall. ISBN 978-0-13-805326-0.
• Liboff, Richard L. (2002). Mecánica cuántica introductoria (4.ª ed.). San Francisco: Addison-Wesley. ISBN 978-0-8053-8714-8.
• Muller-kirsten, Harald JW (2012). Introducción a la mecánica cuántica: ecuación de Schrödinger e integral de trayectoria (2.ª ed.). Singapur: World Scientific Publishing Company. ISBN 978-981-4397-76-6.
• Razavy, Mohsen (2003). Teoría cuántica de la tunelización . River Edge, NJ: World Scientific. ISBN 978-981-238-019-7.OCLC 52498470  .
• Hong, Jooyoo; Vilenkin, Alexander; Winitzki, Serge (2003). "Creación de partículas en un universo de efecto túnel". Physical Review D . 68 (2): 023520. arXiv : gr-qc/0210034 . Bibcode :2003PhRvD..68b3520H. doi :10.1103/PhysRevD.68.023520. ISSN  0556-2821. S2CID  118969589.
• Wolf, EL (2012). Principios de la espectroscopia de efecto túnel de electrones . Serie internacional de monografías sobre física (2.ª ed.). Oxford; Nueva York: Oxford University Press. ISBN 978-0-19-958949-4.OCLC 768067375  .

Wikimedia Commons alberga una categoría multimedia sobre Efecto túnel cuántico .

• Animación, aplicaciones e investigaciones relacionadas con el efecto túnel y otros fenómenos cuánticos (Université Paris Sud)
• Ilustración animada del efecto túnel cuántico
• Ilustración animada del efecto túnel cuántico en un dispositivo RTD
• Solución interactiva de la ecuación del túnel de Schrödinger