Diagrama de Feynman
 |

En física teórica , un diagrama de Feynman es una representación gráfica de las expresiones matemáticas que describen el comportamiento y la interacción de partículas subatómicas . El esquema recibe su nombre del físico estadounidense Richard Feynman , quien introdujo los diagramas en 1948. La interacción de partículas subatómicas puede ser compleja y difícil de entender; los diagramas de Feynman brindan una visualización simple de lo que de otro modo sería una fórmula arcana y abstracta. Según David Kaiser , "desde mediados del siglo XX, los físicos teóricos han recurrido cada vez más a esta herramienta para ayudarlos a realizar cálculos críticos. Los diagramas de Feynman han revolucionado casi todos los aspectos de la física teórica". [1] Si bien los diagramas se aplican principalmente a la teoría cuántica de campos , también se pueden utilizar en otras áreas de la física, como la teoría del estado sólido . Frank Wilczek escribió que los cálculos que le valieron el Premio Nobel de Física en 2004 "habrían sido literalmente impensables sin los diagramas de Feynman, al igual que los cálculos [de Wilczek] que establecieron una ruta hacia la producción y observación de la partícula de Higgs ". [2]
Feynman utilizó la interpretación de Ernst Stueckelberg del positrón como si fuera un electrón moviéndose hacia atrás en el tiempo. [3] Así, las antipartículas se representan como moviéndose hacia atrás a lo largo del eje del tiempo en los diagramas de Feynman.
El cálculo de amplitudes de probabilidad en física teórica de partículas requiere el uso de integrales bastante grandes y complicadas sobre un gran número de variables . Los diagramas de Feynman pueden representar estas integrales gráficamente.
Un diagrama de Feynman es una representación gráfica de una contribución perturbativa a la amplitud de transición o función de correlación de una teoría de campo cuántica o estadística. Dentro de la formulación canónica de la teoría cuántica de campos, un diagrama de Feynman representa un término en la expansión de Wick de la matriz S perturbativa . Alternativamente, la formulación de la integral de trayectorias de la teoría cuántica de campos representa la amplitud de transición como una suma ponderada de todas las historias posibles del sistema desde el estado inicial hasta el final, en términos de partículas o campos. La amplitud de transición se da entonces como el elemento de la matriz S entre los estados inicial y final del sistema cuántico.
| Teoría cuántica de campos |
|---|
 |
| Historia |
Motivación e historia
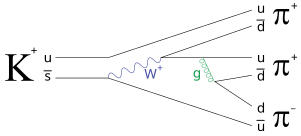
Al calcular las secciones transversales de dispersión en física de partículas , la interacción entre partículas se puede describir partiendo de un campo libre que describe las partículas entrantes y salientes, e incluyendo un hamiltoniano de interacción para describir cómo las partículas se desvían entre sí. La amplitud de dispersión es la suma de cada posible historial de interacción sobre todos los posibles estados intermedios de partículas. El número de veces que actúa el hamiltoniano de interacción es el orden de la expansión de perturbación , y la teoría de perturbación dependiente del tiempo para campos se conoce como la serie de Dyson . Cuando los estados intermedios en tiempos intermedios son estados propios de energía (colecciones de partículas con un momento definido), la serie se denomina teoría de perturbación antigua (o teoría de perturbación dependiente del tiempo/ordenada en el tiempo).
La serie de Dyson se puede reescribir alternativamente como una suma sobre diagramas de Feynman, donde en cada vértice se conservan tanto la energía como el momento , pero donde la longitud del cuatrivector energía-momento no es necesariamente igual a la masa, es decir, las partículas intermedias se denominan off-shell . Los diagramas de Feynman son mucho más fáciles de seguir que los términos "anticuados", porque la forma antigua trata las contribuciones de partículas y antipartículas como separadas. Cada diagrama de Feynman es la suma exponencial de muchos términos antiguos, porque cada línea interna puede representar por separado una partícula o una antipartícula. En una teoría no relativista, no hay antipartículas y no hay duplicación, por lo que cada diagrama de Feynman incluye solo un término.
Feynman dio una receta para calcular la amplitud (las reglas de Feynman, a continuación) para cualquier diagrama dado a partir de un lagrangiano de teoría de campos . Cada línea interna corresponde a un factor del propagador de la partícula virtual ; cada vértice donde se encuentran las líneas da un factor derivado de un término de interacción en el lagrangiano, y las líneas entrantes y salientes llevan una energía, un momento y un espín .
Además de su valor como herramienta matemática, los diagramas de Feynman proporcionan una profunda comprensión física de la naturaleza de las interacciones entre partículas. Las partículas interactúan de todas las formas posibles; de hecho, se permite que las partículas virtuales intermedias se propaguen más rápido que la luz. La probabilidad de cada estado final se obtiene sumando todas esas posibilidades. Esto está estrechamente vinculado a la formulación integral funcional de la mecánica cuántica , también inventada por Feynman (véase formulación de la integral de trayectorias ) .
La aplicación ingenua de tales cálculos a menudo produce diagramas cuyas amplitudes son infinitas , porque las interacciones de partículas a corta distancia requieren un procedimiento de limitación cuidadoso, que incluya las autointeracciones de partículas . La técnica de renormalización , sugerida por Ernst Stueckelberg y Hans Bethe e implementada por Dyson , Feynman, Schwinger y Tomonaga , compensa este efecto y elimina los problemáticos infinitos. Después de la renormalización, los cálculos que utilizan diagramas de Feynman coinciden con los resultados experimentales con una precisión muy alta.
Los diagramas de Feynman y los métodos de integral de trayectoria también se utilizan en mecánica estadística e incluso pueden aplicarse a la mecánica clásica . [4]
Nombres alternativos
Murray Gell-Mann siempre se refirió a los diagramas de Feynman como diagramas de Stueckelberg , en honor a un físico suizo, Ernst Stueckelberg , que ideó una notación similar muchos años antes. Stueckelberg estaba motivado por la necesidad de un formalismo manifiestamente covariante para la teoría cuántica de campos, pero no proporcionó una forma tan automatizada de manejar factores de simetría y bucles, aunque fue el primero en encontrar la interpretación física correcta en términos de trayectorias de partículas hacia adelante y hacia atrás en el tiempo, todo ello sin la integral de trayectoria. [5]
Históricamente, como un dispositivo de contabilidad de la teoría de perturbación covariante, los gráficos se llamaron diagramas de Feynman-Dyson o gráficos de Dyson , [6] porque la integral de trayectoria no era familiar cuando se introdujeron, y la derivación de Freeman Dyson de la teoría de perturbación anticuada tomada de las expansiones perturbativas en mecánica estadística era más fácil de seguir para los físicos entrenados en métodos anteriores. [a] Feynman tuvo que presionar mucho para los diagramas, lo que confundió a los físicos del establishment entrenados en ecuaciones y gráficos. [7]
Representación de la realidad física
En sus presentaciones de interacciones fundamentales , [8] [9] escritas desde la perspectiva de la física de partículas, Gerard 't Hooft y Martinus Veltman dieron buenos argumentos para tomar los diagramas de Feynman originales, no regularizados, como la representación más sucinta de nuestro conocimiento actual sobre la física de la dispersión cuántica de partículas fundamentales . Sus motivaciones son consistentes con las convicciones de James Daniel Bjorken y Sidney Drell : [10]
Los gráficos y las reglas de cálculo de Feynman resumen la teoría cuántica de campos en una forma que está en estrecho contacto con los números experimentales que uno quiere entender. Aunque el enunciado de la teoría en términos de gráficos puede implicar una teoría de perturbaciones , el uso de métodos gráficos en el problema de muchos cuerpos muestra que este formalismo es lo suficientemente flexible como para tratar fenómenos de carácter no perturbativo... Algunas modificaciones de las reglas de cálculo de Feynman pueden sobrevivir a la elaborada estructura matemática de la teoría cuántica de campos canónica local...
En las teorías cuánticas de campos, los diagramas de Feynman se obtienen a partir de un lagrangiano mediante las reglas de Feynman.
La regularización dimensional es un método para regularizar integrales en la evaluación de diagramas de Feynman; les asigna valores que son funciones meromórficas de un parámetro complejo auxiliar d , llamado dimensión. La regularización dimensional escribe una integral de Feynman como una integral que depende de la dimensión del espacio-tiempo d y de los puntos del espacio-tiempo.
Interpretación de la trayectoria de las partículas
Un diagrama de Feynman es una representación de los procesos de la teoría cuántica de campos en términos de interacciones entre partículas . Las partículas están representadas por las líneas del diagrama, que pueden ser onduladas o rectas, con una flecha o sin ella, dependiendo del tipo de partícula. Un punto donde las líneas se conectan con otras líneas es un vértice , y es aquí donde las partículas se encuentran e interactúan: emitiendo o absorbiendo nuevas partículas, desviándose unas a otras o cambiando de tipo.
Hay tres tipos diferentes de líneas: las líneas internas conectan dos vértices, las líneas entrantes se extienden desde "el pasado" hasta un vértice y representan un estado inicial, y las líneas salientes se extienden desde un vértice hasta "el futuro" y representan el estado final (las dos últimas también se conocen como líneas externas ). Tradicionalmente, la parte inferior del diagrama es el pasado y la parte superior el futuro; otras veces, el pasado está a la izquierda y el futuro a la derecha. Al calcular funciones de correlación en lugar de amplitudes de dispersión , no hay pasado ni futuro y todas las líneas son internas. Las partículas comienzan y terminan en pequeñas x, que representan las posiciones de los operadores cuya correlación se está calculando.
Los diagramas de Feynman son una representación gráfica de la contribución a la amplitud total de un proceso que puede ocurrir de varias maneras diferentes. Cuando un grupo de partículas entrantes se dispersan entre sí, el proceso puede considerarse como uno en el que las partículas recorren todos los caminos posibles, incluidos los que van hacia atrás en el tiempo.
Los diagramas de Feynman suelen confundirse con los diagramas de espacio-tiempo y las imágenes de cámara de burbujas porque todos ellos describen la dispersión de partículas. Los diagramas de Feynman son gráficos que representan la interacción de partículas en lugar de la posición física de la partícula durante un proceso de dispersión. A diferencia de una imagen de cámara de burbujas, solo la suma de todos los diagramas de Feynman representa cualquier interacción de partículas dada; las partículas no eligen un diagrama particular cada vez que interactúan. La ley de la suma está de acuerdo con el principio de superposición : cada diagrama contribuye a la amplitud total del proceso.
Descripción
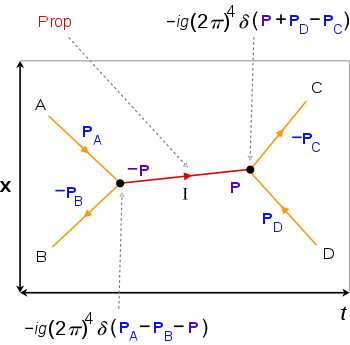
• líneas internas (rojas) para partículas y procesos intermedios, que tienen un factor propagador ("prop"), líneas externas (naranja) para partículas entrantes/salientes hacia/desde vértices (negro) ,
• en cada vértice hay una conservación de 4-momentos usando funciones delta, los 4-momentos que entran al vértice son positivos mientras que los que salen son negativos, los factores en cada vértice y línea interna se multiplican en la integral de amplitud,
• los ejes de espacio x y tiempo t no siempre se muestran, las direcciones de las líneas externas corresponden al paso del tiempo.
Un diagrama de Feynman representa una contribución perturbativa a la amplitud de una transición cuántica desde un estado cuántico inicial a un estado cuántico final.
Por ejemplo, en el proceso de aniquilación electrón-positrón, el estado inicial es un electrón y un positrón, el estado final: dos fotones.
A menudo se supone que el estado inicial está a la izquierda del diagrama y el estado final a la derecha (aunque también se utilizan con bastante frecuencia otras convenciones).
Un diagrama de Feynman consta de puntos, llamados vértices, y líneas unidas a los vértices.
Las partículas en el estado inicial se representan mediante líneas que sobresalen en la dirección del estado inicial (por ejemplo, hacia la izquierda), las partículas en el estado final se representan mediante líneas que sobresalen en la dirección del estado final (por ejemplo, hacia la derecha).
En la electrodinámica cuántica existen dos tipos de partículas: partículas materiales como los electrones o positrones (llamadas fermiones ) y partículas de intercambio (llamadas bosones de gauge ). Se representan en los diagramas de Feynman de la siguiente manera:
- El electrón en el estado inicial se representa mediante una línea sólida, con una flecha que indica el giro de la partícula, por ejemplo, apuntando hacia el vértice (→•).
- El electrón en el estado final se representa mediante una línea, con una flecha que indica el giro de la partícula, por ejemplo, apuntando lejos del vértice: (•→).
- El positrón en el estado inicial está representado por una línea sólida, con una flecha que indica el giro de la partícula, por ejemplo, apuntando lejos del vértice: (←•).
- El positrón en el estado final se representa mediante una línea, con una flecha que indica el giro de la partícula, por ejemplo apuntando hacia el vértice: (•←).
- El fotón virtual en el estado inicial y final está representado por una línea ondulada ( ~• y •~ ).
En QED, un vértice siempre tiene tres líneas unidas a él: una línea bosónica, una línea fermiónica con una flecha hacia el vértice y una línea fermiónica con una flecha que se aleja del vértice.
Los vértices pueden estar conectados por un propagador bosónico o fermiónico . Un propagador bosónico se representa por una línea ondulada que conecta dos vértices (•~•). Un propagador fermiónico se representa por una línea sólida (con una flecha en una u otra dirección) que conecta dos vértices (•←•).
El número de vértices da el orden del término en la expansión de la serie de perturbaciones de la amplitud de transición.
Ejemplo de aniquilación electrón-positrón

La interacción de aniquilación electrón-positrón :
- y + + y − → 2γ
tiene una contribución del diagrama de Feynman de segundo orden que se muestra adyacente:
En el estado inicial (en la parte inferior; tiempo temprano) hay un electrón (e − ) y un positrón (e + ) y en el estado final (en la parte superior; tiempo tardío) hay dos fotones (γ).
Formulación de cuantificación canónica
La amplitud de probabilidad para una transición de un sistema cuántico (entre estados asintóticamente libres) desde el estado inicial |i⟩ al estado final |f ⟩ está dada por el elemento de la matriz
donde S es la matriz S. En términos del operador de evolución temporal U , es simplemente
En la imagen de interacción , esto se expande a
donde H V es el hamiltoniano de interacción y T significa el producto ordenado en el tiempo de los operadores. La fórmula de Dyson expande la exponencial matricial ordenada en el tiempo en una serie de perturbaciones en las potencias de la densidad del hamiltoniano de interacción,
De manera equivalente, con la interacción lagrangiana L V , es
Un diagrama de Feynman es una representación gráfica de un único sumando en la expansión de Wick del producto ordenado en el tiempo en el término de orden n S ( n ) de la serie de Dyson de la matriz S ,
donde N significa el producto ordenado normal de los operadores y (±) se encarga del posible cambio de signo al conmutar los operadores fermiónicos para unirlos para una contracción (un propagador ) y A representa todas las contracciones posibles.
Reglas de Feynman
Los diagramas se dibujan según las reglas de Feynman, que dependen del lagrangiano de interacción. Para el lagrangiano de interacción QED
Al describir la interacción de un campo fermiónico ψ con un campo de calibre bosónico A μ , las reglas de Feynman se pueden formular en el espacio de coordenadas de la siguiente manera:
- Cada coordenada de integración x j está representada por un punto (a veces llamado vértice);
- Un propagador bosónico está representado por una línea ondulada que conecta dos puntos;
- Un propagador fermiónico está representado por una línea sólida que conecta dos puntos;
- Un campo bosónico está representado por una línea ondulada unida al punto x i ;
- Un campo fermiónico ψ ( x i ) se representa mediante una línea sólida unida al punto x i con una flecha hacia el punto;
- Un campo antifermiónico ψ ( x i ) se representa mediante una línea sólida unida al punto x i con una flecha que se aleja del punto;
Ejemplo: procesos de segundo orden en QED
El término de perturbación de segundo orden en la matriz S es
Dispersión de fermiones
 |
La expansión de Wick del integrando da (entre otros) el siguiente término
dónde
es la contracción electromagnética (propagadora) en el calibre de Feynman. Este término está representado por el diagrama de Feynman de la derecha. Este diagrama proporciona contribuciones a los siguientes procesos:
- e − e − dispersión (estado inicial a la derecha, estado final a la izquierda del diagrama);
- e + e + dispersión (estado inicial a la izquierda, estado final a la derecha del diagrama);
- e − e + dispersión (estado inicial en la parte inferior/superior, estado final en la parte superior/inferior del diagrama).
Dispersión Compton y aniquilación/generación de e−mi+pares
Otro término interesante en la expansión es
dónde
es la contracción fermiónica (propagadora).
Formulación de la integral de trayectoria
En una integral de trayectoria , el lagrangiano de campo, integrado sobre todas las historias de campo posibles, define la amplitud de probabilidad para pasar de una configuración de campo a otra. Para que tenga sentido, la teoría de campo debe tener un estado fundamental bien definido , y la integral debe realizarse un poco rotada en tiempo imaginario, es decir, una rotación de Wick . El formalismo de la integral de trayectoria es completamente equivalente al formalismo del operador canónico anterior.
Campo escalar Lagrangiano
Un ejemplo sencillo es el campo escalar relativista libre en d dimensiones, cuya integral de acción es:
La amplitud de probabilidad de un proceso es:
donde A y B son hipersuperficies espaciales que definen las condiciones de contorno. La colección de todos los φ ( A ) en la hipersuperficie inicial da el valor inicial del campo, análogo a la posición inicial para una partícula puntual, y los valores de campo φ ( B ) en cada punto de la hipersuperficie final definen el valor de campo final, que se permite que varíe, dando una amplitud diferente para terminar en valores diferentes. Esta es la amplitud de transición de campo a campo.
La integral de trayectoria proporciona el valor esperado de los operadores entre el estado inicial y final:
y en el límite en que A y B retroceden hacia el pasado infinito y el futuro infinito, la única contribución que importa es la del estado fundamental (esto solo es rigurosamente cierto si la integral de trayectoria se define ligeramente rotada hacia un tiempo imaginario). La integral de trayectoria puede considerarse análoga a una distribución de probabilidad, y es conveniente definirla de modo que multiplicarla por una constante no cambie nada:
El factor de normalización en la parte inferior se llama función de partición del campo y coincide con la función de partición mecánica estadística a temperatura cero cuando se gira en tiempo imaginario.
Las amplitudes iniciales y finales están mal definidas si se piensa en el límite continuo desde el principio, porque las fluctuaciones en el campo pueden volverse ilimitadas. Por lo tanto, la integral de trayectoria puede considerarse como una red cuadrada discreta, con un espaciamiento de red a y el límite a → 0 debe tomarse con cuidado [ aclaración necesaria ] . Si los resultados finales no dependen de la forma de la red o del valor de a , entonces existe el límite continuo.
En una celosía
En una red, (i), el campo se puede expandir en modos de Fourier :
Aquí el dominio de integración está restringido sobre k a un cubo de longitud de lado 2π/a , por lo que no se permiten valores grandes de k . Es importante tener en cuenta que la medida k contiene los factores de 2 π de las transformadas de Fourier , esta es la mejor convención estándar para las integrales k en QFT. La red significa que no se permite que las fluctuaciones en valores grandes de k contribuyan de inmediato, solo comienzan a contribuir en el límite a → 0 . A veces, en lugar de una red, los modos de campo simplemente se cortan en valores altos de k .
También es conveniente, de vez en cuando, considerar que el volumen del espacio-tiempo es finito, de modo que los modos k también son una red. Esto no es estrictamente tan necesario como el límite del espacio-red, porque las interacciones en k no están localizadas, pero es conveniente para hacer un seguimiento de los factores que se encuentran frente a las k -integrales y las funciones delta que conservan el momento que surgirán.
En una red, (ii), la acción debe discretizarse:
donde ⟨ x , y ⟩ es un par de vecinos reticulares más cercanos x e y . La discretización debe considerarse como la definición de lo que significa la derivada ∂ μ φ .
En términos de los modos reticulares de Fourier, la acción se puede escribir:
Para k cerca de cero esto es:
Ahora tenemos la transformada de Fourier continua de la acción original. En un volumen finito, la cantidad d d k no es infinitesimal, sino que se convierte en el volumen de una caja formada por modos de Fourier vecinos, o ( 2π/V )d
.
El campo φ es de valor real, por lo que la transformada de Fourier obedece:
En términos de partes reales e imaginarias, la parte real de φ ( k ) es una función par de k , mientras que la parte imaginaria es impar. La transformada de Fourier evita el doble conteo, por lo que se puede escribir:
sobre un dominio de integración que integra sobre cada par ( k ,− k ) exactamente una vez.
Para un campo escalar complejo con acción
La transformada de Fourier no tiene restricciones:
y la integral es sobre todo k .
Integrar sobre todos los valores diferentes de φ ( x ) es equivalente a integrar sobre todos los modos de Fourier, porque tomar una transformada de Fourier es una transformación lineal unitaria de coordenadas de campo. Cuando cambias las coordenadas en una integral multidimensional mediante una transformación lineal, el valor de la nueva integral viene dado por el determinante de la matriz de transformación. Si
entonces
Si A es una rotación, entonces
de modo que det A = ±1 , y el signo depende de si la rotación incluye una reflexión o no.
La matriz que cambia las coordenadas de φ ( x ) a φ ( k ) se puede leer a partir de la definición de una transformada de Fourier.
y el teorema de inversión de Fourier te dice lo inverso:
que es la conjugada-transpuesta compleja, hasta factores de 2 π . En una red de volumen finito, el determinante es distinto de cero e independiente de los valores del campo.
y la integral de trayectoria es un factor separado en cada valor de k .
El factor d d k es el volumen infinitesimal de una celda discreta en el espacio k , en una caja reticular cuadrada
donde L es la longitud del lado de la caja. Cada factor independiente es una gaussiana oscilatoria y el ancho de la gaussiana diverge a medida que el volumen tiende al infinito.
En tiempo imaginario, la acción euclidiana se vuelve definida positiva y puede interpretarse como una distribución de probabilidad. La probabilidad de que un campo tenga valores φ k es
El valor esperado del campo es el valor esperado estadístico del campo cuando se elige de acuerdo con la distribución de probabilidad:
Dado que la probabilidad de φ k es un producto, el valor de φ k en cada valor separado de k tiene una distribución gaussiana independiente. La varianza de la gaussiana es 1/k2d2dk , que es formalmente infinito, pero eso solo significa que las fluctuaciones son ilimitadas en un volumen infinito. En cualquier volumen finito, la integral se reemplaza por una suma discreta y la varianza de la integral es V/k2 .
Montecarlo
La integral de trayectoria define un algoritmo probabilístico para generar una configuración de campo escalar euclidiano. Elija aleatoriamente las partes reales e imaginarias de cada modo de Fourier en el número de onda k para que sean una variable aleatoria gaussiana con varianza .1/k2 . Esto genera una configuración φ C ( k ) al azar, y la transformada de Fourier da φ C ( x ) . Para campos escalares reales, el algoritmo debe generar solo uno de cada par φ ( k ), φ (− k ) , y hacer que el segundo sea el conjugado complejo del primero.
Para encontrar cualquier función de correlación, genere un campo una y otra vez mediante este procedimiento y encuentre el promedio estadístico:
donde | C | es el número de configuraciones y la suma es el producto de los valores de campo de cada configuración. La función de correlación euclidiana es exactamente la misma que la función de correlación en estadística o mecánica estadística. Las funciones de correlación mecánica cuántica son una continuación analítica de las funciones de correlación euclidianas.
En el caso de campos libres con una acción cuadrática, la distribución de probabilidad es una gaussiana de alta dimensión y el promedio estadístico se obtiene mediante una fórmula explícita. Pero el método de Monte Carlo también funciona bien para las teorías de campos de interacción bosónica donde no existe una forma cerrada para las funciones de correlación.
Propagador escalar
Cada modo se distribuye de forma gaussiana de forma independiente. La esperanza de los modos de campo es fácil de calcular:
para k ≠ k ′ , ya que entonces las dos variables aleatorias gaussianas son independientes y ambas tienen media cero.
En un volumen finito V , cuando los dos valores k coinciden, ya que ésta es la varianza de la gaussiana. En el límite de volumen infinito,
Estrictamente hablando, esto es una aproximación: el propagador reticular es:
Pero cerca de k = 0 , para fluctuaciones de campo largas en comparación con el espaciamiento de la red, las dos formas coinciden.
Las funciones delta contienen factores de 2 π , de modo que cancelan los factores de 2 π en la medida de k integrales.
donde δ D ( k ) es la función delta de Dirac unidimensional ordinaria. Esta convención para las funciones delta no es universal: algunos autores mantienen explícitos los factores de 2 π en las funciones delta (y en la integración k ).
Ecuación de movimiento
La forma del propagador se puede encontrar más fácilmente utilizando la ecuación de movimiento del campo. A partir del lagrangiano, la ecuación de movimiento es:
y en un valor esperado esto dice:
Donde las derivadas actúan sobre x y la identidad es verdadera en todas partes excepto cuando x e y coinciden, y el orden de los operadores importa. La forma de la singularidad puede entenderse a partir de las relaciones de conmutación canónicas como una función delta. Definiendo el propagador de Feynman (euclidiano) Δ como la transformada de Fourier de la función de dos puntos ordenada en el tiempo (la que proviene de la integral de trayectoria):
De modo que:
Si las ecuaciones de movimiento son lineales, el propagador siempre será el recíproco de la matriz en forma cuadrática que define el lagrangiano libre, ya que de esta se obtienen las ecuaciones de movimiento. Esto también es fácil de ver directamente a partir de la integral de trayectoria. El factor de i desaparece en la teoría euclidiana.
Teorema de Wick
Como cada modo de campo es un gaussiano independiente, los valores esperados para el producto de muchos modos de campo obedecen al teorema de Wick :
es cero a menos que los modos de campo coincidan en pares. Esto significa que es cero para un número impar de φ y, para un número par de φ , es igual a una contribución de cada par por separado, con una función delta.
donde la suma se encuentra sobre cada partición de los modos de campo en pares, y el producto se encuentra sobre los pares. Por ejemplo,
Una interpretación del teorema de Wick es que cada inserción de campo puede considerarse como una línea colgante, y el valor esperado se calcula uniendo las líneas en pares, colocando un factor de función delta que garantiza que el momento de cada socio en el par sea igual y dividiendo por el propagador.
Momentos gaussianos superiores: completando el teorema de Wick
Queda por demostrar el teorema de Wick: ¿qué ocurre si más de dos de las s tienen el mismo momento? Si es un número impar, la integral es cero; los valores negativos se cancelan con los valores positivos. Pero si el número es par, la integral es positiva. La demostración anterior suponía que las s solo coincidirían en pares.
Pero el teorema es correcto incluso cuando arbitrariamente muchos de ellos son iguales, y esta es una propiedad notable de la integración gaussiana:
Dividiendo por I ,
Si el teorema de Wick fuera correcto, los momentos superiores vendrían dados por todos los emparejamientos posibles de una lista de 2 n x diferentes :
donde las x son todas la misma variable, el índice es solo para llevar un registro de la cantidad de formas de emparejarlas. La primera x se puede emparejar con otras 2 n − 1 , lo que deja 2 n − 2 . La siguiente x no emparejada se puede emparejar con 2 n − 3 x diferentes , lo que deja 2 n − 4 , y así sucesivamente. Esto significa que el teorema de Wick, sin corregir, dice que el valor esperado de x 2 n debería ser:
Y ésta es, de hecho, la respuesta correcta. Por lo tanto, el teorema de Wick se cumple sin importar cuántos momentos de las variables internas coincidan.
Interacción
Las interacciones se representan mediante contribuciones de orden superior, ya que las contribuciones cuadráticas son siempre gaussianas. La interacción más simple es la autointeracción cuártica, con una acción:
Pronto se aclarará la razón del factor combinatorio 4!. Escribiendo la acción en términos de los modos de Fourier reticulares (o continuos):
Donde S F es la acción libre, cuyas funciones de correlación están dadas por el teorema de Wick. La exponencial de S en la integral de trayectoria puede expandirse en potencias de λ , dando una serie de correcciones a la acción libre.
La integral de trayectoria para la acción interactuante es entonces una serie de potencias de correcciones a la acción libre. El término representado por X debe considerarse como cuatro semirrectas, una para cada factor de φ ( k ) . Las semirrectas se encuentran en un vértice, lo que contribuye a una función delta que garantiza que la suma de los momentos sea igual.
Para calcular una función de correlación en la teoría de interacción, ahora hay una contribución de los términos X. Por ejemplo, la integral de trayectoria para el correlador de cuatro campos:
que en el campo libre sólo era distinto de cero cuando los momentos k eran iguales en pares, ahora es distinto de cero para todos los valores de k . Los momentos de las inserciones φ ( k i ) ahora pueden coincidir con los momentos de las X s en la expansión. Las inserciones también deben considerarse como semirrectas, cuatro en este caso, que llevan un momento k , pero que no está integrado.
La contribución de orden más bajo proviene del primer término no trivial e − S F X en la expansión de Taylor de la acción. El teorema de Wick requiere que los momentos en las semirrectas X , los factores φ ( k ) en X , coincidan con los momentos de las semirrectas externas en pares. La nueva contribución es igual a:
El 4! dentro de X se cancela porque hay exactamente 4! maneras de hacer coincidir las semirrectas en X con las semirrectas externas. Cada una de estas diferentes maneras de hacer coincidir las semirrectas en pares contribuye exactamente una vez, independientemente de los valores de k 1,2,3,4 , según el teorema de Wick.
Diagramas de Feynman
La expansión de la acción en potencias de X da una serie de términos con un número progresivamente mayor de X s. La contribución del término con exactamente n X s se llama de orden n.
Los términos de orden n tienen:
- 4 n semirrectas internas, que son los factores de φ ( k ) a partir de las X . Todas ellas terminan en un vértice y están integradas sobre todos los k posibles .
- semirrectas externas, que provienen de las inserciones φ ( k ) en la integral.
Por el teorema de Wick, cada par de semirrectas deben emparejarse para formar una recta , y esta recta da un factor de
que multiplica la contribución. Esto significa que las dos semirrectas que forman una recta están obligadas a tener momentos iguales y opuestos. La recta en sí debe estar etiquetada con una flecha, dibujada paralela a la recta, y etiquetada con el momento en la recta k . La semirrecta en el extremo de la cola de la flecha lleva momento k , mientras que la semirrecta en el extremo de la cabeza lleva momento − k . Si una de las dos semirrectas es externa, esto mata la integral sobre la interna k , ya que obliga a la interna k a ser igual a la externa k . Si ambas son internas, la integral sobre k permanece.
Los diagramas que se forman uniendo las semirrectas de las X con las semirrectas externas, que representan inserciones, son los diagramas de Feynman de esta teoría. Cada línea lleva un factor de 1/k2 , el propagador, y va de vértice a vértice, o termina en una inserción. Si es interno, se integra sobre él. En cada vértice, el total entrante k es igual al total saliente k .
El número de formas de hacer un diagrama uniendo semirrectas en rectas anula casi por completo los factores factoriales provenientes de la serie de Taylor de la exponencial y el 4! en cada vértice.
Orden de bucle
Un diagrama de bosque es aquel en el que todas las líneas internas tienen un momento que está completamente determinado por las líneas externas y la condición de que el momento entrante y saliente sean iguales en cada vértice. La contribución de estos diagramas es un producto de propagadores, sin ninguna integración. Un diagrama de árbol es un diagrama de bosque conectado.
Un ejemplo de diagrama de árbol es aquel en el que cada una de las cuatro líneas externas termina en una X. Otro es aquel en el que tres líneas externas terminan en una X , y la mitad de la línea restante se une con otra X , y las mitades de línea restantes de esta X se extienden hacia líneas externas. Todos estos son también diagramas de bosque (ya que cada árbol es un bosque); un ejemplo de un bosque que no es un árbol es aquel en el que ocho líneas externas terminan en dos X.
Es fácil verificar que en todos estos casos, los momentos en todas las líneas internas están determinados por los momentos externos y la condición de conservación del momento en cada vértice.
Un diagrama que no es un diagrama de bosque se denomina diagrama de bucles , y un ejemplo es uno en el que dos líneas de una X se unen a líneas externas, mientras que las dos líneas restantes se unen entre sí. Las dos líneas unidas entre sí pueden tener cualquier momento, ya que ambas entran y salen del mismo vértice. Un ejemplo más complicado es uno en el que dos X se unen entre sí haciendo coincidir los catetos entre sí. Este diagrama no tiene líneas externas en absoluto.
La razón por la que los diagramas de bucles se denominan diagramas de bucles es porque el número de k -integrales que quedan sin determinar por la conservación del momento es igual al número de bucles cerrados independientes en el diagrama, donde los bucles independientes se cuentan como en la teoría de homología . La homología tiene un valor real (en realidad, un valor R d ), el valor asociado con cada línea es el momento. El operador de borde lleva cada línea a la suma de los vértices finales con un signo positivo en la cabeza y un signo negativo en la cola. La condición de que se conserve el momento es exactamente la condición de que el borde del grafo ponderado de valor k sea cero.
Un conjunto de valores k válidos se puede redefinir arbitrariamente siempre que haya un bucle cerrado. Un bucle cerrado es una ruta cíclica de vértices adyacentes que nunca vuelve a visitar el mismo vértice. Se puede pensar en un ciclo de este tipo como el límite de una celda hipotética de 2. Las etiquetas k de un grafo que conserva el momento (es decir, que tiene un límite cero) hasta las redefiniciones de k (es decir, hasta los límites de las celdas de 2) definen la primera homología de un grafo. El número de momentos independientes que no se determinan es entonces igual al número de bucles de homología independientes. Para muchos grafos, esto es igual al número de bucles tal como se cuenta de la manera más intuitiva.
Factores de simetría
La cantidad de formas de formar un diagrama de Feynman dado uniendo semirrectas es grande y, según el teorema de Wick, cada forma de emparejar las semirrectas contribuye por igual. A menudo, esto cancela por completo los factoriales en el denominador de cada término, pero la cancelación a veces es incompleta.
El denominador no cancelado se denomina factor de simetría del diagrama. La contribución de cada diagrama a la función de correlación debe dividirse por su factor de simetría.
Por ejemplo, considere el diagrama de Feynman formado a partir de dos líneas externas unidas a una X , y las dos semirrectas restantes en la X unidas entre sí. Hay 4 × 3 maneras de unir las semirrectas externas a la X , y luego solo hay una manera de unir las dos líneas restantes entre sí. La X viene dividida por 4! = 4 × 3 × 2 , pero el número de maneras de unir las semirrectas X para hacer el diagrama es solo 4 × 3, por lo que la contribución de este diagrama se divide por dos.
Para otro ejemplo, considere el diagrama formado al unir todas las semirrectas de una X con todas las semirrectas de otra X . Este diagrama se llama burbuja de vacío , porque no se une a ninguna línea externa. Hay 4! formas de formar este diagrama, pero el denominador incluye un 2! (de la expansión de la exponencial, hay dos X ) y dos factores de 4!. La contribución se multiplica por 4!/¡2 × 4! ¡× 4! = 1/48 .
Otro ejemplo es el diagrama de Feynman formado a partir de dos X s donde cada X se une a dos líneas externas, y las dos semirrectas restantes de cada X se unen entre sí. El número de formas de unir una X a dos líneas externas es 4 × 3, y cualquiera de las X podría unirse a cualquiera de los pares, lo que da un factor adicional de 2. Las dos semirrectas restantes en las dos X s se pueden unir entre sí de dos formas, de modo que el número total de formas de formar el diagrama es 4 × 3 × 4 × 3 × 2 × 2 , mientras que el denominador es 4! × 4! × 2! . El factor de simetría total es 2, y la contribución de este diagrama se divide por 2.
El teorema del factor de simetría da el factor de simetría para un diagrama general: la contribución de cada diagrama de Feynman debe dividirse por el orden de su grupo de automorfismos, el número de simetrías que tiene.
Un automorfismo de un grafo de Feynman es una permutación M de las líneas y una permutación N de los vértices con las siguientes propiedades:
- Si una línea l va del vértice v al vértice v′ , entonces M ( l ) va de N ( v ) a N ( v′ ) . Si la línea no tiene dirección, como ocurre en un campo escalar real, entonces M ( l ) también puede ir de N ( v′ ) a N ( v ) .
- Si una línea l termina en una línea externa, M ( l ) termina en la misma línea externa.
- Si hay diferentes tipos de líneas, M ( l ) debe preservar el tipo.
Este teorema tiene una interpretación en términos de trayectorias de partículas: cuando hay partículas idénticas, la integral sobre todas las partículas intermedias no debe contar dos veces los estados que difieren solo por intercambiar partículas idénticas.
Demostración: Para demostrar este teorema, se nombran todas las líneas internas y externas de un diagrama con un nombre único. Luego se forma el diagrama uniendo una semirrecta con un nombre y luego con la otra semirrecta.
Ahora cuente la cantidad de formas de formar el diagrama nombrado. Cada permutación de las X da un patrón diferente de vinculación de nombres a semirrectas, y este es un factor de n !. Cada permutación de las semirrectas en una sola X da un factor de 4!. Por lo tanto, un diagrama nombrado se puede formar exactamente de tantas formas como el denominador de la expansión de Feynman.
Pero el número de diagramas sin nombre es menor que el número de diagramas con nombre por el orden del grupo de automorfismos del gráfico.
Diagramas conectados:teorema del grupo enlazado
En términos generales, un diagrama de Feynman se denomina conexo si todos los vértices y líneas propagadoras están unidos por una secuencia de vértices y propagadores del propio diagrama. Si se lo considera como un grafo no dirigido, es conexo. La notable relevancia de tales diagramas en las teorías cuánticas de campos se debe al hecho de que son suficientes para determinar la función de partición cuántica Z [ J ] . Más precisamente, los diagramas de Feynman conexos determinan
Para ver esto, hay que recordar que
con D k construido a partir de algún diagrama de Feynman (arbitrario) que se puede pensar que consta de varios componentes conectados C i . Si uno encuentra n i copias (idénticas) de un componente C i dentro del diagrama de Feynman D k uno tiene que incluir un factor de simetría n i ! . Sin embargo, al final cada contribución de un diagrama de Feynman D k a la función de partición tiene la forma genérica
donde i etiqueta los (infinitos) diagramas de Feynman conectados posibles.
Un esquema para crear sucesivamente dichas contribuciones desde D k hasta Z [ J ] se obtiene mediante
y por lo tanto produce
Para establecer la normalización Z 0 = exp W [0] = 1 uno simplemente calcula todos los diagramas de vacío conectados , es decir, los diagramas sin ninguna fuente J (a veces denominados patas externas de un diagrama de Feynman).
El teorema de los grupos enlazados fue demostrado por primera vez para orden cuatro por Keith Brueckner en 1955, y para órdenes infinitos por Jeffrey Goldstone en 1957. [11]
Burbujas de vacío
Una consecuencia inmediata del teorema de los grupos enlazados es que todas las burbujas de vacío, diagramas sin líneas externas, se cancelan al calcular funciones de correlación. Una función de correlación se da mediante una relación de integrales de trayectoria:
La parte superior es la suma de todos los diagramas de Feynman, incluidos los diagramas desconectados que no se vinculan con líneas externas. En términos de los diagramas conectados, el numerador incluye las mismas contribuciones de las burbujas de vacío que el denominador:
Donde la suma de los diagramas E incluye solo aquellos diagramas cuyos componentes conectados terminan en al menos una línea externa. Las burbujas de vacío son las mismas independientemente de las líneas externas y dan un factor multiplicativo general. El denominador es la suma de todas las burbujas de vacío y la división elimina el segundo factor.
Las burbujas de vacío entonces sólo son útiles para determinar el propio Z , que según la definición de la integral de trayectoria es igual a:
donde ρ es la densidad de energía en el vacío. Cada burbuja de vacío contiene un factor de δ ( k ) que pone a cero el k total en cada vértice, y cuando no hay líneas externas, esto contiene un factor de δ (0) , porque la conservación del momento se aplica en exceso. En un volumen finito, este factor puede identificarse como el volumen total del espacio-tiempo. Dividiendo por el volumen, la integral restante para la burbuja de vacío tiene una interpretación: es una contribución a la densidad de energía del vacío.
Fuentes
Las funciones de correlación son la suma de los diagramas de Feynman conectados, pero el formalismo trata los diagramas conectados y desconectados de manera diferente. Las líneas internas terminan en los vértices, mientras que las líneas externas se dirigen a las inserciones. La introducción de fuentes unifica el formalismo, al crear nuevos vértices donde puede terminar una línea.
Las fuentes son campos externos, campos que contribuyen a la acción, pero no son variables dinámicas. Una fuente de campo escalar es otro campo escalar h que contribuye con un término al lagrangiano (de Lorentz):
En la expansión de Feynman, esto aporta términos H con una semirrecta que termina en un vértice. Las rectas en un diagrama de Feynman ahora pueden terminar en un vértice X o en un vértice H , y solo una recta entra en un vértice H. La regla de Feynman para un vértice H es que una recta desde un H con momento k obtiene un factor de h ( k ) .
La suma de los diagramas conexos en presencia de fuentes incluye un término para cada diagrama conexo en ausencia de fuentes, excepto que ahora los diagramas pueden terminar en la fuente. Tradicionalmente, una fuente se representa con una pequeña "×" con una línea que se extiende hacia afuera, exactamente como una inserción.
donde C ( k 1 ,..., k n ) es el diagrama conectado con n líneas externas que llevan el momento como se indica. La suma se aplica a todos los diagramas conectados, como antes.
El campo h no es dinámico, lo que significa que no existe una integral de trayectoria sobre h : h es simplemente un parámetro en el lagrangiano, que varía de un punto a otro. La integral de trayectoria para el campo es:
y es una función de los valores de h en cada punto. Una forma de interpretar esta expresión es que se toma la transformada de Fourier en el espacio de campos. Si hay una densidad de probabilidad en R n , la transformada de Fourier de la densidad de probabilidad es:
La transformada de Fourier es la expectativa de una exponencial oscilatoria. La integral de trayectoria en presencia de una fuente h ( x ) es:
que, en una red, es el producto de una exponencial oscilatoria para cada valor de campo:
La transformada de Fourier de una función delta es una constante que da una expresión formal para una función delta:
Esto te indica cómo se ve una función delta de campo en una integral de trayectoria. Para dos campos escalares φ y η ,
que se integra sobre la coordenada de la transformada de Fourier, sobre h . Esta expresión es útil para cambiar formalmente las coordenadas del campo en la integral de trayectoria, de forma muy similar a como se utiliza una función delta para cambiar las coordenadas en una integral multidimensional ordinaria.
La función de partición ahora es una función del campo h , y la función de partición física es el valor cuando h es la función cero:
Las funciones de correlación son derivadas de la integral de trayectoria con respecto a la fuente:
En el espacio euclidiano, las contribuciones de las fuentes a la acción aún pueden aparecer con un factor de i , de modo que aún realizan una transformada de Fourier.
Girar1/2; "fotones" y "fantasmas"
Girar1/2: Integrales de Grassmann
La integral de trayectoria de campo se puede extender al caso de Fermi, pero solo si se amplía la noción de integración. Una integral de Grassmann de un campo de Fermi libre es un determinante de alta dimensión o Pfaffian , que define el nuevo tipo de integración gaussiana apropiada para los campos de Fermi.
Las dos fórmulas fundamentales de la integración de Grassmann son:
donde M es una matriz arbitraria y ψ , ψ son variables de Grassmann independientes para cada índice i , y
donde A es una matriz antisimétrica, ψ es una colección de variables de Grassmann y 1/2 es para evitar el doble conteo (ya que ψ i ψ j = − ψ j ψ i ).
En notación matricial, donde ψ y η son vectores fila con valores de Grassmann, η y ψ son vectores columna con valores de Grassmann y M es una matriz de valores reales:
donde la última igualdad es una consecuencia de la invariancia de traslación de la integral de Grassmann. Las variables de Grassmann η son fuentes externas para ψ , y la diferenciación con respecto a η reduce los factores de ψ .
De nuevo, en una notación matricial esquemática. El significado de la fórmula anterior es que la derivada con respecto al componente apropiado de η y η da el elemento de matriz de M −1 . Esto es exactamente análogo a la fórmula de integración de la trayectoria bosónica para una integral gaussiana de un campo bosónico complejo:
De modo que el propagador es la inversa de la matriz en la parte cuadrática de la acción tanto en el caso de Bose como en el de Fermi.
Para los campos Grassmann reales, para los fermiones de Majorana , la integral de trayectoria es una forma cuadrática de Pfaffian multiplicada por una fuente, y las fórmulas dan la raíz cuadrada del determinante, tal como lo hacen para los campos bosónicos reales. El propagador sigue siendo el inverso de la parte cuadrática.
El lagrangiano de Dirac libre:
formalmente da las ecuaciones de movimiento y las relaciones de anticonmutación del campo de Dirac, de la misma manera que el lagrangiano de Klein Gordon en una integral de trayectoria ordinaria da las ecuaciones de movimiento y las relaciones de conmutación del campo escalar. Al utilizar la transformada espacial de Fourier del campo de Dirac como una nueva base para el álgebra de Grassmann, la parte cuadrática de la acción de Dirac se vuelve fácil de invertir:
El propagador es la inversa de la matriz M que une ψ ( k ) y ψ ( k ) , ya que diferentes valores de k no se mezclan.
El análogo del teorema de Wick hace coincidir ψ y ψ en pares:
donde S es el signo de la permutación que reordena la secuencia de ψ y ψ para poner los que están emparejados para formar las funciones delta uno al lado del otro, con ψ justo antes de ψ . Dado que un par ψ , ψ es un elemento conmutativo del álgebra de Grassmann, no importa en qué orden estén los pares. Si más de un par ψ , ψ tienen el mismo k , la integral es cero, y es fácil comprobar que la suma sobre los emparejamientos da cero en este caso (siempre hay un número par de ellos). Este es el análogo de Grassmann de los momentos gaussianos superiores que completaron el teorema de Wick bosónico anteriormente.
Las reglas para el giro-1/2Las partículas de Dirac son las siguientes: El propagador es el inverso del operador de Dirac, las líneas tienen flechas como para un campo escalar complejo y el diagrama adquiere un factor global de −1 para cada bucle de Fermi cerrado. Si hay un número impar de bucles de Fermi, el diagrama cambia de signo. Históricamente, la regla −1 fue muy difícil de descubrir para Feynman. La descubrió después de un largo proceso de prueba y error, ya que carecía de una teoría adecuada de la integración de Grassmann.
La regla se desprende de la observación de que el número de líneas de Fermi en un vértice es siempre par. Cada término en el Lagrangiano siempre debe ser bosónico. Un bucle de Fermi se cuenta siguiendo las líneas fermiónicas hasta que se regresa al punto de partida, y luego se eliminan esas líneas del diagrama. La repetición de este proceso eventualmente borra todas las líneas fermiónicas: este es el algoritmo de Euler para 2-colorear un gráfico, que funciona siempre que cada vértice tenga grado par. El número de pasos en el algoritmo de Euler solo es igual al número de ciclos de homología fermiónica independientes en el caso especial común de que todos los términos en el Lagrangiano sean exactamente cuadráticos en los campos de Fermi, de modo que cada vértice tiene exactamente dos líneas fermiónicas. Cuando hay interacciones de cuatro Fermi (como en la teoría efectiva de Fermi de las interacciones nucleares débiles ) hay más k -integrales que bucles de Fermi. En este caso, la regla de conteo debería aplicar el algoritmo de Euler emparejando las líneas de Fermi en cada vértice en pares que juntos formen un factor bosónico del término en el Lagrangiano, y al ingresar a un vértice por una línea, el algoritmo siempre debería salir con la línea asociada.
Para aclarar y demostrar la regla, considere un diagrama de Feynman formado a partir de vértices, términos en el Lagrangiano, con campos de fermiones. El término completo es bosónico, es un elemento conmutativo del álgebra de Grassmann, por lo que el orden en que aparecen los vértices no es importante. Las líneas de Fermi están enlazadas en bucles, y al recorrer el bucle, uno puede reordenar los términos del vértice uno después del otro a medida que uno va dando vueltas sin ningún costo de signo. La excepción es cuando regresa al punto de partida, y la semirrecta final debe unirse con la primera semirrecta no enlazada. Esto requiere una permutación para mover el último ψ para que vaya delante del primer ψ , y esto da el signo.
Esta regla es el único efecto visible del principio de exclusión en las líneas internas. Cuando hay líneas externas, las amplitudes son antisimétricas cuando se intercambian dos inserciones de Fermi para partículas idénticas. Esto es automático en el formalismo de fuentes, porque las fuentes de los campos de Fermi son en sí mismas valoradas por Grassmann.
Giro 1: fotones
El propagador ingenuo para fotones es infinito, ya que el Lagrangiano para el campo A es:
La forma cuadrática que define el propagador no es invertible. La razón es la invariancia de calibración del campo; agregar un gradiente a A no cambia la física.
Para solucionar este problema, es necesario fijar un indicador. La forma más conveniente es exigir que la divergencia de A sea una función f , cuyo valor sea aleatorio de un punto a otro. No hace daño integrar sobre los valores de f , ya que solo determina la elección del indicador. Este procedimiento inserta el siguiente factor en la integral de trayectoria para A :
El primer factor, la función delta, fija el calibre. El segundo factor suma los distintos valores de f que son fijaciones de calibre no equivalentes. Esto es simplemente
La contribución adicional de la fijación del calibre cancela la segunda mitad del Lagrangiano libre, dando como resultado el Lagrangiano de Feynman:
que es como cuatro campos escalares libres independientes, uno para cada componente de A. El propagador de Feynman es:
La única diferencia es que el signo de un propagador es incorrecto en el caso de Lorentz: el componente temporal tiene un propagador de signo opuesto. Esto significa que estos estados de partículas tienen norma negativa: no son estados físicos. En el caso de los fotones, es fácil demostrar mediante métodos de diagramas que estos estados no son físicos: su contribución se cancela con los fotones longitudinales para dejar solo dos contribuciones físicas de polarización de fotones para cualquier valor de k .
Si el promedio sobre f se realiza con un coeficiente diferente de 1/2 , los dos términos no se cancelan completamente. Esto da un lagrangiano covariante con un coeficiente , que no afecta nada:
y el propagador covariante para QED es:
Giro 1: fantasmas no abelianos
Para encontrar las reglas de Feynman para campos de calibre no abelianos, el procedimiento que realiza la fijación del calibre debe corregirse cuidadosamente para tener en cuenta un cambio de variables en la integral de trayectoria.
El factor de fijación del calibre tiene un determinante adicional al hacer estallar la función delta:
Para hallar la forma del determinante, consideremos primero una integral bidimensional simple de una función f que depende únicamente de r , no del ángulo θ . Insertando una integral sobre θ :
El factor de derivada garantiza que al eliminar la función delta en θ se elimine la integral. Al intercambiar el orden de integración,
pero ahora la función delta se puede insertar en y ,
La integral sobre θ simplemente da un factor general de 2 π , mientras que la tasa de cambio de y con un cambio en θ es simplemente x , por lo que este ejercicio reproduce la fórmula estándar para la integración polar de una función radial:
En la integral de trayectoria para un campo de calibre no abeliano, la manipulación análoga es:
El factor que se encuentra al frente es el volumen del grupo de calibración y aporta una constante que puede descartarse. La integral restante es sobre la acción fija de calibración.
Para obtener un calibre covariante, la condición de fijación del calibre es la misma que en el caso abeliano:
Cuya variación bajo una transformación de calibre infinitesimal viene dada por:
donde α es el elemento adjunto del álgebra de Lie en cada punto que realiza la transformación de norma infinitesimal. Esto añade el determinante de Faddeev-Popov a la acción:
que puede reescribirse como una integral de Grassmann introduciendo campos fantasma:
El determinante es independiente de f , por lo que la integral de trayectoria sobre f puede dar el propagador de Feynman (o un propagador covariante) eligiendo la medida para f como en el caso abeliano. La acción fija de calibre completa es entonces la acción de Yang Mills en el calibre de Feynman con una acción fantasma adicional:
Los diagramas se derivan de esta acción. El propagador de los campos de espín 1 tiene la forma habitual de Feynman. Hay vértices de grado 3 con factores de momento cuyos acoplamientos son las constantes de estructura, y vértices de grado 4 cuyos acoplamientos son productos de constantes de estructura. Hay bucles fantasma adicionales, que cancelan los estados temporales y longitudinales en los bucles A.
En el caso abeliano, el determinante para los indicadores covariantes no depende de A , por lo que los fantasmas no contribuyen a los diagramas conectados.
Representación de la trayectoria de partículas
Los diagramas de Feynman fueron descubiertos originalmente por Feynman, por ensayo y error, como una forma de representar la contribución a la matriz S de diferentes clases de trayectorias de partículas.
Representación de Schwinger
El propagador escalar euclidiano tiene una representación sugerente:
El significado de esta identidad (que es una integración elemental) se aclara mediante la transformada de Fourier al espacio real.
La contribución de cualquier valor de τ al propagador es una gaussiana de ancho √ τ . La función de propagación total de 0 a x es una suma ponderada sobre todos los tiempos propios τ de una gaussiana normalizada, la probabilidad de terminar en x después de un recorrido aleatorio del tiempo τ .
La representación integral de trayectoria para el propagador es entonces:
que es una reescritura integral de trayectoria de la representación de Schwinger .
La representación de Schwinger es útil tanto para poner de manifiesto el aspecto de partícula del propagador como para simetrizar denominadores de diagramas de bucles.
Combinando denominadores
La representación de Schwinger tiene una aplicación práctica inmediata en los diagramas de bucles. Por ejemplo, para el diagrama de la teoría φ 4 formado uniendo dos x en dos semirrectas y haciendo que las rectas restantes sean externas, la integral sobre los propagadores internos en el bucle es:
Aquí una línea lleva el momento k y la otra k + p . La asimetría se puede corregir poniendo todo en la representación de Schwinger.
Ahora el exponente depende principalmente de t + t ′ ,
excepto por la pequeña parte asimétrica. Definiendo la variable u = t + t ′ y v = yo/tú , la variable u va de 0 a ∞ , mientras que v va de 0 a 1. La variable u es el tiempo propio total del bucle, mientras que v parametriza la fracción del tiempo propio en la parte superior del bucle frente a la parte inferior.
El jacobiano para esta transformación de variables es fácil de calcular a partir de las identidades:
y el " acuñamiento " da
- .
Esto permite evaluar explícitamente la integral u :
dejando sólo la integral v . Este método, inventado por Schwinger pero generalmente atribuido a Feynman, se llama denominador combinatorio . En abstracto, es la identidad elemental:
Pero esta forma no proporciona la motivación física para introducir v ; v es la proporción de tiempo propio en una de las patas del bucle.
Una vez combinados los denominadores, un desplazamiento de k a k ′ = k + vp simetriza todo:
Esta forma muestra que en el momento en que p 2 es más negativo que cuatro veces la masa de la partícula en el bucle, lo que ocurre en una región física del espacio de Lorentz , la integral tiene un corte. Esto es exactamente cuando el momento externo puede crear partículas físicas.
Cuando el bucle tiene más vértices, hay más denominadores para combinar:
La regla general se desprende de la prescripción de Schwinger para n + 1 denominadores:
La integral sobre los parámetros de Schwinger u i se puede dividir como antes en una integral sobre el tiempo propio total u = u 0 + u 1 ... + u n y una integral sobre la fracción del tiempo propio en todos los segmentos del bucle excepto el primero v i = tú yo/tú para i ∈ {1,2,..., n } . Las v i son positivas y suman menos de 1, de modo que la integral v está sobre un símplex de n dimensiones.
El jacobiano para la transformación de coordenadas se puede calcular como antes:
Uniendo todas estas ecuaciones, se obtiene
Esto da la integral:
donde el símplex es la región definida por las condiciones
así como
La realización de la integral u proporciona la prescripción general para combinar denominadores:
Dado que el numerador del integrando no está involucrado, la misma prescripción funciona para cualquier bucle, sin importar los espines que tengan las patas. La interpretación de los parámetros vi es que son la fracción del tiempo propio total empleado en cada pata.
Dispersión
Las funciones de correlación de una teoría cuántica de campos describen la dispersión de partículas. La definición de "partícula" en la teoría relativista de campos no es evidente, porque si se intenta determinar la posición de modo que la incertidumbre sea menor que la longitud de onda de Compton , la incertidumbre en la energía es lo suficientemente grande como para producir más partículas y antipartículas del mismo tipo a partir del vacío. Esto significa que la noción de un estado de una sola partícula es hasta cierto punto incompatible con la noción de un objeto localizado en el espacio.
En la década de 1930, Wigner dio una definición matemática de los estados de partícula única: son una colección de estados que forman una representación irreducible del grupo de Poincaré. Los estados de partícula única describen un objeto con una masa finita, un momento bien definido y un espín. Esta definición es válida para protones y neutrones, electrones y fotones, pero excluye a los quarks, que están permanentemente confinados, por lo que el punto de vista moderno es más flexible: una partícula es cualquier cosa cuya interacción se puede describir en términos de diagramas de Feynman, que tienen una interpretación como una suma de trayectorias de partículas.
Un operador de campo puede actuar para producir un estado de una partícula a partir del vacío, lo que significa que el operador de campo φ ( x ) produce una superposición de estados de partículas de Wigner. En la teoría de campo libre, el campo produce solo estados de una partícula. Pero cuando hay interacciones, el operador de campo también puede producir estados de 3 partículas, 5 partículas (si no hay simetría +/− también 2, 4, 6 partículas). Para calcular la amplitud de dispersión para estados de una sola partícula solo se requiere un límite cuidadoso, enviando los campos al infinito e integrando sobre el espacio para deshacerse de las correcciones de orden superior.
La relación entre las funciones de dispersión y correlación es el teorema LSZ: la amplitud de dispersión para que n partículas vayan a m partículas en un evento de dispersión está dada por la suma de los diagramas de Feynman que entran en la función de correlación para n + m inserciones de campo, dejando fuera los propagadores de las patas externas.
Por ejemplo, para la interacción λφ 4 de la sección anterior, la contribución de orden λ a la función de correlación (Lorentz) es:
Despojar a los propagadores externos, es decir, eliminar los factores de i/k2 , da la amplitud de dispersión invariante M :
que es una constante, independiente del momento entrante y saliente. La interpretación de la amplitud de dispersión es que la suma de | M | 2 sobre todos los estados finales posibles es la probabilidad del evento de dispersión. Sin embargo, la normalización de los estados de una sola partícula debe elegirse con cuidado para garantizar que M sea un invariante relativista.
Los estados de partículas individuales no relativistas se etiquetan por el momento k y se eligen para que tengan la misma norma en cada valor de k . Esto se debe a que el operador unitario no relativista en los estados de partículas individuales es:
En relatividad, la integral sobre los k estados para una partícula de masa m se integra sobre una hipérbola en el espacio E , k definido por la relación energía-momento:
Si la integral pondera cada punto k por igual, la medida no es invariante respecto de Lorentz. La medida invariante integra sobre todos los valores de k y E , restringiéndose a la hipérbola con una función delta invariante respecto de Lorentz:
Por lo tanto, los k -estados normalizados son diferentes de los k -estados normalizados relativísticamente por un factor de
La amplitud invariante M es entonces la amplitud de probabilidad de que los estados entrantes normalizados relativistamente se conviertan en estados salientes normalizados relativistamente.
Para valores no relativistas de k , la normalización relativista es la misma que la normalización no relativista (hasta un factor constante √ m ). En este límite, la amplitud de dispersión invariante φ 4 sigue siendo constante. Las partículas creadas por el campo φ se dispersan en todas las direcciones con la misma amplitud.
El potencial no relativista, que se dispersa en todas direcciones con una amplitud igual (en la aproximación de Born ), es aquel cuya transformada de Fourier es constante: un potencial de función delta. La dispersión de orden más bajo de la teoría revela la interpretación no relativista de esta teoría: describe una colección de partículas con una repulsión de función delta. Dos de estas partículas tienen aversión a ocupar el mismo punto al mismo tiempo.
Efectos no perturbativos
Si consideramos los diagramas de Feynman como una serie de perturbaciones , no aparecen efectos no perturbativos como el efecto túnel, porque cualquier efecto que llegue a cero más rápido que cualquier polinomio no afecta a la serie de Taylor. Ni siquiera hay estados ligados, ya que en cualquier orden finito las partículas solo se intercambian una cantidad finita de veces y, para crear un estado ligado, la fuerza de unión debe durar eternamente.
Pero este punto de vista es engañoso, porque los diagramas no sólo describen la dispersión, sino que también son una representación de las correlaciones de la teoría de campos de corta distancia. No sólo codifican procesos asintóticos como la dispersión de partículas, sino que también describen las reglas de multiplicación de campos, la expansión del producto del operador . Los procesos de tunelización no perturbativa implican configuraciones de campo que en promedio se hacen grandes cuando la constante de acoplamiento se hace pequeña, pero cada configuración es una superposición coherente de partículas cuyas interacciones locales se describen mediante diagramas de Feynman. Cuando el acoplamiento es pequeño, estos se convierten en procesos colectivos que involucran grandes cantidades de partículas, pero donde las interacciones entre cada una de las partículas son simples. [ cita requerida ] (La serie de perturbaciones de cualquier teoría cuántica de campos interactuante tiene un radio de convergencia cero , lo que complica el límite de la serie infinita de diagramas necesarios (en el límite del acoplamiento que se desvanece) para describir tales configuraciones de campo).
Esto significa que los efectos no perturbativos aparecen asintóticamente en las resumiciones de infinitas clases de diagramas, y estos diagramas pueden ser localmente simples. Los gráficos determinan las ecuaciones locales de movimiento, mientras que las configuraciones permitidas a gran escala describen la física no perturbativa. Pero debido a que los propagadores de Feynman no son locales en el tiempo, traducir un proceso de campo a un lenguaje de partículas coherente no es completamente intuitivo, y solo se ha trabajado explícitamente en ciertos casos especiales. En el caso de estados ligados no relativistas , la ecuación de Bethe-Salpeter describe la clase de diagramas a incluir para describir un átomo relativista. Para la cromodinámica cuántica , las reglas de suma de Shifman-Vainshtein-Zakharov describen modos de campo de longitud de onda larga excitados no perturbativamente en el lenguaje de partículas, pero solo de manera fenomenológica.
El número de diagramas de Feynman en órdenes superiores de la teoría de perturbaciones es muy grande, porque hay tantos diagramas como grafos con un número dado de nodos. Los efectos no perturbativos dejan una huella en la forma en que el número de diagramas y sumas diverge en órdenes superiores. Es sólo porque los efectos no perturbativos aparecen en forma oculta en los diagramas que fue posible analizar los efectos no perturbativos en la teoría de cuerdas, donde en muchos casos una descripción de Feynman es la única disponible.
En la cultura popular
- El uso del diagrama anterior de la partícula virtual que produce un par quark - antiquark fue presentado en la comedia televisiva The Big Bang Theory , en el episodio "La conjetura del tarro del murciélago".
- PhD Comics del 11 de enero de 2012 muestra diagramas de Feynman que visualizan y describen las interacciones académicas cuánticas , es decir, los caminos que siguen los estudiantes de doctorado al interactuar con sus asesores. [12]
- Diagramas de vacío , una historia de ciencia ficción de Stephen Baxter , presenta el diagrama de vacío titular, un tipo específico de diagrama de Feynman.
- Feynman y su esposa, Gweneth Howarth, compraron una Dodge Tradesman Maxivan en 1975 y la pintaron con diagramas de Feynman. [13] La camioneta actualmente es propiedad del diseñador de videojuegos y físico Seamus Blackley . [14] [15] [16] [17] [18] [19] [20] [21] [22] Qantum era la identificación de la matrícula. [23]
Véase también
Notas
- ^ "La contribución de Dyson fue indicar cómo se podían utilizar las ideas visuales de Feynman [...] Se dio cuenta de que los diagramas de Feynman [...] también pueden verse como una representación del contenido lógico de las teorías de campo (tal como se indica en sus expansiones perturbativas)". Schweber, op.cit (1994)
Referencias
- ^ Kaiser, David (2005). "La física y los diagramas de Feynman" (PDF) . American Scientist . 93 (2): 156. doi :10.1511/2005.52.957. Archivado (PDF) desde el original el 27 de mayo de 2012.
- ^ "Por qué los diagramas de Feynman son tan importantes". Revista Quanta . 5 de julio de 2016. Consultado el 16 de junio de 2020 .
- ^ Feynman, Richard (1949). "La teoría de los positrones". Physical Review . 76 (6): 749–759. Bibcode :1949PhRv...76..749F. doi :10.1103/PhysRev.76.749. S2CID 120117564. Archivado desde el original el 2022-08-09 . Consultado el 2021-11-12 .
En esta solución, los "estados de energía negativos" aparecen en una forma que puede representarse (como hizo Stückelberg) en el espacio-tiempo como ondas que se alejan del potencial externo y se desplazan hacia atrás en el tiempo. Experimentalmente, una onda de este tipo corresponde a un positrón que se acerca al potencial y aniquila al electrón.
- ^ Penco, R.; Mauro, D. (2006). "Teoría de perturbaciones a través de diagramas de Feynman en mecánica clásica". Revista Europea de Física . 27 (5): 1241–1250. arXiv : hep-th/0605061 . Código Bibliográfico :2006EJPh...27.1241P. doi :10.1088/0143-0807/27/5/023. S2CID 2895311.
- ↑ George Johnson (julio de 2000). «El jaguar y el zorro». The Atlantic . Consultado el 26 de febrero de 2013 .
- ^ Gribbin, John; Gribbin, Mary (1997). "5". Richard Feynman: una vida en la ciencia . Penguin-Putnam.
- ^ Mlodinow, Leonard (2011). El arco iris de Feynman . Vintage. pág. 29.
- ^ Gerardus 't Hooft, Martinus Veltman, Diagrammar , CERN Yellow Report 1973, reimpreso en G. 't Hooft, Under the Spell of Gauge Principle (World Scientific, Singapur, 1994), Introducción en línea Archivado el 19 de marzo de 2005 en Wayback Machine.
- ^ Martinus Veltman, Diagrammatica: El camino hacia los diagramas de Feynman , Cambridge Lecture Notes in Physics, ISBN 0-521-45692-4
- ^ Bjorken, JD; Drell, SD (1965). Campos cuánticos relativistas . Nueva York: McGraw-Hill. pág. viii. ISBN. 978-0-07-005494-3.
- ^ Fetter, Alexander L.; Walecka, John Dirk (20 de junio de 2003). Teoría cuántica de sistemas de muchas partículas. Courier Corporation. ISBN 978-0-486-42827-7.
- ^ Jorge Cham , Interacción académica – Diagramas de Feynman, 11 de enero de 2012.
- ^ Jepsen, Kathryn (5 de agosto de 2014). "Salvando la furgoneta de Feynman". Revista Symmetry . Consultado el 23 de junio de 2022 .
- ^ Dubner, Stephen J. (7 de febrero de 2024). "El brillante señor Feynman". Freakonomics . Consultado el 9 de febrero de 2024 .
- ^ "Fermilab hoy". www.fnal.gov .
- ^
- https://www.flickr.com/photos/122759998@N03/14430191165
- https://www.flickr.com/photos/jkannenberg/14287569353/in/photostream/
- ^
- https://www.nst.com.my/cbt/2019/04/481648/original-space-van
- mamá, esposa, Feynman, hija, hijo, camioneta, Ensenada, MX
- ^ "La furgoneta de Feynman". 21 de octubre de 2021 – vía www.youtube.com.
- ^
- Caminos para avances teóricos en visualización
- Enero de 2017
- Gráficos y aplicaciones informáticas del IEEE
- 37(4):103-112
- Documento I:10.1109/MCG.2017.3271463
- https://www.researchgate.net/publication/319224539
- ^ "Fermilab | Exposición TUFTE | 12 de abril - 26 de junio de 2014 | Acerca de la exposición". www.fnal.gov .
- ^
- Harald Fritzsch
- https://www.marinabaysands.com/content/dam/singapore/marinabaysands/master/main/home/museum/Feynman/Richard%20Feynman%20by%20Harald%20Fritzsch.pdf
- ^ "Los garabatos del Dr. Feynman". 12 de julio de 2005.
- ^ "Cuántica". Arte de Liz Alzona .
Fuentes
- Veltman, Martinus JG; 'T Hooft, Gerardus (1973). Diagrammar (Reporte). Informe amarillo del CERN. doi :10.5170/CERN-1973-009.
- Kaiser, David (2005). Distinguiendo teorías: la dispersión de los diagramas de Feynman en la física de posguerra . Chicago: University of Chicago Press. ISBN 978-0-226-42266-4.
- Veltman, Martinus (16 de junio de 1994). Diagrammatica: el camino hacia los diagramas de Feynman . Cambridge Lecture Notes in Physics. ISBN 0-521-45692-4.(versión ampliada y actualizada de 't Hooft & Veltman, 1973, citado anteriormente)
- Srednicki, Mark Allen (2006). Teoría cuántica de campos. Guión (edición preliminar). Santa Bárbara, California: Universidad de California, Santa Bárbara . Archivado desde el original el 25 de julio de 2011. Consultado el 28 de enero de 2011 .
- Schweber, Silvan S. (1994). QED y los hombres que la crearon: Dyson, Feynman, Schwinger y Tomonaga . Princeton series in physics. Princeton, NJ: Princeton University Press . ISBN 978-0-691-03327-3.
Enlaces externos
- Artículo de AMS: "Novedades en matemáticas: diagramas de Feynman de dimensión finita"
- Cómo dibujar diagramas de Feynman explicado por Flip Tanedo en Quantumdiaries.com
- Dibujar diagramas de Feynman con la biblioteca C++ FeynDiagram que produce salida PostScript.
- Herramienta de diagramas en línea Una aplicación gráfica para crear diagramas listos para publicar.
- JaxoDraw Un programa Java para dibujar diagramas de Feynman.
- Bowley, Roger; Copeland, Ed (2010). "Diagramas de Feynman". Sesenta símbolos . Brady Haran para la Universidad de Nottingham .






























































![{\displaystyle iW[J]\equiv \ln Z[J].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a03aef8a72b98aa83afeccb54512c30e74dd0762)
![{\displaystyle Z[J]\propto \sum _{k}{D_{k}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c7b6e822c008b3a97c2e25ae9a16d806decc9e7)


![{\displaystyle Z[J]\propto \prod _{i}{\sum _{n_{i}=0}^{\infty }{\frac {C_{i}^{n_{i}}}{n_ {i}!}}}=\exp {\sum _{i}{C_{i}}}\propto \exp {W[J]}\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50886f901a854ec595c3b9727199e105ad57b73f)




![{\displaystyle \log {\big (}Z[h]{\big )}=\sum _{n,C}h(k_{1})h(k_{2})\cdots h(k_{n})C(k_{1},\cdots ,k_{n})\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7bb5547d19ab5fdb64ff700ecc8e3835311e446c)
![{\displaystyle Z[h]=\int e^{iS+i\int h\phi }\,D\phi \,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7ea2bd0c5073e68ceff5ddba15e555ce70f92a6)

![{\displaystyle Z[h]=\int e^{iS}e^{i\int _{x}h(x)\phi (x)}\,D\phi =\left\langle e^{ih\ fi }\right\rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b66d7bcdfcff36ef81756bc3cda53721bd81d685)



![{\displaystyle \left\langle \phi (x)\right\rangle ={\frac {1}{Z}}{\frac {\parcial }{\parcial h(x)}}Z[h]={\frac {\parcial }{\parcial h(x)}}\log {\big (}Z[h]{\big )}\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/370ee6c83d4c8ed003752105106c84371401dfa1)
























































