Paridad (física)

En física , una transformación de paridad (también llamada inversión de paridad ) es la inversión del signo de una coordenada espacial . En tres dimensiones, también puede referirse a la inversión simultánea del signo de las tres coordenadas espaciales (una reflexión puntual ):

$${\displaystyle \mathbf {P} :{\begin{pmatrix}x\\y\\z\end{pmatrix}}\mapsto {\begin{pmatrix}-x\\-y\\-z\end{pmatrix }}.}$$

También puede considerarse como una prueba de quiralidad de un fenómeno físico, en el sentido de que una inversión de paridad transforma un fenómeno en su imagen especular.

Todas las interacciones fundamentales de las partículas elementales , con excepción de la interacción débil , son simétricas bajo paridad. Como se estableció en el experimento de Wu realizado en la Oficina Nacional de Normas de Estados Unidos por el científico chino-estadounidense Chien-Shiung Wu , la interacción débil es quiral y, por lo tanto, proporciona un medio para investigar la quiralidad en física. En su experimento, Wu aprovechó el papel controlador de las interacciones débiles en la desintegración radiactiva de los isótopos atómicos para establecer la quiralidad de la fuerza débil.

Por el contrario, en interacciones que son simétricas bajo paridad, como el electromagnetismo en la física atómica y molecular, la paridad sirve como un poderoso principio de control subyacente a las transiciones cuánticas.

Una representación matricial de P (en cualquier número de dimensiones) tiene un determinante igual a −1 y, por lo tanto, es distinta de una rotación , que tiene un determinante igual a 1. En un plano bidimensional, una inversión simultánea de todas las coordenadas en signo no es una transformación de paridad; es lo mismo que una rotación de 180° .

En mecánica cuántica, las funciones de onda que no cambian ante una transformación de paridad se describen como funciones pares , mientras que aquellas que cambian de signo bajo una transformación de paridad son funciones impares.

En el marco de las rotaciones , los objetos geométricos clásicos pueden clasificarse en escalares , vectores y tensores de rango superior. En física clásica , las configuraciones físicas deben transformarse en virtud de las representaciones de cada grupo de simetría.

La teoría cuántica predice que los estados en un espacio de Hilbert no necesitan transformarse bajo representaciones del grupo de rotaciones, sino solo bajo representaciones proyectivas . La palabra proyectiva se refiere al hecho de que si uno proyecta la fase de cada estado, donde recordamos que la fase general de un estado cuántico no es observable, entonces una representación proyectiva se reduce a una representación ordinaria. Todas las representaciones también son representaciones proyectivas, pero lo inverso no es cierto, por lo tanto, la condición de representación proyectiva en estados cuánticos es más débil que la condición de representación en estados clásicos.

Las representaciones proyectivas de cualquier grupo son isomorfas a las representaciones ordinarias de una extensión central del grupo. Por ejemplo, las representaciones proyectivas del grupo de rotación tridimensional, que es el grupo ortogonal especial SO(3), son representaciones ordinarias del grupo unitario especial SU(2). Las representaciones proyectivas del grupo de rotación que no son representaciones se denominan espinores y, por lo tanto, los estados cuánticos pueden transformarse no solo como tensores sino también como espinores.

Si a esto se añade una clasificación por paridad, éstas pueden extenderse, por ejemplo, a nociones de

• escalares ( P = +1 ) y pseudoescalares ( P = −1 ) que son rotacionalmente invariantes.
• vectores ( P = −1 ) y vectores axiales (también llamados pseudovectores ) ( P = +1 ) que se transforman como vectores bajo rotación.

Se pueden definir reflexiones como

$${\displaystyle V_{x}:{\begin{pmatrix}x\\y\\z\end{pmatrix}}\mapsto {\begin{pmatrix}-x\\y\\z\end{pmatrix}}, }$$

que también tienen determinante negativo y forman una transformación de paridad válida. Luego, al combinarlas con rotaciones (o realizar sucesivamente reflexiones en x , y y z ), se puede recuperar la transformación de paridad particular definida anteriormente. Sin embargo, la primera transformación de paridad dada no funciona en un número par de dimensiones, porque da como resultado un determinante positivo. En dimensiones pares, solo se puede utilizar el último ejemplo de transformación de paridad (o cualquier reflexión de un número impar de coordenadas).

La paridad forma el grupo abeliano debido a la relación . Todos los grupos abelianos tienen solo representaciones irreducibles unidimensionales . Para , hay dos representaciones irreducibles: una es par bajo paridad, , la otra es impar, . Estas son útiles en mecánica cuántica. Sin embargo, como se explica a continuación, en mecánica cuántica los estados no necesitan transformarse bajo representaciones reales de paridad sino solo bajo representaciones proyectivas y, por lo tanto, en principio, una transformación de paridad puede rotar un estado en cualquier fase .${\displaystyle \mathbb {Z} _ {2}}$${\displaystyle {\hat {\mathcal {P}}}^{2}={\hat {1}}}$${\displaystyle \mathbb {Z} _ {2}}$${\displaystyle {\hat {\mathcal {P}}}\phi =+\phi }$${\displaystyle {\hat {\mathcal {P}}}\phi =-\phi }$

Una forma alternativa de escribir la clasificación anterior de escalares, pseudoescalares, vectores y pseudovectores es en términos del espacio de representación en el que se transforma cada objeto. Esto se puede dar en términos del homomorfismo de grupo que define la representación. Para una matriz${\estilo de visualización \rho}$${\displaystyle R\in {\text{O}}(3),}$

• escalares: , la representación trivial${\displaystyle \rho(R)=1}$
• pseudoescalares:${\displaystyle \rho (R)=\det(R)}$
• vectores: , la representación fundamental${\displaystyle \rho(R)=R}$
• pseudovectores:${\displaystyle \rho (R)=\det(R)R.}$

Cuando la representación está restringida a , los escalares y pseudoescalares se transforman de manera idéntica, al igual que los vectores y pseudovectores.${\displaystyle {\text{SO}}(3)}$

La ecuación de movimiento de Newton (si la masa es constante) iguala dos vectores y, por lo tanto, es invariante bajo paridad. La ley de la gravedad también involucra sólo vectores y, por lo tanto, también es invariante bajo paridad.${\displaystyle \mathbf {F} = m\mathbf {a} }$

Sin embargo, el momento angular es un vector axial ,${\displaystyle \mathbf {L}}$$${\displaystyle {\begin{alineado}\mathbf {L} &=\mathbf {r} \times \mathbf {p} \\{\hat {P}}\left(\mathbf {L} \right)&=(-\mathbf {r} )\times (-\mathbf {p} )=\mathbf {L} .\end{alineado}}}$$

En la electrodinámica clásica , la densidad de carga es un escalar, el campo eléctrico, y la corriente son vectores, pero el campo magnético, es un vector axial. Sin embargo, las ecuaciones de Maxwell son invariantes bajo paridad porque el rotacional de un vector axial es un vector.${\estilo de visualización \rho}$${\displaystyle \mathbf {E}}$${\displaystyle \mathbf {j}}$${\displaystyle \mathbf {B}}$

Las dos divisiones principales de las variables físicas clásicas tienen paridad par o impar. La forma en que determinadas variables y vectores se clasifican en una u otra categoría depende de si el número de dimensiones del espacio es par o impar. Las categorías de par o impar que se indican a continuación para la transformación de paridad son una cuestión diferente, pero íntimamente relacionada.

Las respuestas que se dan a continuación son correctas para tres dimensiones espaciales. En un espacio bidimensional, por ejemplo, cuando se limita a permanecer en la superficie de un planeta, algunas de las variables cambian de lado.

Las variables clásicas cuyos signos cambian cuando se invierten en la inversión espacial son predominantemente vectores. Entre ellas se incluyen:

Las variables clásicas, predominantemente cantidades escalares, que no cambian con la inversión espacial incluyen:

En mecánica cuántica, las transformaciones del espacio-tiempo actúan sobre los estados cuánticos . La transformación de paridad, , es un operador unitario , que en general actúa sobre un estado de la siguiente manera: .${\displaystyle {\hat {\mathcal {P}}}}$${\estilo de visualización \psi}$${\displaystyle {\hat {\mathcal {P}}}\,\psi {\left(r\right)}=e^{{i\phi }/{2}}\psi {\left(-r\right)}}$

Se debe tener entonces , ya que una fase global es inobservable. El operador , que invierte la paridad de un estado dos veces, deja el espacio-tiempo invariante, y por lo tanto es una simetría interna que rota sus estados propios por fases . Si es un elemento de un grupo de simetría U(1) continuo de rotaciones de fase, entonces es parte de este U(1) y por lo tanto también es una simetría. En particular, podemos definir , que también es una simetría, y por lo tanto podemos elegir llamar a nuestro operador de paridad, en lugar de . Nótese que y por lo tanto tiene valores propios . Las funciones de onda con valor propio bajo una transformación de paridad son funciones pares , mientras que valor propio corresponde a funciones impares. ^[1] Sin embargo, cuando no existe tal grupo de simetría, puede ser que todas las transformaciones de paridad tengan algunos valores propios que sean fases distintas de .${\displaystyle {\hat {\mathcal {P}}}^{2}\,\psi {\left(r\right)}=e^{i\phi }\psi {\left(r\right)}}$${\displaystyle {\hat {\mathcal {P}}}^{2}}$${\displaystyle e^{i\phi}}$${\displaystyle {\hat {\mathcal {P}}}^{2}}$${\displaystyle e^{iQ}}$${\displaystyle e^{-iQ}}$${\displaystyle {\hat {\mathcal {P}}}'\equiv {\hat {\mathcal {P}}}\,e^{-{iQ}/{2}}}$${\displaystyle {\hat {\mathcal {P}}}'}$${\displaystyle {\hat {\mathcal {P}}}}$${\displaystyle {{\hat {\mathcal {P}}}'}^{2}=1}$${\displaystyle {\hat {\mathcal {P}}}'}$${\estilo de visualización \pm 1}$${\estilo de visualización +1}$${\estilo de visualización -1}$${\estilo de visualización \pm 1}$

En el caso de las funciones de onda electrónicas, los estados pares suelen indicarse con un subíndice g para gerade (en alemán: par) y los estados impares con un subíndice u para ungerade (en alemán: impar). Por ejemplo, el nivel de energía más bajo del ion de la molécula de hidrógeno (H ₂ ⁺ ) está etiquetado y el nivel de energía siguiente (más alto) está etiquetado como . ^[2]${\displaystyle 1\sigma _{g}}$${\displaystyle 1\sigma _{u}}$

Las funciones de onda de una partícula que se mueve dentro de un potencial externo, que es centrosimétrico (energía potencial invariante con respecto a una inversión espacial, simétrica al origen), permanecen invariables o cambian de signo: estos dos estados posibles se denominan estado par o estado impar de las funciones de onda. ^[3]

La ley de conservación de la paridad de partículas establece que, si un conjunto aislado de partículas tiene una paridad definida, dicha paridad permanece invariable en el proceso de evolución del conjunto. Sin embargo, esto no es cierto para la desintegración beta de los núcleos, porque la interacción nuclear débil viola la paridad. ^[4]

La paridad de los estados de una partícula que se mueve en un campo externo esféricamente simétrico está determinada por el momento angular , y el estado de la partícula está definido por tres números cuánticos: la energía total, el momento angular y la proyección del momento angular. ^[3]

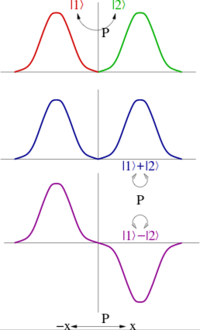
Cuando la paridad genera el grupo abeliano , siempre se pueden tomar combinaciones lineales de estados cuánticos tales que sean pares o impares bajo paridad (ver la figura). Por lo tanto, la paridad de tales estados es ±1. La paridad de un estado multipartícula es el producto de las paridades de cada estado; en otras palabras, la paridad es un número cuántico multiplicativo.${\displaystyle \mathbb {Z} _ {2}}$

En mecánica cuántica, los hamiltonianos son invariantes (simétricos) bajo una transformación de paridad si conmuta con el hamiltoniano. En mecánica cuántica no relativista, esto sucede para cualquier potencial escalar, es decir, , por lo tanto, el potencial es esféricamente simétrico. Los siguientes hechos se pueden demostrar fácilmente:${\displaystyle {\hat {\mathcal {P}}}}$ ${\displaystyle V=V{\left(r\right)}}$

• Si y tienen la misma paridad, entonces donde es el operador de posición .${\displaystyle |\varphi \rangle }$${\displaystyle |\psi \rangle }$${\displaystyle \langle \varphi |{\hat {X}}|\psi \rangle =0}$${\displaystyle {\hat {X}}}$
• Para un estado de momento angular orbital con proyección en el eje z , entonces .${\displaystyle {\bigl |}{\vec {L}},L_{z}{\bigr \rangle }}$${\displaystyle {\vec {L}}}$${\displaystyle L_{z}}$${\displaystyle {\hat {\mathcal {P}}}{\bigl |}{\vec {L}},L_{z}{\bigr \rangle }=\left(-1\right)^{L}{\bigl |}{\vec {L}},L_{z}{\bigr \rangle }}$
• Si , entonces las transiciones dipolares atómicas sólo ocurren entre estados de paridad opuesta. ^[5]${\displaystyle {\bigl [}{\hat {H}},{\hat {\mathcal {P}}}{\bigr ]}=0}$
• Si , entonces un estado propio no degenerado de es también un estado propio del operador de paridad; es decir, una función propia no degenerada de es invariante a o cambia de signo por .${\displaystyle {\bigl [}{\hat {H}},{\hat {\mathcal {P}}}{\bigr ]}=0}$${\displaystyle {\hat {H}}}$${\displaystyle {\hat {H}}}$${\displaystyle {\hat {\mathcal {P}}}}$${\displaystyle {\hat {\mathcal {P}}}}$

Algunas de las funciones propias no degeneradas de no se ven afectadas (son invariantes) por la paridad y las otras simplemente se invierten en signo cuando el operador hamiltoniano y el operador de paridad conmutan:${\displaystyle {\hat {H}}}$${\displaystyle {\hat {\mathcal {P}}}}$$${\displaystyle {\hat {\mathcal {P}}}|\psi \rangle =c\left|\psi \right\rangle ,}$$

donde es una constante, el valor propio de ,${\displaystyle c}$${\displaystyle {\hat {\mathcal {P}}}}$$${\displaystyle {\hat {\mathcal {P}}}^{2}\left|\psi \right\rangle =c\,{\hat {\mathcal {P}}}\left|\psi \right\rangle .}$$

La paridad total de un sistema de muchas partículas es el producto de las paridades de los estados de una partícula. Es -1 si un número impar de partículas se encuentran en estados de paridad impar y +1 en caso contrario. Se utilizan distintas notaciones para indicar la paridad de núcleos, átomos y moléculas.

Los orbitales atómicos tienen paridad (−1) ^ℓ , donde el exponente ℓ es el número cuántico azimutal . La paridad es impar para los orbitales p, f, ... con ℓ = 1, 3, ..., y un estado atómico tiene paridad impar si un número impar de electrones ocupa estos orbitales. Por ejemplo, el estado fundamental del átomo de nitrógeno tiene la configuración electrónica 1s ² 2s ² 2p ³ , y se identifica por el símbolo del término ⁴ S ^o , donde el superíndice o denota paridad impar. Sin embargo, el tercer término excitado a unos 83.300 cm ⁻¹ por encima del estado fundamental tiene la configuración electrónica 1s ² 2s ² 2p ² 3s tiene paridad par ya que solo hay dos electrones 2p, y su símbolo del término es ⁴ P (sin un superíndice o). ^[6]

El hamiltoniano electromagnético completo (rotacional-vibratorio-electrónico-nuclear) de cualquier molécula conmuta con (o es invariante a) la operación de paridad P (o E*, en la notación introducida por Longuet-Higgins ^[7] ) y sus valores propios pueden recibir la etiqueta de simetría de paridad + o - ya que son pares o impares, respectivamente. La operación de paridad implica la inversión de las coordenadas espaciales electrónicas y nucleares en el centro de masa molecular.

Las moléculas centrosimétricas en equilibrio tienen un centro de simetría en su punto medio (el centro de masa nuclear). Esto incluye todas las moléculas diatómicas homonucleares , así como ciertas moléculas simétricas como el etileno , el benceno , el tetrafluoruro de xenón y el hexafluoruro de azufre . Para las moléculas centrosimétricas, el grupo puntual contiene la operación i, que no debe confundirse con la operación de paridad. La operación i implica la inversión de las coordenadas de desplazamiento electrónico y vibracional en el centro de masa nuclear. Para las moléculas centrosimétricas, la operación i conmuta con el hamiltoniano rovibrónico (rotación-vibración-electrónica) y se puede utilizar para etiquetar dichos estados. Los estados electrónicos y vibracionales de las moléculas centrosimétricas no cambian con la operación i o cambian de signo con i . Los primeros se denotan con el subíndice g y se denominan gerade, mientras que los segundos se denotan con el subíndice u y se denominan ungerade. El hamiltoniano electromagnético completo de una molécula centrosimétrica no conmuta con la operación de inversión de grupo puntual i debido al efecto del hamiltoniano hiperfino nuclear. El hamiltoniano hiperfino nuclear puede mezclar los niveles rotacionales de los estados vibrónicos g y u (llamado mezcla orto-para ) y dar lugar a transiciones orto - para ^{[8] [9]}

En los núcleos atómicos, el estado de cada nucleón (protón o neutrón) tiene paridad par o impar, y las configuraciones de nucleones se pueden predecir utilizando el modelo de capas nucleares . En cuanto a los electrones en los átomos, el estado del nucleón tiene paridad general impar si y solo si el número de nucleones en estados de paridad impar es impar. La paridad generalmente se escribe como + (par) o − (impar) después del valor de espín nuclear. Por ejemplo, los isótopos del oxígeno incluyen ¹⁷ O(5/2+), lo que significa que el espín es 5/2 y la paridad es par. El modelo de capas explica esto porque los primeros 16 nucleones están emparejados de modo que cada par tiene espín cero y paridad par, y el último nucleón está en la capa 1d _5/2 , que tiene paridad par ya que ℓ = 2 para el orbital ad. ^[10]

Si se puede demostrar que el estado de vacío es invariante bajo paridad , el hamiltoniano es invariante bajo paridad y las condiciones de cuantificación permanecen sin cambios bajo paridad, entonces se deduce que cada estado tiene buena paridad, y esta paridad se conserva en cualquier reacción.${\displaystyle {\hat {\mathcal {P}}}\left|0\right\rangle =\left|0\right\rangle }$${\displaystyle \left[{\hat {H}},{\hat {\mathcal {P}}}\right]}$

Para demostrar que la electrodinámica cuántica es invariante bajo paridad, tenemos que probar que la acción es invariante y la cuantificación también es invariante. Para simplificar, supondremos que se utiliza la cuantificación canónica ; el estado de vacío es entonces invariante bajo paridad por construcción. La invariancia de la acción se desprende de la invariancia clásica de las ecuaciones de Maxwell. La invariancia del procedimiento de cuantificación canónica se puede calcular, y resulta que depende de la transformación del operador de aniquilación: ^{[ cita requerida ]} donde denota el momento de un fotón y se refiere a su estado de polarización. Esto es equivalente a la afirmación de que el fotón tiene paridad intrínseca impar. De manera similar, se puede demostrar que todos los bosones vectoriales tienen paridad intrínseca impar, y que todos los vectores axiales tienen paridad intrínseca par.$${\displaystyle \mathbf {Pa} (\mathbf {p} ,\pm )\mathbf {P} ^{+}=\mathbf {a} (-\mathbf {p} ,\pm )}$$${\displaystyle \mathbf {p} }$${\displaystyle \pm }$

Una extensión directa de estos argumentos a las teorías de campos escalares muestra que los escalares tienen paridad par. Es decir, , ya que Esto es cierto incluso para un campo escalar complejo. (Los detalles de los espinores se tratan en el artículo sobre la ecuación de Dirac , donde se muestra que los fermiones y los antifermiones tienen paridad intrínseca opuesta).${\displaystyle {\mathsf {P}}\phi (-\mathbf {x} ,t){\mathsf {P}}^{-1}=\phi (\mathbf {x} ,t)}$$${\displaystyle \mathbf {Pa} (\mathbf {p} )\mathbf {P} ^{+}=\mathbf {a} (-\mathbf {p} )}$$

Con los fermiones hay una ligera complicación porque hay más de un grupo de espín .

La aplicación del operador de paridad dos veces deja las coordenadas sin cambios, lo que significa que P ² debe actuar como una de las simetrías internas de la teoría, como máximo cambiando la fase de un estado. ^[11] Por ejemplo, el Modelo Estándar tiene tres simetrías globales U(1) con cargas iguales al número bariónico B , el número leptónico L y la carga eléctrica Q . Por lo tanto, el operador de paridad satisface P ² = e ^{iαB + iβL + iγQ} para alguna elección de α , β y γ . Este operador tampoco es único en el sentido de que siempre se puede construir un nuevo operador de paridad P' multiplicándolo por una simetría interna como P' = P e ^iαB para algún α .

Para ver si el operador de paridad siempre se puede definir para satisfacer P ² = 1 , considere el caso general cuando P ² = Q para alguna simetría interna Q presente en la teoría. El operador de paridad deseado sería P' = P Q ^−1/2 . Si Q es parte de un grupo de simetría continua, entonces Q ^−1/2 existe, pero si es parte de una simetría discreta , entonces este elemento no necesita existir y tal redefinición puede no ser posible. ^[12]

El Modelo Estándar exhibe una simetría (−1) ^F , donde F es el operador de número fermiónico que cuenta cuántos fermiones hay en un estado. Dado que todas las partículas en el Modelo Estándar satisfacen F = B + L , la simetría discreta también es parte del grupo de simetría continua e ^{iα ( B + L ) . Si el operador de paridad satisfizo} P ² = (−1) ^F , entonces puede redefinirse para dar un nuevo operador de paridad que satisfaga P ² = 1 . Pero si el Modelo Estándar se extiende incorporando neutrinos de Majorana , que tienen F = 1 y B + L = 0 , entonces la simetría discreta (−1) ^F ya no es parte del grupo de simetría continua y la redefinición deseada del operador de paridad no puede realizarse. En cambio, satisface P ⁴ = 1 por lo que los neutrinos de Majorana tendrían paridades intrínsecas de ± i .

En 1954, un artículo de William Chinowsky y Jack Steinberger demostró que el pión tiene paridad negativa. ^[13] Estudiaron la desintegración de un "átomo" formado a partir de un deuterón (²
₁yo⁺
) y un pión cargado negativamente (
π⁻
) en un estado con momento angular orbital cero en dos neutrones ( ).${\displaystyle ~\mathbf {L} ={\boldsymbol {0}}~}$${\displaystyle n}$

Los neutrones son fermiones y por lo tanto obedecen a la estadística de Fermi-Dirac , lo que implica que el estado final es antisimétrico. Usando el hecho de que el deuterón tiene espín uno y el pión espín cero junto con la antisimetría del estado final, concluyeron que los dos neutrones deben tener momento angular orbital. La paridad total es el producto de las paridades intrínsecas de las partículas y la paridad extrínseca de la función armónica esférica. Dado que el momento orbital cambia de cero a uno en este proceso, si el proceso debe conservar la paridad total, entonces los productos de las paridades intrínsecas de las partículas iniciales y finales deben tener signo opuesto. Un núcleo de deuterón está hecho de un protón y un neutrón, y así, utilizando la convención antes mencionada de que los protones y neutrones tienen paridades intrínsecas iguales a, argumentaron que la paridad del pión es igual a menos el producto de las paridades de los dos neutrones dividido por la del protón y el neutrón en el deuterón, explícitamente de lo cual concluyeron que el pión es una partícula pseudoescalar .${\displaystyle ~L=1~.}$${\displaystyle ~\left(-1\right)^{L}~.}$${\displaystyle ~+1~}$${\textstyle {\frac {(-1)(1)^{2}}{(1)^{2}}}=-1~,}$

Aunque la paridad se conserva en el electromagnetismo y la gravedad , se viola en interacciones débiles y, tal vez, en algún grado, en interacciones fuertes . ^{[14] [15]} El Modelo Estándar incorpora la violación de la paridad al expresar la interacción débil como una interacción de calibre quiral . Solo los componentes zurdos de las partículas y los componentes diestros de las antipartículas participan en interacciones débiles cargadas en el Modelo Estándar. Esto implica que la paridad no es una simetría de nuestro universo, a menos que exista un sector espejo oculto en el que la paridad se viole en sentido opuesto.

Un oscuro experimento de 1928, llevado a cabo por RT Cox , GC McIlwraith y B. Kurrelmeyer, había informado de una violación de la paridad en desintegraciones débiles , pero, dado que aún no se habían desarrollado los conceptos apropiados, esos resultados no tuvieron impacto. ^[16] En 1929, Hermann Weyl exploró, sin ninguna evidencia, la existencia de una partícula sin masa de dos componentes con espín medio. Esta idea fue rechazada por Pauli , porque implicaba una violación de la paridad. ^[17]

A mediados del siglo XX, varios científicos habían sugerido que la paridad podría no conservarse (en diferentes contextos), pero sin evidencia sólida, estas sugerencias no se consideraron importantes. Luego, en 1956, una revisión y análisis cuidadosos por parte de los físicos teóricos Tsung-Dao Lee y Chen-Ning Yang ^[18] fueron más allá, mostrando que si bien la conservación de la paridad se había verificado en desintegraciones por las interacciones fuertes o electromagnéticas , no se había probado en la interacción débil . Propusieron varias posibles pruebas experimentales directas. En su mayoría fueron ignoradas, ^{[ cita requerida ]} pero Lee pudo convencer a su colega de Columbia Chien-Shiung Wu para que lo intentara. ^{[ cita requerida ]} Necesitaba instalaciones criogénicas especiales y experiencia, por lo que el experimento se realizó en la Oficina Nacional de Normas .

Wu , Ambler , Hayward, Hoppes y Hudson (1957) encontraron una clara violación de la conservación de la paridad en la desintegración beta del cobalto-60 . ^[19] Cuando el experimento estaba llegando a su fin, con una doble verificación en curso, Wu informó a Lee y Yang de sus resultados positivos y, diciendo que los resultados necesitaban un examen más profundo, les pidió que no publicaran los resultados primero. Sin embargo, Lee reveló los resultados a sus colegas de Columbia el 4 de enero de 1957 en una reunión de "almuerzo de viernes" del Departamento de Física de Columbia. ^[20] Tres de ellos, RL Garwin , LM Lederman y RM Weinrich, modificaron un experimento de ciclotrón existente e inmediatamente verificaron la violación de la paridad. ^[21] Retrasaron la publicación de sus resultados hasta que el grupo de Wu estuvo listo, y los dos artículos aparecieron uno tras otro en la misma revista de física.

El descubrimiento de la violación de la paridad explicó el sobresaliente rompecabezas τ–θ en la física de los kaones .

En 2010, se informó que los físicos que trabajaban con el Colisionador de Iones Pesados ​​Relativistas habían creado una burbuja de ruptura de simetría de paridad de corta duración en plasmas de quarks y gluones . Un experimento realizado por varios físicos en la colaboración STAR sugirió que la paridad también puede violarse en la interacción fuerte. ^[15] Se predice que esta violación de paridad local se manifiesta por un efecto magnético quiral . ^{[22] [23]}

A cada partícula se le puede asignar una paridad intrínseca siempre que la naturaleza preserve la paridad. Aunque las interacciones débiles no lo hacen, aún se puede asignar una paridad a cualquier hadrón examinando la reacción de interacción fuerte que la produce, o mediante desintegraciones que no involucran la interacción débil, como la desintegración del mesón rho en piones .

• Simetría C
• Violación de CP
• Teoría electrodébil
• Materia del espejo
• Simetría molecular
• Simetría T

Notas al pie

Citas

• Perkins, Donald H. (2000). Introducción a la física de altas energías . Cambridge University Press. ISBN 9780521621960.
• Sozzi, MS (2008). Simetrías discretas y violación de CP . Oxford University Press . ISBN 978-0-19-929666-8.
• Bigi, II; Sanda, AI (2000). Violación de CP . Cambridge Monographs on Particle Physics, Nuclear Physics and Cosmology. Cambridge University Press . ISBN 0-521-44349-0.
• Weinberg, S. (1995). La teoría cuántica de campos . Cambridge University Press . ISBN 0-521-67053-5.