Paseo aleatorio

Parte de una serie sobre estadísticas
Teoría de la probabilidad
Probabilidad Axiomas Determinismo Sistema Indeterminismo Aleatoriedad
Espacio de probabilidad Espacio muestral Evento Eventos colectivamente exhaustivos Evento elemental Exclusividad mutua Resultado Semifallo Experimento El proceso de Bernoulli Distribución de probabilidad Distribución de Bernoulli Distribución binomial Distribución exponencial Distribución normal Distribución de Pareto Distribución de Poisson Medida de probabilidad Variable aleatoria Proceso de Bernoulli Continuo o discreto Valor esperado Diferencia Cadena de Markov Valor observado Paseo aleatorio Proceso estocástico
Complementary event Joint probability Marginal probability Conditional probability
Independence Conditional independence Law of total probability Law of large numbers Bayes' theorem Boole's inequality
Venn diagram Tree diagram
v t e

En matemáticas , un paseo aleatorio , a veces conocido como el paseo del borracho , es un proceso estocástico que describe un camino que consiste en una sucesión de pasos aleatorios en algún espacio matemático .

Un ejemplo elemental de un paseo aleatorio es el paseo aleatorio en la línea de números enteros que comienza en 0, y en cada paso se mueve +1 o −1 con igual probabilidad . Otros ejemplos incluyen el camino trazado por una molécula mientras viaja en un líquido o un gas (ver movimiento browniano ), la ruta de búsqueda de un animal en busca de alimento , o el precio de una acción fluctuante y la situación financiera de un jugador . Los paseos aleatorios tienen aplicaciones en la ingeniería y en muchos campos científicos, incluyendo la ecología , la psicología , la informática , la física , la química , la biología , la economía y la sociología . El término paseo aleatorio fue introducido por primera vez por Karl Pearson en 1905. ^[1]${\displaystyle \mathbb {Z} }$

Se pueden obtener realizaciones de paseos aleatorios mediante simulación de Monte Carlo . ^[2]

Un modelo popular de paseo aleatorio es el de un paseo aleatorio en una red regular, donde en cada paso la ubicación salta a otro sitio de acuerdo con alguna distribución de probabilidad. En un paseo aleatorio simple , la ubicación solo puede saltar a sitios vecinos de la red, formando un camino de red . En un paseo aleatorio simétrico simple en una red localmente finita, las probabilidades de que la ubicación salte a cada uno de sus vecinos inmediatos son las mismas. El ejemplo mejor estudiado es el paseo aleatorio en la red entera d -dimensional (a veces llamada red hipercúbica) . ^[3]${\displaystyle \mathbb {Z} ^{d}}$

Si el espacio de estados está limitado a dimensiones finitas, el modelo de caminata aleatoria se denomina caminata aleatoria simétrica con borde simple , y las probabilidades de transición dependen de la ubicación del estado porque en los estados de margen y esquina el movimiento es limitado. ^[4]

Un ejemplo elemental de un paseo aleatorio es el paseo aleatorio en la recta de números enteros , , que comienza en 0 y en cada paso se mueve +1 o −1 con igual probabilidad.${\displaystyle \mathbb {Z} }$

Este paseo se puede ilustrar de la siguiente manera. Se coloca un marcador en el cero de la línea numérica y se lanza una moneda. Si cae en cara, el marcador se mueve una unidad a la derecha. Si cae en cruz, el marcador se mueve una unidad a la izquierda. Después de cinco lanzamientos, el marcador podría estar ahora en -5, -3, -1, 1, 3, 5. Con cinco lanzamientos, tres caras y dos cruces, en cualquier orden, caerá en 1. Hay 10 formas de caer en 1 (al sacar tres caras y dos cruces), 10 formas de caer en -1 (al sacar tres cruces y dos caras), 5 formas de caer en 3 (al sacar cuatro caras y una cruz), 5 formas de caer en -3 (al sacar cuatro cruces y una cara), 1 forma de caer en 5 (al sacar cinco caras) y 1 forma de caer en -5 (al sacar cinco cruces). Vea la figura a continuación para ver una ilustración de los posibles resultados de 5 lanzamientos.

Para definir formalmente este paseo, tome variables aleatorias independientes , donde cada variable es 1 o −1, con una probabilidad del 50% para cualquier valor, y establezca y La serie se llama paseo aleatorio simple en . Esta serie (la suma de la secuencia de −1 y 1) da la distancia neta caminada, si cada parte del paseo tiene una longitud de uno. La expectativa de es cero. Es decir, la media de todos los lanzamientos de moneda se acerca a cero a medida que aumenta el número de lanzamientos. Esto se deduce de la propiedad de aditividad finita de la expectativa:${\displaystyle Z_{1},Z_{2},\dots }$${\displaystyle S_{0}=0}$${\textstyle S_{n}=\sum _{j=1}^{n}Z_{j}.}$ ${\displaystyle \{S_{n}\}}$${\displaystyle \mathbb {Z} }$ ${\displaystyle E(S_{n})}$${\displaystyle S_{n}}$$${\displaystyle E(S_{n})=\sum _{j=1}^{n}E(Z_{j})=0.}$$

Un cálculo similar, utilizando la independencia de las variables aleatorias y el hecho de que , muestra que:${\displaystyle E(Z_{n}^{2})=1}$$${\displaystyle E(S_{n}^{2})=\sum _{i=1}^{n}E(Z_{i}^{2})+2\sum _{1\leq i<j\leq n}E(Z_{i}Z_{j})=n.}$$

Esto sugiere que la distancia de traslación esperada después de n pasos debería ser del orden de . De hecho, ^[5]${\displaystyle E(|S_{n}|)\,\!}$ ${\displaystyle {\sqrt {n}}}$$${\displaystyle \lim _{n\to \infty }{\frac {E(|S_{n}|)}{\sqrt {n}}}={\sqrt {\frac {2}{\pi }}}.}$$

Para responder a la pregunta de cuántas veces cruzará un paseo aleatorio una línea divisoria si se le permite seguir caminando eternamente, un simple paseo aleatorio sobre cada punto cruzará cada punto un número infinito de veces. Este resultado tiene muchos nombres: fenómeno del paso de nivel , recurrencia o la ruina del jugador . La razón del último nombre es la siguiente: un jugador con una cantidad finita de dinero acabará perdiendo cuando juegue un juego justo contra un banco con una cantidad infinita de dinero. El dinero del jugador realizará un paseo aleatorio y llegará a cero en algún momento, y el juego habrá terminado.${\displaystyle \mathbb {Z} }$

Si a y b son números enteros positivos, entonces el número esperado de pasos hasta que un paseo aleatorio simple unidimensional que comienza en 0 llega primero a b o − a es ab . La probabilidad de que este paseo llegue a b antes que a − a es , que se puede derivar del hecho de que el paseo aleatorio simple es una martingala . Y estas expectativas y probabilidades de acierto se pueden calcular en la cadena de Markov general del paseo aleatorio unidimensional.${\displaystyle a/(a+b)}$${\displaystyle O(a+b)}$

Algunos de los resultados mencionados anteriormente pueden derivarse de las propiedades del triángulo de Pascal . El número de diferentes paseos de n pasos donde cada paso es +1 o −1 es 2 ⁿ . Para el paseo aleatorio simple, cada uno de estos paseos es igualmente probable. Para que S _n sea igual a un número k es necesario y suficiente que el número de +1 en el paseo exceda a los de −1 en k . De ello se deduce que +1 debe aparecer ( n  +  k )/2 veces entre n pasos de un paseo, por lo tanto, el número de paseos que satisfacen es igual al número de formas de elegir ( n  +  k )/2 elementos de un conjunto de n elementos, ^[6] denotado . Para que esto tenga sentido, es necesario que n  +  k sea un número par, lo que implica que n y k son ambos pares o ambos impares. Por lo tanto, la probabilidad de que sea igual a . Al representar las entradas del triángulo de Pascal en términos de factoriales y utilizar la fórmula de Stirling , se pueden obtener buenas estimaciones de estas probabilidades para valores grandes de .${\displaystyle S_{n}=k}$${\textstyle n \choose (n+k)/2}$${\displaystyle S_{n}=k}$${\textstyle 2^{-n}{n \choose (n+k)/2}}$${\displaystyle n}$

Si el espacio se limita a + para abreviar, la cantidad de formas en que un paseo aleatorio aterrizará en cualquier número dado que tenga cinco lanzamientos se puede mostrar como {0,5,0,4,0,1}.${\displaystyle \mathbb {Z} }$

Esta relación con el triángulo de Pascal se demuestra para valores pequeños de n . En cero vueltas, la única posibilidad será permanecer en cero. Sin embargo, en una vuelta, hay una probabilidad de caer en −1 o una probabilidad de caer en 1. En dos vueltas, un marcador en 1 podría moverse a 2 o volver a cero. Un marcador en −1, podría moverse a −2 o volver a cero. Por lo tanto, hay una probabilidad de caer en −2, dos probabilidades de caer en cero y una probabilidad de caer en 2.

a	-5	-4	-3	-2	-1	0	1	2	3	4	5
${\displaystyle P[S_{0}=k]}$						1
${\displaystyle 2P[S_{1}=k]}$					1		1
${\displaystyle 2^{2}P[S_{2}=k]}$				1		2		1
${\displaystyle 2^{3}P[S_{3}=k]}$			1		3		3		1
${\displaystyle 2^{4}P[S_{4}=k]}$		1		4		6		4		1
${\displaystyle 2^{5}P[S_{5}=k]}$	1		5		10		10		5		1

El teorema del límite central y la ley del logaritmo iterado describen aspectos importantes del comportamiento de los paseos aleatorios simples en . En particular, el primero implica que a medida que n aumenta, las probabilidades (proporcionales a los números en cada fila) se aproximan a una distribución normal .${\displaystyle \mathbb {Z} }$

Para ser precisos, sabiendo que y utilizando la fórmula de Stirling se tiene ${\textstyle \mathbb {P} (X_{n}=k)=2^{-n}{\binom {n}{(n+k)/2}}}$

$${\displaystyle {\log \mathbb {P} (X_{n}=k)}=n\left[\left({1+{\frac {k}{n}}+{\frac {1}{2n}}}\right)\log \left(1+{\frac {k}{n}}\right)+\left({1-{\frac {k}{n}}+{\frac {1}{2n}}}\right)\log \left(1-{\frac {k}{n}}\right)\right]+\log {\frac {\sqrt {2}}{\sqrt {\pi }}}+o(1).}$$

Arreglando la escala , para fijo, y usando la expansión cuando se desvanece, se deduce ${\textstyle k=\lfloor {\sqrt {n}}x\rfloor }$${\textstyle x}$${\textstyle \log(1+{k}/{n})=k/n-k^{2}/2n^{2}+\dots }$${\textstyle k/n}$

$${\displaystyle {\mathbb {P} \left({\frac {X_{n}}{n}}={\frac {\lfloor {\sqrt {n}}x\rfloor }{\sqrt {n}}}\right)}={\frac {1}{\sqrt {n}}}{\frac {1}{2{\sqrt {\pi }}}}e^{-{x^{2}}}(1+o(1)).}$$

Tomando el límite (y observando que corresponde al espaciado de la cuadrícula de escala) se encuentra la densidad gaussiana . En efecto, para una variable aleatoria absolutamente continua con densidad se cumple , con correspondiente a un espaciado infinitesimal.${\textstyle {1}/{\sqrt {n}}}$${\textstyle f(x)={\frac {1}{2{\sqrt {\pi }}}}e^{-{x^{2}}}}$${\textstyle X}$${\textstyle f_{X}}$${\textstyle \mathbb {P} \left(X\in [x,x+dx)\right)=f_{X}(x)dx}$${\textstyle dx}$

Como generalización directa, se pueden considerar los recorridos aleatorios en redes cristalinas (grafos de recubrimiento abeliano de pliegue infinito sobre grafos finitos). En realidad, es posible establecer el teorema del límite central y el teorema de la gran desviación en este contexto. ^{[7] [8]}

Un paseo aleatorio unidimensional también puede verse como una cadena de Markov cuyo espacio de estados está dado por los números enteros Para algún número p que satisface , las probabilidades de transición (la probabilidad P _i,j de moverse del estado i al estado j ) están dadas por${\displaystyle i=0,\pm 1,\pm 2,\dots .}$${\displaystyle \,0<p<1}$$${\displaystyle \,P_{i,i+1}=p=1-P_{i,i-1}.}$$

El paseo aleatorio heterogéneo dibuja en cada paso de tiempo un número aleatorio que determina las probabilidades locales de salto y luego un número aleatorio que determina la dirección real del salto. La cuestión principal es la probabilidad de permanecer en cada uno de los diversos sitios después de los saltos, y en el límite de esta probabilidad cuando es muy grande.${\displaystyle t}$${\displaystyle t}$

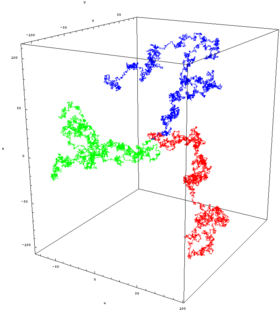
En dimensiones superiores, el conjunto de puntos recorridos aleatoriamente tiene propiedades geométricas interesantes. De hecho, se obtiene un fractal discreto , es decir, un conjunto que exhibe autosimilitud estocástica en grandes escalas. En escalas pequeñas, se puede observar "irregularidad" resultante de la cuadrícula en la que se realiza el recorrido. La trayectoria de un recorrido aleatorio es la colección de puntos visitados, considerados como un conjunto sin tener en cuenta el momento en que el recorrido llegó al punto. En una dimensión, la trayectoria es simplemente todos los puntos entre la altura mínima y la altura máxima alcanzada por el recorrido (ambos son, en promedio, del orden de ).${\displaystyle {\sqrt {n}}}$

Para visualizar el caso bidimensional, podemos imaginar a una persona caminando al azar por una ciudad. La ciudad es efectivamente infinita y está organizada en una cuadrícula de aceras. En cada intersección, la persona elige aleatoriamente una de las cuatro rutas posibles (incluida la ruta original). Formalmente, se trata de un paseo aleatorio por el conjunto de todos los puntos del plano con coordenadas enteras .

Para responder a la pregunta de si la persona regresará alguna vez al punto de partida original del paseo, este es el equivalente bidimensional del problema del paso a nivel discutido anteriormente. En 1921, George Pólya demostró que la persona casi seguramente regresaría al punto de partida en un paseo aleatorio bidimensional, pero para 3 dimensiones o más, la probabilidad de regresar al punto de origen disminuye a medida que aumenta el número de dimensiones. En 3 dimensiones, la probabilidad disminuye a aproximadamente el 34%. ^[9] El matemático Shizuo Kakutani era conocido por referirse a este resultado con la siguiente cita: "Un hombre borracho encontrará su camino a casa, pero un pájaro borracho puede perderse para siempre". ^[10]

La probabilidad de recurrencia es en general , que puede derivarse mediante funciones generadoras ^[11] o el proceso de Poisson. ^[12]${\displaystyle p=1-\left({\frac {1}{\pi ^{d}}}\int _{[-\pi ,\pi ]^{d}}{\frac {\prod _{i=1}^{d}d\theta _{i}}{1-{\frac {1}{d}}\sum _{i=1}^{d}\cos \theta _{i}}}\right)^{-1}}$

Otra variación de esta pregunta, que también fue formulada por Pólya, es: "si dos personas parten del mismo punto de partida, ¿volverán a encontrarse alguna vez?" ^[13] Se puede demostrar que la diferencia entre sus posiciones (dos recorridos aleatorios independientes) también es un recorrido aleatorio simple, por lo que es casi seguro que se volverán a encontrar en un recorrido bidimensional, pero para dimensiones tridimensionales y superiores la probabilidad disminuye con el número de dimensiones. Paul Erdős y Samuel James Taylor también demostraron en 1960 que para dimensiones menores o iguales a 4, dos recorridos aleatorios independientes que parten de dos puntos dados tienen casi con seguridad infinitas intersecciones, pero para dimensiones superiores a 5, es casi seguro que se intersecan solo con una frecuencia finita. ^[14]

La función asintótica para un paseo aleatorio bidimensional a medida que aumenta el número de pasos se da mediante una distribución de Rayleigh . La distribución de probabilidad es una función del radio desde el origen y la longitud del paso es constante para cada paso. Aquí, se supone que la longitud del paso es 1, N es el número total de pasos y r es el radio desde el origen. ^[15]

$${\displaystyle P(r)={\frac {2r}{N}}e^{-r^{2}/N}}$$

Un proceso de Wiener es un proceso estocástico con un comportamiento similar al del movimiento browniano , el fenómeno físico en el que una partícula diminuta se difunde en un fluido. (A veces, el proceso de Wiener se denomina "movimiento browniano", aunque, en sentido estricto, se trata de una confusión entre un modelo y el fenómeno que se modela).

Un proceso de Wiener es el límite de escala del paseo aleatorio en dimensión 1. Esto significa que si hay un paseo aleatorio con pasos muy pequeños, hay una aproximación a un proceso de Wiener (y, con menor precisión, a un movimiento browniano). Para ser más precisos, si el tamaño del paso es ε, uno necesita tomar un paseo de longitud L /ε ² para aproximarse a una longitud de Wiener de L . A medida que el tamaño del paso tiende a 0 (y el número de pasos aumenta proporcionalmente), el paseo aleatorio converge a un proceso de Wiener en un sentido apropiado. Formalmente, si B es el espacio de todos los caminos de longitud L con la topología máxima, y ​​si M es el espacio de medida sobre B con la topología de norma, entonces la convergencia está en el espacio M . De manera similar, un proceso de Wiener en varias dimensiones es el límite de escala del paseo aleatorio en el mismo número de dimensiones.

Un paseo aleatorio es un fractal discreto (una función con dimensiones enteras; 1, 2, ...), pero una trayectoria de proceso de Wiener es un fractal verdadero, y existe una conexión entre los dos. Por ejemplo, tomemos un paseo aleatorio hasta que llegue a un círculo de radio r multiplicado por la longitud del paso. El número promedio de pasos que realiza es r ² . ^{[ cita requerida ]} Este hecho es la versión discreta del hecho de que un paseo de proceso de Wiener es un fractal de dimensión  2 de Hausdorff . ^{[ cita requerida ]}

En dos dimensiones, el número promedio de puntos que un mismo paseo aleatorio tiene en el límite de su trayectoria es r ^4/3 . Esto corresponde al hecho de que el límite de la trayectoria de un proceso de Wiener es un fractal de dimensión 4/3, un hecho predicho por Mandelbrot mediante simulaciones pero demostrado recién en 2000 por Lawler , Schramm y Werner . ^[16]

Un proceso de Wiener disfruta de muchas simetrías que un paseo aleatorio no tiene. Por ejemplo, un paseo de proceso de Wiener es invariante a las rotaciones, pero el paseo aleatorio no lo es, ya que la cuadrícula subyacente no lo es (el paseo aleatorio es invariante a las rotaciones de 90 grados, pero los procesos de Wiener también lo son a las rotaciones de, por ejemplo, 17 grados). Esto significa que, en muchos casos, los problemas en un paseo aleatorio son más fáciles de resolver traduciéndolos a un proceso de Wiener, resolviendo el problema allí y luego traduciendo de nuevo. Por otro lado, algunos problemas son más fáciles de resolver con paseos aleatorios debido a su naturaleza discreta.

El proceso de caminata aleatoria y el proceso de Wiener pueden estar acoplados , es decir, manifestarse en el mismo espacio de probabilidad de una manera dependiente que los obliga a estar bastante cerca. El acoplamiento más simple de este tipo es la incrustación de Skorokhod , pero existen acoplamientos más precisos, como el teorema de aproximación de Komlós–Major–Tusnády .

La convergencia de un paseo aleatorio hacia el proceso de Wiener está controlada por el teorema del límite central y por el teorema de Donsker . Para una partícula en una posición fija conocida en t  = 0, el teorema del límite central nos dice que después de una gran cantidad de pasos independientes en el paseo aleatorio, la posición del caminante se distribuye de acuerdo con una distribución normal de varianza total :

$${\displaystyle \sigma ^{2}={\frac {t}{\delta t}}\,\varepsilon ^{2},}$$

donde t es el tiempo transcurrido desde el inicio del paseo aleatorio, es el tamaño de un paso del paseo aleatorio y es el tiempo transcurrido entre dos pasos sucesivos.${\displaystyle \varepsilon }$${\displaystyle \delta t}$

Esto corresponde a la función de Green de la ecuación de difusión que controla el proceso de Wiener, que sugiere que, después de una gran cantidad de pasos, el camino aleatorio converge hacia un proceso de Wiener.

En 3D, la varianza correspondiente a la función de Green de la ecuación de difusión es:$${\displaystyle \sigma ^{2}=6\,D\,t.}$$

Igualando esta cantidad con la varianza asociada a la posición del caminante aleatorio, se obtiene el coeficiente de difusión equivalente a considerar para el proceso asintótico de Wiener hacia el cual converge el paseo aleatorio después de un gran número de pasos: (válido sólo en 3D).$${\displaystyle D={\frac {\varepsilon ^{2}}{6\delta t}}}$$

Las dos expresiones de la varianza anteriores corresponden a la distribución asociada al vector que une los dos extremos del paseo aleatorio, en 3D. La varianza asociada a cada componente , o es sólo un tercio de este valor (aún en 3D).${\displaystyle {\vec {R}}}$${\displaystyle R_{x}}$${\displaystyle R_{y}}$${\displaystyle R_{z}}$

Para 2D: ^[17]

$${\displaystyle D={\frac {\varepsilon ^{2}}{4\delta t}}.}$$

Para 1D: ^[18]

$${\displaystyle D={\frac {\varepsilon ^{2}}{2\delta t}}.}$$

Un paseo aleatorio que tiene un tamaño de paso que varía según una distribución normal se utiliza como modelo para datos de series de tiempo del mundo real, como los mercados financieros.

Aquí, el tamaño del paso es la distribución normal acumulativa inversa donde 0 ≤  z  ≤ 1 es un número aleatorio distribuido uniformemente, y μ y σ son la media y las desviaciones estándar de la distribución normal, respectivamente.${\displaystyle \Phi ^{-1}(z,\mu ,\sigma )}$

Si μ no es cero, el recorrido aleatorio variará en torno a una tendencia lineal. Si v _s es el valor inicial del recorrido aleatorio, el valor esperado después de n pasos será v _s + n μ.

Para el caso especial donde μ es igual a cero, después de n pasos, la distribución de probabilidad de la distancia de traslación está dada por N (0, n σ ² ), donde N () es la notación para la distribución normal, n es el número de pasos y σ es de la distribución normal acumulativa inversa como se indicó anteriormente.

Prueba: El paseo aleatorio gaussiano puede considerarse como la suma de una secuencia de variables aleatorias independientes e idénticamente distribuidas, X _i de la distribución normal acumulativa inversa con media igual a cero y σ de la distribución normal acumulativa inversa original:

${\displaystyle Z=\sum _{i=0}^{n}{X_{i}},}$

pero tenemos la distribución para la suma de dos variables aleatorias independientes distribuidas normalmente, Z = X + Y , está dada por (ver aquí) . $${\displaystyle {\mathcal {N}}(\mu _{X}+\mu _{Y},\sigma _{X}^{2}+\sigma _{Y}^{2})}$$

En nuestro caso, μ _X = μ _Y = 0 y σ ² _X = σ ² _Y = σ ² da Por inducción, para n pasos tenemos Para pasos distribuidos según cualquier distribución con media cero y una varianza finita (no necesariamente solo una distribución normal), la distancia de traslación cuadrática media después de n pasos es (ver la identidad de Bienaymé )$${\displaystyle {\mathcal {N}}(0,2\sigma ^{2})}$$${\displaystyle Z\sim {\mathcal {N}}(0,n\sigma ^{2}).}$

${\displaystyle {\sqrt {Var(S_{n})}}={\sqrt {E[S_{n}^{2}]}}=\sigma {\sqrt {n}}.}$

Pero para el paseo aleatorio gaussiano, esta es solo la desviación estándar de la distribución de la distancia de traslación después de n pasos. Por lo tanto, si μ es igual a cero, y dado que la distancia de traslación cuadrática media (RMS) es una desviación estándar, existe un 68,27 % de probabilidad de que la distancia de traslación RMS después de n pasos se encuentre entre . Del mismo modo, existe un 50 % de probabilidad de que la distancia de traslación después de n pasos se encuentre entre .${\displaystyle \pm \sigma {\sqrt {n}}}$${\displaystyle \pm 0.6745\sigma {\sqrt {n}}}$

La cantidad de sitios distintos visitados por un único caminante aleatorio se ha estudiado ampliamente para redes cuadradas y cúbicas y para fractales. ^{[19] [20]} Esta cantidad es útil para el análisis de problemas de atrapamiento y reacciones cinéticas. También está relacionada con la densidad vibracional de estados, ^{[21] [22]} procesos de reacciones de difusión ^[23] y propagación de poblaciones en ecología. ^{[24] [25]}${\displaystyle S(t)}$

La tasa de información de un paseo aleatorio gaussiano con respecto a la distancia de error al cuadrado, es decir, su función de distorsión de tasa cuadrática , se da paramétricamente por ^[26] donde . Por lo tanto, es imposible codificar utilizando un código binario de menos de bits y recuperarlo con un error cuadrático medio esperado menor que . Por otro lado, para cualquier , existe un código binario suficientemente grande y de no más de elementos distintos tal que el error cuadrático medio esperado en la recuperación de este código es como máximo .$${\displaystyle R(D_{\theta })={\frac {1}{2}}\int _{0}^{1}\max\{0,\log _{2}\left(S(\varphi )/\theta \right)\}\,d\varphi ,}$$$${\displaystyle D_{\theta }=\int _{0}^{1}\min\{S(\varphi ),\theta \}\,d\varphi ,}$$${\displaystyle S(\varphi )=\left(2\sin(\pi \varphi /2)\right)^{-2}}$${\displaystyle {\{Z_{n}\}_{n=1}^{N}}}$${\displaystyle NR(D_{\theta })}$ ${\displaystyle D_{\theta }}$${\displaystyle \varepsilon >0}$${\displaystyle N\in \mathbb {N} }$${\displaystyle 2^{NR(D_{\theta })}}$${\displaystyle {\{Z_{n}\}_{n=1}^{N}}}$${\displaystyle D_{\theta }-\varepsilon }$

This section needs additional citations for verification. Please help improve this article by adding citations to reliable sources in this section. Unsourced material may be challenged and removed. (February 2013) (Learn how and when to remove this message)

Como se mencionó, la gama de fenómenos naturales que han sido objeto de intentos de descripción mediante algún tipo de paseos aleatorios es considerable, particularmente en física ^{[27] [28]} y química, ^[29] ciencia de los materiales , ^{[30] [31]} y biología. ^{[32] [33] [34]} Las siguientes son algunas aplicaciones específicas de los paseos aleatorios:

• En economía financiera , la hipótesis del paseo aleatorio se utiliza para modelar los precios de las acciones y otros factores. ^[35] Los estudios empíricos encontraron algunas desviaciones de este modelo teórico, especialmente en las correlaciones de corto y largo plazo. Véase precios de las acciones .
• En genética de poblaciones , el recorrido aleatorio describe las propiedades estadísticas de la deriva genética.
• En física , los paseos aleatorios se utilizan como modelos simplificados del movimiento browniano físico y la difusión, como el movimiento aleatorio de moléculas en líquidos y gases. Véase, por ejemplo, la agregación limitada por difusión. También en física, los paseos aleatorios y algunos de los paseos autointeractuantes desempeñan un papel en la teoría cuántica de campos .
• En la fabricación de semiconductores , los recorridos aleatorios se utilizan para analizar los efectos del tratamiento térmico en nodos más pequeños. Se aplica para comprender la difusión de dopantes , defectos , impurezas , etc., durante pasos críticos de fabricación. Los tratamientos de recorrido aleatorio también se utilizan para estudiar la difusión de reactivos, productos y plasma durante los procesos de deposición química de vapor . La difusión continua se ha utilizado para estudiar el flujo de gases, a escalas macroscópicas, en reactores CVD. Sin embargo, las dimensiones más pequeñas y la mayor complejidad nos han obligado a tratarlos con recorrido aleatorio. Esto permite un análisis preciso de los procesos estocásticos, a nivel molecular y más pequeños, en la fabricación de semiconductores.
• En ecología matemática , los recorridos aleatorios se utilizan para describir los movimientos de animales individuales, para apoyar empíricamente procesos de biodifusión y, ocasionalmente, para modelar la dinámica de poblaciones .
• En física de polímeros , el recorrido aleatorio describe una cadena ideal . Es el modelo más simple para estudiar polímeros . ^[36]
• En otros campos de las matemáticas, el recorrido aleatorio se utiliza para calcular soluciones de la ecuación de Laplace , para estimar la medida armónica y para diversas construcciones en análisis y combinatoria .
• En informática , se utilizan recorridos aleatorios para estimar el tamaño de la Web . ^[37]
• En la segmentación de imágenes , se utilizan recorridos aleatorios para determinar las etiquetas (es decir, "objeto" o "fondo") que se asociarán con cada píxel. ^[38] Este algoritmo se conoce normalmente como algoritmo de segmentación de caminante aleatorio .

• En la investigación del cerebro , se utilizan paseos aleatorios y paseos aleatorios reforzados para modelar cascadas de activación de neuronas en el cerebro.
• En la ciencia de la visión , la deriva ocular tiende a comportarse como un paseo aleatorio. ^[39] Según algunos autores, los movimientos oculares fijacionales en general también se describen bien mediante un paseo aleatorio. ^[40]
• En psicología , los paseos aleatorios explican con precisión la relación entre el tiempo necesario para tomar una decisión y la probabilidad de que se tome una determinada decisión. ^[41]
• Los recorridos aleatorios se pueden utilizar para tomar muestras de un espacio de estados que es desconocido o muy grande, por ejemplo, para elegir una página aleatoria de Internet. ^{[ cita requerida ]} En informática , este método se conoce como Markov Chain Monte Carlo (MCMC).

• En redes inalámbricas , se utiliza un recorrido aleatorio para modelar el movimiento de los nodos. ^{[ cita requerida ]}
• Las bacterias móviles realizan caminatas aleatorias sesgadas . ^[42]
• En física, los paseos aleatorios son la base del método de estimación de Fermi . ^{[ cita requerida ]}
• En la web, el sitio web Twitter utiliza recorridos aleatorios para hacer sugerencias de a quién seguir ^[43]
• Dave Bayer y Persi Diaconis han demostrado que 7 barajadas aleatorias son suficientes para mezclar una baraja de cartas (ver más detalles en barajar ). Este resultado se traduce en una afirmación sobre el paseo aleatorio en el grupo simétrico , que es lo que demuestran, con un uso crucial de la estructura del grupo a través del análisis de Fourier.

Se han considerado varios tipos de procesos estocásticos que son similares a los paseos aleatorios puros pero en los que se permite que la estructura simple sea más generalizada. La estructura pura se puede caracterizar por los pasos que se definen mediante variables aleatorias independientes e idénticamente distribuidas . Los paseos aleatorios pueden tener lugar en una variedad de espacios, como grafos , los números enteros, la línea real, el plano o espacios vectoriales de dimensiones superiores, en superficies curvas o variedades de Riemann de dimensiones superiores y en grupos . También es posible definir paseos aleatorios que toman sus pasos en tiempos aleatorios y, en ese caso, la posición X
_adebe definirse para todos los tiempos t ∈ [0, +∞) . Los casos específicos o límites de los paseos aleatorios incluyen los modelos de vuelo y difusión de Lévy, como el movimiento browniano .

Un recorrido aleatorio de longitud k sobre un grafo G posiblemente infinito con raíz 0 es un proceso estocástico con variables aleatorias tales que y es un vértice elegido de manera uniforme al azar entre los vecinos de . Entonces, el número es la probabilidad de que un recorrido aleatorio de longitud k que comience en v termine en w . En particular, si G es un grafo con raíz 0 , es la probabilidad de que un recorrido aleatorio de -pasos regrese a 0 .${\displaystyle X_{1},X_{2},\dots ,X_{k}}$${\displaystyle X_{1}=0}$${\displaystyle {X_{i+1}}}$${\displaystyle X_{i}}$${\displaystyle p_{v,w,k}(G)}$${\displaystyle p_{0,0,2k}}$${\displaystyle 2k}$

Partiendo de la analogía de la sección anterior sobre dimensiones superiores, supongamos ahora que nuestra ciudad ya no es una cuadrícula cuadrada perfecta. Cuando nuestra persona llega a un determinado cruce, elige entre las diversas carreteras disponibles con la misma probabilidad. Por tanto, si el cruce tiene siete salidas, la persona irá a cada una de ellas con una probabilidad de un séptimo. Se trata de un paseo aleatorio en un gráfico. ¿Llegará nuestra persona a su casa? Resulta que, en condiciones más bien suaves, la respuesta sigue siendo sí ^[44], pero, dependiendo del gráfico, la respuesta a la pregunta variante "¿Se volverán a encontrar dos personas?" puede no ser que se encuentren infinitamente a menudo, casi con toda seguridad ^{[45] .}

Un ejemplo de un caso en el que la persona llegará a su casa casi con seguridad es cuando las longitudes de todos los bloques están entre a y b (donde a y b son dos números positivos finitos cualesquiera). Nótese que no asumimos que el gráfico sea plano , es decir, que la ciudad puede contener túneles y puentes. Una forma de demostrar este resultado es utilizando la conexión a las redes eléctricas . Tome un mapa de la ciudad y coloque una resistencia de un ohmio en cada bloque. Ahora mida la "resistencia entre un punto y el infinito". En otras palabras, elija un número R y tome todos los puntos en la red eléctrica con una distancia mayor que R desde nuestro punto y conéctelos. Esta es ahora una red eléctrica finita, y podemos medir la resistencia desde nuestro punto hasta los puntos cableados. Lleve R al infinito. El límite se llama resistencia entre un punto y el infinito . Resulta que lo siguiente es cierto (se puede encontrar una prueba elemental en el libro de Doyle y Snell):

Teorema : un grafo es transitorio si y solo si la resistencia entre un punto y el infinito es finita. No importa qué punto se elija si el grafo es conexo.

En otras palabras, en un sistema transitorio, basta con vencer una resistencia finita para llegar al infinito desde cualquier punto. En un sistema recurrente, la resistencia desde cualquier punto hasta el infinito es infinita.

Esta caracterización de transitoriedad y recurrencia es muy útil, y en concreto nos permite analizar el caso de una ciudad dibujada en el plano con las distancias acotadas.

Un paseo aleatorio en un grafo es un caso muy especial de una cadena de Markov . A diferencia de una cadena de Markov general, el paseo aleatorio en un grafo disfruta de una propiedad llamada simetría temporal o reversibilidad . En términos generales, esta propiedad, también llamada principio de equilibrio detallado , significa que las probabilidades de recorrer un camino dado en una dirección u otra tienen una conexión muy simple entre ellas (si el grafo es regular , son simplemente iguales). Esta propiedad tiene consecuencias importantes.

A partir de la década de 1980, se han realizado muchas investigaciones para conectar las propiedades del gráfico con los paseos aleatorios. Además de la conexión de la red eléctrica descrita anteriormente, existen conexiones importantes con las desigualdades isoperimétricas (ver más aquí) , las desigualdades funcionales como las desigualdades de Sobolev y Poincaré y las propiedades de las soluciones de la ecuación de Laplace . Una parte importante de esta investigación se centró en los gráficos de Cayley de grupos finitamente generados . En muchos casos, estos resultados discretos se trasladan a las variedades y los grupos de Lie o se derivan de ellos .

En el contexto de los grafos aleatorios , en particular el del modelo Erdős–Rényi , se han obtenido resultados analíticos para algunas propiedades de los caminantes aleatorios. Estos incluyen la distribución de los tiempos de primer ^[46] y último golpe ^[47] del caminante, donde el tiempo de primer golpe está dado por la primera vez que el caminante pisa un sitio previamente visitado del grafo, y el tiempo de último golpe corresponde a la primera vez que el caminante no puede realizar un movimiento adicional sin volver a visitar un sitio previamente visitado.

Una buena referencia para el paseo aleatorio en grafos es el libro en línea de Aldous y Fill. Para grupos, consulte el libro de Woess. Si el núcleo de transición es aleatorio en sí mismo (se basa en un entorno ), entonces el paseo aleatorio se denomina "paseo aleatorio en un entorno aleatorio". Cuando la ley del paseo aleatorio incluye la aleatoriedad de , la ley se denomina ley recocida; por otro lado, si se considera fija, la ley se denomina ley apagada. Consulte el libro de Hughes, el libro de Revesz o las notas de la conferencia de Zeitouni.${\displaystyle p(x,y)}$${\displaystyle \omega }$${\displaystyle \omega }$${\displaystyle \omega }$

Podemos pensar en elegir cada arista posible con la misma probabilidad que maximizar la incertidumbre (entropía) localmente. También podríamos hacerlo globalmente: en el paseo aleatorio de entropía máxima (MERW, por sus siglas en inglés) queremos que todos los caminos sean igualmente probables, o en otras palabras: para cada dos vértices, cada camino de longitud dada es igualmente probable. ^[48] Este paseo aleatorio tiene propiedades de localización mucho más fuertes.

Existen varios modelos interesantes de caminos aleatorios en los que cada paso depende del pasado de una manera complicada. Todos son más complejos de resolver analíticamente que el paseo aleatorio habitual; aun así, el comportamiento de cualquier modelo de un caminante aleatorio se puede obtener mediante computadoras. Algunos ejemplos incluyen:

• El paseo que evita el paso por uno mismo . ^[49]

El camino autoevitativo de longitud n en es el camino aleatorio de n pasos que comienza en el origen, hace transiciones solo entre sitios adyacentes en , nunca vuelve a visitar un sitio y se elige uniformemente entre todos esos caminos. En dos dimensiones, debido al autoatrapamiento, un camino autoevitativo típico es muy corto, ^[50] mientras que en una dimensión superior crece más allá de todos los límites. Este modelo se ha utilizado a menudo en física de polímeros (desde la década de 1960).${\displaystyle \mathbb {Z} ^{d}}$${\displaystyle \mathbb {Z} ^{d}}$

• El paseo aleatorio borrado de bucles . ^{[51] [52]}
• El paseo aleatorio reforzado. ^[53]
• El proceso de exploración. ^{[ cita requerida ]}
• El paseo aleatorio multiagente. ^[54]

El paseo aleatorio elegido para maximizar la tasa de entropía tiene propiedades de localización mucho más fuertes.

Paseos aleatorios en los que la dirección del movimiento en un momento dado se correlaciona con la dirección del movimiento en el momento siguiente. Se utiliza para modelar los movimientos de los animales. ^{[55] [56]}

• Paseo aleatorio ramificado
• Movimiento browniano
• Ley del logaritmo iterado
• Vuelo de Lévy
• Hipótesis de alimentación mediante el vuelo de Lévy
• Paseo aleatorio con bucles borrados
• Paseo aleatorio de entropía máxima
• Caminata auto-evitante
• Raíz unitaria

• Aldous, David ; Fill, James Allen (2002). Cadenas de Markov reversibles y recorridos aleatorios en grafos. Archivado desde el original el 27 de febrero de 2019.
• Doyle, Peter G.; Snell, J. Laurie (1984). Paseos aleatorios y redes eléctricas . Carus Mathematical Monographs. Vol. 22. Asociación Matemática de América . arXiv : math.PR/0001057 . ISBN. 978-0-88385-024-4.Sr. 0920811  .
• Feller, William (1968), Introducción a la teoría de la probabilidad y sus aplicaciones (volumen 1). ISBN 0-471-25708-7 
• Hughes, Barry D. (1996), Paseos aleatorios y entornos aleatorios , Oxford University Press. ISBN 0-19-853789-1 
• Norris, James (1998), Cadenas de Markov , Cambridge University Press. ISBN 0-521-63396-6 
• Pólya G.(1921), "Über eine Aufgabe der Wahrscheinlichkeitsrechnung betreffend die Irrfahrt im Strassennetz" Archivado el 4 de marzo de 2016 en Wayback Machine , Mathematische Annalen , 84(1–2):149–160, marzo de 1921.
• Révész, Pal (2013), Paseo aleatorio en entornos aleatorios y no aleatorios (tercera edición) , World Scientific Pub Co. ISBN 978-981-4447-50-8 
• Sunada, Toshikazu (2012). Cristalografía topológica: con vistas al análisis geométrico discreto . Encuestas y tutoriales en ciencias matemáticas aplicadas. Vol. 6. Springer. ISBN 978-4-431-54177-6.
• Weiss G. Aspectos y aplicaciones del paseo aleatorio , Holanda Septentrional, 1994.
• Woess, Wolfgang (2000), Paseos aleatorios en gráficos y grupos infinitos , Cambridge Tracts in Mathematics 138, Cambridge University Press. ISBN 0-521-55292-3 

• Constantes de caminata aleatoria de Pólya
• Paseo aleatorio en el subprograma Java Archivado el 31 de agosto de 2007 en Wayback Machine.
• Paseo aleatorio cuántico
• Estimador de paseo aleatorio gaussiano
• Modelos de conductancia electrónica que utilizan paseos aleatorios de entropía máxima Proyecto de demostraciones de Wolfram