Valores propios y vectores propios

En álgebra lineal , un vector propio ( / ˈaɪɡən- / EYE -gən- ) o vector característico es un vector cuya dirección no cambia (o se invierte) debido a una transformación lineal dada . Más precisamente, un vector propio, , de una transformación lineal, , se escala por un factor constante , , cuando se le aplica la transformación lineal: . El valor propio , valor característico o raíz característica correspondiente es el factor multiplicador (posiblemente negativo).${\displaystyle \mathbf {v}}$${\estilo de visualización T}$${\estilo de visualización \lambda}$${\displaystyle T\mathbf {v} =\lambda \mathbf {v} }$${\estilo de visualización \lambda}$

Geométricamente, los vectores son cantidades multidimensionales con magnitud y dirección, a menudo representadas como flechas. Una transformación lineal rota , estira o corta los vectores sobre los que actúa. Sus vectores propios son aquellos vectores que solo se estiran, sin rotación ni corte. El valor propio correspondiente es el factor por el cual un vector propio se estira o se aplasta. Si el valor propio es negativo, la dirección del vector propio se invierte. ^[1]

Los vectores y valores propios de una transformación lineal sirven para caracterizarla, por lo que desempeñan papeles importantes en todas las áreas en las que se aplica el álgebra lineal, desde la geología hasta la mecánica cuántica . En particular, a menudo se da el caso de que un sistema se representa mediante una transformación lineal cuyas salidas se introducen como entradas a la misma transformación ( retroalimentación ). En una aplicación de este tipo, el valor propio más grande es de particular importancia, porque gobierna el comportamiento a largo plazo del sistema después de muchas aplicaciones de la transformación lineal, y el vector propio asociado es el estado estacionario del sistema.

Consideremos una matriz A y un vector distinto de cero de longitud Si multiplicar A por (denotado por ) simplemente escala por un factor de λ , donde λ es un escalar , entonces se llama vector propio de A , y λ es el valor propio correspondiente. Esta relación se puede expresar como: . ^[2]${\displaystyle n{\times }n}$${\displaystyle \mathbf {v}}$${\displaystyle n.}$${\displaystyle \mathbf {v}}$${\displaystyle A\mathbf {v}}$${\displaystyle \mathbf {v}}$${\displaystyle \mathbf {v}}$${\displaystyle A\mathbf {v} =\lambda \mathbf {v} }$

Existe una correspondencia directa entre matrices cuadradas de n por n y transformaciones lineales de un espacio vectorial de n dimensiones a sí mismo, dada cualquier base del espacio vectorial. Por lo tanto, en un espacio vectorial de dimensión finita, es equivalente definir valores propios y vectores propios utilizando el lenguaje de matrices o el lenguaje de transformaciones lineales. ^{[3] [4]}

La siguiente sección ofrece un punto de vista más general que también cubre los espacios vectoriales de dimensión infinita .

Los valores propios y los vectores propios ocupan un lugar destacado en el análisis de las transformaciones lineales. El prefijo eigen- se adopta de la palabra alemana eigen ( cognado de la palabra inglesa own ) para 'apropiado', 'característico', 'propio'. ^{[5] [6]} Originalmente utilizados para estudiar los ejes principales del movimiento rotacional de cuerpos rígidos , los valores propios y los vectores propios tienen una amplia gama de aplicaciones, por ejemplo en el análisis de estabilidad , análisis de vibraciones , orbitales atómicos , reconocimiento facial y diagonalización de matrices .

En esencia, un vector propio v de una transformación lineal T es un vector distinto de cero que, cuando se le aplica T , no cambia de dirección. La aplicación de T al vector propio solo escala el vector propio por el valor escalar λ , llamado valor propio. Esta condición se puede escribir como la ecuación denominada ecuación de valor propio o ecuación propia . En general, λ puede ser cualquier escalar . Por ejemplo, λ puede ser negativo, en cuyo caso el vector propio invierte la dirección como parte del escalamiento, o puede ser cero o complejo .$${\displaystyle T(\mathbf {v} )=\lambda \mathbf {v} ,}$$

El ejemplo que se muestra aquí, basado en la Mona Lisa , proporciona una ilustración sencilla. Cada punto de la pintura se puede representar como un vector que apunta desde el centro de la pintura hasta ese punto. La transformación lineal en este ejemplo se llama mapeo de cizallamiento . Los puntos en la mitad superior se mueven hacia la derecha y los puntos en la mitad inferior se mueven hacia la izquierda, de manera proporcional a la distancia que se encuentran del eje horizontal que pasa por el medio de la pintura. Por lo tanto, los vectores que apuntan a cada punto en la imagen original se inclinan hacia la derecha o hacia la izquierda y se alargan o acortan mediante la transformación. Los puntos a lo largo del eje horizontal no se mueven en absoluto cuando se aplica esta transformación. Por lo tanto, cualquier vector que apunte directamente a la derecha o a la izquierda sin componente vertical es un vector propio de esta transformación, porque el mapeo no cambia su dirección. Además, todos estos vectores propios tienen un valor propio igual a uno, porque el mapeo tampoco cambia su longitud.

Las transformaciones lineales pueden tomar muchas formas diferentes, mapeando vectores en una variedad de espacios vectoriales, por lo que los vectores propios también pueden tomar muchas formas. Por ejemplo, la transformación lineal podría ser un operador diferencial como , en cuyo caso los vectores propios son funciones llamadas funciones propias que son escaladas por ese operador diferencial, como Alternativamente, la transformación lineal podría tomar la forma de una matriz n por n , en cuyo caso los vectores propios son matrices n por 1. Si la transformación lineal se expresa en la forma de una matriz n por n A , entonces la ecuación de valor propio para una transformación lineal anterior se puede reescribir como la multiplicación de matrices donde el vector propio v es una matriz n por 1. Para una matriz, los valores propios y los vectores propios se pueden usar para descomponer la matriz , por ejemplo, diagonalizándola .${\displaystyle {\frac {d}{dx}}}$$${\displaystyle {\frac {d}{dx}}e^{\lambda x}=\lambda e^{\lambda x}.}$$$${\displaystyle A\mathbf {v} =\lambda \mathbf {v},}$$

Los valores propios y los vectores propios dan lugar a muchos conceptos matemáticos estrechamente relacionados, y el prefijo eigen- se aplica generosamente al nombrarlos:

• El conjunto de todos los vectores propios de una transformación lineal, cada uno emparejado con su valor propio correspondiente, se denomina sistema propio de esa transformación. ^{[7] [8]}
• El conjunto de todos los vectores propios de T correspondientes al mismo valor propio, junto con el vector cero, se denomina espacio propio , o espacio característico de T asociado a ese valor propio. ^[9]
• Si un conjunto de vectores propios de T forma una base del dominio de T , entonces esta base se denomina base propia .

Los valores propios suelen introducirse en el contexto del álgebra lineal o la teoría de matrices . Sin embargo, históricamente, surgieron en el estudio de formas cuadráticas y ecuaciones diferenciales .

En el siglo XVIII, Leonhard Euler estudió el movimiento de rotación de un cuerpo rígido y descubrió la importancia de los ejes principales . ^[a] Joseph-Louis Lagrange se dio cuenta de que los ejes principales son los vectores propios de la matriz de inercia. ^[10]

A principios del siglo XIX, Augustin-Louis Cauchy vio cómo su trabajo podía usarse para clasificar las superficies cuadráticas y lo generalizó a dimensiones arbitrarias. ^[11] Cauchy también acuñó el término racine caractéristique (raíz característica), para lo que ahora se llama valor propio ; su término sobrevive en la ecuación característica . ^[b]

Más tarde, Joseph Fourier utilizó el trabajo de Lagrange y Pierre-Simon Laplace para resolver la ecuación del calor por separación de variables en su famoso libro de 1822 Théorie analytique de la chaleur . ^[12] Charles-François Sturm desarrolló aún más las ideas de Fourier y las llevó a la atención de Cauchy, quien las combinó con sus propias ideas y llegó al hecho de que las matrices simétricas reales tienen valores propios reales. ^[11] Esto fue extendido por Charles Hermite en 1855 a lo que ahora se llaman matrices hermíticas . ^[13]

Casi al mismo tiempo, Francesco Brioschi demostró que los valores propios de las matrices ortogonales se encuentran en el círculo unitario ^[11] y Alfred Clebsch encontró el resultado correspondiente para matrices antisimétricas ^[13] . Finalmente, Karl Weierstrass aclaró un aspecto importante en la teoría de estabilidad iniciada por Laplace, al darse cuenta de que las matrices defectuosas pueden causar inestabilidad ^[11] .

Mientras tanto, Joseph Liouville estudió problemas de valores propios similares a los de Sturm; la disciplina que surgió de su trabajo ahora se llama teoría de Sturm-Liouville . ^[14] Schwarz estudió el primer valor propio de la ecuación de Laplace en dominios generales hacia fines del siglo XIX, mientras que Poincaré estudió la ecuación de Poisson unos años más tarde. ^[15]

A principios del siglo XX, David Hilbert estudió los valores propios de los operadores integrales al considerarlos como matrices infinitas. ^[16] Fue el primero en utilizar la palabra alemana eigen , que significa "propio", ^[6] para denotar valores propios y vectores propios en 1904, ^[c] aunque es posible que haya seguido un uso relacionado de Hermann von Helmholtz . Durante algún tiempo, el término estándar en inglés era "valor propio", pero el término más distintivo "valor propio" es el estándar en la actualidad. ^[17]

El primer algoritmo numérico para calcular valores y vectores propios apareció en 1929, cuando Richard von Mises publicó el método de potencia . Uno de los métodos más populares en la actualidad, el algoritmo QR , fue propuesto independientemente por John GF Francis ^[18] y Vera Kublanovskaya ^[19] en 1961. ^{[20] [21]}

Los valores y vectores propios suelen presentarse a los estudiantes en el contexto de cursos de álgebra lineal centrados en matrices. ^{[22] [23]} Además, las transformaciones lineales sobre un espacio vectorial de dimensión finita se pueden representar utilizando matrices, ^{[3] [4]} lo que es especialmente común en aplicaciones numéricas y computacionales. ^[24]

Consideremos vectores n -dimensionales que se forman como una lista de n escalares, como los vectores tridimensionales$${\displaystyle \mathbf {x} ={\begin{bmatrix}1\\-3\\4\end{bmatrix}}\quad {\mbox{y}}\quad \mathbf {y} ={\begin{bmatrix}-20\\60\\-80\end{bmatrix}}.}$$

Se dice que estos vectores son múltiplos escalares entre sí, o paralelos o colineales , si existe un escalar λ tal que$${\displaystyle \mathbf {x} =\lambda \mathbf {y}.}$$

En este caso, .${\displaystyle \lambda =-{\frac {1}{20}}}$

Consideremos ahora la transformación lineal de vectores n -dimensionales definidos por una matriz n por n A , o donde, para cada fila,$${\displaystyle A\mathbf {v} =\mathbf {w},}$$$${\displaystyle {\begin{bmatrix}A_{11}&A_{12}&\cdots &A_{1n}\\A_{21}&A_{22}&\cdots &A_{2n}\\\vdots &\vdots &\ddots &\vdots \\A_{n1}&A_{n2}&\cdots &A_{nn}\\\end{bmatrix}}{\begin{bmatrix}v_{1}\\v_{2}\\\vdots \\v_{n}\end{bmatrix}}={\begin{bmatrix}w_{1}\\w_{2}\\\vdots \\w_{n}\end{bmatrix}}}$$$${\displaystyle w_{i}=A_{i1}v_{1}+A_{i2}v_{2}+\cdots +A_{in}v_{n}=\sum _{j=1}^{n}A_{ij}v_{j}.}$$

Si ocurre que v y w son múltiplos escalares, es decir si

${\displaystyle A\mathbf {v} =\mathbf {w} =\lambda \mathbf {v},}$

( 1 )

entonces v es un vector propio de la transformación lineal A y el factor de escala λ es el valor propio correspondiente a ese vector propio. La ecuación ( 1 ) es la ecuación del valor propio para la matriz A.

La ecuación ( 1 ) se puede expresar de manera equivalente como

${\displaystyle \left(A-\lambda I\right)\mathbf {v} =\mathbf {0} ,}$

( 2 )

donde I es la matriz identidad n por n y 0 es el vector cero.

La ecuación ( 2 ) tiene una solución v distinta de cero si y solo si el determinante de la matriz ( A − λI ) es cero. Por lo tanto, los valores propios de A son valores de λ que satisfacen la ecuación

${\displaystyle \det(A-\lambda I)=0}$

( 3 )

Utilizando la fórmula de Leibniz para determinantes , el lado izquierdo de la ecuación ( 3 ) es una función polinómica de la variable λ y el grado de este polinomio es n , el orden de la matriz A. Sus coeficientes dependen de las entradas de A , excepto que su término de grado n es siempre (−1) n ^λ n ^. Este polinomio se denomina polinomio característico de A. La ecuación ( 3 ) se denomina ecuación característica o ecuación secular de A.

El teorema fundamental del álgebra implica que el polinomio característico de una matriz n por n A , al ser un polinomio de grado n , puede factorizarse en el producto de n términos lineales,

${\displaystyle \det(A-\lambda I)=(\lambda _{1}-\lambda )(\lambda _{2}-\lambda )\cdots (\lambda _{n}-\lambda ),}$

( 4 )

donde cada λ _i puede ser real pero en general es un número complejo. Los números λ ₁ , λ ₂ , ..., λ _n , que pueden no tener todos valores distintos, son raíces del polinomio y son los valores propios de A .

Como ejemplo breve, que se describe con más detalle en la sección de ejemplos más adelante, considere la matriz$${\displaystyle A={\begin{bmatrix}2&1\\1&2\end{bmatrix}}.}$$

Tomando el determinante de ( A − λI ) , el polinomio característico de A es$${\displaystyle \det(A-\lambda I)={\begin{vmatrix}2-\lambda &1\\1&2-\lambda \end{vmatrix}}=3-4\lambda +\lambda ^{2}. }$$

Si se iguala a cero el polinomio característico, éste tiene raíces en λ=1 y λ=3 , que son los dos valores propios de A. Los vectores propios correspondientes a cada valor propio se pueden encontrar resolviendo los componentes de v en la ecuación . En este ejemplo, los vectores propios son cualquier múltiplo escalar distinto de cero de${\displaystyle \left(A-\lambda I\right)\mathbf {v} =\mathbf {0} }$$${\displaystyle \mathbf {v} _{\lambda =1}={\begin{bmatrix}1\\-1\end{bmatrix}},\quad \mathbf {v} _{\lambda =3}={\begin{bmatrix}1\\1\end{bmatrix}}.}$$

Si las entradas de la matriz A son todas números reales, entonces los coeficientes del polinomio característico también serán números reales, pero los valores propios pueden tener partes imaginarias distintas de cero. Por lo tanto, las entradas de los vectores propios correspondientes también pueden tener partes imaginarias distintas de cero. De manera similar, los valores propios pueden ser números irracionales incluso si todas las entradas de A son números racionales o incluso si son todos números enteros. Sin embargo, si las entradas de A son todas números algebraicos , que incluyen los racionales, los valores propios también deben ser números algebraicos.

Las raíces no reales de un polinomio real con coeficientes reales se pueden agrupar en pares de conjugados complejos , es decir, con los dos miembros de cada par que tienen partes imaginarias que difieren solo en el signo y la misma parte real. Si el grado es impar, entonces, por el teorema del valor intermedio, al menos una de las raíces es real. Por lo tanto, cualquier matriz real con orden impar tiene al menos un valor propio real, mientras que una matriz real con orden par puede no tener ningún valor propio real. Los vectores propios asociados con estos valores propios complejos también son complejos y también aparecen en pares conjugados complejos.

El espectro de una matriz es la lista de valores propios, repetidos según su multiplicidad; en una notación alternativa, el conjunto de valores propios con sus multiplicidades.

Una cantidad importante asociada con el espectro es el valor absoluto máximo de cualquier valor propio, conocido como radio espectral de la matriz.

Sea λ _i un valor propio de una matriz A de n por n . La multiplicidad algebraica μ _A ( λ _i ) del valor propio es su multiplicidad como raíz del polinomio característico, es decir, el entero más grande k tal que ( λ − λ _i ) ^k divide exactamente ese polinomio. ^{[9] [25] [26]}

Supóngase que una matriz A tiene dimensión n y d ≤ n valores propios distintos. Mientras que la ecuación ( 4 ) factoriza el polinomio característico de A en el producto de n términos lineales con algunos términos que potencialmente se repiten, el polinomio característico también puede escribirse como el producto de d términos, cada uno correspondiente a un valor propio distinto y elevado a la potencia de la multiplicidad algebraica,$${\displaystyle \det(A-\lambda I)=(\lambda _{1}-\lambda )^{\mu _{A}(\lambda _{1})}(\lambda _{2}-\ lambda )^{\mu _{A}(\lambda _{2})}\cdots (\lambda _{d}-\lambda )^{\mu _{A}(\lambda _{d})}. }$$

Si d = n entonces el lado derecho es el producto de n términos lineales y esto es lo mismo que la ecuación ( 4 ). El tamaño de la multiplicidad algebraica de cada valor propio está relacionado con la dimensión n como$${\displaystyle {\begin{aligned}1&\leq \mu _{A}(\lambda _{i})\leq n,\\\mu _{A}&=\sum _{i=1}^{d}\mu _{A}\left(\lambda _{i}\right)=n.\end{aligned}}}$$

Si μ _A ( λ _i ) = 1, entonces se dice que λ _i es un valor propio simple . ^[26] Si μ _A ( λ _i ) es igual a la multiplicidad geométrica de λ _i , γ _A ( λ _i ), definida en la siguiente sección, entonces se dice que λ _i es un valor propio semisimple .

Dado un valor propio particular λ de la matriz A de n por n , defina el conjunto E como todos los vectores v que satisfacen la ecuación ( 2 ), $${\displaystyle E=\left\{\mathbf {v} :\left(A-\lambda I\right)\mathbf {v} =\mathbf {0} \right\}.}$$

Por un lado, este conjunto es precisamente el núcleo o espacio nulo de la matriz ( A − λI ). Por otro lado, por definición, cualquier vector distinto de cero que satisfaga esta condición es un vector propio de A asociado a λ . Así, el conjunto E es la unión del vector cero con el conjunto de todos los vectores propios de A asociados a λ , y E es igual al espacio nulo de ( A − λI ). E se denomina espacio propio o espacio característico de A asociado a λ . ^{[27] [9]} En general λ es un número complejo y los vectores propios son matrices complejas n por 1. Una propiedad del espacio nulo es que es un subespacio lineal , por lo que E es un subespacio lineal de .${\displaystyle \mathbb {C} ^{n}}$

Como el espacio propio E es un subespacio lineal, es cerrado bajo la adición. Es decir, si dos vectores u y v pertenecen al conjunto E , escrito u , v ∈ E , entonces ( u + v ) ∈ E o equivalentemente A ( u + v ) = λ ( u + v ) . Esto se puede comprobar utilizando la propiedad distributiva de la multiplicación de matrices. De manera similar, como E es un subespacio lineal, es cerrado bajo la multiplicación escalar. Es decir, si v ∈ E y α es un número complejo, ( α v ) ∈ E o equivalentemente A ( α v ) = λ ( α v ) . Esto se puede comprobar observando que la multiplicación de matrices complejas por números complejos es conmutativa . Siempre que u + v y α v no sean cero, también son vectores propios de A asociados con λ .

La dimensión del espacio propio E asociado con λ , o equivalentemente el número máximo de vectores propios linealmente independientes asociados con λ , se denomina multiplicidad geométrica del valor propio . Debido a que E también es el espacio nulo de ( A − λI ), la multiplicidad geométrica de λ es la dimensión del espacio nulo de ( A − λI ), también llamada nulidad de ( A − λI ), que se relaciona con la dimensión y el rango de ( A − λI ) como${\displaystyle \gamma_{A}(\lambda)}$$${\displaystyle \gamma _{A}(\lambda )=n-\operatorname {rango} (A-\lambda I).}$$

Debido a la definición de valores propios y vectores propios, la multiplicidad geométrica de un valor propio debe ser al menos uno, es decir, cada valor propio tiene al menos un vector propio asociado. Además, la multiplicidad geométrica de un valor propio no puede superar su multiplicidad algebraica. Además, recuerde que la multiplicidad algebraica de un valor propio no puede superar n .$${\displaystyle 1\leq \gamma _{A}(\lambda )\leq \mu _{A}(\lambda )\leq n}$$

Para demostrar la desigualdad , considere cómo la definición de multiplicidad geométrica implica la existencia de vectores propios ortonormales , tales que . Por lo tanto, podemos encontrar una matriz (unitaria) cuyas primeras columnas son estos vectores propios, y cuyas columnas restantes pueden ser cualquier conjunto ortonormal de vectores ortogonales a estos vectores propios de . Entonces tiene rango completo y, por lo tanto, es invertible. Evaluando , obtenemos una matriz cuyo bloque superior izquierdo es la matriz diagonal . Esto se puede ver evaluando lo que el lado izquierdo hace con los vectores base de la primera columna. Al reorganizar y agregar en ambos lados, obtenemos ya que conmuta con . En otras palabras, es similar a , y . Pero a partir de la definición de , sabemos que contiene un factor , lo que significa que la multiplicidad algebraica de debe satisfacer .${\displaystyle \gamma _{A}(\lambda )\leq \mu _{A}(\lambda )}$${\displaystyle \gamma_{A}(\lambda)}$ ${\displaystyle {\boldsymbol {v}}_{1},\,\ldots ,\,{\boldsymbol {v}}_{\gamma _{A}(\lambda )}}$${\displaystyle A{\boldsymbol {v}}_{k}=\lambda {\boldsymbol {v}}_{k}}$${\estilo de visualización V}$${\displaystyle \gamma_{A}(\lambda)}$${\displaystyle n-\gamma _{A}(\lambda )}$${\estilo de visualización A}$${\estilo de visualización V}$${\displaystyle D:=V^{T}AV}$${\displaystyle \lambda I_{\gamma _{A}(\lambda )}}$${\displaystyle -\xi V}$${\displaystyle (A-\xi I)V=V(D-\xi I)}$${\displaystyle I}$${\displaystyle V}$${\displaystyle A-\xi I}$${\displaystyle D-\xi I}$${\displaystyle \det(A-\xi I)=\det(D-\xi I)}$${\displaystyle D}$${\displaystyle \det(D-\xi I)}$${\displaystyle (\xi -\lambda )^{\gamma _{A}(\lambda )}}$${\displaystyle \lambda }$${\displaystyle \mu _{A}(\lambda )\geq \gamma _{A}(\lambda )}$

Supongamos que tiene valores propios distintos , donde la multiplicidad geométrica de es . La multiplicidad geométrica total de , es la dimensión de la suma de todos los espacios propios de los valores propios de , o equivalentemente el número máximo de vectores propios linealmente independientes de . Si , entonces${\displaystyle A}$${\displaystyle d\leq n}$${\displaystyle \lambda _{1},\ldots ,\lambda _{d}}$${\displaystyle \lambda _{i}}$${\displaystyle \gamma _{A}(\lambda _{i})}$${\displaystyle A}$$${\displaystyle {\begin{aligned}\gamma _{A}&=\sum _{i=1}^{d}\gamma _{A}(\lambda _{i}),\\d&\leq \gamma _{A}\leq n,\end{aligned}}}$$${\displaystyle A}$${\displaystyle A}$${\displaystyle \gamma _{A}=n}$

• La suma directa de los espacios propios de todos los valores propios de es el espacio vectorial completo .${\displaystyle A}$${\displaystyle \mathbb {C} ^{n}}$
• Una base de se puede formar a partir de vectores propios linealmente independientes de ; dicha base se denomina base propia${\displaystyle \mathbb {C} ^{n}}$${\displaystyle n}$${\displaystyle A}$
• Cualquier vector en puede escribirse como una combinación lineal de vectores propios de .${\displaystyle \mathbb {C} ^{n}}$${\displaystyle A}$

Sea una matriz arbitraria de números complejos con valores propios . Cada valor propio aparece veces en esta lista, donde es la multiplicidad algebraica del valor propio. Las siguientes son propiedades de esta matriz y sus valores propios:${\displaystyle A}$${\displaystyle n\times n}$${\displaystyle \lambda _{1},\ldots ,\lambda _{n}}$${\displaystyle \mu _{A}(\lambda _{i})}$${\displaystyle \mu _{A}(\lambda _{i})}$

• La traza de , definida como la suma de sus elementos diagonales, es también la suma de todos los valores propios, ^{[28] [29] [30]}${\displaystyle A}$

  ${\displaystyle \operatorname {tr} (A)=\sum _{i=1}^{n}a_{ii}=\sum _{i=1}^{n}\lambda _{i}=\lambda _{1}+\lambda _{2}+\cdots +\lambda _{n}.}$

• El determinante de es el producto de todos sus valores propios, ^{[28] [31] [32]}${\displaystyle A}$

  ${\displaystyle \det(A)=\prod _{i=1}^{n}\lambda _{i}=\lambda _{1}\lambda _{2}\cdots \lambda _{n}.}$

• Los valores propios de la ésima potencia de ; es decir, los valores propios de , para cualquier entero positivo , son .${\displaystyle k}$${\displaystyle A}$${\displaystyle A^{k}}$${\displaystyle k}$${\displaystyle \lambda _{1}^{k},\ldots ,\lambda _{n}^{k}}$
• La matriz es invertible si y sólo si cada valor propio es distinto de cero.${\displaystyle A}$
• Si es invertible, entonces los valores propios de son y la multiplicidad geométrica de cada valor propio coincide. Además, dado que el polinomio característico del inverso es el polinomio recíproco del original, los valores propios comparten la misma multiplicidad algebraica.${\displaystyle A}$${\displaystyle A^{-1}}$${\textstyle {\frac {1}{\lambda _{1}}},\ldots ,{\frac {1}{\lambda _{n}}}}$
• Si es igual a su transpuesta conjugada o, equivalentemente, si es hermítica , entonces todo valor propio es real. Lo mismo se aplica a cualquier matriz real simétrica .${\displaystyle A}$ ${\displaystyle A^{*}}$${\displaystyle A}$
• Si no es solo hermítico sino también positivo-definido , positivo-semidefinido, negativo-definido o negativo-semidefinido, entonces cada valor propio es positivo, no negativo, negativo o no positivo, respectivamente.${\displaystyle A}$
• Si es unitario , cada valor propio tiene valor absoluto .${\displaystyle A}$${\displaystyle |\lambda _{i}|=1}$
• Si es una matriz y son sus valores propios, entonces los valores propios de la matriz (donde es la matriz identidad) son . Además, si , los valores propios de son . De manera más general, para un polinomio los valores propios de la matriz son .${\displaystyle A}$${\displaystyle n\times n}$${\displaystyle \{\lambda _{1},\ldots ,\lambda _{k}\}}$${\displaystyle I+A}$${\displaystyle I}$${\displaystyle \{\lambda _{1}+1,\ldots ,\lambda _{k}+1\}}$${\displaystyle \alpha \in \mathbb {C} }$${\displaystyle \alpha I+A}$${\displaystyle \{\lambda _{1}+\alpha ,\ldots ,\lambda _{k}+\alpha \}}$${\displaystyle P}$${\displaystyle P(A)}$${\displaystyle \{P(\lambda _{1}),\ldots ,P(\lambda _{k})\}}$

Muchas disciplinas tradicionalmente representan los vectores como matrices con una sola columna en lugar de matrices con una sola fila. Por esa razón, la palabra "vector propio" en el contexto de matrices casi siempre se refiere a un vector propio derecho , es decir, un vector columna que multiplica por la derecha la matriz en la ecuación definitoria, ecuación ( 1 ).${\displaystyle n\times n}$${\displaystyle A}$$${\displaystyle A\mathbf {v} =\lambda \mathbf {v} .}$$

El problema de los valores propios y los vectores propios también se puede definir para vectores fila que multiplican por la izquierda la matriz . En esta formulación, la ecuación definitoria es${\displaystyle A}$$${\displaystyle \mathbf {u} A=\kappa \mathbf {u} ,}$$

donde es un escalar y es una matriz. Cualquier vector fila que satisfaga esta ecuación se denomina vector propio izquierdo de y es su valor propio asociado. Tomando la transpuesta de esta ecuación,${\displaystyle \kappa }$${\displaystyle u}$${\displaystyle 1\times n}$${\displaystyle u}$${\displaystyle A}$${\displaystyle \kappa }$$${\displaystyle A^{\textsf {T}}\mathbf {u} ^{\textsf {T}}=\kappa \mathbf {u} ^{\textsf {T}}.}$$

Comparando esta ecuación con la ecuación ( 1 ), se sigue inmediatamente que un vector propio izquierdo de es el mismo que la transpuesta de un vector propio derecho de , con el mismo valor propio. Además, dado que el polinomio característico de es el mismo que el polinomio característico de , los vectores propios izquierdo y derecho de están asociados con los mismos valores propios.${\displaystyle A}$${\displaystyle A^{\textsf {T}}}$${\displaystyle A^{\textsf {T}}}$${\displaystyle A}$${\displaystyle A}$

Supóngase que los vectores propios de A forman una base, o equivalentemente, A tiene n vectores propios linealmente independientes v ₁ , v ₂ , ..., v _n con valores propios asociados λ ₁ , λ ₂ , ..., λ _n . Los valores propios no necesitan ser distintos. Defina una matriz cuadrada Q cuyas columnas sean los n vectores propios linealmente independientes de A ,

${\displaystyle Q={\begin{bmatrix}\mathbf {v} _{1}&\mathbf {v} _{2}&\cdots &\mathbf {v} _{n}\end{bmatrix}}.}$

Dado que cada columna de Q es un vector propio de A , al multiplicar A por Q hacia la derecha se escala cada columna de Q por su valor propio asociado,

${\displaystyle AQ={\begin{bmatrix}\lambda _{1}\mathbf {v} _{1}&\lambda _{2}\mathbf {v} _{2}&\cdots &\lambda _{n}\mathbf {v} _{n}\end{bmatrix}}.}$

Con esto en mente, defina una matriz diagonal Λ donde cada elemento diagonal Λ _ii es el valor propio asociado con la i- ésima columna de Q . Luego

${\displaystyle AQ=Q\Lambda .}$

Como las columnas de Q son linealmente independientes, Q es invertible. Multiplicando ambos lados de la ecuación por Q ⁻¹ ,

${\displaystyle A=Q\Lambda Q^{-1},}$

o en su lugar, multiplicando hacia la izquierda ambos lados por Q ⁻¹ ,

${\displaystyle Q^{-1}AQ=\Lambda .}$

Por lo tanto, A se puede descomponer en una matriz compuesta por sus vectores propios, una matriz diagonal con sus valores propios a lo largo de la diagonal y la inversa de la matriz de vectores propios. Esto se llama descomposición propia y es una transformación de similitud . Se dice que una matriz A de este tipo es similar a la matriz diagonal Λ o diagonalizable . La matriz Q es la matriz de cambio de base de la transformación de similitud. Esencialmente, las matrices A y Λ representan la misma transformación lineal expresada en dos bases diferentes. Los vectores propios se utilizan como base cuando se representa la transformación lineal como Λ.

Por el contrario, supongamos que una matriz A es diagonalizable. Sea P una matriz cuadrada no singular tal que P ⁻¹ AP es una matriz diagonal D . Multiplicando ambas por P , AP = PD . Por lo tanto, cada columna de P debe ser un vector propio de A cuyo valor propio sea el elemento diagonal correspondiente de D . Como las columnas de P deben ser linealmente independientes para que P sea invertible, existen n vectores propios linealmente independientes de A . Entonces se deduce que los vectores propios de A forman una base si y solo si A es diagonalizable.

Una matriz que no es diagonalizable se dice que es defectuosa . Para matrices defectuosas, la noción de vectores propios se generaliza a vectores propios generalizados y la matriz diagonal de valores propios se generaliza a la forma normal de Jordan . Sobre un cuerpo algebraicamente cerrado, cualquier matriz A tiene una forma normal de Jordan y, por lo tanto, admite una base de vectores propios generalizados y una descomposición en espacios propios generalizados .

En el caso hermítico , los valores propios pueden tener una caracterización variacional. El valor propio más grande de es el valor máximo de la forma cuadrática . Un valor de que realiza ese máximo es un vector propio.${\displaystyle H}$ ${\displaystyle \mathbf {x} ^{\textsf {T}}H\mathbf {x} /\mathbf {x} ^{\textsf {T}}\mathbf {x} }$${\displaystyle \mathbf {x} }$

Considere la matriz$${\displaystyle A={\begin{bmatrix}2&1\\1&2\end{bmatrix}}.}$$

La figura de la derecha muestra el efecto de esta transformación sobre las coordenadas de los puntos en el plano. Los vectores propios v de esta transformación satisfacen la ecuación ( 1 ), y los valores de λ para los cuales el determinante de la matriz ( A  −  λI ) es igual a cero son los valores propios.

Tomando el determinante para encontrar el polinomio característico de A ,$${\displaystyle {\begin{aligned}\det(A-\lambda I)&=\left|{\begin{bmatrix}2&1\\1&2\end{bmatrix}}-\lambda {\begin{bmatrix}1&0\\0&1\end{bmatrix}}\right|={\begin{vmatrix}2-\lambda &1\\1&2-\lambda \end{vmatrix}}\\[6pt]&=3-4\lambda +\lambda ^{2}\\[6pt]&=(\lambda -3)(\lambda -1).\end{aligned}}}$$

Al establecer el polinomio característico igual a cero, tiene raíces en λ = 1 y λ = 3 , que son los dos valores propios de A.

Para λ = 1 , la ecuación ( 2 ) se convierte en,$${\displaystyle (A-I)\mathbf {v} _{\lambda =1}={\begin{bmatrix}1&1\\1&1\end{bmatrix}}{\begin{bmatrix}v_{1}\\v_{2}\end{bmatrix}}={\begin{bmatrix}0\\0\end{bmatrix}}}$$$${\displaystyle 1v_{1}+1v_{2}=0}$$

Cualquier vector distinto de cero con v ₁ = − v ₂ resuelve esta ecuación. Por lo tanto, es un vector propio de A correspondiente a λ = 1, al igual que cualquier múltiplo escalar de este vector.$${\displaystyle \mathbf {v} _{\lambda =1}={\begin{bmatrix}v_{1}\\-v_{1}\end{bmatrix}}={\begin{bmatrix}1\\-1\end{bmatrix}}}$$

Para λ = 3 , la ecuación ( 2 ) se convierte en$${\displaystyle {\begin{aligned}(A-3I)\mathbf {v} _{\lambda =3}&={\begin{bmatrix}-1&1\\1&-1\end{bmatrix}}{\begin{bmatrix}v_{1}\\v_{2}\end{bmatrix}}={\begin{bmatrix}0\\0\end{bmatrix}}\\-1v_{1}+1v_{2}&=0;\\1v_{1}-1v_{2}&=0\end{aligned}}}$$

Cualquier vector distinto de cero con v ₁ = v ₂ resuelve esta ecuación. Por lo tanto,$${\displaystyle \mathbf {v} _{\lambda =3}={\begin{bmatrix}v_{1}\\v_{1}\end{bmatrix}}={\begin{bmatrix}1\\1\end{bmatrix}}}$$

es un vector propio de A correspondiente a λ = 3, como lo es cualquier múltiplo escalar de este vector.

Por lo tanto, los vectores v _{λ = 1} y v _{λ = 3} son vectores propios de A asociados a los valores propios λ = 1 y λ = 3 , respectivamente.

Considere la matriz$${\displaystyle A={\begin{bmatrix}2&0&0\\0&3&4\\0&4&9\end{bmatrix}}.}$$

El polinomio característico de A es$${\displaystyle {\begin{aligned}\det(A-\lambda I)&=\left|{\begin{bmatrix}2&0&0\\0&3&4\\0&4&9\end{bmatrix}}-\lambda {\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}}\right|={\begin{vmatrix}2-\lambda &0&0\\0&3-\lambda &4\\0&4&9-\lambda \end{vmatrix}},\\[6pt]&=(2-\lambda ){\bigl [}(3-\lambda )(9-\lambda )-16{\bigr ]}=-\lambda ^{3}+14\lambda ^{2}-35\lambda +22.\end{aligned}}}$$

Las raíces del polinomio característico son 2, 1 y 11, que son los únicos tres valores propios de A. Estos valores propios corresponden a los vectores propios , , y , o cualquier múltiplo distinto de cero de los mismos.${\displaystyle {\begin{bmatrix}1&0&0\end{bmatrix}}^{\textsf {T}}}$ ${\displaystyle {\begin{bmatrix}0&-2&1\end{bmatrix}}^{\textsf {T}}}$${\displaystyle {\begin{bmatrix}0&1&2\end{bmatrix}}^{\textsf {T}}}$

Considere la matriz de permutación cíclica$${\displaystyle A={\begin{bmatrix}0&1&0\\0&0&1\\1&0&0\end{bmatrix}}.}$$

Esta matriz desplaza las coordenadas del vector una posición hacia arriba y desplaza la primera coordenada hacia abajo. Su polinomio característico es 1 −  λ ³ , cuyas raíces son donde es una unidad imaginaria con .$${\displaystyle {\begin{aligned}\lambda _{1}&=1\\\lambda _{2}&=-{\frac {1}{2}}+i{\frac {\sqrt {3}}{2}}\\\lambda _{3}&=\lambda _{2}^{*}=-{\frac {1}{2}}-i{\frac {\sqrt {3}}{2}}\end{aligned}}}$$${\displaystyle i}$${\displaystyle i^{2}=-1}$

Para el valor propio real λ ₁ = 1, cualquier vector con tres entradas iguales distintas de cero es un vector propio. Por ejemplo,$${\displaystyle A{\begin{bmatrix}5\\5\\5\end{bmatrix}}={\begin{bmatrix}5\\5\\5\end{bmatrix}}=1\cdot {\begin{bmatrix}5\\5\\5\end{bmatrix}}.}$$

Para el par conjugado complejo de valores propios imaginarios,$${\displaystyle \lambda _{2}\lambda _{3}=1,\quad \lambda _{2}^{2}=\lambda _{3},\quad \lambda _{3}^{2}=\lambda _{2}.}$$

Entonces y$${\displaystyle A{\begin{bmatrix}1\\\lambda _{2}\\\lambda _{3}\end{bmatrix}}={\begin{bmatrix}\lambda _{2}\\\lambda _{3}\\1\end{bmatrix}}=\lambda _{2}\cdot {\begin{bmatrix}1\\\lambda _{2}\\\lambda _{3}\end{bmatrix}},}$$$${\displaystyle A{\begin{bmatrix}1\\\lambda _{3}\\\lambda _{2}\end{bmatrix}}={\begin{bmatrix}\lambda _{3}\\\lambda _{2}\\1\end{bmatrix}}=\lambda _{3}\cdot {\begin{bmatrix}1\\\lambda _{3}\\\lambda _{2}\end{bmatrix}}.}$$

Por lo tanto, los otros dos vectores propios de A son complejos y son y con valores propios λ ₂ y λ ₃ , respectivamente. Los dos vectores propios complejos también aparecen en un par conjugado complejo,${\displaystyle \mathbf {v} _{\lambda _{2}}={\begin{bmatrix}1&\lambda _{2}&\lambda _{3}\end{bmatrix}}^{\textsf {T}}}$${\displaystyle \mathbf {v} _{\lambda _{3}}={\begin{bmatrix}1&\lambda _{3}&\lambda _{2}\end{bmatrix}}^{\textsf {T}}}$$${\displaystyle \mathbf {v} _{\lambda _{2}}=\mathbf {v} _{\lambda _{3}}^{*}.}$$

Las matrices con entradas solo a lo largo de la diagonal principal se denominan matrices diagonales . Los valores propios de una matriz diagonal son los propios elementos diagonales. Considere la matriz$${\displaystyle A={\begin{bmatrix}1&0&0\\0&2&0\\0&0&3\end{bmatrix}}.}$$

El polinomio característico de A es$${\displaystyle \det(A-\lambda I)=(1-\lambda )(2-\lambda )(3-\lambda ),}$$

que tiene las raíces λ ₁ = 1 , λ ₂ = 2 y λ ₃ = 3 . Estas raíces son los elementos diagonales así como los valores propios de  A .

Cada elemento diagonal corresponde a un vector propio cuyo único componente distinto de cero se encuentra en la misma fila que ese elemento diagonal. En el ejemplo, los valores propios corresponden a los vectores propios,$${\displaystyle \mathbf {v} _{\lambda _{1}}={\begin{bmatrix}1\\0\\0\end{bmatrix}},\quad \mathbf {v} _{\lambda _{2}}={\begin{bmatrix}0\\1\\0\end{bmatrix}},\quad \mathbf {v} _{\lambda _{3}}={\begin{bmatrix}0\\0\\1\end{bmatrix}},}$$

respectivamente, así como múltiplos escalares de estos vectores.

Una matriz cuyos elementos por encima de la diagonal principal son todos cero se denomina matriz triangular inferior , mientras que una matriz cuyos elementos por debajo de la diagonal principal son todos cero se denomina matriz triangular superior . Al igual que con las matrices diagonales, los valores propios de las matrices triangulares son los elementos de la diagonal principal.

Consideremos la matriz triangular inferior,$${\displaystyle A={\begin{bmatrix}1&0&0\\1&2&0\\2&3&3\end{bmatrix}}.}$$

El polinomio característico de A es$${\displaystyle \det(A-\lambda I)=(1-\lambda )(2-\lambda )(3-\lambda ),}$$

que tiene las raíces λ ₁ = 1 , λ ₂ = 2 y λ ₃ = 3 . Estas raíces son los elementos diagonales así como los valores propios de  A .

Estos valores propios corresponden a los vectores propios,$${\displaystyle \mathbf {v} _{\lambda _{1}}={\begin{bmatrix}1\\-1\\{\frac {1}{2}}\end{bmatrix}},\quad \mathbf {v} _{\lambda _{2}}={\begin{bmatrix}0\\1\\-3\end{bmatrix}},\quad \mathbf {v} _{\lambda _{3}}={\begin{bmatrix}0\\0\\1\end{bmatrix}},}$$

respectivamente, así como múltiplos escalares de estos vectores.

Como en el ejemplo anterior, la matriz triangular inferior tiene un polinomio característico que es el producto de sus elementos diagonales,$${\displaystyle A={\begin{bmatrix}2&0&0&0\\1&2&0&0\\0&1&3&0\\0&0&1&3\end{bmatrix}},}$$$${\displaystyle \det(A-\lambda I)={\begin{vmatrix}2-\lambda &0&0&0\\1&2-\lambda &0&0\\0&1&3-\lambda &0\\0&0&1&3-\lambda \end{vmatrix}}=(2-\lambda )^{2}(3-\lambda )^{2}.}$$

Las raíces de este polinomio, y por tanto los valores propios, son 2 y 3. La multiplicidad algebraica de cada valor propio es 2; en otras palabras, ambos son raíces dobles. La suma de las multiplicidades algebraicas de todos los valores propios distintos es μ _A = 4 = n , el orden del polinomio característico y la dimensión de A .

Por otra parte, la multiplicidad geométrica del valor propio 2 es solo 1, porque su espacio propio está abarcado por un solo vector y, por lo tanto, es unidimensional. De manera similar, la multiplicidad geométrica del valor propio 3 es 1 porque su espacio propio está abarcado por un solo vector . La multiplicidad geométrica total γ _A es 2, que es la más pequeña que podría ser para una matriz con dos valores propios distintos. Las multiplicidades geométricas se definen en una sección posterior.${\displaystyle {\begin{bmatrix}0&1&-1&1\end{bmatrix}}^{\textsf {T}}}$${\displaystyle {\begin{bmatrix}0&0&0&1\end{bmatrix}}^{\textsf {T}}}$

Para una matriz hermítica , la norma al cuadrado del componente j de un vector propio normalizado se puede calcular utilizando solo los valores propios de la matriz y los valores propios de la matriz menor correspondiente , donde es la submatriz formada al eliminar la fila y columna j de la matriz original. ^{[33] [34] [35]} Esta identidad también se extiende a matrices diagonalizables y ha sido redescubierta muchas veces en la literatura. ^{[34] [36]}$${\displaystyle |v_{i,j}|^{2}={\frac {\prod _{k}{(\lambda _{i}-\lambda _{k}(M_{j}))}}{\prod _{k\neq i}{(\lambda _{i}-\lambda _{k})}}},}$$${\textstyle M_{j}}$

Las definiciones de valor propio y vectores propios de una transformación lineal T siguen siendo válidas incluso si el espacio vectorial subyacente es un espacio de Hilbert o de Banach de dimensión infinita. Una clase ampliamente utilizada de transformaciones lineales que actúan en espacios de dimensión infinita son los operadores diferenciales en espacios de funciones . Sea D un operador diferencial lineal en el espacio C ^∞ de funciones reales infinitamente diferenciables de un argumento real t . La ecuación del valor propio para D es la ecuación diferencial$${\displaystyle Df(t)=\lambda f(t)}$$

Las funciones que satisfacen esta ecuación son vectores propios de D y se denominan comúnmente funciones propias .

Considere el operador derivado con ecuación de valor propio${\displaystyle {\tfrac {d}{dt}}}$$${\displaystyle {\frac {d}{dt}}f(t)=\lambda f(t).}$$

Esta ecuación diferencial se puede resolver multiplicando ambos lados por dt / f ( t ) e integrando . Su solución, la función exponencial, es la función propia del operador derivada. En este caso, la función propia es en sí misma una función de su valor propio asociado. En particular, para λ = 0, la función propia f ( t ) es una constante.$${\displaystyle f(t)=f(0)e^{\lambda t},}$$

El artículo principal sobre funciones propias ofrece otros ejemplos.

El concepto de valores propios y vectores propios se extiende naturalmente a transformaciones lineales arbitrarias sobre espacios vectoriales arbitrarios. Sea V cualquier espacio vectorial sobre un cuerpo K de escalares y sea T una transformación lineal que aplica V a V ,$${\displaystyle T:V\to V.}$$

Decimos que un vector distinto de cero v ∈ V es un vector propio de T si y solo si existe un escalar λ ∈ K tal que

${\displaystyle T(\mathbf {v} )=\lambda \mathbf {v} .}$

( 5 )

Esta ecuación se denomina ecuación de valor propio para T , y el escalar λ es el valor propio de T correspondiente al vector propio v . T ( v ) es el resultado de aplicar la transformación T al vector v , mientras que λ v es el producto del escalar λ con v . ^{[37] [38]}

Dado un valor propio λ , considere el conjunto$${\displaystyle E=\left\{\mathbf {v} :T(\mathbf {v} )=\lambda \mathbf {v} \right\},}$$

que es la unión del vector cero con el conjunto de todos los vectores propios asociados a  λ . E se denomina espacio propio o espacio característico de T asociado a  λ . ^[39]

Por definición de una transformación lineal,$${\displaystyle {\begin{aligned}T(\mathbf {x} +\mathbf {y} )&=T(\mathbf {x} )+T(\mathbf {y} ),\\T(\alpha \mathbf {x} )&=\alpha T(\mathbf {x} ),\end{aligned}}}$$

para x ,  y  ∈ V y α  ∈ K . Por lo tanto, si u y v son vectores propios de T asociados con el valor propio λ , es decir u ,  v  ∈ E , entonces$${\displaystyle {\begin{aligned}T(\mathbf {u} +\mathbf {v} )&=\lambda (\mathbf {u} +\mathbf {v} ),\\T(\alpha \mathbf {v} )&=\lambda (\alpha \mathbf {v} ).\end{aligned}}}$$

Por lo tanto, tanto u + v como α v son cero o vectores propios de T asociados con λ , es decir, u + v , α v ∈ E , y E está cerrado bajo la adición y la multiplicación escalar. El espacio propio E asociado con λ es, por lo tanto, un subespacio lineal de V . ^[40] Si ese subespacio tiene dimensión 1, a veces se lo denomina línea propia . ^[41]

La multiplicidad geométrica γ _T ( λ ) de un valor propio λ es la dimensión del espacio propio asociado con λ , es decir, el número máximo de vectores propios linealmente independientes asociados con ese valor propio. ^{[9] [26] [42]} Por la definición de valores propios y vectores propios, γ _T ( λ ) ≥ 1 porque cada valor propio tiene al menos un vector propio.

Los espacios propios de T siempre forman una suma directa . En consecuencia, los vectores propios de distintos valores propios son siempre linealmente independientes. Por lo tanto, la suma de las dimensiones de los espacios propios no puede superar la dimensión n del espacio vectorial en el que opera T , y no puede haber más de n valores propios distintos. ^[d]

Cualquier subespacio abarcado por vectores propios de T es un subespacio invariante de T , y la restricción de T a dicho subespacio es diagonalizable. Además, si todo el espacio vectorial V puede ser abarcado por los vectores propios de T , o equivalentemente si la suma directa de los espacios propios asociados con todos los valores propios de T es todo el espacio vectorial V , entonces una base de V llamada base propia puede formarse a partir de vectores propios linealmente independientes de T . Cuando T admite una base propia, T es diagonalizable.

Si λ es un valor propio de T , entonces el operador ( T − λI ) no es biunívoco y, por lo tanto, su inverso ( T − λI ) ⁻¹ no existe. Lo contrario es cierto para espacios vectoriales de dimensión finita, pero no para espacios vectoriales de dimensión infinita. En general, el operador ( T − λI ) puede no tener inverso incluso si λ no es un valor propio.

Por esta razón, en el análisis funcional los valores propios se pueden generalizar al espectro de un operador lineal T como el conjunto de todos los escalares λ para los cuales el operador ( T − λI ) no tiene inverso acotado . El espectro de un operador siempre contiene todos sus valores propios pero no está limitado a ellos.

Se puede generalizar el objeto algebraico que actúa sobre el espacio vectorial, reemplazando un único operador que actúa sobre un espacio vectorial por una representación algebraica : un álgebra asociativa que actúa sobre un módulo . El estudio de tales acciones es el campo de la teoría de la representación .

El concepto teórico de representación de peso es un análogo de los valores propios, mientras que los vectores de peso y los espacios de peso son los análogos de los vectores propios y los espacios propios, respectivamente.

El haz propio de Hecke es un tensor múltiplo de sí mismo y se considera en la correspondencia de Langlands .

Las ecuaciones diferenciales más simples tienen la forma

${\displaystyle x_{t}=a_{1}x_{t-1}+a_{2}x_{t-2}+\cdots +a_{k}x_{t-k}.}$

La solución de esta ecuación para x en términos de t se encuentra utilizando su ecuación característica

${\displaystyle \lambda ^{k}-a_{1}\lambda ^{k-1}-a_{2}\lambda ^{k-2}-\cdots -a_{k-1}\lambda -a_{k}=0,}$

que se puede encontrar apilando en forma matricial un conjunto de ecuaciones que consisten en la ecuación diferencial anterior y las ecuaciones k  – 1 que dan un sistema k -dimensional de primer orden en el vector de variable apilada en términos de su valor una vez rezagado, y tomando la ecuación característica de la matriz de este sistema. Esta ecuación da k raíces características para usar en la ecuación de solución${\displaystyle x_{t-1}=x_{t-1},\ \dots ,\ x_{t-k+1}=x_{t-k+1},}$${\displaystyle {\begin{bmatrix}x_{t}&\cdots &x_{t-k+1}\end{bmatrix}}}$${\displaystyle \lambda _{1},\,\ldots ,\,\lambda _{k},}$

${\displaystyle x_{t}=c_{1}\lambda _{1}^{t}+\cdots +c_{k}\lambda _{k}^{t}.}$

Se utiliza un procedimiento similar para resolver una ecuación diferencial de la forma

${\displaystyle {\frac {d^{k}x}{dt^{k}}}+a_{k-1}{\frac {d^{k-1}x}{dt^{k-1}}}+\cdots +a_{1}{\frac {dx}{dt}}+a_{0}x=0.}$

El cálculo de valores propios y vectores propios es un tema en el que la teoría, tal como se presenta en los libros de texto de álgebra lineal elemental, a menudo está muy lejos de la práctica.

El método clásico consiste en encontrar primero los valores propios y luego calcular los vectores propios para cada valor propio. En varios aspectos, no es adecuado para operaciones aritméticas no exactas, como la de punto flotante .

Los valores propios de una matriz se pueden determinar hallando las raíces del polinomio característico. Esto es fácil en el caso de las matrices, pero la dificultad aumenta rápidamente con el tamaño de la matriz.${\displaystyle A}$${\displaystyle 2\times 2}$

En teoría, los coeficientes del polinomio característico se pueden calcular con exactitud, ya que son sumas de productos de elementos de la matriz; y hay algoritmos que pueden encontrar todas las raíces de un polinomio de grado arbitrario con cualquier precisión requerida . ^[43] Sin embargo, este enfoque no es viable en la práctica porque los coeficientes estarían contaminados por errores de redondeo inevitables , y las raíces de un polinomio pueden ser una función extremadamente sensible de los coeficientes (como lo ejemplifica el polinomio de Wilkinson ). ^[43] Incluso para matrices cuyos elementos son números enteros, el cálculo se vuelve no trivial, porque las sumas son muy largas; el término constante es el determinante , que para una matriz es una suma de diferentes productos. ^[e]${\displaystyle n\times n}$${\displaystyle n!}$

Las fórmulas algebraicas explícitas para las raíces de un polinomio solo existen si el grado es 4 o menos. Según el teorema de Abel-Ruffini, no existe una fórmula algebraica general, explícita y exacta para las raíces de un polinomio con grado 5 o más. (La generalidad importa porque cualquier polinomio con grado es el polinomio característico de alguna matriz compañera de orden ). Por lo tanto, para matrices de orden 5 o más, los valores y vectores propios no se pueden obtener mediante una fórmula algebraica explícita y, por lo tanto, deben calcularse mediante métodos numéricos aproximados . Incluso la fórmula exacta para las raíces de un polinomio de grado 3 es numéricamente impráctica.${\displaystyle n}$${\displaystyle n}$${\displaystyle n}$

Una vez que se conoce el valor (exacto) de un valor propio, se pueden encontrar los vectores propios correspondientes hallando soluciones distintas de cero de la ecuación del valor propio, que se convierte en un sistema de ecuaciones lineales con coeficientes conocidos. Por ejemplo, una vez que se sabe que 6 es un valor propio de la matriz$${\displaystyle A={\begin{bmatrix}4&1\\6&3\end{bmatrix}}}$$

Podemos encontrar sus vectores propios resolviendo la ecuación , es decir${\displaystyle Av=6v}$$${\displaystyle {\begin{bmatrix}4&1\\6&3\end{bmatrix}}{\begin{bmatrix}x\\y\end{bmatrix}}=6\cdot {\begin{bmatrix}x\\y\end{bmatrix}}}$$

Esta ecuación matricial es equivalente a dos ecuaciones lineales que son$${\displaystyle \left\{{\begin{aligned}4x+y&=6x\\6x+3y&=6y\end{aligned}}\right.}$$          ${\displaystyle \left\{{\begin{aligned}-2x+y&=0\\6x-3y&=0\end{aligned}}\right.}$

Ambas ecuaciones se reducen a una única ecuación lineal . Por lo tanto, cualquier vector de la forma , para cualquier número real distinto de cero , es un vector propio de con valor propio .${\displaystyle y=2x}$${\displaystyle {\begin{bmatrix}a&2a\end{bmatrix}}^{\textsf {T}}}$${\displaystyle a}$${\displaystyle A}$${\displaystyle \lambda =6}$

La matriz anterior tiene otro valor propio . Un cálculo similar muestra que los vectores propios correspondientes son las soluciones distintas de cero de , es decir, cualquier vector de la forma , para cualquier número real distinto de cero .${\displaystyle A}$${\displaystyle \lambda =1}$${\displaystyle 3x+y=0}$${\displaystyle {\begin{bmatrix}b&-3b\end{bmatrix}}^{\textsf {T}}}$${\displaystyle b}$

El enfoque inverso, de buscar primero los vectores propios y luego determinar cada valor propio a partir de su vector propio, resulta ser mucho más manejable para las computadoras. El algoritmo más fácil aquí consiste en elegir un vector inicial arbitrario y luego multiplicarlo repetidamente por la matriz (normalizando opcionalmente el vector para mantener sus elementos de tamaño razonable); esto hace que el vector converja hacia un vector propio. Una variación es, en cambio, multiplicar el vector por ; esto hace que converja hacia un vector propio del valor propio más cercano a .${\displaystyle (A-\mu I)^{-1}}$${\displaystyle \mu \in \mathbb {C} }$

Si es (una buena aproximación de) un vector propio de , entonces el valor propio correspondiente se puede calcular como${\displaystyle \mathbf {v} }$${\displaystyle A}$

${\displaystyle \lambda ={\frac {\mathbf {v} ^{*}A\mathbf {v} }{\mathbf {v} ^{*}\mathbf {v} }}}$

donde denota la transpuesta conjugada de .${\displaystyle \mathbf {v} ^{*}}$${\displaystyle \mathbf {v} }$

No se conocían métodos eficientes y precisos para calcular valores propios y vectores propios de matrices arbitrarias hasta que se diseñó el algoritmo QR en 1961. ^[43] La combinación de la transformación de Householder con la descomposición LU da como resultado un algoritmo con mejor convergencia que el algoritmo QR. ^{[ cita requerida ]} Para matrices dispersas hermíticas grandes , el algoritmo de Lanczos es un ejemplo de un método iterativo eficiente para calcular valores propios y vectores propios, entre varias otras posibilidades. ^[43]

La mayoría de los métodos numéricos que calculan los valores propios de una matriz también determinan un conjunto de vectores propios correspondientes como subproducto del cálculo, aunque a veces los implementadores optan por descartar la información del vector propio tan pronto como ya no es necesaria.

Los vectores y valores propios pueden ser útiles para comprender las transformaciones lineales de formas geométricas. La siguiente tabla presenta algunos ejemplos de transformaciones en el plano junto con sus matrices 2×2, valores propios y vectores propios.

Valores propios de transformaciones geométricas

	Escalada	Escala desigual	Rotación	cizallamiento horizontal	Rotación hiperbólica
Ilustración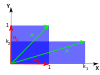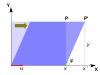
Matriz	${\displaystyle {\begin{bmatrix}k&0\\0&k\end{bmatrix}}}$	${\displaystyle {\begin{bmatrix}k_{1}&0\\0&k_{2}\end{bmatrix}}}$	${\displaystyle {\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \end{bmatrix}}}$	${\displaystyle {\begin{bmatrix}1&k\\0&1\end{bmatrix}}}$	${\displaystyle {\begin{bmatrix}\cosh \varphi &\sinh \varphi \\\sinh \varphi &\cosh \varphi \end{bmatrix}}}$
Polinomio característico	${\displaystyle \ (\lambda -k)^{2}}$	${\displaystyle (\lambda -k_{1})(\lambda -k_{2})}$	${\displaystyle \lambda ^{2}-2\cos(\theta )\lambda +1}$	${\displaystyle \ (\lambda -1)^{2}}$	${\displaystyle \lambda ^{2}-2\cosh(\varphi )\lambda +1}$
Valores propios,${\displaystyle \lambda _{i}}$	${\displaystyle \lambda _{1}=\lambda _{2}=k}$	${\displaystyle {\begin{aligned}\lambda _{1}&=k_{1}\\\lambda _{2}&=k_{2}\end{aligned}}}$	${\displaystyle {\begin{aligned}\lambda _{1}&=e^{i\theta }\\&=\cos \theta +i\sin \theta \\\lambda _{2}&=e^{-i\theta }\\&=\cos \theta -i\sin \theta \end{aligned}}}$	${\displaystyle \lambda _{1}=\lambda _{2}=1}$	${\displaystyle {\begin{aligned}\lambda _{1}&=e^{\varphi }\\&=\cosh \varphi +\sinh \varphi \\\lambda _{2}&=e^{-\varphi }\\&=\cosh \varphi -\sinh \varphi \end{aligned}}}$
Multiplicación algebraica​ ${\displaystyle \mu _{i}=\mu (\lambda _{i})}$	${\displaystyle \mu _{1}=2}$	${\displaystyle {\begin{aligned}\mu _{1}&=1\\\mu _{2}&=1\end{aligned}}}$	${\displaystyle {\begin{aligned}\mu _{1}&=1\\\mu _{2}&=1\end{aligned}}}$	${\displaystyle \mu _{1}=2}$	${\displaystyle {\begin{aligned}\mu _{1}&=1\\\mu _{2}&=1\end{aligned}}}$
Multiplicación geométrica​ ${\displaystyle \gamma _{i}=\gamma (\lambda _{i})}$	${\displaystyle \gamma _{1}=2}$	${\displaystyle {\begin{aligned}\gamma _{1}&=1\\\gamma _{2}&=1\end{aligned}}}$	${\displaystyle {\begin{aligned}\gamma _{1}&=1\\\gamma _{2}&=1\end{aligned}}}$	${\displaystyle \gamma _{1}=1}$	${\displaystyle {\begin{aligned}\gamma _{1}&=1\\\gamma _{2}&=1\end{aligned}}}$
Vectores propios	Todos los vectores distintos de cero	${\displaystyle {\begin{aligned}\mathbf {u} _{1}&={\begin{bmatrix}1\\0\end{bmatrix}}\\\mathbf {u} _{2}&={\begin{bmatrix}0\\1\end{bmatrix}}\end{aligned}}}$	${\displaystyle {\begin{aligned}\mathbf {u} _{1}&={\begin{bmatrix}1\\-i\end{bmatrix}}\\\mathbf {u} _{2}&={\begin{bmatrix}1\\+i\end{bmatrix}}\end{aligned}}}$	${\displaystyle \mathbf {u} _{1}={\begin{bmatrix}1\\0\end{bmatrix}}}$	${\displaystyle {\begin{aligned}\mathbf {u} _{1}&={\begin{bmatrix}1\\1\end{bmatrix}}\\\mathbf {u} _{2}&={\begin{bmatrix}1\\-1\end{bmatrix}}\end{aligned}}}$

La ecuación característica de una rotación es una ecuación cuadrática con discriminante , que es un número negativo siempre que θ no sea un múltiplo entero de 180°. Por lo tanto, excepto en estos casos especiales, los dos valores propios son números complejos, ; y todos los vectores propios tienen entradas no reales. De hecho, excepto en esos casos especiales, una rotación cambia la dirección de cada vector distinto de cero en el plano.${\displaystyle D=-4(\sin \theta )^{2}}$${\displaystyle \cos \theta \pm i\sin \theta }$

Una transformación lineal que convierte un cuadrado en un rectángulo de la misma área (una función de compresión ) tiene valores propios recíprocos.

La descomposición propia de una matriz semidefinida positiva simétrica (PSD) produce una base ortogonal de vectores propios, cada uno de los cuales tiene un valor propio no negativo. La descomposición ortogonal de una matriz PSD se utiliza en el análisis multivariante , donde las matrices de covarianza de la muestra son PSD. Esta descomposición ortogonal se denomina análisis de componentes principales (PCA) en estadística. El PCA estudia las relaciones lineales entre variables. El PCA se realiza en la matriz de covarianza o la matriz de correlación (en la que cada variable se escala para que su varianza de muestra sea igual a uno). Para la matriz de covarianza o correlación, los vectores propios corresponden a los componentes principales y los valores propios a la varianza explicada por los componentes principales. El análisis de componentes principales de la matriz de correlación proporciona una base ortogonal para el espacio de los datos observados: en esta base, los valores propios más grandes corresponden a los componentes principales que están asociados con la mayor parte de la covariabilidad entre una serie de datos observados.

El análisis de componentes principales se utiliza como un medio de reducción de dimensionalidad en el estudio de grandes conjuntos de datos , como los que se encuentran en bioinformática . En la metodología Q , los valores propios de la matriz de correlación determinan el juicio del metodólogo Q sobre la significación práctica (que difiere de la significación estadística de las pruebas de hipótesis ; cf. criterios para determinar el número de factores ). De manera más general, el análisis de componentes principales se puede utilizar como un método de análisis factorial en el modelado de ecuaciones estructurales .

En la teoría de grafos espectrales , un valor propio de un grafo se define como un valor propio de la matriz de adyacencia del grafo , o (cada vez más) de la matriz laplaciana del grafo debido a su operador de Laplace discreto , que es (a veces llamado el laplaciano combinatorio ) o (a veces llamado el laplaciano normalizado ), donde es una matriz diagonal con igual al grado del vértice , y en , la entrada diagonal n es . El n-ésimo vector propio principal de un grafo se define como el vector propio correspondiente al n-ésimo valor propio más grande o al n-ésimo valor propio más pequeño del laplaciano. El primer vector propio principal del grafo también se conoce simplemente como el vector propio principal.${\displaystyle A}$${\displaystyle D-A}$${\displaystyle I-D^{-1/2}AD^{-1/2}}$${\displaystyle D}$${\displaystyle D_{ii}}$${\displaystyle v_{i}}$${\displaystyle D^{-1/2}}$${\displaystyle i}$${\textstyle 1/{\sqrt {\deg(v_{i})}}}$${\displaystyle k}$${\displaystyle k}$${\displaystyle k}$

El vector propio principal se utiliza para medir la centralidad de sus vértices. Un ejemplo es el algoritmo PageRank de Google . El vector propio principal de una matriz de adyacencia modificada del gráfico de la World Wide Web proporciona los rangos de página como sus componentes. Este vector corresponde a la distribución estacionaria de la cadena de Markov representada por la matriz de adyacencia normalizada por filas; sin embargo, la matriz de adyacencia debe modificarse primero para garantizar que exista una distribución estacionaria. El segundo vector propio más pequeño se puede utilizar para dividir el gráfico en grupos, mediante agrupamiento espectral . También hay otros métodos disponibles para el agrupamiento.

Una cadena de Markov se representa mediante una matriz cuyas entradas son las probabilidades de transición entre estados de un sistema. En particular, las entradas no son negativas y cada fila de la matriz suma uno, que es la suma de las probabilidades de transición de un estado a otro estado del sistema. El teorema de Perron-Frobenius proporciona condiciones suficientes para que una cadena de Markov tenga un valor propio dominante único, que gobierna la convergencia del sistema a un estado estable.

Los problemas de valores propios ocurren naturalmente en el análisis de vibraciones de estructuras mecánicas con muchos grados de libertad . Los valores propios son las frecuencias naturales (o frecuencias propias ) de vibración, y los vectores propios son las formas de estos modos vibracionales. En particular, la vibración no amortiguada está gobernada por o$${\displaystyle m{\ddot {x}}+kx=0}$$$${\displaystyle m{\ddot {x}}=-kx}$$

Es decir, la aceleración es proporcional a la posición (es decir, esperamos que sea sinusoidal en el tiempo).${\displaystyle x}$

En dimensiones, se convierte en una matriz de masa y una matriz de rigidez . Las soluciones admisibles son entonces una combinación lineal de soluciones al problema de valor propio generalizado donde es el valor propio y es la frecuencia angular (imaginaria). Los modos de vibración principales son diferentes de los modos de cumplimiento principales, que son los vectores propios de solo. Además, la vibración amortiguada , gobernada por conduce a un llamado problema de valor propio cuadrático .${\displaystyle n}$${\displaystyle m}$${\displaystyle k}$$${\displaystyle kx=\omega ^{2}mx}$$${\displaystyle \omega ^{2}}$${\displaystyle \omega }$${\displaystyle k}$$${\displaystyle m{\ddot {x}}+c{\dot {x}}+kx=0}$$$${\displaystyle \left(\omega ^{2}m+\omega c+k\right)x=0.}$$