Agrupamiento espectral

En las estadísticas multivariadas , las técnicas de agrupamiento espectral hacen uso del espectro ( valores propios ) de la matriz de similitud de los datos para realizar una reducción de la dimensionalidad antes de agruparlos en menos dimensiones. La matriz de similitud se proporciona como entrada y consiste en una evaluación cuantitativa de la similitud relativa de cada par de puntos en el conjunto de datos.

En la aplicación a la segmentación de imágenes, la agrupación espectral se conoce como categorización de objetos basada en segmentación .

Dado un conjunto enumerado de puntos de datos, la matriz de similitud puede definirse como una matriz simétrica , donde representa una medida de la similitud entre puntos de datos con índices y . El enfoque general para el agrupamiento espectral es utilizar un método de agrupamiento estándar (hay muchos métodos de este tipo, k -medias se analiza a continuación) en vectores propios relevantes de una matriz laplaciana de . Hay muchas formas diferentes de definir un laplaciano que tienen diferentes interpretaciones matemáticas, y por lo tanto el agrupamiento también tendrá diferentes interpretaciones. Los vectores propios que son relevantes son los que corresponden a varios valores propios más pequeños del laplaciano, excepto el valor propio más pequeño que tendrá un valor de 0. Para la eficiencia computacional, estos vectores propios a menudo se calculan como los vectores propios correspondientes a los varios valores propios más grandes de una función del laplaciano.${\estilo de visualización A}$${\displaystyle A_{ij}\geq 0}$${\estilo de visualización i}$${\estilo de visualización j}$${\estilo de visualización A}$

Se sabe bien que la agrupación espectral está relacionada con la partición de un sistema de masa-resorte, donde cada masa está asociada con un punto de datos y cada rigidez de resorte corresponde a un peso de un borde que describe una similitud de los dos puntos de datos relacionados, como en el sistema de resorte . Específicamente, la referencia clásica ^[1] explica que el problema de valor propio que describe los modos de vibración transversal de un sistema de masa-resorte es exactamente el mismo que el problema de valor propio para la matriz laplaciana gráfica definida como

${\displaystyle L:=DA}$,

¿Dónde está la matriz diagonal?${\estilo de visualización D}$

${\displaystyle D_{ii}=\sum _{j}A_{ij},}$

y A es la matriz de adyacencia .

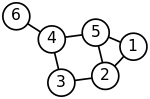
Las masas que están estrechamente conectadas por los resortes en el sistema masa-resorte evidentemente se mueven juntas desde la posición de equilibrio en modos de vibración de baja frecuencia, de modo que los componentes de los vectores propios correspondientes a los valores propios más pequeños del gráfico laplaciano se pueden utilizar para agrupar significativamente las masas. Por ejemplo, suponiendo que todos los resortes y las masas son idénticos en el sistema de resortes bidimensional representado, uno esperaría intuitivamente que las masas conectadas más flojas en el lado derecho del sistema se moverían con la mayor amplitud y en la dirección opuesta al resto de las masas cuando el sistema se sacude, y esta expectativa se confirmará analizando los componentes de los vectores propios del gráfico laplaciano correspondientes a los valores propios más pequeños, es decir, las frecuencias de vibración más pequeñas .

El objetivo de la normalización es hacer que las entradas diagonales de la matriz laplaciana sean todas unitarias, y también escalar las entradas fuera de la diagonal en consecuencia. En un gráfico ponderado, un vértice puede tener un grado alto debido a una pequeña cantidad de aristas conectadas pero con pesos grandes, así como también debido a una gran cantidad de aristas conectadas con pesos unitarios.

Una técnica popular de agrupamiento espectral normalizado es el algoritmo de cortes normalizados o algoritmo Shi-Malik introducido por Jianbo Shi y Jitendra Malik ^[2] , comúnmente utilizado para la segmentación de imágenes . Divide los puntos en dos conjuntos según el vector propio correspondiente al segundo valor propio más pequeño del laplaciano normalizado simétrico definido como${\estilo de visualización (B_{1},B_{2})}$ ${\estilo de visualización v}$

${\displaystyle L^{\text{norma}}:=ID^{-1/2}AD^{-1/2}.}$

El vector es también el vector propio correspondiente al segundo valor propio más grande de la matriz de adyacencia normalizada simétricamente.${\estilo de visualización v}$ ${\displaystyle D^{-1/2}AD^{-1/2}.}$

El laplaciano normalizado de paseo aleatorio (o por la izquierda) se define como

${\displaystyle L^{\text{rw}}:=D^{-1}L=ID^{-1}A}$

y también se puede utilizar para agrupamiento espectral. Un algoritmo matemáticamente equivalente ^[3] toma el vector propio correspondiente al valor propio más grande de la matriz de adyacencia normalizada de caminata aleatoria .${\estilo de visualización u}$$Estilo de visualización P=D-1A$

El vector propio del laplaciano normalizado simétricamente y el vector propio del laplaciano normalizado por la izquierda están relacionados por la identidad${\estilo de visualización v}$${\estilo de visualización u}$${\displaystyle D^{-1/2}v=u.}$

Conociendo la matriz de vectores propios seleccionados, se realiza un mapeo —denominado incrustación espectral— de los puntos de datos originales a un espacio vectorial dimensional utilizando las filas de . Ahora el análisis se reduce a agrupar vectores con componentes, lo que se puede hacer de varias maneras. ${\estilo de visualización n}$${\estilo de visualización k}$${\estilo de visualización V}$${\estilo de visualización n}$${\estilo de visualización k}$${\estilo de visualización V}$${\estilo de visualización k}$

En el caso más simple , el vector propio único seleccionado , llamado vector de Fiedler , corresponde al segundo valor propio más pequeño. Usando los componentes de uno se pueden colocar todos los puntos cuyo componente en es positivo en el conjunto y el resto en , de esta manera se biparticiona el gráfico y se etiquetan los puntos de datos con dos etiquetas. Este enfoque basado en signos sigue la explicación intuitiva de la agrupación espectral a través del modelo de masa-resorte: en el modo de vibración de baja frecuencia que representa el vector de Fiedler , un grupo de puntos de datos identificados con masas fuertemente conectadas entre sí se moverían juntos en una dirección, mientras que en el grupo complementario los puntos de datos identificados con las masas restantes se moverían juntos en la dirección opuesta. El algoritmo se puede usar para la agrupación jerárquica al particionar repetidamente los subconjuntos de la misma manera.${\estilo de visualización k=1}$${\estilo de visualización v}$${\estilo de visualización v,}$${\estilo de visualización v}$$Estilo de visualización B_{+}}$$Estilo de visualización B_{-}}$ ${\estilo de visualización v}$

En el caso general , se puede utilizar cualquier técnica de agrupamiento vectorial, por ejemplo, DBSCAN .${\displaystyle k>1}$

Algoritmo básico

1. Calcular el Laplaciano (o el Laplaciano normalizado)${\estilo de visualización L}$
2. Calcular los primeros vectores propios (los vectores propios correspondientes a los valores propios más pequeños de )${\estilo de visualización k}$${\estilo de visualización k}$${\estilo de visualización L}$
3. Considere la matriz formada por los primeros vectores propios; la fila -ésima define las características del nodo del gráfico${\estilo de visualización k}$${\estilo de visualización l}$${\estilo de visualización l}$
4. Agrupe los nodos del gráfico en función de estas características (por ejemplo, utilizando la agrupación k-means )

Si la matriz de similitud aún no se ha construido explícitamente, la eficiencia del agrupamiento espectral se puede mejorar si la solución al problema de valor propio correspondiente se realiza de manera libre de matriz (sin manipular explícitamente o incluso calcular la matriz de similitud), como en el algoritmo de Lanczos .${\estilo de visualización A}$

En el caso de gráficos de gran tamaño, el segundo valor propio de la matriz laplaciana del gráfico (normalizada) suele estar mal condicionado , lo que conduce a una convergencia lenta de los solucionadores iterativos de valores propios. El preacondicionamiento es una tecnología clave que acelera la convergencia, por ejemplo, en el método LOBPCG sin matriz . La agrupación espectral se ha aplicado con éxito en gráficos grandes identificando primero su estructura de comunidad y luego agrupando las comunidades. ^[4]

La agrupación espectral está estrechamente relacionada con la reducción de dimensionalidad no lineal , y se pueden utilizar técnicas de reducción de dimensión como la incrustación localmente lineal para reducir errores causados ​​por ruido o valores atípicos. ^[5]

Al denotar el número de puntos de datos por , es importante estimar la huella de memoria y el tiempo de cálculo, o el número de operaciones aritméticas (OA) realizadas, como una función de . Sin importar el algoritmo de agrupamiento espectral, los dos elementos costosos principales son la construcción del laplaciano gráfico y la determinación de sus vectores propios para la incrustación espectral. El último paso (determinar las etiquetas a partir de la matriz -por- de vectores propios) es típicamente el menos costoso, ya que solo requiere OA y la creación de solo un vector -por- de las etiquetas en la memoria.${\estilo de visualización n}$${\estilo de visualización n}$${\estilo de visualización k}$${\estilo de visualización n}$${\estilo de visualización k}$${\estilo de visualización kn}$${\estilo de visualización n}$${\estilo de visualización 1}$

La necesidad de construir el laplaciano gráfico es común a todos los métodos de agrupamiento basados ​​en la distancia o la correlación. El cálculo de los vectores propios es específico únicamente del agrupamiento espectral.

El laplaciano de grafos puede construirse, y normalmente se construye, a partir de la matriz de adyacencia. La construcción se puede realizar sin matriz, es decir, sin formar explícitamente la matriz del laplaciano de grafos y sin OA. También se puede realizar en lugar de la matriz de adyacencia sin aumentar la huella de memoria. De cualquier manera, los costos de construir el laplaciano de grafos están determinados esencialmente por los costos de construir la matriz de adyacencia -por- grafo.${\estilo de visualización n}$${\estilo de visualización n}$

Además, un laplaciano normalizado tiene exactamente los mismos vectores propios que la matriz de adyacencia normalizada, pero con el orden de los valores propios invertido. Por lo tanto, en lugar de calcular los vectores propios correspondientes a los valores propios más pequeños del laplaciano normalizado, se pueden calcular de manera equivalente los vectores propios correspondientes a los valores propios más grandes de la matriz de adyacencia normalizada, sin siquiera hablar de la matriz laplaciana.

Las construcciones ingenuas de la matriz de adyacencia de grafos , por ejemplo, utilizando el núcleo RBF, la hacen densa, por lo que se requiere memoria y AO para determinar cada una de las entradas de la matriz. El método de Nystrom ^[6] se puede utilizar para aproximar la matriz de similitud, pero la matriz aproximada no es positiva elemento por elemento, ^[7] es decir, no se puede interpretar como una similitud basada en la distancia.${\estilo de visualización n^{2}}$${\estilo de visualización n^{2}}$${\estilo de visualización n^{2}}$

Los algoritmos para construir la matriz de adyacencia de grafos como una matriz dispersa se basan típicamente en una búsqueda de vecino más cercano , que estima o toma una muestra de un vecindario de un punto de datos dado para los vecinos más cercanos, y calcula las entradas distintas de cero de la matriz de adyacencia comparando solo pares de vecinos. El número de vecinos más cercanos seleccionados determina así el número de entradas distintas de cero, y a menudo es fijo de modo que la huella de memoria de la matriz de adyacencia de grafos -por- es solo , solo se necesitan operaciones aritméticas secuenciales para calcular las entradas distintas de cero, y los cálculos se pueden ejecutar trivialmente en paralelo.${\estilo de visualización n}$${\estilo de visualización n}$${\displaystyle O(n)}$${\displaystyle O(n)}$${\displaystyle O(n)}$

El costo de calcular la matriz -por- (con ) de vectores propios seleccionados del laplaciano del grafo normalmente es proporcional al costo de multiplicación de la matriz laplaciana del grafo -por- por un vector, que varía en gran medida si la matriz laplaciana del grafo es densa o dispersa. Para el caso denso, el costo es . El costo muy comúnmente citado en la literatura proviene de la elección y es claramente engañoso, ya que, por ejemplo, en un agrupamiento espectral jerárquico determinado por el vector de Fiedler .${\estilo de visualización n}$${\estilo de visualización k}$${\displaystyle k\ll n}$${\estilo de visualización n}$${\estilo de visualización n}$${\displaystyle O(n^{2})}$${\displaystyle O(n^{3})}$${\displaystyle k=n}$${\estilo de visualización k=1}$

En el caso escaso de la matriz laplaciana del grafo -por- con entradas distintas de cero, el costo del producto matriz-vector y, por lo tanto, de calcular la matriz -por- con de vectores propios seleccionados es , con el consumo de memoria también solo — ambos son los límites bajos óptimos de complejidad de la agrupación de puntos de datos. Además, los solucionadores de valores propios sin matriz como LOBPCG pueden ejecutarse eficientemente en paralelo, por ejemplo, en múltiples GPU con memoria distribuida, lo que da como resultado no solo agrupaciones de alta calidad, por las que la agrupación espectral es famosa, sino también un rendimiento superior. ^[8]${\estilo de visualización n}$${\estilo de visualización n}$${\displaystyle O(n)}$${\estilo de visualización n}$${\estilo de visualización k}$${\displaystyle k\ll n}$${\displaystyle O(n)}$${\displaystyle O(n)}$${\estilo de visualización n}$

El software libre que implementa la agrupación espectral está disponible en grandes proyectos de código abierto como scikit-learn ^[9] que utiliza LOBPCG ^[10] con preacondicionamiento multigrid ^{[11] [12]} o ARPACK , MLlib para la agrupación de pseudo-vectores propios utilizando el método de iteración de potencia , ^[13] y R. ^[14 ]

Las ideas detrás del agrupamiento espectral pueden no ser obvias de inmediato. Puede ser útil destacar las relaciones con otros métodos. En particular, se puede describir en el contexto de los métodos de agrupamiento kernel, que revelan varias similitudes con otros enfoques. ^[15]

El problema de k -medias del núcleo ponderado ^[16] comparte la función objetivo con el problema de agrupamiento espectral, que se puede optimizar directamente mediante métodos multinivel. ^[17]

En el caso trivial de determinar componentes de gráficos conectados (los grupos óptimos sin bordes cortados), la agrupación espectral también está relacionada con una versión espectral de la agrupación DBSCAN que encuentra componentes conectados por densidad. ^[18]

Ravi Kannan, Santosh Vempala y Adrian Vetta ^[19] propusieron una medida bicriterio para definir la calidad de un agrupamiento determinado. Dijeron que un agrupamiento era un agrupamiento (α, ε) si la conductancia de cada grupo (en el agrupamiento) era al menos α y el peso de los bordes entre grupos era como máximo una fracción ε del peso total de todos los bordes en el gráfico. También analizaron dos algoritmos de aproximación en el mismo artículo.

La agrupación espectral tiene una larga historia. ^{[20] [21] [22] [23] [24] [2] [25]} La agrupación espectral como método de aprendizaje automático fue popularizada por Shi y Malik ^[2] y Ng, Jordan y Weiss. ^[25]

Las ideas y las medidas de red relacionadas con la agrupación espectral también desempeñan un papel importante en una serie de aplicaciones aparentemente diferentes de los problemas de agrupación. Por ejemplo, las redes con particiones espectrales más fuertes tardan más en converger en los modelos de actualización de opiniones que se utilizan en sociología y economía. ^{[26] [27]}

• Propagación por afinidad
• Análisis de componentes principales del núcleo
• Análisis de conglomerados
• Teoría de grafos espectrales