Función cúbica

This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources. Find sources: "Cubic function" – news · newspapers · books · scholar · JSTOR (September 2019)

En matemáticas , una función cúbica es una función de la forma , es decir, una función polinómica de grado tres. En muchos textos, se supone que los coeficientes a , b , c y d son números reales , y la función se considera como una función real que asigna números reales a números reales o como una función compleja que asigna números complejos a números complejos. En otros casos, los coeficientes pueden ser números complejos, y la función es una función compleja que tiene el conjunto de los números complejos como codominio , incluso cuando el dominio está restringido a los números reales.${\displaystyle f(x)=ax^{3}+bx^{2}+cx+d,}$

Al establecer f ( x ) = 0 se obtiene una ecuación cúbica de la forma

${\displaystyle ax^{3}+bx^{2}+cx+d=0,}$

cuyas soluciones se llaman raíces de la función. La derivada de una función cúbica es una función cuadrática .

Una función cúbica con coeficientes reales tiene una o tres raíces reales ( que pueden no ser distintas ); ^[1] todos los polinomios de grado impar con coeficientes reales tienen al menos una raíz real.

La gráfica de una función cúbica siempre tiene un único punto de inflexión . Puede tener dos puntos críticos , un mínimo local y un máximo local. De lo contrario, una función cúbica es monótona . La gráfica de una función cúbica es simétrica con respecto a su punto de inflexión; es decir, es invariante bajo una rotación de media vuelta alrededor de este punto. Hasta una transformación afín , solo hay tres posibles gráficas para funciones cúbicas.

Las funciones cúbicas son fundamentales para la interpolación cúbica .

Los puntos críticos de una función cúbica son sus puntos estacionarios , es decir, los puntos donde la pendiente de la función es cero. ^[2] Por lo tanto, los puntos críticos de una función cúbica f definida por

f ( x ) = ax ³ + bx ² + cx + d ,

ocurren en valores de x tales que la derivada

${\displaystyle 3ax^{2}+2bx+c=0}$

de la función cúbica es cero.

Las soluciones de esta ecuación son los valores x de los puntos críticos y se dan, utilizando la fórmula cuadrática , por

${\displaystyle x_{\text{critical}}={\frac {-b\pm {\sqrt {b^{2}-3ac}}}{3a}}.}$

El signo de la expresión Δ ₀ = b ² – 3 ac dentro de la raíz cuadrada determina el número de puntos críticos. Si es positivo, entonces hay dos puntos críticos, uno es un máximo local y el otro es un mínimo local. Si b ² – 3 ac = 0 , entonces solo hay un punto crítico, que es un punto de inflexión . Si b ² – 3 ac < 0 , entonces no hay puntos críticos (reales). En los dos últimos casos, es decir, si b ² – 3 ac no es positivo, la función cúbica es estrictamente monótona . Véase la figura para un ejemplo del caso Δ ₀ > 0 .

El punto de inflexión de una función es donde esa función cambia de concavidad . ^[3] Un punto de inflexión ocurre cuando la segunda derivada es cero y la tercera derivada es distinta de cero. Por lo tanto, una función cúbica siempre tiene un único punto de inflexión, que ocurre en${\displaystyle f''(x)=6ax+2b,}$

${\displaystyle x_{\text{inflection}}=-{\frac {b}{3a}}.}$

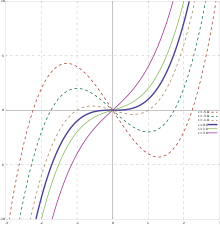
La gráfica de una función cúbica es una curva cúbica , aunque muchas curvas cúbicas no son gráficas de funciones.

Aunque las funciones cúbicas dependen de cuatro parámetros, su gráfica puede tener muy pocas formas. De hecho, la gráfica de una función cúbica siempre es similar a la gráfica de una función de la forma

${\displaystyle y=x^{3}+px.}$

Esta similitud puede construirse como la composición de traslaciones paralelas a los ejes de coordenadas, una homotecia ( escalamiento uniforme ) y, posiblemente, una reflexión ( imagen especular ) con respecto al eje y . Un escalamiento no uniforme adicional puede transformar el gráfico en el gráfico de una de las tres funciones cúbicas.

${\displaystyle {\begin{aligned}y&=x^{3}+x\\y&=x^{3}\\y&=x^{3}-x.\end{aligned}}}$

Esto significa que sólo hay tres gráficos de funciones cúbicas hasta una transformación afín .

Las transformaciones geométricas anteriores se pueden construir de la siguiente manera, partiendo de una función cúbica general ${\displaystyle y=ax^{3}+bx^{2}+cx+d.}$

En primer lugar, si a < 0 , el cambio de variable x → – x permite suponer a > 0 . Tras este cambio de variable, el nuevo gráfico es la imagen especular del anterior, respecto del eje y .

Entonces, el cambio de variable x = x ₁ – ⁠b/3 un⁠ proporciona una función de la forma

${\displaystyle y=ax_{1}^{3}+px_{1}+q.}$

Esto corresponde a una traslación paralela al eje x .

El cambio de variable y = y ₁ + q corresponde a una traslación con respecto al eje y , y da una función de la forma

${\displaystyle y_{1}=ax_{1}^{3}+px_{1}.}$

El cambio de variable corresponde a un escalamiento uniforme, y da, después de la multiplicación por una función de la forma ${\displaystyle \textstyle x_{1}={\frac {x_{2}}{\sqrt {a}}},y_{1}={\frac {y_{2}}{\sqrt {a}}}}$${\displaystyle {\sqrt {a}},}$

${\displaystyle y_{2}=x_{2}^{3}+px_{2},}$

que es la forma más simple que se puede obtener por semejanza.

Entonces, si p ≠ 0 , la escala no uniforme da, después de la división por${\displaystyle \textstyle x_{2}=x_{3}{\sqrt {|p|}},\quad y_{2}=y_{3}{\sqrt {|p|^{3}}}}$${\displaystyle \textstyle {\sqrt {|p|^{3}}},}$

${\displaystyle y_{3}=x_{3}^{3}+x_{3}\operatorname {sgn}(p),}$

donde tiene el valor 1 o –1, dependiendo del signo de p . Si se define la última forma de la función se aplica a todos los casos (con y ).${\displaystyle \operatorname {sgn}(p)}$${\displaystyle \operatorname {sgn}(0)=0,}$${\displaystyle x_{2}=x_{3}}$${\displaystyle y_{2}=y_{3}}$

Para una función cúbica de la forma el punto de inflexión es, por tanto, el origen. Como dicha función es una función impar , su gráfica es simétrica con respecto al punto de inflexión e invariante bajo una rotación de media vuelta alrededor del punto de inflexión. Como estas propiedades son invariantes por semejanza , lo siguiente es cierto para todas las funciones cúbicas.${\displaystyle y=x^{3}+px,}$

La gráfica de una función cúbica es simétrica con respecto a su punto de inflexión y es invariante bajo una rotación de media vuelta alrededor del punto de inflexión.

Las líneas tangentes a la gráfica de una función cúbica en tres puntos colineales interceptan la cúbica nuevamente en puntos colineales. ^[4] Esto se puede ver de la siguiente manera.

Como esta propiedad es invariante bajo un movimiento rígido , se puede suponer que la función tiene la forma

${\displaystyle f(x)=x^{3}+px.}$

Si α es un número real, entonces la tangente a la gráfica de f en el punto ( α , f ( α )) es la recta

{( x , f ( α ) + ( x − α ) f  ′( α )) : x ∈ R } .

Así, el punto de intersección entre esta recta y la gráfica de f se puede obtener resolviendo la ecuación f ( x ) = f ( α ) + ( x − α ) f  ′( α ) , es decir

${\displaystyle x^{3}+px=\alpha ^{3}+p\alpha +(x-\alpha )(3\alpha ^{2}+p),}$

que puede reescribirse

${\displaystyle x^{3}-3\alpha ^{2}x+2\alpha ^{3}=0,}$

y factorizado como

${\displaystyle (x-\alpha )^{2}(x+2\alpha )=0.}$

Entonces, la tangente intercepta la cúbica en

${\displaystyle (-2\alpha ,-8\alpha ^{3}-2p\alpha )=(-2\alpha ,-8f(\alpha )+6p\alpha ).}$

Entonces, la función que asigna un punto ( x , y ) del gráfico al otro punto donde la tangente intercepta el gráfico es

${\displaystyle (x,y)\mapsto (-2x,-8y+6px).}$

Se trata de una transformación afín que transforma puntos colineales en puntos colineales. Esto demuestra el resultado afirmado.

Dados los valores de una función y su derivada en dos puntos, hay exactamente una función cúbica que tiene los mismos cuatro valores, lo que se llama spline de Hermite cúbico .

Existen dos formas estándar de utilizar este hecho. En primer lugar, si se conocen, por ejemplo mediante una medición física, los valores de una función y su derivada en algunos puntos de muestreo, se puede interpolar la función con una función continuamente diferenciable , que es una función cúbica por partes .

Si se conoce el valor de una función en varios puntos, la interpolación cúbica consiste en aproximar la función mediante una función continuamente diferenciable , que es cúbica por partes . Para tener una interpolación definida de manera única, se deben agregar dos restricciones más, como los valores de las derivadas en los puntos extremos, o una curvatura cero en los puntos extremos.

Wikimedia Commons tiene medios relacionados con Funciones cúbicas .

• "Fórmula de Cardano", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• Historia de las ecuaciones cuadráticas, cúbicas y cuárticas en el archivo MacTutor .