Algoritmo QR

En álgebra lineal numérica , el algoritmo QR o iteración QR es un algoritmo de valores propios : es decir, un procedimiento para calcular los valores propios y los vectores propios de una matriz . El algoritmo QR fue desarrollado a finales de la década de 1950 por John GF Francis y por Vera N. Kublanovskaya , trabajando de forma independiente. ^{[1] [2] [3]} La idea básica es realizar una descomposición QR , escribiendo la matriz como un producto de una matriz ortogonal y una matriz triangular superior , multiplicar los factores en orden inverso e iterar.

Formalmente, sea A una matriz real de la que queremos calcular los valores propios, y sea A ₀  := A . En el k -ésimo paso (empezando con k = 0 ), calculamos la descomposición QR A _k = Q _k  R _k donde Q _k es una matriz ortogonal (es decir, Q ^T = Q ⁻¹ ) y R _k es una matriz triangular superior. Luego formamos A _{k +1} = R _k  Q _k . Nótese que entonces todos los A _k son similares y por lo tanto tienen los mismos valores propios. El algoritmo es numéricamente estable porque procede por transformadas de similitud ortogonales .$${\displaystyle A_{k+1}=R_{k}Q_{k}=Q_{k}^{-1}Q_{k}R_{k}Q_{k}=Q_{k}^{-1} A_ {k} Q_ {k} = Q_ {k} ^ {\ mathsf {T}} A_ {k} Q_ {k},}$$

En determinadas condiciones, ^[4] las matrices A _k convergen a una matriz triangular, la forma Schur de A . Los valores propios de una matriz triangular se enumeran en la diagonal y el problema de los valores propios queda resuelto. Para comprobar la convergencia, no resulta práctico exigir ceros exactos, ^{[ cita requerida ]} pero el teorema del círculo de Gershgorin proporciona un límite para el error.

En la forma cruda anterior, las iteraciones son relativamente costosas. Esto se puede mitigar llevando primero la matriz A a la forma Hessenberg superior (que cuesta operaciones aritméticas utilizando una técnica basada en la reducción de Householder ), con una secuencia finita de transformadas de similitud ortogonales, algo así como una descomposición QR de dos lados. ^{[5] [6]} (Para la descomposición QR, los reflectores de Householder se multiplican solo a la izquierda, pero para el caso de Hessenberg se multiplican tanto a la izquierda como a la derecha). Determinar la descomposición QR de una matriz Hessenberg superior cuesta operaciones aritméticas. Además, debido a que la forma Hessenberg ya es casi triangular superior (solo tiene una entrada distinta de cero debajo de cada diagonal), usarla como punto de partida reduce la cantidad de pasos necesarios para la convergencia del algoritmo QR.${\textstyle {\tfrac {10}{3}}n^{3}+{\mathcal {O}}(n^{2})}$${\textstyle 6n^{2}+{\mathcal {O}}(n)}$

Si la matriz original es simétrica , entonces la matriz de Hessenberg superior también es simétrica y, por lo tanto, tridiagonal , y lo mismo ocurre con todas las A _k . En este caso, alcanzar la forma de Hessenberg cuesta operaciones aritméticas utilizando una técnica basada en la reducción de Householder. ^{[5] [6]} Determinar la descomposición QR de una matriz tridiagonal simétrica cuesta operaciones. ^[7]${\textstyle {\tfrac {4}{3}}n^{3}+{\mathcal {O}}(n^{2})}$${\displaystyle {\mathcal {O}}(n)}$

Si una matriz de Hessenberg tiene un elemento para algún , es decir, si uno de los elementos justo debajo de la diagonal es de hecho cero, entonces se descompone en bloques cuyos problemas propios pueden resolverse por separado; un valor propio es un valor propio de la submatriz de las primeras filas y columnas, o un valor propio de la submatriz de las filas y columnas restantes. El propósito del paso de iteración QR es reducir uno de estos elementos de modo que efectivamente un pequeño bloque a lo largo de la diagonal se separe del volumen de la matriz. En el caso de un valor propio real, ese suele ser el bloque en la esquina inferior derecha (en cuyo caso el elemento contiene ese valor propio), mientras que en el caso de un par de valores propios complejos conjugados es el bloque en la esquina inferior derecha.${\estilo de visualización A}$${\displaystyle a_{k,k-1}=0}$${\estilo de visualización k}$${\estilo de visualización k-1}$$estilo de visualización a_{k,k-1}}$${\displaystyle 1\times 1}$$Estilo de visualización a_ {nn}}$${\displaystyle 2\times 2}$

La tasa de convergencia depende de la separación entre los valores propios, por lo que un algoritmo práctico utilizará desplazamientos, ya sean explícitos o implícitos, para aumentar la separación y acelerar la convergencia. Un algoritmo QR simétrico típico aísla cada valor propio (y luego reduce el tamaño de la matriz) con solo una o dos iteraciones, lo que lo hace eficiente y robusto. ^{[ aclaración necesaria ]}

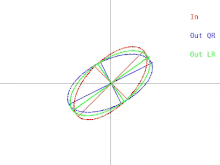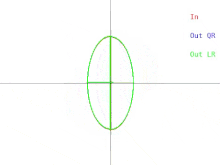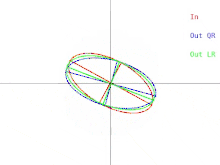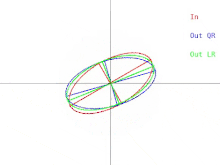
El algoritmo QR básico se puede visualizar en el caso en que A es una matriz simétrica definida positiva. En ese caso, A se puede representar como una elipse en dos dimensiones o como un elipsoide en dimensiones superiores. La relación entre la entrada del algoritmo y una única iteración se puede representar como en la Figura 1 (haga clic para ver una animación). Observe que el algoritmo LR se representa junto con el algoritmo QR.

Una única iteración hace que la elipse se incline o "caiga" hacia el eje x. En el caso en que el semieje mayor de la elipse sea paralelo al eje x, una iteración de QR no hace nada. Otra situación en la que el algoritmo "no hace nada" es cuando el semieje mayor es paralelo al eje y en lugar del eje x. En ese caso, se puede pensar que la elipse se equilibra precariamente sin poder caer en ninguna dirección. En ambas situaciones, la matriz es diagonal. Una situación en la que una iteración del algoritmo "no hace nada" se denomina punto fijo . La estrategia empleada por el algoritmo es la iteración hacia un punto fijo . Observe que un punto fijo es estable mientras que el otro es inestable. Si la elipse se inclinara en dirección opuesta al punto fijo inestable en una cantidad muy pequeña, una iteración de QR haría que la elipse se inclinara en dirección opuesta al punto fijo en lugar de hacia él. Sin embargo, eventualmente el algoritmo convergería a un punto fijo diferente, pero tomaría mucho tiempo.

Vale la pena señalar que encontrar incluso un único vector propio de una matriz simétrica no es computable (en aritmética real exacta según las definiciones en análisis computable ). ^[8] Esta dificultad existe siempre que las multiplicidades de los valores propios de una matriz no sean cognoscibles. Por otro lado, el mismo problema no existe para encontrar valores propios. Los valores propios de una matriz siempre son computables.

Ahora analizaremos cómo se manifiestan estas dificultades en el algoritmo QR básico, como se ilustra en la Figura 2. Recordemos que las elipses representan matrices simétricas definidas positivas. A medida que los dos valores propios de la matriz de entrada se aproximan, la elipse de entrada se transforma en un círculo. Un círculo corresponde a un múltiplo de la matriz identidad. Un casi-círculo corresponde a un casi-múltiplo de la matriz identidad cuyos valores propios son casi iguales a las entradas diagonales de la matriz. Por lo tanto, el problema de encontrar aproximadamente los valores propios se muestra fácil en ese caso. Pero observe lo que sucede con los semiejes de las elipses. Una iteración de QR (o LR) inclina los semiejes cada vez menos a medida que la elipse de entrada se acerca a ser un círculo. Los vectores propios solo se pueden conocer cuando los semiejes son paralelos al eje x y al eje y. El número de iteraciones necesarias para lograr un paralelismo casi absoluto aumenta sin límite a medida que la elipse de entrada se vuelve más circular.

Si bien puede resultar imposible calcular la descomposición propia de una matriz simétrica arbitraria, siempre es posible perturbar la matriz en una cantidad arbitrariamente pequeña y calcular la descomposición propia de la matriz resultante. En el caso en que la matriz se represente como un círculo casi circular, la matriz se puede reemplazar por otra cuya representación sea un círculo perfecto. En ese caso, la matriz es un múltiplo de la matriz identidad y su descomposición propia es inmediata. Sin embargo, tenga en cuenta que la base propia resultante puede estar bastante alejada de la base propia original.

La desaceleración cuando la elipse se vuelve más circular tiene una inversa: resulta que cuando la elipse se estira más -y se vuelve menos circular- entonces la rotación de la elipse se vuelve más rápida. Tal estiramiento puede ser inducido cuando la matriz que representa la elipse se reemplaza con donde es aproximadamente el valor propio más pequeño de . En este caso, la relación de los dos semiejes de la elipse se acerca a . En dimensiones superiores, un desplazamiento como este hace que la longitud del semieje más pequeño de un elipsoide sea pequeña en relación con los otros semiejes, lo que acelera la convergencia al valor propio más pequeño, pero no acelera la convergencia a los otros valores propios. Esto se vuelve inútil cuando el valor propio más pequeño está completamente determinado, por lo que la matriz debe entonces desinflarse , lo que simplemente significa eliminar su última fila y columna.${\estilo de visualización M}$${\displaystyle M-\lambda I}$${\estilo de visualización \lambda}$${\estilo de visualización M}$${\estilo de visualización\infty}$

También es necesario abordar el problema del punto fijo inestable. La heurística de desplazamiento suele estar diseñada para abordar también este problema: los desplazamientos prácticos suelen ser discontinuos y aleatorios. El desplazamiento de Wilkinson, que resulta muy adecuado para matrices simétricas como las que estamos visualizando, es en particular discontinuo.

En la práctica computacional moderna, el algoritmo QR se realiza en una versión implícita que hace que el uso de múltiples desplazamientos sea más fácil de introducir. ^[4] La matriz se lleva primero a la forma Hessenberg superior como en la versión explícita; luego, en cada paso, la primera columna de se transforma a través de una transformación de similitud de Householder de tamaño pequeño a la primera columna de ^{[ aclaración necesaria ]} (o ), donde , de grado , es el polinomio que define la estrategia de desplazamiento (a menudo , donde y son los dos valores propios de la submatriz principal final de , el llamado doble desplazamiento implícito ). Luego se realizan transformaciones de Householder sucesivas de tamaño para devolver la matriz de trabajo a la forma Hessenberg superior. Esta operación se conoce como persecución de abultamiento , debido a la forma peculiar de las entradas distintas de cero de la matriz a lo largo de los pasos del algoritmo. Como en la primera versión, la deflación se realiza tan pronto como una de las entradas subdiagonales de es suficientemente pequeña.${\displaystyle A_{0}=QAQ^{\mathsf {T}}}$$Estilo de visualización A_{k}}$${\displaystyle p(A_{k})}$ ${\displaystyle p(A_{k})e_{1}}$${\displaystyle p(A_{k})}$${\estilo de visualización r}$${\displaystyle p(x)=(x-\lambda )(x-{\bar {\lambda }})}$${\estilo de visualización \lambda}$${\displaystyle {\bar {\lambda }}}$${\displaystyle 2\times 2}$$Estilo de visualización A_{k}}$${\estilo de visualización r+1}$$Estilo de visualización A_{k}}$$Estilo de visualización A_{k}}$

Dado que en la versión implícita moderna del procedimiento no se realizan descomposiciones QR explícitamente, algunos autores, por ejemplo Watkins, ^[9] sugirieron cambiar su nombre a algoritmo Francis . Golub y Van Loan utilizan el término paso QR de Francis .

El algoritmo QR puede considerarse una variación más sofisticada del algoritmo básico de valores propios de "potencia" . Recordemos que el algoritmo de potencia multiplica repetidamente A por un único vector, normalizándose después de cada iteración. El vector converge a un vector propio del valor propio más grande. En cambio, el algoritmo QR trabaja con una base completa de vectores, utilizando la descomposición QR para renormalizar (y ortogonalizar). Para una matriz simétrica A , al converger, AQ = QΛ , donde Λ es la matriz diagonal de valores propios a la que convergió A , y donde Q es una composición de todas las transformaciones de similitud ortogonales necesarias para llegar allí. Por lo tanto, las columnas de Q son los vectores propios.

El algoritmo QR fue precedido por el algoritmo LR , que utiliza la descomposición LU en lugar de la descomposición QR. El algoritmo QR es más estable, por lo que el algoritmo LR rara vez se utiliza en la actualidad. Sin embargo, representa un paso importante en el desarrollo del algoritmo QR.

El algoritmo LR fue desarrollado a principios de la década de 1950 por Heinz Rutishauser , quien trabajaba en ese momento como asistente de investigación de Eduard Stiefel en ETH Zurich . Stiefel sugirió que Rutishauser usara la secuencia de momentos y ₀ ^T A ^k x ₀ , k = 0, 1, ... (donde x ₀ e y ₀ son vectores arbitrarios) para encontrar los valores propios de A . Rutishauser tomó un algoritmo de Alexander Aitken para esta tarea y lo desarrolló en el algoritmo de diferencia de cociente o algoritmo qd . Después de organizar el cálculo en una forma adecuada, descubrió que el algoritmo qd es de hecho la iteración A _k = L _k U _k (descomposición LU), A _{k +1} = U _k L _k , aplicada en una matriz tridiagonal, de la que se desprende el algoritmo LR. ^[10]

Una variante del algoritmo QR , el algoritmo Golub-Kahan-Reinsch , comienza con la reducción de una matriz general a una bidiagonal. ^[11] Esta variante del algoritmo QR para el cálculo de valores singulares fue descrita por primera vez por Golub y Kahan (1965). La subrutina LAPACK DBDSQR implementa este método iterativo, con algunas modificaciones para cubrir el caso en el que los valores singulares son muy pequeños (Demmel y Kahan 1990). Junto con un primer paso que utiliza reflexiones de Householder y, si corresponde, descomposición QR , esto forma la rutina DGESVD para el cálculo de la descomposición de valores singulares . El algoritmo QR también se puede implementar en dimensiones infinitas con los resultados de convergencia correspondientes. ^{[12] [13]}

• Demmel, James ; Kahan, William (1990). "Valores singulares precisos de matrices bidiagonales". Revista SIAM sobre computación científica y estadística . 11 (5): 873–912. CiteSeerX  10.1.1.48.3740 . doi :10.1137/0911052.
• Golub, Gene H. ; Kahan, William (1965). "Cálculo de los valores singulares y pseudoinversos de una matriz". Revista de la Sociedad de Matemáticas Industriales y Aplicadas, Serie B: Análisis numérico . 2 (2): 205–224. Bibcode :1965SJNA....2..205G. doi :10.1137/0702016. JSTOR  2949777.

• Problema de valor propio en PlanetMath .
• Notas sobre bases ortogonales y el funcionamiento del algoritmo QR por Peter J. Olver
• Módulo para el método QR
• Biblioteca C++