Campo (matemáticas)

| Estructuras algebraicas |
|---|
En matemáticas , un cuerpo es un conjunto en el que se definen las operaciones de suma , resta , multiplicación y división y que se comportan como las operaciones correspondientes sobre números racionales y reales . Un cuerpo es, por tanto, una estructura algebraica fundamental que se utiliza ampliamente en álgebra , teoría de números y muchas otras áreas de las matemáticas.
Los campos más conocidos son el campo de los números racionales , el campo de los números reales y el campo de los números complejos . Muchos otros campos, como los campos de funciones racionales , los campos de funciones algebraicas , los campos de números algebraicos y los campos p -ádicos, se utilizan y estudian habitualmente en matemáticas, en particular en teoría de números y geometría algebraica . La mayoría de los protocolos criptográficos se basan en campos finitos , es decir, campos con un número finito de elementos .
La teoría de campos demuestra que la trisección de ángulos y la cuadratura del círculo no se pueden hacer con compás y regla . La teoría de Galois , dedicada a comprender las simetrías de las extensiones de campos , proporciona una elegante prueba del teorema de Abel-Ruffini de que las ecuaciones de quinto grado generales no se pueden resolver en radicales .
Los campos sirven como nociones fundamentales en varios dominios matemáticos. Esto incluye diferentes ramas del análisis matemático , que se basan en campos con estructura adicional. Los teoremas básicos del análisis dependen de las propiedades estructurales del campo de números reales. Lo más importante para fines algebraicos es que cualquier campo puede usarse como escalar para un espacio vectorial , que es el contexto general estándar para el álgebra lineal . Los campos numéricos , los hermanos del campo de números racionales, se estudian en profundidad en la teoría de números . Los campos de funciones pueden ayudar a describir las propiedades de los objetos geométricos.
Definición
De manera informal, un cuerpo es un conjunto, junto con dos operaciones definidas en ese conjunto: una operación de suma escrita como a + b , y una operación de multiplicación escrita como a ⋅ b , las cuales se comportan de manera similar a como se comportan para los números racionales y los números reales , incluida la existencia de un inverso aditivo − a para todos los elementos a , y de un inverso multiplicativo b −1 para cada elemento distinto de cero b . Esto permite considerar también las llamadas operaciones inversas de resta, a − b , y división, a / b , definiendo:
- a − b := a + (− b ) ,
- a / b := a ⋅ b −1 .
Definición clásica
Formalmente, un cuerpo es un conjunto F junto con dos operaciones binarias sobre F llamadas adición y multiplicación . [1] Una operación binaria sobre F es una aplicación F × F → F , es decir, una correspondencia que asocia a cada par ordenado de elementos de F un elemento determinado de forma única de F . [2] [3] El resultado de la adición de a y b se denomina suma de a y b , y se denota a + b . De manera similar, el resultado de la multiplicación de a y b se denomina producto de a y b , y se denota ab o a ⋅ b . Estas operaciones son necesarias para satisfacer las siguientes propiedades, denominadas axiomas de cuerpo (en estos axiomas, a , b y c son elementos arbitrarios del cuerpo F ):
- Asociatividad de la suma y la multiplicación: a + ( b + c ) = ( a + b ) + c , y a ⋅ ( b ⋅ c ) = ( a ⋅ b ) ⋅ c .
- Conmutatividad de la suma y la multiplicación: a + b = b + a , y a ⋅ b = b ⋅ a .
- Identidad aditiva y multiplicativa : existen dos elementos distintos 0 y 1 en F tales que a + 0 = a y a ⋅ 1 = a .
- Inversos aditivos : para cada a en F , existe un elemento en F , denotado − a , llamado inverso aditivo de a , tal que a + (− a ) = 0 .
- Inversos multiplicativos : para cada a ≠ 0 en F , existe un elemento en F , denotado por a −1 o 1/ a , llamado inverso multiplicativo de a , tal que a ⋅ a −1 = 1 .
- Distributividad de la multiplicación sobre la suma: a ⋅ ( b + c ) = ( a ⋅ b ) + ( a ⋅ c ) .
Una definición equivalente, y más sucinta, es: un campo tiene dos operaciones conmutativas, llamadas adición y multiplicación; es un grupo bajo la adición con 0 como identidad aditiva; los elementos distintos de cero son un grupo bajo la multiplicación con 1 como identidad multiplicativa; y la multiplicación se distribuye sobre la adición.
Aún más sucintamente: un campo es un anillo conmutativo donde 0 ≠ 1 y todos los elementos distintos de cero son invertibles bajo la multiplicación.
Definición alternativa
Los campos también pueden definirse de maneras diferentes, pero equivalentes. Alternativamente, se puede definir un campo mediante cuatro operaciones binarias (suma, resta, multiplicación y división) y sus propiedades requeridas. La división por cero está, por definición, excluida. [4] Para evitar los cuantificadores existenciales , los campos pueden definirse mediante dos operaciones binarias (suma y multiplicación), dos operaciones unarias (que producen las inversas aditivas y multiplicativas respectivamente) y dos operaciones nularias (las constantes 0 y 1 ). Estas operaciones están sujetas entonces a las condiciones anteriores. Evitar los cuantificadores existenciales es importante en matemáticas constructivas y computación . [5] Se puede definir de manera equivalente un campo mediante las mismas dos operaciones binarias, una operación unaria (la inversa multiplicativa) y dos constantes (no necesariamente distintas) 1 y −1 , ya que 0 = 1 + (−1) y − a = (−1) a . [a]
Ejemplos
Números racionales
Los números racionales han sido ampliamente utilizados mucho antes de la elaboración del concepto de cuerpo. Son números que pueden escribirse como fracciones a / b , donde a y b son números enteros y b ≠ 0 . El inverso aditivo de dicha fracción es − a / b , y el inverso multiplicativo (siempre que a ≠ 0 ) es b / a , que se puede ver de la siguiente manera:
Los axiomas de campo requeridos de manera abstracta se reducen a propiedades estándar de los números racionales. Por ejemplo, la ley de distributividad se puede demostrar de la siguiente manera: [6]
Números reales y complejos

Los números reales R , con las operaciones habituales de adición y multiplicación, también forman un cuerpo. Los números complejos C están formados por expresiones
- a + bi , con a , b real,
donde i es la unidad imaginaria , es decir, un número (no real) que satisface i 2 = −1 . La suma y la multiplicación de números reales se definen de tal manera que las expresiones de este tipo satisfacen todos los axiomas de cuerpo y, por lo tanto, son válidas para C. Por ejemplo, la ley distributiva impone
- ( a + bi ) ( c + di ) = ac + bci + adi + bdi 2 = ( ac − bd ) + ( bc + ad ) i .
Es inmediato que se trata nuevamente de una expresión del tipo anterior, y por lo tanto los números complejos forman un campo. Los números complejos pueden representarse geométricamente como puntos en el plano , con coordenadas cartesianas dadas por los números reales de su expresión descriptiva, o como flechas desde el origen hasta estos puntos, especificadas por su longitud y un ángulo encerrado con alguna dirección distinta. La adición corresponde entonces a la combinación de las flechas para el paralelogramo intuitivo (sumando las coordenadas cartesianas), y la multiplicación es –menos intuitivamente– la combinación de la rotación y el escalado de las flechas (sumando los ángulos y multiplicando las longitudes). Los campos de números reales y complejos se utilizan en matemáticas, física, ingeniería, estadística y muchas otras disciplinas científicas.
Números construibles
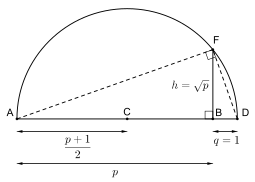
En la antigüedad, varios problemas geométricos se referían a la (in)viabilidad de construir ciertos números con compás y regla . Por ejemplo, los griegos desconocían que, en general, es imposible trisecar un ángulo dado de esta manera. Estos problemas se pueden resolver utilizando el campo de los números construibles . [7] Los números construibles reales son, por definición, longitudes de segmentos de línea que se pueden construir a partir de los puntos 0 y 1 en un número finito de pasos utilizando solo compás y regla . Estos números, dotados de las operaciones de campo de los números reales, restringidas a los números construibles, forman un campo, que incluye propiamente el campo Q de los números racionales. La ilustración muestra la construcción de raíces cuadradas de números construibles, no necesariamente contenidos dentro de Q. Usando el etiquetado en la ilustración, construya los segmentos AB , BD y un semicírculo sobre AD (centro en el punto medio C ), que interseca la línea perpendicular a través de B en un punto F , a una distancia de exactamente de B cuando BD tiene longitud uno.
No todos los números reales son construibles. Se puede demostrar que no es un número construible, lo que implica que es imposible construir con regla y compás la longitud del lado de un cubo con volumen 2 , otro problema planteado por los antiguos griegos.
Un campo con cuatro elementos
| Suma | Multiplicación | ||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
Además de los sistemas numéricos familiares, como los racionales, existen otros ejemplos menos inmediatos de cuerpos. El siguiente ejemplo es un cuerpo que consta de cuatro elementos llamados O , I , A y B . La notación se elige de modo que O desempeñe el papel del elemento de identidad aditiva (denotado como 0 en los axiomas anteriores) e I sea la identidad multiplicativa (denotada como 1 en los axiomas anteriores). Los axiomas de cuerpo se pueden verificar utilizando algo más de teoría de cuerpo o mediante cálculo directo. Por ejemplo,
- A ⋅ ( B + A ) = A ⋅ I = A , que es igual a A ⋅ B + A ⋅ A = I + B = A , como lo requiere la distributividad.
Este campo se llama campo finito o campo de Galois con cuatro elementos, y se denota F 4 o GF(4) . [8] El subconjunto que consiste en O e I (resaltado en rojo en las tablas de la derecha) también es un campo, conocido como campo binario F 2 o GF(2) .
Nociones elementales
En esta sección, F denota un campo arbitrario y a y b son elementos arbitrarios de F.
Consecuencias de la definición
Se tiene a ⋅ 0 = 0 y − a = (−1) ⋅ a . En particular, se puede deducir el inverso aditivo de cada elemento tan pronto como se conoce −1 . [9]
Si ab = 0 entonces a o b deben ser 0 , ya que, si a ≠ 0 , entonces b = ( a −1 a ) b = a −1 ( ab ) = a −1 ⋅ 0 = 0 . Esto significa que todo cuerpo es un dominio integral .
Además, las siguientes propiedades son verdaderas para cualquier elemento a y b :
- -0 = 0
- 1 −1 = 1
- (−(− a )) = a
- (− a ) ⋅ b = a ⋅ (− b ) = −( a ⋅ b )
- ( a −1 ) −1 = a si a ≠ 0
Grupos aditivos y multiplicativos de un cuerpo
Los axiomas de un cuerpo F implican que es un grupo abeliano bajo adición. Este grupo se denomina grupo aditivo del cuerpo y a veces se denota por ( F , +) cuando se denota simplemente como F, lo que podría generar confusión.
De manera similar, los elementos distintos de cero de F forman un grupo abeliano bajo la multiplicación, llamado grupo multiplicativo , y denotado por o simplemente , o F × .
Un cuerpo puede definirse así como un conjunto F equipado con dos operaciones denotadas como una adición y una multiplicación tales que F es un grupo abeliano bajo la adición, es un grupo abeliano bajo la multiplicación (donde 0 es el elemento identidad de la adición), y la multiplicación es distributiva sobre la adición. [b] Por lo tanto, algunas afirmaciones elementales sobre cuerpos pueden obtenerse aplicando hechos generales de grupos . Por ejemplo, los inversos aditivos y multiplicativos − a y a −1 están determinados de forma única por a .
El requisito 1 ≠ 0 se impone por convención para excluir el anillo trivial , que consiste en un solo elemento; esto guía cualquier elección de los axiomas que definen campos.
Todo subgrupo finito del grupo multiplicativo de un cuerpo es cíclico (ver Raíz de la unidad § Grupos cíclicos ).
Característica
Además de la multiplicación de dos elementos de F , es posible definir el producto n ⋅ a de un elemento arbitrario a de F por un entero positivo n como la suma n -veces
- a + a + ... + a (que es un elemento de F .)
Si no existe ningún entero positivo tal que
- n ⋅ 1 = 0 ,
Entonces se dice que F tiene característica 0. [11] Por ejemplo, el campo de números racionales Q tiene característica 0 ya que ningún entero positivo n es cero. De lo contrario, si hay un entero positivo n que satisface esta ecuación, se puede demostrar que el entero positivo más pequeño de esos es un número primo . Generalmente se denota por p y se dice que el campo tiene característica p entonces. Por ejemplo, el campo F 4 tiene característica 2 ya que (en la notación de la tabla de adición anterior) I + I = O.
Si F tiene característica p , entonces p ⋅ a = 0 para todo a en F . Esto implica que
- ( a + b ) p = a p + b p ,
ya que todos los demás coeficientes binomiales que aparecen en la fórmula binomial son divisibles por p . Aquí, a p := a ⋅ a ⋅ ⋯ ⋅ a ( factores p ) es la potencia p ésima, es decir, el producto p -fold del elemento a . Por lo tanto, la función de Frobenius
- F → F : x ↦ x p
es compatible con la adición en F (y también con la multiplicación), y por lo tanto es un homomorfismo de campo. [12] La existencia de este homomorfismo hace que los campos de característica p sean bastante diferentes de los campos de característica 0 .
Subcampos y campos primos
Un subcuerpo E de un cuerpo F es un subconjunto de F que es un cuerpo con respecto a las operaciones de cuerpo de F . Equivalentemente, E es un subconjunto de F que contiene 1 , y está cerrado bajo adición, multiplicación, inverso aditivo e inverso multiplicativo de un elemento distinto de cero. Esto significa que 1 ∊ E , que para todo a , b ∊ E tanto a + b como a ⋅ b están en E , y que para todo a ≠ 0 en E , tanto − a como 1/ a están en E .
Los homomorfismos de campo son aplicaciones φ : E → F entre dos campos tales que φ ( e 1 + e 2 ) = φ ( e 1 ) + φ ( e 2 ) , φ ( e 1 e 2 ) = φ ( e 1 ) φ ( e 2 ) , y φ (1 E ) = 1 F , donde e 1 y e 2 son elementos arbitrarios de E . Todos los homomorfismos de campo son inyectivos . [13] Si φ también es sobreyectivo , se denomina isomorfismo (o los campos E y F se denominan isomorfos).
Un cuerpo se denomina cuerpo primo si no tiene subcuerpos propios (es decir, estrictamente menores). Cualquier cuerpo F contiene un cuerpo primo. Si la característica de F es p (un número primo), el cuerpo primo es isomorfo al cuerpo finito F p introducido a continuación. De lo contrario, el cuerpo primo es isomorfo a Q . [14]
Campos finitos
Los campos finitos (también llamados campos de Galois ) son campos con un número finito de elementos, cuyo número también se conoce como el orden del campo. El ejemplo introductorio anterior F 4 es un campo con cuatro elementos. Su subcampo F 2 es el campo más pequeño, porque por definición un campo tiene al menos dos elementos distintos, 0 y 1 .

Los cuerpos finitos más simples, de orden primo, son más directamente accesibles usando aritmética modular . Para un entero positivo fijo n , la aritmética "módulo n " significa trabajar con los números
- Z / nZ = {0, 1, ..., n − 1}.
La adición y multiplicación en este conjunto se hace realizando la operación en cuestión en el conjunto Z de números enteros, dividiendo por n y tomando el resto como resultado. Esta construcción produce un cuerpo precisamente si n es un número primo . Por ejemplo, tomando el primo n = 2 se obtiene el cuerpo mencionado anteriormente F 2 . Para n = 4 y, de manera más general, para cualquier número compuesto (es decir, cualquier número n que pueda expresarse como un producto n = r ⋅ s de dos números naturales estrictamente menores), Z / n Z no es un cuerpo: el producto de dos elementos distintos de cero es cero ya que r ⋅ s = 0 en Z / n Z , lo que, como se explicó anteriormente, impide que Z / n Z sea un cuerpo. El cuerpo Z / p Z con p elementos ( siendo p primo) construido de esta manera se suele denotar por F p .
Todo cuerpo finito F tiene q = p n elementos, donde p es primo y n ≥ 1. Esta afirmación es válida porque F puede considerarse como un espacio vectorial sobre su cuerpo primo. La dimensión de este espacio vectorial es necesariamente finita, digamos n , lo que implica la afirmación afirmada. [15]
Un campo con q = p n elementos se puede construir como el campo de división del polinomio
- f ( x ) = x q − x .
Un cuerpo de desdoblamiento de este tipo es una extensión de F p en la que el polinomio f tiene q ceros. Esto significa que f tiene tantos ceros como sea posible, ya que el grado de f es q . Para q = 2 2 = 4 , se puede comprobar caso por caso utilizando la tabla de multiplicación anterior que los cuatro elementos de F 4 satisfacen la ecuación x 4 = x , por lo que son ceros de f . Por el contrario, en F 2 , f tiene solo dos ceros (a saber, 0 y 1 ), por lo que f no se desdobla en factores lineales en este cuerpo más pequeño. Desarrollando más a fondo las nociones básicas de la teoría de cuerpos, se puede demostrar que dos cuerpos finitos con el mismo orden son isomorfos. [16] Por lo tanto, es habitual hablar del cuerpo finito con q elementos, denotado por F q o GF( q ) .
Historia
Históricamente, tres disciplinas algebraicas llevaron al concepto de cuerpo: la cuestión de resolver ecuaciones polinómicas, la teoría algebraica de números y la geometría algebraica . [17] Un primer paso hacia la noción de cuerpo fue realizado en 1770 por Joseph-Louis Lagrange , quien observó que permutar los ceros x 1 , x 2 , x 3 de un polinomio cúbico en la expresión
- ( x 1 + ω x 2 + ω 2 x 3 ) 3
( siendo ω una tercera raíz de la unidad ) sólo produce dos valores. De esta manera, Lagrange explicó conceptualmente el método de solución clásico de Scipione del Ferro y François Viète , que procede reduciendo una ecuación cúbica para una incógnita x a una ecuación cuadrática para x 3. [18] Junto con una observación similar para ecuaciones de grado 4 , Lagrange vinculó así lo que eventualmente se convirtió en el concepto de campos y el concepto de grupos. [ 19] Vandermonde , también en 1770, y en mayor medida, Carl Friedrich Gauss , en sus Disquisitiones Arithmeticae (1801), estudiaron la ecuación
- xp = 1
para un primo p y, nuevamente usando lenguaje moderno, el grupo de Galois cíclico resultante . Gauss dedujo que se puede construir un p -gono regular si p = 2 2 k + 1 . Basándose en el trabajo de Lagrange, Paolo Ruffini afirmó (1799) que las ecuaciones de quinto grado (ecuaciones polinómicas de grado 5 ) no se pueden resolver algebraicamente; sin embargo, sus argumentos eran defectuosos. Estas lagunas fueron llenadas por Niels Henrik Abel en 1824. [20] Évariste Galois , en 1832, ideó criterios necesarios y suficientes para que una ecuación polinómica sea resoluble algebraicamente, estableciendo así en efecto lo que hoy se conoce como teoría de Galois . Tanto Abel como Galois trabajaron con lo que hoy se llama un cuerpo de números algebraicos , pero no concibieron ni una noción explícita de cuerpo ni de grupo.
En 1871 Richard Dedekind introdujo, para un conjunto de números reales o complejos que está cerrado bajo las cuatro operaciones aritméticas, la palabra alemana Körper , que significa "cuerpo" o "corpus" (para sugerir una entidad orgánicamente cerrada). El término inglés "campo" fue introducido por Moore (1893). [21]
Por campo entenderemos todo sistema infinito de números reales o complejos tan cerrado en sí mismo y perfecto que la suma, resta, multiplicación y división de cualesquiera dos de estos números dé a su vez un número del sistema.
— Richard Dedekind, 1871 [22]
En 1881 Leopold Kronecker definió lo que llamó un dominio de racionalidad , que es un campo de fracciones racionales en términos modernos. La noción de Kronecker no cubría el campo de todos los números algebraicos (que es un campo en el sentido de Dedekind), pero por otro lado era más abstracta que la de Dedekind en el sentido de que no hacía ninguna suposición específica sobre la naturaleza de los elementos de un campo. Kronecker interpretó un campo como Q (π) de manera abstracta como el campo de funciones racionales Q ( X ) . Antes de esto, se conocían ejemplos de números trascendentales desde el trabajo de Joseph Liouville en 1844, hasta que Charles Hermite (1873) y Ferdinand von Lindemann (1882) demostraron la trascendencia de e y π , respectivamente. [23]
La primera definición clara de un cuerpo abstracto se debe a Weber (1893). [24] En particular, la noción de Heinrich Martin Weber incluía el cuerpo F p . Giuseppe Veronese (1891) estudió el cuerpo de las series de potencias formales, lo que llevó a Hensel (1904) a introducir el cuerpo de los números p -ádicos. Steinitz (1910) sintetizó el conocimiento de la teoría abstracta de cuerpos acumulado hasta entonces. Estudió axiomáticamente las propiedades de los cuerpos y definió muchos conceptos importantes de la teoría de cuerpos. La mayoría de los teoremas mencionados en las secciones Teoría de Galois, Construcción de cuerpos y Nociones elementales se pueden encontrar en el trabajo de Steinitz. Artin y Schreier (1927) vincularon la noción de ordenamientos en un cuerpo , y por tanto el área de análisis, a propiedades puramente algebraicas. [25] Emil Artin desarrolló nuevamente la teoría de Galois entre 1928 y 1942, eliminando la dependencia del teorema del elemento primitivo .
Construyendo campos
Construyendo campos a partir de anillos
Un anillo conmutativo es un conjunto que está equipado con una operación de adición y multiplicación y satisface todos los axiomas de un cuerpo, excepto la existencia de inversos multiplicativos a −1 . [26] Por ejemplo, los números enteros Z forman un anillo conmutativo, pero no un cuerpo: el recíproco de un número entero n no es en sí mismo un número entero, a menos que n = ±1 .
En la jerarquía de estructuras algebraicas, los campos se pueden caracterizar como los anillos conmutativos R en los que cada elemento distinto de cero es una unidad (lo que significa que cada elemento es invertible). De manera similar, los campos son los anillos conmutativos con precisamente dos ideales distintos , (0) y R . Los campos también son precisamente los anillos conmutativos en los que (0) es el único ideal primo .
Dado un anillo conmutativo R , hay dos maneras de construir un cuerpo relacionado con R , es decir, dos maneras de modificar R de modo que todos los elementos distintos de cero se vuelvan invertibles: formando el cuerpo de fracciones y formando cuerpos de residuos. El cuerpo de fracciones de Z es Q , los racionales, mientras que los cuerpos de residuos de Z son los cuerpos finitos F p .
Campo de fracciones
Dado un dominio entero R , su campo de fracciones Q ( R ) se construye con las fracciones de dos elementos de R exactamente como Q se construye a partir de los números enteros. Más precisamente, los elementos de Q ( R ) son las fracciones a / b donde a y b están en R , y b ≠ 0 . Dos fracciones a / b y c / d son iguales si y solo si ad = bc . La operación con las fracciones funciona exactamente como para los números racionales. Por ejemplo,
Es sencillo demostrar que, si el anillo es un dominio integral, el conjunto de las fracciones forma un campo. [27]
El campo F ( x ) de las fracciones racionales sobre un campo (o un dominio integral) F es el campo de fracciones del anillo de polinomios F [ x ] . El campo F (( x )) de la serie de Laurent
sobre un cuerpo F es el cuerpo de fracciones del anillo F [[ x ]] de series de potencias formales (en las que k ≥ 0 ). Sin embargo, dado que cualquier serie de Laurent es una fracción de una serie de potencias dividida por una potencia de x (a diferencia de una serie de potencias arbitraria), la representación de fracciones es menos importante en esta situación.
Campos de residuos
Además del campo de fracciones, que incorpora R de forma inyectiva en un campo, se puede obtener un campo a partir de un anillo conmutativo R mediante una función sobreyectiva sobre un campo F. Cualquier campo obtenido de esta manera es un cociente R / m , donde m es un ideal maximal de R. Si R tiene solo un ideal maximal m , este campo se denomina campo de residuos de R. [28 ]
El ideal generado por un único polinomio f en el anillo de polinomios R = E [ X ] (sobre un cuerpo E ) es máximo si y sólo si f es irreducible en E , es decir, si f no puede expresarse como el producto de dos polinomios en E [ X ] de menor grado . Esto produce un cuerpo
- F = E [ X ] / ( f ( X )).
Este campo F contiene un elemento x (es decir, la clase de residuo de X ) que satisface la ecuación
- f ( x ) = 0.
Por ejemplo, C se obtiene a partir de R mediante la unión del símbolo de unidad imaginaria i , que satisface f ( i ) = 0 , donde f ( X ) = X 2 + 1. Además, f es irreducible sobre R , lo que implica que la función que envía un polinomio f ( X ) ∊ R [ X ] a f ( i ) produce un isomorfismo
Construir campos dentro de un campo más grande
Los campos pueden construirse dentro de un campo contenedor mayor dado. Supóngase que se da un campo E y un campo F que contiene a E como subcampo. Para cualquier elemento x de F , existe un subcampo más pequeño de F que contiene a E y x , llamado subcampo de F generado por x y denotado E ( x ) . [29] El paso de E a E ( x ) se hace referencia adjuntando un elemento a E . De manera más general, para un subconjunto S ⊂ F , existe un subcampo mínimo de F que contiene a E y S , denotado por E ( S ) .
El compuesto de dos subcuerpos E y E ′ de algún cuerpo F es el subcuerpo más pequeño de F que contiene tanto a E como a E ′ . El compuesto se puede utilizar para construir el subcuerpo más grande de F que satisface una cierta propiedad, por ejemplo el subcuerpo más grande de F , que es, en el lenguaje presentado a continuación, algebraico sobre E . [c]
Extensiones de campo
La noción de un subcampo E ⊂ F también puede considerarse desde el punto de vista opuesto, haciendo referencia a que F es una extensión del campo (o simplemente extensión) de E , denotada por
- F / E ,
y leer " F sobre E ".
Un dato básico de una extensión de campo es su grado [ F : E ] , es decir, la dimensión de F como un espacio vectorial E. Satisface la fórmula [30]
- [ G : E ] = [ G : F ] [ F : E ] .
Las extensiones cuyo grado es finito se denominan extensiones finitas. Las extensiones C / R y F 4 / F 2 son de grado 2 , mientras que R / Q es una extensión infinita.
Extensiones algebraicas
Un concepto fundamental en el estudio de las extensiones de campo F / E son los elementos algebraicos . Un elemento x ∈ F es algebraico sobre E si es una raíz de un polinomio con coeficientes en E , es decir, si satisface una ecuación polinómica.
- e n x n + e n −1 x n −1 + ⋯ + e 1 x + e 0 = 0 ,
con e n , ..., e 0 en E , y e n ≠ 0 . Por ejemplo, la unidad imaginaria i en C es algebraica sobre R , e incluso sobre Q , ya que satisface la ecuación
- yo 2 + 1 = 0 .
Una extensión de campo en la que cada elemento de F es algebraico sobre E se denomina extensión algebraica . Cualquier extensión finita es necesariamente algebraica, como se puede deducir de la fórmula de multiplicatividad anterior. [31]
El subcuerpo E ( x ) generado por un elemento x , como se indicó anteriormente, es una extensión algebraica de E si y solo si x es un elemento algebraico. Es decir, si x es algebraico, todos los demás elementos de E ( x ) son necesariamente algebraicos también. Además, el grado de la extensión E ( x ) / E , es decir, la dimensión de E ( x ) como un espacio vectorial E , es igual al grado mínimo n tal que existe una ecuación polinómica que involucra a x , como se indicó anteriormente. Si este grado es n , entonces los elementos de E ( x ) tienen la forma
Por ejemplo, el campo Q ( i ) de los racionales gaussianos es el subcampo de C que consiste en todos los números de la forma a + bi donde tanto a como b son números racionales: los sumandos de la forma i 2 (y de manera similar para exponentes más altos) no tienen que considerarse aquí, ya que a + bi + ci 2 puede simplificarse a a − c + bi .
Bases de trascendencia
El campo de fracciones racionales antes mencionado E ( X ) , donde X es un indeterminado , no es una extensión algebraica de E ya que no existe una ecuación polinómica con coeficientes en E cuyo cero sea X . Los elementos, como X , que no son algebraicos se denominan trascendentales . Hablando informalmente, el indeterminado X y sus potencias no interactúan con elementos de E . Se puede llevar a cabo una construcción similar con un conjunto de indeterminados, en lugar de solo uno.
Una vez más, la extensión de campo E ( x ) / E analizada anteriormente es un ejemplo clave: si x no es algebraica (es decir, x no es una raíz de un polinomio con coeficientes en E ), entonces E ( x ) es isomorfo a E ( X ) . Este isomorfismo se obtiene sustituyendo x por X en fracciones racionales.
Un subconjunto S de un cuerpo F es una base de trascendencia si es algebraicamente independiente (no satisface ninguna relación polinomial) sobre E y si F es una extensión algebraica de E ( S ) . Cualquier extensión de cuerpo F / E tiene una base de trascendencia. [32] Por lo tanto, las extensiones de cuerpo se pueden dividir en extensiones de la forma E ( S ) / E ( extensiones puramente trascendentales ) y extensiones algebraicas.
Operaciones de cierre
Un campo es algebraicamente cerrado si no tiene ninguna extensión algebraica estrictamente mayor o, equivalentemente, si tiene alguna ecuación polinómica
- f n x n + f n −1 x n −1 + ⋯ + f 1 x + f 0 = 0 , con coeficientes f n , ..., f 0 ∈ F , n > 0 ,
tiene una solución x ∊ F . [33] Por el teorema fundamental del álgebra , C es algebraicamente cerrada, es decir, cualquier ecuación polinómica con coeficientes complejos tiene una solución compleja. Los números racionales y reales no son algebraicamente cerrados ya que la ecuación
- x2 + 1=0
no tiene ninguna solución racional o real. Un cuerpo que contiene F se llama clausura algebraica de F si es algebraico sobre F (a grandes rasgos, no demasiado grande en comparación con F ) y es algebraicamente cerrado (lo suficientemente grande como para contener soluciones de todas las ecuaciones polinómicas).
Por lo anterior, C es una clausura algebraica de R . La situación en la que la clausura algebraica es una extensión finita del campo F es bastante especial: por el teorema de Artin-Schreier , el grado de esta extensión es necesariamente 2 , y F es elementalmente equivalente a R . Dichos campos también se conocen como campos cerrados reales .
Todo cuerpo F tiene una clausura algebraica, que además es única salvo isomorfismo (no único). Se denomina comúnmente clausura algebraica y se denota F . Por ejemplo, la clausura algebraica Q de Q se denomina cuerpo de números algebraicos . El cuerpo F suele ser bastante implícito, ya que su construcción requiere el lema del ultrafiltro , un axioma de teoría de conjuntos que es más débil que el axioma de elección . [34] En este sentido, la clausura algebraica de F q , es excepcionalmente simple. Es la unión de los cuerpos finitos que contienen a F q (los de orden q n ). Para cualquier cuerpo algebraicamente cerrado F de característica 0 , la clausura algebraica del cuerpo F (( t )) de la serie de Laurent es el cuerpo de la serie de Puiseux , obtenido mediante la unión de raíces de t . [35]
Campos con estructura adicional
Dado que los campos son omnipresentes en las matemáticas y más allá, se han adaptado varios refinamientos del concepto a las necesidades de áreas matemáticas particulares.
Campos ordenados
Un cuerpo F se denomina cuerpo ordenado si dos elementos cualesquiera pueden compararse, de modo que x + y ≥ 0 y xy ≥ 0 siempre que x ≥ 0 e y ≥ 0 . Por ejemplo, los números reales forman un cuerpo ordenado, con el ordenamiento habitual ≥ . El teorema de Artin-Schreier establece que un cuerpo puede ordenarse si y solo si es un cuerpo formalmente real , lo que significa que cualquier ecuación cuadrática
sólo tiene la solución x 1 = x 2 = ⋯ = x n = 0 . [36] El conjunto de todos los órdenes posibles en un cuerpo fijo F es isomorfo al conjunto de homomorfismos de anillos desde el anillo de Witt W( F ) de formas cuadráticas sobre F , hasta Z . [37]
Un campo arquimediano es un campo ordenado tal que para cada elemento existe una expresión finita
- 1 + 1 + ⋯ + 1
cuyo valor es mayor que ese elemento, es decir, no hay infinitos elementos. Equivalentemente, el cuerpo no contiene infinitesimales (elementos menores que todos los números racionales); o, aún equivalente, el cuerpo es isomorfo a un subcuerpo de R .

Un cuerpo ordenado es Dedekind-completo si todos los límites superiores , límites inferiores (ver corte de Dedekind ) y límites, que deberían existir, existen. Más formalmente, se requiere que cada subconjunto acotado de F tenga un límite superior mínimo. Cualquier cuerpo completo es necesariamente arquimediano, [38] ya que en cualquier cuerpo no arquimediano no hay ni un infinitesimal máximo ni un racional positivo mínimo, de donde la secuencia 1/2, 1/3, 1/4, ... , cada elemento de la cual es mayor que cada infinitesimal, no tiene límite.
Dado que cada subcuerpo propio de los números reales también contiene dichos huecos, R es el único cuerpo ordenado completo, salvo isomorfismo. [39] Varios resultados fundamentales en cálculo se derivan directamente de esta caracterización de los números reales.
Los hiperreales R * forman un cuerpo ordenado que no es arquimediano. Es una extensión de los reales que se obtiene al incluir números infinitos e infinitesimales. Estos son mayores o menores que cualquier número real. Los hiperreales forman la base fundacional del análisis no estándar .
Campos topológicos
Otro refinamiento de la noción de un campo es un campo topológico , en el que el conjunto F es un espacio topológico , tal que todas las operaciones del campo (suma, multiplicación, las funciones a ↦ − a y a ↦ a −1 ) son funciones continuas con respecto a la topología del espacio. [40] La topología de todos los campos discutidos a continuación se induce a partir de una métrica , es decir, una función
- d : F × F → R ,
que mide una distancia entre dos elementos cualesquiera de F .
La completitud de F es otro campo en el que, informalmente hablando, se rellenan los "huecos" del campo original F , si los hay. Por ejemplo, cualquier número irracional x , como x = √ 2 , es un "hueco" en los racionales Q en el sentido de que es un número real que puede aproximarse de forma arbitrariamente cercana mediante números racionales p / q , en el sentido de que la distancia de x y p / q dada por el valor absoluto | x − p / q | es tan pequeña como se desee. La siguiente tabla enumera algunos ejemplos de esta construcción. La cuarta columna muestra un ejemplo de una sucesión cero , es decir, una sucesión cuyo límite (para n → ∞ ) es cero.
| Campo | Métrico | Terminación | secuencia cero |
|---|---|---|---|
| Q | | x − y | ( valor absoluto habitual ) | R | 1/ n |
| Q | obtenido utilizando la valoración p -ádica , para un número primo p | Q p ( números p -ádicos ) | pn |
| F ( t ) ( F cualquier campo) | obtenido utilizando la valoración t -ádica | F (( t )) | en |
El cuerpo Q p se utiliza en teoría de números y análisis p -ádico . El cierre algebraico Q p lleva una norma única que extiende la de Q p , pero no es completo. La completitud de este cierre algebraico, sin embargo, es algebraicamente cerrado. Debido a su analogía aproximada con los números complejos, a veces se lo llama el cuerpo de números complejos p-ádicos y se denota por C p . [41]
Campos locales
Los siguientes campos topológicos se denominan campos locales : [42] [d]
- extensiones finitas de Q p (campos locales de característica cero)
- extensiones finitas de F p (( t )) , el campo de la serie de Laurent sobre F p (campos locales de característica p ).
Estos dos tipos de cuerpos locales comparten algunas similitudes fundamentales. En esta relación, los elementos p ∈ Q p y t ∈ F p (( t )) (denominados uniformizadores ) se corresponden entre sí. La primera manifestación de esto es a un nivel elemental: los elementos de ambos cuerpos pueden expresarse como series de potencias en el uniformizador, con coeficientes en F p . (Sin embargo, dado que la adición en Q p se realiza utilizando el acarreo , lo que no es el caso en F p (( t )) , estos cuerpos no son isomorfos.) Los siguientes hechos muestran que esta similitud superficial es mucho más profunda:
- Cualquier enunciado de primer orden que sea verdadero para casi todos los Q p también es verdadero para casi todos los F p (( t )) . Una aplicación de esto es el teorema de Ax-Kochen que describe los ceros de polinomios homogéneos en Q p .
- Las extensiones suavemente ramificadas de ambos campos se encuentran en biyección una respecto de la otra.
- La unión de raíces arbitrarias de potencias p de p (en Q p ), respectivamente de t (en F p (( t )) ), produce extensiones (infinitas) de estos campos conocidas como campos perfectoides . Sorprendentemente, los grupos de Galois de estos dos campos son isomorfos, lo que constituye el primer atisbo de un notable paralelo entre estos dos campos: [43]
Campos diferenciales
Los campos diferenciales son campos dotados de una derivación , es decir, que permiten tomar derivadas de elementos en el campo. [44] Por ejemplo, el campo R ( X ) , junto con la derivada estándar de polinomios forma un campo diferencial. Estos campos son fundamentales para la teoría diferencial de Galois , una variante de la teoría de Galois que trata con ecuaciones diferenciales lineales .
Teoría de Galois
La teoría de Galois estudia las extensiones algebraicas de un cuerpo mediante el estudio de la simetría en las operaciones aritméticas de adición y multiplicación. Una noción importante en esta área es la de las extensiones finitas de Galois F / E , que son, por definición, aquellas que son separables y normales . El teorema del elemento primitivo muestra que las extensiones finitas separables son necesariamente simples , es decir, de la forma
- F = E [ X ]/ f ( X ) ,
donde f es un polinomio irreducible (como el anterior). [45] Para tal extensión, ser normal y separable significa que todos los ceros de f están contenidos en F y que f solo tiene ceros simples. La última condición siempre se satisface si E tiene característica 0 .
Para una extensión de Galois finita, el grupo de Galois Gal( F / E ) es el grupo de automorfismos de cuerpo de F que son triviales en E (es decir, las biyecciones σ : F → F que preservan la adición y la multiplicación y que envían elementos de E a sí mismos). La importancia de este grupo surge del teorema fundamental de la teoría de Galois , que construye una correspondencia explícita uno a uno entre el conjunto de subgrupos de Gal( F / E ) y el conjunto de extensiones intermedias de la extensión F / E . [46] Por medio de esta correspondencia, las propiedades de la teoría de grupos se traducen en hechos sobre cuerpos. Por ejemplo, si el grupo de Galois de una extensión de Galois como la anterior no es solucionable (no se puede construir a partir de grupos abelianos ), entonces los ceros de f no se pueden expresar en términos de adición, multiplicación y radicales, es decir, expresiones que involucran . Por ejemplo, los grupos simétricos S n no son solucionables para n ≥ 5 . En consecuencia, como se puede demostrar, los ceros de los siguientes polinomios no son expresables mediante sumas, productos y radicales. Para este último polinomio, este hecho se conoce como el teorema de Abel-Ruffini :
- f ( X ) = X 5 − 4 X + 2 (y E = Q ), [47]
- f ( X ) = X n + a n −1 X n −1 + ⋯ + a 0 (donde f se considera un polinomio en E ( a 0 , ..., a n −1 ) , para algunos indeterminados a i , E es cualquier cuerpo y n ≥ 5 ).
El producto tensorial de cuerpos no suele ser un cuerpo. Por ejemplo, una extensión finita F / E de grado n es una extensión de Galois si y sólo si existe un isomorfismo de F -álgebras
- F ⊗ E F ≅ F n .
Este hecho es el comienzo de la teoría de Galois de Grothendieck , una extensión de largo alcance de la teoría de Galois aplicable a los objetos algebro-geométricos. [48]
Invariantes de campos
Los invariantes básicos de un cuerpo F incluyen la característica y el grado de trascendencia de F sobre su cuerpo primo. Este último se define como el número máximo de elementos en F que son algebraicamente independientes sobre el cuerpo primo. Dos cuerpos algebraicamente cerrados E y F son isomorfos precisamente si estos dos datos concuerdan. [49] Esto implica que cualesquiera dos cuerpos algebraicamente cerrados incontables de la misma cardinalidad y la misma característica son isomorfos. Por ejemplo, Q p , C p y C son isomorfos (pero no isomorfos como campos topológicos).
Teoría de modelos de campos
En la teoría de modelos , una rama de la lógica matemática , dos cuerpos E y F se denominan elementalmente equivalentes si cada enunciado matemático que es verdadero para E también lo es para F y viceversa. Se requiere que los enunciados matemáticos en cuestión sean oraciones de primer orden (que involucren 0 , 1 , la adición y la multiplicación). Un ejemplo típico, para n > 0 , n es un entero, es
- φ ( E ) = "cualquier polinomio de grado n en E tiene un cero en E "
El conjunto de tales fórmulas para todo n expresa que E es algebraicamente cerrado. El principio de Lefschetz establece que C es elementalmente equivalente a cualquier cuerpo algebraicamente cerrado F de característica cero. Además, cualquier enunciado fijo φ se cumple en C si y solo si se cumple en cualquier cuerpo algebraicamente cerrado de característica suficientemente alta. [50]
Si U es un ultrafiltro en un conjunto I , y F i es un campo para cada i en I , el ultraproducto de F i con respecto a U es un campo. [51] Se denota por
- ulim i →∞ F i ,
ya que se comporta de varias maneras como un límite de los cuerpos F i : el teorema de Łoś establece que cualquier enunciado de primer orden que se cumple para todos excepto un número finito de F i , también se cumple para el ultraproducto. Aplicado a la oración anterior φ , esto muestra que hay un isomorfismo [e]
De esto también se sigue el teorema de Ax-Kochen mencionado anteriormente y un isomorfismo de los ultraproductos (en ambos casos sobre todos los primos p )
- ulim p Q p ≅ ulim p F p (( t )) .
Además, la teoría de modelos también estudia las propiedades lógicas de varios otros tipos de campos, como los campos cerrados reales o los campos exponenciales (que están equipados con una función exponencial exp : F → F × ). [52]
Grupo absoluto de Galois
Para los cuerpos que no están algebraicamente cerrados (o no están separados), el grupo absoluto de Galois Gal( F ) es fundamentalmente importante: extendiendo el caso de extensiones finitas de Galois descritas anteriormente, este grupo gobierna todas las extensiones finitas separables de F . Por medios elementales, se puede demostrar que el grupo Gal( F q ) es el grupo de Prüfer , la completitud profinita de Z . Esta afirmación subsume el hecho de que las únicas extensiones algebraicas de Gal( F q ) son los cuerpos Gal( F q n ) para n > 0 , y que los grupos de Galois de estas extensiones finitas están dados por
- Gal( F q n / F q ) = Z / n Z .
También se conoce una descripción en términos de generadores y relaciones para los grupos de Galois de cuerpos numéricos p -ádicos (extensiones finitas de Q p ). [53]
Las representaciones de los grupos de Galois y de grupos relacionados como el grupo de Weil son fundamentales en muchas ramas de la aritmética, como el programa de Langlands . El estudio cohomológico de tales representaciones se realiza utilizando la cohomología de Galois . [54] Por ejemplo, el grupo de Brauer , que se define clásicamente como el grupo de F -álgebras simples centrales , puede reinterpretarse como un grupo de cohomología de Galois, es decir
- Br( F ) = H2 ( F , Gm ) .
Teoría K
La teoría K de Milnor se define como
El teorema de isomorfismo de residuos normativos , demostrado alrededor de 2000 por Vladimir Voevodsky , relaciona esto con la cohomología de Galois por medio de un isomorfismo.
La teoría K algebraica está relacionada con el grupo de matrices invertibles con coeficientes del cuerpo dado. Por ejemplo, el proceso de tomar el determinante de una matriz invertible conduce a un isomorfismo K 1 ( F ) = F × . El teorema de Matsumoto muestra que K 2 ( F ) concuerda con K 2 M ( F ) . En grados superiores, la teoría K se aparta de la teoría K de Milnor y sigue siendo difícil de calcular en general.
Aplicaciones
Álgebra lineal y álgebra conmutativa
Si a ≠ 0 , entonces la ecuación
- hacha = b
tiene una solución única x en un cuerpo F , es decir Esta consecuencia inmediata de la definición de un cuerpo es fundamental en el álgebra lineal . Por ejemplo, es un ingrediente esencial de la eliminación gaussiana y de la prueba de que cualquier espacio vectorial tiene una base . [55]
La teoría de módulos (el análogo de los espacios vectoriales sobre anillos en lugar de cuerpos) es mucho más complicada, porque la ecuación anterior puede tener varias soluciones o ninguna. En particular, los sistemas de ecuaciones lineales sobre un anillo son mucho más difíciles de resolver que en el caso de cuerpos, incluso en el caso especialmente simple del anillo Z de los números enteros.
Campos finitos: criptografía y teoría de la codificación
Una rutina criptográfica ampliamente aplicada utiliza el hecho de que la exponenciación discreta, es decir, el cálculo
- a n = a ⋅ a ⋅ ⋯ ⋅ a ( n factores, para un entero n ≥ 1 )
En un campo finito (grande), F q se puede realizar de manera mucho más eficiente que el logaritmo discreto , que es la operación inversa, es decir, determinar la solución n de una ecuación.
- a n = b .
En la criptografía de curva elíptica , la multiplicación en un cuerpo finito se reemplaza por la operación de sumar puntos en una curva elíptica , es decir, las soluciones de una ecuación de la forma
- y 2 = x 3 + ax + b .
Los campos finitos también se utilizan en la teoría de codificación y la combinatoria .
Geometría: campo de funciones

Las funciones de un espacio topológico adecuado X en un campo F se pueden sumar y multiplicar puntualmente, por ejemplo, el producto de dos funciones se define por el producto de sus valores dentro del dominio:
- ( f ⋅ g )( x ) = f ( x ) ⋅ g ( x ) .
Esto hace que estas funciones sean un álgebra F - conmutativa .
Para tener un campo de funciones, se deben considerar álgebras de funciones que sean dominios integrales . En este caso las razones de dos funciones, es decir, expresiones de la forma
formar un campo, llamado campo de funciones.
Esto ocurre en dos casos principales. Cuando X es una variedad compleja X . En este caso, se considera el álgebra de funciones holomorfas , es decir, funciones complejas diferenciables. Sus razones forman el campo de funciones meromórficas en X .
El campo de funciones de una variedad algebraica X (un objeto geométrico definido como los ceros comunes de ecuaciones polinómicas) consiste en razones de funciones regulares , es decir, razones de funciones polinómicas sobre la variedad. El campo de funciones del espacio n -dimensional sobre un campo F es F ( x 1 , ..., x n ) , es decir, el campo que consiste en razones de polinomios en n indeterminados. El campo de funciones de X es el mismo que el de cualquier subvariedad densa abierta . En otras palabras, el campo de funciones es insensible a reemplazar X por una subvariedad (ligeramente) más pequeña.
El campo de funciones es invariante bajo isomorfismo y equivalencia biracional de variedades. Por lo tanto, es una herramienta importante para el estudio de variedades algebraicas abstractas y para la clasificación de variedades algebraicas. Por ejemplo, la dimensión , que es igual al grado de trascendencia de F ( X ) , es invariante bajo equivalencia biracional. [56] Para curvas (es decir, la dimensión es uno), el campo de funciones F ( X ) es muy cercano a X : si X es suave y propio (el análogo de ser compacto ), X puede reconstruirse, hasta el isomorfismo, a partir de su campo de funciones. [f] En dimensiones superiores, el campo de funciones recuerda menos, pero aún información decisiva sobre X . El estudio de los campos de funciones y su significado geométrico en dimensiones superiores se conoce como geometría biracional . El programa de modelo mínimo intenta identificar las variedades algebraicas más simples (en un cierto sentido preciso) con un campo de funciones prescrito.
Teoría de números: campos globales
Los cuerpos globales están en el centro de atención en la teoría algebraica de números y la geometría aritmética . Son, por definición, cuerpos numéricos (extensiones finitas de Q ) o cuerpos funcionales sobre F q (extensiones finitas de F q ( t ) ). En cuanto a los cuerpos locales, estos dos tipos de cuerpos comparten varias características similares, aunque son de característica 0 y característica positiva, respectivamente. Esta analogía de cuerpo funcional puede ayudar a dar forma a las expectativas matemáticas, a menudo primero al comprender las preguntas sobre cuerpos funcionales y luego al tratar el caso del cuerpo numérico. Esto último suele ser más difícil. Por ejemplo, la hipótesis de Riemann sobre los ceros de la función zeta de Riemann (abierta a partir de 2017) puede considerarse paralela a las conjeturas de Weil (probadas en 1974 por Pierre Deligne ).

Los campos ciclotómicos se encuentran entre los campos numéricos más intensamente estudiados. Tienen la forma Q ( ζ n ) , donde ζ n es una raíz primitiva n ésima de la unidad , es decir, un número complejo ζ que satisface ζ n = 1 y ζ m ≠ 1 para todo 0 < m < n . [57] Para n siendo un primo regular , Kummer utilizó campos ciclotómicos para demostrar el Último Teorema de Fermat , que afirma la no existencia de soluciones racionales distintas de cero para la ecuación
- xn + yn = zn .
Los cuerpos locales son compleciones de cuerpos globales. El teorema de Ostrowski afirma que las únicas compleciones de Q , un cuerpo global, son los cuerpos locales Q p y R . El estudio de cuestiones aritméticas en cuerpos globales a veces se puede hacer mirando las cuestiones correspondientes localmente. Esta técnica se llama principio local-global . Por ejemplo, el teorema de Hasse-Minkowski reduce el problema de encontrar soluciones racionales de ecuaciones cuadráticas a resolver estas ecuaciones en R y Q p , cuyas soluciones se pueden describir fácilmente. [58]
A diferencia de los cuerpos locales, los grupos de Galois de los cuerpos globales no se conocen. La teoría inversa de Galois estudia el problema (sin resolver) de si cualquier grupo finito es el grupo de Galois Gal( F / Q ) para algún cuerpo numérico F . [59] La teoría de cuerpos de clase describe las extensiones abelianas , es decir, aquellas con grupo de Galois abeliano, o equivalentemente los grupos de Galois abelianizados de cuerpos globales. Un enunciado clásico, el teorema de Kronecker-Weber , describe la extensión abeliana máxima Q ab de Q : es el cuerpo
- Q ( ζn , n ≥ 2 )
obtenido mediante la unión de todas las raíces n primitivas de la unidad. El Jugendtraum de Kronecker solicita una descripción explícita similar de F ab de los cuerpos numéricos generales F . Para cuerpos cuadráticos imaginarios , , d > 0 , la teoría de la multiplicación compleja describe F ab utilizando curvas elípticas . Para cuerpos numéricos generales, no se conoce una descripción explícita de este tipo.
Nociones relacionadas
Además de la estructura adicional que pueden disfrutar los campos, los campos admiten varias otras nociones relacionadas. Dado que en cualquier campo 0 ≠ 1 , cualquier campo tiene al menos dos elementos. No obstante, existe un concepto de campo con un elemento , que se sugiere que es un límite de los campos finitos F p , ya que p tiende a 1 . [60] Además de los anillos de división, existen varias otras estructuras algebraicas más débiles relacionadas con los campos, como los cuasicampos , los campos cercanos y los semicampos .
También existen clases propias con estructura de campo, que a veces se denominan Campos , con F mayúscula. Los números surreales forman un Campo que contiene a los reales, y serían un campo excepto por el hecho de que son una clase propia, no un conjunto. Los números , un concepto de la teoría de juegos , también forman un Campo de este tipo. [61]
Anillos de división
La eliminación de uno o varios axiomas en la definición de un cuerpo conduce a otras estructuras algebraicas. Como se mencionó anteriormente, los anillos conmutativos satisfacen todos los axiomas de cuerpo excepto la existencia de inversos multiplicativos. La eliminación en cambio de la conmutatividad de la multiplicación conduce al concepto de anillo de división o cuerpo sesgado ; [g] a veces la asociatividad también se debilita. Los únicos anillos de división que son espacios vectoriales R de dimensión finita son el propio R , C (que es un cuerpo) y los cuaterniones H (en los que la multiplicación no es conmutativa). Este resultado se conoce como el teorema de Frobenius . Los octoniones O , para los que la multiplicación no es ni conmutativa ni asociativa, son un álgebra de división alternativa normada , pero no son un anillo de división. Este hecho fue demostrado utilizando métodos de topología algebraica en 1958 por Michel Kervaire , Raoul Bott y John Milnor . [62]
El pequeño teorema de Wedderburn establece que todos los anillos de división finitos son campos.
Notas
- ^ El doble uso a priori del símbolo " − " para denotar una parte de una constante y para los inversos aditivos se justifica por esta última condición.
- ^ De manera equivalente, un campo es una estructura algebraica ⟨ F , +, ⋅, −, −1 , 0, 1⟩ de tipo ⟨2, 2, 1, 1, 0, 0⟩ , tal que 0 −1 no está definido, ⟨ F , +, −, 0⟩ y son grupos abelianos, y ⋅ es distributivo sobre + . [10]
- ^ Otros ejemplos incluyen la extensión máxima no ramificada o la extensión abeliana máxima dentro de F .
- ^ Algunos autores consideran también los campos R y C como campos locales. Por otra parte, estos dos campos, también llamados campos locales de Arquímedes, comparten poca similitud con los campos locales considerados aquí, hasta el punto de que Cassels (1986, p. vi) los califica de "completamente anómalos".
- ^ Tanto C como ulim p F p son algebraicamente cerrados por el teorema de Łoś. Por la misma razón, ambos tienen característica cero. Finalmente, ambos son incontables, por lo que son isomorfos.
- ^ Más precisamente, existe una equivalencia de categorías entre curvas algebraicas propias suaves sobre un campo algebraicamente cerrado F y extensiones de campo finitas de F ( T ) .
- ^ Históricamente, a los anillos de división a veces se los denominaba campos, mientras que a los campos se los llamaba campos conmutativos .
Citas
- ^ Beachy y Blair (2006), Definición 4.1.1, pág. 181
- ^ Fraleigh (1976), pág. 10
- ^ McCoy (1968), pág. 16
- ^ Clark (1984), Capítulo 3
- ^ Mines, Richman y Ruitenburg (1988), §II.2. Véase también el campo Heyting .
- ^ Beachy y Blair (2006), pág. 120, cap. 3
- ^ Artin (1991), Capítulo 13.4
- ^ Lidl y Niederreiter (2008), ejemplo 1.62
- ^ Beachy y Blair (2006), pág. 120, cap. 3
- ^ Wallace (1998), Tomo 2
- ^ Adamson (2007), §I.2, pág. 10
- ^ Escofier (2012), 14.4.2
- ^ Adamson (2007), §I.3
- ^ Adamson (2007), pág. 12
- ^ Lidl y Niederreiter (2008), Lema 2.1, Teorema 2.2
- ^ Lidl y Niederreiter (2008), Teorema 1.2.5
- ^ Kleiner (2007), pág. 63
- ^ Kiernan (1971), pág. 50
- ^ Bourbaki (1994), págs. 75-76
- ^ Corry (2004), pág. 24
- ^ "Usos más antiguos conocidos de algunas palabras de las matemáticas (F)".
- ↑ Dirichlet (1871), pág. 42, traducción de Kleiner (2007), pág. 66
- ^ Bourbaki (1994), pág. 81
- ^ Corry (2004), pág. 33. Véase también Fricke y Weber (1924).
- ^ Bourbaki (1994), pág. 92
- ^ Lang (2002), §II.1
- ^ Artin (1991), §10.6
- ^ Eisenbud (1995), pág. 60
- ^ Jacobson (2009), pág. 213
- ^ Artin (1991), Teorema 13.3.4
- ^ Artin (1991), Corolario 13.3.6
- ^ Bourbaki (1988), Capítulo V, §14, N° 2, Teorema 1
- ^ Artin (1991), §13.9
- ^ Banaschewski (1992). Publicación de Mathoverflow
- ^ Ribenboim (1999), pág. 186, §7.1
- ^ Bourbaki (1988), Capítulo VI, §2.3, Corolario 1
- ^ Lorenz (2008), §22, Teorema 1
- ^ Prestel (1984), Proposición 1.22
- ^ Prestel (1984), Teorema 1.23
- ^ Warner (1989), Capítulo 14
- ^ Gouvêa (1997), §5.7
- ^ Serre (1979)
- ^ Scholze (2014)
- ^ van der Put y Singer (2003), §1
- ^ Lang (2002), Teorema V.4.6
- ^ Lang (2002), §VI.1
- ^ Lang (2002), Ejemplo VI.2.6
- ^ Borceux y Janelidze (2001). Véase también grupo fundamental Étale .
- ^ Gouvêa (2012), Teorema 6.4.8
- ^ Marker, Messmer y Pillay (2006), Corolario 1.2
- ^ Schoutens (2002), §2
- ^ Kuhlmann (2000)
- ^ Jannsen y Wingberg (1982)
- ^ Serre (2002)
- ^ Artin (1991), §3.3
- ^ Eisenbud (1995), §13, Teorema A
- ^ Washington (1997)
- ^ Serre (1996), Capítulo IV
- ^ Serre (1992)
- ^ Tetas (1957)
- ^ Conway (1976)
- ^ Baez (2002)
Referencias
- Adamson, IT (2007), Introducción a la teoría de campos , Dover Publications, ISBN 978-0-486-46266-0
- Allenby, RBJT (1991), Anillos, campos y grupos , Butterworth-Heinemann, ISBN 978-0-340-54440-2
- Artin, Michael (1991), Álgebra , Prentice Hall , ISBN 978-0-13-004763-2, especialmente el capítulo 13
- Artín, Emil ; Schreier, Otto (1927), "Eine Kennzeichnung der reell abgeschlossenen Körper", Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg (en alemán), 5 : 225–231, doi :10.1007/BF02952522, ISSN 0025-5858, JFM 53.0144.01, S2CID 121547404
- Ax, James (1968), "La teoría elemental de los campos finitos", Ann. of Math. , 2, 88 (2): 239–271, doi :10.2307/1970573, JSTOR 1970573
- Baez, John C. (2002), "Los octoniones", Boletín de la Sociedad Matemática Americana , 39 (2): 145–205, arXiv : math/0105155 , doi :10.1090/S0273-0979-01-00934-X, S2CID 586512
- Banaschewski, Bernhard (1992), "Cierre algebraico sin elección", Z. Math. Logik Grundlagen Math. , 38 (4): 383–385, doi :10.1002/malq.19920380136, Zbl 0739.03027
- Beachy, John A; Blair, William D. (2006), Álgebra abstracta (3.ª edición), Waveland Press, ISBN 1-57766-443-4
- Blyth, TS; Robertson, EF (1985), Grupos, anillos y cuerpos: Álgebra a través de la práctica , Cambridge University Press. Véase especialmente el Libro 3 ( ISBN 0-521-27288-2 ) y el Libro 6 ( ISBN 0-521-27291-2 ).
- Borceux, Francis; Janelidze, George (2001), Teorías de Galois , Cambridge University Press, ISBN 0-521-80309-8, Zbl 0978.12004
- Bourbaki, Nicolas (1994), Elementos de la historia de las matemáticas , Springer, doi :10.1007/978-3-642-61693-8, ISBN 3-540-19376-6, Sr. 1290116
- Bourbaki, Nicolas (1988), Álgebra II. Capítulos 4 a 7 , Springer, ISBN 0-387-19375-8
- Cassels, JWS (1986), Campos locales , Textos para estudiantes de la London Mathematical Society, vol. 3, Cambridge University Press, doi :10.1017/CBO9781139171885, ISBN 0-521-30484-9, Sr. 0861410
- Clark, A. (1984), Elementos de álgebra abstracta, Dover Books on Mathematics Series, Dover, ISBN 978-0-486-64725-8
- Conway, John Horton (1976), Sobre números y juegos , Academic Press
- Corry, Leo (2004), Álgebra moderna y el surgimiento de las estructuras matemáticas (2.ª ed.), Birkhäuser, ISBN 3-7643-7002-5, Zbl1044.01008
- Dirichlet, Peter Gustav Lejeune (1871), Dedekind, Richard (ed.), Vorlesungen über Zahlentheorie (Conferencias sobre teoría de números) (en alemán), vol. 1 (2ª ed.), Braunschweig, Alemania: Friedrich Vieweg und Sohn
- Eisenbud, David (1995), Álgebra conmutativa con vistas a la geometría algebraica , Textos de posgrado en matemáticas , vol. 150, Nueva York: Springer-Verlag , doi :10.1007/978-1-4612-5350-1, ISBN 0-387-94268-8, Sr. 1322960
- Escofier, JP (2012), Teoría de Galois , Springer, ISBN 978-1-4613-0191-2
- Fraleigh, John B. (1976), Un primer curso de álgebra abstracta (2.ª ed.), Lectura: Addison-Wesley , ISBN 0-201-01984-1
- Fricke, Robert ; Weber, Heinrich Martin (1924), Lehrbuch der Algebra (en alemán), Vieweg, JFM 50.0042.03
- Gouvêa, Fernando Q. (1997),Números p -ádicos , Universitext (2.ª ed.), Springer
- Gouvêa, Fernando Q. (2012), Una guía para grupos, anillos y campos , Asociación Matemática de América, ISBN 978-0-88385-355-9
- "Campo", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
- Hensel, Kurt (1904), "Über eine neue Begründung der Theorie der algebraischen Zahlen", Journal für die Reine und Angewandte Mathematik (en alemán), 128 : 1–32, ISSN 0075-4102, JFM 35.0227.01
- Jacobson, Nathan (2009), Álgebra básica , vol. 1 (2.ª ed.), Dover, ISBN 978-0-486-47189-1
- Jannsen, Uwe; Wingberg, Kay (1982), "Die Struktur der absolun Galoisgruppe 𝔭-adischer Zahlkörper. [La estructura del grupo absoluto de Galois de campos numéricos 𝔭-ádicos]", Invent. Matemáticas. , 70 (1): 71–98, Bibcode :1982InMat..70...71J, doi :10.1007/bf01393199, MR 0679774, S2CID 119378923
- Kleiner, Israel (2007), Kleiner, Israel (ed.), Una historia del álgebra abstracta , Birkhäuser, doi :10.1007/978-0-8176-4685-1, ISBN 978-0-8176-4684-4, Sr. 2347309
- Kiernan, B. Melvin (1971), "El desarrollo de la teoría de Galois desde Lagrange hasta Artin", Archivo de Historia de las Ciencias Exactas , 8 (1–2): 40–154, doi :10.1007/BF00327219, MR 1554154, S2CID 121442989
- Kuhlmann, Salma (2000), Campos exponenciales ordenados , Fields Institute Monographs, vol. 12, American Mathematical Society, ISBN 0-8218-0943-1, Sr. 1760173
- Lang, Serge (2002), Álgebra , Textos de posgrado en matemáticas, vol. 211 (3.ª ed.), Springer, doi : 10.1007/978-1-4613-0041-0, ISBN 0-387-95385-X
- Lidl, Rudolf; Niederreiter, Harald (2008), Campos finitos (2ª ed.), Cambridge University Press, ISBN 978-0-521-06567-2, Zbl1139.11053
- Lorenz, Falko (2008), Álgebra, Volumen II: Campos con estructuras, álgebras y temas avanzados , Springer, ISBN 978-0-387-72487-4
- Marker, David; Messmer, Margit; Pillay, Anand (2006), Teoría de modelos de campos , Lecture Notes in Logic, vol. 5 (2.ª ed.), Association for Symbolic Logic, CiteSeerX 10.1.1.36.8448 , ISBN 978-1-56881-282-3, Sr. 2215060
- McCoy, Neal H. (1968), Introducción al álgebra moderna, edición revisada , Boston: Allyn and Bacon , LCCN 68015225
- Minas, Ray; Hombre rico, Fred; Ruitenburg, Wim (1988), Un curso de álgebra constructiva , Universitext, Springer, doi :10.1007/978-1-4419-8640-5, ISBN 0-387-96640-4, Sr. 0919949
- Moore, E. Hastings (1893), "Un sistema doblemente infinito de grupos simples", Boletín de la American Mathematical Society , 3 (3): 73–78, doi : 10.1090/S0002-9904-1893-00178-X , MR 1557275
- Prestel, Alexander (1984), Lecciones sobre campos formalmente reales , Lecture Notes in Mathematics, vol. 1093, Springer, doi :10.1007/BFb0101548, ISBN 3-540-13885-4, Sr. 0769847
- Ribenboim, Paulo (1999), La teoría de las valoraciones clásicas , Springer Monographs in Mathematics, Springer, doi :10.1007/978-1-4612-0551-7, ISBN 0-387-98525-5, Sr. 1677964
- Scholze, Peter (2014), "Espacios perfectos y sus aplicaciones" (PDF) , Actas del Congreso Internacional de Matemáticos 2014, Kyung Moon SA, ISBN 978-89-6105-804-9
- Schoutens, Hans (2002), El uso de ultraproductos en álgebra conmutativa , Lecture Notes in Mathematics, vol. 1999, Springer, ISBN 978-3-642-13367-1
- Serre, Jean-Pierre (1996) [1978], Un curso de aritmética. Traducción de Cours d'arithmetique , Texto de posgrado en matemáticas, vol. 7 (2.ª ed.), Springer, ISBN 9780387900407, Zbl0432.10001
- Serre, Jean-Pierre (1979), Campos locales , Textos de posgrado en matemáticas, vol. 67, Springer, ISBN 0-387-90424-7, Sr. 0554237
- Serre, Jean-Pierre (1992), Temas de la teoría de Galois , Jones and Bartlett Publishers, ISBN 0-86720-210-6, Zbl 0746.12001
- Serre, Jean-Pierre (2002), Cohomología de Galois , Springer Monographs in Mathematics, traducido del francés por Patrick Ion , Berlín, Nueva York: Springer-Verlag , ISBN 978-3-540-42192-4, MR 1867431, Zbl 1004.12003
- Sharpe, David (1987), Anillos y factorización , Cambridge University Press, ISBN 0-521-33718-6, Zbl0674.13008
- Steinitz, Ernst (1910), "Algebraische Theorie der Körper" [Teoría algebraica de campos], Journal für die reine und angewandte Mathematik , 1910 (137): 167–309, doi :10.1515/crll.1910.137.167, ISSN 0075- 4102, JFM 41.0445.03, S2CID 120807300
- Tetas, Jacques (1957), "Sur les analogues algébriques des groupes semi-simples complexes", Colloque d'algèbre supérieure, tenu à Bruxelles du 19 au 22 de diciembre de 1956, Centre Belge de Recherches Mathématiques Établissements Ceuterick, Lovaina , París: Librairie Gauthier -Villars, págs. 261–289
- van der Put, M.; Singer, MF (2003), Teoría de Galois de ecuaciones diferenciales lineales, Grundlehren der mathematischen Wissenschaften, vol. 328, saltador
- von Staudt, Karl Georg Christian (1857), Beiträge zur Geometrie der Lage (Contribuciones a la geometría de la posición), vol. 2, Núremberg (Alemania): Bauer y Raspe
- Wallace, DAR (1998), Grupos, anillos y campos , SUMS, vol. 151, Springer
- Warner, Seth (1989), Campos topológicos , Holanda Septentrional, ISBN 0-444-87429-1, Zbl 0683.12014
- Washington, Lawrence C. (1997), Introducción a los campos ciclotómicos , Textos de posgrado en matemáticas, vol. 83 (2.ª ed.), Springer-Verlag, doi :10.1007/978-1-4612-1934-7, ISBN 0-387-94762-0, Sr. 1421575
- Weber, Heinrich (1893), "Die allgemeinen Grundlagen der Galois'schen Gleichungstheorie", Mathematische Annalen (en alemán), 43 (4): 521–549, doi :10.1007/BF01446451, ISSN 0025-5831, JFM 25.0137.01, S2CID 120528969

![{\displaystyle {\begin{aligned}&{\frac {a}{b}}\cdot \left({\frac {c}{d}}+{\frac {e}{f}}\right)\\[6pt]={}&{\frac {a}{b}}\cdot \left({\frac {c}{d}}\cdot {\frac {f}{f}}+{\frac {e}{f}}\cdot {\frac {d}{d}}\right)\\[6pt]={}&{\frac {a}{b}}\cdot \left({\frac {cf}{df}}+{\frac {ed}{fd}}\right)={\frac {a}{b}}\cdot {\frac {cf+ed}{df}}\\[6pt]={}&{\frac {a(cf+ed)}{bdf}}={\frac {acf}{bdf}}+{\frac {aed}{bdf}}={\frac {ac}{bd}}+{\frac {ae}{bf}}\\[6pt]={}&{\frac {a}{b}}\cdot {\frac {c}{d}}+{\frac {a}{b}}\cdot {\frac {e}{f}}.\end{alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fdb74d800a57e82a5c69ce90ed98ddd3e9ebe3bc)

![{\displaystyle {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca071ab504481c2bb76081aacb03f5519930710)




![{\displaystyle \mathbf {R} [X]/\left(X^{2}+1\right)\ {\stackrel {\cong }{\longrightarrow }}\ \mathbf {C} .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca0f1bdfcfbc661e9a16477be8972a3bb7c281c5)



![{\displaystyle {\sqrt[{n}]{~}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55546dcf148dd64ce5d49717847ae757505e67e6)







