- Isaac Newton (1643-1727), en un retrato de 1689 realizado por Godfrey Kneller
- Copia de los Principia de Newton , con correcciones manuscritas para la segunda edición, en la Biblioteca Wren del Trinity College, Cambridge.
- Primera y segunda leyes de Newton, en latín, del libro original Principia Mathematica de 1687
Leyes del movimiento de Newton
| Parte de una serie sobre |
| Mecánica clásica |
|---|
Las leyes de Newton del movimiento son tres leyes físicas que describen la relación entre el movimiento de un objeto y las fuerzas que actúan sobre él. Estas leyes, que constituyen la base de la mecánica newtoniana , pueden resumirse de la siguiente manera:
- Un cuerpo permanece en reposo o en movimiento a velocidad constante en línea recta, excepto en la medida en que actúa sobre él una fuerza.
- En cualquier instante de tiempo, la fuerza neta sobre un cuerpo es igual a la aceleración del cuerpo multiplicada por su masa o, equivalentemente, la tasa a la que el momento del cuerpo cambia con el tiempo.
- Si dos cuerpos ejercen fuerzas entre sí, estas fuerzas tienen la misma magnitud pero direcciones opuestas. [1] [2]
Las tres leyes del movimiento fueron enunciadas por primera vez por Isaac Newton en su Philosophiæ Naturalis Principia Mathematica ( Principios matemáticos de la filosofía natural ), publicada originalmente en 1687. [3] Newton las utilizó para investigar y explicar el movimiento de muchos objetos y sistemas físicos. En el tiempo transcurrido desde Newton, nuevos conocimientos, especialmente en torno al concepto de energía, construyeron el campo de la mecánica clásica sobre sus cimientos. También se han descubierto limitaciones a las leyes de Newton; son necesarias nuevas teorías cuando los objetos se mueven a velocidades muy altas ( relatividad especial ), son muy masivos ( relatividad general ) o son muy pequeños ( mecánica cuántica ).
Prerrequisitos
Las leyes de Newton suelen enunciarse en términos de masas puntuales o de partículas , es decir, cuerpos cuyo volumen es despreciable. Esta es una aproximación razonable para cuerpos reales cuando se puede despreciar el movimiento de las partes internas y cuando la separación entre cuerpos es mucho mayor que el tamaño de cada uno. Por ejemplo, la Tierra y el Sol pueden considerarse como puntuales cuando se considera la órbita del primero alrededor del segundo, pero la Tierra no es puntual cuando se consideran las actividades en su superficie. [nota 1]
La descripción matemática del movimiento, o cinemática , se basa en la idea de especificar posiciones utilizando coordenadas numéricas. El movimiento se representa mediante estos números que cambian con el tiempo: la trayectoria de un cuerpo se representa mediante una función que asigna a cada valor de una variable de tiempo los valores de todas las coordenadas de posición. El caso más simple es unidimensional, es decir, cuando un cuerpo está restringido a moverse solo a lo largo de una línea recta. Su posición puede entonces darse por un solo número, que indica dónde está en relación con algún punto de referencia elegido. Por ejemplo, un cuerpo puede ser libre de deslizarse a lo largo de una pista que va de izquierda a derecha, y por lo tanto su ubicación puede especificarse por su distancia desde un punto cero conveniente, u origen , con números negativos que indican posiciones a la izquierda y números positivos que indican posiciones a la derecha. Si la ubicación del cuerpo en función del tiempo es , entonces su velocidad promedio durante el intervalo de tiempo de a es [6] Aquí, la letra griega ( delta ) se utiliza, por tradición, para significar "cambio en". Una velocidad media positiva significa que la coordenada de posición aumenta en el intervalo en cuestión, una velocidad media negativa indica una disminución neta en ese intervalo y una velocidad media de cero significa que el cuerpo termina el intervalo de tiempo en el mismo lugar en el que comenzó. El cálculo proporciona los medios para definir una velocidad instantánea , una medida de la velocidad y la dirección del movimiento de un cuerpo en un solo momento de tiempo, en lugar de en un intervalo. Una notación para la velocidad instantánea es reemplazar con el símbolo , por ejemplo, Esto denota que la velocidad instantánea es la derivada de la posición con respecto al tiempo. Se puede pensar aproximadamente como la relación entre un cambio infinitesimalmente pequeño en la posición y el intervalo de tiempo infinitesimalmente pequeño en el que ocurre. [7] Más cuidadosamente, la velocidad y todas las demás derivadas se pueden definir utilizando el concepto de límite . [6] Una función tiene un límite de en un valor de entrada dado si la diferencia entre y se puede hacer arbitrariamente pequeña eligiendo una entrada lo suficientemente cercana a . Se escribe: La velocidad instantánea puede definirse como el límite de la velocidad media a medida que el intervalo de tiempo se reduce a cero: La aceleración es a la velocidad lo que la velocidad es a la posición: es la derivada de la velocidad con respecto al tiempo. [nota 2] La aceleración también puede definirse como un límite: En consecuencia, la aceleración es la segunda derivada de la posición, [7] a menudo escrita .
La posición, cuando se considera como un desplazamiento desde un punto de origen, es un vector : una cantidad con magnitud y dirección. [9] : 1 La velocidad y la aceleración también son cantidades vectoriales. Las herramientas matemáticas del álgebra vectorial proporcionan los medios para describir el movimiento en dos, tres o más dimensiones. Los vectores a menudo se denotan con una flecha, como en , o en negrita, como . A menudo, los vectores se representan visualmente como flechas, siendo la dirección del vector la dirección de la flecha y la magnitud del vector indicada por la longitud de la flecha. Numéricamente, un vector puede representarse como una lista; por ejemplo, el vector de velocidad de un cuerpo podría ser , lo que indica que se mueve a 3 metros por segundo a lo largo del eje horizontal y a 4 metros por segundo a lo largo del eje vertical. El mismo movimiento descrito en un sistema de coordenadas diferente se representará con números diferentes, y el álgebra vectorial se puede utilizar para traducir entre estas alternativas. [9] : 4
El estudio de la mecánica se complica por el hecho de que palabras de uso cotidiano como energía se utilizan con un significado técnico. [10] Además, palabras que son sinónimas en el lenguaje cotidiano no lo son en física: fuerza no es lo mismo que potencia o presión , por ejemplo, y masa tiene un significado diferente a peso . [11] [12] : 150 El concepto físico de fuerza hace cuantitativa la idea cotidiana de un empujón o un tirón. Las fuerzas en la mecánica newtoniana a menudo se deben a cuerdas y cuerdas, fricción, esfuerzo muscular, gravedad, etc. Al igual que el desplazamiento, la velocidad y la aceleración, la fuerza es una cantidad vectorial.
Leyes
Primera ley

Traducido del latín, la primera ley de Newton dice:
- Todo objeto persevera en su estado de reposo o de movimiento uniforme en línea recta, excepto en la medida en que se ve obligado a cambiar ese estado por fuerzas impresas sobre él. [nota 3]
La primera ley de Newton expresa el principio de inercia : el comportamiento natural de un cuerpo es moverse en línea recta a velocidad constante. El movimiento de un cuerpo preserva el statu quo, pero las fuerzas externas pueden perturbarlo.
La comprensión moderna de la primera ley de Newton es que ningún observador inercial tiene privilegios sobre otro. El concepto de observador inercial convierte en cuantitativa la idea cotidiana de no sentir efectos del movimiento. Por ejemplo, una persona parada en el suelo mirando pasar un tren es un observador inercial. Si el observador en el suelo ve el tren moviéndose suavemente en línea recta a una velocidad constante, entonces un pasajero sentado en el tren también será un observador inercial: el pasajero del tren no siente movimiento. El principio expresado por la primera ley de Newton es que no hay forma de decir qué observador inercial se está moviendo "realmente" y cuál está "realmente" parado. El estado de reposo de un observador es el estado de movimiento uniforme en línea recta de otro observador, y ningún experimento puede determinar si uno u otro punto de vista es correcto o incorrecto. No hay un estándar absoluto de reposo. [17] [14] : 62–63 [18] : 7–9 El propio Newton creía que existían el espacio y el tiempo absolutos , pero que las únicas medidas de espacio o tiempo accesibles para la experimentación son relativas. [19]
Segunda ley
- El cambio de movimiento de un objeto es proporcional a la fuerza impresa y se realiza en la dirección de la línea recta en la que se imprime la fuerza. [14] : 114
Por "movimiento", Newton se refería a la cantidad ahora llamada momento , que depende de la cantidad de materia contenida en un cuerpo, la velocidad a la que se mueve ese cuerpo y la dirección en la que se mueve. [20] En notación moderna, el momento de un cuerpo es el producto de su masa por su velocidad: donde las tres cantidades pueden cambiar con el tiempo. La segunda ley de Newton, en forma moderna, establece que la derivada temporal del momento es la fuerza: Si la masa no cambia con el tiempo, entonces la derivada actúa solo sobre la velocidad, y por lo tanto la fuerza es igual al producto de la masa por la derivada temporal de la velocidad, que es la aceleración: [21] Como la aceleración es la segunda derivada de la posición con respecto al tiempo, esto también se puede escribir

Las fuerzas que actúan sobre un cuerpo se suman como vectores y, por lo tanto, la fuerza total sobre un cuerpo depende tanto de las magnitudes como de las direcciones de las fuerzas individuales. Cuando la fuerza neta sobre un cuerpo es igual a cero, entonces, según la segunda ley de Newton, el cuerpo no acelera y se dice que está en equilibrio mecánico . Un estado de equilibrio mecánico es estable si, cuando la posición del cuerpo cambia ligeramente, el cuerpo permanece cerca de ese equilibrio. De lo contrario, el equilibrio es inestable.
Una representación visual común de fuerzas que actúan en conjunto es el diagrama de cuerpo libre , que representa esquemáticamente un cuerpo de interés y las fuerzas que se le aplican por influencias externas. [22] Por ejemplo, un diagrama de cuerpo libre de un bloque colocado sobre un plano inclinado puede ilustrar la combinación de fuerza gravitacional, fuerza "normal" , fricción y tensión de la cuerda. [nota 4]
La segunda ley de Newton se presenta a veces como una definición de fuerza, es decir, una fuerza es aquello que existe cuando un observador inercial ve un cuerpo acelerando. Para que esto sea más que una tautología —aceleración implica fuerza, fuerza implica aceleración— también debe hacerse alguna otra afirmación sobre la fuerza. Por ejemplo, se podría especificar una ecuación que detalle la fuerza, como la ley de gravitación universal de Newton . Al insertar una expresión de este tipo en la segunda ley de Newton, se puede escribir una ecuación con poder predictivo. [nota 5] La segunda ley de Newton también se ha considerado como el establecimiento de un programa de investigación para la física, estableciendo que los objetivos importantes de la materia son identificar las fuerzas presentes en la naturaleza y catalogar los componentes de la materia. [14] : 134 [25] : 12-2
Tercera ley
- A toda acción se opone siempre una reacción igual, o bien, las acciones mutuas de dos cuerpos entre sí son siempre iguales y dirigidas a partes contrarias. [14] : 116
.jpg/440px-Iridium-1_Launch_(32312419215).jpg)
Paráfrasis demasiado breves de la tercera ley, como "acción es igual a reacción ", pueden haber causado confusión entre generaciones de estudiantes: la "acción" y la "reacción" se aplican a cuerpos diferentes. Por ejemplo, considere un libro en reposo sobre una mesa. La gravedad de la Tierra atrae hacia abajo el libro. La "reacción" a esa "acción" no es la fuerza de apoyo de la mesa que sostiene el libro, sino la atracción gravitatoria del libro que actúa sobre la Tierra. [nota 6]
La tercera ley de Newton se relaciona con un principio más fundamental, la conservación del momento . Este último sigue siendo cierto incluso en casos en los que la afirmación de Newton no lo es, por ejemplo, cuando los campos de fuerza , así como los cuerpos materiales, tienen momento, y cuando el momento se define correctamente, también en la mecánica cuántica . [nota 7] En la mecánica newtoniana, si dos cuerpos tienen momentos y respectivamente, entonces el momento total del par es , y la tasa de cambio de es Por la segunda ley de Newton, el primer término es la fuerza total sobre el primer cuerpo, y el segundo término es la fuerza total sobre el segundo cuerpo. Si los dos cuerpos están aislados de influencias externas, la única fuerza sobre el primer cuerpo puede ser la del segundo, y viceversa. Por la tercera ley de Newton, estas fuerzas tienen la misma magnitud pero dirección opuesta, por lo que se cancelan cuando se suman, y es constante. Alternativamente, si se sabe que es constante, se deduce que las fuerzas tienen la misma magnitud y dirección opuesta.
Candidatos para leyes adicionales
Varias fuentes han propuesto elevar otras ideas utilizadas en la mecánica clásica a la categoría de leyes de Newton. Por ejemplo, en la mecánica newtoniana, la masa total de un cuerpo formado al unir dos cuerpos más pequeños es la suma de sus masas individuales. Frank Wilczek ha sugerido llamar la atención sobre esta suposición designándola como "Ley Cero de Newton". [33] Otro candidato para una "ley cero" es el hecho de que en cualquier instante, un cuerpo reacciona a las fuerzas que se le aplican en ese instante. [34] Del mismo modo, la idea de que las fuerzas se suman como vectores (o en otras palabras, obedecen al principio de superposición ), y la idea de que las fuerzas cambian la energía de un cuerpo, han sido descritas como una "cuarta ley". [nota 8]
Ejemplos
El estudio del comportamiento de cuerpos masivos utilizando las leyes de Newton se conoce como mecánica newtoniana. Algunos problemas de ejemplo de mecánica newtoniana son particularmente notables por razones conceptuales o históricas.
Movimiento uniformemente acelerado

Si un cuerpo cae desde el reposo cerca de la superficie de la Tierra, entonces, en ausencia de resistencia del aire, se acelerará a una tasa constante. Esto se conoce como caída libre . La velocidad alcanzada durante la caída libre es proporcional al tiempo transcurrido, y la distancia recorrida es proporcional al cuadrado del tiempo transcurrido. [39] Es importante destacar que la aceleración es la misma para todos los cuerpos, independientemente de su masa. Esto se deduce de la combinación de la segunda ley del movimiento de Newton con su ley de gravitación universal . Esta última establece que la magnitud de la fuerza gravitatoria de la Tierra sobre el cuerpo es donde es la masa del cuerpo que cae, es la masa de la Tierra, es la constante de Newton y es la distancia desde el centro de la Tierra hasta la ubicación del cuerpo, que es muy cercana al radio de la Tierra. Al igualar esto a , la masa del cuerpo se cancela en ambos lados de la ecuación, lo que deja una aceleración que depende de , , y , y puede tomarse como constante. Este valor particular de aceleración generalmente se denota como :
Si el cuerpo no se libera desde el reposo, sino que se lanza hacia arriba y/o horizontalmente con una velocidad distinta de cero, entonces la caída libre se convierte en movimiento de proyectil . [40] Cuando se puede descuidar la resistencia del aire, los proyectiles siguen trayectorias en forma de parábola , porque la gravedad afecta el movimiento vertical del cuerpo y no el horizontal. En el pico de la trayectoria del proyectil, su velocidad vertical es cero, pero su aceleración es hacia abajo, como lo es en todo momento. Establecer el vector incorrecto como igual a cero es una confusión común entre los estudiantes de física. [41]
Movimiento circular uniforme

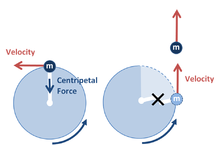
Cuando un cuerpo se encuentra en movimiento circular uniforme, la fuerza que actúa sobre él cambia la dirección de su movimiento, pero no su velocidad. Para un cuerpo que se mueve en un círculo de radio a una velocidad constante , su aceleración tiene una magnitud y está dirigida hacia el centro del círculo. [nota 9] La fuerza necesaria para mantener esta aceleración, llamada fuerza centrípeta , también está dirigida hacia el centro del círculo y tiene magnitud . Muchas órbitas , como la de la Luna alrededor de la Tierra, pueden aproximarse mediante un movimiento circular uniforme. En tales casos, la fuerza centrípeta es la gravedad y, por la ley de gravitación universal de Newton, tiene magnitud , donde es la masa del cuerpo más grande que se orbita. Por lo tanto, la masa de un cuerpo se puede calcular a partir de observaciones de otro cuerpo que orbita a su alrededor. [43] : 130
La bala de cañón de Newton es un experimento mental que interpola entre el movimiento de un proyectil y el movimiento circular uniforme. Una bala de cañón que se lanza débilmente desde el borde de un acantilado alto llegará al suelo en el mismo tiempo que si se dejara caer desde el reposo, porque la fuerza de la gravedad solo afecta al impulso de la bala en la dirección descendente, y su efecto no se ve disminuido por el movimiento horizontal. Si la bala de cañón se lanza con una velocidad horizontal inicial mayor, viajará más lejos antes de llegar al suelo, pero llegará al suelo en el mismo tiempo. Sin embargo, si la bala de cañón se lanza con una velocidad inicial aún mayor, entonces la curvatura de la Tierra se vuelve significativa: el propio suelo se curvará en dirección opuesta a la bala de cañón que cae. Una bala de cañón muy rápida caerá alejándose de la trayectoria inercial en línea recta a la misma velocidad a la que la Tierra se curva debajo de ella; en otras palabras, estará en órbita (imaginándonos que no se ve frenada por la resistencia del aire o los obstáculos). [44]
Movimiento armónico

Consideremos un cuerpo de masa capaz de moverse a lo largo del eje, y supongamos que existe un punto de equilibrio en la posición . Es decir, en , la fuerza neta sobre el cuerpo es el vector cero, y por la segunda ley de Newton, el cuerpo no acelerará. Si la fuerza sobre el cuerpo es proporcional al desplazamiento desde el punto de equilibrio, y está dirigida al punto de equilibrio, entonces el cuerpo realizará un movimiento armónico simple . Escribiendo la fuerza como , la segunda ley de Newton se convierte en Esta ecuación diferencial tiene la solución donde la frecuencia es igual a , y las constantes y se pueden calcular sabiendo, por ejemplo, la posición y la velocidad que tiene el cuerpo en un momento dado, como .
Una razón por la que el oscilador armónico es un ejemplo conceptualmente importante es que es una buena aproximación para muchos sistemas cerca de un equilibrio mecánico estable. [nota 10] Por ejemplo, un péndulo tiene un equilibrio estable en la posición vertical: si está inmóvil allí, permanecerá allí, y si se lo empuja ligeramente, oscilará hacia adelante y hacia atrás. Despreciando la resistencia del aire y la fricción en el pivote, la fuerza sobre el péndulo es la gravedad, y la segunda ley de Newton se convierte en donde es la longitud del péndulo y es su ángulo con la vertical. Cuando el ángulo es pequeño, el seno de es casi igual a (ver serie de Taylor ), y por lo tanto esta expresión se simplifica a la ecuación para un oscilador armónico simple con frecuencia .
Un oscilador armónico puede amortiguarse, a menudo por fricción o arrastre viscoso, en cuyo caso la energía se filtra del oscilador y la amplitud de las oscilaciones disminuye con el tiempo. Además, un oscilador armónico puede ser impulsado por una fuerza aplicada, lo que puede provocar el fenómeno de resonancia . [46]
Objetos con masa variable

La física newtoniana considera que la materia no se crea ni se destruye, aunque puede reorganizarse. Puede darse el caso de que un objeto de interés gane o pierda masa porque se le añade o se le quita materia. En tal situación, las leyes de Newton se pueden aplicar a las piezas individuales de materia, haciendo un seguimiento de qué piezas pertenecen al objeto de interés a lo largo del tiempo. Por ejemplo, si un cohete de masa , que se mueve a una velocidad , expulsa materia a una velocidad relativa al cohete, entonces, donde es la fuerza externa neta (por ejemplo, la atracción gravitatoria de un planeta). [23] : 139
Trabajo y energía
Los físicos desarrollaron el concepto de energía después de la época de Newton, pero se ha convertido en una parte inseparable de lo que se considera física "newtoniana". La energía se puede clasificar en términos generales en cinética , debido al movimiento de un cuerpo, y potencial , debido a la posición de un cuerpo en relación con otros. La energía térmica , la energía transportada por el flujo de calor, es un tipo de energía cinética no asociada con el movimiento macroscópico de los objetos, sino con los movimientos de los átomos y moléculas de los que están hechos. Según el teorema de trabajo-energía , cuando una fuerza actúa sobre un cuerpo mientras ese cuerpo se mueve a lo largo de la línea de la fuerza, la fuerza realiza trabajo sobre el cuerpo, y la cantidad de trabajo realizado es igual al cambio en la energía cinética del cuerpo. [nota 11] En muchos casos de interés, el trabajo neto realizado por una fuerza cuando un cuerpo se mueve en un bucle cerrado (comenzando en un punto, moviéndose a lo largo de una trayectoria y regresando al punto inicial) es cero. Si este es el caso, entonces la fuerza puede escribirse en términos del gradiente de una función llamada potencial escalar : [42] : 303 Esto es cierto para muchas fuerzas, incluida la de la gravedad, pero no para la fricción; de hecho, casi cualquier problema en un libro de texto de mecánica que no involucre fricción puede expresarse de esta manera. [45] : 19 El hecho de que la fuerza pueda escribirse de esta manera puede entenderse a partir de la conservación de la energía . Sin fricción para disipar la energía de un cuerpo en calor, la energía del cuerpo intercambiará entre formas potenciales y cinéticas (no térmicas) mientras que la cantidad total permanece constante. Cualquier ganancia de energía cinética, que ocurre cuando la fuerza neta sobre el cuerpo lo acelera a una velocidad mayor, debe ir acompañada de una pérdida de energía potencial. Entonces, la fuerza neta sobre el cuerpo está determinada por la manera en que disminuye la energía potencial.
Movimiento y rotación de cuerpos rígidos
Un cuerpo rígido es un objeto cuyo tamaño es demasiado grande como para ignorarlo y que mantiene la misma forma a lo largo del tiempo. En la mecánica newtoniana, el movimiento de un cuerpo rígido suele entenderse dividiéndolo en movimiento del centro de masa del cuerpo y movimiento alrededor del centro de masa.
Centro de masa

Los aspectos significativos del movimiento de un cuerpo extenso pueden entenderse imaginando la masa de ese cuerpo concentrada en un único punto, conocido como el centro de masa. La ubicación del centro de masa de un cuerpo depende de cómo se distribuye el material de ese cuerpo. Para una colección de objetos puntuales con masas en posiciones , el centro de masa está ubicado en donde es la masa total del conjunto. En ausencia de una fuerza externa neta, el centro de masa se mueve a una velocidad constante en línea recta. Esto se aplica, por ejemplo, a una colisión entre dos cuerpos. [49] Si la fuerza externa total no es cero, entonces el centro de masa cambia de velocidad como si fuera un cuerpo puntual de masa . Esto se deduce del hecho de que las fuerzas internas dentro del conjunto, las fuerzas que los objetos ejercen entre sí, ocurren en pares equilibrados por la tercera ley de Newton. En un sistema de dos cuerpos con uno mucho más masivo que el otro, el centro de masa coincidirá aproximadamente con la ubicación del cuerpo más masivo. [18] : 22–24
Análogos rotacionales de las leyes de Newton
Cuando las leyes de Newton se aplican a cuerpos extensos en rotación, conducen a nuevas magnitudes que son análogas a las invocadas en las leyes originales. El análogo de la masa es el momento de inercia , la contraparte del momento es el momento angular y la contraparte de la fuerza es el torque .
El momento angular se calcula con respecto a un punto de referencia. [50] Si el vector de desplazamiento desde un punto de referencia a un cuerpo es y el cuerpo tiene momento , entonces el momento angular del cuerpo con respecto a ese punto es, utilizando el producto vectorial , Tomando la derivada temporal del momento angular se obtiene El primer término se desvanece porque y apuntan en la misma dirección. El término restante es el torque, Cuando el torque es cero, el momento angular es constante, al igual que cuando la fuerza es cero, el momento es constante. [18] : 14–15 El torque puede desvanecerse incluso cuando la fuerza no es cero, si el cuerpo está ubicado en el punto de referencia ( ) o si la fuerza y el vector de desplazamiento se dirigen a lo largo de la misma línea.
El momento angular de un conjunto de masas puntuales, y por tanto de un cuerpo extenso, se obtiene sumando las contribuciones de cada uno de los puntos. Esto proporciona un medio para caracterizar la rotación de un cuerpo sobre un eje, sumando los momentos angulares de sus partes individuales. El resultado depende del eje elegido, la forma del cuerpo y la velocidad de rotación. [18] : 28
Sistema gravitacional de múltiples cuerpos

La ley de gravitación universal de Newton establece que cualquier cuerpo atrae a cualquier otro cuerpo a lo largo de la línea recta que los une. El tamaño de la fuerza de atracción es proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia entre ellos. Encontrar la forma de las órbitas que producirá una ley de fuerza del cuadrado inverso se conoce como el problema de Kepler . El problema de Kepler se puede resolver de múltiples formas, incluida la demostración de que el vector de Laplace-Runge-Lenz es constante, [51] o aplicando una transformación de dualidad a un oscilador armónico bidimensional. [52] Independientemente de cómo se resuelva, el resultado es que las órbitas serán secciones cónicas , es decir, elipses (incluidos los círculos), parábolas o hipérbolas . La excentricidad de la órbita, y por lo tanto el tipo de sección cónica, está determinada por la energía y el momento angular del cuerpo en órbita. Los planetas no tienen suficiente energía para escapar del Sol, por lo que sus órbitas son elipses, en una buena aproximación; debido a que los planetas se atraen entre sí, las órbitas reales no son exactamente secciones cónicas.
Si se añade una tercera masa, el problema de Kepler se convierte en el problema de los tres cuerpos, que en general no tiene una solución exacta en forma cerrada . Es decir, no hay forma de partir de las ecuaciones diferenciales implicadas por las leyes de Newton y, después de una secuencia finita de operaciones matemáticas estándar, obtener ecuaciones que expresen los movimientos de los tres cuerpos a lo largo del tiempo. [53] [54] Se pueden aplicar métodos numéricos para obtener resultados útiles, aunque aproximados, para el problema de los tres cuerpos. [55] Las posiciones y velocidades de los cuerpos se pueden almacenar en variables dentro de la memoria de una computadora; las leyes de Newton se utilizan para calcular cómo cambiarán las velocidades en un corto intervalo de tiempo, y conociendo las velocidades, se pueden calcular los cambios de posición durante ese intervalo de tiempo. Este proceso se repite para calcular, aproximadamente, las trayectorias de los cuerpos. En términos generales, cuanto más corto sea el intervalo de tiempo, más precisa será la aproximación. [56]
Caos e imprevisibilidad
Dinámica no lineal

Las leyes de movimiento de Newton permiten la posibilidad del caos . [57] [58] Es decir, cualitativamente hablando, los sistemas físicos que obedecen las leyes de Newton pueden exhibir una dependencia sensible de sus condiciones iniciales: un ligero cambio en la posición o velocidad de una parte de un sistema puede llevar a que todo el sistema se comporte de una manera radicalmente diferente en un corto período de tiempo. Ejemplos notables incluyen el problema de los tres cuerpos, el péndulo doble , el billar dinámico y el problema de Fermi–Pasta–Ulam–Tsingou .
Las leyes de Newton se pueden aplicar a los fluidos al considerar un fluido como compuesto de partes infinitesimales, cada una de las cuales ejerce fuerzas sobre las piezas vecinas. La ecuación del momento de Euler es una expresión de la segunda ley de Newton adaptada a la dinámica de fluidos. [59] [60] Un fluido se describe mediante un campo de velocidad, es decir, una función que asigna un vector de velocidad a cada punto en el espacio y el tiempo. Un objeto pequeño que es transportado por el flujo de fluido puede cambiar de velocidad por dos razones: primero, porque el campo de velocidad en su posición está cambiando con el tiempo, y segundo, porque se mueve a una nueva ubicación donde el campo de velocidad tiene un valor diferente. En consecuencia, cuando la segunda ley de Newton se aplica a una porción infinitesimal de fluido, la aceleración tiene dos términos, una combinación conocida como derivada total o material . La masa de una porción infinitesimal depende de la densidad del fluido , y hay una fuerza neta sobre ella si la presión del fluido varía de un lado a otro. En consecuencia, se convierte en donde es la densidad, es la presión y representa una influencia externa como una atracción gravitatoria. La incorporación del efecto de la viscosidad convierte la ecuación de Euler en una ecuación de Navier-Stokes : donde es la viscosidad cinemática . [59]
Singularidades
Es matemáticamente posible que un conjunto de masas puntuales, que se mueven de acuerdo con las leyes de Newton, lancen algunas de ellas tan fuerte que salgan volando hacia el infinito en un tiempo finito. [61] Este comportamiento no físico, conocido como "singularidad de no colisión", [54] depende de que las masas sean puntuales y capaces de aproximarse entre sí a una distancia arbitraria, así como de la falta de un límite de velocidad relativista en la física newtoniana. [62]
Aún no se sabe si las ecuaciones de Euler y Navier-Stokes muestran un comportamiento análogo al de las soluciones inicialmente suaves que "explotan" en un tiempo finito. La cuestión de la existencia y suavidad de las soluciones de Navier-Stokes es uno de los problemas del Premio del Milenio . [63]
Relación con otras formulaciones de la física clásica
La mecánica clásica se puede formular matemáticamente de múltiples formas diferentes, además de la descripción "newtoniana" (que, por supuesto, incorpora contribuciones de otros tanto antes como después de Newton). El contenido físico de estas diferentes formulaciones es el mismo que el newtoniano, pero proporcionan diferentes perspectivas y facilitan diferentes tipos de cálculos. Por ejemplo, la mecánica lagrangiana ayuda a hacer evidente la conexión entre simetrías y leyes de conservación, y es útil al calcular el movimiento de cuerpos restringidos, como una masa restringida para moverse a lo largo de una pista curva o en la superficie de una esfera. [18] : 48 La mecánica hamiltoniana es conveniente para la física estadística , [64] [65] : 57 conduce a una mayor comprensión de la simetría, [18] : 251 y puede desarrollarse en técnicas sofisticadas para la teoría de perturbaciones . [18] : 284 Debido a la amplitud de estos temas, la discusión aquí se limitará a tratamientos concisos de cómo reformulan las leyes de movimiento de Newton.
Lagrangiano
La mecánica lagrangiana difiere de la formulación newtoniana al considerar trayectorias completas a la vez en lugar de predecir el movimiento de un cuerpo en un solo instante. [18] : 109 Es tradicional en la mecánica lagrangiana denotar la posición con y la velocidad con . El ejemplo más simple es una partícula puntual masiva, cuyo lagrangiano se puede escribir como la diferencia entre sus energías cinética y potencial: donde la energía cinética es y la energía potencial es alguna función de la posición, . El camino físico que tomará la partícula entre un punto inicial y un punto final es el camino para el cual la integral del lagrangiano es "estacionaria". Es decir, el camino físico tiene la propiedad de que pequeñas perturbaciones del mismo, en una primera aproximación, no cambiarán la integral del lagrangiano. El cálculo de variaciones proporciona las herramientas matemáticas para encontrar este camino. [42] : 485 La aplicación del cálculo de variaciones a la tarea de encontrar la trayectoria da como resultado la ecuación de Euler-Lagrange para la partícula. La evaluación de las derivadas parciales del lagrangiano da como resultado que es una reformulación de la segunda ley de Newton. El lado izquierdo es la derivada temporal del momento, y el lado derecho es la fuerza, representada en términos de la energía potencial. [9] : 737
Landau y Lifshitz sostienen que la formulación lagrangiana hace que el contenido conceptual de la mecánica clásica sea más claro que si se parte de las leyes de Newton. [26] La mecánica lagrangiana proporciona un marco conveniente para probar el teorema de Noether , que relaciona las simetrías y las leyes de conservación. [66] La conservación del momento se puede derivar aplicando el teorema de Noether a un lagrangiano para un sistema de múltiples partículas, y por lo tanto, la tercera ley de Newton es un teorema en lugar de una suposición. [18] : 124
Hamiltoniano

En la mecánica hamiltoniana , la dinámica de un sistema se representa mediante una función llamada hamiltoniano, que en muchos casos de interés es igual a la energía total del sistema. [9] : 742 El hamiltoniano es una función de las posiciones y los momentos de todos los cuerpos que forman el sistema, y también puede depender explícitamente del tiempo. Las derivadas temporales de las variables posición y momento se dan mediante derivadas parciales del hamiltoniano, a través de las ecuaciones de Hamilton . [18] : 203 El ejemplo más simple es una masa puntual obligada a moverse en línea recta, bajo el efecto de un potencial. Escribiendo para la coordenada de posición y para el momento del cuerpo, el hamiltoniano es En este ejemplo, las ecuaciones de Hamilton son y Evaluando estas derivadas parciales, la primera ecuación se convierte en que reproduce la afirmación familiar de que el momento de un cuerpo es el producto de su masa y velocidad. La derivada temporal del momento es que, al identificar la derivada negativa del potencial con la fuerza, es simplemente la segunda ley de Newton una vez más. [57] [9] : 742
Al igual que en la formulación lagrangiana, en la mecánica hamiltoniana la conservación del momento se puede derivar utilizando el teorema de Noether, lo que hace que la tercera ley de Newton sea una idea que se deduce en lugar de asumirse. [18] : 251
Entre las propuestas para reformar el currículo introductorio de física estándar hay una que enseña el concepto de energía antes que el de fuerza, esencialmente "mecánica hamiltoniana introductoria". [67] [68]
Hamilton-Jacobi
La ecuación de Hamilton-Jacobi proporciona otra formulación de la mecánica clásica, una que la hace matemáticamente análoga a la óptica ondulatoria . [18] : 284 [69] Esta formulación también utiliza funciones hamiltonianas, pero de una manera diferente a la formulación descrita anteriormente. Las trayectorias tomadas por cuerpos o conjuntos de cuerpos se deducen de una función de posiciones y tiempo . El hamiltoniano se incorpora a la ecuación de Hamilton-Jacobi, una ecuación diferencial para . Los cuerpos se mueven a lo largo del tiempo de tal manera que sus trayectorias son perpendiculares a las superficies de constante , de manera análoga a cómo un rayo de luz se propaga en la dirección perpendicular a su frente de onda. Esto es más simple de expresar para el caso de una sola masa puntual, en la que es una función , y la masa puntual se mueve en la dirección a lo largo de la cual cambia más abruptamente. En otras palabras, el momento de la masa puntual es el gradiente de : La ecuación de Hamilton-Jacobi para una masa puntual es La relación con las leyes de Newton se puede ver al considerar una masa puntual que se mueve en un potencial independiente del tiempo , en cuyo caso la ecuación de Hamilton-Jacobi se convierte en Tomando el gradiente de ambos lados, esto se convierte en Intercambiando el orden de las derivadas parciales en el lado izquierdo y usando las reglas de potencia y cadena en el primer término en el lado derecho, Reuniendo los términos que dependen del gradiente de , Esta es otra reexpresión de la segunda ley de Newton. [70] La expresión entre paréntesis es una derivada total o material como se mencionó anteriormente, [71] en la que el primer término indica cómo la función que se está diferenciando cambia con el tiempo en una ubicación fija, y el segundo término captura cómo una partícula en movimiento verá diferentes valores de esa función a medida que viaja de un lugar a otro:
Relación con otras teorías físicas
Termodinámica y física estadística

En física estadística , la teoría cinética de los gases aplica las leyes de movimiento de Newton a grandes cantidades (normalmente del orden del número de Avogadro ) de partículas. La teoría cinética puede explicar, por ejemplo, la presión que ejerce un gas sobre el recipiente que lo contiene como el agregado de muchos impactos de átomos, cada uno de los cuales imparte una pequeña cantidad de momento. [65] : 62
La ecuación de Langevin es un caso especial de la segunda ley de Newton, adaptada para el caso de describir un objeto pequeño bombardeado estocásticamente por otros aún más pequeños. [72] : 235 Puede escribirse donde es un coeficiente de arrastre y es una fuerza que varía aleatoriamente de un instante a otro, representando el efecto neto de las colisiones con las partículas circundantes. Esto se utiliza para modelar el movimiento browniano . [73]
Electromagnetismo
Las tres leyes de Newton se pueden aplicar a fenómenos que involucran electricidad y magnetismo , aunque existen sutilezas y salvedades.
La ley de Coulomb para la fuerza eléctrica entre dos cuerpos estacionarios cargados eléctricamente tiene una forma matemática muy similar a la ley de gravitación universal de Newton: la fuerza es proporcional al producto de las cargas, inversamente proporcional al cuadrado de la distancia entre ellas y dirigida a lo largo de la línea recta que las une. La fuerza de Coulomb que una carga ejerce sobre otra carga es igual en magnitud a la fuerza que ejerce sobre , y apunta en la dirección exactamente opuesta. La ley de Coulomb es, por tanto, coherente con la tercera ley de Newton. [74]
El electromagnetismo considera que las fuerzas son producidas por campos que actúan sobre cargas. La ley de fuerza de Lorentz proporciona una expresión para la fuerza sobre un cuerpo cargado que se puede introducir en la segunda ley de Newton para calcular su aceleración. [75] : 85 Según la ley de fuerza de Lorentz, un cuerpo cargado en un campo eléctrico experimenta una fuerza en la dirección de ese campo, una fuerza proporcional a su carga y a la intensidad del campo eléctrico. Además, un cuerpo cargado en movimiento en un campo magnético experimenta una fuerza que también es proporcional a su carga, en una dirección perpendicular tanto al campo como a la dirección de movimiento del cuerpo. Utilizando el producto vectorial ,

Si el campo eléctrico se desvanece ( ), entonces la fuerza será perpendicular al movimiento de la carga, tal como en el caso del movimiento circular uniforme estudiado anteriormente, y la carga girará (o más generalmente se moverá en una hélice ) alrededor de las líneas del campo magnético en la frecuencia del ciclotrón . [72] : 222 La espectrometría de masas funciona aplicando campos eléctricos y/o magnéticos a cargas en movimiento y midiendo la aceleración resultante, que por la ley de fuerza de Lorentz produce la relación masa-carga . [76]
Los conjuntos de cuerpos cargados no siempre obedecen la tercera ley de Newton: puede haber un cambio en el momento de un cuerpo sin un cambio compensatorio en el momento de otro. La discrepancia se explica por el momento transportado por el propio campo electromagnético. El momento por unidad de volumen del campo electromagnético es proporcional al vector de Poynting . [77] : 184 [78]
Existe un sutil conflicto conceptual entre el electromagnetismo y la primera ley de Newton: la teoría del electromagnetismo de Maxwell predice que las ondas electromagnéticas viajarán a través del espacio vacío a una velocidad constante y definida. Por lo tanto, algunos observadores inerciales parecen tener un estatus privilegiado sobre los demás, a saber, aquellos que miden la velocidad de la luz y encuentran que es el valor predicho por las ecuaciones de Maxwell. En otras palabras, la luz proporciona un estándar absoluto para la velocidad, pero el principio de inercia sostiene que no debería haber tal estándar. Esta tensión se resuelve en la teoría de la relatividad especial, que revisa las nociones de espacio y tiempo de tal manera que todos los observadores inerciales estarán de acuerdo sobre la velocidad de la luz en el vacío. [nota 12]
Relatividad especial
En la relatividad especial, la regla que Wilczek llamó "Ley Cero de Newton" se rompe: la masa de un objeto compuesto no es simplemente la suma de las masas de las piezas individuales. [81] : 33 La primera ley de Newton, el movimiento inercial, sigue siendo válida. Una forma de la segunda ley de Newton, que la fuerza es la tasa de cambio del momento, también se cumple, al igual que la conservación del momento. Sin embargo, la definición de momento se modifica. Entre las consecuencias de esto está el hecho de que cuanto más rápido se mueve un cuerpo, más difícil es acelerarlo y, por lo tanto, sin importar cuánta fuerza se aplique, un cuerpo no puede acelerarse hasta la velocidad de la luz. Dependiendo del problema en cuestión, el momento en la relatividad especial se puede representar como un vector tridimensional, , donde es la masa en reposo del cuerpo y es el factor de Lorentz , que depende de la velocidad del cuerpo. Alternativamente, el momento y la fuerza se pueden representar como cuatro vectores . [82] : 107
La tercera ley de Newton debe modificarse en la relatividad especial. La tercera ley se refiere a las fuerzas entre dos cuerpos en el mismo momento en el tiempo, y una característica clave de la relatividad especial es que la simultaneidad es relativa. Los eventos que ocurren al mismo tiempo en relación con un observador pueden ocurrir en diferentes momentos en relación con otro. Por lo tanto, en el marco de referencia de un observador dado, la acción y la reacción pueden no ser exactamente opuestas, y el momento total de los cuerpos que interactúan puede no conservarse. La conservación del momento se restaura al incluir el momento almacenado en el campo que describe la interacción de los cuerpos. [83] [84]
La mecánica newtoniana es una buena aproximación a la relatividad especial cuando las velocidades involucradas son pequeñas comparadas con las de la luz. [85] : 131
Relatividad general
La relatividad general es una teoría de la gravedad que va más allá de la de Newton. En la relatividad general, la fuerza gravitacional de la mecánica newtoniana se reimagina como la curvatura del espacio-tiempo . Una trayectoria curva como una órbita, atribuida a una fuerza gravitacional en la mecánica newtoniana, no es el resultado de una fuerza que desvía un cuerpo de una trayectoria recta ideal, sino más bien el intento del cuerpo de caer libremente a través de un fondo que está curvado por la presencia de otras masas. Una observación de John Archibald Wheeler que se ha vuelto proverbial entre los físicos resume la teoría: "El espacio-tiempo le dice a la materia cómo moverse; la materia le dice al espacio-tiempo cómo curvarse". [86] [87] El propio Wheeler pensó en esta relación recíproca como una forma moderna y generalizada de la tercera ley de Newton. [86] La relación entre la distribución de la materia y la curvatura del espacio-tiempo está dada por las ecuaciones de campo de Einstein , que requieren cálculo tensorial para expresarse. [81] : 43 [88]
La teoría de la gravedad newtoniana es una buena aproximación a las predicciones de la relatividad general cuando los efectos gravitacionales son débiles y los objetos se mueven lentamente en comparación con la velocidad de la luz. [79] : 327 [89]
Mecánica cuántica
La mecánica cuántica es una teoría de la física desarrollada originalmente para comprender los fenómenos microscópicos: el comportamiento a escala de moléculas, átomos o partículas subatómicas. En términos generales y vagos, cuanto más pequeño es un sistema, más requerirá un modelo matemático adecuado para comprender los efectos cuánticos. La base conceptual de la física cuántica es muy diferente de la física clásica . En lugar de pensar en cantidades como la posición, el momento y la energía como propiedades que tiene un objeto , se considera qué resultado podría aparecer cuando se realiza una medición de un tipo elegido. La mecánica cuántica permite al físico calcular la probabilidad de que una medición elegida produzca un resultado particular. [90] [91] El valor esperado para una medición es el promedio de los posibles resultados que podría producir, ponderados por sus probabilidades de ocurrencia. [92]
El teorema de Ehrenfest proporciona una conexión entre los valores esperados cuánticos y la segunda ley de Newton, una conexión que es necesariamente inexacta, ya que la física cuántica es fundamentalmente diferente de la clásica. En la física cuántica, la posición y el momento se representan mediante entidades matemáticas conocidas como operadores hermíticos , y la regla de Born se utiliza para calcular los valores esperados de una medición de posición o una medición de momento. Estos valores esperados generalmente cambiarán con el tiempo; es decir, dependiendo del momento en el que (por ejemplo) se realice una medición de posición, variarán las probabilidades de sus diferentes resultados posibles. El teorema de Ehrenfest dice, a grandes rasgos, que las ecuaciones que describen cómo estos valores esperados cambian con el tiempo tienen una forma que recuerda a la segunda ley de Newton. Sin embargo, cuanto más pronunciados sean los efectos cuánticos en una situación dada, más difícil será derivar conclusiones significativas de esta semejanza. [nota 13]
Historia
Los conceptos invocados en las leyes de Newton sobre el movimiento (masa, velocidad, momento, fuerza) tienen predecesores en trabajos anteriores, y el contenido de la física newtoniana se desarrolló aún más después de la época de Newton. Newton combinó el conocimiento de los movimientos celestes con el estudio de los acontecimientos en la Tierra y demostró que una teoría de la mecánica podía abarcar ambos. [nota 14]
Antigüedad y contexto medieval
Aristóteles y el movimiento “violento”
.jpg/440px-Statue_at_the_Aristotle_University_of_Thessaloniki_(cropped).jpg)
(384–322 a. C. )
El tema de la física se remonta a menudo a Aristóteles , pero la historia de los conceptos involucrados está oscurecida por múltiples factores. No es fácil establecer una correspondencia exacta entre los conceptos aristotélicos y los modernos: Aristóteles no distinguió claramente lo que llamaríamos velocidad y fuerza, utilizó el mismo término para densidad y viscosidad , y concibió el movimiento como siempre a través de un medio, en lugar de a través del espacio. Además, algunos conceptos a menudo denominados "aristotélicos" podrían atribuirse mejor a sus seguidores y comentaristas. [97] Estos comentaristas encontraron que la física aristotélica tenía dificultades para explicar el movimiento de proyectiles. [nota 15] Aristóteles dividió el movimiento en dos tipos: "natural" y "violento". El movimiento "natural" de la materia sólida terrestre era caer hacia abajo, mientras que un movimiento "violento" podía empujar un cuerpo hacia los lados. Además, en la física aristotélica, un movimiento "violento" requiere una causa inmediata; Si se separara de la causa de su movimiento "violento", un cuerpo volvería a su comportamiento "natural". Sin embargo, una jabalina continúa moviéndose después de salir de la mano del lanzador. Aristóteles concluyó que el aire alrededor de la jabalina debe estar dotado de la capacidad de mover la jabalina hacia adelante.
Filopono y el impulso
Juan Filópono , un pensador griego bizantino activo durante el siglo VI, encontró esto absurdo: el mismo medio, el aire, era de alguna manera responsable tanto de sostener el movimiento como de impedirlo. Si la idea de Aristóteles fuera cierta, dijo Filópono, los ejércitos lanzarían armas soplando sobre ellas con fuelles. Filópono argumentó que poner un cuerpo en movimiento impartía una cualidad, el ímpetu , que estaría contenida dentro del propio cuerpo. Mientras se mantuviera su ímpetu, el cuerpo continuaría moviéndose. [99] : 47 En los siglos siguientes, versiones de la teoría del ímpetu fueron propuestas por individuos como Nur ad-Din al-Bitruji , Avicena , Abu'l-Barakāt al-Baghdādī , Juan Buridan y Alberto de Sajonia . En retrospectiva, la idea del ímpetu puede verse como un precursor del concepto moderno de momento. [nota 16] La intuición de que los objetos se mueven según algún tipo de impulso persiste en muchos estudiantes de física introductoria. [101]
La inercia y la primera ley
El filósofo francés René Descartes introdujo el concepto de inercia a través de sus "leyes de la naturaleza" en El mundo ( Traité du monde et de la lumière ), escrito entre 1629 y 1633. Sin embargo, El mundo proponía una visión heliocéntrica del mundo, y en 1633 esta visión había dado lugar a un gran conflicto entre Galileo Galilei y la Inquisición católica romana . Descartes conocía esta controversia y no quería involucrarse. El mundo no se publicó hasta 1664, diez años después de su muerte. [102]

(1564-1642)
El concepto moderno de inercia se atribuye a Galileo. Basándose en sus experimentos, Galileo concluyó que el comportamiento "natural" de un cuerpo en movimiento era seguir moviéndose, hasta que algo más interfiriera en él. En Dos nuevas ciencias (1638), Galileo escribió: [103] [104]
Imaginemos cualquier partícula proyectada a lo largo de un plano horizontal sin fricción; entonces sabemos, por lo que se ha explicado más detalladamente en las páginas anteriores, que esta partícula se moverá a lo largo de ese mismo plano con un movimiento uniforme y perpetuo, siempre que el plano no tenga límites.
2.jpg/440px-Frans_Hals_-_Portret_van_René_Descartes_(cropped)2.jpg)
(1596-1650)
Galileo reconoció que en el movimiento de proyectiles, la gravedad de la Tierra afecta el movimiento vertical pero no el horizontal. [105] Sin embargo, la idea de inercia de Galileo no era exactamente la que se codificaría en la primera ley de Newton. Galileo pensaba que un cuerpo que se mueve una gran distancia inercialmente seguiría la curva de la Tierra. Esta idea fue corregida por Isaac Beeckman , Descartes y Pierre Gassendi , quienes reconocieron que el movimiento inercial debería ser un movimiento en línea recta. [106] Descartes publicó sus leyes de la naturaleza (leyes del movimiento) con esta corrección en Principios de filosofía ( Principia Philosophiae ) en 1644, con la parte heliocéntrica atenuada. [107] [102]
Primera Ley de la Naturaleza: Cada cosa abandonada a sí misma continúa en el mismo estado; así, cualquier cuerpo en movimiento continúa moviéndose hasta que algo lo detenga.
Segunda Ley de la Naturaleza: Todo cuerpo que se mueve a su aire se mueve en línea recta; por lo tanto, cualquier cuerpo que se mueva en un círculo siempre tiende a alejarse del centro del círculo.
Según el filósofo estadounidense Richard J. Blackwell , el científico holandés Christiaan Huygens había elaborado su propia versión concisa de la ley en 1656. [108] No se publicó hasta 1703, ocho años después de su muerte, en el párrafo inicial de De Motu Corporum ex Percussione .
Hipótesis I: Todo cuerpo ya en movimiento continuará moviéndose perpetuamente con la misma velocidad y en línea recta a menos que se lo impidan.
Según Huygens, esta ley ya era conocida por Galileo y Descartes entre otros. [108]
La fuerza y la segunda ley

(1629-1695)
Christiaan Huygens, en su Horologium Oscillatorium (1673), planteó la hipótesis de que «por la acción de la gravedad, cualesquiera sean sus fuentes, sucede que los cuerpos se mueven mediante un movimiento compuesto tanto de un movimiento uniforme en una dirección u otra como de un movimiento descendente debido a la gravedad». La segunda ley de Newton generalizó esta hipótesis de la gravedad a todas las fuerzas. [109]
Una característica importante de la física newtoniana es que las fuerzas pueden actuar a distancia sin necesidad de contacto físico. [nota 17] Por ejemplo, el Sol y la Tierra se atraen gravitacionalmente, a pesar de estar separados por millones de kilómetros. Esto contrasta con la idea, defendida por Descartes entre otros, de que la gravedad del Sol mantenía a los planetas en órbita haciéndolos girar en un vórtice de materia transparente, el éter . [116] Newton consideró explicaciones etéreas de la fuerza, pero finalmente las rechazó. [114] El estudio del magnetismo por William Gilbert y otros creó un precedente para pensar en fuerzas inmateriales , [114] e incapaz de encontrar una explicación cuantitativamente satisfactoria de su ley de la gravedad en términos de un modelo etéreo, Newton finalmente declaró: " No finjo ninguna hipótesis ": independientemente de si se pudiera encontrar o no un modelo como los vórtices de Descartes como base de las teorías del movimiento y la gravedad de los Principia , el primer fundamento para juzgarlos deben ser las predicciones acertadas que hicieron. [117] Y, de hecho, desde la época de Newton todos los intentos de crear un modelo de este tipo han fracasado .
Conservación del momento y la tercera ley
.jpg/440px-JKepler_(cropped).jpg)
(1571-1630)
Johannes Kepler sugirió que las atracciones gravitacionales eran recíprocas —que, por ejemplo, la Luna atrae a la Tierra mientras que la Tierra atrae a la Luna— pero no argumentó que tales pares fueran iguales y opuestos. [118] En sus Principios de filosofía (1644), Descartes introdujo la idea de que durante una colisión entre cuerpos, una "cantidad de movimiento" permanece inalterada. Descartes definió esta cantidad de manera un tanto imprecisa al sumar los productos de la velocidad y el "tamaño" de cada cuerpo, donde el "tamaño" para él incorporaba tanto el volumen como el área de superficie. [119] Además, Descartes pensaba en el universo como un plenum , es decir, lleno de materia, por lo que todo movimiento requería que un cuerpo desplazara un medio a medida que se movía.
Durante la década de 1650, Huygens estudió las colisiones entre esferas duras y dedujo un principio que ahora se identifica como la conservación del momento. [120] [121] Christopher Wren deduciría más tarde las mismas reglas para las colisiones elásticas que Huygens, y John Wallis aplicaría la conservación del momento para estudiar las colisiones inelásticas . Newton citó el trabajo de Huygens, Wren y Wallis para apoyar la validez de su tercera ley. [122]
Newton llegó a su conjunto de tres leyes de manera incremental. En un manuscrito de 1684 escrito a Huygens , enumeró cuatro leyes: el principio de inercia, el cambio de movimiento por la fuerza, una declaración sobre el movimiento relativo que hoy se llamaría invariancia galileana y la regla de que las interacciones entre cuerpos no cambian el movimiento de su centro de masa. En un manuscrito posterior, Newton agregó una ley de acción y reacción, al tiempo que decía que esta ley y la ley sobre el centro de masa se implicaban entre sí. Newton probablemente se decidió por la presentación en los Principia, con tres leyes primarias y luego otras declaraciones reducidas a corolarios, durante 1685. [123]
Después de laPrincipios

Newton expresó su segunda ley diciendo que la fuerza sobre un cuerpo es proporcional a su cambio de movimiento, o momento. Cuando escribió los Principia, ya había desarrollado el cálculo (al que llamó " la ciencia de las fluxiones "), pero en los Principia no hizo un uso explícito de él, tal vez porque creía que los argumentos geométricos en la tradición de Euclides eran más rigurosos. [125] : 15 [126] En consecuencia, los Principia no expresan la aceleración como la segunda derivada de la posición, y por lo tanto no dan la segunda ley como . Esta forma de la segunda ley fue escrita (para el caso especial de fuerza constante) al menos ya en 1716, por Jakob Hermann ; Leonhard Euler la emplearía como premisa básica en la década de 1740. [127] Euler fue pionero en el estudio de los cuerpos rígidos [128] y estableció la teoría básica de la dinámica de fluidos. [129] El Traité de mécanique céleste (1798-1825) de cinco volúmenes de Pierre-Simon Laplace abandonó la geometría y desarrolló la mecánica puramente a través de expresiones algebraicas, al tiempo que resolvía cuestiones que los Principia habían dejado abiertas, como una teoría completa de las mareas . [130]
El concepto de energía se convirtió en una parte clave de la mecánica newtoniana en el período posterior a Newton. La solución de Huygens para la colisión de esferas duras mostró que, en ese caso, no solo se conserva el momento, sino también la energía cinética (o, más bien, una cantidad que, en retrospectiva, podemos identificar como la mitad de la energía cinética total). La cuestión de qué se conserva durante todos los demás procesos, como las colisiones inelásticas y el movimiento ralentizado por la fricción, no se resolvió hasta el siglo XIX. Los debates sobre este tema se superpusieron con las disputas filosóficas entre las visiones metafísicas de Newton y Leibniz, y a veces se usaban variantes del término "fuerza" para denotar lo que llamaríamos tipos de energía. Por ejemplo, en 1742, Émilie du Châtelet escribió: "La fuerza muerta consiste en una simple tendencia al movimiento: tal es la de un resorte listo para relajarse; la fuerza viva es la que tiene un cuerpo cuando está en movimiento real". En la terminología moderna, "fuerza muerta" y "fuerza viva" corresponden a la energía potencial y la energía cinética respectivamente. [131] La conservación de la energía no se estableció como un principio universal hasta que se entendió que la energía del trabajo mecánico puede disiparse en calor. [132] [133] Con el concepto de energía dado una base sólida, las leyes de Newton podrían entonces derivarse dentro de formulaciones de la mecánica clásica que ponen la energía en primer lugar, como en las formulaciones lagrangianas y hamiltonianas descritas anteriormente.
Las presentaciones modernas de las leyes de Newton utilizan las matemáticas de los vectores, un tema que no se desarrolló hasta finales del siglo XIX y principios del XX. El álgebra vectorial, iniciada por Josiah Willard Gibbs y Oliver Heaviside , surgió del sistema anterior de cuaterniones inventado por William Rowan Hamilton y lo sustituyó en gran medida . [134] [135]
Véase también
- Leyes del movimiento de Euler
- Historia de la mecánica clásica
- Lista de leyes homónimas
- Lista de ecuaciones de la mecánica clásica
- Lista de leyes científicas que llevan nombres de personas
- Lista de libros de texto sobre mecánica clásica y mecánica cuántica
- La cúpula de Norton
Notas
- ^ Véase, por ejemplo, Zain. [4] : 1-2 David Tong observa: "Una partícula se define como un objeto de tamaño insignificante: por ejemplo, un electrón, una pelota de tenis o un planeta. Obviamente, la validez de esta afirmación depende del contexto..." [5]
- ^ La aceleración negativa incluye tanto la desaceleración (cuando la velocidad actual es positiva) como la aceleración (cuando la velocidad actual es negativa). Para este y otros puntos que a menudo han resultado difíciles para los estudiantes, consulte McDermott et al. [8]
- ^ Según Cohen y Whitman. [2] Para otras expresiones, véase Eddington [13] y Frautschi et al. [14] : 114 La traducción de Andrew Motte de 1729 tradujo el "nisi quatenus" de Newton como a menos que en lugar de excepto en la medida en que, lo que Hoek sostiene que era erróneo. [15] [16]
- ^ Un libro de texto observa que un bloque que se desliza por un plano inclinado es lo que "algunos cínicos consideran el problema más aburrido de toda la física". [23] : 70 Otro bromea: "Nadie sabrá nunca cuántas mentes, ansiosas por aprender los secretos del universo, se encontraron estudiando planos inclinados y poleas, y decidieron cambiarse a una profesión más interesante". [14] : 173
- ^ Por ejemplo, José y Saletan (siguiendo a Mach y Eisenbud [24] ) toman la conservación del momento como un principio físico fundamental y lo tratan como una definición de "fuerza". [18] : 9 Véase también Frautschi et al., [14] : 134 así como Feynman, Leighton y Sands, [25] : 12-1 quienes argumentan que la segunda ley es incompleta sin una especificación de una fuerza por otra ley, como la ley de la gravedad. Kleppner y Kolenkow argumentan que la segunda ley es incompleta sin la tercera ley: un observador que ve un cuerpo acelerar sin una aceleración correspondiente de algún otro cuerpo para compensar concluiría, no que está actuando una fuerza, sino que no es un observador inercial. [23] : 60 Landau y Lifshitz pasan por alto la cuestión comenzando con el formalismo lagrangiano en lugar del newtoniano. [26]
- ^ Véase, por ejemplo, Moebs et al., [27] Gonick y Huffman, [28] Low y Wilson, [29] Stocklmayer et al., [30] Hellingman, [31] y Hodanbosi. [32]
- ^ Véase, por ejemplo, Frautschi et al. [14] : 356
- ^ Para el primero, véase Greiner, [35] o Wachter y Hoeber. [36] Para el segundo, véase Tait [37] y Heaviside. [38]
- ^ Entre las muchas explicaciones de los libros de texto sobre esto se encuentran Frautschi et al. [14] : 104 y Boas. [42] : 287
- ^ Entre los muchos tratamientos de este punto en los libros de texto se encuentran Hand y Finch [45] : 81 y también Kleppner y Kolenkow. [23] : 103
- ^ Los tratamientos se pueden encontrar, por ejemplo, en Chabay et al. [47] y McCallum et al. [48] : 449
- ^ Se pueden encontrar discusiones, por ejemplo, en Frautschi et al., [14] : 215 Panofsky y Phillips, [77] : 272 Goldstein, Poole y Safko, [79] : 277 y Werner. [80]
- ^ Se pueden encontrar detalles en los libros de texto de, por ejemplo, Cohen-Tannoudji et al. [93] : 242 y Peres. [94] : 302
- ^ Como escribe un físico: "La teoría física es posible porque estamos inmersos e incluidos en todo el proceso, porque podemos actuar sobre los objetos que nos rodean. Nuestra capacidad de intervenir en la naturaleza clarifica incluso el movimiento de los planetas alrededor del Sol, masas tan grandes y distancias tan vastas que nuestro papel como participantes parece insignificante. Newton fue capaz de transformar la descripción cinemática del sistema solar de Kepler en una teoría dinámica mucho más poderosa porque añadió conceptos de los métodos experimentales de Galileo: fuerza, masa, momento y gravitación. El observador verdaderamente externo sólo llegará tan lejos como Kepler. Los conceptos dinámicos se formulan sobre la base de lo que podemos establecer, controlar y medir". [95] Véase, por ejemplo, Caspar y Hellman. [96]
- ^ La física aristotélica también tuvo dificultades para explicar la flotabilidad, un punto que Galileo intentó resolver sin éxito completo. [98]
- ^ Anneliese Maier advierte: "El ímpetu no es ni una fuerza, ni una forma de energía, ni un momento en el sentido moderno; comparte algo con todos estos otros conceptos, pero no es idéntico a ninguno de ellos". [100] : 79
- ^ Newton mismo era un alquimista entusiasta . John Maynard Keynes lo llamó "el último de los magos" para describir su lugar en la transición entre la protociencia y la ciencia moderna. [110] [111] Se ha sugerido que la alquimia inspiró la noción de Newton de "acción a distancia", es decir, un cuerpo que ejerce una fuerza sobre otro sin estar en contacto directo. [112] Esta sugerencia gozó de un apoyo considerable entre los historiadores de la ciencia [113] hasta que se hizo posible un estudio más extenso de los artículos de Newton, después de lo cual cayó en desgracia. Sin embargo, parece que la alquimia de Newton influyó en su óptica , en particular, en cómo pensaba sobre la combinación de colores. [114] [115]
Referencias
- ^ Thornton, Stephen T.; Marion, Jerry B. (2004). Dinámica clásica de partículas y sistemas (5.ª ed.). Brooke Cole. pág. 49. ISBN 0-534-40896-6.
- ^ ab Newton, I. (1999). Los Principia, Los principios matemáticos de la filosofía natural . Traducido por Cohen, IB; Whitman, A. Los Ángeles: University of California Press.
- ^ Newton, Isaac; Chittenden, NW; Motte, Andrew; Hill, Theodore Preston (1846). Los Principia de Newton: Los principios matemáticos de la filosofía natural. Bibliotecas de la Universidad de California. Daniel Adee.
- ^ Zain, Samya (2019). Técnicas de mecánica clásica: de la mecánica lagrangiana a la newtoniana. Instituto de Física. ISBN 978-0-750-32076-4.OCLC 1084752471 .
- ^ Tong, David (enero de 2015). «Dinámica clásica: Universidad de Cambridge, parte II, examen final de matemáticas» (PDF) . Universidad de Cambridge . Consultado el 12 de febrero de 2022 .
- ^ ab Hughes-Hallett, Deborah ; McCallum, William G. ; Gleason, Andrew M. ; et al. (2013). Cálculo: de una y varias variables (6.ª ed.). Hoboken, NJ: Wiley. págs. 76–78. ISBN 978-0-470-88861-2.OCLC 794034942 .
- ^ ab Thompson, Silvanus P. ; Gardner, Martin (1998). Cálculo simplificado . Macmillan. págs. 84-85. ISBN 978-0-312-18548-0.OCLC 799163595 .
- ^ McDermott, Lillian C. ; Rosenquist, Mark L.; van Zee, Emily H. (junio de 1987). "Dificultades de los estudiantes para conectar gráficos y física: ejemplos de la cinemática". American Journal of Physics . 55 (6): 503–513. Bibcode :1987AmJPh..55..503M. doi :10.1119/1.15104. ISSN 0002-9505.
- ^ abcde Gbur, Greg (2011). Métodos matemáticos para la física óptica y la ingeniería. Cambridge, Reino Unido: Cambridge University Press. ISBN 978-0-511-91510-9.OCLC 704518582 .
- ^ Driver, Rosalind; Warrington, Lynda (1 de julio de 1985). "Uso del principio de conservación de la energía por parte de los estudiantes en situaciones problemáticas". Educación en Física . 20 (4): 171–176. Bibcode :1985PhyEd..20..171D. doi :10.1088/0031-9120/20/4/308. S2CID 250781921.
- ^ Brookes, David T.; Etkina, Eugenia (25 de junio de 2009). ""Fuerza", ontología y lenguaje". Physical Review Special Topics - Investigación en Educación en Física . 5 (1): 010110. Bibcode :2009PRPER...5a0110B. doi : 10.1103/PhysRevSTPER.5.010110 . ISSN 1554-9178.
- ^ Urona, Paul Peter; Hinrichs, Roger; Dirks, Kim; Sharma, Manjula (2021). Física universitaria. AbiertoStax . ISBN 978-1-947172-01-2.OCLC 895896190 .
- ^ Eddington, Arthur (1929). La naturaleza del mundo físico . Nueva York: Macmillan. pp. 123–125.
- ^ abcdefghij Frautschi, Steven C. ; Olenick, Richard P. ; Apostol, Tom M. ; Goodstein, David L. (2007). El universo mecánico: mecánica y calor (edición avanzada). Cambridge [Cambridgeshire]: Cambridge University Press. ISBN 978-0-521-71590-4.OCLC 227002144 .
- ^ Hoek, D. (2023). "Sólo cambios forzados: una nueva perspectiva sobre la inercia". Filosofía de la ciencia . 90 (1): 60–73. arXiv : 2112.02339 . doi :10.1017/psa.2021.38.
- ^ Pappas, Stephanie (5 de septiembre de 2023). "Se descubre una traducción errónea de la primera ley de Newton casi 300 años después". Scientific American .
- ^ Resnick, Robert (1968). Introducción a la relatividad especial . Wiley. págs. 8-16. OCLC 1120819093.
- ^ abcdefghijklm José, Jorge V. ; Saletan, Eugene J. (1998). Dinámica clásica: un enfoque contemporáneo. Cambridge [Inglaterra]: Cambridge University Press. ISBN 978-1-139-64890-5.OCLC 857769535 .
- ^ Brading, Katherine (agosto de 2019). "Una nota sobre varillas y relojes en los Principia de Newton". Estudios de historia y filosofía de la ciencia, parte B: Estudios de historia y filosofía de la física moderna . 67 : 160–166. Código Bibliográfico : 2019SHPMP..67..160B. doi : 10.1016/j.shpsb.2017.07.004. S2CID 125131430.
- ^ Feather, Norman (1959). Introducción a la física de la masa, la longitud y el tiempo . Reino Unido: University Press. pp. 126–128.
- ^ Resnick, Robert; Halliday, David (1966). "Sección 5-4: Masa; Segunda ley de Newton". Física . John Wiley & Sons. LCCN 66-11527.
- ^ Rosengrant, David; Van Heuvelen, Alan; Etkina, Eugenia (1 de junio de 2009). "¿Los estudiantes utilizan y comprenden los diagramas de cuerpo libre?". Physical Review Special Topics - Physics Education Research . 5 (1): 010108. Bibcode :2009PRPER...5a0108R. doi : 10.1103/PhysRevSTPER.5.010108 . ISSN 1554-9178.
- ^ abcd Kleppner, Daniel; Kolenkow, Robert J. (2014). Introducción a la mecánica (2.ª ed.). Cambridge: Cambridge University Press. ISBN 978-0-521-19811-0.OCLC 854617117 .
- ^ Eisenbud, Leonard (1958). "Sobre las leyes clásicas del movimiento". American Journal of Physics . 26 : 144–159. doi :10.1119/1.1934608.
- ^ ab Feynman, Richard P. ; Leighton, Robert B. ; Sands, Matthew L. (1989) [1965]. Las conferencias Feynman sobre física, volumen 1 . Reading, Mass.: Addison-Wesley Pub. Co. ISBN 0-201-02010-6.OCLC 531535 .
- ^ ab Landau, Lev D .; Lifshitz, Evgeny M. (1969). Mecánica . Curso de física teórica . Vol. 1. Traducido por Sykes, JB; Bell, JS (2.ª ed.). Pergamon Press . pág. vii. ISBN. 978-0-080-06466-6. OCLC 898931862.
Sólo con este enfoque la exposición puede formar un todo lógico y evitar definiciones tautológicas de las magnitudes mecánicas fundamentales. Además, es esencialmente más simple y conduce a los medios más completos y directos de resolver problemas de mecánica.
- ^ Moebs, William; et al. (2023). "5.5 Tercera ley de Newton". Física Universitaria, Volumen 1 . AbiertoStax. pag. 220.ISBN 978-1-947172-20-3.
- ^ Gonick, Larry ; Huffman, Art (1991). La guía de dibujos animados sobre física . HarperPerennial. p. 50. ISBN 0-06-273100-9.
- ^ Low, David J.; Wilson, Kate F. (enero de 2017). "El papel de las estructuras de conocimiento en competencia en el debilitamiento del aprendizaje: la segunda y tercera leyes de Newton". American Journal of Physics . 85 (1): 54–65. Bibcode :2017AmJPh..85...54L. doi :10.1119/1.4972041. ISSN 0002-9505.
- ^ Stocklmayer, Sue ; Rayner, John P.; Gore, Michael M. (octubre de 2012). "Cambiar el orden de las leyes de Newton: por qué y cómo la tercera ley debería ser la primera". The Physics Teacher . 50 (7): 406–409. Bibcode :2012PhTea..50..406S. doi :10.1119/1.4752043. ISSN 0031-921X.
- ^ Hellingman, C. (marzo de 1992). "Revisión de la tercera ley de Newton". Educación en Física . 27 (2): 112–115. Bibcode :1992PhyEd..27..112H. doi :10.1088/0031-9120/27/2/011. ISSN 0031-9120. S2CID 250891975.
- ^ Hodanbosi, Carol (agosto de 1996). Fairman, Jonathan G. (ed.). "Tercera ley del movimiento". www.grc.nasa.gov .
- ^ Wilczek, Frank (2003). "El origen de la masa" (PDF) . MIT Physics Annual 2003. Consultado el 13 de enero de 2022 .
- ^ Scherr, Rachel E. ; Redish, Edward F. (1 de enero de 2005). "La ley cero de Newton: aprender escuchando a nuestros estudiantes". The Physics Teacher . 43 (1): 41–45. Bibcode :2005PhTea..43...41S. doi :10.1119/1.1845990. ISSN 0031-921X.
- ^ Greiner, Walter (2003). Mecánica clásica: partículas puntuales y relatividad. Nueva York: Springer. pág. 135. ISBN. 978-0-387-21851-9.
- ^ Wachter, Armin; Hoeber, Henning (2006). Compendio de física teórica . Nueva York: Springer. pág. 6. ISBN. 978-0-387-25799-0.
- ^ Tait, Peter Guthrie (1889). "Mecánica". Encyclopædia Britannica . Vol. 15 (novena edición). págs. 715–716.
- ^ Heaviside, Oliver (agosto de 1905). "El momento transversal de un electrón". Nature . 72 (1870): 429. Bibcode :1905Natur..72Q.429H. doi : 10.1038/072429a0 . ISSN 0028-0836. S2CID 4016382.
- ^ Nicodemi, Olympia (1 de febrero de 2010). "Galileo y Oresme: ¿Quién es moderno? ¿Quién es medieval?". Revista de Matemáticas . 83 (1): 24–32. doi :10.4169/002557010X479965. ISSN 0025-570X. S2CID 122113958.
- ^ Scholberg, Kate (2020). «Preguntas frecuentes: movimiento de proyectiles». Física 361. Consultado el 16 de enero de 2022 .
- ^ Carli, Marta; Lippiello, Stefania; Pantano, Ornella; Perona, Mario; Tormen, Giuseppe (19 de marzo de 2020). "Evaluación de la capacidad de los estudiantes para utilizar derivadas, integrales y vectores en un contexto puramente matemático y en un contexto físico". Physical Review Physics Education Research . 16 (1): 010111. Bibcode :2020PRPER..16a0111C. doi : 10.1103/PhysRevPhysEducRes.16.010111 . hdl : 11577/3340932 . ISSN 2469-9896. S2CID 215832738.
- ^ abc Boas, Mary L. (2006). Métodos matemáticos en las ciencias físicas (3.ª ed.). Hoboken, Nueva Jersey: Wiley. ISBN 978-0-471-19826-0.OCLC 61332593 .
- ^ Brown, Mike (2010). Cómo maté a Plutón y por qué se lo merecía (1.ª ed.). Nueva York: Spiegel & Grau. ISBN 978-0-385-53108-5. OCLC 495271396.
- ^ Topper, D.; Vincent, DE (1 de enero de 1999). "An analysis of Newton's projectile diagram". Revista Europea de Física . 20 (1): 59–66. Bibcode :1999EJPh...20...59T. doi :10.1088/0143-0807/20/1/018. ISSN 0143-0807. S2CID 250883796.
- ^ ab Hand, Louis N.; Finch, Janet D. (1998). Mecánica analítica. Cambridge: Cambridge University Press. ISBN 0-521-57327-0.OCLC 37903527 .
- ^ Billah, K. Yusuf; Scanlan, Robert H. (1 de febrero de 1991). "Resonancia, falla del puente de Tacoma Narrows y libros de texto de física para estudiantes universitarios" (PDF) . American Journal of Physics . 59 (2): 118–124. Bibcode :1991AmJPh..59..118B. doi :10.1119/1.16590. ISSN 0002-9505.
- ^ Chabay, Ruth ; Sherwood, Bruce; Titus, Aaron (julio de 2019). "Un enfoque unificado y contemporáneo para la enseñanza de la energía en la física introductoria". American Journal of Physics . 87 (7): 504–509. Bibcode :2019AmJPh..87..504C. doi : 10.1119/1.5109519 . ISSN 0002-9505. S2CID 197512796.
- ^ Hughes-Hallett, Deborah ; McCallum, William G .; Gleason, Andrew M .; et al. (2013). Cálculo: simple y multivariable (6ª ed.). Hoboken, Nueva Jersey: Wiley. ISBN 978-0-470-88861-2.OCLC 794034942 .
- ^ Lyublinskaya, Irina E. (enero de 1998). "Colisiones centrales: el caso general". The Physics Teacher . 36 (1): 18–19. Bibcode :1998PhTea..36...18L. doi :10.1119/1.879949. ISSN 0031-921X.
- ^ Close, Hunter G.; Heron, Paula RL (octubre de 2011). "Comprensión del momento angular de las partículas clásicas por parte de los estudiantes". American Journal of Physics . 79 (10): 1068–1078. Bibcode :2011AmJPh..79.1068C. doi :10.1119/1.3579141. ISSN 0002-9505.
- ^ Mungan, Carl E. (1 de marzo de 2005). "Otro comentario sobre "La excentricidad como vector"". Revista Europea de Física . 26 (2): L7–L9. doi :10.1088/0143-0807/26/2/L01. ISSN 0143-0807. S2CID 121740340.
- ^ Saggio, Maria Luisa (1 de enero de 2013). "Transformación de Bohlin: la simetría oculta que conecta a Hooke con Newton". Revista Europea de Física . 34 (1): 129–137. Bibcode :2013EJPh...34..129S. doi :10.1088/0143-0807/34/1/129. ISSN 0143-0807. S2CID 119949261.
- ^ Barrow-Green, junio (1997). Poincaré y el problema de los tres cuerpos . American Mathematical Society. pp. 8–12. Bibcode :1997ptbp.book.....B. ISBN 978-0-8218-0367-7.
- ^ ab Barrow-Green, junio (2008). "El problema de los tres cuerpos". En Gowers, Timothy ; Barrow-Green, junio ; Leader, Imre (eds.). The Princeton Companion to Mathematics . Princeton University Press. págs. 726–728. ISBN 978-0-691-11880-2.OCLC 682200048 .
- ^ Breen, Barbara J.; Weidert, Christine E.; Lindner, John F.; Walker, Lisa May; Kelly, Kasey; Heidtmann, Evan (abril de 2008). "Invitación a la computación paralela vergonzosamente". American Journal of Physics . 76 (4): 347–352. Bibcode :2008AmJPh..76..347B. doi :10.1119/1.2834738. ISSN 0002-9505.
- ^ McCandlish, David (julio de 1973). Shirer, Donald L. (ed.). "Soluciones al problema de los tres cuerpos por computadora". American Journal of Physics . 41 (7): 928–929. doi :10.1119/1.1987423. ISSN 0002-9505.
- ^ ab Masoliver, Jaume; Ros, Ana (1 de marzo de 2011). "Integrabilidad y caos: la incertidumbre clásica". Revista Europea de Física . 32 (2): 431–458. arXiv : 1012.4384 . Bibcode :2011EJPh...32..431M. doi :10.1088/0143-0807/32/2/016. ISSN 0143-0807. S2CID 58892714.
- ^ Laws, Priscilla W. (abril de 2004). "Una unidad sobre oscilaciones, determinismo y caos para estudiantes de física introductoria". American Journal of Physics . 72 (4): 446–452. Bibcode :2004AmJPh..72..446L. doi :10.1119/1.1649964. ISSN 0002-9505.
- ^ ab Zee, Anthony (2020). Física de vuelo nocturno . Princeton University Press. págs. 363–364. ISBN 978-0-691-18254-4.OCLC 1288147292 .
- ^ Han-Kwan, Daniel; Iacobelli, Mikaela (7 de abril de 2021). «De la segunda ley de Newton a las ecuaciones de Euler de fluidos perfectos». Actas de la American Mathematical Society . 149 (7): 3045–3061. arXiv : 2006.14924 . doi : 10.1090/proc/15349 . ISSN: 0002-9939. S2CID : 220127889.
- ^ Saari, Donald G .; Xia, Zhihong (mayo de 1995). "Hacia el infinito en tiempo finito" (PDF) . Avisos de la American Mathematical Society . 42 : 538–546.
- ^ Baez, John C. (2021). "Luchas con el continuo". En Anel, Mathieu; Catren, Gabriel (eds.). Nuevos espacios en física: reflexiones formales y conceptuales . Cambridge University Press. págs. 281–326. arXiv : 1609.01421 . ISBN . 978-1-108-49062-7.OCLC 1195899886 .
- ^ Fefferman, Charles L. (2006). "Existencia y suavidad de la ecuación de Navier-Stokes". En Carlson, James; Jaffe, Arthur ; Wiles, Andrew (eds.). Los problemas del Premio del Milenio (PDF) . Providence, RI: Sociedad Matemática Estadounidense y Instituto de Matemáticas Clay. págs. 57–67. ISBN 978-0-821-83679-8.OCLC 466500872 .
- ^ Ehrenfest, Paul ; Ehrenfest, Tatiana (1990) [1959]. Fundamentos conceptuales del enfoque estadístico en mecánica. Nueva York: Dover Publications. pág. 18. ISBN 0-486-66250-0.OCLC 20934820 .
- ^ ab Kardar, Mehran (2007). Física estadística de partículas . Cambridge University Press . ISBN 978-0-521-87342-0.OCLC 860391091 .
- ^ Byers, Nina (2006). "Emmy Noether". En Byers, Nina; Williams, Gary (eds.). Fuera de las sombras: contribuciones de las mujeres del siglo XX a la física . Cambridge: Cambridge University Press. págs. 83–96. ISBN 978-0-521-82197-1.OCLC 1150964892 .
- ^ LeGresley, Sarah E.; Delgado, Jennifer A.; Bruner, Christopher R.; Murray, Michael J.; Fischer, Christopher J. (13 de septiembre de 2019). "El plan de estudios de cálculo basado en la energía para la introducción a la física mejora el rendimiento de los estudiantes a nivel local y en cursos posteriores". Physical Review Physics Education Research . 15 (2): 020126. Bibcode :2019PRPER..15b0126L. doi : 10.1103/PhysRevPhysEducRes.15.020126 . hdl : 1808/29610 . ISSN 2469-9896. S2CID 203484310.
- ^ Ball, Philip (13 de septiembre de 2019). "Enseñar energía antes que fuerzas". Física . 12 : 100. Bibcode :2019PhyOJ..12..100B. doi :10.1103/Physics.12.100. S2CID 204188746.
- ^ Houchmandzadeh, Bahram (mayo de 2020). "La ecuación de Hamilton-Jacobi: un enfoque alternativo". American Journal of Physics . 88 (5): 353–359. arXiv : 1910.09414 . Código Bibliográfico :2020AmJPh..88..353H. doi :10.1119/10.0000781. ISSN 0002-9505. S2CID 204800598.
- ^ Rosen, Nathan (febrero de 1965). "Estados mixtos en mecánica clásica". Revista estadounidense de física . 33 (2): 146–150. Código Bibliográfico :1965AmJPh..33..146R. doi :10.1119/1.1971282. ISSN 0002-9505.
- ^ Weiner, JH (noviembre de 1974). "Análogos hidrodinámicos con la ecuación de Hamilton-Jacobi". American Journal of Physics . 42 (11): 1026–1028. Bibcode :1974AmJPh..42.1026W. doi :10.1119/1.1987920. ISSN 0002-9505.
- ^ ab Reichl, Linda E. (2016). Un curso moderno de física estadística (4ª ed.). Weinheim, Alemania: Wiley-VCH. ISBN 978-3-527-69048-0.OCLC 966177746 .
- ^ Mermin, N. David (agosto de 1961). "Dos modelos de movimiento browniano". American Journal of Physics . 29 (8): 510–517. Bibcode :1961AmJPh..29..510M. doi :10.1119/1.1937823. ISSN 0002-9505.
- ^ Kneubil, Fabiana B. (1 de noviembre de 2016). "Rompiendo la tercera ley de Newton: casos electromagnéticos". Revista Europea de Física . 37 (6): 065201. Bibcode :2016EJPh...37f5201K. doi :10.1088/0143-0807/37/6/065201. ISSN 0143-0807. S2CID 126380404.
- ^ Tonnelat, Marie-Antoinette (1966). Los principios de la teoría electromagnética y de la relatividad. Dordrecht: D. Reidel. ISBN 90-277-0107-5.OCLC 844001 .
- ^ Chu, Caroline S.; Lebrilla, Carlito B. (2010). "Introducción a las técnicas modernas en espectrometría de masas". En Jue, Thomas (ed.). Aplicaciones biomédicas de la biofísica. Totowa, NJ: Humana Press. págs. 137–154. doi :10.1007/978-1-60327-233-9_6. ISBN 978-1-60327-233-9. Recuperado el 24 de marzo de 2022 .
- ^ de Panofsky, Wolfgang KH ; Phillips, Melba (2005) [1962]. Electricidad y magnetismo clásicos (2.ª ed.). Mineola, NY: Dover Publications. ISBN 0-486-43924-0.OCLC 56526974 .
- ^ Bonga, Béatrice; Poisson, Eric; Yang, Huan (noviembre de 2018). "Balance de momento angular y par propio para una esfera cargada giratoria". American Journal of Physics . 86 (11): 839–848. arXiv : 1805.01372 . Bibcode :2018AmJPh..86..839B. doi :10.1119/1.5054590. ISSN 0002-9505. S2CID 53625857.
- ^ ab Goldstein, Herbert ; Poole, Charles P.; Safko, John L. (2002). Mecánica clásica (3.ª ed.). San Francisco: Addison Wesley. ISBN 0-201-31611-0.OCLC 47056311 .
- ^ Werner, Reinhard F. (9 de octubre de 2014). "Comentario sobre "Lo que hizo Bell"". Revista de Física A: Matemática y Teórica . 47 (42): 424011. Bibcode :2014JPhA...47P4011W. doi :10.1088/1751-8113/47/42/424011. ISSN 1751-8113. S2CID 122180759.
- ^ ab Choquet-Bruhat, Yvonne (2009). Relatividad general y ecuaciones de Einstein. Oxford: Oxford University Press. ISBN 978-0-19-155226-7.OCLC 317496332 .
- ^ Ellis, George FR ; Williams, Ruth M. (2000). Espacio-tiempos planos y curvos (2.ª ed.). Oxford: Oxford University Press. ISBN 0-19-850657-0.OCLC 44694623 .
- ^ French, AP (1968). Relatividad especial . WW Norton and Company. pág. 224. ISBN 0-393-09804-4.
- ^ Havas, Peter (1 de octubre de 1964). "Formulaciones cuatridimensionales de la mecánica newtoniana y su relación con la teoría especial y la teoría general de la relatividad". Reseñas de física moderna . 36 (4): 938–965. Bibcode :1964RvMP...36..938H. doi :10.1103/RevModPhys.36.938. ISSN 0034-6861.
...la suposición habitual de la mecánica newtoniana es que las fuerzas están determinadas por las posiciones simultáneas (y posiblemente sus derivadas) de las partículas, y que están relacionadas por la tercera ley de Newton. Tal suposición no es posible en la relatividad especial ya que la simultaneidad no es un concepto invariante en esa teoría.
- ^ Stavrov, Iva (2020). Curvatura del espacio y el tiempo, con una introducción al análisis geométrico . Providence, Rhode Island: American Mathematical Society. ISBN 978-1-4704-6313-7.OCLC 1202475208 .
- ^ ab Wheeler, John Archibald (18 de junio de 2010). Geones, agujeros negros y espuma cuántica: una vida en física. WW Norton & Company. ISBN 978-0-393-07948-7.
- ^ Kersting, Magdalena (mayo de 2019). "Caída libre en el espacio-tiempo curvo: cómo visualizar la gravedad en la relatividad general". Educación en Física . 54 (3): 035008. Bibcode :2019PhyEd..54c5008K. doi : 10.1088/1361-6552/ab08f5 . hdl : 10852/74677 . ISSN 0031-9120. S2CID 127471222.
- ^ Prescod-Weinstein, Chanda (2021). El cosmos desordenado: un viaje a la materia oscura, el espacio-tiempo y los sueños postergados. Nueva York, NY: Bold Type Books. ISBN 978-1-5417-2470-9.OCLC 1164503847 .
- ^ Goodstein, Judith R. (2018). Los matemáticos italianos de Einstein: Ricci, Levi-Civita y el nacimiento de la relatividad general. Providence, Rhode Island: American Mathematical Society. pág. 143. ISBN 978-1-4704-2846-4.OCLC 1020305599 .
- ^ Mermin, N. David (1993). "Variables ocultas y los dos teoremas de John Bell". Reseñas de Física Moderna . 65 (3): 803–815. arXiv : 1802.10119 . Bibcode :1993RvMP...65..803M. doi :10.1103/RevModPhys.65.803. S2CID 119546199.
Una doctrina cuántica fundamental sostiene que una medición no revela, en general, un valor preexistente de la propiedad medida.
- ^ Schaffer, Kathryn; Barreto Lemos, Gabriela (24 de mayo de 2019). "Eliminación de la cosificación: una introducción al "qué" y al "entonces qué" de la física cuántica". Fundamentos de la ciencia . 26 : 7–26. arXiv : 1908.07936 . doi :10.1007/s10699-019-09608-5. ISSN 1233-1821. S2CID 182656563.
- ^ Marshman, Emily; Singh, Chandralekha (1 de marzo de 2017). "Investigación y mejora de la comprensión de los estudiantes sobre las distribuciones de probabilidad para medir observables físicos en mecánica cuántica". Revista Europea de Física . 38 (2): 025705. Bibcode :2017EJPh...38b5705M. doi : 10.1088/1361-6404/aa57d1 . ISSN 0143-0807. S2CID 126311599.
- ^ Cohen-Tannoudji, Claude ; Diu, Bernardo; Laloë, Franck (2005). Mecánica Cuántica . Traducido por Hemley, Susan Reid; Ostrowsky, Nicole; Ostrowsky, Dan. John Wiley e hijos. ISBN 0-471-16433-X.
- ^ Peres, Asher (1993). Teoría cuántica: conceptos y métodos . Kluwer . ISBN. 0-7923-2549-4.OCLC 28854083 .
- ^ D. Bilodeau, citado en Fuchs, Christopher A. (6 de enero de 2011). Alcanzar la madurez con información cuántica . Cambridge University Press. págs. 310–311. ISBN 978-0-521-19926-1.OCLC 759812415 .
- ^ Caspar, Max (2012) [1959]. Kepler . Traducido por Hellman, C. Doris . Dover. pág. 178. ISBN. 978-0-486-15175-5.OCLC 874097920 .
- ^ Ugaglia, Mónica (2015). "Física hidrostática de Aristóteles". Annali della Scuola Normale Superiore di Pisa. Clases de Letras y Filosofía . 7 (1): 169–199. ISSN 0392-095X. JSTOR 43915795.
- ^ Straulino, S.; Gambi, CMC; Righini, A. (enero de 2011). "Experimentos sobre flotabilidad y tensión superficial siguiendo a Galileo Galilei". American Journal of Physics . 79 (1): 32–36. Bibcode :2011AmJPh..79...32S. doi :10.1119/1.3492721. hdl : 2158/530056 . ISSN 0002-9505.
Aristóteles en su
Física
afirmó que el agua sólida debería tener un peso mayor que el agua líquida para el mismo volumen. Sabemos que esta afirmación es incorrecta porque la densidad del hielo es menor que la del agua (los enlaces de hidrógeno crean una estructura cristalina abierta en la fase sólida), y por esta razón el hielo puede flotar. [...] La teoría aristotélica de la flotabilidad afirma que los cuerpos en un fluido se sostienen por la resistencia del fluido a ser dividido por el objeto que lo penetra, de la misma manera que un gran trozo de madera sostiene un hacha que lo golpea o la miel sostiene una cuchara. Según esta teoría, un barco debería hundirse más en aguas poco profundas que en alta mar, de la misma manera que un hacha puede penetrar fácilmente e incluso romper un pequeño trozo de madera, pero no puede penetrar un trozo grande.
- ^ Sorabji, Richard (2010). "John Philoponus". Philoponus y el rechazo de la ciencia aristotélica (2.ª ed.). Instituto de Estudios Clásicos, Universidad de Londres. ISBN 978-1-905-67018-5. JSTOR 44216227. OCLC 878730683.
- ^ Maier, Anneliese (1982). Sargent, Steven D. (ed.). En el umbral de la ciencia exacta . University of Pennsylvania Press. ISBN 978-0-812-27831-6.OCLC 495305340 .
- ^ Véase, por ejemplo:
- Eaton, Philip; Vavruska, Kinsey; Willoughby, Shannon (25 de abril de 2019). "Explorando las visiones del mundo no newtonianas previas y posteriores a la instrucción, medidas por el Inventario de conceptos de fuerza". Physical Review Physics Education Research . 15 (1): 010123. Bibcode :2019PRPER..15a0123E. doi : 10.1103/PhysRevPhysEducRes.15.010123 . ISSN 2469-9896. S2CID 149482566.
- Robertson, Amy D.; Goodhew, Lisa M.; Scherr, Rachel E .; Heron, Paula RL (marzo de 2021). "El razonamiento de tipo impetuoso como continuo en la física newtoniana". El profesor de física . 59 (3): 185–188. doi :10.1119/10.0003660. ISSN 0031-921X. S2CID 233803836.
- Robertson, Amy D.; Goodhew, Lisa M.; Scherr, Rachel E .; Heron, Paula RL (30 de marzo de 2021). "Recursos conceptuales para estudiantes universitarios para comprender las fuerzas". Physical Review Physics Education Research . 17 (1): 010121. Bibcode :2021PRPER..17a0121R. doi : 10.1103/PhysRevPhysEducRes.17.010121 . ISSN 2469-9896. S2CID 243143427.
- ^ ab Blackwell, Richard J. (1966). "Las leyes del movimiento de Descartes". Isis . 57 (2): 220–234. doi :10.1086/350115. JSTOR 227961. S2CID 144278075.
- ^ Galileo, G. (1954) [1638, 1914]. Crew, H.; De Salvio, A. (eds.). Diálogos sobre dos nuevas ciencias. Dover Publications Inc. pág. 268.
- ^ Galileo, G. (1974) [1638]. Dos nuevas ciencias, incluidos los centros de gravedad y la fuerza de percusión. Traducido por Drake, S. University of Wisconsin Press. pp. 217 [268].
- ^ Hellman, C. Doris (1955). "La ciencia en el Renacimiento: un estudio". Renaissance News . 8 (4): 186–200. doi :10.2307/2858681. ISSN 0277-903X. JSTOR 2858681.
- ^ LoLordo, Antonia (2007). Pierre Gassendi y el nacimiento de la filosofía moderna temprana. Nueva York: Cambridge University Press. pp. 175–180. ISBN 978-0-511-34982-9.OCLC 182818133 .
- ^ Descartes, R. (2008) [1644]. Bennett, J. (ed.). Principios de filosofía (PDF) . Parte II, § 37, 39.
- ^ ab Blackwell, Richard J.; Huygens, Christiaan (1977). "El movimiento de los cuerpos en colisión de Christiaan Huygens". Isis . 68 (4): 574–597. doi :10.1086/351876. JSTOR 230011. S2CID 144406041.
- ^ Pourciau, Bruce (octubre de 2011). "¿Es la segunda ley de Newton realmente la ley de Newton?". American Journal of Physics . 79 (10): 1015–1022. Bibcode :2011AmJPh..79.1015P. doi :10.1119/1.3607433. ISSN 0002-9505.
- ^ Fara, Patricia (15 de agosto de 2003). "¿Newton era newtoniano?". Science . 301 (5635): 920. doi :10.1126/science.1088786. ISSN 0036-8075. S2CID 170120455.
- ^ Higgitt, Rebekah (2015). Ciencia y cultura en el siglo XIX: Recreando a Newton. Nueva York: Taylor & Francis. p. 147. ISBN 978-1-317-31495-0. OCLC 934741893.
- ^ Dobbs, Betty Jo Teeter (1975). Los fundamentos de la alquimia de Newton: o "la caza del Greene Lyon" . Cambridge University Press. págs. 211-212. ISBN. 9780521273817.OCLC 1058581988 .
- ^ West, Richard (1980). Nunca en reposo . Cambridge University Press. pág. 390. ISBN 9780521231435.OCLC 5677169 .
- ^ abc Newman, William R. (2016). "Una reevaluación preliminar de la alquimia de Newton". The Cambridge Companion to Newton (2.ª ed.). Cambridge University Press. págs. 454–484. ISBN 978-1-107-01546-3.OCLC 953450997 .
- ^ Nummedal, Tara (1 de junio de 2020). "William R. Newman. Newton el alquimista: ciencia, enigma y la búsqueda del "fuego secreto" de la naturaleza". Isis . 111 (2): 395–396. doi :10.1086/709344. ISSN 0021-1753. S2CID 243203703.
- ^ Aldersey-Williams, Hugh (2020). Dutch Light: Christiaan Huygens y la creación de la ciencia en Europa. Londres: Picador. ISBN 978-1-5098-9333-1.OCLC 1144105192 .
- ^ Cohen, I. Bernard (1962). "La primera versión inglesa de las hipótesis de Newton non fingo". Isis . 53 (3): 379–388. doi :10.1086/349598. ISSN 0021-1753. JSTOR 227788. S2CID 144575106.
- ^ Jammer, Max (1999) [1962]. Conceptos de fuerza: un estudio sobre los fundamentos de la dinámica . Mineola, NY: Dover Publications. pp. 91, 127. ISBN 978-0-486-40689-3.OCLC 40964671 .
- ^ Slowik, Edward (15 de octubre de 2021). «Descartes' Physics». Stanford Encyclopedia of Philosophy . Consultado el 6 de marzo de 2022 .
- ^ Erlichson, Herman (febrero de 1997). "El joven Huygens resuelve el problema de las colisiones elásticas". American Journal of Physics . 65 (2): 149–154. Bibcode :1997AmJPh..65..149E. doi :10.1119/1.18659. ISSN 0002-9505.
- ^ Smith, George E. (octubre de 2006). "La disputa sobre la vis viva: una controversia en los albores de la dinámica". Physics Today . 59 (10): 31–36. Bibcode :2006PhT....59j..31S. doi :10.1063/1.2387086. ISSN 0031-9228.
- ^ Davies, EB (2009). "Algunas reflexiones sobre los "Principia" de Newton". Revista británica de historia de la ciencia . 42 (2): 211–224. doi :10.1017/S000708740800188X. ISSN 0007-0874. JSTOR 25592244. S2CID 145120248.
- ^ Smith, George E. (diciembre de 2020). "Las leyes del movimiento de Newton". En Schliesser, Eric; Smeenk, Chris (eds.). The Oxford Handbook of Newton . Oxford University Press. En línea antes de la impresión. doi :10.1093/oxfordhb/9780199930418.013.35. ISBN 978-0-199-93041-8.OCLC 972369868 .
- ^ Patterson, Elizabeth C. (diciembre de 1969). "Mary Somerville". The British Journal for the History of Science . 4 (4): 311–339. doi :10.1017/S0007087400010232. ISSN 0007-0874. S2CID 246612625.
En ningún sentido se trató de una mera traducción de la obra de Laplace. En cambio, se esforzó por explicar su método "... mediante el cual se deducían estos resultados a partir de una ecuación general del movimiento de la materia" y por llevar la habilidad matemática del lector al punto en que la exposición de las matemáticas y las ideas de Laplace fuera significativa, para luego ofrecer un resumen en inglés de su gran obra. Se añadieron diagramas cuando fue necesario al texto original y se incluyeron pruebas de varios problemas de mecánica física y astronomía. ... [D]urante casi cien años después de su aparición, el libro continuó sirviendo como libro de texto de matemáticas superiores y astronomía en las escuelas inglesas.
- ^ Baron, Margaret E. (1969). Los orígenes del cálculo infinitesimal (1.ª ed.). Oxford: Pergamon Press. ISBN 978-1-483-28092-9.OCLC 892067655 .
- ^ Dunlop, Katherine (mayo de 2012). "La forma matemática de la medición y el argumento a favor de la Proposición I en los Principia de Newton". Síntesis . 186 (1): 191–229. doi :10.1007/s11229-011-9983-8. ISSN 0039-7857. S2CID 11794836.
- ^ Smith, George (20 de diciembre de 2007). "Philosophae Naturalis Principia Mathematica de Newton". Enciclopedia de Filosofía de Stanford . Consultado el 6 de marzo de 2022 .
- ^ Marquina, JE; Marquina, ML; Marquina, V.; Hernández-Gómez, JJ (1 de enero de 2017). "Leonhard Euler y la mecánica de los cuerpos rígidos". Revista Europea de Física . 38 (1): 015001. Bibcode :2017EJPh...38a5001M. doi :10.1088/0143-0807/38/1/015001. ISSN 0143-0807. S2CID 125948408.
- ^ Hesse, Mary B. (2005) [1961]. Fuerzas y campos: el concepto de acción a distancia en la historia de la física (edición reimpresa de Dover). Mineola, NY: Dover Publications. pág. 189. ISBN 978-0-486-44240-2.OCLC 57579169 .
- ^ Smith, George (19 de diciembre de 2007). "Isaac Newton". Stanford Encyclopedia of Philosophy . Consultado el 6 de marzo de 2022 .
Estos avances en nuestra comprensión del movimiento planetario llevaron a Laplace a producir los cuatro volúmenes principales de su
Traité de mécanique céleste
de 1799 a 1805, una obra que recopila en un solo lugar todos los resultados teóricos y empíricos de la investigación basada en
los Principia
de Newton . A partir de ese momento, la ciencia newtoniana surgió del trabajo de Laplace, no del de Newton.
- ^ Reichenberger, Andrea (junio de 2018). "La interpretación de Émilie Du Châtelet de las leyes del movimiento a la luz de la mecánica del siglo XVIII". Estudios de historia y filosofía de la ciencia, parte A. 69 : 1–11. Bibcode :2018SHPSA..69....1R. doi :10.1016/j.shpsa.2018.01.006. PMID 29857796. S2CID 46923474.
- ^ Frontali, Clara (septiembre de 2014). "Historia de los términos físicos: "energía"". Educación en Física . 49 (5): 564–573. Bibcode :2014PhyEd..49..564F. doi :10.1088/0031-9120/49/5/564. ISSN 0031-9120. S2CID 122097990.
- ^ Gbur, Greg (10 de diciembre de 2018). «Historia de la conservación de la energía: auges, sangre y cerveza (parte 1)». Skulls in the Stars . Consultado el 7 de marzo de 2022 . "Historia de la conservación de la energía: auges, sangre y cerveza (parte 2)". 29 de diciembre de 2018. Consultado el 7 de marzo de 2022 . "Historia de la conservación de la energía: auges, sangre y cerveza (parte 3)". 25 de agosto de 2019. Consultado el 7 de marzo de 2022 .
- ^ Silva, Cibelle Celestino; de Andrade Martins, Roberto (septiembre de 2002). "Vectores polares y axiales versus cuaterniones". American Journal of Physics . 70 (9): 958–963. Bibcode :2002AmJPh..70..958S. doi :10.1119/1.1475326. ISSN 0002-9505.
- ^ Reich, Karin (1996). "El surgimiento del cálculo vectorial en física: las primeras décadas". En Schubring, Gert (ed.). Hermann Günther Graßmann (1809-1877): matemático visionario, científico y erudito neohumanista . Boston Studies in the Philosophy of Science. Vol. 187. Kluwer. págs. 197-210. ISBN 978-9-048-14758-8.OCLC 799299609 .
Lectura adicional
- Las leyes de la dinámica de Newton - Las conferencias Feynman sobre física
- Chakrabarty, Deepto; Dourmashkin, Peter; Tomasik, Michelle; Frebel, Anna ; Vuletic, Vladan (2016). "Mecánica clásica". MIT OpenCourseWare . Consultado el 17 de enero de 2022 .












































































































![{\displaystyle \left[{\frac {\partial }{\partial t}}+{\frac {1}{m}}\left(\mathbf {\nabla } S\cdot \mathbf {\nabla } \right )\right]\mathbf {\nabla } S=-\mathbf {\nabla } V.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba9e3cf63a74bdfb6e4ac08c85c31828ee89fb07)
![{\displaystyle \left[{\frac {\partial }{\partial t}}+{\frac {1}{m}}\left(\mathbf {\nabla } S\cdot \mathbf {\nabla } \right )\right]=\left[{\frac {\partial }{\partial t}}+\mathbf {v} \cdot \mathbf {\nabla } \right]={\frac {d}{dt}}. }](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ba77978a485bdd9eafdda5aa195e2f828c16863)



















