Teoría del caos

La teoría del caos es un área interdisciplinaria de estudio científico y una rama de las matemáticas . Se centra en los patrones subyacentes y las leyes deterministas de los sistemas dinámicos que son altamente sensibles a las condiciones iniciales . Alguna vez se pensó que estos tenían estados completamente aleatorios de desorden e irregularidades. ^[1] La teoría del caos afirma que dentro de la aparente aleatoriedad de los sistemas complejos caóticos , hay patrones subyacentes, interconexión, bucles de retroalimentación constantes , repetición, autosimilitud , fractales y autoorganización . ^[2] El efecto mariposa , un principio subyacente del caos, describe cómo un pequeño cambio en un estado de un sistema no lineal determinista puede resultar en grandes diferencias en un estado posterior (lo que significa que hay una dependencia sensible de las condiciones iniciales). ^[3] Una metáfora para este comportamiento es que una mariposa que bate sus alas en Brasil puede causar un tornado en Texas . ^{[4] [5] [6]}

Pequeñas diferencias en las condiciones iniciales, como las debidas a errores en las mediciones o a errores de redondeo en el cálculo numérico , pueden producir resultados muy divergentes para tales sistemas dinámicos, lo que hace que la predicción a largo plazo de su comportamiento sea imposible en general. ^[7] Esto puede suceder incluso aunque estos sistemas sean deterministas , lo que significa que su comportamiento futuro sigue una evolución única ^[8] y está completamente determinado por sus condiciones iniciales, sin elementos aleatorios involucrados. ^[9] En otras palabras, la naturaleza determinista de estos sistemas no los hace predecibles. ^{[10] [11]} Este comportamiento se conoce como caos determinista , o simplemente caos . La teoría fue resumida por Edward Lorenz como: ^[12]

Caos: Cuando el presente determina el futuro pero el presente aproximado no determina aproximadamente el futuro.

El comportamiento caótico existe en muchos sistemas naturales, incluido el flujo de fluidos, las irregularidades de los latidos del corazón, el tiempo y el clima. ^{[13] [14] [8]} También ocurre espontáneamente en algunos sistemas con componentes artificiales, como el tráfico rodado . ^[2] Este comportamiento se puede estudiar mediante el análisis de un modelo matemático caótico o mediante técnicas analíticas como gráficos de recurrencia y mapas de Poincaré . La teoría del caos tiene aplicaciones en una variedad de disciplinas, incluidas la meteorología , ^[8] la antropología , ^[15] la sociología , la ciencia ambiental , la informática , la ingeniería , la economía , la ecología y la gestión de crisis pandémicas . ^{[16] [17]} La ​​teoría formó la base para campos de estudio como los sistemas dinámicos complejos , la teoría del borde del caos y los procesos de autoensamblaje .

La teoría del caos se ocupa de sistemas deterministas cuyo comportamiento puede, en principio, predecirse. Los sistemas caóticos son predecibles durante un tiempo y luego "parecen" volverse aleatorios. La cantidad de tiempo durante el cual se puede predecir efectivamente el comportamiento de un sistema caótico depende de tres cosas: cuánta incertidumbre se puede tolerar en el pronóstico, con qué precisión se puede medir su estado actual y una escala de tiempo que depende de la dinámica del sistema, llamada tiempo de Lyapunov . Algunos ejemplos de tiempos de Lyapunov son: circuitos eléctricos caóticos, alrededor de 1 milisegundo; sistemas meteorológicos, unos pocos días (no probado); el sistema solar interior, de 4 a 5 millones de años. ^[18] En los sistemas caóticos, la incertidumbre en un pronóstico aumenta exponencialmente con el tiempo transcurrido. Por lo tanto, matemáticamente, duplicar el tiempo de pronóstico más que cuadrar la incertidumbre proporcional en el pronóstico. Esto significa que, en la práctica, no se puede hacer una predicción significativa en un intervalo de más de dos o tres veces el tiempo de Lyapunov. Cuando no se pueden hacer predicciones significativas, el sistema parece aleatorio. ^[19]

En el uso común, "caos" significa "un estado de desorden". ^{[20] [21]} Sin embargo, en la teoría del caos, el término se define con mayor precisión. Aunque no existe una definición matemática universalmente aceptada del caos, una definición comúnmente utilizada, formulada originalmente por Robert L. Devaney , dice que para clasificar un sistema dinámico como caótico, debe tener estas propiedades: ^[22]

1. Debe ser sensible a las condiciones iniciales ,
2. Debe ser topológicamente transitiva ,
3. Debe tener órbitas periódicas densas .

En algunos casos, se ha demostrado que las dos últimas propiedades anteriores implican en realidad sensibilidad a las condiciones iniciales. ^{[23] [24]} En el caso de tiempo discreto, esto es cierto para todos los mapas continuos en espacios métricos . ^[25] En estos casos, si bien a menudo es la propiedad más significativa en la práctica, no es necesario indicar "sensibilidad a las condiciones iniciales" en la definición.

Si la atención se limita a los intervalos , la segunda propiedad implica las otras dos. ^[26] Una definición alternativa y generalmente más débil del caos utiliza sólo las dos primeras propiedades de la lista anterior. ^[27]

La sensibilidad a las condiciones iniciales significa que cada punto de un sistema caótico se aproxima de forma arbitraria a otros puntos que tienen trayectorias o caminos futuros significativamente diferentes. Por lo tanto, un cambio o una perturbación arbitrariamente pequeños de la trayectoria actual pueden dar lugar a un comportamiento futuro significativamente diferente. ^[2]

La sensibilidad a las condiciones iniciales se conoce popularmente como el " efecto mariposa ", llamado así por el título de un artículo presentado por Edward Lorenz en 1972 a la Asociación Americana para el Avance de la Ciencia en Washington, DC, titulado Predictibilidad: ¿el aleteo de las alas de una mariposa en Brasil desencadena un tornado en Texas? [ ^28] El aleteo representa un pequeño cambio en la condición inicial del sistema, que causa una cadena de eventos que impide la predictibilidad de fenómenos a gran escala. Si la mariposa no hubiera aleteado, la trayectoria del sistema en su conjunto podría haber sido muy diferente.

Como se sugiere en el libro de Lorenz titulado La esencia del caos , publicado en 1993, ^[5] "la dependencia sensible puede servir como una definición aceptable del caos". En el mismo libro, Lorenz definió el efecto mariposa como: "El fenómeno de que una pequeña alteración en el estado de un sistema dinámico hará que los estados posteriores difieran en gran medida de los estados que habrían seguido sin la alteración". La definición anterior es coherente con la dependencia sensible de las soluciones en las condiciones iniciales (SDIC). Se desarrolló un modelo de esquí idealizado para ilustrar la sensibilidad de las trayectorias que varían en el tiempo a las posiciones iniciales. ^[5] Se puede determinar un horizonte de predictibilidad antes del inicio de SDIC (es decir, antes de separaciones significativas de las trayectorias cercanas iniciales). ^[29]

Una consecuencia de la sensibilidad a las condiciones iniciales es que si empezamos con una cantidad limitada de información sobre el sistema (como suele ser el caso en la práctica), entonces, más allá de cierto tiempo, el sistema ya no sería predecible. Esto es más frecuente en el caso del clima, que generalmente es predecible solo con una semana de antelación. ^[30] Esto no significa que no se pueda afirmar nada sobre eventos en el futuro lejano, solo que existen algunas restricciones en el sistema. Por ejemplo, sabemos que la temperatura de la superficie de la Tierra no alcanzará naturalmente los 100 °C (212 °F) ni caerá por debajo de los −130 °C (−202 °F) en la Tierra (durante la era geológica actual ), pero no podemos predecir exactamente qué día tendrá la temperatura más alta del año.

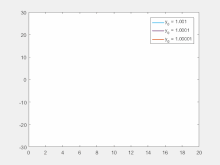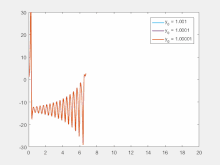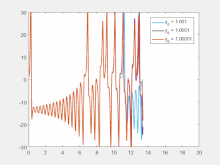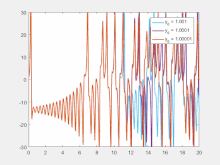
En términos más matemáticos, el exponente de Lyapunov mide la sensibilidad a las condiciones iniciales, en forma de tasa de divergencia exponencial de las condiciones iniciales perturbadas. ^[31] Más específicamente, dadas dos trayectorias iniciales en el espacio de fases que están infinitesimalmente cerca, con una separación inicial , las dos trayectorias terminan divergiendo a una tasa dada por${\displaystyle \delta \mathbf {Z} _ {0}}$

${\displaystyle |\delta \mathbf {Z} (t)|\approx e^{\lambda t}|\delta \mathbf {Z} _{0}|,}$

donde es el tiempo y es el exponente de Lyapunov. La tasa de separación depende de la orientación del vector de separación inicial, por lo que puede existir un espectro completo de exponentes de Lyapunov. El número de exponentes de Lyapunov es igual al número de dimensiones del espacio de fases, aunque es común referirse solo al mayor. Por ejemplo, el exponente máximo de Lyapunov (MLE) es el más utilizado, porque determina la predictibilidad general del sistema. Un MLE positivo generalmente se toma como una indicación de que el sistema es caótico. ^[8]${\estilo de visualización t}$${\estilo de visualización \lambda}$

Además de la propiedad mencionada anteriormente, también existen otras propiedades relacionadas con la sensibilidad de las condiciones iniciales, entre las que se incluyen, por ejemplo, la mezcla teórica de medidas (como se analiza en la teoría ergódica ) y las propiedades de un sistema K. ^[11 ]

Un sistema caótico puede tener secuencias de valores para la variable en evolución que se repiten exactamente, dando lugar a un comportamiento periódico a partir de cualquier punto de esa secuencia. Sin embargo, dichas secuencias periódicas se repelen en lugar de atraerse, lo que significa que si la variable en evolución está fuera de la secuencia, por muy cerca que esté, no entrará en ella y, de hecho, divergirá de ella. Por lo tanto, para casi todas las condiciones iniciales, la variable evoluciona caóticamente con un comportamiento no periódico.

La mezcla topológica (o la condición más débil de transitividad topológica) significa que el sistema evoluciona con el tiempo de modo que cualquier región dada o conjunto abierto de su espacio de fases eventualmente se superpone con cualquier otra región dada. Este concepto matemático de "mezcla" corresponde a la intuición estándar, y la mezcla de tintes o fluidos de colores es un ejemplo de un sistema caótico.

La mezcla topológica suele omitirse en las explicaciones populares sobre el caos, que equiparan el caos con la sensibilidad a las condiciones iniciales. Sin embargo, la dependencia sensible a las condiciones iniciales por sí sola no produce caos. Por ejemplo, considere el sistema dinámico simple producido al duplicar repetidamente un valor inicial. Este sistema tiene una dependencia sensible a las condiciones iniciales en todas partes, ya que cualquier par de puntos cercanos eventualmente se vuelve muy separado. Sin embargo, este ejemplo no tiene mezcla topológica y, por lo tanto, no tiene caos. De hecho, tiene un comportamiento extremadamente simple: todos los puntos excepto 0 tienden al infinito positivo o negativo.

Se dice que una función es topológicamente transitiva si para cualquier par de conjuntos abiertos no vacíos , existe tal que . La transitividad topológica es una versión más débil de la mezcla topológica . Intuitivamente, si una función es topológicamente transitiva, entonces dado un punto x y una región V , existe un punto y cerca de x cuya órbita pasa por V . Esto implica que es imposible descomponer el sistema en dos conjuntos abiertos. ^[32]${\displaystyle f:X\a X}$ ${\displaystyle U,V\subconjunto X}$${\displaystyle k>0}$${\displaystyle f^{k}(U)\cap V\neq \conjunto vacío}$

Un teorema importante relacionado es el teorema de transitividad de Birkhoff. Es fácil ver que la existencia de una órbita densa implica transitividad topológica. El teorema de transitividad de Birkhoff establece que si X es un segundo espacio métrico completo numerable , entonces la transitividad topológica implica la existencia de un conjunto denso de puntos en X que tienen órbitas densas. ^[33]

Para que un sistema caótico tenga órbitas periódicas densas significa que cada punto en el espacio está arbitrariamente cerca de órbitas periódicas. ^{[32] El} mapa logístico unidimensional definido por x → 4 x (1 – x ) es uno de los sistemas más simples con densidad de órbitas periódicas. Por ejemplo,  →  → (o aproximadamente 0.3454915 → 0.9045085 → 0.3454915) es una órbita (inestable) de período 2, y existen órbitas similares para los períodos 4, 8, 16, etc. (de hecho, para todos los períodos especificados por el teorema de Sharkovskii ). ^[34]${\displaystyle {\tfrac {5-{\sqrt {5}}}{8}}}$${\displaystyle {\tfrac {5+{\sqrt {5}}}{8}}}$${\displaystyle {\tfrac {5-{\sqrt {5}}}{8}}}$

El teorema de Sharkovskii es la base de la prueba de Li y Yorke ^[35] (1975) de que cualquier sistema unidimensional continuo que exhibe un ciclo regular de período tres también mostrará ciclos regulares de cualquier otra longitud, así como órbitas completamente caóticas.

Algunos sistemas dinámicos, como el mapa logístico unidimensional definido por x → 4 x (1 – x ), son caóticos en todas partes, pero en muchos casos el comportamiento caótico se encuentra solo en un subconjunto del espacio de fases. Los casos de mayor interés surgen cuando el comportamiento caótico tiene lugar en un atractor , ya que entonces un gran conjunto de condiciones iniciales conduce a órbitas que convergen a esta región caótica. ^[36]

Una manera fácil de visualizar un atractor caótico es empezar con un punto en la cuenca de atracción del atractor y luego simplemente trazar su órbita subsiguiente. Debido a la condición de transitividad topológica, es probable que esto produzca una imagen de todo el atractor final y, de hecho, ambas órbitas que se muestran en la figura de la derecha dan una imagen de la forma general del atractor de Lorenz. Este atractor resulta de un modelo tridimensional simple del sistema meteorológico de Lorenz . El atractor de Lorenz es quizás uno de los diagramas de sistemas caóticos más conocidos, probablemente porque no solo es uno de los primeros, sino también uno de los más complejos y, como tal, da lugar a un patrón muy interesante que, con un poco de imaginación, parece las alas de una mariposa.

A diferencia de los atractores de punto fijo y los ciclos límite , los atractores que surgen de sistemas caóticos, conocidos como atractores extraños , tienen un gran detalle y complejidad. Los atractores extraños ocurren tanto en sistemas dinámicos continuos (como el sistema de Lorenz) como en algunos sistemas discretos (como el mapa de Hénon ). Otros sistemas dinámicos discretos tienen una estructura de repulsión llamada conjunto de Julia , que se forma en el límite entre cuencas de atracción de puntos fijos. Los conjuntos de Julia pueden considerarse como repelentes extraños. Tanto los atractores extraños como los conjuntos de Julia suelen tener una estructura fractal , y se puede calcular la dimensión fractal para ellos.

A diferencia de las soluciones caóticas de un solo tipo, estudios recientes que utilizan modelos de Lorenz ^{[40] [41]} han enfatizado la importancia de considerar varios tipos de soluciones. Por ejemplo, pueden aparecer soluciones caóticas y no caóticas coexistentes dentro del mismo modelo (por ejemplo, el sistema de doble péndulo) utilizando las mismas configuraciones de modelado pero diferentes condiciones iniciales. Los hallazgos de coexistencia de atractores, obtenidos a partir de modelos de Lorenz clásicos y generalizados, ^{[37] [38] [39]} sugirieron una visión revisada de que "la totalidad del clima posee una naturaleza dual de caos y orden con una predictibilidad distinta", en contraste con la visión convencional de que "el clima es caótico".

Los sistemas caóticos discretos, como el mapa logístico , pueden exhibir atractores extraños independientemente de su dimensionalidad . En cambio, para los sistemas dinámicos continuos , el teorema de Poincaré-Bendixson muestra que un atractor extraño solo puede surgir en tres o más dimensiones. Los sistemas lineales de dimensión finita nunca son caóticos; para que un sistema dinámico muestre un comportamiento caótico, debe ser no lineal o de dimensión infinita.

El teorema de Poincaré-Bendixson establece que una ecuación diferencial bidimensional tiene un comportamiento muy regular. El atractor de Lorenz que se analiza a continuación se genera mediante un sistema de tres ecuaciones diferenciales como:

${\displaystyle {\begin{aligned}{\frac {\mathrm {d} x}{\mathrm {d} t}}&=\sigma y-\sigma x,\\{\frac {\mathrm {d} y}{\mathrm {d} t}}&=\rho x-xz-y,\\{\frac {\mathrm {d} z}{\mathrm {d} t}}&=xy-\beta z.\end{aligned}}}$

donde , , y forman el estado del sistema , es el tiempo, y , , son los parámetros del sistema . Cinco de los términos del lado derecho son lineales, mientras que dos son cuadráticos; un total de siete términos. Otro atractor caótico bien conocido es generado por las ecuaciones de Rössler , que tienen solo un término no lineal de siete. Sprott ^[42] encontró un sistema tridimensional con solo cinco términos, que tenía solo un término no lineal, que exhibe caos para ciertos valores de parámetros. Zhang y Heidel ^{[43] [44]} demostraron que, al menos para sistemas cuadráticos disipativos y conservativos, los sistemas cuadráticos tridimensionales con solo tres o cuatro términos en el lado derecho no pueden exhibir un comportamiento caótico. La razón es, simplemente, que las soluciones a tales sistemas son asintóticas a una superficie bidimensional y, por lo tanto, las soluciones se comportan bien.${\estilo de visualización x}$${\estilo de visualización y}$${\estilo de visualización z}$${\estilo de visualización t}$${\estilo de visualización \sigma}$${\estilo de visualización \rho}$${\estilo de visualización \beta}$

Si bien el teorema de Poincaré-Bendixson muestra que un sistema dinámico continuo en el plano euclidiano no puede ser caótico, los sistemas continuos bidimensionales con geometría no euclidiana aún pueden exhibir algunas propiedades caóticas. ^[45] Quizás sorprendentemente, el caos también puede ocurrir en sistemas lineales, siempre que sean de dimensión infinita. ^[46] Se está desarrollando una teoría del caos lineal en una rama del análisis matemático conocida como análisis funcional .

El conjunto anterior de tres ecuaciones diferenciales ordinarias se ha denominado modelo tridimensional de Lorenz. ^[47] Desde 1963, se han desarrollado modelos de Lorenz de mayor dimensión en numerosos estudios ^{[48] [49] [37] [38]} para examinar el impacto de un mayor grado de no linealidad, así como su efecto colectivo con el calentamiento y las disipaciones, en la estabilidad de la solución.

La generalización directa de mapas discretos acoplados ^[50] se basa en la integral de convolución que media la interacción entre mapas distribuidos espacialmente: ,${\displaystyle \psi _{n+1}({\vec {r}},t)=\int K({\vec {r}}-{\vec {r}}^{,},t)f [\psi _{n}({\vec {r}}^{,},t)]d{\vec {r}}^{,}}$

donde el núcleo es el propagador derivado como función de Green de un sistema físico relevante, ^[51] podría ser un mapa logístico o un mapa complejo . Para ejemplos de mapas complejos pueden servir el conjunto de Julia o el mapa de Ikeda . Cuando se consideran problemas de propagación de ondas a distancia con longitud de onda , el núcleo puede tener una forma de función de Green para la ecuación de Schrödinger :. ^{[52] [53]}${\displaystyle K({\vec {r}}-{\vec {r}}^{,},t)}$${\displaystyle f[\psi_{n}({\vec {r}},t)]}$${\displaystyle \psi \rightarrow G\psi [1-\tanh(\psi )]}$ ${\displaystyle f[\psi ]=\psi ^{2}}$${\displaystyle \psi _{n+1}=A+B\psi _{n}e^{i(|\psi _{n}|^{2}+C)}}$${\displaystyle L=ct}$${\displaystyle \lambda =2\pi /k}$${\displaystyle K}$

${\displaystyle K({\vec {r}}-{\vec {r}}^{,},L)={\frac {ik\exp[ikL]}{2\pi L}}\exp[{\frac {ik|{\vec {r}}-{\vec {r}}^{,}|^{2}}{2L}}]}$.

En física , el tirón es la tercera derivada de la posición con respecto al tiempo. Por lo tanto, las ecuaciones diferenciales de la forma

${\displaystyle J\left({\overset {...}{x}},{\ddot {x}},{\dot {x}},x\right)=0}$

A veces se denominan ecuaciones jerk . Se ha demostrado que una ecuación jerk, que es equivalente a un sistema de tres ecuaciones diferenciales ordinarias, no lineales y de primer orden, es en cierto sentido la configuración mínima para soluciones que muestran un comportamiento caótico. Esto motiva el interés matemático en los sistemas jerk. Los sistemas que involucran una cuarta derivada o superior se denominan en consecuencia sistemas hyperjerk. ^[54]

El comportamiento de un sistema de sacudidas se describe mediante una ecuación de sacudidas y, para ciertas ecuaciones de sacudidas, los circuitos electrónicos simples pueden modelar soluciones. Estos circuitos se conocen como circuitos de sacudidas.

Una de las propiedades más interesantes de los circuitos jerk es la posibilidad de comportamiento caótico. De hecho, ciertos sistemas caóticos bien conocidos, como el atractor de Lorenz y el mapa de Rössler , se describen convencionalmente como un sistema de tres ecuaciones diferenciales de primer orden que pueden combinarse en una única ecuación jerk (aunque bastante complicada). Otro ejemplo de una ecuación jerk con no linealidad en la magnitud de es:${\displaystyle x}$

${\displaystyle {\frac {\mathrm {d} ^{3}x}{\mathrm {d} t^{3}}}+A{\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}+{\frac {\mathrm {d} x}{\mathrm {d} t}}-|x|+1=0.}$

Aquí, A es un parámetro ajustable. Esta ecuación tiene una solución caótica para A = 3/5 y se puede implementar con el siguiente circuito de sacudidas; la no linealidad requerida se logra mediante los dos diodos:

En el circuito anterior, todas las resistencias tienen el mismo valor, excepto , y todos los condensadores tienen el mismo tamaño. La frecuencia dominante es . La salida del amplificador operacional 0 corresponderá a la variable x, la salida de 1 corresponde a la primera derivada de x y la salida de 2 corresponde a la segunda derivada.${\displaystyle R_{A}=R/A=5R/3}$${\displaystyle 1/2\pi RC}$

Circuitos similares solo requieren un diodo ^[55] o ningún diodo en absoluto. ^[56]

Véase también el conocido circuito de Chua , una de las bases para los generadores de números aleatorios verdaderos caóticos. ^[57] La ​​facilidad de construcción del circuito lo ha convertido en un ejemplo omnipresente en el mundo real de un sistema caótico.

En las condiciones adecuadas, el caos evoluciona espontáneamente hacia un patrón de sincronización. En el modelo de Kuramoto , cuatro condiciones son suficientes para producir sincronización en un sistema caótico. Algunos ejemplos incluyen la oscilación acoplada de los péndulos de Christiaan Huygens , las luciérnagas, las neuronas , la resonancia del Puente del Milenio de Londres y grandes conjuntos de uniones de Josephson . ^[58]

Además, desde el punto de vista de la física teórica, el caos dinámico en sí mismo, en su manifestación más general, es un orden espontáneo. La esencia aquí es que la mayoría de los órdenes en la naturaleza surgen de la ruptura espontánea de varias simetrías. Esta gran familia de fenómenos incluye la elasticidad, la superconductividad, el ferromagnetismo y muchos otros. Según la teoría supersimétrica de la dinámica estocástica , el caos, o más precisamente, su generalización estocástica, también es parte de esta familia. La simetría correspondiente que se rompe es la supersimetría topológica que está oculta en todas las ecuaciones diferenciales estocásticas (parciales) , y el parámetro de orden correspondiente es una encarnación teórica de campo del efecto mariposa. ^[59]

James Clerk Maxwell fue el primero en enfatizar el " efecto mariposa ", y es visto como uno de los primeros en discutir la teoría del caos, con trabajos en las décadas de 1860 y 1870. ^{[60] [61] [62]} Uno de los primeros defensores de la teoría del caos fue Henri Poincaré . En la década de 1880, mientras estudiaba el problema de los tres cuerpos , descubrió que puede haber órbitas que no sean periódicas, y sin embargo no aumenten para siempre ni se acerquen a un punto fijo. ^{[63] [64] [65]} En 1898, Jacques Hadamard publicó un influyente estudio del movimiento caótico de una partícula libre deslizándose sin fricción sobre una superficie de curvatura negativa constante, llamado " billar de Hadamard ". ^{[66] Hadamard pudo demostrar que todas las trayectorias son inestables, en el sentido de que todas las trayectorias de partículas divergen exponencialmente entre sí, con un} exponente de Lyapunov positivo .

La teoría del caos comenzó en el campo de la teoría ergódica . Estudios posteriores, también sobre el tema de las ecuaciones diferenciales no lineales , fueron realizados por George David Birkhoff , ^[67] Andrey Nikolaevich Kolmogorov , ^{[68] [69] [70]} Mary Lucy Cartwright y John Edensor Littlewood , ^[71] y Stephen Smale . ^[72] Aunque no se había observado movimiento planetario caótico, los experimentalistas habían encontrado turbulencia en el movimiento de fluidos y oscilación no periódica en circuitos de radio sin el beneficio de una teoría para explicar lo que estaban viendo.

A pesar de las ideas iniciales de la primera mitad del siglo XX, la teoría del caos se formalizó como tal solo después de mediados de siglo, cuando se hizo evidente para algunos científicos que la teoría lineal , la teoría de sistemas predominante en ese momento, simplemente no podía explicar el comportamiento observado de ciertos experimentos como el del mapa logístico . Lo que se había atribuido a la imprecisión de la medida y al simple " ruido " fue considerado por los teóricos del caos como un componente completo de los sistemas estudiados. En 1959, Boris Valerianovich Chirikov propuso un criterio para la aparición del caos clásico en sistemas hamiltonianos ( criterio de Chirikov ). Aplicó este criterio para explicar algunos resultados experimentales sobre el confinamiento de plasma en trampas de espejo abierto. ^{[73] [74]} Esta se considera como la primera teoría física del caos, que logró explicar un experimento concreto. Y el propio Boris Chirikov es considerado como un pionero en el caos clásico y cuántico. ^{[75] [76] [77]}

El principal catalizador para el desarrollo de la teoría del caos fue la computadora electrónica. Gran parte de las matemáticas de la teoría del caos implican la iteración repetida de fórmulas matemáticas simples, lo que sería poco práctico si se hiciera a mano. Las computadoras electrónicas hicieron que estos cálculos repetidos fueran prácticos, mientras que las figuras e imágenes hicieron posible visualizar estos sistemas. Como estudiante de posgrado en el laboratorio de Chihiro Hayashi en la Universidad de Kioto, Yoshisuke Ueda estaba experimentando con computadoras analógicas y notó, el 27 de noviembre de 1961, lo que llamó "fenómenos de transición aleatoria". Sin embargo, su asesor no estuvo de acuerdo con sus conclusiones en ese momento, y no le permitió informar sobre sus hallazgos hasta 1970. ^{[78] [79]}

Edward Lorenz fue uno de los pioneros de la teoría. Su interés por el caos surgió accidentalmente a través de su trabajo sobre predicción meteorológica en 1961. ^[13] Lorenz y su colaboradora Ellen Fetter y Margaret Hamilton ^[80] estaban usando una computadora digital simple, una Royal McBee LGP-30 , para ejecutar simulaciones meteorológicas. Querían ver una secuencia de datos nuevamente y, para ahorrar tiempo, comenzaron la simulación en el medio de su curso. Lo hicieron ingresando una impresión de los datos que correspondían a las condiciones en el medio de la simulación original. Para su sorpresa, el clima que la máquina comenzó a predecir era completamente diferente del cálculo anterior. Lo rastrearon hasta la impresión de la computadora. La computadora trabajaba con una precisión de 6 dígitos, pero la impresión redondeaba las variables a un número de 3 dígitos, por lo que un valor como 0,506127 se imprimía como 0,506. Esta diferencia es minúscula y el consenso en ese momento habría sido que no debería tener ningún efecto práctico. Sin embargo, Lorenz descubrió que pequeños cambios en las condiciones iniciales producían grandes cambios en los resultados a largo plazo. ^[81] El descubrimiento de Lorenz, que dio su nombre a los atractores de Lorenz , mostró que incluso el modelado atmosférico detallado no puede, en general, realizar predicciones meteorológicas precisas a largo plazo.

En 1963, Benoit Mandelbrot , estudiando teoría de la información , descubrió que el ruido en muchos fenómenos (incluidos los precios de las acciones y los circuitos telefónicos ) estaba modelado como un conjunto de Cantor , un conjunto de puntos con rugosidad y detalle infinitos. ^[82] Mandelbrot describió tanto el "efecto Noé" (en el que pueden ocurrir cambios repentinos discontinuos) como el "efecto Joseph" (en el que la persistencia de un valor puede ocurrir por un tiempo, pero cambiar repentinamente después). ^{[83] [84]} En 1967, publicó " ¿Cuánto mide la costa de Gran Bretaña? Autosimilitud estadística y dimensión fraccionaria ", mostrando que la longitud de una costa varía con la escala del instrumento de medición, se parece a sí misma en todas las escalas y es infinita en longitud para un dispositivo de medición infinitesimalmente pequeño. ^[85] Argumentando que una bola de hilo aparece como un punto cuando se la ve desde lejos (0-dimensional), una bola cuando se la ve bastante cerca (3-dimensional), o una hebra curva (unidimensional), argumentó que las dimensiones de un objeto son relativas al observador y pueden ser fraccionarias. Un objeto cuya irregularidad es constante en diferentes escalas ("autosimilitud") es un fractal (los ejemplos incluyen la esponja de Menger , la junta de Sierpiński y la curva o copo de nieve de Koch , que es infinitamente larga pero encierra un espacio finito y tiene una dimensión fractal de alrededor de 1,2619). En 1982, Mandelbrot publicó La geometría fractal de la naturaleza , que se convirtió en un clásico de la teoría del caos. ^[86]

En diciembre de 1977, la Academia de Ciencias de Nueva York organizó el primer simposio sobre el caos, al que asistieron David Ruelle, Robert May , James A. Yorke (creador del término "caos" tal como se usa en matemáticas), Robert Shaw y el meteorólogo Edward Lorenz. Al año siguiente, Pierre Coullet y Charles Tresser publicaron "Itérations d'endomorphismes et groupe de renormalisation", y el artículo de Mitchell Feigenbaum "Quantitative Universality for a Class of Nonlinear Transformations" finalmente apareció en una revista, después de 3 años de rechazos de los árbitros. ^{[87] [88]} Así, Feigenbaum (1975) y Coullet & Tresser (1978) descubrieron la universalidad en el caos, lo que permitió la aplicación de la teoría del caos a muchos fenómenos diferentes.

En 1979, Albert J. Libchaber , durante un simposio organizado en Aspen por Pierre Hohenberg , presentó su observación experimental de la cascada de bifurcación que conduce al caos y la turbulencia en los sistemas de convección de Rayleigh-Bénard . Fue galardonado con el Premio Wolf en Física en 1986 junto con Mitchell J. Feigenbaum por sus inspiradores logros. ^[89]

En 1986, la Academia de Ciencias de Nueva York organizó junto con el Instituto Nacional de Salud Mental y la Oficina de Investigación Naval la primera conferencia importante sobre el caos en biología y medicina. Allí, Bernardo Huberman presentó un modelo matemático de la disfunción del seguimiento ocular entre personas con esquizofrenia . ^[90] Esto condujo a una renovación de la fisiología en la década de 1980 a través de la aplicación de la teoría del caos, por ejemplo, en el estudio de los ciclos cardíacos patológicos .

En 1987, Per Bak , Chao Tang y Kurt Wiesenfeld publicaron un artículo en Physical Review Letters ^[91] describiendo por primera vez la criticidad autoorganizada (SOC), considerada uno de los mecanismos por los cuales surge la complejidad en la naturaleza.

Junto con enfoques basados ​​principalmente en laboratorio, como el estudio de la pila de arena de Bak-Tang-Wiesenfeld , muchas otras investigaciones se han centrado en sistemas naturales o sociales a gran escala que se sabe (o se sospecha) que muestran un comportamiento invariante en la escala . Aunque estos enfoques no siempre fueron bien recibidos (al menos inicialmente) por los especialistas en los temas examinados, el SOC se ha establecido como un fuerte candidato para explicar una serie de fenómenos naturales, incluidos los terremotos (que, mucho antes de que se descubriera el SOC, eran conocidos como una fuente de comportamiento invariante de escala como la ley de Gutenberg-Richter que describe la distribución estadística de los tamaños de los terremotos y la ley de Omori ^[92] que describe la frecuencia de las réplicas), las erupciones solares , las fluctuaciones en los sistemas económicos como los mercados financieros (las referencias al SOC son comunes en la econofísica ), la formación del paisaje, los incendios forestales , los deslizamientos de tierra , las epidemias y la evolución biológica (donde el SOC se ha invocado, por ejemplo, como el mecanismo dinámico detrás de la teoría de los " equilibrios puntuados " propuesta por Niles Eldredge y Stephen Jay Gould ). Dadas las implicaciones de una distribución libre de escala de los tamaños de los eventos, algunos investigadores han sugerido que otro fenómeno que debería considerarse un ejemplo de SOC es la ocurrencia de guerras . Estas investigaciones del SOC han incluido tanto intentos de modelado (ya sea desarrollando nuevos modelos o adaptando los existentes a las particularidades de un sistema natural dado) como análisis de datos exhaustivos para determinar la existencia y/o las características de las leyes de escala natural.

También en 1987 James Gleick publicó Chaos: Making a New Science , que se convirtió en un best-seller e introdujo los principios generales de la teoría del caos así como su historia al público en general. ^[93] Inicialmente dominio de unos pocos individuos aislados, la teoría del caos emergió progresivamente como una disciplina transdisciplinaria e institucional, principalmente bajo el nombre de análisis de sistemas no lineales . Aludiendo al concepto de cambio de paradigma de Thomas Kuhn expuesto en La estructura de las revoluciones científicas (1962), muchos "caólogos" (como algunos se describieron a sí mismos) afirmaron que esta nueva teoría era un ejemplo de tal cambio, una tesis sostenida por Gleick.

La disponibilidad de computadoras más baratas y potentes amplía la aplicabilidad de la teoría del caos. Actualmente, la teoría del caos sigue siendo un área activa de investigación, ^[94] que involucra muchas disciplinas diferentes como matemáticas , topología , física , ^[95] sistemas sociales , ^[96] modelado de población , biología , meteorología , astrofísica , teoría de la información , neurociencia computacional , gestión de crisis pandémicas , ^{[16] [17]} etc.

A lo largo de su carrera, el profesor Edward Lorenz fue autor de un total de 61 artículos de investigación, de los cuales 58 fueron de su exclusiva autoría. ^[97] A partir de la conferencia de 1960 en Japón, Lorenz se embarcó en un viaje de desarrollo de diversos modelos destinados a descubrir el SDIC y las características caóticas. Una revisión reciente de la progresión del modelo de Lorenz ^{[98] [99]} que abarca desde 1960 hasta 2008 reveló su destreza en el empleo de diversos sistemas físicos para ilustrar fenómenos caóticos. Estos sistemas abarcaban sistemas cuasigeostróficos, la ecuación de vorticidad conservativa, las ecuaciones de convección de Rayleigh-Bénard y las ecuaciones de aguas poco profundas. Además, a Lorenz se le puede atribuir la aplicación temprana del mapa logístico para explorar soluciones caóticas, un hito que logró antes que sus colegas (por ejemplo, Lorenz 1964 ^[100] ).

En 1972, Lorenz acuñó el término "efecto mariposa" como metáfora para analizar si una pequeña perturbación podría llegar a crear un tornado con una estructura tridimensional, organizada y coherente. Si bien está relacionado con el efecto mariposa original basado en la dependencia sensible de las condiciones iniciales, su variante metafórica conlleva matices distintivos. Para conmemorar este hito, se publicó oficialmente un libro reimpreso que contiene artículos invitados que profundizan nuestra comprensión de ambos efectos mariposa para celebrar el 50 aniversario del efecto mariposa metafórico. ^[101]

La dependencia sensible de las condiciones iniciales (es decir, el efecto mariposa) se ha ilustrado utilizando el siguiente folclore: ^[93]

Con base en lo anterior, muchas personas creen erróneamente que el impacto de una pequeña perturbación inicial aumenta monótonamente con el tiempo y que cualquier pequeña perturbación puede eventualmente producir un gran impacto en las integraciones numéricas. Sin embargo, en 2008, Lorenz afirmó que no sentía que este verso describiera el verdadero caos sino que ilustraba mejor el fenómeno más simple de la inestabilidad y que el verso sugiere implícitamente que los pequeños eventos posteriores no revertirán el resultado. ^[102] Con base en el análisis, el verso solo indica divergencia, no acotación. ^[6] La acotación es importante para el tamaño finito de un patrón de mariposa. ^{[6] [102] [103]} En un estudio reciente, ^[104] la característica del verso mencionado anteriormente fue denotada recientemente como "dependencia sensible al tiempo finito".

Aunque la teoría del caos nació a partir de la observación de patrones climáticos, se ha vuelto aplicable a una variedad de otras situaciones. Algunas áreas que se benefician de la teoría del caos hoy son la geología , las matemáticas , la biología , la informática , la economía , ^{[106] [107 ] [108]} la ingeniería , ^{[109] [110]} las finanzas , ^{[111] [ 112] [ 113] [114] [115]} la meteorología , la filosofía , la antropología , ^[15] la física , ^{[116] [117] [118]} la política , ^{[119] [120]} la dinámica de poblaciones , ^[121] y la robótica . A continuación se enumeran algunas categorías con ejemplos, pero esta no es de ninguna manera una lista completa ya que están apareciendo nuevas aplicaciones.

La teoría del caos se ha utilizado durante muchos años en criptografía . En las últimas décadas, el caos y la dinámica no lineal se han utilizado en el diseño de cientos de primitivas criptográficas . Estos algoritmos incluyen algoritmos de cifrado de imágenes , funciones hash , generadores de números pseudoaleatorios seguros , cifrados de flujo , marcas de agua y esteganografía . ^[122] La mayoría de estos algoritmos se basan en mapas caóticos unimodales y una gran parte de estos algoritmos utilizan los parámetros de control y la condición inicial de los mapas caóticos como sus claves. ^[123] Desde una perspectiva más amplia, sin pérdida de generalidad, las similitudes entre los mapas caóticos y los sistemas criptográficos son la principal motivación para el diseño de algoritmos criptográficos basados ​​en el caos. ^[122] Un tipo de cifrado, clave secreta o clave simétrica , se basa en la difusión y la confusión , que está bien modelada por la teoría del caos. ^[124] Otro tipo de computación, la computación de ADN , cuando se combina con la teoría del caos, ofrece una forma de cifrar imágenes y otra información. ^[125] Se ha demostrado que muchos de los algoritmos criptográficos de ADN-Caos no son seguros o se sugiere que la técnica aplicada no es eficiente. ^{[126] [127] [128]}

La robótica es otro campo que recientemente se ha beneficiado de la teoría del caos. En lugar de que los robots actúen mediante un proceso de ensayo y error para refinar su interacción con el entorno, se ha utilizado la teoría del caos para construir un modelo predictivo . ^{[129] Los robots bípedos} que caminan de forma pasiva han mostrado dinámicas caóticas . ^[130]

Durante más de cien años, los biólogos han estado haciendo un seguimiento de las poblaciones de diferentes especies con modelos de población . La mayoría de los modelos son continuos , pero recientemente los científicos han podido implementar modelos caóticos en ciertas poblaciones. ^[131] Por ejemplo, un estudio sobre modelos de lince canadiense mostró que había un comportamiento caótico en el crecimiento de la población. ^[132] El caos también se puede encontrar en sistemas ecológicos, como la hidrología . Si bien un modelo caótico para la hidrología tiene sus deficiencias, todavía hay mucho que aprender al observar los datos a través de la lente de la teoría del caos. ^[133] Otra aplicación biológica se encuentra en la cardiotocografía . La vigilancia fetal es un delicado equilibrio entre la obtención de información precisa y la no invasiva posible. Se pueden obtener mejores modelos de señales de advertencia de hipoxia fetal a través del modelado caótico. ^[134]

Como señala Perry, la modelización de series temporales caóticas en ecología se ve facilitada por las restricciones. ^{[135] : 176, 177} Siempre existe una dificultad potencial para distinguir el caos real del caos que solo está en el modelo. ^{[135] : 176, 177} Por lo tanto, tanto la restricción en el modelo como los datos duplicados de series temporales para la comparación serán útiles para restringir el modelo a algo cercano a la realidad, por ejemplo Perry & Wall 1984. ^{[135] : 176, 177} La coevolución gen por gen a veces muestra dinámicas caóticas en las frecuencias de los alelos . ^[136] Agregar variables exagera esto: el caos es más común en modelos que incorporan variables adicionales para reflejar facetas adicionales de poblaciones reales. ^{[136] El propio} Robert M. May realizó algunos de estos estudios fundamentales de coevolución de cultivos, y esto a su vez ayudó a dar forma a todo el campo. ^[136] Incluso en un entorno estable, la simple combinación de un cultivo y un patógeno puede dar lugar a oscilaciones cuasi periódicas o caóticas en la población de patógenos . ^{[137] : 169}

Es posible que los modelos económicos también puedan mejorarse mediante la aplicación de la teoría del caos, pero predecir la salud de un sistema económico y qué factores influyen más en él es una tarea extremadamente compleja. ^[138] Los sistemas económicos y financieros son fundamentalmente diferentes de los de las ciencias naturales clásicas, ya que los primeros son inherentemente estocásticos por naturaleza, ya que resultan de las interacciones de las personas, y por lo tanto es poco probable que los modelos deterministas puros proporcionen representaciones precisas de los datos. La literatura empírica que prueba el caos en economía y finanzas presenta resultados muy mixtos, en parte debido a la confusión entre pruebas específicas para el caos y pruebas más generales para relaciones no lineales. ^[139]

El caos se puede detectar en economía mediante el análisis de cuantificación de recurrencia . De hecho, Orlando et al. ^[140], mediante el llamado índice de correlación de cuantificación de recurrencia, pudieron detectar cambios ocultos en series temporales. Luego, se empleó la misma técnica para detectar transiciones de fases laminares (regulares) a turbulentas (caóticas), así como diferencias entre variables macroeconómicas y resaltar características ocultas de la dinámica económica. ^[141] Finalmente, la teoría del caos podría ayudar a modelar cómo opera una economía, así como a incorporar shocks debido a eventos externos como COVID-19. ^[142]

Debido a la dependencia sensible de las soluciones en las condiciones iniciales (SDIC), también conocida como efecto mariposa, los sistemas caóticos como el modelo de Lorenz de 1963 implican un horizonte de predictibilidad finito. Esto significa que, si bien es posible realizar predicciones precisas durante un período de tiempo finito, no son factibles durante un lapso de tiempo infinito. Considerando la naturaleza de las soluciones caóticas de Lorenz, el comité dirigido por Charney et al. en 1966 ^[143] extrapoló un tiempo de duplicación de cinco días a partir de un modelo de circulación general, lo que sugiere un límite de predictibilidad de dos semanas. Esta conexión entre el tiempo de duplicación de cinco días y el límite de predictibilidad de dos semanas también se registró en un informe de 1969 del Programa de Investigación Atmosférica Global (GARP). ^[144] Para reconocer las influencias directas e indirectas combinadas del modelo de Mintz y Arakawa y los modelos de Lorenz, así como el liderazgo de Charney et al., Shen et al. ^[145] se refieren al límite de predictibilidad de dos semanas como la "Hipótesis del límite de predictibilidad", estableciendo una analogía con la Ley de Moore.

En los modelos de lenguaje grandes impulsados ​​por IA, las respuestas pueden mostrar sensibilidades a factores como alteraciones en el formato y variaciones en las indicaciones. Estas sensibilidades son similares a los efectos mariposa. ^[146] Aunque clasificar los modelos de lenguaje grandes impulsados ​​por IA como sistemas caóticos deterministas clásicos plantea desafíos, se pueden emplear enfoques y técnicas inspirados en el caos (como el modelado de conjuntos) para extraer información confiable de estos modelos de lenguaje expansivos (ver también " Efecto mariposa en la cultura popular ").

En química, predecir la solubilidad de los gases es esencial para la fabricación de polímeros , pero los modelos que utilizan optimización de enjambre de partículas (PSO) tienden a converger en los puntos equivocados. Se ha creado una versión mejorada de PSO introduciendo el caos, que evita que las simulaciones se atasquen. ^[147] En mecánica celeste , especialmente al observar asteroides, la aplicación de la teoría del caos conduce a mejores predicciones sobre cuándo estos objetos se acercarán a la Tierra y otros planetas. ^[148] Cuatro de las cinco lunas de Plutón giran caóticamente. En física cuántica e ingeniería eléctrica , el estudio de grandes conjuntos de uniones Josephson se benefició enormemente de la teoría del caos. ^[149] Más cerca de casa, las minas de carbón siempre han sido lugares peligrosos donde las frecuentes fugas de gas natural causan muchas muertes. Hasta hace poco, no había una forma fiable de predecir cuándo ocurrirían. Pero estas fugas de gas tienen tendencias caóticas que, cuando se modelan adecuadamente, se pueden predecir con bastante precisión. ^[150]

La teoría del caos se puede aplicar fuera de las ciencias naturales, pero históricamente casi todos estos estudios han adolecido de falta de reproducibilidad, validez externa deficiente y/o falta de atención a la validación cruzada, lo que ha dado como resultado una precisión predictiva deficiente (si es que se ha intentado alguna vez predecir fuera de la muestra). Glass ^[151] y Mandell y Selz ^[152] han descubierto que hasta ahora ningún estudio de EEG ha indicado la presencia de atractores extraños u otros signos de comportamiento caótico.

Redington y Reidbord (1992) intentaron demostrar que el corazón humano podía mostrar rasgos caóticos. Monitorearon los cambios en los intervalos entre latidos cardíacos de una sola paciente de psicoterapia a medida que pasaba por períodos de intensidad emocional variable durante una sesión de terapia. Los resultados, sin duda, no fueron concluyentes. No sólo había ambigüedades en los diversos gráficos que los autores produjeron para supuestamente mostrar evidencia de dinámica caótica (análisis espectral, trayectoria de fase y gráficos de autocorrelación), sino que también cuando intentaron calcular un exponente de Lyapunov como confirmación más definitiva del comportamiento caótico, los autores descubrieron que no podían hacerlo de manera confiable. ^[153]

En su artículo de 1995, Metcalf y Allen ^[154] sostuvieron que descubrieron en el comportamiento animal un patrón de duplicación de períodos que conduce al caos. Los autores examinaron una respuesta bien conocida llamada polidipsia inducida por un programa, por la cual un animal privado de alimento durante ciertos períodos de tiempo beberá cantidades inusuales de agua cuando finalmente se le presente el alimento. El parámetro de control (r) que opera aquí fue la duración del intervalo entre las comidas, una vez reanudadas. Los autores fueron cuidadosos al probar una gran cantidad de animales e incluir muchas réplicas, y diseñaron su experimento de modo de descartar la probabilidad de que los cambios en los patrones de respuesta fueran causados ​​por diferentes puntos de partida para r.

Las series temporales y los primeros gráficos de retardo proporcionan el mejor respaldo a las afirmaciones realizadas, mostrando una marcha bastante clara desde la periodicidad a la irregularidad a medida que se incrementaban los tiempos de alimentación. Por otra parte, los diversos gráficos de trayectorias de fase y los análisis espectrales no coinciden lo suficientemente bien con los otros gráficos o con la teoría general como para llevar inexorablemente a un diagnóstico caótico. Por ejemplo, las trayectorias de fase no muestran una progresión definida hacia una complejidad cada vez mayor (y alejándose de la periodicidad); el proceso parece bastante confuso. Además, donde Metcalf y Allen vieron períodos de dos y seis en sus gráficos espectrales, hay espacio para interpretaciones alternativas. Toda esta ambigüedad requiere una explicación serpenteante y post hoc para demostrar que los resultados se ajustan a un modelo caótico.

Al adaptar un modelo de orientación profesional para incluir una interpretación caótica de la relación entre los empleados y el mercado laboral, Amundson y Bright descubrieron que se pueden hacer mejores sugerencias a las personas que tienen dificultades para tomar decisiones profesionales. ^[155] Las organizaciones modernas se consideran cada vez más como sistemas complejos y adaptativos abiertos con estructuras naturales fundamentales no lineales, sujetas a fuerzas internas y externas que pueden contribuir al caos. Por ejemplo, la formación de equipos y el desarrollo de grupos se investigan cada vez más como un sistema inherentemente impredecible, ya que la incertidumbre de que diferentes personas se conozcan por primera vez hace que la trayectoria del equipo sea incognoscible. ^[156]

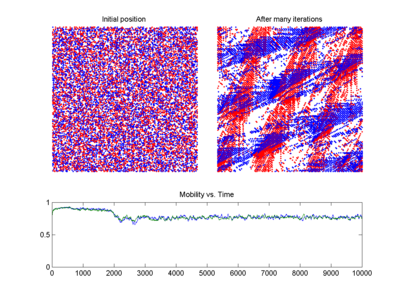
La previsión del tráfico puede beneficiarse de las aplicaciones de la teoría del caos. Unas predicciones más precisas de cuándo se producirá una congestión permitirían tomar medidas para dispersarla antes de que se produzca. La combinación de los principios de la teoría del caos con algunos otros métodos ha dado lugar a un modelo de predicción a corto plazo más preciso (véase el gráfico del modelo de tráfico BML a la derecha). ^[157]

La teoría del caos se ha aplicado a los datos ambientales del ciclo del agua (también a los datos hidrológicos ), como las precipitaciones y el caudal de los ríos. ^[158] Estos estudios han arrojado resultados controvertidos, porque los métodos para detectar una firma caótica suelen ser relativamente subjetivos. Los primeros estudios tendían a "tener éxito" en la detección del caos, mientras que los estudios y metaanálisis posteriores pusieron en tela de juicio esos estudios y proporcionaron explicaciones de por qué es poco probable que estos conjuntos de datos presenten una dinámica caótica de baja dimensión. ^[159]

Ejemplos de sistemas caóticos

Otros temas relacionados

Gente

• Sharkovskii, AN (1964). "Coexistencia de ciclos de una proyección continua de la línea en sí misma". Ukrainian Math. J. 16 : 61–71.
• Li, TY ; Yorke, JA (1975). "Period Three Implies Chaos" (PDF) . American Mathematical Monthly . 82 (10): 985–92. Bibcode :1975AmMM...82..985L. CiteSeerX  10.1.1.329.5038 . doi :10.2307/2318254. JSTOR  2318254. Archivado desde el original (PDF) el 29 de diciembre de 2009 . Consultado el 12 de agosto de 2009 .
• Alemansour, Hamed; Miandoab, Ehsan Maani; Pishkenari, Hossein Nejat (marzo de 2017). "Efecto del tamaño en el comportamiento caótico de los nanoresonadores". Communications in Nonlinear Science and Numerical Simulation . 44 : 495–505. Bibcode :2017CNSNS..44..495A. doi :10.1016/j.cnsns.2016.09.010.
• Crutchfield ; Tucker; Morrison; JD Farmer ; Packard ; NH; Shaw ; RS (diciembre de 1986). "Caos". Scientific American . 255 (6): 38–49 (bibliografía p.136). Código Bibliográfico :1986SciAm.255d..38T. doi :10.1038/scientificamerican1286-46.Versión en línea (Nota: el volumen y la página citados para el texto en línea difieren de los citados aquí. La cita aquí es de una fotocopia, lo que es consistente con otras citas encontradas en línea que no proporcionan vistas del artículo. El contenido en línea es idéntico al texto impreso. Las variaciones de cita están relacionadas con el país de publicación).
• Kolyada, SF (2004). "Sensibilidad de Li-Yorke y otros conceptos del caos". Ukrainian Math. J. 56 ( 8): 1242–57. doi :10.1007/s11253-005-0055-4. S2CID  207251437.
• Day, RH; Pavlov, OV (2004). "Computación del caos económico". Economía computacional . 23 (4): 289–301. arXiv : 2211.02441 . doi :10.1023/B:CSEM.0000026787.81469.1f. S2CID  119972392. SSRN  806124.
• Strelioff, C.; Hübler, A. (2006). "Predicción del caos a medio plazo" (PDF) . Phys. Rev. Lett . 96 (4): 044101. Bibcode :2006PhRvL..96d4101S. doi :10.1103/PhysRevLett.96.044101. PMID  16486826. 044101. Archivado desde el original (PDF) el 2013-04-26.
• Hübler, A.; Foster, G.; Phelps, K. (2007). "Gestión del caos: pensar fuera de la caja" (PDF) . Complexity . 12 (3): 10–13. Bibcode :2007Cmplx..12c..10H. doi :10.1002/cplx.20159. Archivado desde el original (PDF) el 2012-10-30 . Consultado el 2011-07-17 .
• Motter, Adilson E.; Campbell, David K. (2013). "Caos a los 50". Physics Today . 66 (5): 27. arXiv : 1306.5777 . Código Bibliográfico :2013PhT....66e..27M. doi :10.1063/PT.3.1977. S2CID  54005470.

• Alligood, KT; Sauer, T.; Yorke, JA (1997). Caos: una introducción a los sistemas dinámicos. Springer-Verlag. ISBN 978-0-387-94677-1.
• Baker, GL (1996). Caos, dispersión y mecánica estadística . Cambridge University Press. ISBN 978-0-521-39511-3.
• Badii, R.; Politi A. (1997). Complejidad: estructuras jerárquicas y escalamiento en física. Cambridge University Press. ISBN 978-0-521-66385-4.
• Collet, Pierre; Eckmann, Jean-Pierre (1980). Mapas iterados en el intervalo como sistemas dinámicos . Birkhauser. ISBN 978-0-8176-4926-5.
• Devaney, Robert L. (2003). Introducción a los sistemas dinámicos caóticos (2.ª ed.). Westview Press. ISBN 978-0-8133-4085-2.
• Robinson, Clark (1995). Sistemas dinámicos: estabilidad, dinámica simbólica y caos . CRC Press. ISBN 0-8493-8493-1.
• Feldman, DP (2012). Caos y fractales: una introducción elemental. Oxford University Press. ISBN 978-0-19-956644-0Archivado desde el original el 31 de diciembre de 2019. Consultado el 29 de diciembre de 2016 .
• Gollub, JP; Baker, GL (1996). Dinámica caótica. Cambridge University Press. ISBN 978-0-521-47685-0.
• Guckenheimer, John ; Holmes, Philip (1983). Oscilaciones no lineales, sistemas dinámicos y bifurcaciones de campos vectoriales . Springer-Verlag. ISBN 978-0-387-90819-9.
• Gulick, Denny (1992). Encuentros con el caos . McGraw-Hill. ISBN 978-0-07-025203-5.
• Gutzwiller, Martin (1990). Caos en la mecánica clásica y cuántica. Springer-Verlag. ISBN 978-0-387-97173-5.
• Hoover, William Graham (2001) [1999]. Reversibilidad temporal, simulación por ordenador y caos. World Scientific. ISBN 978-981-02-4073-8.
• Kautz, Richard (2011). Caos: la ciencia del movimiento aleatorio predecible. Oxford University Press. ISBN 978-0-19-959458-0.
• Kiel, L. Douglas; Elliott, Euel W. (1997). Teoría del caos en las ciencias sociales. Perseus Publishing. ISBN 978-0-472-08472-2.
• Moon, Francis (1990). Dinámica caótica y fractal. Springer-Verlag. ISBN 978-0-471-54571-2.
• Orlando, Giuseppe; Pisarchick, Alexander; Stoop, Ruedi (2021). No linealidades en economía. Modelado dinámico y econometría en economía y finanzas. Vol. 29. doi :10.1007/978-3-030-70982-2. ISBN 978-3-030-70981-5. Número de identificación del sujeto  239756912.
• Ott, Edward (2002). Caos en sistemas dinámicos. Cambridge University Press. ISBN 978-0-521-01084-9.
• Strogatz, Steven (2000). Dinámica no lineal y caos. Perseus Publishing. ISBN 978-0-7382-0453-6.
• Sprott, Julien Clinton (2003). Caos y análisis de series temporales. Oxford University Press. ISBN 978-0-19-850840-3.
• Tél, Tamás; Gruiz, Márton (2006). Dinámica caótica: una introducción basada en la mecánica clásica. Prensa de la Universidad de Cambridge. ISBN 978-0-521-83912-9.
• Teschl, Gerald (2012). Ecuaciones diferenciales ordinarias y sistemas dinámicos. Providence : American Mathematical Society . ISBN 978-0-8218-8328-0.
• Thompson JM, Stewart HB (2001). Dinámica no lineal y caos . John Wiley and Sons Ltd. ISBN 978-0-471-87645-8.
• Tufillaro; Reilly (1992). Un enfoque experimental de la dinámica no lineal y el caos . American Journal of Physics. Vol. 61. Addison-Wesley. p. 958. Bibcode :1993AmJPh..61..958T. doi :10.1119/1.17380. ISBN 978-0-201-55441-0.
• Wiggins, Stephen (2003). Introducción a los sistemas dinámicos aplicados y al caos . Springer. ISBN 978-0-387-00177-7.
• Zaslavsky, George M. (2005). Caos hamiltoniano y dinámica fraccional . Oxford University Press. ISBN 978-0-19-852604-9.

• Christophe Letellier, Caos en la naturaleza , World Scientific Publishing Company, 2012, ISBN 978-981-4374-42-2 . 
• Abraham, Ralph H.; Ueda, Yoshisuke, eds. (2000). La vanguardia del caos: memorias de los primeros días de la teoría del caos. World Scientific Series on Nonlinear Science Series A. Vol. 39. World Scientific. Bibcode :2000cagm.book.....A. doi :10.1142/4510. ISBN 978-981-238-647-2.
• Barnsley, Michael F. (2000). Fractales por todas partes. Morgan Kaufmann. ISBN 978-0-12-079069-2.
• Bird, Richard J. (2003). Caos y vida: complejidad y orden en la evolución y el pensamiento. Columbia University Press. ISBN 978-0-231-12662-5.
• John Briggs y David Peat, Espejo turbulento: una guía ilustrada de la teoría del caos y la ciencia de la totalidad , Harper Perennial 1990, 224 págs.
• John Briggs y David Peat, Siete lecciones de vida del caos: sabiduría espiritual de la ciencia del cambio , Harper Perennial 2000, 224 págs.
• Cunningham, Lawrence A. (1994). "De los paseos aleatorios a los colapsos caóticos: la genealogía lineal de la hipótesis del mercado de capitales eficiente". George Washington Law Review . 62 : 546.
• Predrag Cvitanović , Universalidad en el caos , Adam Hilger 1989, 648 págs.
• Leon Glass y Michael C. Mackey, De los relojes al caos: los ritmos de la vida, Princeton University Press 1988, 272 pp.
• James Gleick , Caos: Creación de una nueva ciencia , Nueva York: Penguin, 1988. 368 pp.
• John Gribbin. Simplicidad profunda . Penguin Press Science. Penguin Books.
• L Douglas Kiel, Euel W Elliott (ed.), Teoría del caos en las ciencias sociales: fundamentos y aplicaciones , University of Michigan Press, 1997, 360 págs.
• Arvind Kumar, Caos, fractales y autoorganización: nuevas perspectivas sobre la complejidad en la naturaleza , National Book Trust, 2003.
• Hans Lauwerier, Fractales , Princeton University Press, 1991.
• Edward Lorenz , La esencia del caos , University of Washington Press, 1996.
• Marshall, Alan (2002). La unidad de la naturaleza: totalidad y desintegración en la ecología y la ciencia . doi :10.1142/9781860949548. ISBN 9781860949548.
• David Peak y Michael Frame, Caos bajo control: el arte y la ciencia de la complejidad , Freeman, 1994.
• Heinz-Otto Peitgen y Dietmar Saupe (Eds.), La ciencia de las imágenes fractales , Springer 1988, 312 págs.
• Nuria Perpinya , Caos, virus, calma. La Teoría del Caos aplicada al desórden artístico, social y político , Páginas de Espuma, 2021.
• Clifford A. Pickover , Computadoras, patrones, caos y belleza: gráficos de un mundo invisible , St Martins Pr 1991.
• Clifford A. Pickover , Caos en el país de las maravillas: aventuras visuales en un mundo fractal , St Martins Pr 1994.
• Ilya Prigogine e Isabelle Stengers , Orden en el caos , Bantam 1984.
• Peitgen, Heinz-Otto; Richter, Peter H. (1986). La belleza de los fractales . doi :10.1007/978-3-642-61717-1. ISBN 978-3-642-61719-5.
• David Ruelle , Azar y caos , Princeton University Press 1993.
• Ivars Peterson , El reloj de Newton: caos en el sistema solar , Freeman, 1993.
• Ian Roulstone; John Norbury (2013). Invisible en la tormenta: el papel de las matemáticas en la comprensión del clima. Princeton University Press. ISBN 978-0691152721.
• Ruelle, D. (1989). Evolución caótica y atractores extraños . doi :10.1017/CBO9780511608773. ISBN 9780521362726.
• Manfred Schroeder, Fractales, caos y leyes de potencia , Freeman, 1991.
• Smith, Peter (1998). Explicando el caos . doi :10.1017/CBO9780511554544. ISBN 9780511554544.
• Ian Stewart , ¿Dios juega a los dados?: Las matemáticas del caos , Blackwell Publishers, 1990.
• Steven Strogatz , Sync: La ciencia emergente del orden espontáneo , Hyperion, 2003.
• Yoshisuke Ueda, El camino al caos , producción aérea, 1993.
• M. Mitchell Waldrop, Complejidad: la ciencia emergente al borde del orden y el caos , Simon & Schuster, 1992.
• Antonio Sawaya, Análisis de series de tiempo financieras: enfoque de caos y neurodinámica , Lambert, 2012.

Wikimedia Commons tiene medios relacionados con Teoría del caos .

• "Caos", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• Grupo de Investigación en Dinámica No Lineal con Animaciones en Flash
• El grupo Caos de la Universidad de Maryland
• El hipertexto del caos. Una introducción al caos y los fractales
• ChaosBook.org Un libro de texto avanzado de posgrado sobre el caos (sin fractales)
• Sociedad para la teoría del caos en psicología y ciencias de la vida
• Grupo de investigación en dinámica no lineal en el CSDC, Florencia , Italia
• Dinámica no lineal: cómo la ciencia comprende el caos, charla presentada por Sunny Auyang, 1998.
• Dinámica no lineal. Modelos de bifurcación y caos por Elmer G. Wiens
• El caos de Gleick (fragmento) Archivado el 2 de febrero de 2007 en Wayback Machine.
• Grupo de Análisis, Modelado y Predicción de Sistemas de la Universidad de Oxford
• Una página sobre la ecuación de Mackey-Glass
• Ansiedad extrema: las matemáticas del caos (2008) Documental de la BBC dirigido por David Malone
• La teoría del caos de la evolución: artículo publicado en Newscientist que presenta similitudes entre la evolución y los sistemas no lineales, incluida la naturaleza fractal de la vida y el caos.
• Jos Leys, Étienne Ghys y Aurélien Alvarez, Chaos, A Mathematical Adventure. Nueve películas sobre sistemas dinámicos, el efecto mariposa y la teoría del caos, destinadas a un público amplio.
• "Chaos Theory", charla en BBC Radio 4 con Susan Greenfield, David Papineau y Neil Johnson ( In Our Time , 16 de mayo de 2002)
• Caos: La ciencia del efecto mariposa (2019) una explicación presentada por Derek Muller

•  Este artículo incorpora texto de una obra de contenido libre . Licencia CC-BY (declaración de licencia/permiso). Texto tomado de Three Kinds of Butterfly Effects within Lorenz Models​, Bo-Wen Shen, Roger A. Pielke, Sr., Xubin Zeng, Jialin Cui, Sara Faghih-Naini, Wei Paxson y Robert Atlas, MDPI. Enciclopedia.