Constante de disociación ácida

Ácidos y bases
Número de aceptor Ácido Reacción ácido-base Homeostasis ácido-base Fuerza del ácido Función de acidez Anfoterismo Base Soluciones tampón Constante de disociación Número de donante Química del equilibrio Extracción Función de acidez de Hammett pH Afinidad de protones Autoionización del agua Valoración Catálisis ácida de Lewis Pareja de Lewis frustrada Ácido de Lewis quiral Modelo ECW
Tipos de ácidos
Brønsted–Lowry Ametralladora Mineral Orgánico Óxido Fuerte Superácidos Débil Sólido
Tipos de base
Brønsted–Lowry Ametralladora Orgánico Óxido Fuerte Superbases No nucleofílico Débil
en a mi

En química , una constante de disociación ácida (también conocida como constante de acidez o constante de ionización ácida ; denotada como )${\displaystyle K_{a}}$ es una medida cuantitativa de la fuerza de un ácido en solución . Es la constante de equilibrio de una reacción química .

${\displaystyle {\ce {HA <=> A^- + H^+}}}$

conocido como disociación en el contexto de las reacciones ácido-base . La especie química HA es un ácido que se disocia en A ⁻ , llamada la base conjugada del ácido, y un ion hidrógeno , H ⁺ . ^[a] Se dice que el sistema está en equilibrio cuando las concentraciones de sus componentes no cambian con el tiempo, porque las reacciones tanto hacia adelante como hacia atrás ocurren al mismo ritmo. ^[1]

La constante de disociación se define por ^[b]

${\displaystyle K_{\text{a}}=\mathrm {\frac {[A^{-}][H^{+}]}{[HA]}} ,}$o por su forma logarítmica

${\displaystyle \mathrm {p} K_{{\ce {a}}}=-\log _{10}K_{\text{a}}=\log _{10}{\frac {{\ce {[HA]}}}{[{\ce {A^-}}][{\ce {H+}}]}}}$

donde las cantidades entre corchetes representan las concentraciones molares de las especies en equilibrio. ^{[c] [2]} Por ejemplo, un ácido débil hipotético que tiene K _a  = 10 ⁻⁵ , el valor de log K _a es el exponente (−5), dando p K _a  = 5. Para el ácido acético , K _a  = 1,8 x 10 ⁻⁵ , por lo que p K _a es aproximadamente 5. Un K _a más alto corresponde a un ácido más fuerte (un ácido que está más disociado en el equilibrio). La forma p K _a se utiliza a menudo porque proporciona una escala logarítmica conveniente , donde un p K _a más bajo corresponde a un ácido más fuerte.

La constante de disociación de un ácido es una consecuencia directa de la termodinámica subyacente de la reacción de disociación; el valor de p K _a es directamente proporcional al cambio de energía libre de Gibbs estándar para la reacción. El valor de p K _a cambia con la temperatura y se puede entender cualitativamente con base en el principio de Le Châtelier : cuando la reacción es endotérmica , K _a aumenta y p K _a disminuye con el aumento de la temperatura; lo opuesto es cierto para las reacciones exotérmicas .

El valor de p K _a también depende de la estructura molecular del ácido de muchas maneras. Por ejemplo, Pauling propuso dos reglas: una para los sucesivos p K _a de los ácidos polipróticos (ver Ácidos polipróticos a continuación) y otra para estimar el p K _a de los oxiácidos basándose en el número de grupos =O y −OH (ver Factores que afectan los valores de pKa a continuación). Otros factores estructurales que influyen en la magnitud de la constante de disociación del ácido incluyen los efectos inductivos , los efectos mesoméricos y los enlaces de hidrógeno . Las ecuaciones de tipo Hammett se han aplicado con frecuencia a la estimación de p K _a . ^{[3] [4]}

El comportamiento cuantitativo de los ácidos y bases en solución sólo puede entenderse si se conocen sus valores p K _a . En particular, el pH de una solución puede predecirse cuando se conocen la concentración analítica y los valores p K _a de todos los ácidos y bases; a la inversa, es posible calcular la concentración de equilibrio de los ácidos y bases en solución cuando se conoce el pH. Estos cálculos encuentran aplicación en muchas áreas diferentes de la química, la biología, la medicina y la geología. Por ejemplo, muchos compuestos utilizados para la medicación son ácidos o bases débiles, y el conocimiento de los valores p K _a , junto con el coeficiente de partición octanol-agua , puede utilizarse para estimar el grado en que el compuesto entra en el torrente sanguíneo. Las constantes de disociación ácida también son esenciales en la química acuática y la oceanografía química , donde la acidez del agua juega un papel fundamental. En los organismos vivos, la homeostasis ácido-base y la cinética enzimática dependen de los valores p K _a de los muchos ácidos y bases presentes en la célula y en el cuerpo. En química, el conocimiento de los valores de p K _a es necesario para la preparación de soluciones tampón y también es un prerrequisito para una comprensión cuantitativa de la interacción entre ácidos o bases e iones metálicos para formar complejos . Experimentalmente, los valores de p K _a se pueden determinar mediante titulación potenciométrica (pH) , pero para valores de p K _a menores de aproximadamente 2 o mayores de aproximadamente 11, pueden requerirse mediciones espectrofotométricas o de RMN debido a dificultades prácticas con las mediciones de pH.

Según la definición molecular original de Arrhenius , un ácido es una sustancia que se disocia en solución acuosa, liberando el ion hidrógeno H ⁺ (un protón): ^[5]

${\displaystyle {\ce {HA <=> A- + H+}}}$

La constante de equilibrio para esta reacción de disociación se conoce como constante de disociación . El protón liberado se combina con una molécula de agua para dar un ion hidronio (u oxonio) H ₃ O ⁺ (los protones desnudos no existen en solución), por lo que Arrhenius propuso posteriormente que la disociación debería escribirse como una reacción ácido-base :

${\displaystyle {\ce {HA + H2O <=> A- + H3O+}}}$

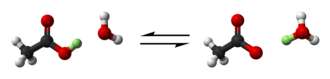
Brønsted y Lowry generalizaron esto a una reacción de intercambio de protones: ^{[6] [7] [8]}

${\displaystyle {\text{acid}}+{\text{base }}{\ce {<=>}}{\text{ conjugate base}}+{\text{conjugate acid}}}$

El ácido pierde un protón, dejando una base conjugada; el protón se transfiere a la base, creando un ácido conjugado. Para soluciones acuosas de un ácido HA, la base es agua; la base conjugada es A ⁻ y el ácido conjugado es el ion hidronio. La definición de Brønsted–Lowry se aplica a otros solventes, como el dimetilsulfóxido : el solvente S actúa como una base, aceptando un protón y formando el ácido conjugado SH ⁺ .

${\displaystyle {\ce {HA + S <=> A- + SH+}}}$

En la química de soluciones, es común utilizar H ⁺ como abreviatura del ion hidrógeno solvatado, independientemente del solvente. En solución acuosa, H ⁺ denota un ion hidronio solvatado en lugar de un protón. ^{[9] [10]}

La designación de un ácido o una base como "conjugado" depende del contexto. El ácido conjugado BH ⁺ de una base B se disocia según

${\displaystyle {\ce {BH+ + OH- <=> B + H2O}}}$

que es el reverso del equilibrio

${\displaystyle {\ce {H2O}}{\text{ (acid)}}+{\ce {B}}{\text{ (base) }}{\ce {<=> OH-}}{\text{ (conjugate base)}}+{\ce {BH+}}{\text{ (conjugate acid)}}}$

El ion hidróxido OH ⁻ , una base bien conocida, actúa aquí como base conjugada del agua ácida. Por lo tanto, los ácidos y las bases se consideran simplemente como donantes y aceptores de protones respectivamente.

Una definición más amplia de disociación ácida incluye la hidrólisis , en la que se producen protones mediante la división de las moléculas de agua. Por ejemplo, _el ácido bórico ( B(OH) ₃ ) produce H3O ⁺ como si fuera un donador de protones, [ ^11] pero se ha confirmado mediante espectroscopia Raman que esto se debe al equilibrio de hidrólisis: ^[12]

${\displaystyle {\ce {B(OH)3 + 2 H2O <=> B(OH)4- + H3O+}}}$

De manera similar, la hidrólisis de iones metálicos hace que iones como [Al(H ₂ O) ₆ ] ³⁺ se comporten como ácidos débiles: ^[13]

${\displaystyle {\ce {[Al(H2O)6]^3+ + H2O <=> [Al(H2O)5(OH)]^2+ + H3O+}}}$

Según la definición original de Lewis , un ácido es una sustancia que acepta un par de electrones para formar un enlace covalente coordinado . ^[14]

Una constante de disociación ácida es un ejemplo particular de una constante de equilibrio . La disociación de un ácido monoprótico , HA, en solución diluida se puede escribir como

${\displaystyle {\ce {HA <=> A- + H+}}}$

La constante de equilibrio termodinámico se${\displaystyle K^{\ominus }}$ puede definir mediante ^[15 ]

${\displaystyle K^{\ominus }={\frac {\{{\ce {A^-}}\}\{{\ce {H+}}\}}{{\ce {\{HA\}}}}}}$

donde representa la actividad , en equilibrio, de la especie química X. es adimensional ya que la actividad es adimensional. Las actividades de los productos de disociación se colocan en el numerador, las actividades de los reactivos se colocan en el denominador. Véase el coeficiente de actividad para una derivación de esta expresión.${\displaystyle \{X\}}$${\displaystyle K^{\ominus }}$

Dado que la actividad es el producto de la concentración y el coeficiente de actividad ( γ ), la definición también podría escribirse como

${\displaystyle K^{\ominus }={{\frac {[{\ce {A^-}}][{\ce {H+}}]}{{\ce {[HA]}}}}\Gamma },\quad \Gamma ={\frac {\gamma _{{\ce {A^-}}}\ \gamma _{{\ce {H+}}}}{\gamma _{{\ce {HA}}}\ }}}$

donde representa la concentración de HA y ⁠ ⁠ es un cociente de coeficientes de actividad.${\displaystyle [{\text{HA}}]}$${\displaystyle \Gamma }$

Para evitar las complicaciones que implica el uso de actividades, las constantes de disociación se determinan , cuando es posible, en un medio de alta fuerza iónica , es decir, en condiciones en las que se puede suponer que ⁠ ⁠${\displaystyle \Gamma }$ es siempre constante. ^[15] Por ejemplo, el medio podría ser una solución de  nitrato de sodio 0,1 molar (M) o perclorato de potasio 3 M. Con esta suposición,

${\displaystyle K_{\text{a}}={\frac {K^{\ominus }}{\Gamma }}=\mathrm {\frac {[A^{-}][H^{+}]}{[HA]}} }$

${\displaystyle \mathrm {p} K_{{\ce {a}}}=-\log _{10}{\frac {[{\ce {A^-}}][{\ce {H^+}}]}{[{\ce {HA}}]}}=\log _{10}{\frac {{\ce {[HA]}}}{[{\ce {A^-}}][{\ce {H+}}]}}}$

Se obtiene. Sin embargo, es importante tener en cuenta que todos los valores de constante de disociación publicados se refieren al medio iónico específico utilizado en su determinación y que se obtienen valores diferentes con diferentes condiciones, como se muestra para el ácido acético en la ilustración anterior. Cuando las constantes publicadas se refieren a una fuerza iónica distinta de la requerida para una aplicación particular, se pueden ajustar mediante la teoría de iones específicos (SIT) y otras teorías. ^[16]

Una constante de equilibrio acumulativa, denotada por ⁠ ⁠${\displaystyle \mathrm {\beta } ,}$ está relacionada con el producto de constantes escalonadas, denotadas por ⁠ ⁠${\displaystyle \mathrm {K} .}$ Para un ácido dibásico, la relación entre las constantes escalonadas y las constantes generales es la siguiente

${\displaystyle {\ce {H2A <=> A^2- + 2H+}}}$

${\displaystyle \beta _{2}={\frac {{\ce {[H2A]}}}{[{\ce {A^2-}}][{\ce {H+}}]^{2}}}}$

${\displaystyle \log \beta _{2}=\mathrm {p} K_{{\ce {a1}}}+\mathrm {p} K_{{\ce {a2}}}}$

Obsérvese que en el contexto de la formación de complejos metal-ligando, las constantes de equilibrio para la formación de complejos metálicos se definen habitualmente como constantes de asociación . En ese caso, las constantes de equilibrio para la protonación del ligando también se definen como constantes de asociación. La numeración de las constantes de asociación es inversa a la numeración de las constantes de disociación; en este ejemplo${\displaystyle \log \beta _{1}=\mathrm {p} K_{{\ce {a2}}}}$

Cuando se discuten las propiedades de los ácidos, es habitual especificar las constantes de equilibrio como constantes de disociación ácida, denotadas por K _a , con valores numéricos dados por el símbolo p K _a .

${\displaystyle K_{\text{dissoc}}={\frac {{\ce {[A- ][H+]}}}{{\ce {[HA]}}}}:\mathrm {p} K_{\text{a}}=-\log K_{\text{dissoc}}}$

Por otro lado, se utilizan constantes de asociación para las bases.

${\displaystyle K_{\text{assoc}}={\frac {{\ce {[HA]}}}{{\ce {[A- ][H+]}}}}}$

Sin embargo, los programas informáticos de uso general que se utilizan para derivar valores de constantes de equilibrio a partir de datos experimentales utilizan constantes de asociación tanto para ácidos como para bases. Debido a que las constantes de estabilidad para un complejo metal-ligando siempre se especifican como constantes de asociación, la protonación del ligando también debe especificarse como una reacción de asociación. ^[17] Las definiciones muestran que el valor de una constante de disociación de un ácido es el recíproco del valor de la constante de asociación correspondiente:

${\displaystyle K_{\text{dissoc}}={\frac {1}{K_{\text{assoc}}}}}$

${\displaystyle \log K_{\text{dissoc}}=-\log K_{\text{assoc}}}$

${\displaystyle \mathrm {p} K_{\text{dissoc}}=-\mathrm {p} K_{\text{assoc}}}$

Notas

1. Para un ácido o base dado en agua, p K _a + p K _b = p K _w , la constante de autoionización del agua .
2. La constante de asociación para la formación de un complejo supramolecular puede denotarse como K _a ; en tales casos, "a" representa "asociación", no "ácido".
3. En el caso de los ácidos polipróticos, la numeración de las constantes de asociación escalonada es inversa a la numeración de las constantes de disociación. Por ejemplo, en el caso del ácido fosfórico (los detalles se encuentran en la sección de ácidos polipróticos que aparece a continuación):

${\displaystyle {\begin{aligned}\log K_{{\text{assoc}},1}&=\mathrm {p} K_{{\text{dissoc}},3}\\\log K_{{\text{assoc}},2}&=\mathrm {p} K_{{\text{dissoc}},2}\\\log K_{{\text{assoc}},3}&=\mathrm {p} K_{{\text{dissoc}},1}\end{aligned}}}$

Todas las constantes de equilibrio varían con la temperatura según la ecuación de van 't Hoff ^[18]

${\displaystyle {\frac {\mathrm {d} \ln \left(K\right)}{\mathrm {d} T}}={\frac {\Delta H^{\ominus }}{RT^{2}}}}$

⁠ ⁠${\displaystyle R}$ es la constante de los gases y ⁠ ⁠${\displaystyle T}$ es la temperatura absoluta . Por lo tanto, para las reacciones exotérmicas , el cambio de entalpía estándar , ⁠ ⁠${\displaystyle \Delta H^{\ominus }}$ , es negativo y K disminuye con la temperatura. Para las reacciones endotérmicas , ⁠ ⁠${\displaystyle \Delta H^{\ominus }}$ es positivo y K aumenta con la temperatura.

El cambio de entalpía estándar para una reacción es en sí mismo una función de la temperatura, según la ley de termoquímica de Kirchhoff :

${\displaystyle \left({\frac {\partial \Delta H}{\partial T}}\right)_{p}=\Delta C_{p}}$

donde ⁠ ⁠${\displaystyle \Delta C_{p}}$ es el cambio de capacidad térmica a presión constante. En la práctica ⁠ ⁠${\displaystyle \Delta H^{\ominus }}$ puede considerarse constante en un rango pequeño de temperaturas.

En la ecuación

${\displaystyle K_{\mathrm {a} }=\mathrm {\frac {[A^{-}][H^{+}]}{[HA]}} ,}$

K _a parece tener dimensiones de concentración. Sin embargo, como , la constante de equilibrio, ⁠ ⁠ , no puede tener una dimensión física. Esta aparente paradoja se puede resolver de varias maneras. ${\displaystyle \Delta G=-RT\ln K}$${\displaystyle K}$

1. Supongamos que el cociente de coeficientes de actividad tiene un valor numérico de 1, de modo que ⁠ ⁠${\displaystyle K}$ tiene el mismo valor numérico que la constante de equilibrio termodinámico .${\displaystyle K^{\ominus }}$
2. Expresar cada valor de concentración como la relación c/c ⁰ , donde c ⁰ es la concentración en un estado estándar [hipotético], con un valor numérico de 1, por definición. ^[19]
3. Expresar las concentraciones en la escala de fracción molar . Como la fracción molar no tiene dimensión, el cociente de concentraciones será, por definición, un número puro.

Los procedimientos (1) y (2) dan valores numéricos idénticos para una constante de equilibrio. Además, dado que una concentración es simplemente proporcional${\displaystyle c_{i}}$ a la fracción molar y${\displaystyle x_{i}}$ la densidad :${\displaystyle \rho }$

${\displaystyle c_{i}={\frac {x_{i}\rho }{M}}}$

y dado que la masa molar es una constante${\displaystyle M}$ en soluciones diluidas, un valor constante de equilibrio determinado usando (3) será simplemente proporcional a los valores obtenidos con (1) y (2).

Es una práctica común en bioquímica citar un valor con una dimensión como, por ejemplo, " K _a = 30 mM" para indicar la escala, milimolar (mM) o micromolar (μM) de los valores de concentración utilizados para su cálculo.

Un ácido se clasifica como "fuerte" cuando la concentración de sus especies no disociadas es demasiado baja para ser medida. ^{[6] Cualquier ácido acuoso con} _un valor de p K a menor que 0 está casi completamente desprotonado y se considera un ácido fuerte . ^[20] Todos estos ácidos transfieren sus protones al agua y forman la especie catiónica del disolvente (H ₃ O ⁺ en solución acuosa) de modo que todos tienen esencialmente la misma acidez, un fenómeno conocido como nivelación del disolvente . ^{[21] [22]} Se dice que están completamente disociados en solución acuosa porque la cantidad de ácido no disociado, en equilibrio con los productos de disociación, está por debajo del límite de detección . Del mismo modo, cualquier base acuosa con una constante de asociación p K _b menor que aproximadamente 0, correspondiente a p K _a mayor que aproximadamente 14, se nivela a OH ⁻ y se considera una base fuerte . ^[22]

El ácido nítrico , con un valor p K de alrededor de −1,7, se comporta como un ácido fuerte en soluciones acuosas con un pH mayor que 1. ^[23] A valores de pH más bajos se comporta como un ácido débil.

Los valores de p K _a para ácidos fuertes se han estimado por medios teóricos. ^[24] Por ejemplo, el valor de p K _{a del} HCl acuoso se ha estimado en −9,3.

Después de reordenar la expresión que define K _a , y poner pH = −log ₁₀ [H ⁺ ] , se obtiene ^[25]

${\displaystyle \mathrm {pH} =\mathrm {p} K_{\text{a}}+\log \mathrm {\frac {[A^{-}]}{[HA]}} }$

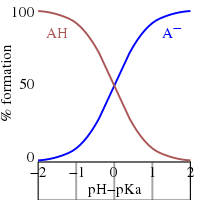
Esta es la ecuación de Henderson-Hasselbalch , de la que se pueden extraer las siguientes conclusiones.

• En la semineutralización la relación[Un ⁻ ]/[JA]⁠ = 1 ; dado que log(1) = 0 , el pH en la semineutralización es numéricamente igual a p K _a . Por el contrario, cuando pH = p K _a , la concentración de HA es igual a la concentración de A ⁻ .
• La región tampón se extiende sobre el rango aproximado p K _a  ± 2. El tamponamiento es débil fuera del rango p K _a  ± 1. A pH ≤ p K _a − 2 se dice que la sustancia está completamente protonada y a pH ≥ p K _a + 2 está completamente disociada (desprotonada).
• Si se conoce el pH, se puede calcular la relación, que es independiente de la concentración analítica del ácido.

En el agua, los valores de p K a mensurables _varían desde aproximadamente -2 para un ácido fuerte hasta aproximadamente 12 para un ácido muy débil (o base fuerte).

Se puede preparar una solución tampón de un pH deseado como una mezcla de un ácido débil y su base conjugada. En la práctica, la mezcla se puede crear disolviendo el ácido en agua y agregando la cantidad necesaria de ácido o base fuerte. Cuando se conocen el p K _a y la concentración analítica del ácido, el grado de disociación y el pH de una solución de un ácido monoprótico se pueden calcular fácilmente utilizando una tabla ICE .

Un ácido poliprótico es un compuesto que puede perder más de un protón. Las constantes de disociación escalonada se definen para la pérdida de un solo protón. La constante para la disociación del primer protón se puede denotar como K _a1 y las constantes para la disociación de protones sucesivos como K _a2 , etc. El ácido fosfórico , H ₃ PO ₄ , es un ejemplo de ácido poliprótico, ya que puede perder tres protones.

Equilibrio	p K definición y valor [26]
${\displaystyle {\ce {H3PO4 <=> H2PO4- + H+}}}$	${\displaystyle \mathrm {p} K_{{\ce {a1}}}=\log _{10}{\frac {[{\ce {H_3PO_4}}]}{[{\ce {H_2PO_4^{-}}}][{\ce {H^+}}]}}=2.14}$
${\displaystyle {\ce {H2PO4- <=> HPO4^2- + H+}}}$	${\displaystyle \mathrm {p} K_{{\ce {a2}}}=\log _{10}{\frac {[{\ce {H_2PO_4^{-}}}]}{[{\ce {HPO_4^{2-}}}][{\ce {H^+}}]}}=7.2}$
${\displaystyle {\ce {HPO4^2- <=> PO4^3- + H+}}}$	${\displaystyle \mathrm {p} K_{{\ce {a3}}}=\log _{10}{\frac {[{\ce {HPO4^2-}}]}{[{\ce {PO4^3-}}][{\ce {H+}}]}}=12.37}$

Cuando la diferencia entre valores p K sucesivos es de aproximadamente cuatro o más, como en este ejemplo, cada especie puede considerarse un ácido por derecho propio; ^[27] De hecho, las sales de H
₂correos⁻
₄Puede cristalizarse a partir de una solución ajustando el pH a aproximadamente 5,5 y sales de HPO2−4Puede cristalizarse a partir de una solución ajustando el pH a aproximadamente 10. El diagrama de distribución de especies muestra que las concentraciones de los dos iones son máximas a pH 5,5 y 10.

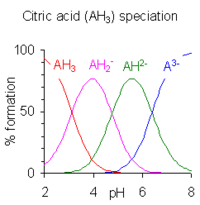
Cuando la diferencia entre valores de p K sucesivos es menor que aproximadamente cuatro, existe una superposición entre el rango de pH de existencia de las especies en equilibrio. Cuanto menor sea la diferencia, mayor será la superposición. El caso del ácido cítrico se muestra a la derecha; las soluciones de ácido cítrico se tamponan en todo el rango de pH de 2,5 a 7,5.

Según la primera regla de Pauling, los valores p K sucesivos de un ácido dado aumentan (p K _a2 > p K _a1 ) . ^[28] Para los oxiácidos con más de un hidrógeno ionizable en el mismo átomo, los valores p K _{a a} menudo aumentan alrededor de 5 unidades por cada protón eliminado, ^{[29] [30]} como en el ejemplo del ácido fosfórico mencionado anteriormente.

En la tabla anterior se puede observar que el segundo protón se elimina de una especie con carga negativa. Como el protón lleva una carga positiva, se necesita trabajo adicional para eliminarlo, por lo que p K _a2 es mayor que p K _a1 . p K _a3 es mayor que p K _a2 porque hay una mayor separación de cargas. Cuando se encuentra una excepción a la regla de Pauling, indica que también se está produciendo un cambio importante en la estructura. En el caso de VO+2(aq), el vanadio es octaédrico , de 6 coordenadas, mientras que el ácido vanádico es tetraédrico , de 4 coordenadas. Esto significa que se liberan cuatro "partículas" con la primera disociación, pero solo dos "partículas" con las otras disociaciones, lo que da como resultado una contribución de entropía mucho mayor al cambio de energía libre de Gibbs estándar para la primera reacción que para las otras.

Equilibrio	pK a​
${\displaystyle {\ce {[VO2(H2O)4]+ <=> H3VO4 + H+ + 2H2O}}}$	${\displaystyle \mathrm {p} K_{a_{1}}=4.2}$
${\displaystyle {\ce {H3VO4 <=> H2VO4- + H+}}}$	${\displaystyle \mathrm {p} K_{a_{2}}=2.60}$
${\displaystyle {\ce {H2VO4- <=> HVO4^2- + H+}}}$	${\displaystyle \mathrm {p} K_{a_{3}}=7.92}$
${\displaystyle {\ce {HVO4^2- <=> VO4^3- + H+}}}$	${\displaystyle \mathrm {p} K_{a_{4}}=13.27}$

Para las sustancias en solución, el punto isoeléctrico (p I ) se define como el pH en el que la suma, ponderada por el valor de la carga, de las concentraciones de las especies con carga positiva es igual a la suma ponderada de las concentraciones de las especies con carga negativa. En el caso de que haya una especie de cada tipo, el punto isoeléctrico se puede obtener directamente de los valores p K . Tomemos el ejemplo de la glicina , definida como AH. Hay dos equilibrios de disociación a considerar.

${\displaystyle {\ce {AH2+<=>AH~+H+\qquad [AH][H+]={\mathit {K}}_{1}[AH2+]}}}$

${\displaystyle {\ce {AH<=>A^{-}~+H+\qquad [A^{-}][H+]={\mathit {K}}_{2}[AH]}}}$

Sustituya la expresión para [AH] de la segunda ecuación en la primera ecuación.

${\displaystyle {\ce {[A^{-}][H+]^{2}={\mathit {K}}_{1}{\mathit {K}}_{2}[AH2+]}}}$

En el punto isoeléctrico la concentración de las especies cargadas positivamente, AH+2, es igual a la concentración de la especie cargada negativamente, A ⁻ , por lo que

${\displaystyle [{\ce {H+}}]^{2}=K_{1}K_{2}}$

Por lo tanto, tomando cologaritmos , el pH viene dado por

${\displaystyle \mathrm {p} I={\frac {\mathrm {p} K_{1}+\mathrm {p} K_{2}}{2}}}$

Los valores de p I de los aminoácidos se enumeran en aminoácido proteinogénico . Cuando más de dos especies cargadas están en equilibrio entre sí, puede ser necesario un cálculo de especiación completo.

La constante de equilibrio K _b para una base se define generalmente como la constante de asociación para la protonación de la base, B, para formar el ácido conjugado, HB ⁺ .

${\displaystyle {\ce {B + H2O <=> HB+ + OH-}}}$

Utilizando un razonamiento similar al utilizado anteriormente

${\displaystyle {\begin{aligned}K_{\text{b}}&=\mathrm {\frac {[HB^{+}][OH^{-}]}{[B]}} \\\mathrm {p} K_{\text{b}}&=-\log _{10}\left(K_{\text{b}}\right)\end{aligned}}}$

K _b está relacionado con K _a para el ácido conjugado. En el agua, la concentración del ion hidróxido , [OH ⁻ ] , está relacionada con la concentración del ion hidrógeno por K _w = [H ⁺ ][OH ⁻ ] , por lo tanto

${\displaystyle \mathrm {[OH^{-}]} ={\frac {K_{\mathrm {w} }}{\mathrm {[H^{+}]} }}}$

Sustituyendo la expresión para [OH ⁻ ] en la expresión para K _b se obtiene

${\displaystyle K_{\text{b}}={\frac {[\mathrm {HB^{+}} ]K_{\text{w}}}{\mathrm {[B][H^{+}]} }}={\frac {K_{\text{w}}}{K_{\text{a}}}}}$

Cuando se determinan K _a , K _b y K _{w en las mismas condiciones de temperatura y fuerza iónica, se deduce, tomando} cologaritmos , que p K _b  = p K _w  − p K _a . En soluciones acuosas a 25 °C, p K _w es 13,9965, ^[31] por lo que

${\displaystyle \mathrm {p} K_{\text{b}}\approx 14-\mathrm {p} K_{\text{a}}}$

con suficiente precisión para la mayoría de los propósitos prácticos. En efecto, no hay necesidad de definir p K _b por separado de p K _a , ^[32] pero se hace aquí ya que a menudo solo se pueden encontrar valores de p K _b en la literatura más antigua.

Para un ion metálico hidrolizado, K _b también se puede definir como una constante de disociación escalonada.

${\displaystyle \mathrm {M} _{p}({\ce {OH}})_{q}\leftrightharpoons \mathrm {M} _{p}({\ce {OH}})_{q-1}^{+}+{\ce {OH-}}}$

${\displaystyle K_{\mathrm {b} }={\frac {[\mathrm {M} _{p}({\ce {OH}})_{q-1}^{+}][{\ce {OH-}}]}{[\mathrm {M} _{p}({\ce {OH}})_{q}]}}}$

Este es el recíproco de una constante de asociación para la formación del complejo.

Debido a que la relación p K _b  = p K _w  − p K _a se cumple solo en soluciones acuosas (aunque se aplican relaciones análogas para otros solventes anfóteros), las subdisciplinas de la química como la química orgánica que generalmente tratan con soluciones no acuosas generalmente no usan p K _b como una medida de basicidad. En cambio, se cita el p K _a del ácido conjugado, denotado por p K _aH , cuando se necesita cuantificar la basicidad. Para la base B y su ácido conjugado BH ⁺ en equilibrio, esto se define como

${\displaystyle \mathrm {p} K_{\mathrm {aH} }(\mathrm {B} )=\mathrm {p} K_{\mathrm {a} }({\ce {BH+}})=-\log _{10}{\Big (}{\frac {[{\ce {B}}][{\ce {H+}}]}{[{\ce {BH+}}]}}{\Big )}}$

Un valor más alto de p K _aH corresponde a una base más fuerte. Por ejemplo, los valores p K _aH (C ₅ H ₅ N) = 5,25 y p K _aH ((CH ₃ CH ₂ ) ₃ N) = 10,75 indican que (CH ₃ CH ₂ ) ₃ N (trietilamina) es una base más fuerte que C ₅ H ₅ N (piridina).

Una sustancia anfótera es aquella que puede actuar como ácido o como base, dependiendo del pH. El agua (abajo) es anfótera. Otro ejemplo de molécula anfótera es el ion bicarbonato HCO−3Esa es la base conjugada de la molécula de ácido carbónico H2CO3 en el equilibrio.

${\displaystyle {\ce {H2CO3 + H2O <=> HCO3- + H3O+}}}$

pero también el ácido conjugado del ion carbonato CO2−3en (el reverso del) equilibrio

${\displaystyle {\ce {HCO3- + OH- <=> CO3^2- + H2O}}}$

Los equilibrios del ácido carbónico son importantes para la homeostasis ácido-base en el cuerpo humano.

Un aminoácido también es anfótero con la complicación añadida de que la molécula neutra está sujeta a un equilibrio ácido-base interno en el que el grupo amino básico atrae y une el protón del grupo carboxilo ácido, formando un zwitterión .

${\displaystyle {\ce {NH2CHRCO2H <=> NH3+CHRCO2-}}}$

A un pH inferior a aproximadamente 5, tanto el grupo carboxilato como el grupo amino están protonados. A medida que aumenta el pH, el ácido se disocia de acuerdo con

${\displaystyle {\ce {NH3+CHRCO2H <=> NH3+CHRCO2- + H+}}}$

A un pH alto puede producirse una segunda disociación.

${\displaystyle {\ce {NH3+CHRCO2- <=> NH2CHRCO2- + H+}}}$

Por lo tanto, la molécula de aminoácido es anfótera porque puede estar protonada o desprotonada.

La molécula de agua puede ganar o perder un protón. Se dice que es anfiprótica . El equilibrio de ionización se puede escribir

${\displaystyle {\ce {H2O <=> OH- + H+}}}$

donde en solución acuosa H ⁺ denota un protón solvatado . A menudo esto se escribe como el ion hidronio H3O ⁺ , pero esta fórmula no es exacta porque de hecho hay solvatación por más de una molécula de agua _{y especies} como H5O+2, H7O_​​+3, y H ₉ O+4También están presentes. ^[33]

La constante de equilibrio está dada por

${\displaystyle K_{\text{a}}=\mathrm {\frac {[H^{+}][OH^{-}]}{[H_{2}O]}} }$

En soluciones en las que las concentraciones de soluto no son muy altas, se puede suponer que la concentración [H ₂ O] es constante, independientemente del soluto o solutos; esta expresión puede entonces reemplazarse por

${\displaystyle K_{\text{w}}=[\mathrm {H} ^{+}][\mathrm {OH} ^{-}]\,}$

La constante de autoionización del agua, K _w , es, por tanto, un caso especial de constante de disociación ácida. También se puede definir una forma logarítmica análoga a p K _a

${\displaystyle \mathrm {p} K_{\text{w}}=-\log _{10}\left(K_{\text{w}}\right)}$

Estos datos se pueden modelar mediante una parábola con

${\displaystyle \mathrm {p} K_{\mathrm {w} }=14.94-0.04209\ T+0.0001718\ T^{2}}$

De esta ecuación, p K _w  = 14 a 24,87 °C. A esa temperatura, tanto los iones de hidrógeno como los de hidróxido tienen una concentración de 10 ⁻⁷  M.

Será más probable que un disolvente promueva la ionización de una molécula ácida disuelta en las siguientes circunstancias: ^[35]

1. Es un disolvente prótico , capaz de formar enlaces de hidrógeno.
2. Tiene un alto número de donantes , lo que lo convierte en una fuerte base de Lewis .
3. Tiene una constante dieléctrica alta (permitividad relativa), lo que lo convierte en un buen disolvente para especies iónicas.

Los valores de p K _a de los compuestos orgánicos se obtienen a menudo utilizando los disolventes apróticos dimetilsulfóxido (DMSO) ^[35] y acetonitrilo (ACN). ^[36]

El DMSO se utiliza ampliamente como alternativa al agua porque tiene una constante dieléctrica más baja que la del agua y es menos polar, por lo que disuelve sustancias no polares e hidrófobas con mayor facilidad. Tiene un rango de p K a medible _de aproximadamente 1 a 30. El acetonitrilo es menos básico que el DMSO y, por lo tanto, en general, los ácidos son más débiles y las bases son más fuertes en este solvente. Algunos valores de p K a a 25 °C para acetonitrilo (ACN) _[ 37 ^{] [38] [39]} y dimetilsulfóxido (DMSO). ^[40] se muestran en las siguientes tablas. Se incluyen valores para el agua a modo de comparación.

La ionización de los ácidos es menor en un disolvente ácido que en agua. Por ejemplo, el cloruro de hidrógeno es un ácido débil cuando se disuelve en ácido acético . Esto se debe a que el ácido acético es una base mucho más débil que el agua.

${\displaystyle {\ce {HCl + CH3CO2H <=> Cl- + CH3C(OH)2+}}}$

${\displaystyle {\text{acid}}+{\text{base }}{\ce {<=>}}{\text{ conjugate base}}+{\text{conjugate acid}}}$

Compare esta reacción con lo que sucede cuando el ácido acético se disuelve en el disolvente más ácido, ácido sulfúrico puro: ^[41]

${\displaystyle {\ce {H2SO4 + CH3CO2H <=> HSO4- + CH3C(OH)2+}}}$

La improbable especie de diol geminal CH ₃ C(OH)+2es estable en estos entornos. Para soluciones acuosas, la escala de pH es la función de acidez más conveniente . ^[42] Se han propuesto otras funciones de acidez para medios no acuosos, siendo la más notable la función de acidez de Hammett , H ₀ , para medios superácidos y su versión modificada H ₋ para medios superbásicos . ^[43]

En disolventes apróticos, los oligómeros , como el conocido dímero de ácido acético , pueden formarse mediante enlaces de hidrógeno. Un ácido también puede formar enlaces de hidrógeno con su base conjugada. Este proceso, conocido como homoconjugación , tiene el efecto de mejorar la acidez de los ácidos, reduciendo sus valores efectivos de p K _a , al estabilizar la base conjugada. La homoconjugación mejora el poder donador de protones del ácido toluenosulfónico en solución de acetonitrilo en un factor de casi 800. ^[44]

En soluciones acuosas no se produce homoconjugación porque el agua forma enlaces de hidrógeno más fuertes con la base conjugada que el ácido.

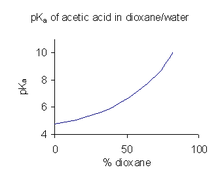
Cuando un compuesto tiene una solubilidad limitada en agua, es una práctica común (en la industria farmacéutica, por ejemplo) determinar los valores de p K _a en una mezcla de solventes como agua/ dioxano o agua/ metanol , en la que el compuesto es más soluble. ^[46] En el ejemplo que se muestra a la derecha, el valor de p K _a aumenta abruptamente con el aumento del porcentaje de dioxano a medida que disminuye la constante dieléctrica de la mezcla.

_Un valor de p K a obtenido en un disolvente mixto no se puede utilizar directamente para soluciones acuosas. La razón de esto es que cuando el disolvente está en su estado estándar, su actividad se define como uno. Por ejemplo, el estado estándar de la mezcla de agua:dioxano con una relación de mezcla de 9:1 es precisamente esa mezcla de disolventes, sin solutos añadidos. Para obtener el valor de p K _a para su uso con soluciones acuosas, se debe extrapolar a una concentración de codisolvente cero a partir de los valores obtenidos a partir de varias mezclas de codisolventes.

Estos hechos se ven oscurecidos por la omisión del disolvente en la expresión que normalmente se utiliza para definir p K _a , pero los valores de p K _a obtenidos en un disolvente mixto determinado se pueden comparar entre sí, lo que da lugar a concentraciones ácidas relativas. Lo mismo ocurre con los valores de p K _a obtenidos en un disolvente no acuoso particular, como el DMSO.

No se ha desarrollado una escala universal, independiente del disolvente, para las constantes de disociación ácida, ya que no se conoce ninguna forma de comparar los estados estándar de dos disolventes diferentes.

La segunda regla de Pauling es que el valor del primer p K _a para ácidos de fórmula XO _m (OH) _n depende principalmente del número de grupos oxo m , y es aproximadamente independiente del número de grupos hidroxi n , y también del átomo central X. Los valores aproximados de p K _a son 8 para m  = 0, 2 para m  = 1, −3 para m  = 2 y < −10 para m  = 3. ^[28] Alternativamente, se han propuesto varias fórmulas numéricas incluyendo p K _a  = 8 − 5 m (conocida como regla de Bell ), ^{[29] [47]} p K _a  = 7 − 5 m , ^{[30] [48]} o p K _a  = 9 − 7 m . ^[29] La dependencia de m se correlaciona con el estado de oxidación del átomo central, X: cuanto mayor sea el estado de oxidación, más fuerte será el oxiácido.

Por ejemplo, p K _a para HClO es 7,2, para HClO ₂ es 2,0, para HClO ₃ es −1 y HClO ₄ es un ácido fuerte ( p K _a ≪ 0 ). ^[7] La ​​mayor acidez al añadir un grupo oxo se debe a la estabilización de la base conjugada por deslocalización de su carga negativa sobre un átomo de oxígeno adicional. ^[47] Esta regla puede ayudar a asignar la estructura molecular: por ejemplo, el ácido fosforoso , que tiene la fórmula molecular H ₃ PO ₃ , tiene un p K _a cercano a 2, lo que sugirió que la estructura es HPO(OH) ₂ , como se confirmó más tarde por espectroscopia de RMN , y no P(OH) ₃ , que se esperaría que tuviera un p K _a cercano a 8. ^[48]

Los efectos inductivos y los efectos mesoméricos afectan los valores de p K _a . Un ejemplo sencillo lo proporciona el efecto de reemplazar los átomos de hidrógeno en el ácido acético por el átomo de cloro, más electronegativo. El efecto de atracción de electrones del sustituyente facilita la ionización, por lo que los valores sucesivos de p K _a disminuyen en la serie 4,7, 2,8, 1,4 y 0,7 cuando están presentes 0, 1, 2 o 3 átomos de cloro. ^[49] La ecuación de Hammett proporciona una expresión general para el efecto de los sustituyentes. ^[50]

log( K _a ) = log( K⁰
_a) + ρσ.

K _a es la constante de disociación de un compuesto sustituido, K⁰
_aes la constante de disociación cuando el sustituyente es hidrógeno, ρ es una propiedad del compuesto no sustituido y σ tiene un valor particular para cada sustituyente. Una gráfica de log( K _a ) en función de σ es una línea recta con intersección en log( K⁰
_a) y pendiente ρ. Este es un ejemplo de una relación de energía libre lineal ya que log( K _a ) es proporcional al cambio de energía libre estándar. Hammett originalmente ^[51] formuló la relación con datos del ácido benzoico con diferentes sustituyentes en las posiciones orto y para : algunos valores numéricos están en la ecuación de Hammett . Este y otros estudios permitieron ordenar los sustituyentes según su poder de atracción o liberación de electrones , y distinguir entre efectos inductivos y mesoméricos. ^{[52] [53]}

Los alcoholes normalmente no se comportan como ácidos en agua, pero la presencia de un doble enlace adyacente al grupo OH puede disminuir sustancialmente el p K _a por el mecanismo de tautomería ceto-enólica . El ácido ascórbico es un ejemplo de este efecto. La dicetona 2,4-pentanodiona ( acetilacetona ) también es un ácido débil debido al equilibrio ceto-enólico. En compuestos aromáticos, como el fenol , que tienen un sustituyente OH, la conjugación con el anillo aromático en su conjunto aumenta en gran medida la estabilidad de la forma desprotonada.

Los efectos estructurales también pueden ser importantes. La diferencia entre el ácido fumárico y el ácido maleico es un ejemplo clásico. El ácido fumárico es el ácido (E)-1,4-but-2-enedioico, un isómero trans , mientras que el ácido maleico es el isómero cis correspondiente , es decir, el ácido (Z)-1,4-but-2-enedioico (véase isomería cis-trans ). El ácido fumárico tiene valores de p K _a de aproximadamente 3,0 y 4,5. Por el contrario, el ácido maleico tiene valores de p K _a de aproximadamente 1,5 y 6,5. La razón de esta gran diferencia es que cuando se elimina un protón del isómero cis (ácido maleico), se forma un fuerte enlace de hidrógeno intramolecular con el grupo carboxilo restante cercano. Esto favorece la formación del maleato H ⁺ y se opone a la eliminación del segundo protón de esa especie. En el isómero trans , los dos grupos carboxilo están siempre muy separados, por lo que no se observan enlaces de hidrógeno. ^[54]

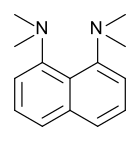
La esponja de protones , 1,8-bis(dimetilamino)naftaleno, tiene _{un valor de p} K de 12,1. Es una de las bases de amina más fuertes conocidas. La alta basicidad se atribuye al alivio de la tensión durante la protonación y a los fuertes enlaces de hidrógeno internos. ^{[55] [56]}

En esta sección también se deben mencionar los efectos del disolvente y la solvatación. Resulta que estas influencias son más sutiles que las de un medio dieléctrico mencionado anteriormente. Por ejemplo, el orden de basicidad esperado (por los efectos electrónicos de los sustituyentes de metilo) y observado en fase gaseosa de las metilaminas, Me ₃ N > Me ₂ NH > MeNH ₂ > NH ₃ , se cambia por el agua a Me ₂ NH > MeNH ₂ > Me ₃ N > NH ₃ . Las moléculas de metilamina neutras están unidas por enlaces de hidrógeno a las moléculas de agua principalmente a través de una interacción aceptora, N–HOH, y solo ocasionalmente solo un enlace donador más, NH–OH ₂ . Por lo tanto, las metilaminas se estabilizan aproximadamente en la misma medida por hidratación, independientemente del número de grupos metilo. En marcado contraste, los cationes de metilamonio correspondientes siempre utilizan todos los protones disponibles para el enlace donador NH–OH ₂ . La estabilización relativa de los iones de metilamonio disminuye con el número de grupos metilo, lo que explica el orden de basicidad del agua de las metilaminas. ^[4]

Una constante de equilibrio está relacionada con el cambio de energía de Gibbs estándar para la reacción, por lo que para una constante de disociación ácida

${\displaystyle \Delta G^{\ominus }=-RT\ln K_{\text{a}}\approx 2.303RT\ \mathrm {p} K_{\text{a}}}$.

R es la constante de los gases y T es la temperatura absoluta . Nótese que p K _a = −log( K _a ) y 2,303 ≈ ln (10) . A 25 °C, Δ G ^⊖ en kJ·mol ⁻¹ ≈ 5,708 p K _a (1 kJ·mol ⁻¹ = 1000 julios por mol ). La energía libre se compone de un término de entalpía y un término de entropía . ^[11]

${\displaystyle \Delta G^{\ominus }=\Delta H^{\ominus }-T\Delta S^{\ominus }}$

El cambio de entalpía estándar se puede determinar por calorimetría o utilizando la ecuación de van 't Hoff , aunque es preferible el método calorimétrico. Cuando se han determinado tanto el cambio de entalpía estándar como la constante de disociación ácida, el cambio de entropía estándar se calcula fácilmente a partir de la ecuación anterior. En la siguiente tabla, los términos de entropía se calculan a partir de los valores experimentales de p K _a y Δ H ^⊖ . Los datos se seleccionaron críticamente y se refieren a 25 °C y fuerza iónica cero, en agua. ^[11]

El primer punto a destacar es que, cuando p K _a es positivo, el cambio de energía libre estándar para la reacción de disociación también es positivo. En segundo lugar, algunas reacciones son exotérmicas y otras endotérmicas , pero, cuando Δ H ^⊖ es negativo, T ΔS ^⊖ es el factor dominante, que determina que Δ G ^⊖ sea positivo. Por último, la contribución de la entropía siempre es desfavorable ( Δ S ^⊖ < 0 ) en estas reacciones. Los iones en solución acuosa tienden a orientar las moléculas de agua circundantes, lo que ordena la solución y disminuye la entropía. La contribución de un ion a la entropía es la entropía molar parcial que a menudo es negativa, especialmente para iones pequeños o muy cargados. ^[57] La ​​ionización de un ácido neutro implica la formación de dos iones de modo que la entropía disminuye ( Δ S ^⊖ < 0 ). En la segunda ionización del mismo ácido, ahora hay tres iones y el anión tiene carga, por lo que la entropía disminuye nuevamente.

Tenga en cuenta que el cambio de energía libre estándar para la reacción corresponde a los cambios de los reactivos en sus estados estándar a los productos en sus estados estándar. El cambio de energía libre en el equilibrio es cero, ya que los potenciales químicos de los reactivos y los productos son iguales en el equilibrio.

La determinación experimental de los valores de p K _a se realiza habitualmente mediante titulaciones , en un medio de alta fuerza iónica y a temperatura constante. ^[58] Un procedimiento típico sería el siguiente. Una solución del compuesto en el medio se acidifica con un ácido fuerte hasta el punto en que el compuesto está completamente protonado. Luego, la solución se titula con una base fuerte hasta que se hayan eliminado todos los protones. En cada punto de la titulación, se mide el pH utilizando un electrodo de vidrio y un medidor de pH . Las constantes de equilibrio se encuentran ajustando los valores de pH calculados a los valores observados, utilizando el método de mínimos cuadrados . ^[59]

El volumen total de la base fuerte añadida debe ser pequeño en comparación con el volumen inicial de la solución de titulación para mantener la fuerza iónica casi constante. Esto garantizará que p K _a permanezca invariable durante la titulación.

A la derecha se muestra una curva de titulación calculada para el ácido oxálico. El ácido oxálico tiene valores de p K _a de 1,27 y 4,27. Por lo tanto, las regiones tampón estarán centradas en pH 1,3 y 4,3. Las regiones tampón contienen la información necesaria para obtener los valores de p _K a a medida que cambian las concentraciones de ácido y base conjugada a lo largo de una región tampón.

Entre las dos regiones tampón hay un punto final, o punto de equivalencia , a aproximadamente pH 3. Este punto final no es nítido y es típico de un ácido diprótico cuyas regiones tampón se superponen en una pequeña cantidad: p K _a2  − p K _a1 es aproximadamente tres en este ejemplo. (Si la diferencia en los valores de p K fuera de aproximadamente dos o menos, el punto final no sería perceptible). El segundo punto final comienza aproximadamente a pH 6,3 y es nítido. Esto indica que se han eliminado todos los protones. Cuando esto es así, la solución no está tamponada y el pH aumenta abruptamente al agregar una pequeña cantidad de base fuerte. Sin embargo, el pH no continúa aumentando indefinidamente. Una nueva región tampón comienza aproximadamente a pH 11 (p K _w  − 3), que es donde la autoionización del agua se vuelve importante.

Es muy difícil medir valores de pH inferiores a dos en solución acuosa con un electrodo de vidrio , porque la ecuación de Nernst se rompe con valores de pH tan bajos. Para determinar valores de p K inferiores a aproximadamente 2 o superiores a aproximadamente 11, se pueden utilizar mediciones espectrofotométricas ^{[60] [61]} o de RMN ^{[62] [63]} en lugar de, o combinadas con, mediciones de pH.

Cuando no se puede emplear el electrodo de vidrio, como en el caso de las soluciones no acuosas, se utilizan con frecuencia métodos espectrofotométricos. ^[38] Estos pueden implicar mediciones de absorbancia o fluorescencia . En ambos casos, se supone que la cantidad medida es proporcional a la suma de las contribuciones de cada especie fotoactiva; con las mediciones de absorbancia, se supone que se aplica la ley de Beer-Lambert .

La calorimetría de titulación isotérmica (ITC) se puede utilizar para determinar tanto el valor de p K como la entalpía estándar correspondiente para la disociación ácida. ^[64] Los fabricantes de instrumentos suministran el software para realizar los cálculos para sistemas simples.

Las soluciones acuosas con agua normal no se pueden utilizar para las mediciones de RMN ¹ H, sino que se debe utilizar agua pesada , D ₂ O , en su lugar. Sin embargo, los datos de RMN ¹³ C se pueden utilizar con agua normal y los espectros de RMN ^{1 H se pueden utilizar con medios no acuosos. Las cantidades medidas con RMN son} desplazamientos químicos promediados en el tiempo , ya que el intercambio de protones es rápido en la escala de tiempo de RMN. Se pueden medir otros desplazamientos químicos, como los de ^{31 P.}

Para algunos ácidos polipróticos, la disociación (o asociación) ocurre en más de un sitio no equivalente, ^[4] y la constante de equilibrio macroscópica observada, o macroconstante, es una combinación de microconstantes que involucran especies distintas. Cuando un reactivo forma dos productos en paralelo, la macroconstante es una suma de dos microconstantes. Esto es cierto, por ejemplo, para la desprotonación del aminoácido cisteína , que existe en solución como un zwitterión neutro HS−CH ₂ −CH(NH${\displaystyle K=K_{X}+K_{Y}.}$ +3)−COO ⁻ . Las dos microconstantes representan la desprotonación ya sea en azufre o en nitrógeno, y la suma de las macroconstantes aquí es la constante de disociación ácida ^[65]${\displaystyle K_{\mathrm {a} }=K_{\mathrm {a} }{\ce {(-SH)}}+K_{\mathrm {a} }{\ce {(-NH3+)}}.}$

De manera similar, una base como la espermina tiene más de un sitio donde puede ocurrir la protonación. Por ejemplo, la monoprotonación puede ocurrir en un grupo terminal −NH2 o en grupos internos −NH− . Los valores _de Kb para la disociación de la espermina protonada en uno u otro de los sitios son ejemplos de microconstantes _. No se pueden determinar directamente por medio de mediciones de pH, absorbancia, fluorescencia o RMN; un valor de Kb medido _es la suma de los valores de K para las microrreacciones.

${\displaystyle K_{\text{b}}=K_{\text{terminal}}+K_{\text{internal}}}$

Sin embargo, el sitio de protonación es muy importante para la función biológica, por lo que se han desarrollado métodos matemáticos para la determinación de microconstantes. ^[66]

Cuando dos reactivos forman un único producto en paralelo, la macroconstante ^[65] Por ejemplo, el equilibrio mencionado anteriormente para la espermina puede considerarse en términos de valores de K _a de dos ácidos conjugados tautoméricos , con macroconstante En este caso Esto es equivalente a la expresión anterior ya que es proporcional a${\displaystyle 1/K=1/K_{X}+1/K_{Y}.}$${\displaystyle 1/K_{\text{a}}=1/K_{{\text{a}},{\text{terminal}}}+1/K_{{\text{a}},{\text{internal}}}.}$${\displaystyle K_{\mathrm {b} }}$${\displaystyle 1/K_{\mathrm {a} }.}$

Cuando un reactivo experimenta dos reacciones en serie, la macroconstante de la reacción combinada es el producto de la microconstante de los dos pasos. Por ejemplo, el zwitterión de cisteína mencionado anteriormente puede perder dos protones, uno del azufre y otro del nitrógeno, y la macroconstante total para perder dos protones es el producto de dos constantes de disociación ^[65]. Esto también se puede escribir en términos de constantes logarítmicas como${\displaystyle K=K_{\mathrm {a} }{\ce {(-SH)}}K_{\mathrm {a} }{\ce {(-NH3+)}}.}$${\displaystyle \mathrm {p} K=\mathrm {p} K_{\mathrm {a} }{\ce {(-SH)}}+\mathrm {p} K_{\mathrm {a} }{\ce {(-NH3+)}}.}$

El conocimiento de los valores de p K _a es importante para el tratamiento cuantitativo de sistemas que involucran equilibrios ácido-base en solución. Existen muchas aplicaciones en bioquímica ; por ejemplo, los valores de p K _a de las proteínas y las cadenas laterales de aminoácidos son de gran importancia para la actividad de las enzimas y la estabilidad de las proteínas. ^[67] Los valores de p K _a de las proteínas no siempre se pueden medir directamente, pero se pueden calcular utilizando métodos teóricos. Las soluciones tampón se utilizan ampliamente para proporcionar soluciones a pH fisiológico o cercano al mismo para el estudio de reacciones bioquímicas; ^[68] el diseño de estas soluciones depende del conocimiento de los valores de p K _a de sus componentes. Las soluciones tampón importantes incluyen MOPS , que proporciona una solución con pH 7,2, y tricina , que se utiliza en la electroforesis en gel . ^{[69] [70]} El tamponamiento es una parte esencial de la fisiología ácido-base, incluida la homeostasis ácido-base , ^[71] y es clave para comprender trastornos como el trastorno ácido-base . ^{[72] [73] [74]} El punto isoeléctrico de una molécula dada es una función de sus valores p K , por lo que diferentes moléculas tienen diferentes puntos isoeléctricos. Esto permite una técnica llamada enfoque isoeléctrico , ^[75] que se utiliza para la separación de proteínas mediante electroforesis en gel de poliacrilamida en 2-D .

Las soluciones tampón también desempeñan un papel clave en la química analítica . Se utilizan siempre que sea necesario fijar el pH de una solución en un valor particular. En comparación con una solución acuosa, el pH de una solución tampón es relativamente insensible a la adición de una pequeña cantidad de ácido fuerte o base fuerte. La capacidad tampón ^[76] de una solución tampón simple es mayor cuando pH = p K _a . En la extracción ácido-base , la eficiencia de extracción de un compuesto en una fase orgánica, como un éter , se puede optimizar ajustando el pH de la fase acuosa utilizando un tampón apropiado. En el pH óptimo, se maximiza la concentración de la especie eléctricamente neutra; dicha especie es más soluble en disolventes orgánicos que tienen una constante dieléctrica baja que en agua. Esta técnica se utiliza para la purificación de ácidos y bases débiles. ^[77]

Un indicador de pH es un ácido débil o una base débil que cambia de color en el rango de pH de transición, que es aproximadamente p K _a  ± 1. El diseño de un indicador universal requiere una mezcla de indicadores cuyos valores p K _a adyacentes difieren en aproximadamente dos, de modo que sus rangos de pH de transición simplemente se superponen.

En farmacología , la ionización de un compuesto altera su comportamiento físico y sus macropropiedades, como la solubilidad y la lipofilicidad (log  p ). Por ejemplo, la ionización de cualquier compuesto aumentará la solubilidad en agua, pero disminuirá la lipofilicidad. Esto se aprovecha en el desarrollo de fármacos para aumentar la concentración de un compuesto en la sangre ajustando el p K _a de un grupo ionizable. ^[78]

El conocimiento de los valores de p K _a es importante para la comprensión de los complejos de coordinación , que se forman por la interacción de un ion metálico, M ^m+ , que actúa como un ácido de Lewis , con un ligando , L, que actúa como una base de Lewis . Sin embargo, el ligando también puede sufrir reacciones de protonación, por lo que la formación de un complejo en solución acuosa podría representarse simbólicamente por la reacción

${\displaystyle [{\ce {M(H2O)_{\mathit {n}}}}]^{m+}+{\ce {LH<=>}}\ [{\ce {M(H2O)}}_{n-1}{\ce {L}}]^{(m-1)+}+{\ce {H3O+}}}$

Para determinar la constante de equilibrio de esta reacción, en la que el ligando pierde un protón, se debe conocer el p K _{a del ligando protonado. En la práctica, el ligando puede ser poliprótico; por ejemplo} , el EDTA ⁴⁻ puede aceptar cuatro protones; en ese caso, se deben conocer todos los valores de p K _a . Además, el ion metálico está sujeto a hidrólisis , es decir, se comporta como un ácido débil, por lo que también se deben conocer los valores de p K para las reacciones de hidrólisis. ^[79]

Para evaluar el riesgo asociado con un ácido o una base puede ser necesario conocer los valores de p K _a . ^[80] Por ejemplo, el cianuro de hidrógeno es un gas muy tóxico, porque el ion cianuro inhibe la enzima que contiene hierro citocromo c oxidasa . El cianuro de hidrógeno es un ácido débil en solución acuosa con un p K _a de aproximadamente 9. En soluciones fuertemente alcalinas, por encima de pH 11, por ejemplo, se deduce que el cianuro de sodio está "totalmente disociado", por lo que el riesgo debido al gas cianuro de hidrógeno se reduce mucho. Una solución ácida, por otro lado, es muy peligrosa porque todo el cianuro está en su forma ácida. La ingestión de cianuro por vía oral es potencialmente fatal, independientemente del pH, debido a la reacción con la citocromo c oxidasa.

En la ciencia ambiental, los equilibrios ácido-base son importantes para lagos ^[81] y ríos; ^{[82] [83]} por ejemplo, los ácidos húmicos son componentes importantes de las aguas naturales. Otro ejemplo ocurre en la oceanografía química : ^[84] para cuantificar la solubilidad del hierro (III) en agua de mar a varias salinidades , se calculan los valores de p K _a para la formación de los productos de hidrólisis del hierro (III) Fe(OH) ²⁺ , Fe(OH)+2y Fe(OH) ₃ , junto con el producto de solubilidad del hidróxido de hierro . ^[85]

Existen múltiples técnicas para determinar el p K _a de una sustancia química, lo que genera algunas discrepancias entre las distintas fuentes. Los valores medidos correctamente suelen tener una diferencia de 0,1 unidades entre sí. Los datos presentados aquí se tomaron a 25 °C en agua. ^{[7] [86]} Se pueden encontrar más valores en la sección Termodinámica, más arriba. Se puede encontrar una tabla de p K _a de ácidos carbonados, medidos en DMSO, en la página sobre carbaniones .

• Acidosis
• Ácidos en el vino : tartárico , málico y cítrico son los principales ácidos del vino.
• Alcalosis
• Gasometría arterial
• Equilibrio químico
• Conductividad (electrolítica)
• Mecanismo de Grotthuss : cómo se transfieren los protones entre los iones hidronio y las moléculas de agua, lo que explica la movilidad iónica excepcionalmente alta del protón (animación).
• Función de acidez de Hammett : medida de acidez que se utiliza para soluciones muy concentradas de ácidos fuertes, incluidos los superácidos .
• Número de transporte de iones
• Acidificación de los océanos : la disolución del dióxido de carbono atmosférico afecta el pH del agua de mar . La reacción depende del carbono inorgánico total y de los equilibrios de solubilidad con carbonatos sólidos como la caliza y la dolomita .
• Ley de dilución
• pCO2
• pH
• Diagrama de predominancia : se relaciona con los equilibrios que involucran polioxianiones . Se necesitan valores de p K a para construir estos _diagramas .
• Afinidad de protones : una medida de basicidad en la fase gaseosa.
• Constantes de estabilidad de los complejos : la formación de un complejo a menudo puede verse como una competencia entre un protón y un ion metálico por un ligando, que es el producto de la disociación de un ácido.