Ecuación de Van 't Hoff
Relación entre la temperatura y la constante de equilibrio de una reacción química

La ecuación de Van 't Hoff relaciona el cambio en la constante de equilibrio , K eq , de una reacción química con el cambio en la temperatura , T , dado el cambio de entalpía estándar , Δ r H ⊖ , para el proceso. El subíndice significa "reacción" y el superíndice significa "estándar". Fue propuesta por el químico holandés Jacobus Henricus van 't Hoff en 1884 en su libro Études de Dynamique chimique ( Estudios de química dinámica ). [1] a {\estilo de visualización r} ⊖ {\displaystyle \ominus}

La ecuación de Van 't Hoff se ha utilizado ampliamente para explorar los cambios en las funciones de estado en un sistema termodinámico . El diagrama de Van 't Hoff , que se deriva de esta ecuación, es especialmente eficaz para estimar el cambio en la entalpía y la entropía de una reacción química .

Ecuación

Resumen y usos

La presión estándar , , se utiliza para definir el estado de referencia para la ecuación de Van 't Hoff, que es [2] [3] PAG 0 {\estilo de visualización P^{0}}

d d yo En ⁡ K mi q = Δ a yo ⊖ R yo 2 {\displaystyle {\frac {d}{dT}}\ln K_{\mathrm {eq} }={\frac {\Delta _{r}H^{\ominus }}{RT^{2}}}}

donde ln denota el logaritmo natural , es la constante de equilibrio termodinámico y R es la constante de los gases ideales . Esta ecuación es exacta a cualquier temperatura y a todas las presiones, derivada del requisito de que la energía libre de Gibbs de la reacción sea estacionaria en un estado de equilibrio químico . K mi q {\displaystyle K_{eq}}

En la práctica, la ecuación se suele integrar entre dos temperaturas bajo el supuesto de que la entalpía de reacción estándar es constante (y además, también se supone a menudo que es igual a su valor a temperatura estándar ). Dado que en la realidad y la entropía de reacción estándar varían con la temperatura para la mayoría de los procesos, [4] la ecuación integrada es solo aproximada. En la práctica, también se realizan aproximaciones a los coeficientes de actividad dentro de la constante de equilibrio. Δ a yo ⊖ {\displaystyle \Delta _{r}H^{\ominus }} Δ a yo ⊖ {\displaystyle \Delta _{r}H^{\ominus }} Δ a S ⊖ {\displaystyle \Delta _{r}S^{\ominus }}

Un uso importante de la ecuación integrada es estimar una nueva constante de equilibrio a una nueva temperatura absoluta suponiendo un cambio de entalpía estándar constante en el rango de temperaturas. Para obtener la ecuación integrada, es conveniente reescribir primero la ecuación de Van 't Hoff como [2]

d En ⁡ K mi q d 1 yo = − Δ a yo ⊖ R . {\displaystyle {\frac {d\ln K_{\mathrm {eq} }}{d{\frac {1}{T}}}}=-{\frac {\Delta _{r}H^{\ominus }}{R}}.}

La integral definida entre las temperaturas T 1 y T 2 es entonces

En ⁡ K 2 K 1 = Δ a yo ⊖ R ( 1 yo 1 − 1 yo 2 ) . {\displaystyle \ln {\frac {K_{2}}{K_{1}}}={\frac {\Delta _{r}H^{\ominus }}{R}}\left({\frac {1}{T_{1}}}-{\frac {1}{T_{2}}}\right).}

En esta ecuación, K 1 es la constante de equilibrio a temperatura absoluta T 1 , y K 2 es la constante de equilibrio a temperatura absoluta T 2 .

Desarrollo a partir de la termodinámica

Combinando la conocida fórmula de la energía libre de Gibbs de reacción

Δ a GRAMO ⊖ = Δ a yo ⊖ − yo Δ a S ⊖ , {\displaystyle \Delta _{r}G^{\ominus }=\Delta _{r}H^{\ominus }-T\Delta _{r}S^{\ominus },}

donde S es la entropía del sistema, con la ecuación de la isoterma de energía libre de Gibbs: [5]

Δ a GRAMO ⊖ = − R yo En ⁡ K mi q , {\displaystyle \Delta _{r}G^{\ominus }=-RT\ln K_{\mathrm {eq} },}

Nosotros obtenemos

En ⁡ K mi q = − Δ a yo ⊖ R yo + Δ a S ⊖ R . {\displaystyle \ln K_{\mathrm {eq} }=-{\frac {\Delta _{r}H^{\ominus }}{RT}}+{\frac {\Delta _{r}S^{\ominus }}{R}}.}

La diferenciación de esta expresión con respecto a la variable T , suponiendo que tanto y como son independientes de T, da como resultado la ecuación de Van 't Hoff. Se espera que estas suposiciones no sean del todo válidas para grandes variaciones de temperatura. Δ a yo ⊖ {\displaystyle \Delta _{r}H^{\ominus }} Δ a S ⊖ {\displaystyle \Delta _{r}S^{\ominus }}

Siempre que y sean constantes, la ecuación anterior da ln K como una función lineal de ⁠ Δ a yo ⊖ {\displaystyle \Delta _{r}H^{\ominus }} Δ a S ⊖ {\displaystyle \Delta _{r}S^{\ominus }} 1/yo⁠ y por lo tanto se conoce como la forma lineal de la ecuación de Van 't Hoff. Por lo tanto, cuando el rango de temperatura es lo suficientemente pequeño como para que la entalpía de reacción estándar y la entropía de reacción sean esencialmente constantes, un gráfico del logaritmo natural de la constante de equilibrio versus la temperatura recíproca da una línea recta. La pendiente de la línea se puede multiplicar por la constante de gas R para obtener el cambio de entalpía estándar de la reacción, y la intersección se puede multiplicar por R para obtener el cambio de entropía estándar.

Isoterma de Van 't Hoff

La isoterma de Van 't Hoff se puede utilizar para determinar la dependencia de la temperatura de la energía libre de Gibbs de la reacción para reacciones en estados no estándar a una temperatura constante: [6]

( d GRAMO d o ) yo , pag = Δ a GRAMO = Δ a GRAMO ⊖ + R yo En ⁡ Q a , {\displaystyle \left({\frac {dG}{d\xi }}\right)_{T,p}=\Delta _{\mathrm {r} }G=\Delta _{\mathrm {r} } G^{\ominus }+RT\ln Q_{\mathrm {r} },}

donde es la energía libre de Gibbs de la reacción en estados no estándar a temperatura , es la energía libre de Gibbs para la reacción a , es la extensión de la reacción , y Q r es el cociente de reacción termodinámico . Dado que , la dependencia de la temperatura de ambos términos puede describirse mediante ecuaciones de Van t'Hoff como una función de T . Esto encuentra aplicaciones en el campo de la electroquímica , particularmente en el estudio de la dependencia de la temperatura de las celdas voltaicas. Δ a GRAMO {\displaystyle \Delta _{\mathrm {r} }G} yo {\estilo de visualización T} Δ a GRAMO ⊖ {\displaystyle \Delta _{r}G^{\ominus }} ( yo , PAG 0 ) {\displaystyle (T,P^{0})} o {\estilo de visualización \xi} Δ a GRAMO ⊖ = − R yo En ⁡ K mi q {\displaystyle \Delta _{r}G^{\ominus }=-RT\ln K_{eq}}

La isoterma también se puede utilizar a temperatura fija para describir la Ley de Acción de Masas . Cuando una reacción está en equilibrio , Q r = K eq y . De lo contrario, la isoterma de Van 't Hoff predice la dirección en la que el sistema debe cambiar para alcanzar el equilibrio; cuando Δ r G < 0 , la reacción se mueve en la dirección hacia adelante, mientras que cuando Δ r G > 0 , la reacción se mueve en la dirección hacia atrás. Véase Equilibrio químico . Δ a GRAMO = 0 {\displaystyle \Delta _ {\mathrm {r} }G=0}

La trama de Van 't Hoff

Para una reacción reversible , la constante de equilibrio se puede medir a una variedad de temperaturas. Estos datos se pueden representar gráficamente con ln K eq en el eje y y1/yo⁠ en el eje x . Los datos deben tener una relación lineal, cuya ecuación se puede encontrar ajustando los datos utilizando la forma lineal de la ecuación de Van 't Hoff

En ⁡ K mi q = − Δ a yo ⊖ R yo + Δ a S ⊖ R . {\displaystyle \ln K_{\mathrm {eq} }=-{\frac {\Delta _{r}H^{\ominus }}{RT}}+{\frac {\Delta _{r}S^{\ominus }}{R}}.}

Este gráfico se denomina "diagrama de Van 't Hoff" y se utiliza ampliamente para estimar la entalpía y la entropía de una reacción química . A partir de este gráfico, − ⁠ΔrH​​/R⁠ es la pendiente, y ⁠ΔrS​​/R⁠ es la intersección del ajuste lineal.

Al medir la constante de equilibrio , K eq , a diferentes temperaturas, se puede utilizar el diagrama de Van 't Hoff para evaluar una reacción cuando cambia la temperatura. [7] [8] Conociendo la pendiente y la intersección del diagrama de Van 't Hoff, la entalpía y la entropía de una reacción se pueden obtener fácilmente utilizando

Δ a yo = − R × pendiente , Δ a S = R × interceptar . {\displaystyle {\begin{aligned}\Delta _{r}H&=-R\times {\text{pendiente}},\\\Delta _{r}S&=R\times {\text{intersección}}.\end{aligned}}}

El diagrama de Van 't Hoff se puede utilizar para determinar rápidamente la entalpía de una reacción química, tanto de forma cualitativa como cuantitativa. Este cambio en la entalpía puede ser positivo o negativo, lo que da lugar a dos formas principales del diagrama de Van 't Hoff.

Reacciones endotérmicas

Diagrama de Van 't Hoff para una reacción endotérmica

En una reacción endotérmica , se absorbe calor, lo que hace que el cambio de entalpía neta sea positivo. Por lo tanto, según la definición de la pendiente:

pendiente = − Δ a yo R , {\displaystyle {\text{pendiente}}=-{\frac {\Delta _{r}H}{R}},}

Cuando la reacción es endotérmica , Δ r H > 0 (y la constante del gas R > 0 ), entonces

pendiente = − Δ a yo R < 0. {\displaystyle {\text{pendiente}}=-{\frac {\Delta _{r}H}{R}}<0.}

Por lo tanto, para una reacción endotérmica, el diagrama de Van 't Hoff siempre debe tener una pendiente negativa.

Reacciones exotérmicas

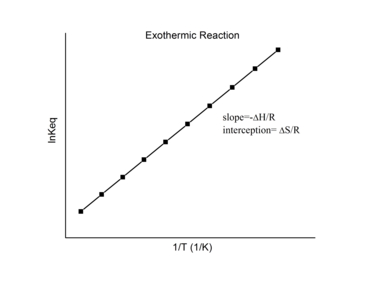
Diagrama de Van 't Hoff para una reacción exotérmica

En una reacción exotérmica se libera calor, lo que hace que el cambio de entalpía neta sea negativo. Por lo tanto, según la definición de la pendiente:

pendiente = − Δ a yo R , {\displaystyle {\text{pendiente}}=-{\frac {\Delta _{r}H}{R}},}

Para una reacción exotérmica Δ r H < 0 , entonces

pendiente = − Δ a yo R > 0. {\displaystyle {\text{pendiente}}=-{\frac {\Delta _{r}H}{R}}>0.}

Por lo tanto, para una reacción exotérmica, el gráfico de Van 't Hoff siempre debe tener una pendiente positiva.

Propagación de errores

A primera vista, utilizando el hecho de que Δ r G ⊖ = − RT ln K = Δ r H ⊖ − T Δ r S ⊖ parecería que dos mediciones de K serían suficientes para poder obtener un valor preciso de Δ r H ⊖ :

Δ a yo ⊖ = R En ⁡ K 1 − En ⁡ K 2 1 yo 2 − 1 yo 1 , {\displaystyle \Delta _{r}H^{\ominus }=R{\frac {\ln K_{1}-\ln K_{2}}{{\frac {1}{T_{2}}}-{\frac {1}{T_{1}}}}},}

donde K 1 y K 2 son los valores de la constante de equilibrio obtenidos a las temperaturas T 1 y T 2 respectivamente. Sin embargo, la precisión de los valores Δ r H ⊖ obtenidos de esta manera depende en gran medida de la precisión de los valores de la constante de equilibrio medidos.

El uso de la propagación de errores muestra que el error en Δ r H ⊖ será aproximadamente 76 kJ/mol multiplicado por la incertidumbre experimental en (ln K 1 − ln K 2 ) , o aproximadamente 110 kJ/mol multiplicado por la incertidumbre en los valores de ln K. Se aplican consideraciones similares a la entropía de la reacción obtenida a partir de Δ r S ⊖ = ⁠1/yo⁠ (Δ H ⊖ + RT ln K ) .

En particular, cuando se miden las constantes de equilibrio a tres o más temperaturas, los valores de Δ r H ⊖ y Δ r S ⊖ se obtienen a menudo mediante un ajuste en línea recta . [9] La expectativa es que el error se reducirá con este procedimiento, aunque la suposición de que la entalpía y la entropía de la reacción son constantes puede resultar correcta o no. Si hay una dependencia significativa de la temperatura en una o ambas cantidades, debería manifestarse en un comportamiento no lineal en el diagrama de Van 't Hoff; sin embargo, presumiblemente se necesitarían más de tres puntos de datos para observar esto.

Aplicaciones del diagrama de Van 't Hoff

Análisis de Van 't Hoff

Análisis de Van 't Hoff

En la investigación biológica, el diagrama de Van 't Hoff también se denomina análisis de Van 't Hoff. [10] Es más eficaz para determinar el producto favorecido en una reacción. Puede obtener resultados diferentes a los de la calorimetría directa, como la calorimetría diferencial de barrido o la calorimetría de titulación isotérmica, debido a diversos efectos distintos del error experimental. [11]

Supongamos que se forman dos productos B y C en una reacción:

aA + dD → bB ,
aA + dD → cC .

En este caso, K eq puede definirse como la relación entre B y C en lugar de la constante de equilibrio.

Cuando ⁠B/do⁠ > 1, B es el producto favorecido y los datos del gráfico de Van 't Hoff estarán en la región positiva.

Cuando ⁠B/do< 1, C es el producto favorecido y los datos del gráfico de Van 't Hoff estarán en la región negativa.

Utilizando esta información, un análisis de Van 't Hoff puede ayudar a determinar la temperatura más adecuada para un producto deseado.

En 2010, se utilizó un análisis de Van 't Hoff para determinar si el agua forma preferentemente un enlace de hidrógeno con el extremo C o el extremo N del aminoácido prolina. [12] La constante de equilibrio para cada reacción se encontró a una variedad de temperaturas, y se creó un diagrama de Van 't Hoff. Este análisis mostró que entálpicamente, el agua prefería el enlace de hidrógeno con el extremo C , pero entrópicamente era más favorable al enlace de hidrógeno con el extremo N. Específicamente, encontraron que el enlace de hidrógeno del extremo C se favorecía por 4.2–6.4 kJ/mol. El enlace de hidrógeno del extremo N se favorecía por 31–43 J/(K mol).

Estos datos por sí solos no permitieron concluir en qué sitio el agua se unirá preferentemente mediante enlaces de hidrógeno, por lo que se utilizaron experimentos adicionales. Se determinó que a temperaturas más bajas, la especie favorecida entálpicamente, el agua unida mediante enlaces de hidrógeno al extremo C , era la preferida. A temperaturas más altas, la especie favorecida entrópicamente, el agua unida mediante enlaces de hidrógeno al extremo N , era la preferida.

Estudios mecanísticos

Diagrama de Van 't Hoff en el estudio de mecanismos

Una reacción química puede experimentar diferentes mecanismos de reacción a diferentes temperaturas. [13]

En este caso, se puede utilizar un diagrama de Van 't Hoff con dos o más ajustes lineales. Cada ajuste lineal tiene una pendiente y una intersección diferentes, lo que indica diferentes cambios en la entalpía y la entropía para cada mecanismo distinto. El diagrama de Van 't Hoff se puede utilizar para encontrar el cambio de entalpía y entropía para cada mecanismo y el mecanismo preferido a diferentes temperaturas.

Δ a yo 1 = − R × pendiente 1 , Δ a S 1 = R × interceptar 1 ; Δ a yo 2 = − R × pendiente 2 , Δ a S 2 = R × interceptar 2 . {\displaystyle {\begin{aligned}\Delta _{r}H_{1}&=-R\times {\text{pendiente}}_{1},&\Delta _{r}S_{1}&=R\times {\text{intersección}}_{1};\\[5pt]\Delta _{r}H_{2}&=-R\times {\text{pendiente}}_{2},&\Delta _{r}S_{2}&=R\times {\text{intersección}}_{2}.\end{aligned}}}

En la figura de ejemplo, la reacción experimenta el mecanismo 1 a alta temperatura y el mecanismo 2 a baja temperatura.

Dependencia de la temperatura

Diagrama de Van 't Hoff dependiente de la temperatura

Si la entalpía y la entropía son aproximadamente constantes a medida que la temperatura varía en un cierto rango, entonces el gráfico de Van 't Hoff es aproximadamente lineal cuando se traza en ese rango. Sin embargo, en algunos casos la entalpía y la entropía cambian drásticamente con la temperatura. Una aproximación de primer orden es suponer que los dos productos de reacción diferentes tienen diferentes capacidades térmicas. Incorporar esta suposición produce un término adicional ⁠do/T2​⁠ en la expresión de la constante de equilibrio en función de la temperatura. Luego, se puede utilizar un ajuste polinomial para analizar datos que exhiben una entalpía estándar de reacción no constante: [14]

En ⁡ K mi q = a + b yo + do yo 2 , {\displaystyle \ln K_{\mathrm {eq}}=a+{\frac {b}{T}}+{\frac {c}{T^{2}}},}

dónde

Δ a yo = − R ( b + 2 do yo ) , Δ a S = R ( a − do yo 2 ) . {\displaystyle {\begin{aligned}\Delta _{r}H&=-R\left(b+{\frac {2c}{T}}\right),\\\Delta _{r}S&=R\left(a-{\frac {c}{T^{2}}}\right).\end{aligned}}}

De esta forma, la entalpía y la entropía de una reacción se pueden determinar a temperaturas específicas incluso cuando existe una dependencia de la temperatura.

Autoensamblaje de surfactantes

La relación de Van 't Hoff es particularmente útil para la determinación de la entalpía de micelización Δ H⊖
mde surfactantes a partir de la dependencia de la temperatura de la concentración micelar crítica (CMC):

d d yo En ⁡ do METRO do = Δ yo metro ⊖ R yo 2 . {\displaystyle {\frac {d}{dT}}\ln \mathrm {CMC} ={\frac {\Delta H_{\mathrm {m} }^{\ominus }}{RT^{2}}}.}

Sin embargo, la relación pierde su validez cuando el número de agregación también depende de la temperatura, y en su lugar se debe utilizar la siguiente relación: [15]

R T 2 ( ∂ ∂ T ln ⁡ C M C ) P = − Δ r H m ⊖ ( N ) + T ( ∂ ∂ N ( G N + 1 − G N ) ) T , P ( ∂ N ∂ T ) P , {\displaystyle RT^{2}\left({\frac {\partial }{\partial T}}\ln \mathrm {CMC} \right)_{P}=-\Delta _{r}H_{\mathrm {m} }^{\ominus }(N)+T\left({\frac {\partial }{\partial N}}\left(G_{N+1}-G_{N}\right)\right)_{T,P}\left({\frac {\partial N}{\partial T}}\right)_{P},}

donde G N + 1 y G N son las energías libres del surfactante en una micela con número de agregación N + 1 y N respectivamente. Este efecto es particularmente relevante para surfactantes etoxilados no iónicos [16] o copolímeros de bloque de polioxipropileno-polioxietileno (Poloxamers, Pluronics, Synperonics). [17] La ​​ecuación extendida puede ser explotada para la extracción de números de agregación de micelas autoensambladas a partir de termogramas calorimétricos de barrido diferencial . [18]

Véase también

Referencias

  1. ^ Biografía en el sitio web del premio Nobel. Nobelprize.org (1 de marzo de 1911). Consultado el 8 de noviembre de 2013.
  2. ^ ab Atkins, Peter; De Paula, Julio (10 de marzo de 2006). Química física (8.ª ed.). WH Freeman and Company. pág. 212. ISBN 978-0-7167-8759-4.
  3. ^ Ives, DJG (1971). Termodinámica química . Química universitaria. Macdonald Technical and Scientific. ISBN 978-0-356-03736-3.
  4. ^ Craig, Norman (1996). "Diagramas de entropía". J. Chem. Educ . 73 (8): 710. Código Bibliográfico :1996JChEd..73..710C. doi :10.1021/ed073p710.
  5. ^ Dickerson, RE; Geis, I. (1976). Química, materia y universo . Estados Unidos: WA Benjamin Inc. ISBN 978-0-19-855148-5.
  6. ^ Monk, Paul (2004). Química física: comprensión de nuestro mundo químico . Wiley. pág. 162. ISBN 978-0471491811.
  7. ^ Kim, Tae Woo (2012). "Concatenación [2] dinámica de macrociclos autoensamblados de Pd(II) en agua". Chem. Lett . 41 : 70. doi :10.1246/cl.2012.70.
  8. ^ Ichikawa, Takayuki (2010). "Propiedades termodinámicas de amidas metálicas determinadas por isotermas de presión-composición de amoníaco" (PDF) . J. Chem. Thermodynamics . 42 : 140. doi :10.1016/j.jct.2009.07.024.
  9. ^ Chang, Raymond; Thoman, Jr., John W. (2014). Química física para las ciencias químicas . EE. UU.: University Science Books. págs. 322–325. ISBN 978-1-891389-69-6.
  10. ^ "Análisis de Van 't Hoff". Grupo de Análisis y Diseño de Proteínas.
  11. ^ Cooper, Alan (2018), Roberts, Gordon; Watts, Anthony (eds.), "Análisis de Van't Hoff y variables termodinámicas ocultas", Enciclopedia de biofísica , Berlín, Heidelberg: Springer, págs. 1–4, doi :10.1007/978-3-642-35943-9_10066-1, ISBN 978-3-642-35943-9, consultado el 4 de julio de 2023
  12. ^ Prell, James; Williams E. (2010). "La entropía impulsa una molécula de agua unida desde el extremo C al N en la prolina protonada". J. Am. Chem. Soc . 132 (42): 14733–5. doi :10.1021/ja106167d. PMID  20886878.
  13. ^ Chatake, Toshiyuki (2010). "Un enfoque para la cristalización del ADN utilizando el proceso térmico reversible de dúplex de ADN". Cryst. Growth Des . 10 (3): 1090. doi :10.1021/cg9007075.
  14. ^ David, Victor (28 de abril de 2011). "Desviación de la dependencia de van 't Hoff en RP-LC inducida por interconversión tautomérica observada para cuatro compuestos". Journal of Separation Science . 34 (12): 1423–8. doi :10.1002/jssc.201100029. PMID  21538875.
  15. ^ Holtzer, Alfred; Holtzer, Marilyn F. (1 de mayo de 2002). "Uso de la relación de van 't Hoff en la determinación de la entalpía de formación de micelas". The Journal of Physical Chemistry . 78 (14): 1442–1443. doi :10.1021/j100607a026.
  16. ^ Heerklotz, Heiko; Tsamaloukas, Alekos; Kita-Tokarczyk, Katarzyna; Strunz, Pavel; Gutberlet, Thomas (25 de noviembre de 2004). "Caracterización estructural, volumétrica y termodinámica de una transición de esfera a varilla micelar". Revista de la Sociedad Química Estadounidense . 126 (50): 16544–16552. doi :10.1021/ja045525w. PMID  15600359.
  17. ^ Taboada, Pablo; Mosquera, Victor; Attwood, David; Yang, Zhuo; Booth, Colin (5 de junio de 2003). "Entalpía de micelización de un copoli(oxietileno/oxipropileno) de dibloque mediante calorimetría de titulación isotérmica. Comparación con el valor de Van 't Hoff". Química física Química Física . 5 (12): 2625–2627. Código Bibliográfico :2003PCCP....5.2625T. doi :10.1039/b303108j.
  18. ^ Chiappisi, Leonardo; Lazzara, Giuseppe; Gradzielski, Michael; Milioto, Stefana (6 de diciembre de 2012). "Descripción cuantitativa de termogramas de autoagregación inducidos por temperatura determinados por calorimetría diferencial de barrido" (PDF) . Langmuir . 28 (51): 17609–17616. doi :10.1021/la303599d. hdl : 10447/96872 . PMID  23171124.
Retrieved from "https://en.wikipedia.org/w/index.php?title=Van_%27t_Hoff_equation&oldid=1239556406"