Círculo de quintas
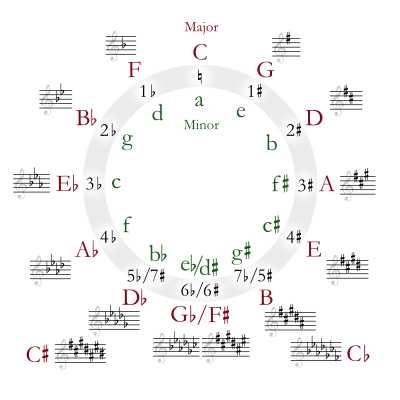
En teoría musical , el círculo de quintas (a veces también ciclo de quintas ) es una forma de organizar las notas como una secuencia de quintas perfectas . Comenzando en un Do y utilizando el sistema estándar de afinación para la música occidental ( temperamento igual de 12 tonos ), la secuencia es: Do, Sol, Re, La, Mi, Si, Fa ♯ /Sol ♭ , Do ♯ /Re ♭ , Sol ♯ /La ♭ , Re ♯ /Mi ♭ , La ♯ /Si ♭ , Fa y Do. Este orden coloca las armaduras de clave más estrechamente relacionadas unas con otras.
La afinación de temperamento igual de doce tonos divide cada octava en doce semitonos equivalentes y el círculo de quintas conduce a un do siete octavas por encima del punto de partida. Si las quintas están afinadas con una relación de frecuencia exacta de 3:2 (el sistema de afinación conocido como entonación justa ), esto no es así (el círculo no se "cierra").
Definición
El círculo de quintas organiza las notas en una secuencia de quintas perfectas , generalmente representadas como un círculo con las notas (y sus correspondientes tonalidades) en orden horario. Puede verse en sentido antihorario como un círculo de cuartas. Las progresiones armónicas en la música occidental suelen utilizar tonalidades adyacentes en este sistema, lo que lo convierte en una referencia útil para la composición y la armonía musical. [1]
La parte superior del círculo muestra la tonalidad de Do mayor, sin sostenidos ni bemoles . Siguiendo en el sentido de las agujas del reloj, las notas ascienden en quintas. Las armaduras de clave asociadas con esas notas cambian en consecuencia: la tonalidad de Sol tiene un sostenido, la tonalidad de Re tiene dos sostenidos, y así sucesivamente. Siguiendo en el sentido contrario a las agujas del reloj desde la parte superior del círculo, las notas cambian en quintas descendentes y las armaduras de clave cambian en consecuencia: la tonalidad de Fa tiene un bemol, la tonalidad de Si bemol tiene dos bemoles, y así sucesivamente. Algunas tonalidades (en la parte inferior del círculo) se pueden escribir en sostenidos o en bemoles .
Comenzando en cualquier tono y ascendiendo una quinta, se generan todos los tonos antes de regresar a la clase de tono inicial (una clase de tono consiste en todas las notas indicadas por una letra dada, independientemente de la octava; todas las "C", por ejemplo, pertenecen a la misma clase de tono). Moviéndose en sentido antihorario, los tonos descienden una quinta, pero ascendiendo una cuarta perfecta conducirá a la misma nota una octava más alta (por lo tanto, en la misma clase de tono). Moviéndose en sentido antihorario desde C podría considerarse como descender una quinta a F, o ascender una cuarta a F.
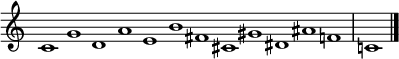 Círculo de quintas en el sentido de las agujas del reloj dentro de una octava |  Círculo de quintas en sentido antihorario dentro de una octava
|
Estructura y uso
Armaduras de clave diatónica
Cada tono puede servir como tónica de una tonalidad mayor o menor , y cada una de estas tonalidades tendrá una escala diatónica asociada a ella. El diagrama circular muestra el número de sostenidos o bemoles en cada armadura de tonalidad , con la tonalidad mayor indicada por una letra mayúscula y la tonalidad menor indicada por una letra minúscula. Las tonalidades mayores y menores que tienen la misma armadura de tonalidad se denominan relativas mayores y relativas menores entre sí.
Modulación y progresión de acordes
La música tonal suele modularse hacia un nuevo centro tonal cuya tonalidad difiere de la original en solo un bemol o un sostenido. Estas tonalidades estrechamente relacionadas están separadas por una quinta y, por lo tanto, son adyacentes en el círculo de quintas. Las progresiones de acordes también suelen moverse entre acordes cuyas raíces están relacionadas por una quinta perfecta, lo que hace que el círculo de quintas sea útil para ilustrar la "distancia armónica" entre acordes.

El círculo de quintas se utiliza para organizar y describir la función armónica o tonal de los acordes . [2] Los acordes pueden progresar en un patrón de cuartas perfectas ascendentes (que también se consideran quintas perfectas descendentes) en "sucesión funcional". Esto se puede demostrar "... mediante el círculo de quintas (en el que, por lo tanto, el grado II de la escala está más cerca de la dominante que el grado IV de la escala)". [3] En esta perspectiva, el centro tónico o tonal se considera el punto final de una progresión de acordes derivada del círculo de quintas.

Según Harmony in Western Music de Richard Franko Goldman , "el acorde IV está, en los mecanismos más simples de relaciones diatónicas, a mayor distancia de I. En términos del círculo [descendente] de quintas, se aleja de I, en lugar de acercarse a él". [4] Afirma que la progresión I–ii–V–I (una cadencia auténtica ) se sentiría más final o resuelta que I–IV–I (una cadencia plagal ). Goldman [5] coincide con Nattiez, quien sostiene que "el acorde en el cuarto grado aparece mucho antes que el acorde en II, y el I final posterior, en la progresión I–IV–vii o –iii–vi–ii–V–I", y también está más alejado de la tónica allí. [6] (En este y otros artículos relacionados, los números romanos en mayúsculas indican tríadas mayores, mientras que los números romanos en minúsculas indican tríadas menores).
Cierre de círculo en sistemas de afinación no iguales
El uso de la proporción exacta de frecuencias de 3:2 para definir una quinta perfecta ( entonación justa ) no da como resultado un retorno a la clase de tono de la nota inicial después de recorrer el círculo de quintas. La afinación de temperamento igual de doce tonos produce quintas que regresan a un tono exactamente siete octavas por encima del tono inicial y hace que la proporción de frecuencia del semitono cromático sea la misma que la del semitono diatónico. La quinta temperada estándar tiene una proporción de frecuencia de 2 7/12 :1 (o aproximadamente 1,498307077:1), aproximadamente dos centésimas más estrecha que una quinta afinada justamente.
Ascender doce quintas afinadas correctamente no cierra el círculo por un exceso de aproximadamente 23,46 centésimas , aproximadamente un cuarto de semitono , un intervalo conocido como coma pitagórica . Si se limita a doce tonos por octava, la afinación pitagórica acorta notablemente el ancho de una de las doce quintas, lo que la hace severamente disonante . Esta quinta anómala se llama quinta de lobo , una referencia humorística a un lobo aullando una nota desafinada. La quinta media no extendida de un cuarto de coma utiliza once quintas ligeramente más estrechas que la quinta igualmente temperada, y requiere una quinta de lobo mucho más ancha e incluso más disonante para cerrar el círculo. Los sistemas de afinación más complejos basados en la entonación justa, como la afinación de límite 5 , utilizan como máximo ocho quintas afinadas correctamente y al menos tres quintas no justas (algunas ligeramente más estrechas y otras ligeramente más anchas que la quinta justa) para cerrar el círculo.
Afinaciones de temperamento igual con más de doce notas
En la actualidad, con la llegada de los teclados electrónicos isomorfos , se pueden utilizar afinaciones de temperamento igual con más de doce notas por octava para cerrar el círculo de quintas de otras afinaciones. Por ejemplo, el temperamento igual de 31 tonos se aproxima mucho a la afinación de tono medio de un cuarto de coma, y el temperamento igual de 53 tonos se aproxima mucho a la afinación pitagórica.
Historia


El círculo de quintas se desarrolló a finales del siglo XVII y principios del siglo XVIII para teorizar la modulación de la era barroca (véase § Era barroca).
El primer diagrama de círculo de quintas aparece en la Grammatika (1677) del compositor y teórico Nikolay Diletsky , que pretendía presentar la teoría musical como una herramienta para la composición. [7] Fue "el primero de su tipo, destinado a enseñar a una audiencia rusa cómo escribir composiciones polifónicas de estilo occidental".
Un diagrama de círculo de quintas fue creado de forma independiente por el compositor y teórico alemán Johann David Heinichen en su Neu erfundene und gründliche Anweisung (1711), [8] al que llamó "Círculo Musical" (en alemán: Musicalischer Circul ). [9] [10] Esto también fue publicado en su Der General-Bass in der Composition (1728).
Heinichen colocó la tonalidad menor relativa junto a la tonalidad mayor, lo que no reflejaba la proximidad real de las tonalidades. Johann Mattheson (1735) y otros intentaron mejorar esto: David Kellner (1737) propuso tener las tonalidades mayores en un círculo y las tonalidades menores relativas en un segundo círculo interior. Esto se desarrolló más tarde en el espacio de acordes , incorporando también la menor paralela. [11]
Algunas fuentes implican que el círculo de quintas era conocido en la antigüedad, por Pitágoras . [12] [13] [14] Esto es un malentendido y un anacronismo. [15] La afinación por quintas (la llamada afinación pitagórica ) data de la antigua Mesopotamia; [16] ver Música de Mesopotamia § Teoría musical , aunque no extendieron esto a una escala de doce notas, deteniéndose en siete. La coma pitagórica fue calculada por Euclides y por matemáticos chinos (en el Huainanzi ); ver Coma pitagórica § Historia . Así, se sabía en la antigüedad que un ciclo de doce quintas era casi exactamente siete octavas (más prácticamente, alternar quintas ascendentes y cuartas descendentes era casi exactamente una octava). Sin embargo, este era un conocimiento teórico, y no se utilizó para construir una escala repetitiva de doce tonos, ni para modular. Esto se hizo más tarde en el temperamento medio y el temperamento igual de doce tonos , que permitían la modulación sin dejar de estar afinado, pero no se desarrolló en Europa hasta alrededor de 1500. Aunque se popularizó como el círculo de quintas, sus orígenes etimológicos anglosajones se remontan al nombre "rueda de quintas".
Usar
En piezas musicales de la era de la música barroca y de la era clásica de la música , así como en la música popular occidental , la música tradicional y la música folclórica , cuando las piezas o canciones se modulan a una nueva tonalidad, estas modulaciones suelen estar asociadas al círculo de quintas.
En la práctica, las composiciones rara vez hacen uso de todo el círculo de quintas. Más comúnmente, los compositores hacen uso de "la idea compositiva del 'ciclo' de quintas, cuando la música se mueve consistentemente a través de un segmento más pequeño o más grande de los recursos estructurales tonales que el círculo representa de manera abstracta". [17] La práctica habitual es derivar la progresión del círculo de quintas a partir de los siete tonos de la escala diatónica, en lugar de la gama completa de doce tonos presentes en la escala cromática. En esta versión diatónica del círculo, una de las quintas no es una quinta verdadera: es un tritono (o una quinta disminuida), por ejemplo, entre F y B en la escala diatónica "natural" (es decir, sin sostenidos ni bemoles). He aquí cómo se deriva el círculo de quintas, a través de la permutación de la escala mayor diatónica:

Y de la escala menor (natural):

La siguiente es la secuencia básica de acordes que se pueden construir sobre la línea de bajo mayor:

Y sobre el menor:

Añadir séptimas a los acordes crea una mayor sensación de impulso hacia adelante en la armonía:

Época barroca
Según Richard Taruskin , Arcangelo Corelli fue el compositor más influyente en establecer el patrón como un "tropo" armónico estándar : "Fue precisamente en la época de Corelli, a finales del siglo XVII, que el círculo de quintas estaba siendo 'teorizado' como el principal propulsor del movimiento armónico, y fue Corelli más que cualquier otro compositor quien puso esa nueva idea en práctica". [18]
La progresión en círculo de quintas aparece con frecuencia en la música de JS Bach . En el siguiente fragmento, de Jauchzet Gott en allen Landen , BWV 51 , incluso cuando la línea de bajo solista implica, en lugar de indicar, los acordes implicados:

Handel utiliza una progresión en círculo de quintas como base para el movimiento Passacaglia de su Suite para clavecín n.º 6 en sol menor.

Los compositores barrocos aprendieron a realzar la "fuerza propulsora" de la armonía engendrada por el círculo de quintas "añadiendo séptimas a la mayoría de los acordes constituyentes". "Estas séptimas, al ser disonancias, crean la necesidad de resolución, convirtiendo así cada progresión del círculo en un aliviador y reestimulador simultáneo de la tensión armónica... Por lo tanto, se aprovechan para fines expresivos". [19] Hay pasajes llamativos que ilustran el uso de séptimas en el aria "Pena tiranna" de la ópera Amadigi di Gaula de Handel de 1715 :

– y en el arreglo para teclado de Bach del Concierto para oboe y cuerdas de Alessandro Marcello .
![{ << \new PianoStaff << \new Staff = "acordes" << \magnifyStaff #2/3 \new Voice \relative c' { \key f \major \set Score.tempoHideNote = ##t \tempo 4 = 40 \time 3/4 \mark \markup { \abs-fontsize #10 { \bold { Adagio } } } d8 ddddd | eeeeee | gggggg | \stemUp d'( f) \stemNeutral f( la) a( c16 bes) | bes2 \mdent r4 | \break c,8( mi16 re) mi8( sol16 fa) sol8( bes16 la) | a2 \mdent r4 | bes,16( c32 a bes16 d32 cis) d16( e32 cis d16 f32 e) f16( g32 e f16 a32 g) | \break g2 \mdent r4 | a,32( gis abab cis b) cis( d cis dedefefg! fgfge) | f4 \mdent s4 } \new Voz \relativa c' { s2. | s | \stemDown e8 eeeee | f8 } \new Pentagrama << \magnifyPentagrama #2/3 \new Voz \relativa c' { \clave f \mayor \clave f \tiempo 3/4 R2. | d8 ddddd | \stemUp cis cis cis cis cis cis cis | d <d f>[ <d f> <d f> <d f> <d f>] | <d f> <d f> <d f> <d f> <d f> <d f> | eeeeee | <c e> <c e> <c e> <c e> <c e> <c e> | dddddd | <bes d> <bes d> <bes d> <bes d> <bes d> <bes d> | cis cis cis cis cis cis | d[ d] s4 } \new Voz \relativa c' { \clef F s2. | s | \stemDown a8 aaaaa | re, r r4 r | sol8 ggggg | do8 ccccc | fa, fffff | bes bes bes bes bes bes | mi, eeeee | aaaaaa | re,[ re] s4 } \addlyrics \with { alignAboveContext = "acordes" } { \override LyricText.font-size = #-1.5 _ _ _ _ _ _ Dm \markup{\concat{Gm\super{7}}} _ _ _ _ _ C _ _ _ _ _ \markup{\concat{F\super{maj7}}} _ _ _ _ _ Si♭ _ _ _ _ _ \markup{\concat{Em\super{7(♭5)}}} _ _ _ _ _ \markup{\concat{A\super{7}}} _ _ _ _ _ Dm } >> >> >> \new Staff \with { \omit Compás \magnifyStaff #2/3 firstClef = ##f } \relative c' { \hide Staff.KeySignature \key f \major \clef bass {\stopStaff s2. ss \startStaff \hide Tallo d8 sssssg, ssssscsssssf, sssss bes ssssse, sssssassssd,}} >> } \layout { line-width = #150 }](http://upload.wikimedia.org/score/2/r/2rj0hc4pt0k6grm4sbdi8k7nqi1sdl7/2rj0hc4p.png)
Siglo XIX
El Impromptu en mi bemol mayor, D 899, de Franz Schubert contiene armonías que se mueven en un círculo modificado de quintas:

El movimiento Intermezzo del Cuarteto de cuerdas n.º 2 de Mendelssohn tiene un segmento corto con movimiento de círculo de quintas (el ii° se sustituye por iv):

"El niño se duerme" de Robert Schumann, de sus Kinderszenen, utiliza la progresión, cambiándola al final: la pieza termina en un acorde de la menor, en lugar de la tónica esperada de mi menor.

En la ópera de Wagner , El ocaso de los dioses , se produce un ciclo de progresión de quintas en la música que va desde el final del prólogo hasta la primera escena del primer acto, ambientada en el imponente salón de los ricos gibichungos. "El estatus y la reputación están escritos en todos los motivos asignados a Gunther", [20] jefe del clan gibichungo:
![{<< \new ChoirStaff << \relative c' { \magnifyStaff #3/4 \set Score.tempoHideNote = ##t \tempo 4 = 60 \time 3/4 \set Staff.midiInstrument = #"trumpet" \transposition f'^"en F" \p \grace {s16 s} ees2( d4) | ees2(d4) | cis2. ~ cis4 rr | R2. | R | R | R | R | R } \new Staff \with{ \magnifyStaff #3/4 } << \new Voice \relative c' { \override Hairpin.minimum-length = #3 \set Staff.midiInstrument = #"trumpet" \transposition e'^ "en E" \p \grace {s16 s} \hide \pp <g bes>2( <bes g>4) | <g bes>2( <bes g>4) | <bes d>4.( <g bes>8 <a c>4 | <bes d>2.) |<bes d>4.( <g bes>8 <a c>4 ) | <bes d>2 ees4-! | c2._"(marc.)" | s2. | R | R } \new Voz \relativa c' { \stemDown \hide \p \grace {s16 s} s2. | s | s | s | s | s2 ees4-! | c2. | d4-! bes2 | R2. | R2. \bar "|." } >> >> \relative c' { \magnifyStaff # 3/4 \set Staff.midiInstrument = #"trombón" \transposición e^"en E" \p \grace {s16 s} \hide \pp g'2. ~ gramo ~ gramo ~ gramo | g~g2 bes4-! | g2._"(marco.)" | d'4-! bes2 | c2_"tenue." r4 | \pp d2 r4 } \new ChoirStaff << \relative c' { \magnifyStaff #3/4 \clef tenor \set Staff.midiInstrument = #"trombón" \p \grace {s16 s} aes2( g4) | aes2(g4) | fis2. ~ fis | fis~fis2 b4-! | g2._"(marco.)" | cis4-! b2 | b2_"tenue." r4 | \pp ais2 r4 } \relative c' { \magnifyStaff #3/4 \clef F \set Staff.midiInstrument = #"trombón" \p \grace {s16 s} \hide \pp <b, d>2. | < b d> | <b d> ~ <b d> | <b d> ~ <b d>2 <b g'>4-! | <e g>2._"(marc.)" | <fis a>4-! <d fis>2 | <e g>_"dim." r4 | \pp <cis fis>2 r4 } >> \relative c' { \magnifyStaff #3/4 \clef F \set Staff.midiInstrument = #"trombón" \ p \grace {s16 s} \hide \pp f,,!2( g4) | f!2( g4) | gis2. ~ gis | g! ~ g2 e4 ~ e a8._"(marc.)"[ g16 fis8. e16] | d2 g4( | cis,2_"dim.") r4 | \pp fis2 r4 } \relative c' { \magnifyStaff #3/ 4 \clef F \set Staff.midiInstrument = #"timbales" \p \grace {b,16 b} b4 rr | \grace {b16 b} b4 rr | \grace {b16 b} b4 rr | rbb | \grace { b16 b} b4 rr | rb f' | b, rr | R2. | R | R } \relative c' { \magnifyStaff #3/4 \clef F \set Staff.midiInstrument = #"tuba" \p \grace { s16 s} R2. | R2 | R2 | R2 | r4 re,, ~ e a8._"(marc.)"[ g16 fis8. e16] | d2 g4( cis,2_"dim." ) r4 | \pp fis2 r4 } >> } \layout { ancho-de-linea = #150 }](http://upload.wikimedia.org/score/b/9/b9cg7s9gxq732qwfg97n25bgulyaxon/b9cg7s9g.png)
Jazz y música popular
La popularidad duradera del círculo de quintas como recurso para la construcción de formas y como tropo musical expresivo es evidente en la cantidad de canciones populares " estándar " compuestas durante el siglo XX. También es un vehículo favorito para la improvisación entre los músicos de jazz, ya que el círculo de quintas ayuda a los compositores a comprender los intervalos, las relaciones de acordes y las progresiones.
- Bart Howard , " Llévame a la luna "
La canción se inicia con un patrón de frases descendentes –en esencia, el estribillo de la canción– presentadas con una previsibilidad tranquilizadora, casi como si la dirección futura de la melodía estuviera dictada por las cinco notas iniciales. La progresión armónica, por su parte, rara vez se aparta del círculo de quintas. [21]
- Jerome Kern , “ Todas las cosas que eres ” [22]
- Ray Noble , " Cherokee ". Muchos músicos de jazz han encontrado esto particularmente desafiante ya que el octavo central avanza tan rápidamente a través del círculo, "creando una serie de progresiones II-V-I que pasan temporalmente por varias tonalidades ". [23]
- Kosma, Prévert y Mercer, “ Hojas de otoño ” [24]
- The Beatles , " Nunca me darás tu dinero " [25] [ se necesita una fuente no primaria ]
- Mike Oldfield , " Encantamientos " [26]
- Carlos Santana , " Europa (El grito de la Tierra, la sonrisa del Cielo) " [ cita requerida ]
- Gloria Gaynor , " Sobreviviré " [27] [ se necesita una fuente no primaria ]
- Pet Shop Boys , " Es un pecado " [28] [ se necesita una fuente no primaria ]
- Donna Summer , " Love to Love you, Baby " [29] [ se necesita una fuente no primaria ]
Conceptos relacionados
Círculo diatónico de quintas
El círculo diatónico de quintas es el círculo de quintas que abarca solo los miembros de la escala diatónica. Por lo tanto, contiene una quinta disminuida, en do mayor entre si y fa. Ver estructura implica multiplicidad . La progresión circular es comúnmente un círculo de quintas a través de los acordes diatónicos, incluido un acorde disminuido . A continuación se muestra una progresión circular en do mayor con los acordes I–IV–vii o –iii–vi–ii–V–I.
Círculo cromático
El círculo de quintas está estrechamente relacionado con el círculo cromático , que también organiza las clases de tonos de temperamento igual de una afinación particular en un orden circular. Una diferencia clave entre los dos círculos es que el círculo cromático puede entenderse como un espacio continuo donde cada punto del círculo corresponde a una clase de tono concebible , y cada clase de tono concebible corresponde a un punto del círculo. Por el contrario, el círculo de quintas es fundamentalmente una estructura discreta dispuesta a través de intervalos distintos , y no hay una forma obvia de asignar clases de tono a cada uno de sus puntos. En este sentido, los dos círculos son matemáticamente bastante diferentes.
Sin embargo, para cualquier entero positivo N , las clases de tono en el temperamento igual de N tonos pueden representarse por el grupo cíclico de orden N , o equivalentemente, las clases de residuo módulo igual a N , . En el temperamento igual de doce tonos, el grupo tiene cuatro generadores, que pueden identificarse con los semitonos ascendentes y descendentes y las quintas perfectas ascendentes y descendentes. El generador de semitonos da lugar al círculo cromático , mientras que la cuarta perfecta y la quinta perfecta dan lugar al círculo de quintas. En la mayoría de las demás afinaciones, como en el temperamento igual de 31 , se pueden utilizar muchos más intervalos como generador y, como resultado, son posibles muchos más círculos.
Relación con la escala cromática

El círculo de quintas o cuartas puede representarse a partir de la escala cromática mediante la multiplicación , y viceversa. Para representar entre el círculo de quintas y la escala cromática (en notación entera ) se multiplica por 7 ( M7 ), y para el círculo de cuartas se multiplica por 5 ( P5 ).
En el temperamento igual de doce tonos, uno puede comenzar con una tupla ordenada de 12 números enteros ( fila de tonos ):
- (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11)
Representando las notas de la escala cromática: 0 = C, 2 = D, 4 = E, 5 = F, 7 = G, 9 = A, 11 = B, 1 = C ♯ , 3 = D ♯ , 6 = F ♯ , 8 = G ♯ , 10 = A ♯ . Ahora multiplica todo el 12-tono por 7:
- (0, 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77)
y luego aplicar una reducción módulo 12 a cada uno de los números (restar 12 de cada número tantas veces como sea necesario hasta que el número sea menor que 12):
- (0, 7, 2, 9, 4, 11, 6, 1, 8, 3, 10, 5)
que es equivalente a
- (C, G, D, A, E, B, F ♯ , C ♯ , G ♯ , D ♯ , A ♯ , F)
que es el círculo de quintas. Esto es enarmónicamente equivalente a:
- (C, G, D, A, E, B, G ♭ , D ♭ , A ♭ , E ♭ , B ♭ , F).
Equivalentes enarmónicos, tonalidades teóricas y espiral de quintas


Las afinaciones de temperamento igual no utilizan la proporción exacta de frecuencias de 3:2 que define una quinta perfecta, mientras que la entonación justa utiliza esta proporción exacta. Ascender por quintas en temperamento igual conduce a un regreso a la clase de tono inicial: comenzar con un Do y ascender por quintas conduce a otro Do después de un cierto número de iteraciones. Esto no ocurre si se utiliza una proporción exacta de 3:2 (solo entonación). El ajuste realizado en la afinación de temperamento igual se llama coma pitagórica . Debido a esta diferencia, los tonos que son enarmónicamente equivalentes en temperamentos iguales (como Do ♯ y Re ♭ en temperamento igual de 12 tonos, o Do ♯ y Re ♭ en temperamento igual de 12 tonos) son enarmónicamente equivalentes. en 19 temperamento igual ) no son equivalentes cuando se utiliza solo la entonación.
en 19 temperamento igual ) no son equivalentes cuando se utiliza solo la entonación.
En la entonación justa, la secuencia de quintas puede visualizarse como una espiral, no como un círculo: una secuencia de doce quintas da como resultado una " bomba de coma " según la coma pitagórica, que se visualiza como un ascenso de un nivel en la espiral. Véase también § Cierre de círculo en sistemas de afinación no iguales.
Sin equivalencias enarmónicas, continuar una secuencia de quintas da como resultado notas con alteraciones dobles (sostenidas dobles o bemoles dobles), o incluso alteraciones triples o cuádruples. En la mayoría de las afinaciones de temperamento igual, estas pueden reemplazarse por notas enarmónicamente equivalentes.
Las tonalidades con dobles o triples sostenidos y bemoles en las armaduras se denominan tonalidades teóricas ; son redundantes en el temperamento igual de doce tonos, por lo que su uso es extremadamente raro, pero si el número de notas por octava no es múltiplo de 12, se distinguen. La notación en estos casos no está estandarizada.

El comportamiento predeterminado de LilyPond (en la imagen de arriba) escribe los sostenidos o bemoles simples en el orden del círculo de quintas, antes de proceder a los sostenidos o bemoles dobles. Este es el formato utilizado en A World Requiem de John Foulds , Op. 60, [31] que termina con la armadura de clave de sol ♯ mayor, como se muestra arriba. Los sostenidos en la armadura de clave de sol ♯ mayor aquí proceden de do ♯ , sol ♯ , re ♯ , la ♯ , mi ♯ , si ♯ , fa. .
.
Los sostenidos o bemoles individuales en la armadura de clave a veces se repiten como cortesía, por ejemplo, en el Suplemento a la teoría de la modulación de Max Reger , que contiene armaduras de clave menor en re bemol en las páginas 42 a 45. Estas tienen un si bemol al principio y también un si bemol. Al final (con un símbolo doble bemol), va Si ♭ , Mi ♭ , La ♭ , Re ♭ , Sol ♭ , Do ♭ , Fa ♭ , Si
Al final (con un símbolo doble bemol), va Si ♭ , Mi ♭ , La ♭ , Re ♭ , Sol ♭ , Do ♭ , Fa ♭ , Si La convención de LilyPond y Foulds suprimiría el B ♭ inicial . A veces, los signos dobles se escriben al principio de la armadura, seguidos de los signos simples. Por ejemplo, la armadura de F ♭ se escribe como B
La convención de LilyPond y Foulds suprimiría el B ♭ inicial . A veces, los signos dobles se escriben al principio de la armadura, seguidos de los signos simples. Por ejemplo, la armadura de F ♭ se escribe como B , E ♭ , A ♭ , D ♭ , G ♭ , C ♭ , F ♭ . Esta convención es utilizada por Victor Ewald, [32] por el programa Finale y por algunos trabajos teóricos.
, E ♭ , A ♭ , D ♭ , G ♭ , C ♭ , F ♭ . Esta convención es utilizada por Victor Ewald, [32] por el programa Finale y por algunos trabajos teóricos.
Véase también
- Acorde de aproximación
- Forma sonata
- Buen temperamento
- Tabla de texto del círculo de quintas
- Constelación de tono
- Grupo multiplicativo de números enteros módulo n
- Multiplicación (música)
- Círculo de tercios
Notas
Referencias
- ^ Michael Pilhofer y Holly Day (23 de febrero de 2009). "El círculo de quintas: una breve historia", www.dummies.com.
- ^ Broekhuis, Rogier (11 de octubre de 2022). «Rueda de quintas: función armónica». Rueda de quintas . Consultado el 5 de octubre de 2023 .
- ^ Nattiez 1990, pág. 225.
- ^ Goldman 1965, pág. 68.
- ^ Goldman 1965, capítulo 3.
- ^ Nattiez 1990, pág. 226.
- ^ Jensen 1992, págs. 306-307
- ^ Johann David Heinichen, Neu erfundene und gründliche Anweisung (1711), pág. 261
- ^ Barnett 2002, pág. 444.
- ^ Lester 1989, págs. 110-112.
- ^ Lerdahl, Fred (2005). Tonal Pitch Space. Nueva York: Oxford University Press. pág. 42. ISBN 0195178297.
- ^ "¡Guía completa del Círculo de Quintas!". 17 de enero de 2021.
- ^ "El Círculo de Quintas dejado en claro".
- ^ "Dummies - El aprendizaje es fácil".
- ^ Fraser, Peter A. (2001), The Development of Musical Tuning Systems (PDF) , pp. 9, 13, archivado desde el original (PDF) el 1 de julio de 2013 , consultado el 24 de mayo de 2020
- ^ Dumbrill, Richard J. (2005). La arqueomusicología del Próximo Oriente antiguo . Victoria, BC, pág. 18. ISBN 978-1412055383.
{{cite book}}: Mantenimiento de CS1: falta la ubicación del editor ( enlace ) - ^ Whittall, A. (2002, p. 259) "Círculo de quintas", artículo en Latham, E. (ed.) The Oxford Companion to Music . Oxford University Press.
- ^ Taruskin 2010, pág. 184.
- ^ Taruskin 2010, pág. 188.
- ^ Scruton, R. (2016, p. 121) El anillo de la verdad: la sabiduría del Anillo del Nibelungo de Wagner . Londres, Allen Lane.
- ^ Gioia 2012, pág. 115.
- ^ Gioia 2012, pág. 16.
- ^ Scott, Richard J. (2003, pág. 123) Progresiones de acordes para compositores . Bloomington Indiana, Writers Club Press.
- ^ Kostka, Stefan ; Payne, Dorothy; Almén, Byron (2013). Armonía tonal con una introducción a la música del siglo XX (7.ª ed.). Nueva York: McGraw-Hill. pp. 46, 238. ISBN 978-0-07-131828-0.
- ^ "Nunca me das tu dinero" (1989, págs. 1099-1100, compases 1-16) The Beatles Partituras completas . Hal Leonard.
- ^ Oakes, Tim (junio de 1980). "Mike Oldfield". Músico internacional y mundo de la grabación . Consultado el 19 de febrero de 2021 a través de Tubular.net.
- ^ Fekaris, D. y Perren, FJ (1978) "Sobreviviré". Polygram International Publishing.
- ^ Tennant, N. y Lowe, C. (1987, compases 1–8) "Es un pecado". Sony/ATV Music Publishing (Reino Unido) Ltd.
- ^ Moroder, G. , Bellote, P. y Summer, D. (1975, compases 11-14) "Love to Love you, Baby" 1976, Bulle Music
- ^ McCartin 1998, pág. 364.
- ^ "Foulds, John, Un Réquiem Mundial, Op. 60, págs. 153 y siguientes".
- ^ "Ewald, Victor, Quinteto n.º 4 en la bemol, Op. 8 para quinteto de metales [211.01]".
Fuentes
- Barnett, Gregory (2002). "Organización tonal en la teoría musical del siglo XVII". En Thomas Christensen (ed.). The Cambridge History of Western Music Theory . Cambridge: Cambridge University Press. págs. 407–455.
- Gioia, Ted (2012). Los estándares del jazz: una guía del repertorio . Oxford University Press. ISBN 9780199769155.
- Goldman, Richard Franko (1965). Armonía en la música occidental . Nueva York: WW Norton.
- Jensen, Claudia R. (verano de 1992). "Un trabajo teórico de la Moscovia de finales del siglo XVII: "Grammatika" de Nikolai Diletskii y el primer círculo de quintas". Revista de la Sociedad Americana de Musicología . 45 (2): 305–331. doi :10.2307/831450. JSTOR 831450.
- Lester, Joel (1989). Entre modos y claves: teoría alemana 1592-1802 . Stuyvesant: Pendragon Press.
- McCartin, Brian J. (noviembre de 1998). "Preludio a la geometría musical". The College Mathematics Journal . 29 (5): 354–370. doi :10.1080/07468342.1998.11973971. JSTOR 2687250. Archivado desde el original el 17 de mayo de 2008. Consultado el 29 de julio de 2008 .
- Nattiez, Jean-Jacques (1990). Música y discurso: hacia una semiología de la música , traducido por Carolyn Abbate. Princeton, Nueva Jersey: Princeton University Press. ISBN 0-691-02714-5 . (Publicado originalmente en francés, como Musicologie générale et sémiologie . París: C. Bourgois, 1987. ISBN 2-267-00500-X ).
- Taruskin, Richard (2010). La historia de Oxford de la música occidental: la música en los siglos XVII y XVIII . Oxford University Press.
Lectura adicional
- D'Indy, Vicente (1903). Curso de composición musical . París: A. Durand et fils.
- Lester, Joel. Entre modos y claves: teoría alemana, 1592-1802. 1990.
- Miller, Michael. Guía completa para idiotas sobre teoría musical, 2.ª ed. [Indianápolis, IN]: Alpha, 2005. ISBN 1-59257-437-8 .
- Purwins, Hendrik (2005). "Perfiles de clases de altura tonal: circularidad de altura tonal y tonalidad relativas: experimentos, modelos, análisis computacional de música y perspectivas". Tesis doctoral. Berlín: Technische Universität Berlin .
- Purwins, Hendrik, Benjamin Blankertz y Klaus Obermayer (2007). "Modelos toroidales en teoría tonal y análisis de clases de altura". en: Computing in Musicology 15 ("Teoría tonal para la era digital"): 73–98.
Enlaces externos
- Descifrando el Círculo de Vths
- Círculo interactivo de quintas
- Herramienta interactiva para componer círculos de quintas
- Círculo de quintas interactivo para guitarristas


