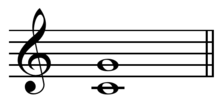
Quinta perfecta
| Inverso | cuarta perfecta |
|---|---|
| Nombre | |
| Otros nombres | diapente |
| Abreviatura | P5 |
| Tamaño | |
| Semitonos | 7 |
| Clase de intervalo | 5 |
| Sólo intervalo | 3:2 |
| Centavos | |
| Temperamento igual de 12 tonos | 700 |
| Solo entonación | 701.955 [1] |
En teoría musical , una quinta perfecta es el intervalo musical correspondiente a un par de tonos con una relación de frecuencia de 3:2, o muy cercana.
En la música clásica de la cultura occidental , una quinta es el intervalo que va desde la primera hasta la última de las cinco primeras notas consecutivas de una escala diatónica . [2] La quinta perfecta (a menudo abreviada P5 ) abarca siete semitonos , mientras que la quinta disminuida abarca seis y la quinta aumentada abarca ocho semitonos. Por ejemplo, el intervalo de do a sol es una quinta perfecta, ya que la nota sol se encuentra siete semitonos por encima de do.
La quinta perfecta puede derivarse de la serie armónica como el intervalo entre el segundo y el tercer armónico. En una escala diatónica, la nota dominante es una quinta perfecta por encima de la nota tónica .
La quinta perfecta es más consonante o estable que cualquier otro intervalo, excepto el unísono y la octava . Se encuentra por encima de la raíz de todos los acordes mayores y menores (tríadas) y sus extensiones . Hasta finales del siglo XIX, se la solía denominar por uno de sus nombres griegos, diapente . [3] Su inversión es la cuarta perfecta . La octava de la quinta es la duodécima.
Una quinta perfecta está al comienzo de " Twinkle, Twinkle, Little Star "; el tono del primer "twinkle" es la nota raíz y el tono del segundo "twinkle" es una quinta perfecta por encima de ella.
Definiciones alternativas
El término perfecto identifica a la quinta justa como perteneciente al grupo de intervalos perfectos (incluyendo el unísono , la cuarta justa y la octava ), llamados así por sus relaciones tonales simples y su alto grado de consonancia . [4] Cuando un instrumento con solo doce notas por octava (como el piano) se afina usando la afinación pitagórica , una de las doce quintas (la quinta lobo ) suena severamente discordante y difícilmente puede calificarse como "perfecta", si este término se interpreta como "altamente consonante". Sin embargo, cuando se usa la ortografía enarmónica correcta , la quinta lobo en la afinación pitagórica o temperamento medio no es en realidad una quinta perfecta sino una sexta disminuida (por ejemplo G ♯ – E ♭ ).
Los intervalos perfectos también se definen como aquellos intervalos naturales cuyas inversiones también son naturales, donde natural, a diferencia de alterado, designa aquellos intervalos entre una nota base y otra nota en la escala diatónica mayor que comienza en esa nota base (por ejemplo, los intervalos de do a do, re, mi, fa, sol, la, si, do, sin sostenidos ni bemoles); esta definición lleva a que los intervalos perfectos sean solo el unísono , la cuarta , la quinta y la octava , sin apelar a grados de consonancia. [5]
El término perfecto también se ha utilizado como sinónimo de justo , para distinguir los intervalos afinados a proporciones de números enteros pequeños de aquellos que están "templados" o "imperfectos" en varios otros sistemas de afinación, como el temperamento igual . [6] [7] El unísono perfecto tiene una relación de tono de 1:1, la octava perfecta de 2:1, la cuarta perfecta de 4:3 y la quinta perfecta de 3:2.
Dentro de esta definición, otros intervalos también pueden llamarse perfectos, por ejemplo una tercera perfecta (5:4) [8] o una sexta mayor perfecta (5:3). [9]
Otras cualidades
Además de la quinta perfecta, existen otros dos tipos o calidades de quintas: la quinta disminuida , que es un semitono cromático menor, y la quinta aumentada , que es un semitono cromático mayor. En términos de semitonos, estas son equivalentes al tritono (o cuarta aumentada) y a la sexta menor , respectivamente.
Relación de tono


La relación de afinación justa de una quinta perfecta es 3:2 (también conocida, en la teoría musical antigua, como hemiola ), [11] [12] lo que significa que la nota superior produce tres vibraciones en la misma cantidad de tiempo que la nota inferior produce dos. La quinta perfecta se puede escuchar cuando se afina un violín : si las cuerdas adyacentes se ajustan a la relación exacta de 3:2, el resultado es un sonido suave y consonante, y el violín suena afinado.
Los instrumentos de teclado, como el piano, normalmente utilizan una versión de quinta perfecta con temperamento igual , lo que permite que el instrumento pueda tocar en todas las tonalidades . En el temperamento igual de 12 tonos, las frecuencias de la quinta perfecta temperada están en la proporción de aproximadamente 1,498307. Una quinta perfecta con temperamento igual, definida como 700 centésimas , es aproximadamente dos centésimas más estrecha que una quinta perfecta justa, que es aproximadamente 701,955 centésimas.
Kepler exploró la afinación musical en términos de proporciones enteras y definió una "quinta imperfecta inferior" como una proporción de tono de 40:27 y una "quinta imperfecta mayor" como una proporción de tono de 243:160. [13] Su proporción de quinta perfecta inferior de 1,48148 (680 cents) es mucho más "imperfecta" que la afinación de temperamento igual (700 cents) de 1,4983 (en relación con el ideal de 1,50). Hermann von Helmholtz utiliza la proporción de 301:200 (708 cents) como un ejemplo de una quinta imperfecta; contrasta la proporción de una quinta en temperamento igual (700 cents) con una "quinta perfecta" (3:2), y analiza la audibilidad de los pulsos que resultan de una afinación tan "imperfecta". [14]
Utilizar en armonía
WE Heathcote describe la octava como la representación de la unidad primordial dentro de la tríada, una unidad superior producida a partir del proceso sucesivo: "primero la octava, luego la quinta, luego la tercera, que es la unión de las dos anteriores". [15] Hermann von Helmholtz sostiene que algunos intervalos, a saber, la cuarta, la quinta y la octava perfectas, "se encuentran en todas las escalas musicales conocidas", aunque el editor de la traducción inglesa de su libro señala que la cuarta y la quinta pueden ser intercambiables o indeterminadas. [16]
La quinta perfecta es un elemento básico en la construcción de tríadas mayores y menores , y sus extensiones . Debido a que estos acordes aparecen con frecuencia en gran parte de la música, la quinta perfecta aparece con la misma frecuencia. Sin embargo, dado que muchos instrumentos contienen una quinta perfecta como sobretono , no es inusual omitir la quinta de un acorde (especialmente en la posición fundamental).
La quinta justa también está presente en los acordes de séptima, así como en las armonías de "tercianas altas" (armonías que consisten en más de cuatro tonos apilados en terceras por encima de la fundamental). La presencia de una quinta justa puede, de hecho, suavizar los intervalos disonantes de estos acordes, como en el acorde de séptima mayor , en el que la disonancia de una séptima mayor se suaviza mediante la presencia de dos quintas justas.
Los acordes también se pueden construir apilando quintas, lo que produce armonías quintales. Tales armonías están presentes en la música más moderna, como la música de Paul Hindemith . Esta armonía también aparece en La consagración de la primavera de Stravinsky en la "Danza de los adolescentes", donde cuatro trompetas en do , una trompeta piccolo y una trompa tocan un acorde quintal en si bemol de cinco tonos. [17]
Quinta desnuda, quinta abierta o quinta vacía

Una quinta desnuda, una quinta abierta o una quinta vacía es un acorde que contiene solo una quinta perfecta sin tercera. Los acordes finales de Viderunt omnes y Sederunt Principes de Pérotin , Messe de Nostre Dame de Guillaume de Machaut , el Kyrie en el Réquiem de Mozart y el primer movimiento de la Novena Sinfonía de Bruckner son todos ejemplos de piezas que terminan en una quinta abierta. Estos acordes son comunes en la música medieval , el canto de arpa sacra y en toda la música rock . En la música hard rock , metal y punk , la guitarra eléctrica saturada o distorsionada puede hacer que las terceras suenen turbias mientras que las quintas desnudas permanecen nítidas. Además, los pasajes rápidos basados en acordes son más fáciles de tocar al combinar las cuatro formas de mano de guitarra más comunes en una sola. Los músicos de rock se refieren a ellos como acordes de potencia . Los acordes de potencia a menudo incluyen duplicación de octavas (es decir, su nota baja se duplica una octava más alta, por ejemplo, F3–C4–F4).
En la música tradicional , por ejemplo, en la música asiática y en algunos géneros musicales andinos de origen precolombino, como el k'antu y el sikuri , se utiliza a veces una quinta vacía . La misma melodía está guiada por quintas y octavas paralelas durante toda la pieza.
Los compositores occidentales pueden utilizar el intervalo para darle a un pasaje un sabor exótico. [18] Las quintas vacías también se utilizan a veces para darle a una cadencia una cualidad ambigua, ya que la quinta desnuda no indica una tonalidad mayor o menor.
Uso en afinación y sistemas tonales
La quinta perfecta, junto con la octava , constituye la base de la afinación pitagórica . Una quinta perfecta ligeramente estrechada es asimismo la base de la afinación de tonos medios . [ cita requerida ]
El círculo de quintas es un modelo de espacio tonal para la escala cromática (círculo cromático), que considera la proximidad como el número de quintas perfectas necesarias para llegar de una nota a otra, en lugar de la adyacencia cromática.
Véase también
Referencias
- ^
- ^ Don Michael Randel (2003), "Intervalo", Harvard Dictionary of Music , cuarta edición (Cambridge, Massachusetts: Harvard University Press): pág. 413.
- ^ William Smith y Samuel Cheetham (1875). Diccionario de antigüedades cristianas. Londres: John Murray. pág. 550. ISBN 9780790582290.
- ^ Pistón, Walter ; De Voto, Mark (1987). Armonía (5ª ed.). Nueva York: WW Norton. pag. 15.ISBN 0-393-95480-3.Las octavas, los intervalos perfectos, las terceras y las sextas se clasifican como "intervalos consonánticos", pero las terceras y las sextas se califican como "consonancias imperfectas".
- ^ Kenneth McPherson Bradley (1908). Armonía y análisis. CF Summy. pág. 17.
- ^ Charles Knight (1843). Penny Cyclopaedia. Sociedad para la Difusión del Conocimiento Útil. pág. 356.
- ^ John Stillwell (2006). Anhelo de lo imposible . AK Peters. pág. 21. ISBN 1-56881-254-X.
quinta perfecta quinta imperfecta temperada.
- ^ Llewelyn Southworth Lloyd (1970). Música y sonido. Ayer Publishing. pág. 27. ISBN 0-8369-5188-3.
- ^ John Broadhouse (1892). Acústica musical. W. Reeves. pág. 277.
proporción perfecta de sexta mayor.
- ^ por John Fonville (verano de 1991). " La entonación justa extendida de Ben Johnston : una guía para intérpretes". Perspectivas de la nueva música . 29 (2): 109 (106–137). doi :10.2307/833435. JSTOR 833435.
- ^ Willi Apel (1972). "Hemiola, hemiolia" . Diccionario de música de Harvard (2.ª ed.). Cambridge, Massachusetts: Harvard University Press. pág. 382. ISBN 0-674-37501-7.
- ^ Randel, Don Michael , ed. (2003). "Hemiola, hemiola". Diccionario de música de Harvard: cuarta edición . Diccionario de música de Harvard (4.ª ed.). Cambridge, Massachusetts: Harvard University Press. pág. 389. ISBN 0-674-01163-5.
- ^ Johannes Kepler (2004). Stephen Hawking (ed.). Armonías del mundo . Running Press. pág. 22. ISBN 0-7624-2018-9.
- ^ Hermann von Helmholtz (1912). Sobre las sensaciones del sonido como base fisiológica de la teoría de la música. Longmans, Green. pp. 199, 313. ISBN 9781419178931.
quinta perfecta quinta imperfecta temperada de Helmholtz
- ^ WE Heathcote (1888), "Ensayo introductorio", en Moritz Hauptmann , La naturaleza de la armonía y el metro, traducido y editado por WE Heathcote (Londres: Swan Sonnenschein), pág. xx.
- ^ Hermann von Helmholtz (1912). Sobre las sensaciones del sonido como base fisiológica de la teoría de la música. Longmans, Green. pág. 253. ISBN 9781419178931.
quinta perfecta quinta imperfecta temperada de Helmholtz
- ^ Pistón y DeVoto 1987, págs. 503–505.
- ^ Scott Miller, "Inside The King and I", New Line Theatre , consultado el 28 de diciembre de 2012
![{\displaystyle ({\sqrt[{12}]{2}})^{7}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb23db3674c3081c7995b2e899d4d6c8f36159bb)
