Equilibrio químico

Parte de una serie sobre
Química
Ciencia de la materia
Índice Describir Glosario Historia ( línea de tiempo )
Componentes clave Asunto Fase Vínculo Reacción química Ion Reacción ácido-base Redox Equilibrio químico Ley química
Sucursales Química analítica Bioquímica Química orgánica Química inorgánica Química física
Investigación Químico ( lista ) Lista de premios de química Lista de revistas Lista de problemas sin resolver
Portal de química  Categoría
en a mi

En una reacción química , el equilibrio químico es el estado en el que tanto los reactivos como los productos están presentes en concentraciones que no tienen tendencia a cambiar con el tiempo, de modo que no hay cambios observables en las propiedades del sistema . ^[1] Este estado se produce cuando la reacción directa se produce a la misma velocidad que la reacción inversa . Las velocidades de reacción de las reacciones directa e inversa generalmente no son cero, pero son iguales. Por lo tanto, no hay cambios netos en las concentraciones de los reactivos y los productos. Tal estado se conoce como equilibrio dinámico . ^{[2] [3]}

El concepto de equilibrio químico fue desarrollado en 1803, después de que Berthollet descubriera que algunas reacciones químicas son reversibles . ^[4] Para que cualquier mezcla de reacción exista en equilibrio, las velocidades de las reacciones directa e inversa (inversa) deben ser iguales. En la siguiente ecuación química , las flechas apuntan en ambas direcciones para indicar el equilibrio. ^[5] A y B son especies químicas reactivas , S y T son especies de productos, y α , β , σ y τ son los coeficientes estequiométricos de los respectivos reactivos y productos:

α  A + β  B ⇌ σ  S + τ  T

Se dice que la posición de concentración de equilibrio de una reacción se encuentra "muy a la derecha" si, en el equilibrio, se consumen casi todos los reactivos. Por el contrario, se dice que la posición de equilibrio está "muy a la izquierda" si casi no se forma ningún producto a partir de los reactivos.

Guldberg y Waage (1865), basándose en las ideas de Berthollet, propusieron la ley de acción de masas :

${\displaystyle {\begin{aligned}{\text{forward reaction rate}}&=k_{+}{\ce {A}}^{\alpha }{\ce {B}}^{\beta }\\{\text{backward reaction rate}}&=k_{-}{\ce {S}}^{\sigma }{\ce {T}}^{\tau }\end{aligned}}}$

donde A, B, S y T son masas activas y k ₊ y k− son constantes de velocidad _. Como en el equilibrio las velocidades de avance y retroceso son iguales:

${\displaystyle k_{+}\left\{{\ce {A}}\right\}^{\alpha }\left\{{\ce {B}}\right\}^{\beta }=k_{-}\left\{{\ce {S}}\right\}^{\sigma }\left\{{\ce {T}}\right\}^{\tau }}$

y la relación de las constantes de velocidad también es una constante, ahora conocida como constante de equilibrio .

${\displaystyle K_{c}={\frac {k_{+}}{k_{-}}}={\frac {\{{\ce {S}}\}^{\sigma }\{{\ce {T}}\}^{\tau }}{\{{\ce {A}}\}^{\alpha }\{{\ce {B}}\}^{\beta }}}}$

Por convención, los productos forman el numerador . Sin embargo, la ley de acción de masas es válida solo para reacciones concertadas de un solo paso que pasan por un solo estado de transición y no es válida en general porque las ecuaciones de velocidad no siguen, en general, la estequiometría de la reacción como habían propuesto Guldberg y Waage (véase, por ejemplo, la sustitución alifática nucleofílica por S _N 1 o la reacción de hidrógeno y bromo para formar bromuro de hidrógeno ). Sin embargo, la igualdad de las velocidades de reacción hacia adelante y hacia atrás es una condición necesaria para el equilibrio químico, aunque no es suficiente para explicar por qué se produce el equilibrio.

A pesar de las limitaciones de esta derivación, la constante de equilibrio de una reacción es, de hecho, una constante, independiente de las actividades de las distintas especies implicadas, aunque depende de la temperatura, como se observa en la ecuación de van 't Hoff . La adición de un catalizador afectará tanto a la reacción directa como a la reacción inversa de la misma manera y no tendrá efecto sobre la constante de equilibrio. El catalizador acelerará ambas reacciones, aumentando así la velocidad a la que se alcanza el equilibrio. ^{[2] [6]}

Aunque las concentraciones de equilibrio macroscópico son constantes en el tiempo, las reacciones ocurren a nivel molecular. Por ejemplo, en el caso del ácido acético disuelto en agua y que forma iones acetato e hidronio ,

CH3CO2H + _H2O ⇌ _CH3CO​​_​​−2+ _H3O ⁺​

Un protón puede saltar de una molécula de ácido acético a una molécula de agua y luego a un anión acetato para formar otra molécula de ácido acético y dejar inalterada la cantidad de moléculas de ácido acético. Este es un ejemplo de equilibrio dinámico . Los equilibrios, como el resto de la termodinámica, son fenómenos estadísticos, promedios del comportamiento microscópico.

El principio de Le Châtelier (1884) predice el comportamiento de un sistema en equilibrio cuando se producen cambios en sus condiciones de reacción. Si se altera un equilibrio dinámico al cambiar las condiciones, la posición de equilibrio se mueve para revertir parcialmente el cambio . Por ejemplo, agregar más S (a la reacción química anterior) desde el exterior provocará un exceso de productos, y el sistema intentará contrarrestarlo aumentando la reacción inversa y empujando el punto de equilibrio hacia atrás (aunque la constante de equilibrio permanecerá igual).

Si se añade ácido mineral a la mezcla de ácido acético, aumentando la concentración del ion hidronio, la cantidad de disociación debe disminuir a medida que la reacción se desplaza hacia la izquierda de acuerdo con este principio. Esto también se puede deducir de la expresión de la constante de equilibrio para la reacción:

${\displaystyle K={\frac {\{{\ce {CH3CO2-}}\}\{{\ce {H3O+}}\}}{{\ce {\{CH3CO2H\}}}}}}$

Si {H ₃ O ⁺ } aumenta {CH ₃ CO ₂ H} debe aumentar y CH ₃ CO−2debe disminuir. El H2O _se deja fuera, ya que es el disolvente y su concentración permanece alta y casi constante.

Una versión cuantitativa viene dada por el cociente de reacción .

JW Gibbs sugirió en 1873 que el equilibrio se alcanza cuando la energía libre de Gibbs del potencial químico del sistema está en su valor mínimo (suponiendo que la reacción se lleva a cabo a una temperatura y presión constantes). Esto significa que la derivada de la energía de Gibbs con respecto a la coordenada de reacción (una medida del grado de reacción que ha ocurrido, que va desde cero para todos los reactivos hasta un máximo para todos los productos) se anula (porque dG = 0), lo que indica un punto estacionario . Esta derivada se denomina energía de Gibbs de reacción (o cambio de energía) y corresponde a la diferencia entre los potenciales químicos de los reactivos y los productos en la composición de la mezcla de reacción. ^[1] Este criterio es necesario y suficiente. Si una mezcla no está en equilibrio, la liberación del exceso de energía de Gibbs (o energía de Helmholtz en reacciones de volumen constante) es la "fuerza impulsora" para que la composición de la mezcla cambie hasta que se alcance el equilibrio. La constante de equilibrio se puede relacionar con el cambio de energía libre de Gibbs estándar para la reacción mediante la ecuación

${\displaystyle \Delta _{r}G^{\ominus }=-RT\ln K_{\mathrm {eq} }}$

donde R es la constante universal de los gases y T la temperatura .

Cuando los reactivos se disuelven en un medio de alta fuerza iónica, el cociente de los coeficientes de actividad puede considerarse constante. En ese caso, el cociente de concentración , K _c ,

${\displaystyle K_{\ce {c}}={\frac {[{\ce {S}}]^{\sigma }[{\ce {T}}]^{\tau }}{[{\ce {A}}]^{\alpha }[{\ce {B}}]^{\beta }}}}$

donde [A] es la concentración de A, etc., es independiente de la concentración analítica de los reactivos. Por esta razón, las constantes de equilibrio para soluciones se determinan generalmente en medios de alta fuerza iónica. K _c varía con la fuerza iónica , la temperatura y la presión (o el volumen). Del mismo modo, K _p para los gases depende de la presión parcial . Estas constantes son más fáciles de medir y se encuentran en los cursos de química de la escuela secundaria.

A temperatura y presión constantes, se debe considerar la energía libre de Gibbs , G , mientras que a temperatura y volumen constantes, se debe considerar la energía libre de Helmholtz , A , para la reacción; y a energía interna y volumen constantes, se debe considerar la entropía, S , para la reacción.

El caso de volumen constante es importante en geoquímica y química atmosférica donde las variaciones de presión son significativas. Nótese que, si los reactivos y productos estuvieran en estado estándar (completamente puros), entonces no habría reversibilidad ni equilibrio. De hecho, necesariamente ocuparían volúmenes disjuntos de espacio. La mezcla de los productos y reactivos contribuye a un gran aumento de entropía (conocido como entropía de mezcla ) a estados que contienen mezclas iguales de productos y reactivos y da lugar a un mínimo distintivo en la energía de Gibbs como una función del grado de reacción. ^[7] El cambio de energía de Gibbs estándar, junto con la energía de Gibbs de mezcla, determinan el estado de equilibrio. ^{[8] [9]}

En este artículo se considera únicamente el caso de presión constante . La relación entre la energía libre de Gibbs y la constante de equilibrio se puede determinar considerando los potenciales químicos . ^[1]

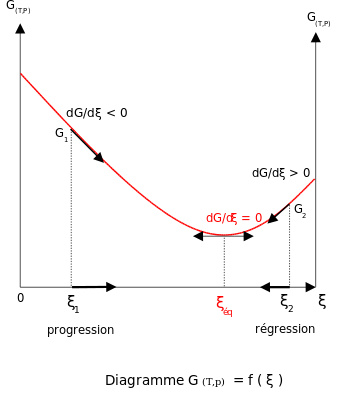
A temperatura y presión constantes en ausencia de voltaje aplicado, la energía libre de Gibbs , G , para la reacción depende únicamente de la extensión de la reacción : ξ (letra griega xi ), y solo puede disminuir de acuerdo con la segunda ley de la termodinámica . Esto significa que la derivada de G con respecto a ξ debe ser negativa si ocurre la reacción; en el equilibrio, esta derivada es igual a cero.

${\displaystyle \left({\frac {dG}{d\xi }}\right)_{T,p}=0~}$:      equilibrio

Para cumplir con la condición termodinámica de equilibrio, la energía de Gibbs debe ser estacionaria, es decir, la derivada de G con respecto a la extensión de la reacción, ξ , debe ser cero. Se puede demostrar que, en este caso, la suma de los potenciales químicos por los coeficientes estequiométricos de los productos es igual a la suma de los correspondientes a los reactivos. ^[10] Por lo tanto, la suma de las energías de Gibbs de los reactivos debe ser igual a la suma de las energías de Gibbs de los productos.

${\displaystyle \alpha \mu _{\mathrm {A} }+\beta \mu _{\mathrm {B} }=\sigma \mu _{\mathrm {S} }+\tau \mu _{\mathrm {T} }\,}$

donde μ es en este caso una energía de Gibbs molar parcial, un potencial químico . El potencial químico de un reactivo A es una función de la actividad , {A} de ese reactivo.

${\displaystyle \mu _{\mathrm {A} }=\mu _{A}^{\ominus }+RT\ln\{\mathrm {A} \}\,}$

(donde μ^o
_Unes el potencial químico estándar ).

La definición de la ecuación de energía de Gibbs interactúa con la relación termodinámica fundamental para producir

${\displaystyle dG=Vdp-SdT+\sum _{i=1}^{k}\mu _{i}dN_{i}}$.

Insertando dN _i  = ν _i  dξ en la ecuación anterior se obtiene un coeficiente estequiométrico ( ) y un diferencial que denota la reacción que ocurre en una extensión infinitesimal ( dξ ). A presión y temperatura constantes las ecuaciones anteriores se pueden escribir como${\displaystyle \nu _{i}~}$

${\displaystyle \left({\frac {dG}{d\xi }}\right)_{T,p}=\sum _{i=1}^{k}\mu _{i}\nu _{i}=\Delta _{\mathrm {r} }G_{T,p}}$

que es el "cambio de energía libre de Gibbs" para la reacción . Esto da como resultado:

${\displaystyle \Delta _{\mathrm {r} }G_{T,p}=\sigma \mu _{\mathrm {S} }+\tau \mu _{\mathrm {T} }-\alpha \mu _{\mathrm {A} }-\beta \mu _{\mathrm {B} }\,}$.

Sustituyendo los potenciales químicos:

${\displaystyle \Delta _{\mathrm {r} }G_{T,p}=(\sigma \mu _{\mathrm {S} }^{\ominus }+\tau \mu _{\mathrm {T} }^{\ominus })-(\alpha \mu _{\mathrm {A} }^{\ominus }+\beta \mu _{\mathrm {B} }^{\ominus })+(\sigma RT\ln\{\mathrm {S} \}+\tau RT\ln\{\mathrm {T} \})-(\alpha RT\ln\{\mathrm {A} \}+\beta RT\ln\{\mathrm {B} \})}$,

La relación se convierte en:

${\displaystyle \Delta _{\mathrm {r} }G_{T,p}=\sum _{i=1}^{k}\mu _{i}^{\ominus }\nu _{i}+RT\ln {\frac {\{\mathrm {S} \}^{\sigma }\{\mathrm {T} \}^{\tau }}{\{\mathrm {A} \}^{\alpha }\{\mathrm {B} \}^{\beta }}}}$

${\displaystyle \sum _{i=1}^{k}\mu _{i}^{\ominus }\nu _{i}=\Delta _{\mathrm {r} }G^{\ominus }}$:

que es el cambio de energía de Gibbs estándar para la reacción que se puede calcular utilizando tablas termodinámicas. El cociente de reacción se define como:

${\displaystyle Q_{\mathrm {r} }={\frac {\{\mathrm {S} \}^{\sigma }\{\mathrm {T} \}^{\tau }}{\{\mathrm {A} \}^{\alpha }\{\mathrm {B} \}^{\beta }}}}$

Por lo tanto,

${\displaystyle \left({\frac {dG}{d\xi }}\right)_{T,p}=\Delta _{\mathrm {r} }G_{T,p}=\Delta _{\mathrm {r} }G^{\ominus }+RT\ln Q_{\mathrm {r} }}$

En equilibrio:

${\displaystyle \left({\frac {dG}{d\xi }}\right)_{T,p}=\Delta _{\mathrm {r} }G_{T,p}=0}$

conduciendo a:

${\displaystyle 0=\Delta _{\mathrm {r} }G^{\ominus }+RT\ln K_{\mathrm {eq} }}$

y

${\displaystyle \Delta _{\mathrm {r} }G^{\ominus }=-RT\ln K_{\mathrm {eq} }}$

La obtención del valor del cambio de energía de Gibbs estándar, permite el cálculo de la constante de equilibrio.

Para un sistema reaccional en equilibrio: Q _r  =  K _eq ; ξ  =  ξ _eq .

• Si se modifican las actividades de los constituyentes, el valor del cociente de reacción cambia y se vuelve diferente de la constante de equilibrio: Q _r  ≠  K _eq y entonces$${\displaystyle \left({\frac {dG}{d\xi }}\right)_{T,p}=\Delta _{\mathrm {r} }G^{\ominus }+RT\ln Q_{\mathrm {r} }~}$$$${\displaystyle \Delta _{\mathrm {r} }G^{\ominus }=-RT\ln K_{eq}~}$$$${\displaystyle \left({\frac {dG}{d\xi }}\right)_{T,p}=RT\ln \left({\frac {Q_{\mathrm {r} }}{K_{\mathrm {eq} }}}\right)~}$$
• Si la actividad de un reactivo i aumenta, el cociente de reacción disminuye. Entonces, y La reacción se desplazará hacia la derecha (es decir, en dirección hacia adelante, y por lo tanto se formarán más productos).$${\displaystyle Q_{\mathrm {r} }={\frac {\prod (a_{j})^{\nu _{j}}}{\prod (a_{i})^{\nu _{i}}}}~,}$$$${\displaystyle Q_{\mathrm {r} }<K_{\mathrm {eq} }~}$$$${\displaystyle \left({\frac {dG}{d\xi }}\right)_{T,p}<0~}$$
• Si la actividad de un producto j aumenta, entonces y La reacción se desplazará hacia la izquierda (es decir, en la dirección inversa, y por lo tanto se formarán menos productos).$${\displaystyle Q_{\mathrm {r} }>K_{\mathrm {eq} }~}$$$${\displaystyle \left({\frac {dG}{d\xi }}\right)_{T,p}>0~}$$

Tenga en cuenta que las actividades y las constantes de equilibrio son números adimensionales.

La expresión de la constante de equilibrio se puede reescribir como el producto de un cociente de concentración, K _c y un cociente de coeficiente de actividad , Γ .

${\displaystyle K={\frac {[\mathrm {S} ]^{\sigma }[\mathrm {T} ]^{\tau }...}{[\mathrm {A} ]^{\alpha }[\mathrm {B} ]^{\beta }...}}\times {\frac {{\gamma _{\mathrm {S} }}^{\sigma }{\gamma _{\mathrm {T} }}^{\tau }...}{{\gamma _{\mathrm {A} }}^{\alpha }{\gamma _{\mathrm {B} }}^{\beta }...}}=K_{\mathrm {c} }\Gamma }$

[A] es la concentración del reactivo A, etc. En principio, es posible obtener valores de los coeficientes de actividad, γ. Para las soluciones, se pueden utilizar ecuaciones como la ecuación de Debye–Hückel o extensiones como la ecuación de Davies ^[11], la teoría de interacción iónica específica o las ecuaciones de Pitzer ^{[12] . Software (abajo)} Sin embargo, esto no siempre es posible. Es una práctica común asumir que Γ es una constante y utilizar el cociente de concentración en lugar de la constante de equilibrio termodinámico. También es una práctica general utilizar el término constante de equilibrio en lugar del más preciso cociente de concentración . Esta práctica se seguirá aquí.

Para las reacciones en fase gaseosa se utiliza la presión parcial en lugar de la concentración y el coeficiente de fugacidad en lugar del coeficiente de actividad. En el mundo real, por ejemplo, al fabricar amoniaco en la industria, se deben tener en cuenta los coeficientes de fugacidad. La fugacidad, f , es el producto de la presión parcial y el coeficiente de fugacidad. El potencial químico de una especie en la fase gaseosa real se da por

${\displaystyle \mu =\mu ^{\ominus }+RT\ln \left({\frac {f}{\mathrm {bar} }}\right)=\mu ^{\ominus }+RT\ln \left({\frac {p}{\mathrm {bar} }}\right)+RT\ln \gamma }$

Por lo tanto, la expresión general que define una constante de equilibrio es válida tanto para la fase de solución como para la fase gaseosa. ^{[ cita requerida ]}

En solución acuosa, las constantes de equilibrio se determinan generalmente en presencia de un electrolito "inerte", como el nitrato de sodio , NaNO ₃ , o el perclorato de potasio , KClO ₄ . La fuerza iónica de una solución se expresa mediante

${\displaystyle I={\frac {1}{2}}\sum _{i=1}^{N}c_{i}z_{i}^{2}}$

donde c _i y z _i representan la concentración y la carga iónica del tipo de ion i , y la suma se toma sobre todos los N tipos de especies cargadas en solución. Cuando la concentración de sal disuelta es mucho mayor que las concentraciones analíticas de los reactivos, los iones que se originan de la sal disuelta determinan la fuerza iónica, y la fuerza iónica es efectivamente constante. Dado que los coeficientes de actividad dependen de la fuerza iónica, los coeficientes de actividad de las especies son efectivamente independientes de la concentración. Por lo tanto, la suposición de que Γ es constante está justificada. El cociente de concentración es un simple múltiplo de la constante de equilibrio. ^[13]

${\displaystyle K_{\mathrm {c} }={\frac {K}{\Gamma }}}$

Sin embargo, K _c varía con la fuerza iónica. Si se mide en una serie de fuerzas iónicas diferentes, el valor puede extrapolarse a una fuerza iónica cero. ^[12] El cociente de concentración obtenido de esta manera se conoce, paradójicamente, como una constante de equilibrio termodinámico.

Antes de utilizar un valor publicado de una constante de equilibrio en condiciones de fuerza iónica diferentes de las condiciones utilizadas en su determinación, el valor debe ajustarse ^{mediante el software (abajo)} .

Una mezcla puede parecer no tener tendencia a cambiar, aunque no esté en equilibrio. Por ejemplo, una mezcla de SO ₂ y O ₂ es metaestable , ya que existe una barrera cinética para la formación del producto, SO ₃ .

2SO2 + _{O2 ⇌} 2SO3_​

La barrera se puede superar cuando también está presente un catalizador en la mezcla, como en el proceso de contacto , pero el catalizador no afecta las concentraciones de equilibrio.

Asimismo, la formación de bicarbonato a partir de dióxido de carbono y agua es muy lenta en condiciones normales.

CO2 ₊ 2 H2O _⇌ HCO−3+ _H3O ⁺​

pero casi instantánea en presencia de la enzima catalítica anhidrasa carbónica .

Cuando sustancias puras (líquidos o sólidos) están involucradas en equilibrios sus actividades no aparecen en la constante de equilibrio ^[14] porque sus valores numéricos se consideran uno.

Aplicando la fórmula general para una constante de equilibrio al caso específico de una solución diluida de ácido acético en agua se obtiene

CH ₃ CO ₂ H + H ₂ O ⇌ CH ₃ CO ₂ ⁻ + H ₃ O ⁺

${\displaystyle K_{\mathrm {c} }={\frac {\mathrm {[{CH_{3}CO_{2}}^{-}][{H_{3}O}^{+}]} }{\mathrm {[{CH_{3}CO_{2}H}][{H_{2}O}]} }}}$

En el caso de todas las soluciones, excepto en las muy concentradas, el agua puede considerarse un líquido "puro" y, por lo tanto, tiene una actividad de uno. Por lo tanto, la expresión de la constante de equilibrio suele escribirse como

${\displaystyle K={\frac {\mathrm {[{CH_{3}CO_{2}}^{-}][{H_{3}O}^{+}]} }{\mathrm {[{CH_{3}CO_{2}H}]} }}=K_{\mathrm {c} }}$.

Un caso particular es la autoionización del agua.

2H2O ⇌ _H3O ⁺ + OH ⁻_​

Debido a que el agua es el disolvente y tiene una actividad de uno, la constante de autoionización del agua se define como

${\displaystyle K_{\mathrm {w} }=\mathrm {[H^{+}][OH^{-}]} }$

Es perfectamente legítimo escribir [H ⁺ ] para la concentración del ion hidronio , ya que el estado de solvatación del protón es constante (en soluciones diluidas) y, por lo tanto, no afecta las concentraciones de equilibrio. K _w varía con la variación de la fuerza iónica y/o la temperatura.

Las concentraciones de H ⁺ y OH− ^no son cantidades independientes. Lo más común es que [OH− ^] se reemplace por K _w [H ⁺ ] ⁻¹ en expresiones de constantes de equilibrio que, de otro modo, incluirían el ion hidróxido .

Los sólidos tampoco aparecen en la expresión de la constante de equilibrio, si se los considera puros y, por lo tanto, sus actividades se consideran una sola. Un ejemplo es la reacción de Boudouard : ^[14]

2CO ⇌ CO ₂ + C

para lo cual la ecuación (sin carbono sólido) se escribe como:

${\displaystyle K_{\mathrm {c} }={\frac {\mathrm {[CO_{2}]} }{\mathrm {[CO]^{2}} }}}$

Consideremos el caso de un ácido dibásico H ₂ A. Al disolverse en agua, la mezcla contendrá H ₂ A, HA ⁻ y A ²⁻ . Este equilibrio se puede dividir en dos pasos en cada uno de los cuales se libera un protón.

${\displaystyle {\begin{array}{rl}{\ce {H2A <=> HA^- + H+}}:&K_{1}={\frac {{\ce {[HA-][H+]}}}{{\ce {[H2A]}}}}\\{\ce {HA- <=> A^2- + H+}}:&K_{2}={\frac {{\ce {[A^{2-}][H+]}}}{{\ce {[HA-]}}}}\end{array}}}$

K ₁ y K ₂ son ejemplos de constantes de equilibrio escalonado . La constante de equilibrio general , β _D , es el producto de las constantes escalonadas.

${\displaystyle {\ce {{H2A}<=>{A^{2-}}+{2H+}}}}$:     ${\displaystyle \beta _{{\ce {D}}}={\frac {{\ce {[A^{2-}][H^+]^2}}}{{\ce {[H_2A]}}}}=K_{1}K_{2}}$

Tenga en cuenta que estas constantes son constantes de disociación porque los productos del lado derecho de la expresión de equilibrio son productos de disociación. En muchos sistemas, es preferible utilizar constantes de asociación.

${\displaystyle {\begin{array}{ll}{\ce {A^2- + H+ <=> HA-}}:&\beta _{1}={\frac {{\ce {[HA^-]}}}{{\ce {[A^{2-}][H+]}}}}\\{\ce {A^2- + 2H+ <=> H2A}}:&\beta _{2}={\frac {{\ce {[H2A]}}}{{\ce {[A^{2-}][H+]^2}}}}\end{array}}}$

β ₁ y β ₂ son ejemplos de constantes de asociación. Claramente β ₁  =  ⁠1/K2_​⁠ y β ₂  =  ⁠1/βD_​⁠ ; log  β ₁  = p K ₂ y log  β ₂  = p K ₂  + p K ₁ ^[15] Para sistemas de equilibrio múltiple, véase también: teoría de reacciones de respuesta .

El efecto del cambio de temperatura sobre una constante de equilibrio viene dado por la ecuación de van 't Hoff

${\displaystyle {\frac {d\ln K}{dT}}={\frac {\Delta H_{\mathrm {m} }^{\ominus }}{RT^{2}}}}$

Por lo tanto, para las reacciones exotérmicas (Δ H es negativo), K disminuye con un aumento de la temperatura, pero, para las reacciones endotérmicas , (Δ H es positivo) K aumenta con un aumento de la temperatura. Una formulación alternativa es

${\displaystyle {\frac {d\ln K}{d(T^{-1})}}=-{\frac {\Delta H_{\mathrm {m} }^{\ominus }}{R}}}$

A primera vista, esto parece ofrecer un medio para obtener la entalpía molar estándar de la reacción mediante el estudio de la variación de K con la temperatura. Sin embargo, en la práctica, el método no es confiable porque la propagación de errores casi siempre da como resultado errores muy grandes en los valores calculados de esta manera.

El efecto del campo eléctrico sobre el equilibrio ha sido estudiado por Manfred Eigen ^{[16] [17]} entre otros.

El equilibrio se puede clasificar ampliamente como equilibrio heterogéneo y homogéneo. ^[18] El equilibrio homogéneo consiste en reactivos y productos que pertenecen a la misma fase, mientras que el equilibrio heterogéneo entra en juego para reactivos y productos en diferentes fases.

• En fase gaseosa: motores de cohetes ^[19]
• La síntesis industrial, como el amoníaco en el proceso Haber-Bosch (mostrado a la derecha), se lleva a cabo a través de una sucesión de pasos de equilibrio que incluyen procesos de adsorción .
• Química atmosférica
• Agua de mar y otras aguas naturales: oceanografía química
• Distribución entre dos fases
  • Coeficiente de distribución log D : importante para productos farmacéuticos donde la lipofilicidad es una propiedad significativa de un fármaco.
  • Extracción líquido-líquido , Intercambio iónico , Cromatografía
  • Producto de solubilidad
  • Captación y liberación de oxígeno por la hemoglobina en la sangre.
• Equilibrios ácido-base: constante de disociación ácida , hidrólisis , soluciones tampón , indicadores , homeostasis ácido-base
• Complejación metal-ligando: agentes secuestrantes , terapia de quelación , reactivos de contraste para resonancia magnética , equilibrio de Schlenk
• Formación de aductos: química huésped-anfitrión , química supramolecular , reconocimiento molecular , tetróxido de dinitrógeno
• En ciertas reacciones oscilantes , la aproximación al equilibrio no es asintótica sino en forma de una oscilación amortiguada. ^[14]
• La ecuación de Nernst relacionada en electroquímica da la diferencia en el potencial del electrodo en función de las concentraciones redox.
• Cuando las moléculas de cada lado del equilibrio pueden reaccionar de forma irreversible en reacciones secundarias, la relación del producto final se determina de acuerdo con el principio de Curtin-Hammett .

En estas aplicaciones se utilizan términos como constante de estabilidad, constante de formación, constante de unión, constante de afinidad, constante de asociación y constante de disociación. En bioquímica, es habitual dar unidades para las constantes de unión, que sirven para definir las unidades de concentración utilizadas cuando se determinó el valor de la constante.

Cuando el único equilibrio es el de la formación de un aducto 1:1 como composición de una mezcla, existen muchas formas de calcular la composición de una mezcla. Por ejemplo, consulte la tabla ICE para conocer un método tradicional de cálculo del pH de una solución de un ácido débil.

Hay tres enfoques para el cálculo general de la composición de una mezcla en equilibrio.

1. El enfoque más básico es manipular las diversas constantes de equilibrio hasta que las concentraciones deseadas se expresen en términos de constantes de equilibrio medidas (equivalentes a medir potenciales químicos) y condiciones iniciales.
2. Minimizar la energía de Gibbs del sistema. ^{[20] [21]}
3. Satisfacer la ecuación de balance de masa . Las ecuaciones de balance de masa son simplemente enunciados que demuestran que la concentración total de cada reactivo debe ser constante según la ley de conservación de la masa .

En general, los cálculos son bastante complicados o complejos. Por ejemplo, en el caso de un ácido dibásico, H ₂ A disuelto en agua, los dos reactivos pueden especificarse como la base conjugada , A ²⁻ , y el protón , H ⁺ . Las siguientes ecuaciones de balance de masa podrían aplicarse igualmente bien a una base como el 1,2-diaminoetano , en cuyo caso la base en sí se designa como el reactivo A:

${\displaystyle T_{\mathrm {A} }=\mathrm {[A]+[HA]+[H_{2}A]} \,}$

${\displaystyle T_{\mathrm {H} }=\mathrm {[H]+[HA]+2[H_{2}A]-[OH]} \,}$

siendo T _A la concentración total de la especie A. Nótese que es habitual omitir las cargas iónicas al escribir y utilizar estas ecuaciones.

Cuando se conocen las constantes de equilibrio y se especifican las concentraciones totales, hay dos ecuaciones en dos "concentraciones libres" desconocidas [A] y [H]. Esto se deduce del hecho de que [HA] =  β ₁ [A][H], [H ₂ A] =  β ₂ [A][H] ² y [OH] =  K _w [H] ⁻¹

${\displaystyle T_{\mathrm {A} }=\mathrm {[A]} +\beta _{1}\mathrm {[A][H]} +\beta _{2}\mathrm {[A][H]} ^{2}\,}$

${\displaystyle T_{\mathrm {H} }=\mathrm {[H]} +\beta _{1}\mathrm {[A][H]} +2\beta _{2}\mathrm {[A][H]} ^{2}-K_{w}[\mathrm {H} ]^{-1}\,}$

De esta forma, las concentraciones de los "complejos" se calculan a partir de las concentraciones libres y las constantes de equilibrio. Las expresiones generales aplicables a todos los sistemas con dos reactivos, A y B, serían

${\displaystyle T_{\mathrm {A} }=[\mathrm {A} ]+\sum _{i}p_{i}\beta _{i}[\mathrm {A} ]^{p_{i}}[\mathrm {B} ]^{q_{i}}}$

${\displaystyle T_{\mathrm {B} }=[\mathrm {B} ]+\sum _{i}q_{i}\beta _{i}[\mathrm {A} ]^{p_{i}}[\mathrm {B} ]^{q_{i}}}$

Es fácil ver cómo esto puede extenderse a tres o más reactivos.

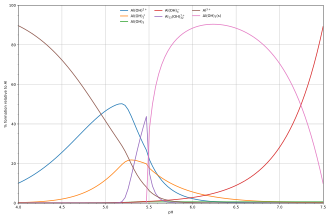
La composición de las soluciones que contienen los reactivos A y H es fácil de calcular en función del pH[H] . Cuando se conoce el valor de [H], la concentración libre [A] se calcula a partir de la ecuación de balance de masa en A.

El diagrama adjunto muestra un ejemplo de la hidrólisis del ácido de Lewis de aluminio Al ³⁺ _(aq) ^[22] y muestra las concentraciones de especies para una solución 5 × 10 ⁻⁶  M de una sal de aluminio en función del pH. Cada concentración se muestra como un porcentaje del aluminio total.

El diagrama anterior ilustra el punto de que puede formarse un precipitado que no es una de las especies principales en el equilibrio de la solución. A un pH justo por debajo de 5,5, las principales especies presentes en una solución de 5 μM de Al ³⁺ son hidróxidos de aluminio Al(OH) ²⁺ , AlOH+2y Al ₁₃ (OH)7+32, pero al aumentar el pH, el Al(OH) ₃ precipita de la solución. Esto ocurre porque el Al(OH) _{3 tiene una} energía reticular muy grande . A medida que aumenta el pH , sale cada vez más Al(OH) _{3 de la solución. Este es un ejemplo del} principio de Le Châtelier en acción: aumentar la concentración del ion hidróxido hace que precipite más hidróxido de aluminio, lo que elimina el hidróxido de la solución. Cuando la concentración de hidróxido se vuelve lo suficientemente alta, el aluminato soluble, Al(OH)−4, se forma.

Otro caso común en el que se produce la precipitación es cuando un catión metálico interactúa con un ligando aniónico para formar un complejo eléctricamente neutro. Si el complejo es hidrófobo , se precipitará del agua. Esto ocurre con el ion níquel Ni ²⁺ y la dimetilglioxima (dmgH ₂ ): en este caso, la energía reticular del sólido no es especialmente grande, pero supera con creces la energía de solvatación de la molécula Ni(dmgH) ₂ .

En equilibrio, a una temperatura y presión específicas, y sin fuerzas externas, la energía libre de Gibbs G es mínima:

${\displaystyle dG=\sum _{j=1}^{m}\mu _{j}\,dN_{j}=0}$

donde μ _j es el potencial químico de la especie molecular j y N _j es la cantidad de especie molecular j . Puede expresarse en términos de actividad termodinámica como:

${\displaystyle \mu _{j}=\mu _{j}^{\ominus }+RT\ln {A_{j}}}$

donde es el potencial químico en el estado estándar, R es la constante del gas, T es la temperatura absoluta y A _j es la actividad.${\displaystyle \mu _{j}^{\ominus }}$

En un sistema cerrado no pueden entrar ni salir partículas, aunque pueden combinarse de diversas formas. El número total de átomos de cada elemento permanecerá constante. Esto significa que la minimización anterior debe estar sujeta a las restricciones:

${\displaystyle \sum _{j=1}^{m}a_{ij}N_{j}=b_{i}^{0}}$

donde a _ij es el número de átomos del elemento i en la molécula j y b⁰
_yoes el número total de átomos del elemento i , que es una constante, ya que el sistema es cerrado. Si hay un total de k tipos de átomos en el sistema, entonces habrá k ecuaciones de este tipo. Si hay iones involucrados, se agrega una fila adicional a la matriz a _ij que especifica la carga respectiva en cada molécula, que sumará cero.

Este es un problema estándar en optimización , conocido como minimización restringida . El método más común para resolverlo es mediante el método de multiplicadores de Lagrange ^{[23] [19]} (aunque se pueden utilizar otros métodos).

Definir:

${\displaystyle {\mathcal {G}}=G+\sum _{i=1}^{k}\lambda _{i}\left(\sum _{j=1}^{m}a_{ij}N_{j}-b_{i}^{0}\right)=0}$

donde λ _i son los multiplicadores de Lagrange, uno para cada elemento. Esto permite que cada uno de los N _j y λ _j se trate de forma independiente, y se puede demostrar utilizando las herramientas del cálculo multivariante que la condición de equilibrio está dada por

${\displaystyle 0={\frac {\partial {\mathcal {G}}}{\partial N_{j}}}=\mu _{j}+\sum _{i=1}^{k}\lambda _{i}a_{ij}}$

${\displaystyle 0={\frac {\partial {\mathcal {G}}}{\partial \lambda _{i}}}=\sum _{j=1}^{m}a_{ij}N_{j}-b_{i}^{0}}$

(Para demostración, véase multiplicadores de Lagrange .) Este es un conjunto de ecuaciones ( m  +  k ) en incógnitas ( m  +  k ) (las N _j y las λ _i ) y, por lo tanto, se puede resolver para las concentraciones de equilibrio N _j siempre que las actividades químicas se conozcan como funciones de las concentraciones a la temperatura y presión dadas. (En el caso ideal, las actividades son proporcionales a las concentraciones.) (Véase Bases de datos termodinámicas para sustancias puras .) Nótese que la segunda ecuación son solo las restricciones iniciales para la minimización.

Este método de cálculo de concentraciones químicas de equilibrio es útil para sistemas con una gran cantidad de moléculas diferentes. El uso de ecuaciones de conservación de elementos atómicos k para la restricción de masa es sencillo y reemplaza el uso de ecuaciones de coeficientes estequiométricos. ^[19] Los resultados son consistentes con los especificados por ecuaciones químicas. Por ejemplo, si el equilibrio se especifica mediante una sola ecuación química: ^[24]

${\displaystyle \sum _{j=0}^{m}\nu _{j}R_{j}=0}$

donde ν _j es el coeficiente estequiométrico para la molécula j (negativo para reactivos, positivo para productos) y R _j es el símbolo de la molécula j , una ecuación correctamente balanceada obedecerá:

${\displaystyle \sum _{j=1}^{m}a_{ij}\nu _{j}=0}$

Multiplicando la primera condición de equilibrio por ν _j y utilizando la ecuación anterior se obtiene:

${\displaystyle 0=\sum _{j=1}^{m}\nu _{j}\mu _{j}+\sum _{j=1}^{m}\sum _{i=1}^{k}\nu _{j}\lambda _{i}a_{ij}=\sum _{j=1}^{m}\nu _{j}\mu _{j}}$

Como anteriormente, definiendo ΔG

${\displaystyle \Delta G=\sum _{j=1}^{m}\nu _{j}\mu _{j}=\sum _{j=1}^{m}\nu _{j}(\mu _{j}^{\ominus }+RT\ln(\{R_{j}\}))=\Delta G^{\ominus }+RT\ln \left(\prod _{j=1}^{m}\{R_{j}\}^{\nu _{j}}\right)=\Delta G^{\ominus }+RT\ln(K_{c})}$

donde K _c es la constante de equilibrio y ΔG será cero en el equilibrio.

Existen procedimientos análogos para la minimización de otros potenciales termodinámicos . ^[19]

• Van Zeggeren, F.; Storey, SH (1970). El cálculo de los equilibrios químicos . Cambridge University Press.Se ocupa principalmente de los equilibrios en fase gaseosa.
• Leggett, DJ, ed. (1985). Métodos computacionales para la determinación de constantes de formación . Plenum Press.
• Martell, AE; Motekaitis, RJ (1992). La determinación y el uso de constantes de estabilidad . Wiley-VCH.

• Medios relacionados con Equilibrios químicos en Wikimedia Commons