Balance de masa

En física , un balance de masa , también llamado balance de materiales , es una aplicación de la conservación de la masa ^[1] al análisis de sistemas físicos . Al tener en cuenta el material que entra y sale de un sistema, se pueden identificar flujos de masa que podrían haber sido desconocidos o difíciles de medir sin esta técnica. La ley de conservación exacta utilizada en el análisis del sistema depende del contexto del problema, pero todas giran en torno a la conservación de la masa, es decir, que la materia no puede desaparecer ni crearse espontáneamente. ^{[2] : 59–62}

Por lo tanto, los balances de masa se utilizan ampliamente en ingeniería y análisis ambientales . Por ejemplo, la teoría del balance de masa se utiliza para diseñar reactores químicos , para analizar procesos alternativos para producir sustancias químicas, así como para modelar la dispersión de la contaminación y otros procesos de sistemas físicos. Los balances de masa forman la base del diseño de ingeniería de procesos. ^[3] Las técnicas de análisis estrechamente relacionadas y complementarias incluyen el balance de población , el balance de energía y el balance de entropía algo más complejo . Estas técnicas son necesarias para el diseño y análisis exhaustivos de sistemas como el ciclo de refrigeración .

En el monitoreo ambiental , el término cálculos de balance de masa se utiliza para describir ecuaciones de balance de masa que se utilizan para evaluar los datos de monitoreo (comparando entradas y salidas, etc.). En biología , la teoría del balance de energía dinámica para la organización metabólica hace un uso explícito del balance de masa y energía.

La forma general citada para un balance de masa es: La masa que ingresa a un sistema debe, por conservación de la masa, salir del sistema o acumularse dentro del sistema .

Matemáticamente, el balance de masa para un sistema sin reacción química es el siguiente: ^{[2] : 59–62}

$${\displaystyle {\text{Input}}={\text{Output}}+{\text{Accumulation}}}$$

En sentido estricto, la ecuación anterior se aplica también a sistemas con reacciones químicas si los términos de la ecuación de balance se toman como referencia a la masa total, es decir, la suma de todas las especies químicas del sistema. En ausencia de una reacción química, la cantidad de cualquier especie química que entre y salga será la misma; esto da lugar a una ecuación para cada especie presente en el sistema. Sin embargo, si este no es el caso, entonces la ecuación de balance de masa debe modificarse para permitir la generación o el agotamiento (consumo) de cada especie química. Algunos utilizan un término en esta ecuación para dar cuenta de las reacciones químicas, que será negativo para el agotamiento y positivo para la generación. Sin embargo, la forma convencional de esta ecuación está escrita para dar cuenta tanto de un término positivo de generación (es decir, producto de la reacción) como de un término negativo de consumo (los reactivos utilizados para producir los productos). Aunque en general un término dará cuenta del balance total del sistema, si esta ecuación de balance se aplica a una especie individual y luego a todo el proceso, ambos términos son necesarios. Esta ecuación modificada se puede utilizar no sólo para sistemas reactivos, sino también para balances de población como los que surgen en problemas de mecánica de partículas . La ecuación se presenta a continuación; observe que se simplifica a la ecuación anterior en el caso de que el término de generación sea cero. ^{[2] : 59–62}

$${\displaystyle {\text{Input}}+{\text{Generation}}={\text{Output}}+{\text{Accumulation}}\ +{\text{Consumption}}}$$

• En ausencia de una reacción nuclear, el número de átomos que entran y salen debe permanecer igual, incluso en presencia de una reacción química.
• Para que se forme un equilibrio, los límites del sistema deben estar claramente definidos.
• Se pueden realizar balances de masa en sistemas físicos a múltiples escalas.
• Los balances de masa se pueden simplificar con el supuesto de estado estable , en el que el término de acumulación es cero.

Un ejemplo sencillo puede ilustrar el concepto. Consideremos la situación en la que un lodo fluye hacia un tanque de sedimentación para eliminar los sólidos del tanque. Los sólidos se recogen en el fondo mediante una cinta transportadora parcialmente sumergida en el tanque y el agua sale por una salida de desbordamiento.

En este ejemplo, hay dos sustancias: sólidos y agua. La salida de desbordamiento de agua lleva una mayor concentración de agua en relación con los sólidos, en comparación con la entrada de lodo, y la salida de la cinta transportadora lleva una mayor concentración de sólidos en relación con el agua.

Supuestos

• Estado estable
• Sistema no reactivo

Análisis

Supongamos que la composición de entrada de la suspensión (en masa) es 50% sólida y 50% agua, con un flujo másico de100  kg / min . Se supone que el tanque está funcionando en estado estable y, como tal, la acumulación es cero, por lo que la entrada y la salida deben ser iguales tanto para los sólidos como para el agua. Si sabemos que la eficiencia de eliminación del tanque de lodos es del 60 %, entonces la salida de agua contendrá20  kg / min de sólidos (40% veces100  kg / min por 50% de sólidos). Si medimos el caudal de los sólidos y el agua combinados, y se muestra que la salida de agua es65  kg / min , entonces la cantidad de agua que sale por la cinta transportadora debe ser5  kg / min . Esto nos permite determinar completamente cómo se ha distribuido la masa en el sistema con solo información limitada y utilizando las relaciones de balance de masa en los límites del sistema. El balance de masa para este sistema se puede describir en forma de tabla:

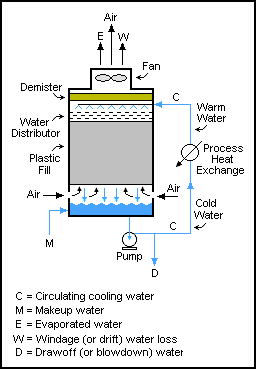
Los balances de masa se pueden realizar en sistemas que tienen flujos cíclicos. En estos sistemas, las corrientes de salida se devuelven a la entrada de una unidad, a menudo para su posterior reprocesamiento. ^{[2] : 97–105}

Estos sistemas son comunes en los circuitos de molienda , donde el grano se tritura y luego se tamiza para permitir que solo las partículas finas salgan del circuito y las partículas más grandes se devuelven al molino de rodillos (triturador). Sin embargo, los flujos de reciclaje no se limitan de ninguna manera a las operaciones de mecánica de sólidos; también se utilizan en flujos de líquidos y gases. Un ejemplo de ello es en las torres de enfriamiento , donde el agua se bombea a través de una torre muchas veces, y solo se extrae una pequeña cantidad de agua en cada paso (para evitar la acumulación de sólidos) hasta que se ha evaporado o ha salido con el agua extraída. El balance de masa para el agua es M = D + W + E.

El uso del reciclaje ayuda a aumentar la conversión general de los productos de entrada, lo que resulta útil para procesos de baja conversión por paso (como el proceso Haber ).

Un balance de masa también puede realizarse de forma diferencial . El concepto es el mismo que el de un balance de masa grande, pero se realiza en el contexto de un sistema límite (por ejemplo, se puede considerar el caso límite en el tiempo o, más comúnmente, en el volumen). Un balance de masa diferencial se utiliza para generar ecuaciones diferenciales que pueden proporcionar una herramienta eficaz para modelar y comprender el sistema objetivo.

El balance de masa diferencial generalmente se resuelve en dos pasos: primero se debe obtener un conjunto de ecuaciones diferenciales gobernantes y luego se deben resolver estas ecuaciones, ya sea analíticamente o, para problemas menos manejables, numéricamente.

Los siguientes sistemas son buenos ejemplos de las aplicaciones del balance de masa diferencial:

1. Reactor discontinuo ideal (agitado)
2. Reactor de tanque ideal, también llamado reactor de tanque agitado continuo (CSTR)
3. Reactor de flujo de tapón ideal (PFR)

El reactor discontinuo completamente mezclado ideal es un sistema cerrado. Se suponen condiciones isotérmicas y la mezcla evita los gradientes de concentración a medida que las concentraciones de reactivo disminuyen y las concentraciones de producto aumentan con el tiempo. ^{[4] : 40–41} Muchos libros de texto de química asumen implícitamente que el sistema estudiado puede describirse como un reactor discontinuo cuando escriben sobre cinética de reacción y equilibrio químico . El balance de masa para una sustancia A se convierte en

$${\displaystyle {\begin{array}{ccccccc}{\text{IN}}&+&{\text{PROD}}&=&{\text{OUT}}&+&{\text{ACC}}\\0&+&r_{\rm {A}}V&=&0&+&\displaystyle {\frac {dn_{\rm {A}}}{dt}}\end{array}}}$$

dónde

• r _A denota la velocidad a la que se produce la sustancia A;
• V es el volumen (que puede ser constante o no);
• n _{A es} el número de moles ( n ) de sustancia A.

En un reactor de lotes alimentados, algunos reactivos o ingredientes se añaden de forma continua o en pulsos (compare la preparación de papilla mezclando primero todos los ingredientes y luego dejándolos hervir, lo que se puede describir como un reactor por lotes, o mezclando primero solo agua y sal y dejándolos hervir antes de agregar los demás ingredientes, lo que se puede describir como un reactor de lotes alimentados). Los balances de masa para los reactores de lotes alimentados se vuelven un poco más complicados.

En el primer ejemplo, mostraremos cómo utilizar un balance de masa para derivar una relación entre el porcentaje de exceso de aire para la combustión de un combustible a base de hidrocarburos y el porcentaje de oxígeno en el gas producto de la combustión. En primer lugar, el aire seco normal contiene0,2095  moles de oxígeno por mol de aire, por lo que hay un mol de O
₂en4,773 moles de aire seco. Para la combustión estequiométrica , las relaciones entre la masa del aire y la masa de cada elemento combustible en un fueloil son:

$${\displaystyle {\begin{array}{rccc}{\text{Carbon:}}&{\frac {\text{mass of air}}{\text{mass of C}}}&=&{\frac {4.773\times 28.96}{12.01}}&=&11.51\\[2pt]{\text{Hydrogen:}}&{\frac {\text{mass of air}}{\text{mass of H}}}&=&{\frac {{\frac {1}{4}}(4.773)\times 28.96}{1.008}}&=&34.28\\[6pt]{\text{Sulfur:}}&{\frac {\text{mass of air}}{\text{mass of S}}}&=&{\frac {4.773\times 28.96}{32.06}}&=&4.31\end{array}}}$$

Considerando la precisión de los procedimientos analíticos típicos, una ecuación para la masa de aire por masa de combustible en combustión estequiométrica es:

$${\displaystyle {\frac {\text{mass of air}}{\text{mass of fuel}}}=\mathrm {AFR} _{\text{mass}}=11.5\,w_{\rm {C}}+34.3\,w_{\rm {H}}+(w_{\rm {S}}-w_{\rm {O}})}$$

donde w _C , w _H , w _S , w _O se refieren a la fracción de masa de cada elemento en el combustible, el azufre que se quema a SO ₂ y _{la masa} AFR se refiere a la relación aire-combustible en unidades de masa.

Para1  kg de fueloil que contiene 86,1% de C, 13,6% de H, 0,2% de O y 0,1% de S la masa estequiométrica del aire es14,56 kg , por lo que AFR = 14,56. La masa del producto de combustión es entonces15,56 kg . En estequiometría exacta, O
₂debe estar ausente. Con un exceso de aire del 15 por ciento, el AFR = 16,75 y la masa del gas producto de la combustión es17,75 kg , que contiene0,505 kg de oxígeno en exceso. Por lo tanto, el gas de combustión contiene un 2,84 por ciento de O
₂en masa. Las relaciones entre el porcentaje de exceso de aire y el % de O
₂En el gas de combustión se expresan con precisión mediante ecuaciones cuadráticas, válidas en el rango de 0 a 30 por ciento de exceso de aire:

$${\displaystyle {\begin{aligned}&\%{\text{ excess air}}=1.2804\times (\%{\ce {O2}}{\text{ in combustion gas}})^{2}+4.49\times (\%{\ce {O2}}{\text{ in combustion gas}})\\[4pt]&\%{\ce {O2}}{\text{ in combustion gas}}=-0.00138\times (\%{\text{ excess air}})^{2}+0.210\times (\%{\text{ excess air}})\end{aligned}}}$$

En el segundo ejemplo, utilizaremos la ley de acción de masas para derivar la expresión de una constante de equilibrio químico .

Supongamos que tenemos un reactor cerrado en el que ocurre la siguiente reacción reversible en fase líquida:

$${\displaystyle a\mathrm {A} +b\mathrm {B} \leftrightarrow c\mathrm {C} +d\mathrm {D} }$$

El balance de masa para la sustancia A se convierte en

$${\displaystyle {\begin{array}{ccccccc}{\text{IN}}&+&{\text{PROD}}&=&{\text{OUT}}&+&{\text{ACC}}\\0&+&r_{\rm {A}}V&=&0&+&\displaystyle {\frac {dn_{\mathrm {A} }}{dt}}\end{array}}}$$

Como tenemos una reacción en fase líquida, podemos (normalmente) asumir un volumen constante y, dado que obtenemos${\displaystyle n_{\rm {A}}=V*C_{\rm {A}}}$

$${\displaystyle r_{\rm {A}}V=V{\frac {dC_{\rm {A}}}{dt}}}$$

o

$${\displaystyle r_{\rm {A}}={\frac {dC_{\rm {A}}}{dt}}}$$

En muchos libros de texto se da esta definición de velocidad de reacción sin especificar la suposición implícita de que estamos hablando de la velocidad de reacción en un sistema cerrado con una sola reacción. Este es un error desafortunado que ha confundido a muchos estudiantes a lo largo de los años.

Según la ley de acción de masas, la velocidad de reacción directa se puede escribir como

$${\displaystyle r_{1}=k_{1}[\mathrm {A} ]^{a}[\mathrm {B} ]^{b}}$$

y la tasa de reacción hacia atrás como

$${\displaystyle r_{-1}=k_{-1}[\mathrm {C} ]^{c}[\mathrm {D} ]^{d}}$$

La velocidad a la que se produce la sustancia A es, por tanto,

$${\displaystyle r_{\mathrm {A} }=a(r_{-1}-r_{1})}$$

y como en el equilibrio la concentración de A es constante obtenemos

$${\displaystyle r_{\mathrm {A} }=a(r_{-1}-r_{1})={\frac {dC_{\mathrm {A} }}{dt}}=0}$$

o, reorganizado

$${\displaystyle {\frac {k_{1}}{k_{-1}}}={\frac {[\mathrm {C} ]^{c}[\mathrm {D} ]^{d}}{[\mathrm {A} ]^{a}[\mathrm {B} ]^{b}}}=K_{eq}}$$

El reactor de tanque de mezcla continua es un sistema abierto con una corriente de entrada de reactivos y una corriente de efluente de productos. ^{[4] : 41} Un lago puede considerarse como un reactor de tanque, y los lagos con tiempos de rotación largos (por ejemplo, con bajas relaciones de flujo a volumen) pueden considerarse para muchos propósitos como continuamente agitados (por ejemplo, homogéneos en todos los aspectos). El balance de masa se convierte entonces en

$${\displaystyle {\begin{array}{ccccccc}{\text{IN}}&+&{\text{PROD}}&=&{\text{OUT}}&+&{\text{ACC}}\\Q_{0}\cdot C_{\rm {A,0}}&+&r_{\rm {A}}\cdot V&=&Q\cdot C_{\rm {A}}&+&\displaystyle {\frac {dn_{\rm {A}}}{dt}}\end{array}}}$$

dónde

• Q ₀ es el flujo volumétrico en el sistema;
• Q es el flujo volumétrico que sale del sistema;
• C _A,0 es la concentración de A en la entrada ;
• C _A es la concentración de A en el flujo de salida .

En un sistema abierto nunca se puede alcanzar un equilibrio químico. Sin embargo, sí se puede alcanzar un estado estacionario en el que todas las variables de estado (temperatura, concentraciones, etc.) permanezcan constantes ( ACC = 0 ).

Consideremos una bañera en la que hay disuelta un poco de sal de baño. Ahora llenamos más agua, manteniendo el tapón inferior puesto. ¿Qué sucede?

Como no hay reacción, PROD = 0 y como no hay flujo de salida Q = 0. El balance de masa se convierte en

$${\displaystyle {\begin{array}{ccccccc}{\text{IN}}&+&{\text{PROD}}&=&{\text{OUT}}&+&{\text{ACC}}\\Q_{0}\cdot C_{\rm {A,0}}&+&0&=&0\cdot C_{\rm {A}}&+&\displaystyle {\frac {dn_{\rm {A}}}{dt}}\end{array}}}$$

o

$${\displaystyle Q_{0}\cdot C_{\rm {A,0}}={\frac {dC_{\rm {A}}V}{dt}}=V{\frac {dC_{\rm {A}}}{dt}}+C_{\rm {A}}{\frac {dV}{dt}}}$$

Sin embargo, utilizando un balance de masa para el volumen total, es evidente que y que Por lo tanto obtenemos${\displaystyle {\tfrac {dV}{dt}}=Q_{0}}$${\displaystyle V=V_{t=0}+Q_{0}t.}$

$${\displaystyle {\frac {dC_{\rm {A}}}{dt}}={\frac {Q_{0}}{(V_{t=0}+Q_{0}t)}}\left(C_{\rm {A,0}}-C_{\rm {A}}\right)}$$

Nótese que no hay reacción y, por lo tanto, no hay velocidad de reacción ni ley de velocidad involucradas, y sin embargo . Por lo tanto, podemos sacar la conclusión de que la velocidad de reacción no se puede definir de manera general utilizando . Primero se debe escribir un balance de masa antes de poder encontrar un vínculo entre y la velocidad de reacción. Sin embargo, muchos libros de texto definen la velocidad de reacción como${\displaystyle {\tfrac {dC_{\rm {A}}}{dt}}\neq 0}$${\displaystyle {\tfrac {dC}{dt}}}$${\displaystyle {\tfrac {dC}{dt}}}$

$${\displaystyle r={\frac {dC_{\mathrm {A} }}{dt}}}$$

sin mencionar que esta definición supone implícitamente que el sistema es cerrado, tiene un volumen constante y que solo hay una reacción.

El reactor de flujo tapón idealizado es un sistema abierto que se asemeja a un tubo sin mezcla en la dirección del flujo, pero con una mezcla perfecta perpendicular a la dirección del flujo, que se utiliza a menudo para sistemas como ríos y tuberías de agua si el flujo es turbulento. Cuando se realiza un balance de masa para un tubo, primero se considera una parte infinitesimal del tubo y se realiza un balance de masa sobre ella utilizando el modelo de reactor de tanque ideal. ^{[4] : 46–47} Ese balance de masa se integra luego sobre todo el volumen del reactor para obtener:

$${\displaystyle {\frac {d(Q\cdot C_{\rm {A}})}{dV}}=r_{\rm {A}}}$$

En soluciones numéricas, por ejemplo cuando se utilizan computadoras, el tubo ideal a menudo se traduce a una serie de reactores de tanque, ya que se puede demostrar que un PFR es equivalente a un número infinito de tanques agitados en serie, pero este último es a menudo más fácil de analizar, especialmente en estado estable.

En realidad, los reactores a menudo no son ideales, y se utilizan combinaciones de los modelos de reactores anteriores para describir el sistema. No solo las velocidades de reacción química, sino también las velocidades de transferencia de masa pueden ser importantes en la descripción matemática de un sistema, especialmente en sistemas heterogéneos . ^[5]

Como la velocidad de una reacción química depende de la temperatura, a menudo es necesario realizar un balance de energía (a menudo un balance de calor en lugar de un balance de energía completo) y balances de masa para describir completamente el sistema. Puede ser necesario un modelo de reactor diferente para el balance de energía: un sistema que está cerrado con respecto a la masa puede estar abierto con respecto a la energía, por ejemplo, ya que el calor puede ingresar al sistema a través de la conducción .

En las plantas de procesos industriales, si se tiene en cuenta que la masa que entra y sale de cualquier parte de una planta de procesos debe equilibrarse, se pueden emplear algoritmos de validación y conciliación de datos para corregir los caudales medidos, siempre que exista suficiente redundancia de mediciones de caudal para permitir la conciliación estadística y la exclusión de mediciones que puedan detectarse como erróneas. Dado que todos los valores medidos en el mundo real contienen errores inherentes, las mediciones conciliadas proporcionan una mejor base que los valores medidos para la elaboración de informes financieros, la optimización y los informes reglamentarios. Existen paquetes de software que hacen que esto sea comercialmente factible a diario.

• Cálculos de balance de materiales
• Fundamentos del balance de materiales
• El balance de materiales para reactores químicos
• Balance de materia y energía
• Método de control de procesos de balance de calor y materia para plantas petroquímicas y refinerías de petróleo, Patente de Estados Unidos 6751527
• Morris, Arthur E.; Geiger, Gordon; Fine, H. Alan (2011). Manual sobre cálculos de balance de materiales y energía en el procesamiento de materiales (3.ª ed.). Wiley . ISBN 978-1-118-06565-5.