Temperatura
| Temperatura | |
|---|---|
 Vibración térmica de un segmento de la hélice alfa de una proteína . Su amplitud aumenta con la temperatura. | |
Símbolos comunes | yo |
| Unidad SI | K |
Otras unidades | °C , °F , °R , °Rø , °Ré , °N , °D , °L , °W |
| Intensivo ? | Sí |
Derivaciones de otras magnitudes | , |
| Dimensión | |
La temperatura es una magnitud física que expresa cuantitativamente el atributo de calor o frío. La temperatura se mide con un termómetro . Refleja la energía cinética promedio de los átomos que vibran y chocan entre sí y que forman una sustancia.
Los termómetros se calibran en varias escalas de temperatura que históricamente se han basado en varios puntos de referencia y sustancias termométricas para su definición. Las escalas más comunes son la escala Celsius con el símbolo de unidad °C (antes llamada centígrado ), la escala Fahrenheit (°F) y la escala Kelvin (K), esta última utilizada predominantemente para fines científicos. El kelvin es una de las siete unidades básicas del Sistema Internacional de Unidades (SI).
El cero absoluto , es decir, cero kelvin o −273,15 °C, es el punto más bajo en la escala de temperatura termodinámica . Experimentalmente, se puede aproximar mucho, pero no alcanzarlo, como se reconoce en la tercera ley de la termodinámica . Sería imposible extraer energía en forma de calor de un cuerpo a esa temperatura.
La temperatura es importante en todos los campos de las ciencias naturales , incluida la física , la química , las ciencias de la Tierra , la astronomía , la medicina , la biología , la ecología , la ciencia de los materiales , la metalurgia , la ingeniería mecánica y la geografía, así como en la mayoría de los aspectos de la vida diaria.
Efectos
Muchos procesos físicos están relacionados con la temperatura; algunos de ellos se detallan a continuación:
- Las propiedades físicas de los materiales, incluida la fase ( sólida , líquida , gaseosa o plasma ), la densidad , la solubilidad , la presión de vapor , la conductividad eléctrica , la dureza , la resistencia al desgaste , la conductividad térmica , la resistencia a la corrosión y la resistencia.
- la velocidad y el grado en que ocurren las reacciones químicas [1]
- La cantidad y las propiedades de la radiación térmica emitida desde la superficie de un objeto.
- La temperatura del aire afecta a todos los organismos vivos.
- la velocidad del sonido , que en un gas es proporcional a la raíz cuadrada de la temperatura absoluta [2]
Balanza
Esta sección necesita citas adicionales para su verificación . ( Enero de 2021 ) |
Las escalas de temperatura necesitan dos valores para su definición: el punto elegido como cero grados y las magnitudes de la unidad incremental de temperatura.
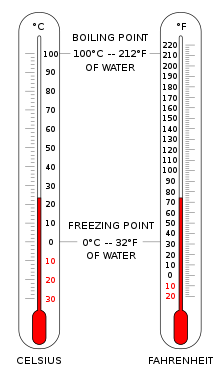
La escala Celsius (°C) se utiliza para mediciones de temperatura comunes en la mayor parte del mundo. Es una escala empírica que se desarrolló históricamente, lo que llevó a su punto cero.0 °C se define como el punto de congelación del agua , y100 °C como punto de ebullición del agua, ambos a presión atmosférica al nivel del mar. Se le llamó escala centígrada debido al intervalo de 100 grados. [3] Desde la estandarización del kelvin en el Sistema Internacional de Unidades, se ha redefinido posteriormente en términos de los puntos de fijación equivalentes en la escala Kelvin, de modo que un incremento de temperatura de un grado Celsius es lo mismo que un incremento de un kelvin, aunque numéricamente las escalas difieren en un desfase exacto de 273,15.
La escala Fahrenheit es de uso común en los Estados Unidos. El agua se congela a32 °F y hierve a212 °F a presión atmosférica a nivel del mar.
Cero absoluto
En el cero absoluto de temperatura, no se puede extraer energía de la materia en forma de calor, un hecho expresado en la tercera ley de la termodinámica . A esta temperatura, la materia no contiene energía térmica macroscópica, pero aún tiene energía de punto cero mecánico cuántico como predice el principio de incertidumbre , aunque esto no entra en la definición de temperatura absoluta. Experimentalmente, el cero absoluto solo se puede aproximar muy de cerca; nunca se puede alcanzar (la temperatura más baja alcanzada experimentalmente es 38 pK). [4] Teóricamente, en un cuerpo a una temperatura de cero absoluto, todo movimiento clásico de sus partículas ha cesado y están en completo reposo en este sentido clásico. El cero absoluto, definido como0 K , es exactamente igual a−273,15 °C , o-459,67 °F .
Escalas absolutas
En referencia a la constante de Boltzmann , a la distribución de Maxwell-Boltzmann y a la definición mecánica estadística de entropía de Boltzmann , a diferencia de la definición de Gibbs, [5] para partículas microscópicas que se mueven independientemente, sin tener en cuenta la energía potencial entre partículas, por acuerdo internacional, se define una escala de temperatura y se dice que es absoluta porque es independiente de las características de sustancias termométricas particulares y mecanismos de termómetro . Aparte del cero absoluto, no tiene una temperatura de referencia. Se conoce como la escala Kelvin , ampliamente utilizada en ciencia y tecnología. El kelvin (el nombre de la unidad se escribe con una 'k' minúscula ) es la unidad de temperatura en el Sistema Internacional de Unidades (SI). La temperatura de un cuerpo en un estado de equilibrio termodinámico siempre es positiva en relación con el cero absoluto.
Además de la escala Kelvin acordada internacionalmente, también existe una escala de temperatura termodinámica , inventada por Lord Kelvin , también con su cero numérico en el cero absoluto de temperatura, pero directamente relacionada con conceptos termodinámicos puramente macroscópicos, incluida la entropía macroscópica , aunque microscópicamente referible a la definición mecánica estadística de Gibbs de entropía para el conjunto canónico , que tiene en cuenta la energía potencial entre partículas, así como el movimiento de partículas independientes para que pueda dar cuenta de las mediciones de temperaturas cercanas al cero absoluto. [5] Esta escala tiene una temperatura de referencia en el punto triple del agua, cuyo valor numérico se define mediante mediciones utilizando la escala Kelvin acordada internacionalmente antes mencionada.
Escala Kelvin
Muchas mediciones científicas utilizan la escala de temperatura Kelvin (símbolo de unidad: K), llamada así en honor al físico que la definió por primera vez . Es una escala absoluta . Su punto cero numérico,0 K , es el cero absoluto de temperatura. Desde mayo de 2019, el kelvin se define a través de la teoría cinética de partículas y la mecánica estadística. En el Sistema Internacional de Unidades (SI), la magnitud del kelvin se define en términos de la constante de Boltzmann , cuyo valor se define como fijo por convención internacional. [6] [7]
Mecánica estadísticaversusescalas de temperatura termodinámicas
Desde mayo de 2019, la magnitud del kelvin se define en relación con fenómenos microscópicos, caracterizados en términos de mecánica estadística. Anteriormente, pero desde 1954, el Sistema Internacional de Unidades definió una escala y unidad para el kelvin como temperatura termodinámica , utilizando como segundo punto de referencia la temperatura del punto triple del agua, reproducible de manera fiable, siendo el primer punto de referencia0 K en el cero absoluto. [ cita requerida ]
Históricamente, la temperatura del punto triple del agua se definía exactamente como 273,16 K. Hoy en día es una cantidad medida empíricamente. El punto de congelación del agua a presión atmosférica al nivel del mar se produce a una temperatura muy cercana a la del punto triple del agua.273,15 kilos (0°C ).
Clasificación de escalas
Existen varios tipos de escalas de temperatura. Puede resultar conveniente clasificarlas en escalas de base empírica y escalas de base teórica. Las escalas de temperatura empíricas son históricamente más antiguas, mientras que las escalas de base teórica surgieron a mediados del siglo XIX. [8] [9]
Escalas empíricas
Las escalas de temperatura basadas en datos empíricos se basan directamente en mediciones de propiedades físicas macroscópicas simples de los materiales. Por ejemplo, la longitud de una columna de mercurio, confinada en un tubo capilar con paredes de vidrio, depende en gran medida de la temperatura y es la base del muy útil termómetro de mercurio en vidrio. Estas escalas son válidas solo dentro de rangos convenientes de temperatura. Por ejemplo, por encima del punto de ebullición del mercurio , un termómetro de mercurio en vidrio es impracticable. La mayoría de los materiales se expanden con el aumento de temperatura, pero algunos materiales, como el agua, se contraen con el aumento de temperatura en un rango específico, y entonces son poco útiles como materiales termométricos. Un material no es útil como termómetro cerca de una de sus temperaturas de cambio de fase, por ejemplo, su punto de ebullición.
A pesar de estas limitaciones, la mayoría de los termómetros que se utilizan en la práctica son de tipo empírico. En particular, se utilizaron para la calorimetría , que contribuyó en gran medida al descubrimiento de la termodinámica. Sin embargo, la termometría empírica tiene serios inconvenientes cuando se la juzga como base de la física teórica. Los termómetros de base empírica, más allá de su base como simples mediciones directas de propiedades físicas ordinarias de materiales termométricos, pueden recalibrarse mediante el uso del razonamiento físico teórico, y esto puede ampliar su rango de adecuación.
Escalas teóricas
Las escalas de temperatura basadas en la teoría se basan directamente en argumentos teóricos, especialmente los de la teoría cinética y la termodinámica. Se materializan de manera más o menos ideal en dispositivos y materiales físicos factibles en la práctica. Las escalas de temperatura basadas en la teoría se utilizan para proporcionar estándares de calibración para termómetros prácticos basados en la experiencia.
Báscula mecánica estadística microscópica
En física, la escala de temperatura convencional acordada internacionalmente se denomina escala Kelvin. Se calibra a través del valor internacionalmente acordado y prescrito de la constante de Boltzmann, [6] [7] que se refiere a los movimientos de partículas microscópicas, como átomos, moléculas y electrones, que constituyen el cuerpo cuya temperatura se va a medir. A diferencia de la escala de temperatura termodinámica inventada por Kelvin, la temperatura Kelvin convencional actual no se define a través de la comparación con la temperatura de un estado de referencia de un cuerpo estándar, ni en términos de termodinámica macroscópica.
Aparte del cero absoluto de temperatura, la temperatura Kelvin de un cuerpo en un estado de equilibrio termodinámico interno se define mediante mediciones de propiedades físicas elegidas adecuadamente, como las que tienen explicaciones teóricas conocidas con precisión en términos de la constante de Boltzmann . [ cita requerida ] Esa constante se refiere a tipos elegidos de movimiento de partículas microscópicas en la constitución del cuerpo. En esos tipos de movimiento, las partículas se mueven individualmente, sin interacción mutua. Tales movimientos suelen verse interrumpidos por colisiones entre partículas, pero para la medición de la temperatura, los movimientos se eligen de modo que, entre colisiones, se sepa que los segmentos no interactivos de sus trayectorias son accesibles para una medición precisa. Para este propósito, se descarta la energía potencial entre partículas.
En un gas ideal y en otros cuerpos comprendidos teóricamente, la temperatura Kelvin se define como proporcional a la energía cinética promedio de partículas microscópicas que se mueven de manera no interactiva, que se puede medir mediante técnicas adecuadas. La constante de proporcionalidad es un simple múltiplo de la constante de Boltzmann. Si se emiten moléculas, átomos o electrones [10] [11] desde un material y se miden sus velocidades, el espectro de sus velocidades a menudo casi obedece a una ley teórica llamada distribución de Maxwell-Boltzmann , que proporciona una medición bien fundamentada de las temperaturas para las que se cumple la ley. [12] Todavía no se han realizado experimentos exitosos de este mismo tipo que utilicen directamente la distribución de Fermi-Dirac para la termometría, pero tal vez eso se logre en el futuro. [13]
La velocidad del sonido en un gas se puede calcular teóricamente a partir de las características moleculares del gas , la temperatura, la presión y la constante de Boltzmann. Para un gas de características moleculares y presión conocidas, esto proporciona una relación entre la temperatura y la constante de Boltzmann. Esas cantidades se pueden conocer o medir con mayor precisión que las variables termodinámicas que definen el estado de una muestra de agua en su punto triple. En consecuencia, tomando el valor de la constante de Boltzmann como una referencia definida principalmente de un valor exactamente definido, una medición de la velocidad del sonido puede proporcionar una medición más precisa de la temperatura del gas. [14]
La medición del espectro de la radiación electromagnética de un cuerpo negro tridimensional ideal puede proporcionar una medición precisa de la temperatura porque la frecuencia de la radiancia espectral máxima de la radiación del cuerpo negro es directamente proporcional a la temperatura del cuerpo negro; esto se conoce como ley de desplazamiento de Wien y tiene una explicación teórica en la ley de Planck y la ley de Bose-Einstein .
La medición del espectro de potencia de ruido producido por una resistencia eléctrica también puede proporcionar una medición precisa de la temperatura. La resistencia tiene dos terminales y es, en efecto, un cuerpo unidimensional. La ley de Bose-Einstein para este caso indica que la potencia de ruido es directamente proporcional a la temperatura de la resistencia y al valor de su resistencia y al ancho de banda del ruido. En una banda de frecuencia dada, la potencia de ruido tiene contribuciones iguales de cada frecuencia y se denomina ruido de Johnson . Si se conoce el valor de la resistencia, se puede encontrar la temperatura. [15] [16]
Escala termodinámica macroscópica
Históricamente, hasta mayo de 2019, la definición de la escala Kelvin era la inventada por Kelvin, basada en una relación de cantidades de energía en procesos en una máquina de Carnot ideal, enteramente en términos de termodinámica macroscópica. [ cita requerida ] Esa máquina de Carnot debía funcionar entre dos temperaturas, la del cuerpo cuya temperatura se quería medir, y una de referencia, la de un cuerpo a la temperatura del punto triple del agua. Entonces la temperatura de referencia, la del punto triple, se definió como exactamente273,16 K. Desde mayo de 2019, este valor no está fijado por definición, sino que se mide a través de fenómenos microscópicos, en los que interviene la constante de Boltzmann, como se ha descrito anteriormente. La definición mecánica estadística microscópica no tiene una temperatura de referencia.
Gas ideal
Un material en el que se puede basar una escala de temperatura definida macroscópicamente es el gas ideal . La presión ejercida por un volumen y una masa fijos de un gas ideal es directamente proporcional a su temperatura. Algunos gases naturales muestran propiedades tan cercanas a las ideales en un rango de temperatura adecuado que se pueden utilizar para la termometría; esto fue importante durante el desarrollo de la termodinámica y sigue siendo de importancia práctica hoy en día. [17] [18] Sin embargo, el termómetro de gas ideal no es teóricamente perfecto para la termodinámica. Esto se debe a que la entropía de un gas ideal en su cero absoluto de temperatura no es una cantidad semidefinida positiva, lo que pone al gas en violación de la tercera ley de la termodinámica. A diferencia de los materiales reales, el gas ideal no se licúa ni se solidifica, sin importar cuán frío esté. Pensando de manera alternativa, la ley de los gases ideales se refiere al límite de temperatura infinitamente alta y presión cero; estas condiciones garantizan movimientos no interactivos de las moléculas constituyentes. [19] [20] [21]
Enfoque de la teoría cinética
La magnitud del kelvin ahora se define en términos de la teoría cinética, derivada del valor de la constante de Boltzmann .
La teoría cinética proporciona una explicación microscópica de la temperatura para algunos cuerpos de material, especialmente gases, basada en que los sistemas macroscópicos están compuestos de muchas partículas microscópicas, como moléculas e iones de varias especies, siendo todas las partículas de una especie iguales. Explica los fenómenos macroscópicos a través de la mecánica clásica de las partículas microscópicas. El teorema de equipartición de la teoría cinética afirma que cada grado clásico de libertad de una partícula que se mueve libremente tiene una energía cinética promedio de k B T /2 donde k B denota la constante de Boltzmann . [ cita requerida ] El movimiento de traslación de la partícula tiene tres grados de libertad, de modo que, excepto a temperaturas muy bajas donde predominan los efectos cuánticos, la energía cinética de traslación promedio de una partícula que se mueve libremente en un sistema con temperatura T será 3 k B T /2 .
Las moléculas, como el oxígeno (O 2 ), tienen más grados de libertad que los átomos esféricos individuales: experimentan movimientos rotacionales y vibracionales, así como traslaciones. El calentamiento produce un aumento de la temperatura debido a un aumento de la energía cinética de traslación media de las moléculas. El calentamiento también hará que, a través de la equipartición , aumente la energía asociada a los modos vibracional y rotacional. Por lo tanto, un gas diatómico requerirá un mayor aporte de energía para aumentar su temperatura en una cierta cantidad, es decir, tendrá una mayor capacidad calorífica que un gas monoatómico.
Como se ha indicado anteriormente, la velocidad del sonido en un gas se puede calcular a partir de las características moleculares del gas, la temperatura, la presión y la constante de Boltzmann. Si se toma el valor de la constante de Boltzmann como referencia primaria definida con un valor exactamente definido, una medición de la velocidad del sonido puede proporcionar una medición más precisa de la temperatura del gas. [14]
Es posible medir la energía cinética media de las partículas microscópicas constituyentes si se les permite escapar del conjunto del sistema a través de un pequeño orificio en la pared que lo contiene. Es necesario medir el espectro de velocidades y calcular el promedio a partir de ahí. No es necesariamente el caso de que las partículas que escapan y se miden tengan la misma distribución de velocidad que las partículas que permanecen en el conjunto del sistema, pero a veces es posible obtener una buena muestra.
Enfoque termodinámico
| Termodinámica |
|---|
 |
La temperatura es una de las magnitudes principales en el estudio de la termodinámica . Antiguamente, la magnitud del kelvin se definía en términos termodinámicos, pero hoy en día, como se mencionó anteriormente, se define en términos de la teoría cinética.
Se dice que la temperatura termodinámica es absoluta por dos razones. Una es que su carácter formal es independiente de las propiedades de materiales particulares. La otra razón es que su cero es, en cierto sentido, absoluto, ya que indica ausencia de movimiento clásico microscópico de las partículas constituyentes de la materia, de modo que tienen un calor específico límite de cero para temperatura cero, de acuerdo con la tercera ley de la termodinámica. Sin embargo, una temperatura termodinámica de hecho tiene un valor numérico definido que ha sido elegido arbitrariamente por la tradición y depende de la propiedad de materiales particulares; es simplemente menos arbitraria que las escalas de "grados" relativos como Celsius y Fahrenheit . Al ser una escala absoluta con un punto fijo (cero), solo queda un grado de libertad para la elección arbitraria, en lugar de dos como en las escalas relativas. Para la escala Kelvin desde mayo de 2019, por convención internacional, se ha optado por utilizar el conocimiento de los modos de funcionamiento de varios dispositivos termométricos, apoyándose en teorías cinéticas microscópicas sobre el movimiento molecular. La escala numérica se establece mediante una definición convencional del valor de la constante de Boltzmann , que relaciona la temperatura macroscópica con la energía cinética microscópica promedio de partículas como las moléculas. Su valor numérico es arbitrario y existe una escala de temperatura absoluta alternativa, menos utilizada, llamada escala Rankine , diseñada para alinearse con la escala Fahrenheit como la Kelvin con la Celsius.
La definición termodinámica de temperatura se debe a Kelvin. Está enmarcada en términos de un dispositivo idealizado llamado máquina de Carnot , imaginado para funcionar en un ciclo continuo ficticio de procesos sucesivos que atraviesan un ciclo de estados de su cuerpo de trabajo. La máquina absorbe una cantidad de calor Q 1 de un depósito caliente y pasa una cantidad menor de calor residual Q 2 < 0 a un depósito frío. La energía térmica neta absorbida por el cuerpo de trabajo se pasa, como trabajo termodinámico, a un depósito de trabajo, y se considera que es la salida de la máquina. Se imagina que el ciclo se ejecuta tan lentamente que en cada punto del ciclo el cuerpo de trabajo está en un estado de equilibrio termodinámico. Por lo tanto, se imagina que los procesos sucesivos del ciclo se ejecutan de manera reversible sin producción de entropía . Entonces, la cantidad de entropía absorbida del depósito caliente cuando el cuerpo de trabajo se calienta es igual a la que pasa al depósito frío cuando el cuerpo de trabajo se enfría. Luego, las temperaturas absolutas o termodinámicas, T 1 y T 2 , de los yacimientos se definen de manera que [22]
| (1) |
La ley cero de la termodinámica permite utilizar esta definición para medir la temperatura absoluta o termodinámica de un cuerpo de interés arbitrario, haciendo que el otro reservorio de calor tenga la misma temperatura que el cuerpo de interés.
El trabajo original de Kelvin, que postulaba la temperatura absoluta, se publicó en 1848. Se basaba en el trabajo de Carnot, anterior a la formulación de la primera ley de la termodinámica. Carnot no tenía una comprensión sólida del calor ni un concepto específico de entropía. Escribió sobre el término "calórico" y dijo que todo el calórico que pasaba del depósito caliente pasaba al depósito frío. Kelvin escribió en su artículo de 1848 que su escala era absoluta en el sentido de que se definía "independientemente de las propiedades de cualquier tipo particular de materia". Su publicación definitiva, que establece la definición que acabamos de exponer, se imprimió en 1853, y se leyó en 1851. [23] [24] [25] [26]
Los detalles numéricos se resolvían anteriormente haciendo que uno de los depósitos de calor fuera una celda en el punto triple del agua, que se definió con una temperatura absoluta de 273,16 K. [27] Hoy en día, el valor numérico se obtiene a partir de la medición mediante la definición internacional mecánica estadística microscópica, como se indicó anteriormente.
Variabilidad intensa
En términos termodinámicos, la temperatura es una variable intensiva porque es igual a un coeficiente diferencial de una variable extensiva con respecto a otra, para un cuerpo dado. Por lo tanto, tiene las dimensiones de una relación de dos variables extensivas. En termodinámica, a menudo se considera que dos cuerpos están conectados por el contacto con una pared común, que tiene algunas propiedades de permeabilidad específicas. Dicha permeabilidad específica puede referirse a una variable intensiva específica. Un ejemplo es una pared diatérmica que es permeable solo al calor; la variable intensiva para este caso es la temperatura. Cuando los dos cuerpos han estado conectados a través de la pared específicamente permeable durante mucho tiempo y se han asentado en un estado estacionario permanente, las variables intensivas relevantes son iguales en los dos cuerpos; para una pared diatérmica, esta afirmación a veces se denomina la ley cero de la termodinámica. [28] [29] [30]
En particular, cuando el cuerpo se describe indicando su energía interna U , una variable extensiva, como una función de su entropía S , también una variable extensiva, y otras variables de estado V , N , con U = U ( S , V , N ), entonces la temperatura es igual a la derivada parcial de la energía interna con respecto a la entropía: [29] [30] [31]
| (2) |
De la misma manera, cuando el cuerpo se describe expresando su entropía S como una función de su energía interna U , y otras variables de estado V , N , con S = S ( U , V , N ) , entonces el recíproco de la temperatura es igual a la derivada parcial de la entropía con respecto a la energía interna: [29] [31] [32]
| (3) |
La definición anterior, ecuación (1), de la temperatura absoluta, se debe a Kelvin. Se refiere a sistemas cerrados a la transferencia de materia y hace especial hincapié en los procedimientos directamente experimentales. Una presentación de la termodinámica por parte de Gibbs comienza en un nivel más abstracto y trata de sistemas abiertos a la transferencia de materia; en este desarrollo de la termodinámica, las ecuaciones (2) y (3) anteriores son en realidad definiciones alternativas de la temperatura. [33]
Equilibrio termodinámico local
Los cuerpos del mundo real a menudo no están en equilibrio termodinámico y no son homogéneos. Para el estudio mediante métodos de termodinámica irreversible clásica, un cuerpo suele dividirse espacial y temporalmente conceptualmente en "células" de pequeño tamaño. Si las condiciones de equilibrio termodinámico clásico para la materia se cumplen con una buena aproximación en una de esas "células", entonces es homogénea y existe una temperatura para ella. Si esto es así para cada "célula" del cuerpo, entonces se dice que prevalece el equilibrio termodinámico local en todo el cuerpo. [34] [35] [36] [37] [38]
Tiene sentido, por ejemplo, decir de la variable extensiva U , o de la variable extensiva S , que tiene una densidad por unidad de volumen o una cantidad por unidad de masa del sistema, pero no tiene sentido hablar de densidad de temperatura por unidad de volumen o cantidad de temperatura por unidad de masa del sistema. Por otra parte, no tiene sentido hablar de energía interna en un punto, mientras que cuando prevalece el equilibrio termodinámico local, tiene sentido hablar de temperatura en un punto. En consecuencia, la temperatura puede variar de un punto a otro en un medio que no está en equilibrio termodinámico global, pero en el que sí lo hay.
Así, cuando en un cuerpo prevalece el equilibrio termodinámico local, la temperatura puede considerarse como una propiedad local que varía espacialmente en ese cuerpo, y esto se debe a que la temperatura es una variable intensiva.
Teoría básica
| Conjugate variables of thermodynamics | ||||||||
|
La temperatura es una medida de la cualidad del estado de un material. [39] La cualidad puede considerarse una entidad más abstracta que cualquier escala de temperatura particular que la mida, y algunos autores la denominan picor . [40] [41] [42] La cualidad del picor se refiere al estado del material solo en una localidad particular y, en general, aparte de los cuerpos que se mantienen en un estado estable de equilibrio termodinámico, el picor varía de un lugar a otro. No es necesariamente el caso de que un material en un lugar particular esté en un estado estable y casi lo suficientemente homogéneo como para permitirle tener un picor o temperatura bien definidos. El picor puede representarse de forma abstracta como una variedad unidimensional . Cada escala de temperatura válida tiene su propio mapa uno a uno en la variedad de picor. [43] [44]
Cuando dos sistemas en contacto térmico están a la misma temperatura no hay transferencia de calor entre ellos. Cuando existe una diferencia de temperatura, el calor fluye espontáneamente del sistema más caliente al sistema más frío hasta que están en equilibrio térmico . Esta transferencia de calor se produce por conducción o por radiación térmica. [45] [46] [47] [48] [49] [50] [51] [52]
Los físicos experimentales, como Galileo y Newton , [53] descubrieron que existen infinitas escalas de temperatura empíricas . Sin embargo, la ley cero de la termodinámica dice que todas miden la misma cualidad. Esto significa que, para un cuerpo en su propio estado de equilibrio termodinámico interno, cualquier termómetro correctamente calibrado, del tipo que sea, que mida la temperatura del cuerpo, registra una misma temperatura. Para un cuerpo que no se encuentra en su propio estado de equilibrio termodinámico interno, diferentes termómetros pueden registrar diferentes temperaturas, dependiendo respectivamente de los mecanismos de funcionamiento de los termómetros.
Cuerpos en equilibrio termodinámico
Para la física experimental, el calor significa que, al comparar dos cuerpos cualesquiera dados en sus respectivos equilibrios termodinámicos separados , dos termómetros empíricos dados adecuadamente con lecturas de escala numérica concordarán en cuál es el más caliente de los dos cuerpos dados, o en que tienen la misma temperatura. [54] Esto no requiere que los dos termómetros tengan una relación lineal entre sus lecturas de escala numérica, pero sí requiere que la relación entre sus lecturas numéricas sea estrictamente monótona . [55] [56] Se puede tener un sentido definido de mayor calor, independientemente de la calorimetría , de la termodinámica y de las propiedades de materiales particulares, a partir de la ley de desplazamiento de Wien de la radiación térmica : la temperatura de un baño de radiación térmica es proporcional , por una constante universal, a la frecuencia del máximo de su espectro de frecuencia ; esta frecuencia es siempre positiva, pero puede tener valores que tienden a cero . La radiación térmica se define inicialmente para una cavidad en equilibrio termodinámico. Estos hechos físicos justifican una afirmación matemática de que el calor existe en una variedad unidimensional ordenada . Esta es una característica fundamental de la temperatura y de los termómetros para los cuerpos en su propio equilibrio termodinámico. [8] [43] [44] [57] [58]
A excepción de un sistema que experimenta un cambio de fase de primer orden , como la fusión del hielo, cuando un sistema cerrado recibe calor, sin un cambio en su volumen y sin un cambio en los campos de fuerza externos que actúan sobre él, su temperatura aumenta. Para un sistema que experimenta un cambio de fase tan lento que la desviación del equilibrio termodinámico puede despreciarse, su temperatura permanece constante mientras el sistema recibe calor latente . Por el contrario, una pérdida de calor de un sistema cerrado, sin cambio de fase, sin cambio de volumen y sin un cambio en los campos de fuerza externos que actúan sobre él, disminuye su temperatura. [59]
Cuerpos en estado estacionario pero no en equilibrio termodinámico
Mientras que para los cuerpos en sus propios estados de equilibrio termodinámico, la noción de temperatura requiere que todos los termómetros empíricos estén de acuerdo en cuál de los dos cuerpos es el más caliente o que están a la misma temperatura, este requisito no es seguro para los cuerpos que están en estados estables aunque no en equilibrio termodinámico. Entonces, bien puede ser que diferentes termómetros empíricos discrepen sobre cuál es el más caliente, y si esto es así, entonces al menos uno de los cuerpos no tiene una temperatura termodinámica absoluta bien definida. Sin embargo, cualquier cuerpo dado y cualquier termómetro empírico adecuado aún pueden sustentar nociones de calor y temperatura empíricas, no absolutas, para un rango adecuado de procesos. Este es un tema de estudio en termodinámica del no equilibrio . [ cita requerida ]
Cuerpos que no se encuentran en estado estacionario
Cuando un cuerpo no se encuentra en estado estacionario, la noción de temperatura se vuelve aún menos segura que para un cuerpo en estado estacionario que no se encuentra en equilibrio termodinámico. Esto también es un tema de estudio en la termodinámica del no equilibrio .
Axiomática del equilibrio termodinámico
Para el tratamiento axiomático del equilibrio termodinámico, desde la década de 1930, se ha vuelto habitual referirse a una ley cero de la termodinámica . La versión minimalista habitualmente enunciada de dicha ley postula solo que todos los cuerpos, que cuando están conectados térmicamente estarían en equilibrio térmico, se debe decir que tienen la misma temperatura por definición, pero por sí misma no establece la temperatura como una cantidad expresada como un número real en una escala. Una versión físicamente más informativa de dicha ley considera la temperatura empírica como un gráfico en una variedad de calor. [43] [58] [60] Mientras que la ley cero permite las definiciones de muchas escalas empíricas diferentes de temperatura, la segunda ley de la termodinámica selecciona la definición de una única temperatura absoluta preferida , única hasta un factor de escala arbitrario, de ahí el nombre de temperatura termodinámica . [8] [43] [61] [62] [63] [64] Si se considera la energía interna como una función del volumen y la entropía de un sistema homogéneo en equilibrio termodinámico, la temperatura absoluta termodinámica aparece como la derivada parcial de la energía interna con respecto a la entropía a volumen constante. Su origen natural, intrínseco o punto nulo es el cero absoluto en el que la entropía de cualquier sistema es mínima. Aunque esta es la temperatura absoluta más baja descrita por el modelo, la tercera ley de la termodinámica postula que el cero absoluto no puede ser alcanzado por ningún sistema físico.
Capacidad calorífica
Cuando la transferencia de energía hacia o desde un cuerpo se realiza únicamente en forma de calor, el estado del cuerpo cambia. Dependiendo del entorno y de las paredes que lo separan del cuerpo, son posibles diversos cambios en el cuerpo. Entre ellos se incluyen reacciones químicas, aumento de presión, aumento de temperatura y cambio de fase. Para cada tipo de cambio en condiciones específicas, la capacidad térmica es la relación entre la cantidad de calor transferida y la magnitud del cambio. [65]
Por ejemplo, si el cambio es un aumento de temperatura a volumen constante, sin cambio de fase ni cambio químico, entonces la temperatura del cuerpo aumenta y su presión aumenta. La cantidad de calor transferido, Δ Q , dividida por el cambio de temperatura observado, Δ T , es la capacidad térmica del cuerpo a volumen constante:
- C V = Δ Q Δ T . {\displaystyle C_{V}={\frac {\Delta Q}{\Delta T}}.}
Si se mide la capacidad calorífica de una cantidad bien definida de sustancia , el calor específico es la medida del calor necesario para aumentar la temperatura de dicha cantidad unitaria en una unidad de temperatura. Por ejemplo, para aumentar la temperatura del agua en un kelvin (equivalente a un grado Celsius) se necesitan 4186 julios por kilogramo (J/kg).
Medición

La medición de la temperatura mediante termómetros y escalas de temperatura científicos modernos se remonta al menos a principios del siglo XVIII, cuando Daniel Gabriel Fahrenheit adaptó un termómetro (cambiándolo por el de mercurio ) y una escala, ambos desarrollados por Ole Christensen Rømer . La escala de Fahrenheit todavía se utiliza en los Estados Unidos para aplicaciones no científicas.
La temperatura se mide con termómetros que pueden calibrarse en distintas escalas de temperatura . En la mayor parte del mundo (excepto en Belice , Myanmar , Liberia y Estados Unidos ), se utiliza la escala Celsius para la mayoría de los propósitos de medición de temperatura. La mayoría de los científicos miden la temperatura utilizando la escala Celsius y la temperatura termodinámica utilizando la escala Kelvin , que es la escala Celsius desplazada de modo que su punto nulo es0 K =−273,15 °C o cero absoluto . Muchos campos de ingeniería en los EE. UU., en particular la alta tecnología y las especificaciones federales de los EE. UU. (civiles y militares), también utilizan las escalas Kelvin y Celsius. Otros campos de ingeniería en los EE. UU. también dependen de la escala Rankine (una escala Fahrenheit desplazada) cuando trabajan en disciplinas relacionadas con la termodinámica, como la combustión .
Unidades
La unidad básica de temperatura en el Sistema Internacional de Unidades (SI) es el kelvin . Su símbolo es K.
Para aplicaciones cotidianas, a menudo es conveniente utilizar la escala Celsius, en la que0 °C corresponde muy de cerca al punto de congelación del agua y100 °C es su punto de ebullición a nivel del mar. Debido a que las gotas de líquido suelen existir en las nubes a temperaturas bajo cero,0 °C se define mejor como el punto de fusión del hielo. En esta escala, una diferencia de temperatura de 1 grado Celsius es lo mismo que un incremento de 1 kelvin , pero la escala se compensa con la temperatura a la que se derrite el hielo (273,15 K ).
Por acuerdo internacional, [66] hasta mayo de 2019, las escalas Kelvin y Celsius se definían por dos puntos fijos: el cero absoluto y el punto triple del agua oceánica estándar de Viena , que es agua especialmente preparada con una mezcla específica de isótopos de hidrógeno y oxígeno. El cero absoluto se definía como0 K y−273,15 °C . Es la temperatura a la que cesa todo movimiento de traslación clásico de las partículas que componen la materia y se encuentran en completo reposo en el modelo clásico. Sin embargo, desde el punto cero en la mecánica cuántica, el movimiento permanece y tiene una energía asociada, la energía del punto cero . La materia está en su estado fundamental , [67] y no contiene energía térmica . Las temperaturas273,16 K ySe definieron 0,01 °C como los del punto triple del agua. Esta definición sirvió para los siguientes propósitos: fijó la magnitud del kelvin como exactamente 1 parte en 273,16 partes de la diferencia entre el cero absoluto y el punto triple del agua; estableció que un kelvin tiene exactamente la misma magnitud que un grado en la escala Celsius; y estableció la diferencia entre los puntos nulos de estas escalas como273,15 kilos (0 K =-273,15 °C y273,16 K =0,01 °C ). Desde 2019 existe una nueva definición basada en la constante de Boltzmann, [68] pero las escalas apenas han cambiado.
En Estados Unidos, la escala Fahrenheit es la más utilizada. En esta escala, el punto de congelación del agua corresponde a32 °F y el punto de ebullición a212 °F . La escala Rankine, todavía utilizada en los campos de la ingeniería química en los EE. UU., es una escala absoluta basada en el incremento de Fahrenheit.
Escalas históricas
Las siguientes escalas de temperatura se utilizan o se han utilizado históricamente para medir la temperatura:
- Escala Kelvin
- Escala Celsius
- Escala Fahrenheit
- Escala de Rankine
- Escala de Delisle
- Escala de Newton
- Escala de Réaumur
- Escala de Rømer
Física del plasma
El campo de la física del plasma se ocupa de fenómenos de naturaleza electromagnética que involucran temperaturas muy altas. Es habitual expresar la temperatura como energía en una unidad relacionada con el electronvoltio o kiloelectronvoltio ( eV/ k B o keV/ k B ). La energía correspondiente, que es dimensionalmente distinta de la temperatura, se calcula entonces como el producto de la constante de Boltzmann por la temperatura, . Entonces, 1 eV/ k B es 11 605 K . En el estudio de la materia de QCD se encuentran rutinariamente temperaturas del orden de unos pocos cientos de MeV/ k B , equivalentes a aproximadamente10 12 K .
Continuo o discreto
Cuando se mide la variación de la temperatura en una región del espacio o del tiempo, ¿las mediciones de temperatura resultan ser continuas o discretas? Existe una idea errónea generalizada de que dichas mediciones de temperatura siempre deben ser continuas. [69] Esta idea errónea se origina en parte de la visión histórica asociada con la continuidad de las cantidades físicas clásicas , que establece que las cantidades físicas deben asumir cada valor intermedio entre un valor inicial y un valor final. [69] [70] Sin embargo, la imagen clásica solo es verdadera en los casos en que la temperatura se mide en un sistema que está en equilibrio , es decir, la temperatura puede no ser continua fuera de estas condiciones. [69] Para los sistemas fuera del equilibrio, como en las interfaces entre materiales (por ejemplo, una interfaz metal/no metal o una interfaz líquido-vapor), las mediciones de temperatura pueden mostrar discontinuidades pronunciadas en el tiempo y el espacio. [69] Por ejemplo, Fang y Ward fueron algunos de los primeros autores en informar con éxito discontinuidades de temperatura de hasta 7,8 K en la superficie de gotas de agua en evaporación. [71] Esto se informó a escalas intermoleculares, o a la escala del camino libre medio de las moléculas que es típicamente del orden de unos pocos micrómetros en gases [72] a temperatura ambiente. En términos generales, las discontinuidades de temperatura se consideran normas en lugar de excepciones en casos de transferencia de calor interfacial. [73] Esto se debe al cambio abrupto en las propiedades vibracionales o térmicas de los materiales a través de tales interfaces que impiden la transferencia instantánea de calor y el establecimiento del equilibrio térmico (un prerrequisito para tener una temperatura de equilibrio uniforme a través de la interfaz). [74] [75] Además, las mediciones de temperatura a escala macro (escala de observación típica) pueden ser demasiado granulares, ya que promedian la información térmica microscópica en función de la escala del volumen de muestra representativo del sistema de control y, por lo tanto, es probable que las discontinuidades de temperatura a escala micro puedan pasarse por alto en tales promedios. [69] Este promedio puede incluso producir resultados incorrectos o engañosos en muchos casos de mediciones de temperatura, incluso a escala macro, y por lo tanto es prudente examinar la información microfísica cuidadosamente antes de promediar o suavizar cualquier posible discontinuidad de temperatura en un sistema, ya que dichas discontinuidades no siempre se pueden promediar o suavizar. [69] [76]Las discontinuidades de temperatura, en lugar de ser simplemente anomalías, han mejorado sustancialmente nuestra comprensión y nuestras capacidades predictivas en relación con la transferencia de calor a pequeña escala. [69] [73] [74] [75] [76]
Fundamentación teórica
Históricamente, existen varios enfoques científicos para la explicación de la temperatura: la descripción termodinámica clásica basada en variables empíricas macroscópicas que se pueden medir en un laboratorio; la teoría cinética de los gases que relaciona la descripción macroscópica con la distribución de probabilidad de la energía del movimiento de las partículas de gas; y una explicación microscópica basada en la física estadística y la mecánica cuántica . Además, los tratamientos rigurosos y puramente matemáticos han proporcionado un enfoque axiomático a la termodinámica clásica y la temperatura. [77] La física estadística proporciona una comprensión más profunda al describir el comportamiento atómico de la materia y deriva propiedades macroscópicas de promedios estadísticos de estados microscópicos, incluidos los estados clásicos y cuánticos. En la descripción física fundamental, la temperatura puede medirse directamente en unidades de energía. Sin embargo, en los sistemas prácticos de medición para la ciencia, la tecnología y el comercio, como el sistema métrico moderno de unidades, las descripciones macroscópicas y microscópicas están interrelacionadas por la constante de Boltzmann , un factor de proporcionalidad que escala la temperatura a la energía cinética media microscópica.
La descripción microscópica en mecánica estadística se basa en un modelo que analiza un sistema en sus partículas fundamentales de materia o en un conjunto de osciladores clásicos o mecánicos cuánticos y considera el sistema como un conjunto estadístico de microestados . Como colección de partículas materiales clásicas, la temperatura es una medida de la energía media de movimiento, llamada energía cinética traslacional , de las partículas, ya sea en sólidos, líquidos, gases o plasmas. La energía cinética, un concepto de la mecánica clásica , es la mitad de la masa de una partícula por su velocidad al cuadrado. En esta interpretación mecánica del movimiento térmico, las energías cinéticas de las partículas materiales pueden residir en la velocidad de las partículas de su movimiento traslacional o vibracional o en la inercia de sus modos rotacionales. En los gases perfectos monatómicos y, aproximadamente, en la mayoría de los gases y en los metales simples, la temperatura es una medida de la energía cinética traslacional media de las partículas, 3/2 k B T . También determina la función de distribución de probabilidad de la energía. En materia condensada, y particularmente en sólidos, esta descripción puramente mecánica es a menudo menos útil y el modelo de oscilador proporciona una mejor descripción para dar cuenta de los fenómenos mecánicos cuánticos. La temperatura determina la ocupación estadística de los microestados del conjunto. La definición microscópica de temperatura solo tiene sentido en el límite termodinámico , es decir, para grandes conjuntos de estados o partículas, para cumplir con los requisitos del modelo estadístico.
La energía cinética también se considera un componente de la energía térmica . La energía térmica puede dividirse en componentes independientes atribuidos a los grados de libertad de las partículas o a los modos de osciladores en un sistema termodinámico . En general, el número de estos grados de libertad que están disponibles para la equipartición de la energía depende de la temperatura, es decir, la región de energía de las interacciones en consideración. Para los sólidos, la energía térmica está asociada principalmente con las vibraciones de sus átomos o moléculas alrededor de su posición de equilibrio. En un gas monoatómico ideal , la energía cinética se encuentra exclusivamente en los movimientos puramente traslacionales de las partículas. En otros sistemas, los movimientos vibratorios y rotacionales también contribuyen a los grados de libertad.
Teoría cinética de los gases

Maxwell y Boltzmann desarrollaron una teoría cinética que proporciona una comprensión fundamental de la temperatura en los gases. [78] Esta teoría también explica la ley de los gases ideales y la capacidad térmica observada de los gases monoatómicos (o "nobles" ). [79] [80] [81]
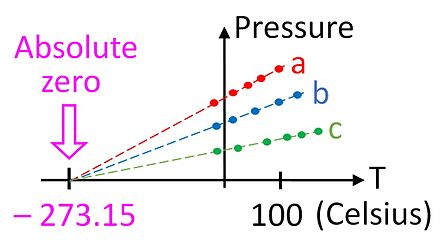
La ley de los gases ideales se basa en relaciones empíricas observadas entre la presión ( p ), el volumen ( V ) y la temperatura ( T ), y fue reconocida mucho antes de que se desarrollara la teoría cinética de los gases (ver las leyes de Boyle y Charles ). La ley de los gases ideales establece: [82]
donde n es el número de moles de gas y R = 8.314 462 618 ... J⋅mol −1 ⋅K −1 [ 83] es la constante del gas .
Esta relación nos da la primera pista de que existe un cero absoluto en la escala de temperatura, ya que solo se cumple si la temperatura se mide en una escala absoluta como la de Kelvin. La ley de los gases ideales permite medir la temperatura en esta escala absoluta utilizando el termómetro de gas . La temperatura en kelvin se puede definir como la presión en pascales de un mol de gas en un recipiente de un metro cúbico, dividida por la constante de los gases.
Aunque no es un dispositivo especialmente práctico, el termómetro de gas proporciona una base teórica esencial para calibrar todos los termómetros. En la práctica, no es posible utilizar un termómetro de gas para medir la temperatura del cero absoluto, ya que los gases se condensan en un líquido mucho antes de que la temperatura llegue a cero. Sin embargo, es posible extrapolar la temperatura al cero absoluto utilizando la ley de los gases ideales, como se muestra en la figura.
La teoría cinética supone que la presión es causada por la fuerza asociada con los átomos individuales que chocan contra las paredes, y que toda la energía es energía cinética traslacional . Utilizando un sofisticado argumento de simetría, [84] Boltzmann dedujo lo que ahora se llama la función de distribución de probabilidad de Maxwell-Boltzmann para la velocidad de las partículas en un gas ideal. A partir de esa función de distribución de probabilidad , la energía cinética promedio (por partícula) de un gas ideal monoatómico es [80] [85]
donde la constante de Boltzmann k B es la constante del gas ideal dividida por el número de Avogadro , y es la raíz cuadrada de la velocidad media . [86] Esta proporcionalidad directa entre la temperatura y la energía cinética molecular media es un caso especial del teorema de equipartición , y se cumple solo en el límite clásico de un gas perfecto . No se cumple exactamente para la mayoría de las sustancias.
Ley cero de la termodinámica
Cuando dos cuerpos que de otro modo estarían aislados se conectan entre sí mediante un camino físico rígido e impermeable a la materia, se produce una transferencia espontánea de energía en forma de calor desde el más caliente al más frío de ellos. Finalmente, alcanzan un estado de equilibrio térmico mutuo , en el que la transferencia de calor ha cesado y las respectivas variables de estado de los cuerpos se han estabilizado y se han vuelto inmutables. [87] [88] [89]
Una afirmación de la ley cero de la termodinámica es que si dos sistemas están cada uno en equilibrio térmico con un tercer sistema, entonces también están en equilibrio térmico entre sí. [90] [91] [92]
Esta afirmación ayuda a definir la temperatura, pero no completa, por sí sola, la definición. Una temperatura empírica es una escala numérica para el calor de un sistema termodinámico. Tal calor puede definirse como existente en una variedad unidimensional , que se extiende entre caliente y frío. A veces se afirma que la ley cero incluye la existencia de una variedad única y universal de calor, y de escalas numéricas en ella, de modo de proporcionar una definición completa de la temperatura empírica. [60] Para ser adecuado para la termometría empírica, un material debe tener una relación monótona entre el calor y alguna variable de estado fácilmente medible, como la presión o el volumen, cuando todas las demás coordenadas relevantes son fijas. Un sistema excepcionalmente adecuado es el gas ideal , que puede proporcionar una escala de temperatura que coincide con la escala Kelvin absoluta. La escala Kelvin se define sobre la base de la segunda ley de la termodinámica.
Segunda ley de la termodinámica
Como alternativa a considerar o definir la ley cero de la termodinámica, el desarrollo histórico de la termodinámica fue definir la temperatura en términos de la segunda ley de la termodinámica , que trata de la entropía . [ cita requerida ] La segunda ley establece que cualquier proceso dará como resultado la inexistencia de cambios o un aumento neto de la entropía del universo. Esto se puede entender en términos de probabilidad.
Por ejemplo, en una serie de lanzamientos de monedas, un sistema perfectamente ordenado sería aquel en el que en cada lanzamiento sale cara o en cada lanzamiento sale cruz. Esto significa que el resultado es siempre 100% el mismo. Por el contrario, son posibles muchos resultados mixtos ( desordenados ), y su número aumenta con cada lanzamiento. Finalmente, las combinaciones de ~50% caras y ~50% cruces dominan, y obtener un resultado significativamente diferente de 50/50 se vuelve cada vez más improbable. Así, el sistema progresa naturalmente a un estado de máximo desorden o entropía.
Como la temperatura rige la transferencia de calor entre dos sistemas y el universo tiende a progresar hacia un máximo de entropía, se espera que exista alguna relación entre la temperatura y la entropía. Un motor térmico es un dispositivo para convertir energía térmica en energía mecánica, lo que da como resultado la realización de trabajo. Un análisis del motor térmico de Carnot proporciona las relaciones necesarias. De acuerdo con la conservación de la energía y la energía como una función de estado que no cambia durante un ciclo completo, el trabajo de un motor térmico durante un ciclo completo es igual al calor neto, es decir, la suma del calor introducido en el sistema a alta temperatura, q H > 0, y el calor residual emitido a baja temperatura, q C < 0. [93]
La eficiencia es el trabajo dividido por el calor aportado:
| (4) |
donde w cy es el trabajo realizado por ciclo. La eficiencia depende únicamente de | q C |/ q H . Como q C y q H corresponden a la transferencia de calor a las temperaturas T C y T H , respectivamente, | q C |/ q H debería ser alguna función de estas temperaturas:
| (5) |
El teorema de Carnot establece que todos los motores reversibles que funcionan entre los mismos depósitos de calor son igualmente eficientes. [ cita requerida ] Por lo tanto, un motor térmico que funciona entre T 1 y T 3 debe tener la misma eficiencia que uno que consta de dos ciclos, uno entre T 1 y T 2 y el segundo entre T 2 y T 3 . Esto solo puede ser el caso si
Lo que implica
Como la primera función es independiente de T 2 , esta temperatura debe cancelarse en el lado derecho, lo que significa que f ( T 1 , T 3 ) tiene la forma g ( T 1 )/ g ( T 3 ) (es decir, f ( T 1 , T 3 ) = f ( T 1 , T 2 ) f ( T 2 , T 3 ) = g ( T 1 )/ g ( T 2 ) · g ( T 2 )/ g ( T 3 ) = g ( T 1 )/ g ( T 3 )) , donde g es una función de una sola temperatura. Ahora se puede elegir una escala de temperatura con la propiedad de que
| (6) |
Sustituyendo (6) en (4) obtenemos una relación para la eficiencia en términos de temperatura:
| (7) |
Para T C = 0 K la eficiencia es del 100% y esa eficiencia se vuelve mayor que el 100% por debajo de 0 K. Dado que una eficiencia mayor que el 100% viola la primera ley de la termodinámica, esto implica que 0 K es la temperatura mínima posible. De hecho, la temperatura más baja jamás obtenida en un sistema macroscópico fue de 20 nK, que se logró en 1995 en el NIST. Restando el lado derecho de (5) de la porción media y reordenando se obtiene [22] [93]
donde el signo negativo indica calor expulsado del sistema. Esta relación sugiere la existencia de una función de estado, S , cuyo cambio se desvanece característicamente durante un ciclo completo si se define por
| (8) |
donde el subíndice indica un proceso reversible. Esta función corresponde a la entropía del sistema, que se describió anteriormente. Reordenando (8) se obtiene una fórmula para la temperatura en términos de elementos infinitesimales ficticios cuasi-reversibles de entropía y calor:
| (9) |
Para un sistema de volumen constante donde la entropía S ( E ) es una función de su energía E , d E = d q rev y (9) da
| (10) |
es decir, el recíproco de la temperatura es la tasa de aumento de la entropía con respecto a la energía a volumen constante.
Definición de mecánica estadística
La mecánica estadística define la temperatura en función de los grados de libertad fundamentales de un sistema. La ecuación (10) es la relación que define la temperatura, donde la entropía se define (hasta una constante) por el logaritmo del número de microestados del sistema en el macroestado dado (como se especifica en el conjunto microcanónico ):
donde es la constante de Boltzmann y W es el número de microestados con la energía E del sistema (degeneración).
Cuando dos sistemas con diferentes temperaturas se ponen en conexión puramente térmica, el calor fluirá del sistema de mayor temperatura al de menor temperatura; termodinámicamente esto se entiende por la segunda ley de la termodinámica: El cambio total en entropía después de una transferencia de energía del sistema 1 al sistema 2 es:
y por tanto es positivo si
Desde el punto de vista de la mecánica estadística, el número total de microestados en el sistema combinado 1 + sistema 2 es , cuyo logaritmo (por la constante de Boltzmann) es la suma de sus entropías; por lo tanto, un flujo de calor de alta a baja temperatura, que produce un aumento de la entropía total, es más probable que cualquier otro escenario (normalmente es mucho más probable), ya que hay más microestados en el macroestado resultante.
Temperatura generalizada a partir de estadísticas de partículas individuales
Es posible extender la definición de temperatura incluso a sistemas de pocas partículas, como en un punto cuántico . La temperatura generalizada se obtiene considerando conjuntos temporales en lugar de conjuntos de configuración-espacio dados en mecánica estadística en el caso de intercambio térmico y de partículas entre un pequeño sistema de fermiones ( N incluso menor que 10) con un sistema de ocupación simple/doble. El conjunto gran canónico cuántico finito , [94] obtenido bajo la hipótesis de ergodicidad y ortodicidad, [95] permite expresar la temperatura generalizada a partir de la relación entre el tiempo medio de ocupación y el del sistema de ocupación simple/doble: [96]
donde E F es la energía de Fermi . Esta temperatura generalizada tiende a la temperatura ordinaria cuando N tiende al infinito.
Temperatura negativa
En las escalas de temperatura empíricas que no están referidas al cero absoluto, una temperatura negativa es una temperatura por debajo del punto cero de la escala utilizada. Por ejemplo, el hielo seco tiene una temperatura de sublimación de−78,5 °C que equivale a−109,3 °F . [97] En la escala absoluta Kelvin, esta temperatura es194,6 K. Ningún cuerpo de materia puede ser llevado a una temperatura exacta.0 K (la temperatura del cuerpo idealmente más frío posible) por cualquier proceso practicable finito; esto es una consecuencia de la tercera ley de la termodinámica . [98] [99] [100]
La teoría cinética interna establece que la temperatura de un cuerpo de materia no puede adoptar valores negativos. Sin embargo, la escala de temperatura termodinámica no está tan limitada.
Un cuerpo de materia puede definirse conceptualmente en términos de grados de libertad microscópicos, es decir, espines de partículas, un subsistema con una temperatura distinta a la del cuerpo entero. Cuando el cuerpo está en su estado de equilibrio termodinámico interno, las temperaturas de todo el cuerpo y del subsistema deben ser las mismas. Las dos temperaturas pueden diferir cuando, mediante el trabajo a través de campos de fuerza impuestos externamente, se puede transferir energía hacia y desde el subsistema, independientemente del resto del cuerpo; entonces, el cuerpo entero no está en su propio estado de equilibrio termodinámico interno. Existe un límite superior de energía que un subsistema de espín de este tipo puede alcanzar.
Considerando que el subsistema está en un estado temporal de equilibrio termodinámico virtual, es posible obtener una temperatura negativa en la escala termodinámica. La temperatura termodinámica es la inversa de la derivada de la entropía del subsistema para su energía interna. A medida que aumenta la energía interna del subsistema, la entropía aumenta durante un cierto rango, pero finalmente alcanza un valor máximo y luego comienza a disminuir a medida que los estados de energía más altos comienzan a llenarse. En el punto de máxima entropía, la función de temperatura muestra el comportamiento de una singularidad porque la pendiente de la entropía como función de la energía disminuye a cero y luego se vuelve negativa. A medida que la entropía del subsistema alcanza su máximo, su temperatura termodinámica tiende al infinito positivo, cambiando al infinito negativo cuando la pendiente se vuelve negativa. Tales temperaturas negativas son más altas que cualquier temperatura positiva. Con el tiempo, cuando el subsistema se expone al resto del cuerpo, que tiene una temperatura positiva, la energía se transfiere como calor del subsistema de temperatura negativa al sistema de temperatura positiva. [101] La temperatura de la teoría cinética no está definida para tales subsistemas.
Ejemplos
.jpg/440px-A_Guide_to_Cosmic_Temperatures_(SVS14374_-_Cosmic_Temperatures_Infographic_Final_Full).jpg)
| Temperatura | Longitud de onda de emisión máxima [a] de la radiación del cuerpo negro | ||
|---|---|---|---|
| Kelvin | Celsius | ||
| Cero absoluto (precisamente por definición) | 0 K | -273,15 °C | Infinidad |
| Temperatura del cuerpo negro del agujero negro en el centro de nuestra galaxia, Sagitario A* [b] | 15 mil | −273,149 999 999 999 985 °C | 2,5 × 10 8 kilómetros (1,7 UA ) |
| Temperatura más baja alcanzada [4] | 38 pK | −273,149 999 999 962 °C | 76 263 kilómetros |
Condensado de Bose-Einstein más frío [c] | 450 pK | −273.149 999 999 55 °C | 6400 kilómetros |
| Un milikelvin (precisamente por definición) | 0,001 K | -273,149 °C | 2.897 77 m (radio, banda FM ) [d] |
| Fondo cósmico de microondas (medición de 2013) | 2,7260 K | -270,424 °C | 0,001 063 01 m (microondas de longitud de onda milimétrica) |
| Punto triple del agua (anteriormente por definición) [e] | 273,16 K | 0,01 °C | 10 608,3 nm ( IR de longitud de onda larga ) |
| Punto de ebullición del agua [A] | 373,1339 K | 99,9839 °C | 7 766 .03 nm (IR de longitud de onda media) |
| Punto de fusión del hierro | 1811 K | 1538 °C | 1600 nm ( infrarrojo lejano ) |
| Lámpara incandescente [B] | 2500 kilovatios | ≈2200 °C | 1160 nm ( infrarrojo cercano ) [C] |
| Superficie visible del Sol [D] [f] | 5778 K | 5505 °C | 501,5 nm ( luz verde-azul ) |
Canal del rayo [E] | 28 kK | 28 000 °C | 100 nm ( luz ultravioleta lejana) |
| Núcleo del Sol [E] | 16 MK | 16 millones de °C | 0,18 nm ( rayos X ) |
| Arma termonuclear (temperatura máxima) [E] [g] | 350 MK | 350 millones de °C | 8,3 × 10 −3 nm ( rayos gamma ) |
Máquina Z de Sandia National Labs [E] [h] | 2 porteros | 2 mil millones de °C | 1,4 × 10 −3 nm (rayos gamma) [F] |
| Núcleo de una estrella de gran masa en su último día [E] [i] | 3 porteros | 3 mil millones de °C | 1 × 10 −3 nm (rayos gamma) |
| Sistema binario de estrellas de neutrones en fusión [E] [j] | 350 GC | 350 mil millones de °C | 8 × 10 −6 nm (rayos gamma) |
Colisionador relativista de iones pesados [E] [103] | 1 TK | 1 billón de °C | 3 × 10 −6 nm (rayos gamma) |
Colisiones de protones contra núcleos en el CERN [E] [104] | 10 TK | 10 billones de °C | 3 × 10 −7 nm (rayos gamma) |
- A Para el agua oceánica media estándar de Viena a una atmósfera estándar (101,325 kPa ) cuando se calibra estrictamente según la definición de dos puntos de temperatura termodinámica.
- B ElEl valor de 2500 K es aproximado.273,15 K la diferencia entre K y °C se redondea a300 K para evitar falsas precisiones en el valor Celsius.
- C Para un cuerpo negro verdadero (que los filamentos de tungsteno no son). La emisividad de los filamentos de tungsteno es mayor en longitudes de onda más cortas, lo que los hace parecer más blancos.
- D Temperatura efectiva de la fotosfera.273,15 K la diferencia entre K y °C se redondea a273 K para evitar falsas precisiones en el valor Celsius.
- E El273,15 K La diferencia entre K y °C está dentro de la precisión de estos valores.
- F Para un cuerpo negro verdadero (que no era el plasma). La emisión dominante de la máquina Z se originó a partir de40 electrones MK (emisiones de rayos X suaves) dentro del plasma.
Véase también
- Temperatura atmosférica – Magnitud física que expresa calor y frío en la atmósfera.
- Temperatura corporal : Capacidad de un organismo de mantener su temperatura corporal dentro de ciertos límites (termorregulación)
- Temperatura de color : propiedad de las fuentes de luz relacionada con la radiación del cuerpo negro
- Temperatura de bulbo seco : temperatura del aire medida con un termómetro protegido de la radiación y la humedad.
- Conducción térmica : proceso mediante el cual se transfiere calor dentro de un objeto.
- Transferencia de calor por convección : transferencia de calor debida a los efectos combinados de advección y difusión.Pages displaying short descriptions of redirect targets
- Registro instrumental de temperatura : temperatura media de la superficie de la TierraPages displaying short descriptions of redirect targets
- ISO 1 – Temperatura estándar ISO, 20 °C
- Escala Internacional de Temperatura de 1990 ( ITS-90 ): escala de temperatura práctica
- Deflectometría por láser Schlieren
- Lista de ciudades por temperatura media
- El demonio de Maxwell – Experimento mental de 1867
- Órdenes de magnitud (temperatura) : comparación de un amplio rango de temperaturas
- Temperatura del aire exterior – Término de aviación
- Temperatura de Planck : Unidades definidas únicamente por constantes físicasPages displaying short descriptions of redirect targets
- Escala Rankine : escala de temperatura absoluta en grados Fahrenheit
- Conducción de calor relativista : modelo compatible con la relatividad especial
- Mediciones de temperatura por satélite : mediciones de la temperatura atmosférica, de la superficie terrestre o del mar mediante satélites.Pages displaying short descriptions of redirect targets
- Escala de temperatura – Método para medir la temperatura cuantitativamente
- Temperatura de la superficie del mar : temperatura del agua cerca de la superficie del océano.
- Temperatura de estancamiento
- Radiación térmica : radiación electromagnética generada por el movimiento térmico de las partículas.
- Termocepción – Sensación y percepción de la temperatura
- Temperatura termodinámica (absoluta) : medida de la temperatura relativa al cero absoluto .
- Termografía : imágenes infrarrojas utilizadas para revelar la temperatura.
- Termómetro – Dispositivo para medir la temperatura
- Temperatura virtual – Temperatura virtual de una parcela de aire húmedo
- Temperatura de bulbo húmedo : estimación de la temperatura aparente que afecta a los humanos
- Temperatura de bulbo húmedo : temperatura leída con un termómetro cubierto con un paño empapado en agua.
Notas y referencias
- Notas
- ^ Las longitudes de onda de emisión citadas corresponden a cuerpos negros en equilibrio. Valor recomendado por CODATA 20062.897 7685 (51) × 10 −3 m K utilizado para la constante b de la ley de desplazamiento de Wien .
- ^ Esta es la radiación de Hawking para un agujero negro de Schwarzschild de masa M =4.145 × 10 6 M ☉ . Es demasiado débil para ser observado.
- ^ En 2003, investigadores del MIT consiguieron una temperatura de 450 ±80 pK en un condensado de Bose-Einstein (BEC) de átomos de sodio . Cita: Cooling Bose-Einstein Condensates Below 500 Picokelvin , AE Leanhardt et al ., Science 301 , 12 de septiembre de 2003, pág. 1515. La longitud de onda de cuerpo negro de emisión máxima de este récord, de 6400 kilómetros, es aproximadamente el radio de la Tierra.
- ^ La longitud de onda de emisión máxima de2.897 77 m es una frecuencia de103,456 MHz
- ^ Desde 2019, Kelvin ahora se define en la constante de Boltzmann , de modo que el punto triple es273,16 ± 0,0001 K
- ^ La medición se realizó en 2002 y tiene una incertidumbre de ±3 kelvin. Una medición de 1989 Archivado el 11 de febrero de 2010 en Wayback Machine produjo un valor de 5777,0 ±2,5 K. Cita: Panorama del Sol (Capítulo 1, notas de clase sobre Física Solar, División de Física Teórica, Departamento de Ciencias Físicas, Universidad de Helsinki).
- ^ El valor de 350 MK es la temperatura máxima de pico del combustible de fusión en un arma termonuclear de la configuración Teller-Ulam (comúnmente conocida como bomba de hidrógeno ). Las temperaturas máximas en los núcleos de las bombas de fisión de tipo Gadget (comúnmente conocidas como bombas atómicas ) están en el rango de 50 a 100 MK. Cita: Preguntas frecuentes sobre armas nucleares, 3.2.5 Materia a altas temperaturas. Enlace a la página web correspondiente. Archivado el 3 de mayo de 2007 en Wayback Machine. Todos los datos a los que se hace referencia se recopilaron de fuentes disponibles públicamente.
- ^ La temperatura máxima para una gran cantidad de materia se logró mediante una máquina de potencia pulsada utilizada en experimentos de física de fusión. El término cantidad a gran escala establece una distinción con respecto a las colisiones en aceleradores de partículas, en las que la temperatura alta se aplica solo a los restos de dos partículas subatómicas o núcleos en un instante determinado. La temperatura >2 GK se logró durante un período de aproximadamente diez nanosegundos durante el disparo Z1137 . De hecho, los iones de hierro y manganeso en el plasma promediaron 3,58 ± 0,41 GK (309 ± 35 keV) durante 3 ns (ns 112 a 115). Calentamiento viscoso de iones en un pellizco Z magnetohidrodinámicamente inestable a más de 2 × 109 Kelvin, MG Haines et al. , Physical Review Letters 96 (2006) 075003. Enlace al comunicado de prensa de Sandia. Archivado el 30 de mayo de 2010 en Wayback Machine .
- ^ Temperatura central de una estrella de gran masa (>8–11 masas solares) después de que abandona la secuencia principal en el diagrama de Hertzsprung-Russell y comienza el proceso alfa (que dura un día) de fusión del silicio-28 en elementos más pesados en los siguientes pasos: azufre-32 → argón-36 → calcio-40 → titanio-44 → cromo-48 → hierro-52 → níquel-56. A los pocos minutos de terminar la secuencia, la estrella explota como una supernova de tipo II . Cita: Holland, Arthur; Williams, Mark. "Evolución estelar: la vida y la muerte de nuestros vecinos luminosos". GS265 . Universidad de Michigan. Archivado desde el original el 16 de enero de 2009.Se pueden encontrar enlaces más informativos aquí "Capítulo 21 Explosiones estelares". Archivado desde el original el 2013-04-11 . Consultado el 2016-02-08 ., y aquí "Trans". Archivado desde el original el 14 de agosto de 2011. Consultado el 8 de febrero de 2016 ., y un tratado conciso sobre las estrellas de la NASA se encuentra aquí "NASA - Star". Archivado desde el original el 24 de octubre de 2010. Consultado el 12 de octubre de 2010 ..
- ^ Basado en un modelo informático que predijo una temperatura interna máxima de 30 MeV (350 GK) durante la fusión de un sistema binario de estrellas de neutrones (que produce un estallido de rayos gamma). Las estrellas de neutrones en el modelo tenían 1,2 y 1,6 masas solares respectivamente, eran aproximadamente20 km de diámetro y orbitaban alrededor de su baricentro (centro de masa común) a aproximadamente390 Hz durante los últimos milisegundos antes de que se fusionaran por completo. La porción de 350 GK era un pequeño volumen ubicado en el núcleo común en desarrollo del par y variaba desde aproximadamenteDe 1 a 7 km de diámetro en un lapso de tiempo de alrededor de 5 ms. Imagine dos objetos del tamaño de una ciudad con una densidad inimaginable orbitando uno alrededor del otro a la misma frecuencia que la nota musical G4 (la 28.ª tecla blanca de un piano). También es digno de mención que a 350 GK, el neutrón promedio tiene una velocidad vibratoria del 30 % de la velocidad de la luz y una masa relativista ( m ) un 5 % mayor que su masa en reposo ( m 0 ). Formación de toros en fusiones de estrellas de neutrones y estallidos cortos de rayos gamma bien localizados Archivado el 22 de noviembre de 2017 en Wayback Machine , R. Oechslin et al . del Instituto Max Planck de Astrofísica. Archivado el 3 de abril de 2005 en Wayback Machine , arXiv:astro-ph/0507099 v2, 22 de febrero de 2006. Un resumen en HTML Archivado el 9 de noviembre de 2010 en Wayback Machine .
- Citas
- ^ Organismo Internacional de Energía Atómica (1974). Descargas térmicas en centrales nucleares: su gestión e impactos ambientales: informe preparado por un grupo de expertos como resultado de una reunión de expertos celebrada en Viena del 23 al 27 de octubre de 1972. Organismo Internacional de Energía Atómica.
- ^ Watkinson, John (2001). El arte del audio digital. Taylor y Francisco. ISBN 978-0-240-51587-8.
- ^ Middleton, WEK (1966), págs. 89-105.
- ^ de Joanna Thompson (14 de octubre de 2021). "Los científicos acaban de batir el récord de la temperatura más fría jamás registrada en un laboratorio". Live Science . Consultado el 28 de abril de 2023 .
- ^ por Jaynes, ET (1965), págs. 391–398.
- ^ ab Cryogenic Society Archivado el 7 de noviembre de 2020 en Wayback Machine (2019).
- ^ Proyecto de Resolución A "Sobre la revisión del Sistema Internacional de Unidades (SI)" que se presentará a la CGPM en su 26ª reunión (2018) (PDF) , archivado desde el original (PDF) el 2018-04-29 , consultado el 2019-10-20
- ^ abc Truesdell, CA (1980), Secciones 11 B, 11H, págs. 306–310, 320–332.
- ^ Quinn, T. J. (1983).
- ^ Germer, LH (1925). 'La distribución de las velocidades iniciales entre los electrones termoiónicos', Phys. Rev. , 25 : 795–807. aquí
- ^ Turvey, K. (1990). 'Prueba de validez de las estadísticas maxwellianas para electrones emitidos termoiónicamente desde un cátodo de óxido', European Journal of Physics , 11 (1): 51–59. aquí
- ^ Zeppenfeld, M., Englert, BGU, Glöckner, R., Prehn, A., Mielenz, M., Sommer, C., van Buuren, LD, Motsch, M., Rempe, G. (2012).
- ^ Miller, J. (2013).
- ^ ab de Podesta, M., Underwood, R., Sutton, G., Morantz, P, Harris, P, Mark, DF, Stuart, FM, Vargha, G., Machin, M. (2013). Una medición de baja incertidumbre de la constante de Boltzmann, Metrologia , 50 (4): S213–S216, BIPM & IOP Publishing Ltd
- ^ Quinn, TJ (1983), págs. 98-107.
- ^ Schooley, JF (1986), págs. 138-143.
- ^ Quinn, TJ (1983), págs. 61–83.
- ^ Schooley, JF (1986), págs. 115-138.
- ^ Adkins, CJ (1968/1983), págs. 119-120.
- ^ Buchdahl, HA (1966), págs. 137-138.
- ^ Tschoegl, NW (2000), pág. 88.
- ^ ab Fermi, E. (1956). Termodinámica . Dover Publications (aún en imprenta). pág. 48.
ecuación (64).
. - ^ Thomson, W. (Lord Kelvin) (1848).
- ^ Thomson, W. (Lord Kelvin) (1851).
- ^ Partington, JR (1949), págs. 175-177.
- ^ Roberts, JK, Miller, AR (1928/1960), págs. 321–322.
- ^ Quinn, TJ (1983). Temperatura , Academic Press, Londres, ISBN 0-12-569680-9 , págs. 160–162.
- ^ Tisza, L. (1966). Termodinámica generalizada , MIT Press, Cambridge MA, págs. 47, 57.
- ^ abc Münster, A. (1970), Termodinámica clásica , traducido por ES Halberstadt, Wiley–Interscience, Londres, ISBN 0-471-62430-6 , pp. 49, 69.
- ^ ab Bailyn, M. (1994). Un estudio de la termodinámica , American Institute of Physics Press, Nueva York, ISBN 0-88318-797-3 , págs. 14-15, 214.
- ^ ab Callen, HB (1960/1985), Termodinámica y una introducción a la termoestadística , (primera edición 1960), segunda edición 1985, John Wiley & Sons, Nueva York, ISBN 0-471-86256-8 , págs. 146–148.
- ^ Kondepudi, D., Prigogine, I. (1998). Termodinámica moderna. De los motores térmicos a las estructuras disipativas , John Wiley, Chichester, ISBN 0-471-97394-7 , págs. 115-116.
- ^ Tisza, L. (1966). Termodinámica generalizada , MIT Press, Cambridge MA, pág. 58.
- ^ Milne, EA (1929). El efecto de las colisiones en el equilibrio radiativo monocromático, Monthly Notices of the Royal Astronomical Society, 88 : 493–502.
- ^ Gyarmati, I. (1970). Termodinámica del no equilibrio. Teoría de campos y principios variacionales , traducido por E. Gyarmati y WF Heinz, Springer, Berlín, págs. 63–66.
- ^ Glansdorff, P., Prigogine, I. , (1971). Teoría termodinámica de la estructura, estabilidad y fluctuaciones , Wiley, Londres, ISBN 0-471-30280-5 , págs. 14–16.
- ^ Bailyn, M. (1994). Un estudio de la termodinámica , American Institute of Physics Press, Nueva York, ISBN 0-88318-797-3 , págs. 133-135.
- ^ Callen, HB (1960/1985), Termodinámica y una introducción a la termoestadística , (primera edición 1960), segunda edición 1985, John Wiley & Sons, Nueva York, ISBN 0-471-86256-8 , págs. 309–310.
- ^ Bryan, GH (1907). Termodinámica. Tratado introductorio que trata principalmente de los primeros principios y sus aplicaciones directas , BG Teubner, Leipzig, pág. 3. «Termodinámica de George Hartley Bryan». Archivado desde el original el 18 de noviembre de 2011. Consultado el 2 de octubre de 2011 .
- ^ Pippard, AB (1957/1966), pág. 18.
- ^ Adkins, CJ (1968/1983), pág. 20.
- ^ Bryan, GH (1907). Thermodynamics. An Introductory Treatise treating generally with First Principles and their Direct Applications (Termodinámica. Un tratado introductorio que trata principalmente de los primeros principios y sus aplicaciones directas ), BG Teubner, Leipzig, p. 5: "... cuando se habla de un cuerpo que se calienta o se enfría, siempre se implica un aumento de temperatura, ya que el calor y el frío de un cuerpo son términos cualitativos que solo pueden referirse a la temperatura". "Thermodynamics by George Hartley Bryan". Archivado desde el original el 18 de noviembre de 2011. Consultado el 2 de octubre de 2011 .
- ^ abcd Mach, E. (1900). Die Principien der Wärmelehre. Historisch-kritisch entwickelt , Johann Ambrosius Barth, Leipzig, sección 22, págs. 56–57.
- ^ ab Serrin, J. (1986). Capítulo 1, 'Un esquema de la estructura termodinámica', págs. 3–32, especialmente pág. 6, en Nuevas perspectivas en termodinámica , editado por J. Serrin, Springer, Berlín, ISBN 3-540-15931-2 .
- ^ Maxwell, JC (1872). Teoría del calor , tercera edición, Longmans, Green, Londres, pág. 32.
- ^ Tait, PG (1884). Heat , Macmillan, Londres, Capítulo VII, págs. 39-40.
- ^ Planck, M. (1897/1903). Tratado de termodinámica , traducido por A. Ogg, Longmans, Green, Londres, págs. 1–2.
- ^ Planck, M. (1914), The Theory of Heat Radiation Archivado el 18 de noviembre de 2011 en Wayback Machine , segunda edición, traducida al inglés por M. Masius, Blakiston's Son & Co., Filadelfia, reimpresa por Kessinger.
- ^ JS Dugdale (1996). Entropía y su interpretación física . Taylor & Francis. pág. 13. ISBN 978-0-7484-0569-5.
- ^ F. Reif (1965). Fundamentos de física estadística y térmica . McGraw-Hill. pág. 102. ISBN. 9780070518001.
- ^ MJ Moran; HN Shapiro (2006). "1.6.1". Fundamentos de termodinámica en ingeniería (5.ª ed.). John Wiley & Sons, Ltd. pág. 14. ISBN 978-0-470-03037-0.
- ^ TW Leland, Jr. "Principios básicos de la termodinámica clásica y estadística" (PDF) . p. 14. Archivado (PDF) desde el original el 28 de septiembre de 2011.
En consecuencia, identificamos la temperatura como una fuerza impulsora que hace que se transfiera algo llamado calor.
- ^ Tait, PG (1884). Heat , Macmillan, Londres, Capítulo VII, págs. 42, 103–117.
- ^ Beattie, JA, Oppenheim, I. (1979). Principios de termodinámica , Elsevier Scientific Publishing Company, Ámsterdam, ISBN 978-0-444-41806-7 , pág. 29.
- ^ Landsberg, PT (1961). Termodinámica con ilustraciones estadísticas cuánticas , Interscience Publishers, Nueva York, pág. 17.
- ^ Thomsen, JS (1962). "Una reformulación de la ley cero de la termodinámica". Am. J. Phys . 30 (4): 294–296. Código Bibliográfico :1962AmJPh..30..294T. doi : 10.1119/1.1941991 .
- ^ Maxwell, JC (1872). Teoría del calor , tercera edición, Longman's, Green & Co, Londres, pág. 45.
- ^ ab Pitteri, M. (1984). Sobre los fundamentos axiomáticos de la temperatura, Apéndice G6 en las págs. 522–544 de Termodinámica racional , C. Truesdell, segunda edición, Springer, Nueva York, ISBN 0-387-90874-9 .
- ^ Truesdell, C., Bharatha, S. (1977). Los conceptos y la lógica de la termodinámica clásica como teoría de los motores térmicos, rigurosamente construida sobre los cimientos establecidos por S. Carnot y F. Reech , Springer, Nueva York, ISBN 0-387-07971-8 , pág. 20.
- ^ ab Serrin, J. (1978). Los conceptos de termodinámica, en Contemporary Developments in Continuum Mechanics and Partial Differential Equations. Proceedings of the International Symposium on Continuum Mechanics and Partial Differential Equations, Río de Janeiro, agosto de 1977 , editado por GM de La Penha, LAJ Medeiros, Holanda Septentrional, Ámsterdam, ISBN 0-444-85166-6 , pp. 411–451.
- ^ Maxwell, JC (1872). Teoría del calor , tercera edición, Longmans, Green, Londres, págs. 155-158.
- ^ Tait, PG (1884). Heat , Macmillan, Londres, Capítulo VII, Sección 95, págs. 68-69.
- ^ Buchdahl, HA (1966), pág. 73.
- ^ Kondepudi, D. (2008). Introducción a la termodinámica moderna , Wiley, Chichester, ISBN 978-0-470-01598-8 , Sección 32, págs. 106–108.
- ^ Green, Don; Perry, Robert H. (2008). Manual de ingenieros químicos de Perry, octava edición (8.ª ed.). McGraw-Hill Education. pág. 660. ISBN 978-0071422949.
- ^ El kelvin en el folleto del SI Archivado el 26 de septiembre de 2007 en Wayback Machine.
- ^ "Cero absoluto". Calphad.com. Archivado desde el original el 8 de julio de 2011. Consultado el 16 de septiembre de 2010 .
- ^ Definición acordada por la 26ª Conferencia General de Pesas y Medidas (CGPM) Archivado el 9 de octubre de 2020 en Wayback Machine en noviembre de 2018, implementado el 20 de mayo de 2019
- ^ abcdefg Jha, Aditya; Campbell, Douglas; Montelle, Clemency; Wilson, Phillip L. (30 de julio de 2023). "Sobre la falacia del continuo: ¿es la temperatura una función continua?". Fundamentos de la física . 53 (4): 69. Bibcode :2023FoPh...53...69J. doi : 10.1007/s10701-023-00713-x . ISSN 1572-9516.
- ^ van Strien, Marij (1 de octubre de 2015). "Continuidad en la naturaleza y en las matemáticas: Boltzmann y Poincaré". Síntesis . 192 (10): 3275–3295. doi :10.1007/s11229-015-0701-9. ISSN 1573-0964. S2CID 255075377.
- ^ Fang, G.; Ward, CA (1999-01-01). "Temperatura medida cerca de la interfaz de un líquido en evaporación". Physical Review E . 59 (1): 417–428. Bibcode :1999PhRvE..59..417F. doi :10.1103/PhysRevE.59.417.
- ^ Newell, Homer E. (12 de febrero de 1960). "El entorno espacial: mientras el hombre espera con ansias el vuelo al espacio, descubre que las regiones exteriores no son completamente desconocidas". Science . 131 (3398): 385–390. doi :10.1126/science.131.3398.385. ISSN 0036-8075. PMID 14426791.
- ^ ab Chen, Gang (1 de agosto de 2022). "Sobre la imagen molecular y la discontinuidad de la temperatura interfacial durante la evaporación y la condensación". Revista internacional de transferencia de calor y masa . 191 : 122845. arXiv : 2201.07318 . doi :10.1016/j.ijheatmasstransfer.2022.122845. ISSN 0017-9310. S2CID 246036409.
- ^ ab Cahill, D; et al. (27 de diciembre de 2022). "Transporte térmico a nanoescala". Journal of Applied Physics . 93 (2): 793–818. doi :10.1063/1.1524305. hdl : 2027.42/70161 . S2CID 15327316 . Consultado el 2 de agosto de 2023 .
- ^ ab Chen, Jie; Xu, Xiangfan; Zhou, Jun; Li, Baowen (22 de abril de 2022). "Resistencia térmica interfacial: pasado, presente y futuro". Reseñas de Física Moderna . 94 (2): 025002. Bibcode :2022RvMP...94b5002C. doi :10.1103/RevModPhys.94.025002. S2CID 248350864.
- ^ ab Aursand, Eskil; Ytrehus, Tor (1 de julio de 2019). "Comparación de modelos de evaporación de teoría cinética para películas delgadas líquidas". Revista internacional de flujo multifásico . 116 : 67–79. doi :10.1016/j.ijmultiphaseflow.2019.04.007. hdl : 11250/2594950 . ISSN 0301-9322. S2CID 146056093.
- ^ C. Carathéodory (1909). "Untersuchungen über die Grundlagen der Thermodynamik". Annalen Matemáticas . 67 (3): 355–386. doi :10.1007/BF01450409. S2CID 118230148.
- ^ Swendsen, Robert (marzo de 2006). "Mecánica estadística de coloides y definición de entropía de Boltzmann" (PDF) . American Journal of Physics . 74 (3): 187–190. Código Bibliográfico :2006AmJPh..74..187S. doi :10.1119/1.2174962. S2CID 59471273. Archivado desde el original (PDF) el 28 de febrero de 2020.
- ^ Balescu, R. (1975). Mecánica estadística de equilibrio y no equilibrio , Wiley, Nueva York, ISBN 0-471-04600-0 , págs. 148-154.
- ^ ab Kittel, Charles ; Kroemer, Herbert (1980). Física térmica (2.ª ed.). WH Freeman Company. págs. 391–397. ISBN 978-0-7167-1088-2.
- ^ Kondepudi, DK (1987). "Aspectos microscópicos implicados en la segunda ley". Fundamentos de la física . 17 (7): 713–722. Bibcode :1987FoPh...17..713K. doi :10.1007/BF01889544. S2CID 120576357.
- ^ Las conferencias de Feynman sobre física. 39–5 La ley de los gases ideales
- ^ "Valor CODATA 2022: constante molar de gas". Referencia del NIST sobre constantes, unidades e incertidumbre . NIST . Mayo de 2024. Consultado el 18 de mayo de 2024 .
- ^ "Teoría cinética". galileo.phys.virginia.edu . Archivado desde el original el 16 de julio de 2017 . Consultado el 27 de enero de 2018 .
- ^ Tolman, RC (1938). Los principios de la mecánica estadística , Oxford University Press, Londres, págs. 93, 655.
- ^ Peter Atkins, Julio de Paula (2006). Química física (8.ª ed.). Oxford University Press. pág. 9.
- ^ Maxwell, JC (1872). Teoría del calor , tercera edición, Longman's, Green & Co, Londres, pág. 32.
- ^ Bailyn, M. (1994). A Survey of Thermodynamics , American Institute of Physics Press, Nueva York, ISBN 0-88318-797-3 , pág. 23, "..., si existe un gradiente de temperatura, ..., entonces debe producirse un flujo de calor, ..., para lograr una temperatura uniforme".
- ^ Guggenheim, EA (1967). Termodinámica. Un tratamiento avanzado para químicos y físicos , North-Holland Publishing Company , Ámsterdam, (1.ª edición, 1949), quinta edición, 1965, pág. 8, "... se irán ajustando gradualmente hasta que finalmente alcancen el equilibrio mutuo, después del cual, por supuesto, no habrá más cambios".
- ^ Bailyn, M. (1994). Un estudio de la termodinámica , American Institute of Physics Press, Nueva York, ISBN 0-88318-797-3 , pág. 22.
- ^ Guggenheim, EA (1967). Termodinámica. Un tratamiento avanzado para químicos y físicos , North-Holland Publishing Company , Ámsterdam, (1.ª edición, 1949), quinta edición, 1965, pág. 8: "Si dos sistemas están en equilibrio térmico con un tercer sistema, entonces están en equilibrio térmico entre sí".
- ^ Buchdahl, HA (1966). The Concepts of Classical Thermodynamics , Cambridge University Press, Cambridge, pág. 29: "... si cada uno de dos sistemas está en equilibrio con un tercer sistema, entonces están en equilibrio entre sí".
- ^ ab Planck, M. (1945). Tratado de termodinámica . Dover Publications. pág. §90 y §137.
ecuaciones (39), (40) y (65).
. - ^ Prati, E. (2010). "El conjunto gran canónico cuántico finito y la temperatura a partir de estadísticas de un solo electrón para un dispositivo mesoscópico". J. Stat. Mech . 1 (1): P01003. arXiv : 1001.2342 . Bibcode :2010JSMTE..01..003P. doi :10.1088/1742-5468/2010/01/P01003. S2CID 118339343.arxiv.org Archivado el 22 de noviembre de 2017 en Wayback Machine
- ^ "Hacer realidad el sueño de Boltzmann: simulaciones por ordenador en mecánica estadística moderna" (PDF) . Archivado (PDF) desde el original el 13 de abril de 2014. Consultado el 11 de abril de 2014 .
- ^ Prati, E.; et al. (2010). "Medición de la temperatura de un sistema electrónico mesoscópico mediante estadísticas de electrones individuales". Applied Physics Letters . 96 (11): 113109. arXiv : 1002.0037 . Código Bibliográfico :2010ApPhL..96k3109P. doi :10.1063/1.3365204. S2CID 119209143. Archivado desde el original el 2016-05-14 . Consultado el 2022-03-02 .arxiv.org Archivado el 22 de noviembre de 2017 en Wayback Machine
- ^ Escuela de Ciencias del Agua. "El dióxido de carbono congelado (hielo seco) se sublima directamente y se convierte en vapor". USGS .
- ^ Guggenheim, EA (1967) [1949], Termodinámica. Un tratamiento avanzado para químicos y físicos (quinta edición), Ámsterdam: North-Holland Publishing Company , pág. 157:"Es imposible mediante cualquier procedimiento, por idealizado que sea, reducir la temperatura de cualquier sistema a temperatura cero en un número finito de operaciones finitas".
- ^ Pippard, AB (1957/1966). Elements of Classical Thermodynamics for Advanced Students of Physics , publicación original de 1957, reimpresión de 1966, Cambridge University Press, Cambridge, página 51: " No es posible alcanzar el cero absoluto mediante ninguna serie finita de procesos " .
- ^ Tisza, L. (1966). Termodinámica generalizada , MIT Press, Cambridge MA, página 96: "Es imposible alcanzar el cero absoluto como resultado de una secuencia finita de operaciones".
- ^ Kittel, Charles ; Kroemer, Herbert (1980). Física térmica (2.ª ed.). WH Freeman Company. pág. Apéndice E. ISBN 978-0-7167-1088-2.
- ^ SVS (3 de agosto de 2023). «Estudio de visualización científica de la NASA | Una guía sobre las temperaturas cósmicas». SVS . Consultado el 6 de agosto de 2023 .
- ^ Resultados de la investigación de Stefan Bathe utilizando el detector PHENIX Archivado el 20 de noviembre de 2008 en Wayback Machine en el Relativistic Heavy Ion Collider Archivado el 3 de marzo de 2016 en Wayback Machine en el Brookhaven National Laboratory Archivado el 24 de junio de 2012 en Wayback Machine en Upton, Nueva York. Bathe ha estudiado las colisiones oro-oro, deuterón-oro y protón-protón para probar la teoría de la cromodinámica cuántica, la teoría de la fuerza fuerte que mantiene unidos los núcleos atómicos. Enlace al comunicado de prensa. Archivado el 11 de febrero de 2009 en Wayback Machine
- ^ ¿ Cómo estudian los físicos las partículas? Archivado el 11 de octubre de 2007 en Wayback Machine por CERN Archivado el 7 de julio de 2012 en Wayback Machine .
Bibliografía de referencias citadas
- Adkins, CJ (1968/1983). Termodinámica del equilibrio , (1.ª edición, 1968), tercera edición, 1983, Cambridge University Press, Cambridge, Reino Unido, ISBN 0-521-25445-0 .
- Buchdahl, HA (1966). Los conceptos de la termodinámica clásica , Cambridge University Press, Cambridge.
- Jaynes, ET (1965). Entropías de Gibbs vs. Boltzmann, American Journal of Physics , 33 (5), 391–398.
- Middleton, WEK (1966). Una historia del termómetro y su uso en metrología , Johns Hopkins Press, Baltimore.
- Miller, J (2013). "Moléculas enfriadas por vía optoeléctrica". Physics Today . 66 (1): 12–14. Bibcode :2013PhT....66a..12M. doi : 10.1063/pt.3.1840 .
- Partington, JR (1949). Tratado avanzado de química física , volumen 1, Principios fundamentales. Propiedades de los gases , Longmans, Green & Co., Londres, págs. 175-177.
- Pippard, AB (1957/1966). Elementos de termodinámica clásica para estudiantes avanzados de física , publicación original en 1957, reimpresión en 1966, Cambridge University Press, Cambridge, Reino Unido.
- Quinn, TJ (1983). Temperatura , Academic Press, Londres, ISBN 0-12-569680-9 .
- Schooley, JF (1986). Termometría , CRC Press, Boca Raton, ISBN 0-8493-5833-7 .
- Roberts, JK, Miller, AR (1928/1960). Heat and Thermodynamics (primera edición, 1928), quinta edición, Blackie & Son Limited, Glasgow.
- Thomson, W. (Lord Kelvin) (1848). En una escala termométrica absoluta basada en la teoría de Carnot sobre la fuerza motriz del calor y calculada a partir de las observaciones de Regnault, Proc. Camb. Phil. Soc. (1843/1863) 1 , No. 5: 66–71.
- Thomson, W. (Lord Kelvin) (marzo de 1851). "Sobre la teoría dinámica del calor, con resultados numéricos deducidos del equivalente de una unidad térmica del Sr. Joule y las observaciones de M. Regnault sobre el vapor". Transactions of the Royal Society of Edinburgh . XX (parte II): 261–268, 289–298.
- Truesdell, CA (1980). La tragicómica historia de la termodinámica, 1822-1854 , Springer, Nueva York, ISBN 0-387-90403-4 .
- Tschoegl, NW (2000). Fundamentos de la termodinámica del equilibrio y del estado estacionario , Elsevier, Ámsterdam, ISBN 0-444-50426-5 .
- Zeppenfeld, M.; Englert, BGU; Glockner, R.; Prehn, A.; Mielenz, M.; Sommer, C.; van Buuren, LD; Motsch, M.; Rempe, G. (2012). "Enfriamiento por Sysiphus de moléculas poliatómicas atrapadas eléctricamente". Naturaleza . 491 (7425): 570–573. arXiv : 1208.0046 . Código Bib :2012Natur.491..570Z. doi : 10.1038/naturaleza11595. PMID 23151480. S2CID 4367940.
Lectura adicional
- Chang, Hasok (2004). Inventando la temperatura: medición y progreso científico . Oxford: Oxford University Press. ISBN 978-0-19-517127-3 .
- Zemansky, Mark Waldo (1964). Temperaturas muy bajas y muy altas . Princeton, NJ: Van Nostrand.
Enlaces externos
- Mapa actual de las temperaturas superficiales globales



















































