Espectroscopia ultrasónica resonante

La espectroscopia ultrasónica resonante ( RUS ) es una técnica de laboratorio utilizada en geología y ciencia de los materiales para medir propiedades fundamentales de los materiales que involucran la elasticidad . Esta técnica se basa en el hecho de que los objetos sólidos tienen frecuencias naturales en las que vibran cuando se excitan mecánicamente. La frecuencia natural depende de la elasticidad, el tamaño y la forma del objeto; la RUS explota esta propiedad de los sólidos para determinar el tensor elástico del material. La gran ventaja de esta técnica es que todo el tensor elástico se obtiene de una sola muestra de cristal en una sola medición rápida. ^[1] A frecuencias más bajas o más generales, este método se conoce como espectroscopia de resonancia acústica .

El interés por las propiedades elásticas hizo su entrada con los filósofos del siglo XVII, pero la teoría real de la elasticidad, que indicaba que las constantes elásticas de un material podían obtenerse midiendo las velocidades del sonido en ese material, fue resumida sólo doscientos años después. En 1964, DB Frasier y RC LeCraw utilizaron la solución calculada en 1880 por G. Lamè y H. Lamb para resolver el problema directo, y luego la invirtieron gráficamente, en lo que puede ser la primera medición de RUS. Sin embargo, tuvimos que esperar la participación de la comunidad geofísica, interesada en determinar la estructura interior de la Tierra , para resolver el problema inverso : en 1970 tres geofísicos mejoraron el método anterior e introdujeron el término técnica de esfera resonante (RST). Emocionado por los alentadores resultados obtenidos con muestras lunares , uno de ellos encargó a uno de sus estudiantes la tarea de ampliar el método para su uso con muestras en forma de cubo. Este método, conocido actualmente como método de resonancia de paralelepípedo rectangular (RPR), fue ampliado por I. Ohno en 1976. Finalmente, a finales de los años 1980, A. Migliori y J. Maynard ampliaron los límites de la técnica en términos de carga y mediciones electrónicas de bajo nivel, y con W. Visscher llevaron los algoritmos informáticos a su estado actual, introduciendo el término final de espectroscopia ultrasónica resonante (RUS). ^[2]

En primer lugar, se debe resolver el problema de calcular las frecuencias naturales en términos de las dimensiones de la muestra, la masa y un conjunto de constantes elásticas hipotéticas (el problema directo). Luego, se debe aplicar un algoritmo de inversión no lineal para encontrar las constantes elásticas a partir de las frecuencias naturales medidas (el problema inverso ).

Todas las mediciones de RUS se realizan en muestras que son vibradores libres. Debido a que no existe una solución analítica completa para las vibraciones libres de sólidos, se debe confiar en aproximaciones. Los métodos de elementos finitos se basan en equilibrar las fuerzas aplicadas a un elemento de volumen diferencial y luego calcular su respuesta. Los métodos de minimización de energía , por otro lado, determinan la energía mínima y, por lo tanto, la configuración de equilibrio para el objeto. Entre las técnicas de minimización de energía, la minimización lagrangiana es la más utilizada en los análisis de RUS debido a su ventaja en velocidad (un orden de magnitud menor que los métodos de elementos finitos).

El procedimiento comienza con un objeto de volumen V, delimitado por su superficie libre S. El lagrangiano está dado por

${\displaystyle L=\int _ {V}(KE-PE)dV(1)}$

donde KE es la densidad de energía cinética

${\displaystyle KE={\frac {1}{2}}\sum _{i}\rho \omega ^{2}u_{i}^{2}(2)}$

y PE es la densidad de energía potencial

${\displaystyle PE={\frac {1}{2}}\sum _{i,j,k,l}c_{i,j,k,l}{\frac {du_{i}}{dx_{j}}}{\frac {du_{k}}{dx_{l}}}(3)}$

Aquí, es el componente i del vector de desplazamiento , ω es la frecuencia angular de la dependencia armónica del tiempo, es un componente del tensor de rigidez elástica y ρ es la densidad . Los subíndices i, j, etc., se refieren a las direcciones de coordenadas cartesianas .${\displaystyle u_{i}}$${\displaystyle c_{i,j,k,l}}$

Para encontrar el mínimo del lagrangiano, calcule la diferencial de L en función de u, la variación arbitraria de u en V y en S. Esto da:

${\displaystyle \delta L=\int _{V}{\Bigl \{}\sum _{i}{\Bigl [}\rho \omega ^{2}u_{i}-\sum _{j,k,l}c_{i,j,k,l}{\frac {\delta ^{2}u_{k}}{\delta x_{j}\delta x_{l}}}{\Bigr ]}\delta u_{i}{\Bigr \}}dV-\int _{S}{\Bigl \{}\sum _{i}{\Bigl [}\sum _{j,k,l}{\vec {n}}c_{i,j,k,l}{\frac {\delta u_{k}}{\delta x_{l}}}{\Bigr ]}du_{i}{\Bigr \}}dS(4)}$

Como es arbitrario en V y en S, ambos términos entre corchetes deben ser cero. ^[3] Si se iguala el primer término a cero, se obtiene la ecuación de onda elástica . El segundo término entre corchetes es una expresión de las condiciones de contorno de la superficie libre ; es el vector unitario normal a S. Para un cuerpo libre (tal como lo suponemos), el último término suma cero y se puede ignorar.${\displaystyle u_{i}}$${\displaystyle {\vec {n}}}$

Así, el conjunto de que satisface las condiciones mencionadas anteriormente son aquellos desplazamientos que corresponden a que ω sea una frecuencia normal del sistema. Esto sugiere que las vibraciones normales de un objeto (Fig. 1) pueden calcularse aplicando un método variacional (en nuestro caso el método variacional de Rayleigh-Ritz , explicado en el párrafo siguiente) para determinar tanto las frecuencias normales como la descripción de las oscilaciones físicas. ^[4] Para citar a Visscher, obtener ambas ecuaciones a partir del lagrangiano básico es "una casualidad matemática que puede haber ocurrido durante un lapso en la vigilancia de Murphy ". ^[5]${\displaystyle u_{i}}$

La puesta en práctica de este enfoque requiere la expansión de la función lagrangiana en un conjunto de funciones base adecuadas a la geometría del cuerpo, sustituyendo dicha expresión en la ecuación (1) y reduciendo el problema al de diagonalizar una matriz N×N ( problema de valores propios ). Los puntos estacionarios del lagrangiano se encuentran resolviendo el problema de valores propios resultante de la ecuación (4), es decir,${\displaystyle u_{i}}$

${\displaystyle \omega ^{2}Ea=\Gamma a(5)}$

donde an son las aproximaciones al movimiento expandido en un conjunto base completo, E proviene del término de energía cinética y Γ proviene del término de energía elástica . El orden de las matrices es ~10^3 para obtener buenas aproximaciones.

La ecuación (5) determina las frecuencias de resonancia a partir de los módulos elásticos . ^[3]

El problema inverso de deducir las constantes elásticas a partir de un espectro medido de resonancias mecánicas no tiene solución analítica , por lo que debe resolverse mediante métodos computacionales. Para el método indirecto, se calcula un espectro de frecuencia resonante inicial (n=1,2,...) utilizando valores estimados para las constantes elásticas y las dimensiones y densidad de la muestra conocidas. La diferencia entre el espectro de frecuencia de resonancia calculado y medido (n=1,2,...) se cuantifica mediante una función de figura de mérito ,$estilo de visualización f_{n}^{cal}}$${\displaystyle f_{n}^{mea}}$

${\displaystyle F=\sum_{n}w_{n}(f_{n}^{cal}-f_{n}^{mea})^{2}(6)}$

donde (n=1,2,...) son coeficientes de ponderación que reflejan la confianza en las mediciones de resonancia individuales. Luego, se busca minimizar la función F mediante la regresión de los valores de todas las constantes elásticas utilizando un software informático desarrollado para este proceso. ^[6]$Estilo de visualización w_{n}$

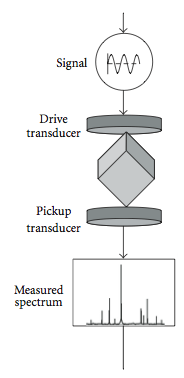
El método más común para detectar el espectro resonante mecánico se ilustra en la Fig. 2, donde una pequeña muestra con forma de paralelepípedo se sostiene ligeramente entre dos transductores piezoeléctricos . Un transductor se utiliza para generar una onda elástica de amplitud constante y frecuencia variable , mientras que el otro se utiliza para detectar la resonancia de la muestra. A medida que se barre un rango de frecuencia, se registra una secuencia de picos de resonancia . La posición de estos picos se produce en las frecuencias naturales (a partir de las cuales se determinan las constantes elásticas) y el factor de calidad Q (una medida de cuán estrecha es la resonancia) proporciona información sobre la disipación de la energía elástica .$Estilo de visualización f_{n}$

A diferencia de una medida ultrasónica convencional, en un método que hace resonar la muestra no se requiere un fuerte acoplamiento entre el transductor y la muestra, porque la muestra se comporta como un amplificador natural . ^[2] Más bien, manteniendo al mínimo el par entre ellos, se obtiene una buena aproximación a las condiciones de contorno de la superficie libre y se tiende a preservar también la Q. Para mediciones de temperatura variable, la muestra se mantiene entre los extremos de dos varillas amortiguadoras que unen la muestra a los transductores (Fig. 3) porque los transductores deben mantenerse a temperatura ambiente . En términos de presión , por el contrario, hay un límite de solo unos pocos bares, porque la aplicación de presiones más altas conduce a la amortiguación de las resonancias de la muestra. ^[1]

El RUS se puede aplicar a una gran variedad de tamaños de muestras, con un mínimo del orden de unos pocos cientos de micrómetros , pero para la medición de la elasticidad mineral se utiliza en muestras típicamente de entre 1 mm y 1 cm de tamaño.

La muestra, ya sea un agregado policristalino completamente denso o un monocristal , se mecaniza hasta obtener una forma regular. ^[1] En teoría, se puede utilizar cualquier forma de muestra, pero se obtiene un ahorro sustancial en tiempo de cálculo utilizando resonadores paralelepípedos rectangulares (RPR), esféricos o cilíndricos (menos ahorro de tiempo con cilindros).

Dado que la precisión de la medida depende estrictamente de la precisión en la preparación de la muestra, se toman varias precauciones: los RPR se preparan con los bordes paralelos a las direcciones cristalográficas; para los cilindros, solo el eje puede coincidir con la simetría de la muestra . El RUS rara vez se utiliza para muestras de simetría inferior y, para muestras isotrópicas , la alineación es irrelevante. Para las simetrías superiores, es conveniente tener bordes de longitudes diferentes para evitar una resonancia redundante.

Las mediciones en monocristales requieren la orientación de los ejes cristalográficos de la muestra con los bordes del RPR, para descuidar el cálculo de la orientación y tratar solo los módulos elásticos . ^[4]

Las muestras policristalinas deben ser idealmente completamente densas, libres de grietas y sin orientación preferencial de los granos. Las muestras de monocristal deben estar libres de defectos internos como paredes gemelas . Las superficies de todas las muestras deben estar pulidas hasta quedar planas y las caras opuestas deben ser paralelas. Una vez preparadas, la densidad debe medirse con precisión, ya que escala todo el conjunto de módulos elásticos. ^[1]

Los transductores ultrasónicos RUS están diseñados para hacer contacto de punto seco con la muestra. Esto se debe al requisito de condiciones de contorno de superficie libre para el cálculo de módulos elásticos a partir de frecuencias. Para los RPR, esto requiere un contacto muy ligero entre las esquinas de la muestra y los transductores. Las esquinas se utilizan porque proporcionan un acoplamiento elásticamente débil, lo que reduce la carga, y porque nunca son puntos nodales vibracionales. Un contacto suficientemente débil garantiza que no se requiera corrección transducida. ^[4]

Como herramienta versátil para caracterizar las propiedades elásticas de los materiales sólidos , la RUS ha encontrado aplicaciones en una variedad de campos. En las geociencias, una de las aplicaciones más importantes está relacionada con la determinación de las velocidades sísmicas en el interior de la Tierra . En un trabajo reciente, ^[7] por ejemplo, se midieron las constantes elásticas de la forsterita hidratada hasta 14,1 GPa a temperatura ambiente. Este estudio mostró que los módulos de volumen y de corte de los agregados de la forsterita hidratada aumentan con la presión a una tasa mayor que los de la fase anhidra correspondiente . Esto implica que en condiciones ambientales, VP y VS de la forsterita hidratada son más lentas que las de la anhidra; por el contrario, con el aumento de la presión y, en consecuencia, de la profundidad, VP _y VS _de la forsterita hidratada superan a las de la anhidra. Además, la hidratación disminuye la relación VP _/ VS _de la forsterita, la anisotropía azimutal máxima de la onda de compresión y la división máxima de la onda de corte . Estos datos nos ayudan a delimitar la composición del manto de la Tierra y a distinguir las regiones de enriquecimiento de hidrógeno de las regiones de alta temperatura o de fusión parcial.