Material de Maxwell

Un material Maxwell es el modelo más simple de material viscoelástico que muestra propiedades de un líquido típico. Muestra flujo viscoso en la escala de tiempo larga, pero resistencia elástica adicional a deformaciones rápidas. ^[1] Recibe su nombre de James Clerk Maxwell , quien propuso el modelo en 1867. ^{[2] [3]} También se lo conoce como fluido Maxwell. Una generalización de la relación escalar a una ecuación tensorial carece de motivación a partir de modelos más microscópicos y no cumple con el concepto de objetividad del material. Sin embargo, estos criterios se cumplen con el modelo de Maxwell de convección superior .

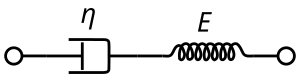
El modelo de Maxwell está representado por un amortiguador puramente viscoso y un resorte puramente elástico conectados en serie, ^[4] como se muestra en el diagrama. Si, en cambio, conectamos estos dos elementos en paralelo, ^[4] obtenemos el modelo generalizado de un material sólido Kelvin–Voigt .

En la configuración de Maxwell, bajo una tensión axial aplicada, la tensión total y la deformación total se pueden definir de la siguiente manera: ^[1]${\displaystyle \sigma _{\mathrm {Total} }}$${\displaystyle \varepsilon _{\mathrm {Total} }}$

${\displaystyle \sigma _{\mathrm {Total}}=\sigma _{\rm {D}}=\sigma _{\rm {S}}}$

${\displaystyle \varepsilon _{\mathrm {Total} }=\varepsilon _{\rm {D}}+\varepsilon _{\rm {S}}}$

donde el subíndice D indica la tensión-deformación en el amortiguador y el subíndice S indica la tensión-deformación en el resorte. Tomando la derivada de la deformación con respecto al tiempo, obtenemos:

${\displaystyle {\frac {d\varepsilon _{\mathrm {Total}}}{dt}}={\frac {d\varepsilon _{\rm {D}}}{dt}}+{\frac {d\varepsilon _{\rm {S}}}{dt}}={\frac {\sigma }{\eta }}+{\frac {1}{E}}{\frac {d\sigma }{dt}}}$

donde E es el módulo elástico y η es el coeficiente de viscosidad del material. Este modelo describe el amortiguador como un fluido newtoniano y modela el resorte con la ley de Hooke .

En un material Maxwell, la tensión σ , la deformación ε y sus tasas de cambio con respecto al tiempo t están regidas por ecuaciones de la forma: ^[1]

${\displaystyle {\frac {1}{E}}{\frac {d\sigma }{dt}}+{\frac {\sigma }{\eta }}={\frac {d\varepsilon }{dt}}}$

o, en notación de puntos:

${\displaystyle {\frac {\dot {\sigma }}{E}}+{\frac {\sigma }{\eta }}={\dot {\varepsilon }}}$

La ecuación se puede aplicar tanto a la tensión de corte como a la tensión uniforme en un material. En el primer caso, la viscosidad corresponde a la de un fluido newtoniano . En el segundo caso, tiene un significado ligeramente diferente que relaciona la tensión y la velocidad de deformación.

El modelo se aplica generalmente al caso de pequeñas deformaciones. Para las grandes deformaciones, debemos incluir cierta no linealidad geométrica. Para la forma más sencilla de generalizar el modelo de Maxwell, consulte el modelo de Maxwell de convección superior .

Si un material de Maxwell se deforma repentinamente y se somete a una tensión de , la tensión decae en una escala de tiempo característica de , conocida como tiempo de relajación . El fenómeno se conoce como relajación de la tensión .${\displaystyle \varepsilon _{0}}$${\displaystyle {\frac {\eta }{E}}}$

La imagen muestra la dependencia de la tensión adimensional con respecto al tiempo adimensional :${\displaystyle {\frac {\sigma (t)}{E\varepsilon _{0}}}}$${\displaystyle {\frac {E}{\eta }}t}$

Si liberamos el material en el tiempo , entonces el elemento elástico volverá a su posición original en el valor de${\displaystyle t_{1}}$

${\displaystyle \varepsilon _{\mathrm {back} }=-{\frac {\sigma (t_{1})}{E}}=\varepsilon _{0}\exp \left(-{\frac {E}{\eta }}t_{1}\right).}$

Dado que el elemento viscoso no volvería a su longitud original, el componente irreversible de la deformación se puede simplificar a la siguiente expresión:

${\displaystyle \varepsilon _{\mathrm {irreversible} }=\varepsilon _{0}\left[1-\exp \left(-{\frac {E}{\eta }}t_{1}\right)\right].}$

Si un material Maxwell se somete repentinamente a una tensión , entonces el elemento elástico se deformaría repentinamente y el elemento viscoso se deformaría a una velocidad constante:${\displaystyle \sigma _{0}}$

${\displaystyle \varepsilon (t)={\frac {\sigma _{0}}{E}}+t{\frac {\sigma _{0}}{\eta }}}$

Si en algún momento liberamos el material, entonces la deformación del elemento elástico sería la deformación elástica y la deformación del elemento viscoso no cambiaría:${\displaystyle t_{1}}$

${\displaystyle \varepsilon _{\mathrm {reversible} }={\frac {\sigma _{0}}{E}},}$

${\displaystyle \varepsilon _{\mathrm {irreversible} }=t_{1}{\frac {\sigma _{0}}{\eta }}.}$

El modelo de Maxwell no presenta fluencia ya que modela la deformación como una función lineal del tiempo.

Si se aplica una pequeña tensión durante un tiempo suficientemente prolongado, las deformaciones irreversibles se hacen grandes. Por lo tanto, el material de Maxwell es un tipo de líquido.

Si un material Maxwell está sujeto a una tasa de deformación constante , entonces la tensión aumenta, alcanzando un valor constante de ${\displaystyle {\dot {\epsilon }}}$

${\displaystyle \sigma =\eta {\dot {\varepsilon }}}$

En general

${\displaystyle \sigma (t)=\eta {\dot {\varepsilon }}(1-e^{-Et/\eta })}$

El módulo dinámico complejo de un material Maxwell sería:

${\displaystyle E^{*}(\omega )={\frac {1}{1/E-i/(\omega \eta )}}={\frac {E\eta ^{2}\omega ^{2}+i\omega E^{2}\eta }{\eta ^{2}\omega ^{2}+E^{2}}}}$

Por tanto, los componentes del módulo dinámico son:

${\displaystyle E_{1}(\omega )={\frac {E\eta ^{2}\omega ^{2}}{\eta ^{2}\omega ^{2}+E^{2}}}={\frac {(\eta /E)^{2}\omega ^{2}}{(\eta /E)^{2}\omega ^{2}+1}}E={\frac {\tau ^{2}\omega ^{2}}{\tau ^{2}\omega ^{2}+1}}E}$

y

${\displaystyle E_{2}(\omega )={\frac {\omega E^{2}\eta }{\eta ^{2}\omega ^{2}+E^{2}}}={\frac {(\eta /E)\omega }{(\eta /E)^{2}\omega ^{2}+1}}E={\frac {\tau \omega }{\tau ^{2}\omega ^{2}+1}}E}$

La imagen muestra el espectro de relajación del material de Maxwell. La constante de tiempo de relajación es .${\displaystyle \tau \equiv \eta /E}$

Curva azul	módulo elástico adimensional${\displaystyle {\frac {E_{1}}{E}}}$
Curva rosa	módulo de pérdidas adimensional${\displaystyle {\frac {E_{2}}{E}}}$
Curva amarilla	viscosidad aparente adimensional${\displaystyle {\frac {E_{2}}{\omega \eta }}}$
Eje X	frecuencia adimensional${\displaystyle \omega \tau }$

• Material de hamburguesas
• Modelo de Maxwell generalizado
• Material de Kelvin-Voigt
• Modelo Oldroyd-B
• Modelo sólido lineal estándar
• Modelo de Maxwell con convección superior