Velocidad de la luz
 | |
| Valor exacto | |
|---|---|
| metros por segundo | 299 792 458 |
| Valores aproximados (hasta tres dígitos significativos) | |
| kilómetros por hora | 1 080 000 000 |
| millas por segundo | 186 000 |
| millas por hora [1] | 671 000 000 |
| unidades astronómicas por día | 173 [Nota 1] |
| parsecs por año | 0,307 [Nota 2] |
| Tiempos aproximados de recorrido de la señal luminosa | |
| Distancia | Tiempo |
| un pie | 1,0 ns |
| un metro | 3,3 ns |
| De la órbita geoestacionaria a la Tierra | 119 ms |
| la longitud del ecuador de la Tierra | 134 ms |
| De la Luna a la Tierra | 1,3 segundos |
| Del Sol a la Tierra (1 UA ) | 8,3 minutos |
| un año luz | 1,0 año |
| un parsec | 3,26 años |
| desde la estrella más cercana al Sol (1,3 piezas ) | 4,2 años |
| Desde la galaxia más cercana a la Tierra | 70 000 años |
| a través de la Vía Láctea | 87 400 años |
| De la galaxia de Andrómeda a la Tierra | 2,5 millones de años |
| Relatividad especial |
|---|
 |
La velocidad de la luz en el vacío , comúnmente denominada c , es una constante física universal que es exactamente igual a 299.792.458 metros por segundo (aproximadamente 300.000 kilómetros por segundo; 186.000 millas por segundo; 671 millones de millas por hora). [Nota 3] Según la teoría especial de la relatividad , c es el límite superior de la velocidad a la que la materia o energía convencional (y, por lo tanto, cualquier señal que transporte información ) puede viajar a través del espacio . [4] [5] [6]
Todas las formas de radiación electromagnética , incluida la luz visible , viajan a la velocidad de la luz. Para muchos propósitos prácticos, la luz y otras ondas electromagnéticas parecerán propagarse instantáneamente, pero para distancias largas y mediciones muy sensibles, su velocidad finita tiene efectos notables. Gran parte de la luz de las estrellas observada en la Tierra proviene del pasado distante, lo que permite a los humanos estudiar la historia del universo al observar objetos distantes. Al comunicarse con sondas espaciales distantes , las señales pueden tardar minutos u horas en viajar. En informática , la velocidad de la luz fija el retraso mínimo de comunicación definitivo . La velocidad de la luz se puede utilizar en mediciones de tiempo de vuelo para medir grandes distancias con una precisión extremadamente alta.
En 1676, Ole Rømer demostró por primera vez que la luz no viaja instantáneamente estudiando el movimiento aparente de la luna de Júpiter , Ío . En los siglos siguientes se realizaron mediciones cada vez más precisas de su velocidad. En un artículo publicado en 1865, James Clerk Maxwell propuso que la luz era una onda electromagnética y, por lo tanto, viajaba a una velocidad c . [7] En 1905, Albert Einstein postuló que la velocidad de la luz c con respecto a cualquier marco de referencia inercial es una constante e independiente del movimiento de la fuente de luz. [8] Exploró las consecuencias de ese postulado derivando la teoría de la relatividad y, al hacerlo, demostró que el parámetro c tenía relevancia fuera del contexto de la luz y el electromagnetismo.
Las partículas sin masa y las perturbaciones de campo , como las ondas gravitacionales , también viajan a velocidad c en el vacío. Dichas partículas y ondas viajan a c independientemente del movimiento de la fuente o del marco de referencia inercial del observador . Las partículas con masa en reposo distinta de cero pueden acelerarse para acercarse a c, pero nunca pueden alcanzarla, independientemente del marco de referencia en el que se mida su velocidad. En la teoría de la relatividad , c interrelaciona el espacio y el tiempo y aparece en la famosa equivalencia masa-energía , E = mc 2 . [9]
En algunos casos, los objetos o las ondas pueden parecer viajar más rápido que la luz (por ejemplo, las velocidades de fase de las ondas, la aparición de ciertos objetos astronómicos de alta velocidad y determinados efectos cuánticos ). Se entiende que la expansión del universo supera la velocidad de la luz más allá de un cierto límite .
La velocidad a la que la luz se propaga a través de materiales transparentes , como el vidrio o el aire, es menor que c ; de manera similar, la velocidad de las ondas electromagnéticas en los cables de alambre es menor que c . La relación entre c y la velocidad v a la que viaja la luz en un material se denomina índice de refracción n del material ( n = do/en ). Por ejemplo, para la luz visible, el índice de refracción del vidrio suele rondar 1,5, lo que significa que la luz en el vidrio viaja a do/1.5≈ 200 000 km/s ( 124 000 mi/s) ; el índice de refracción del aire para la luz visible es de aproximadamente 1,0003 , por lo que la velocidad de la luz en el aire es aproximadamente 90 km/s (56 mi/s) más lenta que c .
Valor numérico, notación y unidades
La velocidad de la luz en el vacío se suele denotar con una c minúscula , que significa "constante" o del latín celeritas (que significa "rapidez, celeridad"). En 1856, Wilhelm Eduard Weber y Rudolf Kohlrausch habían utilizado c para una constante diferente que más tarde se demostró que era igual a √ 2 veces la velocidad de la luz en el vacío. Históricamente, el símbolo V se utilizó como símbolo alternativo para la velocidad de la luz, introducido por James Clerk Maxwell en 1865. En 1894, Paul Drude redefinió c con su significado moderno. Einstein utilizó V en sus artículos originales en alemán sobre la relatividad especial en 1905, pero en 1907 cambió a c , que para entonces se había convertido en el símbolo estándar para la velocidad de la luz. [10] [11]
A veces se utiliza c para la velocidad de las ondas en cualquier medio material, y c 0 para la velocidad de la luz en el vacío. [12] Esta notación con subíndices, que está respaldada en la literatura oficial del SI, [13] tiene la misma forma que las constantes electromagnéticas relacionadas: a saber, μ 0 para la permeabilidad del vacío o constante magnética, ε 0 para la permitividad del vacío o constante eléctrica, y Z 0 para la impedancia del espacio libre . Este artículo utiliza c exclusivamente para la velocidad de la luz en el vacío.
Uso en sistemas de unidades
Desde 1983, la constante c se define en el Sistema Internacional de Unidades (SI) exactamente como 299 792 458 m/s ; esta relación se utiliza para definir el metro como exactamente la distancia que recorre la luz en el vacío en 1 ⁄299 792 458 de unsegundo. Al utilizar el valor de c , así como una medición precisa delsegundo, se puede establecer un estándar para el metro.[14]Comoconstante física dimensional, el valor numérico de c es diferente para diferentes sistemas de unidades. Por ejemplo, enunidades imperiales, la velocidad de la luz es aproximadamente186 282 millas por segundo, [Nota 4] o aproximadamente 1 pie por nanosegundo. [Nota 5] [15] [16]
En las ramas de la física en las que c aparece a menudo, como en la relatividad, es habitual utilizar sistemas de unidades de medida naturales o el sistema de unidades geometrizadas donde c = 1. [17] [18] Al utilizar estas unidades, c no aparece explícitamente porque la multiplicación o división por 1 no afecta al resultado. Su unidad de segundo luz por segundo sigue siendo relevante, incluso si se omite.
Papel fundamental en la física
La velocidad a la que las ondas de luz se propagan en el vacío es independiente tanto del movimiento de la fuente de ondas como del marco de referencia inercial del observador. [Nota 6] Esta invariancia de la velocidad de la luz fue postulada por Einstein en 1905, [8] después de estar motivado por la teoría del electromagnetismo de Maxwell y la falta de evidencia de movimiento contra el éter luminífero . [19] Desde entonces ha sido confirmada consistentemente por muchos experimentos. [Nota 7] Solo es posible verificar experimentalmente que la velocidad bidireccional de la luz (por ejemplo, de una fuente a un espejo y viceversa) es independiente del marco, porque es imposible medir la velocidad unidireccional de la luz (por ejemplo, de una fuente a un detector distante) sin alguna convención sobre cómo deben sincronizarse los relojes en la fuente y en el detector. [20] [21]
Al adoptar la sincronización de Einstein para los relojes, la velocidad unidireccional de la luz se vuelve igual a la velocidad bidireccional de la luz por definición. [20] [21] La teoría especial de la relatividad explora las consecuencias de esta invariancia de c con el supuesto de que las leyes de la física son las mismas en todos los marcos de referencia inerciales. [22] [23] Una consecuencia es que c es la velocidad a la que todas las partículas y ondas sin masa, incluida la luz, deben viajar en el vacío. [24] [Nota 8]
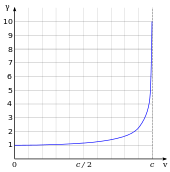
La relatividad especial tiene muchas implicaciones contraintuitivas y verificadas experimentalmente. [26] Estas incluyen la equivalencia de masa y energía ( E = mc 2 ) , contracción de la longitud (los objetos en movimiento se acortan), [Nota 9] y dilatación del tiempo (los relojes en movimiento funcionan más lentamente). El factor γ por el cual las longitudes se contraen y los tiempos se dilatan se conoce como el factor de Lorentz y está dado por γ = (1 − v 2 / c 2 ) −1/2 , donde v es la velocidad del objeto. La diferencia de γ con respecto a 1 es insignificante para velocidades mucho más lentas que c , como la mayoría de las velocidades cotidianas -en cuyo caso la relatividad especial se aproxima estrechamente a la relatividad galileana- pero aumenta a velocidades relativistas y diverge hasta el infinito a medida que v se acerca a c . Por ejemplo, un factor de dilatación del tiempo de γ = 2 ocurre a una velocidad relativa del 86,6 % de la velocidad de la luz ( v = 0,866 c ). De manera similar, un factor de dilatación del tiempo de γ = 10 ocurre al 99,5 % de la velocidad de la luz ( v = 0,995 c ).
Los resultados de la relatividad especial se pueden resumir tratando el espacio y el tiempo como una estructura unificada conocida como espacio-tiempo (con c relacionando las unidades de espacio y tiempo), y requiriendo que las teorías físicas satisfagan una simetría especial llamada invariancia de Lorentz , cuya formulación matemática contiene el parámetro c . [29] La invariancia de Lorentz es un supuesto casi universal para las teorías físicas modernas, como la electrodinámica cuántica , la cromodinámica cuántica , el Modelo Estándar de física de partículas y la relatividad general . Como tal, el parámetro c es omnipresente en la física moderna, apareciendo en muchos contextos que no están relacionados con la luz. Por ejemplo, la relatividad general predice que c es también la velocidad de la gravedad y de las ondas gravitacionales , [30] y las observaciones de ondas gravitacionales han sido consistentes con esta predicción. [31] En marcos de referencia no inerciales (espacio-tiempo curvado gravitacionalmente o marcos de referencia acelerados ), la velocidad local de la luz es constante e igual a c , pero la velocidad de la luz puede diferir de c cuando se mide desde un marco de referencia remoto, dependiendo de cómo se extrapolen las mediciones a la región. [32]
En general, se supone que las constantes fundamentales como c tienen el mismo valor en todo el espacio-tiempo, lo que significa que no dependen de la ubicación y no varían con el tiempo. Sin embargo, en varias teorías se ha sugerido que la velocidad de la luz puede haber cambiado con el tiempo . [33] [34] No se ha encontrado evidencia concluyente de tales cambios, pero siguen siendo objeto de investigación en curso. [35] [36]
En general, se supone que la velocidad bidireccional de la luz es isótropa , lo que significa que tiene el mismo valor independientemente de la dirección en la que se mida. Las observaciones de las emisiones de los niveles de energía nuclear en función de la orientación de los núcleos emisores en un campo magnético (véase el experimento de Hughes-Drever ) y de los resonadores ópticos giratorios (véase los experimentos con resonadores ) han puesto límites estrictos a la posible anisotropía bidireccional . [37] [38]
Límite superior de velocidad
Según la relatividad especial, la energía de un objeto con masa en reposo m y velocidad v está dada por γmc 2 , donde γ es el factor de Lorentz definido anteriormente. Cuando v es cero, γ es igual a uno, lo que da lugar a la famosa fórmula E = mc 2 para la equivalencia masa-energía. El factor γ se acerca al infinito cuando v se acerca a c , y se necesitaría una cantidad infinita de energía para acelerar un objeto con masa a la velocidad de la luz. La velocidad de la luz es el límite superior para las velocidades de los objetos con masa en reposo positiva, y los fotones individuales no pueden viajar más rápido que la velocidad de la luz. [39] Esto se establece experimentalmente en muchas pruebas de energía y momento relativistas . [40]

En términos más generales, es imposible que las señales o la energía viajen más rápido que c . Un argumento para esto se desprende de la implicación contraintuitiva de la relatividad especial conocida como la relatividad de la simultaneidad . Si la distancia espacial entre dos eventos A y B es mayor que el intervalo de tiempo entre ellos multiplicado por c, entonces hay marcos de referencia en los que A precede a B, otros en los que B precede a A y otros en los que son simultáneos. Como resultado, si algo viajara más rápido que c en relación con un marco de referencia inercial, estaría viajando hacia atrás en el tiempo en relación con otro marco, y se violaría la causalidad . [Nota 10] [43] En un marco de referencia de este tipo, se podría observar un "efecto" antes de su "causa". Tal violación de la causalidad nunca se ha registrado, [21] y conduciría a paradojas como la del antiteléfono taquiónico . [44]
Observaciones y experimentos más rápidos que la luz
Existen situaciones en las que puede parecer que la materia, la energía o la señal portadora de información viajan a velocidades superiores a c , pero no es así. Por ejemplo, como se analiza en la sección sobre la propagación de la luz en un medio que aparece más adelante, muchas velocidades de onda pueden superar c . La velocidad de fase de los rayos X a través de la mayoría de los vidrios puede superar habitualmente c , [45] pero la velocidad de fase no determina la velocidad a la que las ondas transmiten la información. [46]
Si un rayo láser se desplaza rápidamente sobre un objeto distante, el punto de luz puede moverse más rápido que c , aunque el movimiento inicial del punto se retrasa debido al tiempo que tarda la luz en llegar al objeto distante a la velocidad c . Sin embargo, las únicas entidades físicas que se mueven son el láser y la luz emitida por él, que viaja a la velocidad c desde el láser hasta las distintas posiciones del punto. De manera similar, una sombra proyectada sobre un objeto distante puede moverse más rápido que c , después de un retraso en el tiempo. [47] En ninguno de los casos la materia, la energía o la información viajan más rápido que la luz. [48]
La tasa de cambio en la distancia entre dos objetos en un marco de referencia con respecto al cual ambos se mueven (su velocidad de cierre ) puede tener un valor superior a c . Sin embargo, esto no representa la velocidad de ningún objeto individual medido en un único marco inercial. [48]
Ciertos efectos cuánticos parecen transmitirse instantáneamente y, por lo tanto, más rápido que c , como en la paradoja EPR . Un ejemplo involucra los estados cuánticos de dos partículas que pueden estar entrelazadas . Hasta que se observe cualquiera de las partículas, existen en una superposición de dos estados cuánticos. Si las partículas están separadas y se observa el estado cuántico de una partícula, el estado cuántico de la otra partícula se determina instantáneamente. Sin embargo, es imposible controlar qué estado cuántico adoptará la primera partícula cuando se la observa, por lo que la información no se puede transmitir de esta manera. [48] [49]
Otro efecto cuántico que predice la ocurrencia de velocidades superiores a la de la luz se denomina efecto Hartman : en determinadas condiciones, el tiempo que necesita una partícula virtual para atravesar una barrera es constante, independientemente del espesor de la misma. [50] [51] Esto podría dar como resultado que una partícula virtual cruce un gran espacio más rápido que la luz. Sin embargo, no se puede enviar información utilizando este efecto. [52]
El llamado movimiento superlumínico se observa en ciertos objetos astronómicos, [53] como los chorros relativistas de las radiogalaxias y los cuásares . Sin embargo, estos chorros no se mueven a velocidades superiores a la de la luz: el aparente movimiento superlumínico es un efecto de proyección causado por objetos que se mueven cerca de la velocidad de la luz y se aproximan a la Tierra en un ángulo pequeño con respecto a la línea de visión: como la luz que se emitió cuando el chorro estaba más lejos tardó más en llegar a la Tierra, el tiempo entre dos observaciones sucesivas corresponde a un tiempo más largo entre los instantes en que se emitieron los rayos de luz. [54]
Un experimento de 2011 en el que se observó que los neutrinos viajaban más rápido que la luz resultó deberse a un error experimental. [55] [56]
En los modelos del universo en expansión , cuanto más alejadas están las galaxias entre sí, más rápido se alejan. Por ejemplo, se infiere que las galaxias alejadas de la Tierra se alejan de ella a velocidades proporcionales a sus distancias. Más allá de un límite llamado esfera de Hubble , la velocidad a la que aumenta su distancia de la Tierra se vuelve mayor que la velocidad de la luz. [57] Estas tasas de recesión, definidas como el aumento de la distancia propia por tiempo cosmológico , no son velocidades en un sentido relativista. Las velocidades de recesión cosmológica más rápidas que la luz son solo un artefacto de coordenadas .
Propagación de la luz
En física clásica , la luz se describe como un tipo de onda electromagnética . El comportamiento clásico del campo electromagnético se describe mediante las ecuaciones de Maxwell , que predicen que la velocidad c con la que se propagan las ondas electromagnéticas (como la luz) en el vacío está relacionada con la capacitancia e inductancia distribuidas del vacío, también conocidas respectivamente como la constante eléctrica ε 0 y la constante magnética μ 0 , mediante la ecuación [58]
En la física cuántica moderna , el campo electromagnético se describe mediante la teoría de la electrodinámica cuántica (EDQ). En esta teoría, la luz se describe mediante las excitaciones fundamentales (o cuantos) del campo electromagnético, llamadas fotones . En la EQQ, los fotones son partículas sin masa y, por lo tanto, según la relatividad especial, viajan a la velocidad de la luz en el vacío. [24]
Se han considerado extensiones de la QED en las que el fotón tiene una masa. En tal teoría, su velocidad dependería de su frecuencia, y la velocidad invariante c de la relatividad especial sería entonces el límite superior de la velocidad de la luz en el vacío. [32] No se ha observado variación de la velocidad de la luz con la frecuencia en pruebas rigurosas, lo que pone límites estrictos a la masa del fotón. [59] El límite obtenido depende del modelo utilizado: si el fotón masivo se describe mediante la teoría de Proca , [60] el límite superior experimental para su masa es de aproximadamente 10 −57 gramos ; [61] si la masa del fotón se genera mediante un mecanismo de Higgs , el límite superior experimental es menos agudo, m ≤10 −14 eV/ c 2 (aproximadamente 2 × 10 −47 g). [60]
Otra razón para que la velocidad de la luz varíe con su frecuencia sería el fracaso de la relatividad especial para aplicarse a escalas arbitrariamente pequeñas, como predicen algunas teorías propuestas de gravedad cuántica . En 2009, la observación del estallido de rayos gamma GRB 090510 no encontró evidencia de una dependencia de la velocidad del fotón con la energía, lo que apoya restricciones estrictas en modelos específicos de cuantificación del espacio-tiempo sobre cómo esta velocidad se ve afectada por la energía del fotón para energías que se acercan a la escala de Planck . [62]
En un medio
En un medio, la luz no suele propagarse a una velocidad igual a c ; además, los distintos tipos de ondas de luz viajarán a distintas velocidades. La velocidad a la que se propagan las crestas y valles individuales de una onda plana (una onda que llena todo el espacio, con una sola frecuencia ) se denomina velocidad de fase v p . Una señal física con una extensión finita (un pulso de luz) viaja a una velocidad diferente. La envolvente general del pulso viaja a la velocidad de grupo v g , y su parte más temprana viaja a la velocidad frontal v f . [63]
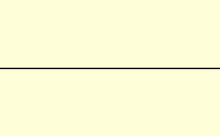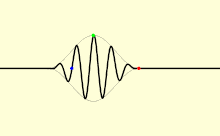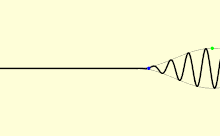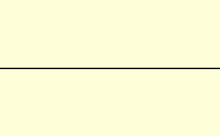
La velocidad de fase es importante para determinar cómo viaja una onda de luz a través de un material o de un material a otro. A menudo se representa en términos de un índice de refracción . El índice de refracción de un material se define como la relación entre c y la velocidad de fase v p en el material: los índices de refracción más altos indican velocidades más bajas. El índice de refracción de un material puede depender de la frecuencia, intensidad, polarización o dirección de propagación de la luz; sin embargo, en muchos casos, puede tratarse como una constante dependiente del material. El índice de refracción del aire es aproximadamente 1,0003. [64] Los medios más densos, como el agua , [65] el vidrio , [66] y el diamante , [67] tienen índices de refracción de alrededor de 1,3, 1,5 y 2,4, respectivamente, para la luz visible.
En materiales exóticos como los condensados de Bose-Einstein cerca del cero absoluto, la velocidad efectiva de la luz puede ser de sólo unos pocos metros por segundo. Sin embargo, esto representa un retraso de absorción y re-radiación entre átomos, como lo son todas las velocidades más lentas que c en las sustancias materiales. Como un ejemplo extremo de la luz "ralentizada" en la materia, dos equipos independientes de físicos afirmaron haber logrado que la luz se "detuviera por completo" haciéndola pasar a través de un condensado de Bose-Einstein del elemento rubidio . La descripción popular de la luz "detenida" en estos experimentos se refiere sólo a la luz que se almacena en los estados excitados de los átomos, y luego se vuelve a emitir en un momento arbitrario posterior, estimulada por un segundo pulso láser. Durante el tiempo en que se había "detenido", había dejado de ser luz. Este tipo de comportamiento es generalmente cierto a nivel microscópico en todos los medios transparentes que "ralentizan" la velocidad de la luz. [68]
En los materiales transparentes, el índice de refracción es generalmente mayor que 1, lo que significa que la velocidad de fase es menor que c . En otros materiales, es posible que el índice de refracción sea menor que 1 para algunas frecuencias; en algunos materiales exóticos es incluso posible que el índice de refracción sea negativo. [69] El requisito de que no se viole la causalidad implica que las partes real e imaginaria de la constante dieléctrica de cualquier material, correspondientes respectivamente al índice de refracción y al coeficiente de atenuación , están vinculadas por las relaciones de Kramers-Kronig . [70] [71] En términos prácticos, esto significa que en un material con un índice de refracción menor que 1, la onda será absorbida rápidamente. [72]
Un pulso con diferentes velocidades de grupo y fase (lo que ocurre si la velocidad de fase no es la misma para todas las frecuencias del pulso) se difumina con el tiempo, un proceso conocido como dispersión . Ciertos materiales tienen una velocidad de grupo excepcionalmente baja (o incluso cero) para las ondas de luz, un fenómeno llamado luz lenta . [73] Lo opuesto, velocidades de grupo superiores a c , se propuso teóricamente en 1993 y se logró experimentalmente en 2000. [74] Incluso debería ser posible que la velocidad de grupo se volviera infinita o negativa, con pulsos que viajan instantáneamente o hacia atrás en el tiempo. [63]
Ninguna de estas opciones permite transmitir información a una velocidad superior a c . Es imposible transmitir información con un pulso de luz a una velocidad superior a la de la primera parte del pulso (la velocidad frontal). Se puede demostrar que esta es (bajo ciertas suposiciones) siempre igual a c . [63]
Es posible que una partícula viaje a través de un medio más rápido que la velocidad de fase de la luz en ese medio (pero aún más lento que c ). Cuando una partícula cargada hace eso en un material dieléctrico , se emite el equivalente electromagnético de una onda de choque , conocida como radiación Cherenkov . [75]
Efectos prácticos de la finitud
La velocidad de la luz es importante para las telecomunicaciones : el tiempo de retardo en el trayecto de ida y vuelta es mayor que cero. Esto se aplica desde escalas pequeñas hasta astronómicas. Por otro lado, algunas técnicas dependen de la velocidad finita de la luz, por ejemplo, en las mediciones de distancias.
Pequeñas escalas
En las computadoras , la velocidad de la luz impone un límite a la rapidez con la que se pueden enviar datos entre procesadores . Si un procesador opera a 1 gigahercio , una señal puede viajar solo un máximo de aproximadamente 30 centímetros (1 pie) en un solo ciclo de reloj; en la práctica, esta distancia es incluso más corta ya que la placa de circuito impreso refracta y ralentiza las señales. Por lo tanto, los procesadores deben colocarse cerca unos de otros, así como los chips de memoria , para minimizar las latencias de comunicación, y se debe tener cuidado al enrutar los cables entre ellos para garantizar la integridad de la señal . Si las frecuencias de reloj continúan aumentando, la velocidad de la luz puede eventualmente convertirse en un factor limitante para el diseño interno de chips individuales . [76] [77]
Grandes distancias en la Tierra
Dado que la circunferencia ecuatorial de la Tierra es de aproximadamente40 075 km y eso que c es aproximadamente300 000 km/s , el tiempo teórico más corto para que un fragmento de información recorra la mitad del globo a lo largo de la superficie es de unos 67 milisegundos. Cuando la luz viaja en fibra óptica (un material transparente ), el tiempo de tránsito real es mayor, en parte porque la velocidad de la luz es aproximadamente un 35% más lenta en la fibra óptica, dependiendo de su índice de refracción n . [Nota 11] Las líneas rectas son raras en las comunicaciones globales y el tiempo de viaje aumenta cuando las señales pasan a través de interruptores electrónicos o regeneradores de señales. [79]
Aunque esta distancia es en gran medida irrelevante para la mayoría de las aplicaciones, la latencia se vuelve importante en campos como el comercio de alta frecuencia , donde los operadores buscan obtener pequeñas ventajas al entregar sus transacciones a las bolsas fracciones de segundo antes que otros operadores. Por ejemplo, los operadores han estado cambiando a comunicaciones de microondas entre centros comerciales, debido a la ventaja que tienen las ondas de radio que viajan a una velocidad cercana a la de la luz a través del aire sobre las señales de fibra óptica comparativamente más lentas . [80] [81]
Vuelos espaciales y astronomía

De manera similar, las comunicaciones entre la Tierra y las naves espaciales no son instantáneas. Existe un breve retraso entre la fuente y el receptor, que se hace más notorio a medida que aumentan las distancias. Este retraso fue significativo para las comunicaciones entre el control terrestre y el Apolo 8 cuando se convirtió en la primera nave espacial tripulada en orbitar la Luna : para cada pregunta, la estación de control terrestre tuvo que esperar al menos tres segundos para que llegara la respuesta. [82]
El retraso en las comunicaciones entre la Tierra y Marte puede variar entre cinco y veinte minutos, dependiendo de las posiciones relativas de los dos planetas. Como consecuencia de ello, si un robot en la superficie de Marte tuviera un problema, sus controladores humanos no se darían cuenta hasta aproximadamente entre cuatro y veinticuatro minutos después. A partir de entonces, las órdenes tardarían otros cuatro o veinticuatro minutos en llegar desde la Tierra a Marte. [83] [84]
Recibir luz y otras señales de fuentes astronómicas distantes lleva mucho más tiempo. Por ejemplo, se necesitan 13 mil millones (13 × 109 ) años para que la luz viaje a la Tierra desde las galaxias lejanas vistas en las imágenes del Campo Ultraprofundo del Hubble . [85] [86] Esas fotografías, tomadas hoy, capturan imágenes de las galaxias tal como aparecían hace 13 mil millones de años, cuando el universo tenía menos de mil millones de años. [85] El hecho de que los objetos más distantes parezcan ser más jóvenes, debido a la velocidad finita de la luz, permite a los astrónomos inferir la evolución de las estrellas , de las galaxias y del universo mismo. [87]
Las distancias astronómicas a veces se expresan en años luz , especialmente en publicaciones y medios de divulgación científica . [88] Un año luz es la distancia que recorre la luz en un año juliano , alrededor de 9461 mil millones de kilómetros, 5879 mil millones de millas o 0,3066 parsecs . En cifras redondas, un año luz son casi 10 billones de kilómetros o casi 6 billones de millas. Próxima Centauri , la estrella más cercana a la Tierra después del Sol, está a unos 4,2 años luz de distancia. [89]
Medición de distancia
Los sistemas de radar miden la distancia a un objetivo por el tiempo que tarda un pulso de onda de radio en regresar a la antena del radar después de ser reflejado por el objetivo: la distancia al objetivo es la mitad del tiempo de tránsito de ida y vuelta multiplicado por la velocidad de la luz. Un receptor del Sistema de Posicionamiento Global (GPS) mide su distancia a los satélites GPS basándose en el tiempo que tarda una señal de radio en llegar desde cada satélite, y a partir de estas distancias calcula la posición del receptor. Debido a que la luz viaja aproximadamente300 000 kilómetros (186 000 mi ) en un segundo, estas mediciones de pequeñas fracciones de segundo deben ser muy precisas. El experimento Lunar Laser Ranging , la astronomía de radar y la Deep Space Network determinan distancias a la Luna, [90] planetas [91] y naves espaciales, [92] respectivamente, midiendo los tiempos de tránsito de ida y vuelta.
Medición
Existen diferentes formas de determinar el valor de c . Una de ellas es medir la velocidad real a la que se propagan las ondas de luz, lo que se puede hacer en diversas configuraciones astronómicas y terrestres. También es posible determinar c a partir de otras leyes físicas en las que aparece, por ejemplo, determinando los valores de las constantes electromagnéticas ε 0 y μ 0 y utilizando su relación con c . Históricamente, los resultados más precisos se han obtenido determinando por separado la frecuencia y la longitud de onda de un haz de luz, con su producto igual a c . Esto se describe con más detalle en la sección "Interferometría" a continuación.
En 1983 se definió el metro como "la longitud del camino recorrido por la luz en el vacío durante un intervalo de tiempo de 1 ⁄299 792 458 de segundo",[93]fijando el valor de la velocidad de la luz en299 792 458 m/s por definición, como se describe a continuación. En consecuencia, las mediciones precisas de la velocidad de la luz dan como resultado una determinación precisa del metro en lugar de un valor preciso de c .
Mediciones astronómicas

El espacio exterior es un entorno conveniente para medir la velocidad de la luz debido a su gran escala y al vacío casi perfecto . Normalmente, se mide el tiempo que necesita la luz para recorrer una distancia de referencia en el Sistema Solar , como el radio de la órbita de la Tierra. Históricamente, estas mediciones se podían realizar con bastante precisión, en comparación con la precisión con la que se conoce la longitud de la distancia de referencia en unidades terrestres.
Ole Christensen Rømer utilizó una medición astronómica para hacer la primera estimación cuantitativa de la velocidad de la luz en el año 1676. [94] [95] Cuando se miden desde la Tierra, los períodos de las lunas que orbitan un planeta distante son más cortos cuando la Tierra se acerca al planeta que cuando la Tierra se aleja de él. La diferencia es pequeña, pero el tiempo acumulado se vuelve significativo cuando se mide a lo largo de meses. La distancia recorrida por la luz desde el planeta (o su luna) hasta la Tierra es más corta cuando la Tierra está en el punto de su órbita más cercano a su planeta que cuando la Tierra está en el punto más alejado de su órbita, siendo la diferencia en la distancia el diámetro de la órbita de la Tierra alrededor del Sol. El cambio observado en el período orbital de la luna es causado por la diferencia en el tiempo que tarda la luz en atravesar la distancia más corta o más larga. Rømer observó este efecto para la luna principal más interna de Júpiter, Ío , y dedujo que la luz tarda 22 minutos en cruzar el diámetro de la órbita de la Tierra. [94]

Otro método consiste en utilizar la aberración de la luz , descubierta y explicada por James Bradley en el siglo XVIII. [96] Este efecto resulta de la suma vectorial de la velocidad de la luz que llega desde una fuente distante (como una estrella) y la velocidad de su observador (véase el diagrama de la derecha). Un observador en movimiento ve así la luz que viene de una dirección ligeramente diferente y, en consecuencia, ve la fuente en una posición desplazada respecto de su posición original. Dado que la dirección de la velocidad de la Tierra cambia continuamente a medida que la Tierra orbita alrededor del Sol, este efecto hace que la posición aparente de las estrellas se mueva. A partir de la diferencia angular en la posición de las estrellas (máximo 20,5 segundos de arco ) [97] es posible expresar la velocidad de la luz en términos de la velocidad de la Tierra alrededor del Sol, que con la duración conocida de un año se puede convertir en el tiempo necesario para viajar del Sol a la Tierra. En 1729, Bradley utilizó este método para derivar que la luz viajaba10 210 veces más rápido que la Tierra en su órbita (la cifra moderna es10 066 veces más rápido) o, equivalentemente, que la luz tardaría 8 minutos y 12 segundos en viajar desde el Sol a la Tierra. [96]
Unidad astronómica
Una unidad astronómica (UA) es aproximadamente la distancia promedio entre la Tierra y el Sol. Fue redefinida en 2012 como exactamente149 597 870 700 m . [98] [99] Anteriormente la UA no se basaba en el Sistema Internacional de Unidades sino en términos de la fuerza gravitacional ejercida por el Sol en el marco de la mecánica clásica. [Nota 12] La definición actual utiliza el valor recomendado en metros para la definición anterior de la unidad astronómica, que se determinaba mediante medición. [98] Esta redefinición es análoga a la del metro y asimismo tiene el efecto de fijar la velocidad de la luz a un valor exacto en unidades astronómicas por segundo (a través de la velocidad exacta de la luz en metros por segundo). [101]
Anteriormente, la inversa de c expresada en segundos por unidad astronómica se medía comparando el tiempo que tardaban las señales de radio en llegar a diferentes naves espaciales en el Sistema Solar, con su posición calculada a partir de los efectos gravitacionales del Sol y varios planetas. Al combinar muchas de estas mediciones, se podía obtener un valor de ajuste óptimo para el tiempo de luz por unidad de distancia. Por ejemplo, en 2009, la mejor estimación, aprobada por la Unión Astronómica Internacional (UAI), era: [102] [103]
- tiempo de luz por unidad de distancia: t au = 499.004 783 836 (10) s ,
- c = 0,002 003 988 804 10 (4) UA/s = 173.144 632 674 (3) UA/día .
La incertidumbre relativa en estas mediciones es de 0,02 partes por mil millones (2 × 10 −11 ), equivalente a la incertidumbre en las mediciones de longitud basadas en la Tierra por interferometría. [104] Dado que el metro se define como la longitud recorrida por la luz en un cierto intervalo de tiempo, la medición del tiempo luz en términos de la definición anterior de la unidad astronómica también puede interpretarse como la medición de la longitud de una UA (definición antigua) en metros. [Nota 13]
Técnicas de tiempo de vuelo

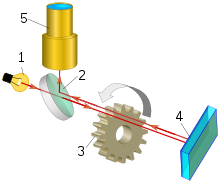
- Fuente de luz
- Espejo semitransparente con división de haz
- Rueda dentada rompedora del haz de luz
- Espejo remoto
- Tubo telescópico
Un método para medir la velocidad de la luz consiste en medir el tiempo que tarda la luz en llegar a un espejo situado a una distancia conocida y volver. Este es el principio de funcionamiento que sustenta los experimentos de Hippolyte Fizeau y Léon Foucault .
El sistema utilizado por Fizeau consiste en un haz de luz dirigido hacia un espejo situado a 8 kilómetros de distancia. En el trayecto desde la fuente hasta el espejo, el haz pasa por una rueda dentada giratoria. A una determinada velocidad de rotación, el haz pasa por un hueco en el camino de ida y por otro en el de vuelta, pero a velocidades ligeramente superiores o inferiores, el haz incide en un diente y no atraviesa la rueda. Conociendo la distancia entre la rueda y el espejo, el número de dientes de la rueda y la velocidad de rotación, se puede calcular la velocidad de la luz. [105]
El método de Foucault reemplaza la rueda dentada por un espejo giratorio. Como el espejo sigue girando mientras la luz viaja hacia el espejo distante y de regreso, la luz se refleja desde el espejo giratorio en un ángulo diferente en su camino de ida y vuelta. A partir de esta diferencia de ángulo, se puede calcular la velocidad de rotación conocida y la distancia al espejo distante: la velocidad de la luz. [106] Foucault utilizó este aparato para medir la velocidad de la luz en el aire en comparación con el agua, basándose en una sugerencia de François Arago . [107]
En la actualidad, con osciloscopios con resoluciones temporales inferiores a un nanosegundo, se puede medir directamente la velocidad de la luz cronometrando el retardo de un pulso de luz de un láser o un LED reflejado en un espejo. Este método es menos preciso (con errores del orden del 1%) que otras técnicas modernas, pero a veces se utiliza como experimento de laboratorio en las clases de física de la universidad. [108]
Constantes electromagnéticas
Una opción para derivar c que no depende directamente de una medición de la propagación de ondas electromagnéticas es utilizar la relación entre c y la permitividad del vacío ε 0 y la permeabilidad del vacío μ 0 establecida por la teoría de Maxwell: c 2 = 1/( ε 0 μ 0 ). La permitividad del vacío se puede determinar midiendo la capacitancia y las dimensiones de un condensador , mientras que el valor de la permeabilidad del vacío se fijaba históricamente exactamente en4π × 10 −7 H⋅m −1 a través de la definición del amperio . Rosa y Dorsey utilizaron este método en 1907 para encontrar un valor de299 710 ± 22 km/s . Su método dependía de tener una unidad estándar de resistencia eléctrica, el " ohmio internacional ", y por lo tanto su precisión estaba limitada por la forma en que se definiera este estándar. [109] [110]
Resonancia de cavidad

Otra forma de medir la velocidad de la luz es medir independientemente la frecuencia f y la longitud de onda λ de una onda electromagnética en el vacío. El valor de c se puede encontrar entonces utilizando la relación c = fλ . Una opción es medir la frecuencia de resonancia de un resonador de cavidad . Si también se conocen las dimensiones de la cavidad de resonancia, estas se pueden utilizar para determinar la longitud de onda de la onda. En 1946, Louis Essen y AC Gordon-Smith establecieron la frecuencia para una variedad de modos normales de microondas de una cavidad de microondas de dimensiones conocidas con precisión. Las dimensiones se establecieron con una precisión de aproximadamente ±0,8 μm utilizando medidores calibrados por interferometría. [109] Como la longitud de onda de los modos se conocía a partir de la geometría de la cavidad y de la teoría electromagnética , el conocimiento de las frecuencias asociadas permitió un cálculo de la velocidad de la luz. [109] [111]
El resultado de Essen-Gordon-Smith,299 792 ± 9 km/s , fue sustancialmente más precisa que las encontradas mediante técnicas ópticas. [109] En 1950, mediciones repetidas de Essen establecieron un resultado de299 792,5 ± 3,0 km /s . [112]
Es posible realizar una demostración casera de esta técnica utilizando un horno microondas y alimentos como malvaviscos o margarina: si se retira el plato giratorio para que los alimentos no se muevan, se cocinarán más rápido en los antinodos (los puntos en los que la amplitud de onda es mayor), donde comenzarán a derretirse. La distancia entre dos de esos puntos es la mitad de la longitud de onda de las microondas; midiendo esta distancia y multiplicando la longitud de onda por la frecuencia de las microondas (que suele aparecer en la parte posterior del horno, normalmente 2450 MHz), se puede calcular el valor de c , "a menudo con un error inferior al 5%". [113] [114]
Interferometría

La interferometría es otro método para encontrar la longitud de onda de la radiación electromagnética para determinar la velocidad de la luz. [Nota 14] Un haz de luz coherente (por ejemplo, de un láser ), con una frecuencia conocida ( f ), se divide para seguir dos caminos y luego se recombina. Al ajustar la longitud del camino mientras se observa el patrón de interferencia y se mide cuidadosamente el cambio en la longitud del camino, se puede determinar la longitud de onda de la luz ( λ ). Luego, la velocidad de la luz se calcula utilizando la ecuación c = λf .
Antes de la llegada de la tecnología láser, se utilizaban fuentes de radio coherentes para las mediciones interferométricas de la velocidad de la luz. [116] La determinación interferométrica de la longitud de onda se vuelve menos precisa con la longitud de onda y, por lo tanto, los experimentos estaban limitados en precisión por la longitud de onda larga (~4 mm (0,16 pulgadas)) de las ondas de radio. La precisión se puede mejorar utilizando luz con una longitud de onda más corta, pero entonces se vuelve difícil medir directamente la frecuencia de la luz. [117]
Una forma de evitar este problema es empezar con una señal de baja frecuencia cuya frecuencia se pueda medir con precisión y, a partir de esta señal, sintetizar progresivamente señales de mayor frecuencia cuya frecuencia se pueda vincular a la señal original. A continuación, se puede sincronizar un láser con la frecuencia y se puede determinar su longitud de onda mediante interferometría. [117] Esta técnica se debió a un grupo de la Oficina Nacional de Normas (que más tarde se convirtió en el Instituto Nacional de Normas y Tecnología ). La utilizaron en 1972 para medir la velocidad de la luz en el vacío con una incertidumbre fraccionaria de3,5 × 10 −9 . [117] [118]
Historia
Hasta principios de la época moderna no se sabía si la luz viajaba instantáneamente o a una velocidad finita muy rápida. El primer estudio registrado sobre este tema se realizó en la antigua Grecia . Los antiguos griegos, los eruditos árabes y los científicos europeos clásicos debatieron sobre este tema durante mucho tiempo hasta que Rømer proporcionó el primer cálculo de la velocidad de la luz. La teoría de la relatividad especial de Einstein postula que la velocidad de la luz es constante independientemente del marco de referencia. Desde entonces, los científicos han proporcionado mediciones cada vez más precisas.
| <1638 | Galileo , linternas cubiertas | inconcluso [119] [120] [121] : 1252 [Nota 15] | |
| <1667 | Accademia del Cimento , faroles cubiertos | inconcluso [121] : 1253 [122] | |
| 1675 | Rømer y Huygens , lunas de Júpiter | 220 000 000 [95] [123] | -27% |
| 1729 | James Bradley , aberración de la luz | 301 000 000 [105] | +0,40% |
| 1849 | Hippolyte Fizeau , rueda dentada | 315 000 000 [105] | +5,1% |
| 1862 | Léon Foucault , espejo giratorio | 298 000 000 ± 500 000 [105] | -0,60% |
| 1875 | Werner Siemens | 260 000 000 [124] | |
| 1893 | Heinrich Hertz | 200 000 000 [125] | |
| 1907 | Rosa y Dorsey, constantes EM | 299 710 000 ± 30 000 [109] [110] | -280 ppm |
| 1926 | Albert A. Michelson , espejo giratorio | 299 796 000 ± 4000 [126] | +12 ppm |
| 1950 | Resonador de cavidad de Essen y Gordon-Smith | 299 792 500 ± 3000 [112] | +0,14 ppm |
| 1958 | KD Froome, radiointerferometría | 299 792 500 ± 100 [116] | +0,14 ppm |
| 1972 | Evenson et al. , interferometría láser | 299 792 456 ,2 ± 1,1 [118] | -0,006 ppm |
| 1983 | 17ª CGPM, definición del metro | 299 792 458 (exacto) [93] | |
Historia temprana
Empédocles (c. 490–430 a. C.) fue el primero en proponer una teoría de la luz [127] y afirmó que la luz tiene una velocidad finita. [128] Sostuvo que la luz era algo en movimiento y, por lo tanto, debía tardar un tiempo en viajar. Aristóteles argumentó, por el contrario, que "la luz se debe a la presencia de algo, pero no es un movimiento". [129] Euclides y Ptolomeo propusieron la teoría de la emisión de Empédocles sobre la visión, según la cual la luz se emite desde el ojo, lo que permite la visión. Basándose en esa teoría, Herón de Alejandría argumentó que la velocidad de la luz debe ser infinita porque los objetos distantes, como las estrellas, aparecen inmediatamente al abrir los ojos. [130]
Los primeros filósofos islámicos inicialmente estuvieron de acuerdo con la visión aristotélica de que la luz no tenía velocidad de viaje. En 1021, Alhazen (Ibn al-Haytham) publicó el Libro de Óptica , en el que presentó una serie de argumentos que descartaban la teoría de la emisión de la visión a favor de la teoría de la intromisión ahora aceptada, en la que la luz se mueve desde un objeto hacia el ojo. [131] Esto llevó a Alhazen a proponer que la luz debe tener una velocidad finita, [129] [132] [133] y que la velocidad de la luz es variable, disminuyendo en cuerpos más densos. [133] [134] Argumentó que la luz es materia sustancial, cuya propagación requiere tiempo, incluso si este está oculto a los sentidos. [135] También en el siglo XI, Abū Rayhān al-Bīrūnī estuvo de acuerdo en que la luz tiene una velocidad finita, y observó que la velocidad de la luz es mucho más rápida que la velocidad del sonido. [136]
En el siglo XIII, Roger Bacon argumentó que la velocidad de la luz en el aire no era infinita, utilizando argumentos filosóficos respaldados por los escritos de Alhazen y Aristóteles. [137] [138] En la década de 1270, Witelo consideró la posibilidad de que la luz viajara a una velocidad infinita en el vacío, pero que se desacelerara en cuerpos más densos. [139]
A principios del siglo XVII, Johannes Kepler creía que la velocidad de la luz era infinita, ya que el espacio vacío no presenta ningún obstáculo para ella. René Descartes argumentó que si la velocidad de la luz fuera finita, el Sol, la Tierra y la Luna estarían notablemente desalineados durante un eclipse lunar . Aunque este argumento falla cuando se tiene en cuenta la aberración de la luz , esta última no se reconoció hasta el siglo siguiente. [140] Como tal desalineación no se había observado, Descartes concluyó que la velocidad de la luz era infinita. Descartes especuló que si se descubriera que la velocidad de la luz era finita, todo su sistema de filosofía podría ser demolido. [129] A pesar de esto, en su derivación de la ley de Snell , Descartes asumió que algún tipo de movimiento asociado con la luz era más rápido en medios más densos. [141] [142] Pierre de Fermat derivó la ley de Snell utilizando el supuesto opuesto, cuanto más denso es el medio, más lento viaja la luz. Fermat también argumentó a favor de una velocidad finita de la luz. [143]
Primeros intentos de medición
En 1629, Isaac Beeckman propuso un experimento en el que una persona observa el destello de un cañón reflejándose en un espejo a aproximadamente una milla (1,6 km) de distancia. En 1638, Galileo Galilei propuso un experimento, con una aparente afirmación de haberlo realizado algunos años antes, para medir la velocidad de la luz observando el retraso entre descubrir una linterna y su percepción a cierta distancia. No pudo distinguir si el viaje de la luz era instantáneo o no, pero concluyó que si no lo era, debía ser extraordinariamente rápido. [119] [120] En 1667, la Accademia del Cimento de Florencia informó que había realizado el experimento de Galileo, con las linternas separadas por aproximadamente una milla, pero no se observó ningún retraso. [144] El retraso real en este experimento habría sido de aproximadamente 11 microsegundos .
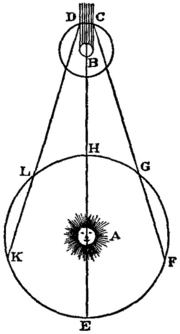
La primera estimación cuantitativa de la velocidad de la luz fue realizada en 1676 por Ole Rømer. [94] [95] A partir de la observación de que los períodos de la luna más interior de Júpiter, Ío, parecían ser más cortos cuando la Tierra se acercaba a Júpiter que cuando se alejaba de él, concluyó que la luz viaja a una velocidad finita y estimó que la luz tarda 22 minutos en cruzar el diámetro de la órbita de la Tierra. Christiaan Huygens combinó esta estimación con una estimación del diámetro de la órbita de la Tierra para obtener una estimación de la velocidad de la luz de220 000 km/s , lo que supone un 27% menos que el valor real. [123]
En su libro Opticks de 1704 , Isaac Newton informó sobre los cálculos de Rømer de la velocidad finita de la luz y dio un valor de "siete u ocho minutos" para el tiempo que tarda la luz en viajar desde el Sol a la Tierra (el valor moderno es 8 minutos 19 segundos). [145] Newton se preguntó si las sombras del eclipse de Rømer estaban coloreadas. Al escuchar que no lo estaban, concluyó que los diferentes colores viajaban a la misma velocidad. En 1729, James Bradley descubrió la aberración estelar . [96] A partir de este efecto, determinó que la luz debe viajar 10.210 veces más rápido que la Tierra en su órbita (la cifra moderna es 10.066 veces más rápida) o, equivalentemente, que la luz tardaría 8 minutos 12 segundos en viajar desde el Sol a la Tierra. [96]
Conexiones con el electromagnetismo
En el siglo XIX, Hippolyte Fizeau desarrolló un método para determinar la velocidad de la luz basándose en mediciones del tiempo de vuelo en la Tierra y reportó un valor de315 000 km/s . [146] Su método fue mejorado por Léon Foucault , quien obtuvo un valor de298 000 km/s en 1862. [105] En el año 1856, Wilhelm Eduard Weber y Rudolf Kohlrausch midieron la relación entre las unidades electromagnéticas y electrostáticas de carga, 1/ √ ε 0 μ 0 , descargando una botella de Leyden , y descubrieron que su valor numérico era muy cercano a la velocidad de la luz medida directamente por Fizeau. Al año siguiente, Gustav Kirchhoff calculó que una señal eléctrica en un cable sin resistencia viaja a lo largo del cable a esta velocidad. [147]
A principios de la década de 1860, Maxwell demostró que, según la teoría del electromagnetismo en la que estaba trabajando, las ondas electromagnéticas se propagan en el espacio vacío [148] a una velocidad igual a la relación Weber/Kohlrausch antes mencionada, y llamando la atención sobre la proximidad numérica de este valor a la velocidad de la luz medida por Fizeau, propuso que la luz es de hecho una onda electromagnética. [149] Maxwell respaldó su afirmación con su propio experimento publicado en Philosophical Transactions de 1868, que determinaba la relación entre las unidades electrostáticas y electromagnéticas de la electricidad. [150]
"Éter luminífero"
Las propiedades ondulatorias de la luz eran bien conocidas desde Thomas Young . En el siglo XIX, los físicos creían que la luz se propagaba en un medio llamado éter (o éter). Pero en el caso de la fuerza eléctrica, se parece más a la fuerza gravitacional de la ley de Newton. No se requería un medio de transmisión. Después de que la teoría de Maxwell unificara la luz y las ondas eléctricas y magnéticas, se favoreció la idea de que tanto la luz como las ondas eléctricas y magnéticas se propagaran en el mismo medio etéreo (o llamado éter luminífero ). [151]

En aquella época se creía que el espacio vacío estaba lleno de un medio de fondo llamado éter luminífero en el que existía el campo electromagnético. Algunos físicos pensaban que este éter actuaba como un marco de referencia preferido para la propagación de la luz y, por lo tanto, debería ser posible medir el movimiento de la Tierra con respecto a este medio, midiendo la isotropía de la velocidad de la luz. A partir de la década de 1880 se realizaron varios experimentos para intentar detectar este movimiento, el más famoso de los cuales es el experimento realizado por Albert A. Michelson y Edward W. Morley en 1887. [152] [153] Se descubrió que el movimiento detectado siempre era nulo (dentro del margen de error de observación). Los experimentos modernos indican que la velocidad bidireccional de la luz es isotrópica (la misma en todas las direcciones) con una precisión de 6 nanómetros por segundo. [154]
Debido a este experimento, Hendrik Lorentz propuso que el movimiento del aparato a través del éter puede hacer que el aparato se contraiga a lo largo de su longitud en la dirección del movimiento, y supuso además que la variable tiempo para los sistemas en movimiento también debe cambiarse en consecuencia ("tiempo local"), lo que llevó a la formulación de la transformación de Lorentz . Basándose en la teoría del éter de Lorentz , Henri Poincaré (1900) demostró que este tiempo local (de primer orden en v / c ) está indicado por relojes que se mueven en el éter, que están sincronizados bajo el supuesto de una velocidad de luz constante. En 1904, especuló que la velocidad de la luz podría ser una velocidad límite en dinámica, siempre que se confirmen todos los supuestos de la teoría de Lorentz. En 1905, Poincaré hizo que la teoría del éter de Lorentz coincidiera plenamente en términos observacionales con el principio de relatividad . [155] [156]
Relatividad especial
En 1905, Einstein postuló desde el principio que la velocidad de la luz en el vacío, medida por un observador que no acelera, es independiente del movimiento de la fuente o del observador. Utilizando esto y el principio de relatividad como base, derivó la teoría especial de la relatividad , en la que la velocidad de la luz en el vacío c figuraba como una constante fundamental, que también aparecía en contextos no relacionados con la luz. Esto hizo inútil el concepto de éter estacionario (al que Lorentz y Poincaré todavía se adhirieron) y revolucionó los conceptos de espacio y tiempo. [157] [158]
Mayor precisión dedoy redefinición del metro y del segundo
En la segunda mitad del siglo XX se hicieron grandes progresos en la mejora de la precisión de las mediciones de la velocidad de la luz, primero mediante técnicas de resonancia de cavidad y más tarde mediante técnicas de interferómetro láser. Estas se vieron favorecidas por nuevas definiciones más precisas del metro y el segundo. En 1950, Louis Essen determinó la velocidad como299 792 ,5 ± 3,0 km/s , utilizando resonancia de cavidad. [112] Este valor fue adoptado por la 12.ª Asamblea General de la Unión Radiocientífica en 1957. En 1960, el metro se redefinió en términos de la longitud de onda de una línea espectral particular del criptón-86 y, en 1967, el segundo se redefinió en términos de la frecuencia de transición hiperfina del estado fundamental del cesio-133 . [159]
En 1972, utilizando el método del interferómetro láser y las nuevas definiciones, un grupo de la Oficina Nacional de Normas de Estados Unidos en Boulder, Colorado, determinó que la velocidad de la luz en el vacío era c = 299 792 456 ,2 ± 1,1 m/s . Esto era 100 veces menos incierto que el valor aceptado anteriormente. La incertidumbre restante se relacionaba principalmente con la definición del metro. [Nota 16] [118] Como experimentos similares encontraron resultados comparables para c , la 15.ª Conferencia General de Pesas y Medidas en 1975 recomendó utilizar el valor299 792 458 m/s para la velocidad de la luz. [162]
Definida como una constante explícita
En 1983, la 17.ª reunión de la Conferencia General de Pesas y Medidas (CGPM) concluyó que las longitudes de onda de las mediciones de frecuencia y un valor dado de la velocidad de la luz son más reproducibles que el estándar anterior. Mantuvieron la definición de segundo de 1967, por lo que la frecuencia hiperfina de cesio determinaría ahora tanto el segundo como el metro. Para ello, redefinieron el metro como "la longitud del camino recorrido por la luz en el vacío durante un intervalo de tiempo de 1/299 792 458 de segundo". [93]
Como resultado de esta definición, el valor de la velocidad de la luz en el vacío es exactamente299 792 458 m/s [163] [164] y se ha convertido en una constante definida en el sistema SI de unidades. [14] Las técnicas experimentales mejoradas que, antes de 1983, habrían medido la velocidad de la luz ya no afectan el valor conocido de la velocidad de la luz en unidades SI, sino que permiten una realización más precisa del metro midiendo con mayor exactitud la longitud de onda del criptón-86 y otras fuentes de luz. [165] [166]
En 2011, la CGPM manifestó su intención de redefinir las siete unidades básicas del SI utilizando lo que denomina "la formulación de la constante explícita", en la que cada "unidad se define indirectamente especificando explícitamente un valor exacto para una constante fundamental bien reconocida", como se hizo para la velocidad de la luz. Propuso una redacción nueva, pero completamente equivalente, de la definición del metro: "El metro, símbolo m, es la unidad de longitud; su magnitud se establece fijando el valor numérico de la velocidad de la luz en el vacío para que sea exactamente igual a299 792 458 cuando se expresa en la unidad SI ms −1 ." [167] Este fue uno de los cambios que se incorporaron en la revisión de 2019 del SI , también denominada Nuevo SI . [168]
Véase también
Notas
- ^ Valor exacto: (299 792 458 ×86 400 /149 597 870 700 ) AU/día .
- ^ Valor exacto: (999 992 651 π /10 246 429 500 ) pc/a .
- ^ Es exacto porque, por un acuerdo internacional de 1983, un metro se define como la longitud del camino recorrido por la luz en el vacío durante un intervalo de tiempo de 1 ⁄299 792 458 segundo. Este valor en particular se eligió para proporcionar una definición más precisa del metro que aún coincidiera lo más posible con la definición utilizada anteriormente. Véase, por ejemplo, elsitio webdel NIST[2]o la explicación dePenrose.[3]El segundo, a su vez, se define como la duración del tiempo ocupado por9 192 631 770 ciclos de la radiación emitida por un átomo de cesio -133 en una transición entre dos estados de energía especificados . [2]
- ^ La velocidad de la luz en el sistema imperial es exactamente
- 186 282 millas ,698 yardas ,2 pies y 5+21/127pulgadas por segundo.
- ^ El valor exacto es 149 896 229/152 400 000 pie/ns ≈ 0,98 pie/ns .
- ^ Sin embargo, la frecuencia de la luz puede depender del movimiento de la fuente con respecto al observador, debido al efecto Doppler .
- ^ Véase el experimento de Michelson-Morley y el experimento de Kennedy-Thorndike , por ejemplo.
- ^ Debido a que los neutrinos tienen una masa pequeña pero distinta de cero, viajan a través del espacio vacío muy levemente más lentamente que la luz . Sin embargo, debido a que pasan a través de la materia mucho más fácilmente que la luz, en teoría hay ocasiones en las que la señal de neutrinos de un evento astronómico podría llegar a la Tierra antes que una señal óptica, como las supernovas . [25]
- ^ Mientras que los objetos en movimiento se miden como más cortos a lo largo de la línea de movimiento relativo, también se los ve como si estuvieran rotando. Este efecto, conocido como rotación de Terrell , se debe a los diferentes tiempos que tarda la luz de las distintas partes del objeto en llegar al observador. [27] [28]
- ^ Se ha especulado que el efecto Scharnhorst permite que las señales viajen ligeramente más rápido que c , pero se ha cuestionado la validez de esos cálculos, [41] y parece que las condiciones especiales en las que podría ocurrir este efecto impedirían usarlo para violar la causalidad. [42]
- ^ Un valor típico para el índice de refracción de la fibra óptica está entre 1,518 y 1,538. [78]
- ^ La unidad astronómica se definió como el radio de una órbita newtoniana circular no perturbada alrededor del Sol de una partícula con masa infinitesimal, moviéndose con una frecuencia angular de 0,017 202 098 95 radianes (aproximadamente 1 ⁄365.256 898 de una revolución) por día.[100]
- ^ Sin embargo, en este grado de precisión, los efectos de la relatividad general deben tenerse en cuenta al interpretar la longitud. El metro se considera una unidad de longitud propia , mientras que la UA se utiliza habitualmente como unidad de longitud observada en un marco de referencia dado. Los valores citados aquí siguen esta última convención y son compatibles con TDB . [103]
- ^ Una discusión detallada del interferómetro y su uso para determinar la velocidad de la luz se puede encontrar en Vaughan (1989). [115]
- ^ Según Galileo, las linternas que utilizó estaban "a una distancia corta, menos de una milla". Suponiendo que la distancia no fuera mucho menor que una milla, y que "alrededor de una trigésima de segundo es el intervalo de tiempo mínimo distinguible a simple vista", Boyer señala que, en el mejor de los casos, se podría decir que el experimento de Galileo estableció un límite inferior de aproximadamente 60 millas por segundo para la velocidad de la luz. [120]
- ^ Entre 1960 y 1983 el metro se definió como "la longitud igual a1 650 763 .73 longitudes de onda en el vacío de la radiación correspondiente a la transición entre los niveles 2p 10 y 5d 5 del átomo de criptón-86". [160] Se descubrió en la década de 1970 que esta línea espectral no era simétrica, lo que ponía un límite a la precisión con la que se podía realizar la definición en experimentos de interferometría. [161]
Referencias
- ^ Larson, Ron; Hostetler, Robert P. (2007). Álgebra elemental e intermedia: un curso combinado, edición de apoyo para estudiantes (cuarta edición ilustrada). Cengage Learning. pág. 197. ISBN 978-0-618-75354-3.
- ^ ab "Definiciones de las unidades base del SI". physics.nist.gov . 29 de mayo de 2019 . Consultado el 8 de febrero de 2022 .
- ^ Penrose, R (2004). El camino a la realidad: una guía completa de las leyes del universo . Vintage Books. págs. 410–411. ISBN 978-0-679-77631-4...
el estándar más preciso para el metro se
define
convenientemente de modo que haya exactamente 299 792 458 de ellos corresponden a la distancia recorrida por la luz en un segundo estándar, lo que da un valor para el metro que coincide con gran exactitud con la regla del metro estándar de París, ahora insuficientemente precisa.
- ^ Moses Fayngold (2008). Relatividad especial y cómo funciona (edición ilustrada). John Wiley & Sons. pág. 497. ISBN 978-3-527-40607-4.Extracto de la página 497.
- ^ Albert Shadowitz (1988). Relatividad especial (edición revisada). Courier Corporation. pág. 79. ISBN 978-0-486-65743-1.Extracto de la página 79.
- ^ Peres, Asher ; Terno, Daniel R. (6 de enero de 2004). "Información cuántica y teoría de la relatividad". Reseñas de Física Moderna . 76 (1): 93–123. arXiv : quant-ph/0212023 . Bibcode :2004RvMP...76...93P. doi :10.1103/RevModPhys.76.93. ISSN 0034-6861. S2CID 7481797.
- ^ Gibbs, Philip (1997). "¿Cómo se mide la velocidad de la luz?". Preguntas frecuentes sobre física y relatividad . Archivado desde el original el 21 de agosto de 2015.
- ^ ab Stachel, JJ (2002). Einstein de "B" a "Z" - Volumen 9 de Estudios de Einstein. Saltador. pag. 226.ISBN 978-0-8176-4143-6.
- ^ Véase, por ejemplo:
- Feigenbaum, Mitchell J. ; Mermin, N. David (enero de 1988). "E = mc2". American Journal of Physics . 56 (1): 18–21. Bibcode :1988AmJPh..56...18F. doi :10.1119/1.15422. ISSN 0002-9505.
- Uzan, JP; Leclercq, B (2008). Las leyes naturales del universo: comprensión de las constantes fundamentales. Springer. pp. 43–44. ISBN 978-0-387-73454-5.
- ^ Gibbs, P. (2004) [1997]. "¿Por qué c es el símbolo de la velocidad de la luz?". Preguntas frecuentes sobre física de Usenet . Universidad de California, Riverside . Archivado desde el original el 25 de marzo de 2010. Consultado el 16 de noviembre de 2009 ."Los orígenes de la letra c utilizada para la velocidad de la luz se remontan a un artículo de 1856 de Weber y Kohlrausch [...] Al parecer, Weber quería que c significara "constante" en su ley de fuerza, pero hay pruebas de que físicos como Lorentz y Einstein estaban acostumbrados a una convención común según la cual c podía utilizarse como variable de velocidad. Este uso se remonta a los textos latinos clásicos en los que c significaba "celeritas", es decir, "velocidad".
- ^ Mendelson, KS (2006). "La historia de c ". American Journal of Physics . 74 (11): 995–997. Código Bibliográfico :2006AmJPh..74..995M. doi :10.1119/1.2238887. ISSN 0002-9505.
- ^ Véase, por ejemplo:
- Lide, DR (2004). Manual de química y física del CRC. CRC Press . Págs. 2–9. ISBN. 978-0-8493-0485-9.
- Harris, JW; et al. (2002). Manual de Física. Springer. pág. 499. ISBN 978-0-387-95269-7.
- Whitaker, JC (2005). Manual de electrónica. CRC Press. pág. 235. ISBN 978-0-8493-1889-4.
- Cohen, ER; et al. (2007). Cantidades, unidades y símbolos en química física (3.ª ed.). Royal Society of Chemistry . p. 184. ISBN 978-0-85404-433-7.
- ^ Oficina Internacional de Pesas y Medidas (2006), El Sistema Internacional de Unidades (SI) (PDF) (8.ª ed.), pág. 112, ISBN 92-822-2213-6, archivado (PDF) del original el 4 de junio de 2021 , consultado el 16 de diciembre de 2021
- ^ ab Véase, por ejemplo:
- Sydenham, PH (2003). "Medición de longitud". En Boyes, W (ed.). Instrumentation Reference Book (3.ª ed.). Butterworth–Heinemann . p. 56. ISBN 978-0-7506-7123-1... si la velocidad de la luz se define como un número fijo, entonces, en principio, el estándar
de tiempo servirá como estándar de longitud ...
- "Valor CODATA: Velocidad de la luz en el vacío". Referencia del NIST sobre constantes, unidades e incertidumbre . NIST . Consultado el 21 de agosto de 2009 .
- Jespersen, J.; Fitz-Randolph, J.; Robb, J. (1999). De los relojes de sol a los relojes atómicos: comprensión del tiempo y la frecuencia (reimpresión de la Oficina Nacional de Normas 1977, 2.ª ed.). Courier Dover . p. 280. ISBN 978-0-486-40913-9.
- Sydenham, PH (2003). "Medición de longitud". En Boyes, W (ed.). Instrumentation Reference Book (3.ª ed.). Butterworth–Heinemann . p. 56. ISBN 978-0-7506-7123-1... si la velocidad de la luz se define como un número fijo, entonces, en principio, el estándar
- ^ Mermin, N. David (2005). Ya era hora: entender la relatividad de Einstein. Princeton: Princeton University Press. pág. 22. ISBN 0-691-12201-6.OCLC 57283944 .
- ^ "Nanosegundos asociados con Grace Hopper". Museo Nacional de Historia Estadounidense . Consultado el 1 de marzo de 2022.
Grace Murray Hopper
(1906-1992), matemática que se convirtió en oficial naval y científica informática durante la Segunda Guerra Mundial, comenzó a distribuir estos "nanosegundos" de cable a fines de la década de 1960 para demostrar cómo el diseño de componentes más pequeños produciría computadoras más rápidas.
- ^ Lawrie, ID (2002). "Apéndice C: Unidades naturales". Un gran recorrido unificado por la física teórica (2.ª ed.). CRC Press. pág. 540. ISBN 978-0-7503-0604-1.
- ^ Hsu, L. (2006). "Apéndice A: Sistemas de unidades y el desarrollo de las teorías de la relatividad". Una visión más amplia de la relatividad: implicaciones generales de la invariancia de Lorentz y Poincaré (2.ª ed.). World Scientific . págs. 427–428. ISBN 978-981-256-651-5.
- ^ Einstein, A. (1905). "Zur Elektrodynamik bewegter Körper". Annalen der Physik (manuscrito enviado) (en alemán). 17 (10): 890–921. Código bibliográfico : 1905AnP...322..891E. doi : 10.1002/andp.19053221004 .Traducción al español: Perrett, W. Walker, J (ed.). "Sobre la electrodinámica de los cuerpos en movimiento". Fourmilab . Traducido por Jeffery, G. B. . Consultado el 27 de noviembre de 2009 .
- ^ ab Hsu, J.-P.; Zhang, YZ (2001). Invariancia de Lorentz y Poincaré. Serie avanzada sobre ciencia física teórica. Vol. 8. World Scientific . pp. 543ff. ISBN 978-981-02-4721-8.
- ^ abc Zhang, YZ (1997). Relatividad especial y sus fundamentos experimentales. Serie avanzada sobre ciencia física teórica. Vol. 4. World Scientific . págs. 172–173. ISBN 978-981-02-2749-4. Consultado el 23 de julio de 2009 .
- ^ d'Inverno, R. (1992). Introducción a la relatividad de Einstein. Oxford University Press. pp. 19-20. ISBN 978-0-19-859686-8.
- ^ Sriranjan, B. (2004). "Postulados de la teoría especial de la relatividad y sus consecuencias". La teoría especial de la relatividad . PHI Learning Pvt. Ltd., pp. 20 y siguientes. ISBN 978-81-203-1963-9.
- ^ ab Ellis, George FR ; Williams, Ruth M. (2000). Espacio-tiempos planos y curvos (2.ª ed.). Oxford: Oxford University Press. pág. 12. ISBN 0-19-850657-0.OCLC 44694623 .
- ^ Antonioli, Pietro; Fienberg, Richard Tresch; Fleurot, Fabrice; Fukuda, Yoshiyuki; Fulgione, Walter; Habig, Alec; Heise, Jaret; McDonald, Arthur B.; Mills, Corrinne; Namba, Toshio; Robinson, Leif J. (2 de septiembre de 2004). "SNEWS: el sistema de alerta temprana de supernovas". New Journal of Physics . 6 : 114. arXiv : astro-ph/0406214 . Código Bibliográfico :2004NJPh....6..114A. doi :10.1088/1367-2630/6/1/114. ISSN 1367-2630. S2CID 119431247.
- ^ Roberts, T.; Schleif, S. (2007). Dlugosz, JM (ed.). "¿Cuál es la base experimental de la relatividad especial?". Usenet Physics FAQ . Universidad de California, Riverside . Archivado desde el original el 15 de octubre de 2009. Consultado el 27 de noviembre de 2009 .
- ^ Terrell, J. (1959). "Invisibilidad de la contracción de Lorentz". Physical Review . 116 (4): 1041–1045. Código Bibliográfico :1959PhRv..116.1041T. doi :10.1103/PhysRev.116.1041.
- ^ Penrose, R. (1959). "La forma aparente de una esfera que se mueve relativistamente". Actas de la Sociedad Filosófica de Cambridge . 55 (1): 137–139. Bibcode :1959PCPS...55..137P. doi :10.1017/S0305004100033776. S2CID 123023118.
- ^ Hartle, JB (2003). Gravedad: una introducción a la relatividad general de Einstein. Addison-Wesley . págs. 52-59. ISBN. 978-981-02-2749-4.
- ^ Hartle, JB (2003). Gravedad: una introducción a la relatividad general de Einstein . Addison-Wesley . pág. 332. ISBN. 978-981-02-2749-4.
- ^ Véase, por ejemplo:
- Abbott, BP; et al. (2017). "Ondas gravitacionales y rayos gamma de una fusión de estrellas de neutrones binarias: GW170817 y GRB 170817A". The Astrophysical Journal Letters . 848 (2): L13. arXiv : 1710.05834 . Código Bibliográfico :2017ApJ...848L..13A. doi : 10.3847/2041-8213/aa920c .
- Cornish, Neil; Blas, Diego; Nardini, Germano (18 de octubre de 2017). "Limitar la velocidad de la gravedad con observaciones de ondas gravitacionales". Physical Review Letters . 119 (16): 161102. arXiv : 1707.06101 . Bibcode :2017PhRvL.119p1102C. doi :10.1103/PhysRevLett.119.161102. PMID 29099221. S2CID 206300556.
- Liu, Xiaoshu; He, Vincent F.; Mikulski, Timothy M.; Palenova, Daria; Williams, Claire E.; Creighton, Jolien; Tasson, Jay D. (7 de julio de 2020). "Medición de la velocidad de las ondas gravitacionales de la primera y segunda serie de observaciones de Advanced LIGO y Advanced Virgo". Physical Review D . 102 (2): 024028. arXiv : 2005.03121 . Código Bibliográfico :2020PhRvD.102b4028L. doi :10.1103/PhysRevD.102.024028. S2CID 220514677.
- ^ ab Gibbs, P. (1997) [1996]. Carlip, S. (ed.). "¿Es constante la velocidad de la luz?". Usenet Physics FAQ . Universidad de California, Riverside . Archivado desde el original el 2 de abril de 2010. Consultado el 26 de noviembre de 2009 .
- ^ Ellis, TFG; Uzan, J.-P. (2005). "'c' es la velocidad de la luz, ¿no?". American Journal of Physics . 73 (3): 240–227. arXiv : gr-qc/0305099 . Bibcode :2005AmJPh..73..240E. doi :10.1119/1.1819929. S2CID 119530637.
La posibilidad de que las constantes fundamentales puedan variar durante la evolución del universo ofrece una ventana excepcional hacia teorías de dimensiones superiores y probablemente esté vinculada con la naturaleza de la energía oscura que hace que el universo se acelere hoy.
- ^ Mota, DF (2006). Variaciones de la constante de estructura fina en el espacio y el tiempo (PhD). arXiv : astro-ph/0401631 . Código Bibliográfico :2004astro.ph..1631M.
- ^ Uzan, J.-P. (2003). "Las constantes fundamentales y su variación: estado observacional y motivaciones teóricas". Reseñas de Física Moderna . 75 (2): 403. arXiv : hep-ph/0205340 . Código Bibliográfico :2003RvMP...75..403U. doi :10.1103/RevModPhys.75.403. S2CID 118684485.
- ^ Amelino-Camelia, G. (2013). "Fenomenología de la gravedad cuántica". Living Reviews in Relativity . 16 (1): 5. arXiv : 0806.0339 . Bibcode :2013LRR....16....5A. doi : 10.12942/lrr-2013-5 . PMC 5255913 . PMID 28179844.
- ^ Herrmann, S.; Senger, A.; Möhle, K.; Nagel, M.; Kovalchuk, EV; Peters, A. (2009). "Experimento de cavidad óptica rotatoria que prueba la invariancia de Lorentz en el nivel 10 −17 ". Physical Review D . 80 (100): 105011. arXiv : 1002.1284 . Código Bibliográfico :2009PhRvD..80j5011H. doi :10.1103/PhysRevD.80.105011. S2CID 118346408.
- ^ Lang, KR (1999). Fórmulas astrofísicas (3.ª ed.). Birkhäuser. pág. 152. ISBN 978-3-540-29692-8.
- ^ Véase, por ejemplo:
- "Es oficial: las máquinas del tiempo no funcionan". Los Angeles Times . 25 de julio de 2011.
- "Profesores de la HKUST demuestran que los fotones individuales no superan la velocidad de la luz". Universidad de Ciencia y Tecnología de Hong Kong . 19 de julio de 2011.
- Shanchao Zhang; JF Chen; Chang Liu; MMT Loy; GKL Wong; Shengwang Du (16 de junio de 2011). "Precursor óptico de un fotón único" (PDF) . Physical Review Letters . 106 (243602): 243602. Bibcode :2011PhRvL.106x3602Z. doi :10.1103/physrevlett.106.243602. PMID 21770570.
- ^ Fowler, M. (marzo de 2008). "Notes on Special Relativity" (PDF) . Universidad de Virginia. pág. 56. Consultado el 7 de mayo de 2010 .
- ^ Véase, por ejemplo:
- Ben-Menahem, Shahar (noviembre de 1990). "Causalidad entre placas conductoras". Physics Letters B . 250 (1–2): 133–138. Bibcode :1990PhLB..250..133B. doi :10.1016/0370-2693(90)91167-A. OSTI 1449261.
- Fearn, H. (10 de noviembre de 2006). "Relaciones de dispersión y causalidad: ¿requiere la causalidad relativista que n (ω) → 1 cuando ω → ∞?". Journal of Modern Optics . 53 (16–17): 2569–2581. Bibcode :2006JMOp...53.2569F. doi :10.1080/09500340600952085. ISSN 0950-0340. S2CID 119892992.
- Fearn, H. (mayo de 2007). "¿Pueden las señales de luz viajar más rápido que c en vacíos no triviales en un espacio-tiempo plano? Causalidad relativista II". Física láser . 17 (5): 695–699. arXiv : 0706.0553 . Código Bibliográfico :2007LaPhy..17..695F. doi :10.1134/S1054660X07050155. ISSN 1054-660X. S2CID 61962.
- ^ Liberati, S.; Sonego, S.; Visser, M. (2002). "Señales más rápidas que c , relatividad especial y causalidad". Anales de Física . 298 (1): 167–185. arXiv : gr-qc/0107091 . Código Bibliográfico :2002AnPhy.298..167L. doi :10.1006/aphy.2002.6233. S2CID 48166.
- ^ Taylor, EF ; Wheeler, JA (1992). Física del espacio-tiempo. WH Freeman. págs. 74-75. ISBN 978-0-7167-2327-1.
- ^ Tolman, RC (2009) [1917]. "Velocidades mayores que la de la luz". La teoría de la relatividad del movimiento (edición reimpresa). BiblioLife . p. 54. ISBN 978-1-103-17233-7.
- ^ Hecht, E. (1987). Óptica (2.ª ed.). Addison-Wesley. pág. 62. ISBN 978-0-201-11609-0.
- ^ Quimby, RS (2006). Fotónica y láseres: una introducción. John Wiley and Sons. pág. 9. ISBN 978-0-471-71974-8.
- ^ Wertheim, M. (20 de junio de 2007). "The Shadow Goes". The New York Times . Consultado el 21 de agosto de 2009 .
- ^ abc Gibbs, P. (1997). "¿Es posible viajar o comunicarse más rápido que la luz?". Usenet Physics FAQ . Universidad de California, Riverside . Archivado desde el original el 10 de marzo de 2010. Consultado el 20 de agosto de 2008 .
- ^ Véase, por ejemplo:
- Sakurai, JJ (1994). Tuan, SF (ed.). Mecánica cuántica moderna (edición revisada). Addison-Wesley. págs. 231–232. ISBN 978-0-201-53929-5.
- Peres, Asher (1993). Teoría cuántica: conceptos y métodos . Kluwer . Pág. 170. ISBN. 0-7923-2549-4.OCLC 28854083 .
- Caves, Carlton M. (2015). "La ciencia de la información cuántica: ya no está en auge". OSA Century of Optics . Optica . págs. 320–326. arXiv : 1302.1864 . ISBN 978-1-943-58004-0
Era natural soñar que las correlaciones cuánticas podrían usarse para comunicaciones más rápidas que la luz, pero esta especulación fue rápidamente derribada y el derribo estableció el principio de que los estados cuánticos no pueden copiarse
.
- ^ Muga, JG; Mayato, RS; Egusquiza, IL, eds. (2007). El tiempo en la mecánica cuántica. Saltador. pag. 48.ISBN 978-3-540-73472-7.
- ^ Hernández-Figueroa, HE; Zamboni-Rached, M.; Recami, E. (2007). Ondas Localizadas. Wiley Interciencia . pag. 26.ISBN 978-0-470-10885-7.
- ^ Wynne, K. (2002). "Causalidad y naturaleza de la información" (PDF) . Optics Communications . 209 (1–3): 84–100. Bibcode :2002OptCo.209...85W. doi :10.1016/S0030-4018(02)01638-3. Archivado desde el original (PDF) el 25 de marzo de 2009.
- ^ Rees, M. (1966). "La aparición de fuentes de radio con expansión relativista". Nature . 211 (5048): 468. Bibcode :1966Natur.211..468R. doi :10.1038/211468a0. S2CID 41065207.
- ^ Chase, IP "Velocidad superlumínica aparente de las galaxias". Usenet Physics FAQ . Universidad de California, Riverside . Consultado el 26 de noviembre de 2009 .
- ^ Reich, Eugenie Samuel (2 de abril de 2012). «Los líderes del proyecto de neutrinos en conflicto renuncian». Nature News . doi :10.1038/nature.2012.10371. S2CID 211730430 . Consultado el 11 de febrero de 2022 .
- ^ OPERA Collaboration (12 de julio de 2012). "Medición de la velocidad de los neutrinos con el detector OPERA en el haz CNGS". Journal of High Energy Physics . 2012 (10): 93. arXiv : 1109.4897 . Bibcode :2012JHEP...10..093A. doi :10.1007/JHEP10(2012)093. S2CID 17652398.
- ^ Harrison, ER (2003). Máscaras del universo. Cambridge University Press. pág. 206. ISBN 978-0-521-77351-5.
- ^ Panofsky, WKH; Phillips, M. (1962). Electricidad clásica y magnetismo . Addison-Wesley. pág. 182. ISBN. 978-0-201-05702-7.
- ^ Véase, por ejemplo:
- Schaefer, BE (1999). "Límites severos en las variaciones de la velocidad de la luz con la frecuencia". Physical Review Letters . 82 (25): 4964–4966. arXiv : astro-ph/9810479 . Código Bibliográfico :1999PhRvL..82.4964S. doi :10.1103/PhysRevLett.82.4964. S2CID 119339066.
- Ellis, J.; Mavromatos, NE ; Nanopoulos, DV; Sakharov, AS (2003). "Análisis de gravedad cuántica de estallidos de rayos gamma utilizando wavelets". Astronomía y astrofísica . 402 (2): 409–424. arXiv : astro-ph/0210124 . Bibcode :2003A&A...402..409E. doi :10.1051/0004-6361:20030263. S2CID 15388873.
- Füllekrug, M. (2004). "Estudio de la velocidad de la luz con ondas de radio a frecuencias extremadamente bajas". Physical Review Letters . 93 (4): 043901. Bibcode :2004PhRvL..93d3901F. doi :10.1103/PhysRevLett.93.043901. PMID 15323762.
- Bartlett, DJ; Desmond, H.; Ferreira, PG; Jasche, J. (17 de noviembre de 2021). "Restricciones en la gravedad cuántica y la masa de fotones de los estallidos de rayos gamma". Physical Review D . 104 (10): 103516. arXiv : 2109.07850 . Bibcode :2021PhRvD.104j3516B. doi :10.1103/PhysRevD.104.103516. ISSN 2470-0010. S2CID 237532210.
- ^ ab Adelberger, E.; Dvali, G.; Gruzinov, A. (2007). "Masa de fotón limitada destruida por vórtices". Physical Review Letters . 98 (1): 010402. arXiv : hep-ph/0306245 . Código Bibliográfico :2007PhRvL..98a0402A. doi :10.1103/PhysRevLett.98.010402. PMID 17358459. S2CID 31249827.
- ^ Sidharth, BG (2008). El universo termodinámico. World Scientific . pág. 134. ISBN 978-981-281-234-6.
- ^ Amelino-Camelia, G. (2009). "Astrofísica: Explosión de apoyo a la relatividad". Nature . 462 (7271): 291–292. Bibcode :2009Natur.462..291A. doi : 10.1038/462291a . PMID 19924200. S2CID 205051022.
- ^ abc Milonni, Peter W. (2004). Luz rápida, luz lenta y luz para zurdos. CRC Press. pp. 25 y siguientes . ISBN 978-0-7503-0926-4.
- ^ de Podesta, M. (2002). Entendiendo las propiedades de la materia. CRC Press. p. 131. ISBN 978-0-415-25788-6.
- ^ "Constantes ópticas de H2O, D2O (Agua, agua pesada, hielo)". refractiveindex.info . Mikhail Polyanskiy . Consultado el 7 de noviembre de 2017 .
- ^ "Constantes ópticas del vidrio sódico-cálcico". refractiveindex.info . Mikhail Polyanskiy . Consultado el 7 de noviembre de 2017 .
- ^ "Constantes ópticas de C (Carbono, diamante, grafito)". refractiveindex.info . Mikhail Polyanskiy . Consultado el 7 de noviembre de 2017 .
- ^ Cromie, William J. (24 de enero de 2001). «Los investigadores ahora pueden detener y reiniciar la luz». Harvard University Gazette . Archivado desde el original el 28 de octubre de 2011. Consultado el 8 de noviembre de 2011 .
- ^ Milonni, PW (2004). Luz rápida, luz lenta y luz para zurdos. CRC Press. p. 25. ISBN 978-0-7503-0926-4.
- ^ Toll, JS (1956). "Causalidad y la relación de dispersión: fundamentos lógicos". Physical Review . 104 (6): 1760–1770. Código Bibliográfico :1956PhRv..104.1760T. doi :10.1103/PhysRev.104.1760.
- ^ Wolf, Emil (2001). "Analiticidad, causalidad y relaciones de dispersión". Obras seleccionadas de Emil Wolf: con comentarios. River Edge, NJ: World Scientific. págs. 577–584. ISBN 978-981-281-187-5.OCLC 261134839 .
- ^ Libbrecht, KG; Libbrecht, MW (diciembre de 2006). "Medición interferométrica de la absorción resonante y el índice de refracción en gas rubidio" (PDF) . American Journal of Physics . 74 (12): 1055–1060. Bibcode :2006AmJPh..74.1055L. doi :10.1119/1.2335476. ISSN 0002-9505.
- ^ Véase, por ejemplo:
- Hau, LV ; Harris, SE ; Dutton, Z. ; Behroozi, CH (1999). "Reducción de la velocidad de la luz a 17 metros por segundo en un gas atómico ultrafrío" (PDF) . Nature . 397 (6720): 594–598. Bibcode :1999Natur.397..594V. doi :10.1038/17561. S2CID 4423307.
- Liu, C.; Dutton, Z .; Behroozi, CH; Hau, LV (2001). "Observación del almacenamiento de información óptica coherente en un medio atómico utilizando pulsos de luz detenidos" (PDF) . Nature . 409 (6819): 490–493. Bibcode :2001Natur.409..490L. doi :10.1038/35054017. PMID 11206540. S2CID 1894748.
- Bajcsy, M.; Zibrov, AS; Lukin, MD (2003). "Pulsos estacionarios de luz en un medio atómico". Nature . 426 (6967): 638–641. arXiv : quant-ph/0311092 . Bibcode :2003Natur.426..638B. doi :10.1038/nature02176. PMID 14668857. S2CID 4320280.
- Dumé, B. (2003). «Encender y apagar la luz». Physics World . Instituto de Física. Archivado desde el original el 5 de diciembre de 2008 . Consultado el 8 de diciembre de 2008 .
- ^ Véase, por ejemplo:
- Chiao, RY (1993). "Propagación superlumínica (pero causal) de paquetes de ondas en medios transparentes con poblaciones atómicas invertidas". Physical Review A . 48 (1): R34–R37. Bibcode :1993PhRvA..48...34C. doi :10.1103/PhysRevA.48.R34. PMID 9909684.
- Wang, LJ; Kuzmich, A.; Dogariu, A. (2000). "Propagación de luz superlumínica asistida por ganancia". Nature . 406 (6793): 277–279. doi :10.1038/35018520. PMID 10917523. S2CID 4358601.
- Whitehouse, D. (19 de julio de 2000). "Beam Smashes Light Barrier". BBC News . Consultado el 9 de febrero de 2022 .
- Gbur, Greg (26 de febrero de 2008). "La luz rompe su propio límite de velocidad: cómo funcionan las artimañas 'superlumínicas'" . Consultado el 9 de febrero de 2022 .
- ^ Cherenkov, Pavel A. (1934). "Видимое свечение чистых жидкостей под действием γ-радиации" [Emisión visible de líquidos puros por acción de la radiación γ]. Doklady Akademii Nauk SSSR . 2 : 451.Reimpreso: Cherenkov, PA (1967). "Видимое свечение чистых жидкостей под действием γ-радиации" [Emisión visible de líquidos puros por acción de la radiación γ]. Usp. Fiz. Nauk . 93 (10): 385. doi :10.3367/ufnr.0093.196710n.0385., y en AN Gorbunov; EP Čerenkova, eds. (1999). Pavel Alekseyevich Čerenkov: Chelovek i Otkrytie [ Pavel Alekseyevich Čerenkov: el hombre y el descubrimiento ]. Moscú: Nauka. págs. 149-153.
- ^ Parhami, B. (1999). Introducción al procesamiento paralelo: algoritmos y arquitecturas. Plenum Press . p. 5. ISBN 978-0-306-45970-2.
- ^ Imbs, D.; Raynal, Michel (2009). Malyshkin, V. (ed.). Memorias transaccionales de software: un enfoque para la programación multinúcleo. 10.ª Conferencia internacional, PaCT 2009, Novosibirsk, Rusia, 31 de agosto – 4 de septiembre de 2009. Springer. pág. 26. ISBN 978-3-642-03274-5.
- ^ Midwinter, JE (1991). Fibras ópticas para transmisión (2.ª edición). Krieger Publishing Company. ISBN 978-0-89464-595-2.
- ^ "Límite de velocidad teórico vs. real de Ping". Pingdom . Junio de 2007. Archivado desde el original el 2 de septiembre de 2010. Consultado el 5 de mayo de 2010 .
- ^ Buchanan, Mark (11 de febrero de 2015). «Física en finanzas: Comercio a la velocidad de la luz». Nature . 518 (7538): 161–163. Bibcode :2015Natur.518..161B. doi : 10.1038/518161a . PMID 25673397.
- ^ "El tiempo es dinero cuando se trata de microondas" . Financial Times . 10 de mayo de 2013. Archivado desde el original el 10 de diciembre de 2022 . Consultado el 25 de abril de 2014 .
- ^ "Día 4: Órbitas lunares 7, 8 y 9". Diario de vuelo del Apolo 8. NASA. Archivado desde el original el 4 de enero de 2011. Consultado el 16 de diciembre de 2010 .
- ^ Ormston, Thomas (8 de mayo de 2012). «Retraso temporal entre Marte y la Tierra – Mars Express». MARS EXPRESS, misión de la ESA al Planeta Rojo . Consultado el 16 de julio de 2024 .
- ^ Parisi, Megan; Panontin, Tina; Wu, Shu-Chieh; Mctigue, Kaitlin; Vera, Alonso (2023). "Efectos del retraso de la comunicación en las misiones de vuelos espaciales tripulados". Sistemas aeroespaciales centrados en el ser humano y aplicaciones de sostenibilidad . 98 . AHFE Open Acces. doi :10.54941/ahfe1003920. ISBN 978-1-958651-74-2.
- ^ ab "El Hubble llega al "país desconocido" de las galaxias primigenias" (Nota de prensa). Instituto Científico del Telescopio Espacial . 5 de enero de 2010.
- ^ "Litografía de campo ultraprofundo del Hubble" (PDF) . NASA . Consultado el 4 de febrero de 2010 .
- ^ Mack, Katie (2021). El fin de todo (Astrofísicamente hablando). Londres: Penguin Books. pp. 18-19. ISBN 978-0-141-98958-7.OCLC 1180972461 .
- ^ "La UAI y las unidades astronómicas". Unión Astronómica Internacional . Consultado el 11 de octubre de 2010 .
- ^ Se puede encontrar más información en "StarChild Question of the Month for March 2000". StarChild . NASA. 2000 . Consultado el 22 de agosto de 2009 .
- ^ Dickey, JO; et al. (julio de 1994). "Medición de distancias por láser lunar: un legado continuo del programa Apolo" (PDF) . Science . 265 (5171): 482–490. Bibcode :1994Sci...265..482D. doi :10.1126/science.265.5171.482. PMID 17781305. S2CID 10157934.
- ^ Standish, EM (febrero de 1982). "Las efemérides planetarias del JPL". Mecánica celestial . 26 (2): 181–186. Código Bibliográfico :1982CeMec..26..181S. doi :10.1007/BF01230883. S2CID 121966516.
- ^ Berner, JB; Bryant, SH; Kinman, PW (noviembre de 2007). "Medición de rangos tal como se practica en la red del espacio profundo" (PDF) . Actas del IEEE . 95 (11): 2202–2214. doi :10.1109/JPROC.2007.905128. S2CID 12149700.
- ^ abc «Resolución 1 de la 17ª CGPM». BIPM. 1983. Consultado el 23 de agosto de 2009 .
- ^ abc Cohen, IB (1940). "Roemer y la primera determinación de la velocidad de la luz (1676)". Isis . 31 (2): 327–379. doi :10.1086/347594. hdl : 2027/uc1.b4375710 . S2CID 145428377.
- ^ abc "Demostración sobre el movimiento de la luz trouvé par M. Rŏmer de l'Académie Royale des Sciences" [Demostración sobre el movimiento de la luz encontrado por el Sr. Römer de la Real Academia de Ciencias] (PDF) . Journal des sçavans (en francés): 233–236. 1676.
Traducido en "Una demostración sobre el movimiento de la luz, comunicada desde París, en el Journal des Sçavans, y aquí traducida al inglés". Philosophical Transactions of the Royal Society . 12 (136): 893–895. 1677. Bibcode :1677RSPT...12..893.. doi : 10.1098/rstl.1677.0024 .
Reproducido en Hutton, C.; Shaw, G.; Pearson, R., eds. (1809). "Sobre el movimiento de la luz por M. Romer". Las Transacciones Filosóficas de la Royal Society de Londres, desde su inicio en 1665, en el año 1800: Abreviado . Vol. II. De 1673 a 1682. Londres: C. & R. Baldwin. págs. 397–398.
El relato publicado en el Journal des sçavans se basó en un informe que Rømer leyó en la Academia Francesa de Ciencias en noviembre de 1676 (Cohen, 1940, p. 346). - ^ abcd Bradley, J. (1729). "Explicación de un nuevo descubrimiento del movimiento de las estrellas fijas". Philosophical Transactions . 35 : 637–660.
- ^ Duffett-Smith, P. (1988). Astronomía práctica con calculadora . Cambridge University Press. pág. 62. ISBN 978-0-521-35699-2.Extracto de la página 62.
- ^ ab "Resolución B2 sobre la redefinición de la unidad astronómica de longitud" (PDF) . Unión Astronómica Internacional. 2012.
- ^ "Suplemento 2014: Actualizaciones de la 8.ª edición (2006) del folleto SI" (PDF) . El Sistema Internacional de Unidades . Oficina Internacional de Pesas y Medidas: 14. 2014.
- ^ Oficina Internacional de Pesas y Medidas (2006), El Sistema Internacional de Unidades (SI) (PDF) (8.ª ed.), pág. 126, ISBN 92-822-2213-6, archivado (PDF) del original el 4 de junio de 2021 , consultado el 16 de diciembre de 2021
- ^ Brumfiel, Geoff (14 de septiembre de 2012). "La unidad astronómica se fija". Nature . doi :10.1038/nature.2012.11416. ISSN 1476-4687. S2CID 123424704.
- ^ Ver lo siguiente:
- Pitjeva, EV; Standish, EM (2009). "Propuestas para las masas de los tres asteroides más grandes, la relación de masas Luna-Tierra y la unidad astronómica". Mecánica celeste y astronomía dinámica . 103 (4): 365–372. Código Bibliográfico :2009CeMDA.103..365P. doi :10.1007/s10569-009-9203-8. S2CID 121374703.
- «Constantes astrodinámicas». Dinámica del sistema solar . Laboratorio de propulsión a chorro . Consultado el 10 de febrero de 2022 .
- ^ ab Grupo de trabajo de la IAU sobre estándares numéricos para la astronomía fundamental. «IAU WG on NSFA Current Best Estimates». Observatorio Naval de los Estados Unidos . Archivado desde el original el 8 de diciembre de 2009. Consultado el 25 de septiembre de 2009 .
- ^ "Guía de longitud para principiantes del NPL". Laboratorio Nacional de Física del Reino Unido . Archivado desde el original el 31 de agosto de 2010. Consultado el 28 de octubre de 2009 .
- ^ abcde Gibbs, P. (1997). «¿Cómo se mide la velocidad de la luz?». Usenet Physics FAQ . Universidad de California, Riverside. Archivado desde el original el 21 de agosto de 2015. Consultado el 13 de enero de 2010 .
- ^ Fowler, M. "La velocidad de la luz". Universidad de Virginia . Consultado el 21 de abril de 2010 .
- ^ Hughes, Stephan (2012). Catchers of the Light: Las vidas olvidadas de los hombres y mujeres que fotografiaron por primera vez los cielos. ArtDeCiel Publishing. pág. 210. ISBN 978-1-62050-961-6.
- ^ Véase, por ejemplo:
- Cooke, J.; Martin, M.; McCartney, H.; Wilf, B. (1968). "Determinación directa de la velocidad de la luz como experimento de laboratorio de física general". American Journal of Physics . 36 (9): 847. Bibcode :1968AmJPh..36..847C. doi :10.1119/1.1975166.
- Aoki, K.; Mitsui, T. (2008). "Un pequeño experimento de sobremesa para la medición directa de la velocidad de la luz". American Journal of Physics . 76 (9): 812–815. arXiv : 0705.3996 . Bibcode :2008AmJPh..76..812A. doi :10.1119/1.2919743. S2CID 117454437.
- James, MB; Ormond, RB; Stasch, AJ (1999). "Medición de la velocidad de la luz para la miríada". American Journal of Physics . 67 (8): 681–714. Bibcode :1999AmJPh..67..681J. doi :10.1119/1.19352.
- ^ abcde Essen, L.; Gordon-Smith, AC (1948). "La velocidad de propagación de las ondas electromagnéticas derivada de las frecuencias resonantes de un resonador de cavidad cilíndrica". Actas de la Royal Society of London A . 194 (1038): 348–361. Bibcode :1948RSPSA.194..348E. doi : 10.1098/rspa.1948.0085 . JSTOR 98293.
- ^ ab Rosa, EB ; Dorsey, NE (1907). "Una nueva determinación de la relación entre la unidad electromagnética y la unidad electrostática de electricidad". Boletín de la Oficina de Normas . 3 (6): 433. doi : 10.6028/bulletin.070 .
- ^ Essen, L. (1947). "Velocidad de las ondas electromagnéticas". Nature . 159 (4044): 611–612. Código Bibliográfico :1947Natur.159..611E. doi :10.1038/159611a0. S2CID 4101717.
- ^ abc Essen, L. (1950). "La velocidad de propagación de las ondas electromagnéticas derivada de las frecuencias resonantes de un resonador de cavidad cilíndrica". Actas de la Royal Society of London A . 204 (1077): 260–277. Bibcode :1950RSPSA.204..260E. doi :10.1098/rspa.1950.0172. JSTOR 98433. S2CID 121261770.
- ^ Stauffer, RH (abril de 1997). "Encontrar la velocidad de la luz con malvaviscos". The Physics Teacher . 35 (4): 231. Bibcode :1997PhTea..35..231S. doi :10.1119/1.2344657 . Consultado el 15 de febrero de 2010 .
- ^ "BBC Look East at the speed of light" (BBC mira al este a la velocidad de la luz). Sitio web de la BBC Norfolk . Consultado el 15 de febrero de 2010 .
- ^ Vaughan, JM (1989). El interferómetro Fabry-Perot. CRC Press. pp. 47, 384–391. ISBN 978-0-85274-138-2.
- ^ ab Froome, KD (1958). "Una nueva determinación de la velocidad en el espacio libre de las ondas electromagnéticas". Actas de la Royal Society de Londres. Serie A, Ciencias matemáticas y físicas . 247 (1248): 109–122. Bibcode :1958RSPSA.247..109F. doi :10.1098/rspa.1958.0172. JSTOR 100591. S2CID 121444888.
- ^ abc Sullivan, DB (2001). "Velocidad de la luz a partir de mediciones directas de frecuencia y longitud de onda". En Lide, DR (ed.). Un siglo de excelencia en mediciones, estándares y tecnología (PDF) . CRC Press. págs. 191–193. ISBN 978-0-8493-1247-2. Archivado desde el original (PDF) el 13 de agosto de 2009.
- ^ abc Evenson, KM; et al. (1972). "Velocidad de la luz a partir de mediciones directas de frecuencia y longitud de onda del láser estabilizado con metano". Physical Review Letters . 29 (19): 1346–1349. Código Bibliográfico :1972PhRvL..29.1346E. doi :10.1103/PhysRevLett.29.1346. S2CID 120300510.
- ^ ab Galilei, G. (1954) [1638]. Diálogos sobre dos nuevas ciencias. Crew, H.; de Salvio A. (trad.). Dover Publications . p. 43. ISBN 978-0-486-60099-4Archivado desde el original el 30 de enero de 2019 . Consultado el 29 de enero de 2019 .
- ^ abc Boyer, CB (1941). "Estimaciones tempranas de la velocidad de la luz". Isis . 33 (1): 24. doi :10.1086/358523. S2CID 145400212.
- ^ ab Foschi, Renato; Leone, Matteo (2009), "Galileo, medición de la velocidad de la luz y los tiempos de reacción", Perception , 38 (8): 1251–1259, doi :10.1068/p6263, hdl : 2318/132957 , PMID 19817156, S2CID 11747908
- ^ Magalotti, Lorenzo (2001) [1667], Saggi di Naturali Esperienze fatte nell' Accademia del Cimento (digital, edición en línea), Florencia: Istituto e Museo di Storia delle Scienze, págs. 265–266 , consultado el 25 de septiembre de 2015
- ^ ab Huygens, C. (1690). Traitée de la Lumière (en francés). Pierre van der Aa. págs. 8–9.
- ^ Buchwald, Jed; Yeang, Chen-Pang; Stemeroff, Noah; Barton, Jenifer; Harrington, Quinn (1 de marzo de 2021). «Lo que Heinrich Hertz descubrió sobre las ondas eléctricas en 1887-1888». Archivo de Historia de las Ciencias Exactas . 75 (2): 125–171. doi :10.1007/s00407-020-00260-1. ISSN 1432-0657. S2CID 253895826.
- ^ Hertz, Heinrich (1893). Ondas eléctricas . Londres: Macmillan and Co.
- ^ Michelson, AA (1927). "Medición de la velocidad de la luz entre el monte Wilson y el monte San Antonio". The Astrophysical Journal . 65 : 1. Bibcode :1927ApJ....65....1M. doi :10.1086/143021.
- ^ Weiner, John; Nunes, Frederico (2013). Interacción luz-materia: física e ingeniería a nanoescala (edición ilustrada). OUP Oxford. p. 1. ISBN 978-0-19-856766-0.Extracto de la página 1.
- ^ Sarton, G. (1993). La ciencia antigua a través de la edad de oro de Grecia. Courier Dover . p. 248. ISBN 978-0-486-27495-9.
- ^ abc MacKay, RH; Oldford, RW (2000). "Método científico, método estadístico y la velocidad de la luz". Ciencia estadística . 15 (3): 254–278. doi : 10.1214/ss/1009212817 .(haga clic en “Antecedentes históricos” en el índice)
- ^ Ahmed, Sherif Sayed (2014). Imágenes electrónicas por microondas con matrices multiestáticas planas. Logos Verlag Berlin. p. 1. ISBN 978-3-8325-3621-3.Extracto de la página 1
- ^ Gross, CG (1999). "El fuego que sale del ojo". Neurocientífico . 5 : 58–64. doi :10.1177/107385849900500108. S2CID 84148912.
- ^ Hamarneh, S. (1972). "Reseña: Hakim Mohammed Said, Ibn al-Haitham ". Isis . 63 (1): 119. doi :10.1086/350861.
- ^ ab Lester, PM (2005). Comunicación visual: imágenes con mensajes . Thomson Wadsworth . págs. 10-11. ISBN 978-0-534-63720-0.
- ^ O'Connor, JJ ; Robertson, EF "Abu Ali al-Hasan ibn al-Haytham". Archivo MacTutor de Historia de las Matemáticas . Universidad de San Andrés . Consultado el 12 de enero de 2010 .
- ^ Lauginie, P. (2004). Medición de la velocidad de la luz: ¿por qué? ¿Velocidad de qué? (PDF) . Quinta Conferencia Internacional de Historia de la Ciencia en Educación Científica. Keszthely, Hungría. pp. 75–84. Archivado desde el original (PDF) el 4 de julio de 2015. Consultado el 12 de agosto de 2017 .
- ^ O'Connor, JJ; Robertson, EF "Abu han Muhammad ibn Ahmad al-Biruni". Archivo MacTutor de Historia de las Matemáticas . Universidad de San Andrés . Consultado el 12 de enero de 2010 .
- ^ Lindberg, DC (1996). Roger Bacon y los orígenes de Perspectiva en la Edad Media: una edición crítica y traducción al inglés de Perspectiva de Bacon, con introducción y notas. Oxford University Press. p. 143. ISBN 978-0-19-823992-5.
- ^ Lindberg, DC (1974). "Síntesis en óptica a finales del siglo XIII". En Edward Grant (ed.). Un libro de consulta sobre ciencia medieval . Harvard University Press. pág. 396. ISBN 978-0-674-82360-0.
- ^ Marshall, P. (1981). "Nicole Oresme sobre la naturaleza, la reflexión y la velocidad de la luz". Isis . 72 (3): 357–374 [367–374]. doi :10.1086/352787. S2CID 144035661.
- ^ Sakellariadis, Spyros (1982). "La prueba experimental de Descartes de la velocidad infinita de la luz y la réplica de Huygens". Archivo de Historia de las Ciencias Exactas . 26 (1): 1–12. doi :10.1007/BF00348308. ISSN 0003-9519. JSTOR 41133639. S2CID 118187860.
- ^ Cajori, Florian (1922). Una historia de la física en sus ramas elementales: incluida la evolución de los laboratorios físicos. Macmillan. pág. 76.
- ^ Smith, A. Mark (1987). "La teoría de la luz y la refracción de Descartes: un discurso sobre el método". Transactions of the American Philosophical Society . 77 (3): i–92. doi :10.2307/1006537. ISSN 0065-9746. JSTOR 1006537.
- ^ Boyer, Carl Benjamin (1959). El arco iris: del mito a las matemáticas . Thomas Yoseloff. págs. 205-206. OCLC 763848561.
- ^ Foschi, Renato; Leone, Matteo (agosto de 2009). "Galileo, medición de la velocidad de la luz y los tiempos de reacción". Percepción . 38 (8): 1251–1259. doi :10.1068/p6263. hdl : 2318/132957 . ISSN 0301-0066. PMID 19817156. S2CID 11747908.
- ^ Newton, I. (1704). "Prop. XI". Óptica.El texto de la Prop. XI es idéntico entre la primera (1704) y la segunda (1719) edición.
- ^ Guarnieri, M. (2015). "Dos milenios de luz: el largo camino hacia las ondas de Maxwell". Revista de electrónica industrial IEEE . 9 (2): 54–56, 60. doi :10.1109/MIE.2015.2421754. S2CID 20759821.
- ^ Kirchhoff, G. (1857). "Über die Bewegung der Elektricität". Ana. Física. 178 (12): 529–244. Código bibliográfico : 1857AnP...178..529K. doi : 10.1002/andp.18571781203.
- ^ Véase, por ejemplo:
- Giordano, Nicholas J. (2009). Física universitaria: razonamiento y relaciones. Cengage Learning. pág. 787. ISBN 978-0-534-42471-8.Extracto de la página 787
- Bergmann, Peter Gabriel (1992). El enigma de la gravitación. Courier Dover Publications. pág. 17. ISBN 978-0-486-27378-5.Extracto de la página 17
- Bais, Sander (2005). Las ecuaciones: iconos del conocimiento . Harvard University Press. pág. 40. ISBN 978-0-674-01967-6.Extracto de la página 40
- ^ O'Connor, JJ; Robertson, EF (noviembre de 1997). "James Clerk Maxwell". Facultad de Matemáticas y Estadística, Universidad de St Andrews . Archivado desde el original el 28 de enero de 2011. Consultado el 13 de octubre de 2010 .
- ^ Campbell, Lewis; Garnett, William; Rautio, James C. "La vida de James Clerk Maxwell", pág. 544, ISBN 978-1-77375-139-9 .
- ^ Watson, EC (1 de septiembre de 1957). "Sobre las relaciones entre la luz y la electricidad". American Journal of Physics . 25 (6): 335–343. Bibcode :1957AmJPh..25..335W. doi :10.1119/1.1934460. ISSN 0002-9505.
- ^ Consoli, Maurizio; Pluchino, Alessandro (2018). Experimentos de Michelson-Morley: un enigma para la física y la historia de la ciencia. World Scientific. págs. 118-119. ISBN 978-9-813-27818-9. Recuperado el 4 de mayo de 2020 .
- ^ Michelson, AA; Morley, EW (1887). "Sobre el movimiento relativo de la Tierra y el éter luminífero". Revista estadounidense de ciencias . 34 (203): 333–345. doi :10.1366/0003702874447824. S2CID 98374065.
- ^ French, AP (1983). Relatividad especial . Van Nostrand Reinhold. págs. 51-57. ISBN 978-0-442-30782-0.
- ^ Darrigol, O. (2000). Electrodinámica desde Ampére hasta Einstein . Clarendon Press. ISBN 978-0-19-850594-5.
- ^ Galison, P. (2003). Los relojes de Einstein, los mapas de Poincaré: imperios del tiempo . WW Norton. ISBN 978-0-393-32604-8.
- ^ Miller, AI (1981). Teoría especial de la relatividad de Albert Einstein. Surgimiento (1905) e interpretación temprana (1905-1911) . Addison-Wesley. ISBN 978-0-201-04679-3.
- ^ Pais, A. (1982). Sutil es el Señor: La ciencia y la vida de Albert Einstein . Oxford University Press. ISBN 978-0-19-520438-4.
- ^ «Resolución 1 de la 15ª CGPM». BIPM . 1967. Archivado desde el original el 11 de abril de 2021 . Consultado el 14 de marzo de 2021 .
- ^ "Resolución 6 de la 15ª CGPM". BIPM . 1967 . Consultado el 13 de octubre de 2010 .
- ^ Barger, R.; Hall, J. (1973). "Longitud de onda de la línea de absorción de metano saturada por láser de 3,39 μm". Applied Physics Letters . 22 (4): 196. Bibcode :1973ApPhL..22..196B. doi :10.1063/1.1654608. S2CID 1841238.
- ^ "Resolución 2 de la 15ª CGPM". BIPM. 1975. Consultado el 9 de septiembre de 2009 .
- ^ Taylor, EF ; Wheeler, JA (1992). Física del espacio-tiempo: Introducción a la relatividad especial (2.ª ed.). Macmillan. pág. 59. ISBN 978-0-7167-2327-1.
- ^ Penzes, WB (2009). "Cronología de la definición del metro" (PDF) . NIST . Consultado el 11 de enero de 2010 .
- ^ Adams, S. (1997). Relatividad: Introducción a la física del espacio-tiempo. CRC Press. pág. 140. ISBN 978-0-7484-0621-0
Una consecuencia peculiar de este sistema de definiciones es que cualquier refinamiento futuro en nuestra capacidad para medir
c
no cambiará la velocidad de la luz (que es un número definido), ¡pero sí cambiará la longitud del metro!
- ^ Rindler, W. (2006). Relatividad: especial, general y cosmológica (2.ª ed.). Oxford University Press. pág. 41. ISBN 978-0-19-856731-8.
Téngase en cuenta que [...] las mejoras en la precisión experimental modificarán el medidor en relación con las longitudes de onda atómicas, ¡pero no el valor de la velocidad de la luz!
- ^ "La formulación de la "constante explícita"". BIPM . 2011. Archivado desde el original el 11 de agosto de 2014.
- ^ Véase, por ejemplo:
- Conover, Emily (2 de noviembre de 2016). «Las unidades de medida están experimentando una actualización fundamental». Science News . Consultado el 6 de febrero de 2022 .
- Knotts, Sandra; Mohr, Peter J.; Phillips, William D. (enero de 2017). "Introducción al nuevo SI". The Physics Teacher . 55 (1): 16–21. Bibcode :2017PhTea..55...16K. doi :10.1119/1.4972491. ISSN 0031-921X. S2CID 117581000.
- «Redefinición del SI». Instituto Nacional de Normas y Tecnología . 11 de mayo de 2018. Consultado el 6 de febrero de 2022 .
Lectura adicional
Referencias históricas
- Romer, O. (1676). "Démonstration touchant le mouvement de la lumière trouvé par M. Römer de l'Academie Royale des Sciences" (PDF) . Journal des sçavans (en francés): 223–236. Archivado desde el original (PDF) el 8 de septiembre de 2022 . Consultado el 10 de marzo de 2020 .
- Traducido como "Una demostración sobre el movimiento de la luz". Philosophical Transactions of the Royal Society . 12 (136): 893–894. 1677. Bibcode :1677RSPT...12..893.. doi : 10.1098/rstl.1677.0024 . Archivado desde el original el 29 de julio de 2007.
- Halley, E. (1694). "Monsieur Cassini, sus nuevas y exactas tablas para los eclipses del primer satélite de Júpiter, reducidas al estilo juliano y al meridiano de Londres". Philosophical Transactions of the Royal Society . 18 (214): 237–256. Bibcode :1694RSPT...18..237C. doi : 10.1098/rstl.1694.0048 .
- Fizeau, HL (1849). "Sur una experiencia relativa a la vitesse de propagation de la lumière" (PDF) . Comptes rendus de l'Académie des sciences (en francés). 29 : 90–92, 132.
- Foucault, JL (1862). "Determinación experimental de la vitesse de la lumière: paralaje del sol". Comptes rendus de l'Académie des sciences (en francés). 55 : 501–503, 792–796.
- Michelson, AA (1878). "Determinación experimental de la velocidad de la luz". Actas de la Asociación Estadounidense para el Avance de la Ciencia . 27 : 71–77.
- Michelson, AA; Pease, FG ; Pearson, F. (1935). "Medición de la velocidad de la luz en un vacío parcial". Astrophysical Journal . 82 (2091): 26–61. Bibcode :1935ApJ....82...26M. doi :10.1086/143655. PMID 17816642. S2CID 123010613.
- Newcomb, S. (1886). "La velocidad de la luz". Nature . 34 (863): 29–32. Bibcode :1886Natur..34...29.. doi : 10.1038/034029c0 .
- Perrotín, J. (1900). "Sur la vitesse de la lumière". Comptes rendus de l'Académie des sciences (en francés). 131 : 731–734.
Referencias modernas
- Brillouin, L. (1960). Propagación de ondas y velocidad de grupo . Academic Press .
- Jackson, JD (1975). Electrodinámica clásica (2.ª ed.). John Wiley & Sons. ISBN 978-0-471-30932-1.
- Keiser, G. (2000). Comunicaciones por fibra óptica (3.ª ed.). McGraw-Hill. pág. 32. ISBN 978-0-07-232101-2.
- Ng, YJ (2004). "Espuma cuántica y fenomenología de la gravedad cuántica". En Amelino-Camelia, G; Kowalski-Glikman, J (eds.). Efectos de la escala de Planck en astrofísica y cosmología . Springer. pp. 321ff. ISBN. 978-3-540-25263-4.
- Helmcke, J.; Riehle, F. (2001). "La física detrás de la definición del metro". En Quinn, TJ; Leschiutta, S.; Tavella, P. (eds.). Avances recientes en metrología y constantes fundamentales . IOS Press . pág. 453. ISBN. 978-1-58603-167-1.
- Duff, MJ (2004). "Comentario sobre la variación temporal de constantes fundamentales". arXiv : hep-th/0208093 .
Enlaces externos
- "Prueba de la velocidad de la luz en un tubo de vacío de una milla de longitud". Popular Science Monthly , septiembre de 1930, págs. 17-18.
- Definición del metro (Oficina Internacional de Pesas y Medidas, BIPM)
- Velocidad de la luz en el vacío (Instituto Nacional de Estándares y Tecnología, NIST)
- Galería de datos: Velocidad de la luz de Michelson (estimación de ubicación univariante) (descargar datos recopilados por Albert A. Michelson )
- Subluminal (applet de Java de Greg Egan que muestra los límites de información de velocidad de grupo)
- Discusión ligera sobre la adición de velocidades
- Velocidad de la luz (Sesenta símbolos, Departamento de Física de la Universidad de Nottingham [vídeo])
- La velocidad de la luz, debate en BBC Radio 4 ( In Our Time , 30 de noviembre de 2006)
- Velocidad de la luz (Contador en vivo – Ilustraciones)
- Velocidad de la luz: demostraciones animadas
- "La velocidad de la luz", Albert A. Nicholson, Scientific American , 28 de septiembre de 1878, pág. 193






