Espacio tridimensional

Este artículo incluye una lista de referencias generales , pero carece de suficientes citas en línea correspondientes . Ayúdenos a mejorar este artículo introduciendo citas más precisas. ( Abril de 2016 ) ( Aprenda cómo y cuándo eliminar este mensaje )

En geometría , un espacio tridimensional ( espacio 3D , 3-espacio o, raramente, espacio tridimensional ) es un espacio matemático en el que se requieren tres valores ( coordenadas ) para determinar la posición de un punto . Lo más común es que se trate del espacio euclidiano tridimensional , es decir, el espacio euclidiano de dimensión tres, que modela el espacio físico . Los espacios tridimensionales más generales se denominan 3-variedades . El término también puede referirse coloquialmente a un subconjunto del espacio, una región tridimensional (o dominio 3D ), ^[1] una figura sólida .

Técnicamente, una tupla de n números puede entenderse como las coordenadas cartesianas de una ubicación en un espacio euclidiano n -dimensional. El conjunto de estas n -tuplas se denota comúnmente y puede identificarse con el par formado por un espacio euclidiano n -dimensional y un sistema de coordenadas cartesianas . Cuando n = 3 , este espacio se denomina${\displaystyle \mathbb {R} ^{n},}$espacio euclidiano tridimensional (o simplemente "espacio euclidiano" cuando el contexto es claro). ^[2] En física clásica , sirve como modelo del universo físico , en el que existe toda la materia conocida. Cuando se considera la teoría de la relatividad , puede considerarse un subespacio local del espacio-tiempo . ^[3] Si bien este espacio sigue siendo la forma más convincente y útil de modelar el mundo tal como se experimenta, ^[4] es solo un ejemplo de una gran variedad de espacios en tres dimensiones llamados 3-variedades . En este ejemplo clásico, cuando los tres valores se refieren a mediciones en diferentes direcciones ( coordenadas ), se pueden elegir tres direcciones cualesquiera, siempre que estas direcciones no se encuentren en el mismo plano . Además, si estas direcciones son perpendiculares por pares , los tres valores a menudo se etiquetan con los términos ancho /ancho , altura /profundidad y longitud .

Los libros XI a XIII de los Elementos de Euclides tratan de la geometría tridimensional. El libro XI desarrolla nociones de ortogonalidad y paralelismo de líneas y planos, y define los sólidos, incluidos los paralelepípedos, las pirámides, los prismas, las esferas, los octaedros, los icosaedros y los dodecaedros. El libro XII desarrolla nociones de semejanza de sólidos. El libro XIII describe la construcción de los cinco sólidos platónicos regulares en una esfera.

En el siglo XVII, el espacio tridimensional se describía con coordenadas cartesianas , con la llegada de la geometría analítica desarrollada por René Descartes en su obra La Géométrie y Pierre de Fermat en el manuscrito Ad locos planos et solidos isagoge (Introducción a los lugares planos y sólidos), que no se publicó durante la vida de Fermat. Sin embargo, solo la obra de Fermat se ocupó del espacio tridimensional.

En el siglo XIX, los avances en la geometría del espacio tridimensional llegaron con el desarrollo de los cuaterniones por parte de William Rowan Hamilton . De hecho, fue Hamilton quien acuñó los términos escalar y vector , y fueron definidos por primera vez dentro de su marco geométrico para los cuaterniones . El espacio tridimensional podía entonces ser descrito por cuaterniones que tenían un componente escalar que se desvanecía, es decir, . Aunque Hamilton no lo estudió explícitamente, esto introdujo indirectamente nociones de base, aquí dadas por los elementos cuaterniones , así como el producto escalar y el producto vectorial , que corresponden a (el negativo de) la parte escalar y la parte vectorial del producto de dos cuaterniones vectoriales.${\displaystyle q=a+ui+vj+wk}$${\estilo de visualización a=0}$${\estilo de visualización i,j,k}$

No fue hasta Josiah Willard Gibbs que estos dos productos fueron identificados por derecho propio, y la notación moderna para el producto escalar y vectorial se introdujo en sus notas de enseñanza en el aula, que también se encuentran en el libro de texto de 1901 Análisis vectorial escrito por Edwin Bidwell Wilson basado en las conferencias de Gibbs.

También durante el siglo XIX se produjeron avances en el formalismo abstracto de los espacios vectoriales, con el trabajo de Hermann Grassmann y Giuseppe Peano , este último fue el primero en dar la definición moderna de los espacios vectoriales como una estructura algebraica.

Geometría
Proyectar una esfera a un plano
Describir Historia ( Cronología )
Sucursales Euclidiano No euclidiano Elíptico Esférico Hiperbólico Geometría no arquimediana Descriptivo Afín Sintético Analítico Algebraico Aritmética Diofántico Diferencial Riemanniano Simpléctico Diferencial discreto Complejo Finito Discreto/Combinatorio Digital Convexo Computacional Fractal Incidencia Geometría no conmutativa Geometría algebraica no conmutativa
Conceptos Características Dimensión Construcciones con regla y compás Ángulo Curva Diagonal Ortogonalidad ( perpendicular ) Paralelo Vértice Congruencia Semejanza Simetría
Cero-dimensional Punto
Unidimensional Línea segmento rayo Longitud
Bidimensional Avión Área Polígono Triángulo Altitud Hipotenusa Teorema de Pitágoras Paralelogramo Cuadrado Rectángulo Rombo Romboidal Cuadrilátero Trapecio Cometa Círculo Diámetro Circunferencia Área
Tridimensional Volumen Cubo cuboides Cilindro Dodecaedro Icosaedro Octaedro Pirámide Sólido platónico Esfera Tetraedro
Cuatro - / otras dimensiones Teseracto Hiperesfera
Geometrias
por nombre Aida Aryabhata Ahmes Alhazen Apollonius Archimedes Atiyah Baudhayana Bolyai Brahmagupta Cartan Coxeter Descartes Euclid Euler Gauss Gromov Hilbert Huygens Jyeṣṭhadeva Kātyāyana Khayyám Klein Lobachevsky Manava Minkowski Minggatu Pascal Pythagoras Parameshvara Poincaré Riemann Sakabe Sijzi al-Tusi Veblen Virasena Yang Hui al-Yasamin Zhang List of geometers
by period BCE Ahmes Baudhayana Manava Pythagoras Euclid Archimedes Apollonius 1–1400s Zhang Kātyāyana Aryabhata Brahmagupta Virasena Alhazen Sijzi Khayyám al-Yasamin al-Tusi Yang Hui Parameshvara 1400s–1700s Jyeṣṭhadeva Descartes Pascal Huygens Minggatu Euler Sakabe Aida 1700s–1900s Gauss Lobachevsky Bolyai Riemann Klein Poincaré Hilbert Minkowski Cartan Veblen Coxeter Present day Atiyah Gromov
v t e

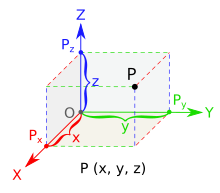
En matemáticas, la geometría analítica (también llamada geometría cartesiana) describe cada punto en el espacio tridimensional por medio de tres coordenadas. Se dan tres ejes de coordenadas , cada uno perpendicular a los otros dos en el origen , el punto en el que se cruzan. Por lo general, se etiquetan x , y y z . En relación con estos ejes, la posición de cualquier punto en el espacio tridimensional está dada por un triple ordenado de números reales , cada número da la distancia de ese punto desde el origen medida a lo largo del eje dado, que es igual a la distancia de ese punto desde el plano determinado por los otros dos ejes. ^[5]

Otros métodos populares para describir la ubicación de un punto en el espacio tridimensional incluyen las coordenadas cilíndricas y las coordenadas esféricas , aunque existe una cantidad infinita de métodos posibles. Para obtener más información, consulte Espacio euclidiano .

A continuación se muestran imágenes de los sistemas mencionados anteriormente.

• 
  Sistema de coordenadas cartesianas
• 
  Sistema de coordenadas cilíndricas
• 
  Sistema de coordenadas esféricas

Dos puntos distintos siempre determinan una línea (recta) . Tres puntos distintos son colineales o determinan un único plano . Por otra parte, cuatro puntos distintos pueden ser colineales, coplanares o determinar todo el espacio.

Dos rectas distintas pueden intersecarse, ser paralelas o ser oblicuas . Dos rectas paralelas, o dos rectas que se intersectan , se encuentran en un único plano, por lo que las rectas oblicuas son rectas que no se encuentran ni se encuentran en un plano común.

Dos planos distintos pueden encontrarse en una línea común o ser paralelos (es decir, no encontrarse). Tres planos distintos, ninguno de los cuales es paralelo a un par, pueden encontrarse en una línea común, encontrarse en un único punto común o no tener ningún punto en común. En el último caso, las tres líneas de intersección de cada par de planos son paralelas entre sí.

Una recta puede estar en un plano dado, intersectar dicho plano en un único punto o ser paralela al plano. En este último caso, habrá rectas en el plano que sean paralelas a la recta dada.

Un hiperplano es un subespacio de una dimensión menor que la dimensión del espacio completo. Los hiperplanos de un espacio tridimensional son los subespacios bidimensionales, es decir, los planos. En términos de coordenadas cartesianas, los puntos de un hiperplano satisfacen una única ecuación lineal , por lo que los planos en este espacio tridimensional se describen mediante ecuaciones lineales. Una línea se puede describir mediante un par de ecuaciones lineales independientes, cada una de las cuales representa un plano que tiene esta línea como intersección común.

El teorema de Varignon establece que los puntos medios de cualquier cuadrilátero forman un paralelogramo y, por lo tanto, son coplanares.${\displaystyle \mathbb {R} ^{3}}$

Una esfera en el espacio tridimensional (también llamada biesfera porque es un objeto bidimensional) consiste en el conjunto de todos los puntos en el espacio tridimensional a una distancia fija r de un punto central P. El sólido encerrado por la esfera se llama bola (o, más precisamente, 3-bola ).

El volumen de la pelota viene dado por

$${\displaystyle V={\frac {4}{3}}\pi r^{3},}$$y el área de la superficie de la esfera es Otro tipo de esfera surge de una 4-bola, cuya superficie tridimensional es la 3-esfera : puntos equidistantes al origen del espacio euclidiano R ⁴ . Si un punto tiene coordenadas, P ( x , y , z , w ) , entonces x ² + y ² + z ² + w ² = 1 caracteriza aquellos puntos en la 3-esfera unitaria centrada en el origen.$${\displaystyle A=4\pi r^{2}.}$$

Esta esfera tridimensional es un ejemplo de una variedad tridimensional: un espacio que "se parece localmente" a un espacio tridimensional. En términos topológicos precisos, cada punto de la esfera tridimensional tiene un entorno que es homeomorfo a un subconjunto abierto del espacio tridimensional.

En tres dimensiones, hay nueve politopos regulares: los cinco sólidos platónicos convexos y los cuatro poliedros de Kepler-Poinsot no convexos .

Politopos regulares en tres dimensiones

Clase	Sólidos platónicos					Poliedros de Kepler-Poinsot
Simetría	T.D.​	Oh​		Yo soy
Grupo Coxeter	Un 3 , [3,3]	B3 , [4,3 ]		H3 , [5,3 ]
Orden	24	48		120
Poliedro regular	{3,3}	{4,3}	{3,4}	{5,3}	{3,5}	{5/2,5}	{5,5/2}	{5/2,3}	{3,5/2}

Una superficie generada al girar una curva plana alrededor de una línea fija en su plano como eje se denomina superficie de revolución . La curva plana se denomina generatriz de la superficie. Una sección de la superficie, formada al intersecar la superficie con un plano perpendicular (ortogonal) al eje, es un círculo.

Ejemplos sencillos se dan cuando la generatriz es una línea. Si la línea generatriz interseca la línea del eje, la superficie de revolución es un cono circular recto cuyo vértice es el punto de intersección. Sin embargo, si la generatriz y el eje son paralelos, entonces la superficie de revolución es un cilindro circular .

En analogía con las secciones cónicas , el conjunto de puntos cuyas coordenadas cartesianas satisfacen la ecuación general de segundo grado, es decir, donde A , B , C , F , G , H , J , K , L y M son números reales y no todos A , B , C , F , G y H son cero, se llama superficie cuádrica . ^[6]$${\displaystyle Ax^{2}+By^{2}+Cz^{2}+Fxy+Gyz+Hxz+Jx+Ky+Lz+M=0,}$$

Hay seis tipos de superficies cuádricas no degeneradas :

1. Elipsoide
2. Hiperboloide de una lámina
3. Hiperboloide de dos láminas
4. Cono elíptico
5. Paraboloide elíptico
6. Paraboloide hiperbólico

Las superficies cuadráticas degeneradas son el conjunto vacío, un único punto, una única línea, un único plano, un par de planos o un cilindro cuadrático (una superficie que consiste en una sección cónica no degenerada en un plano π y todas las líneas de R ³ a través de esa cónica que son normales a π ). ^[6] Los conos elípticos a veces también se consideran superficies cuadráticas degeneradas.

Tanto el hiperboloide de una lámina como el paraboloide hiperbólico son superficies regladas , es decir, pueden estar formadas por una familia de rectas. De hecho, cada una tiene dos familias de rectas generadoras, los miembros de cada familia son disjuntos y cada miembro de una familia interseca, con una sola excepción, a todos los miembros de la otra familia. ^[7] Cada familia se llama régulo .

Otra forma de ver el espacio tridimensional se encuentra en el álgebra lineal , donde la idea de independencia es crucial. El espacio tiene tres dimensiones porque la longitud de una caja es independiente de su ancho. En el lenguaje técnico del álgebra lineal, el espacio es tridimensional porque cada punto en el espacio puede describirse mediante una combinación lineal de tres vectores independientes .

Un vector se puede representar como una flecha. La magnitud del vector es su longitud y su dirección es la dirección hacia la que apunta la flecha. Un vector se puede representar mediante un triple ordenado de números reales. Estos números se denominan componentes del vector.${\displaystyle \mathbb {R} ^{3}}$

El producto escalar de dos vectores A = [ A ₁ , A ₂ , A ₃ ] y B = [ B ₁ , B ₂ , B ₃ ] se define como: ^[8]

${\displaystyle \mathbf {A} \cdot \mathbf {B} =A_{1}B_{1}+A_{2}B_{2}+A_{3}B_{3}=\sum _{i=1}^{3}A_{i}B_{i}.}$

La magnitud de un vector A se denota por || A || . El producto escalar de un vector A = [ A ₁ , A ₂ , A ₃ ] consigo mismo es

${\displaystyle \mathbf {A} \cdot \mathbf {A} =\|\mathbf {A} \|^{2}=A_{1}^{2}+A_{2}^{2}+A_{3}^{2},}$

Lo cual da

${\displaystyle \|\mathbf {A} \|={\sqrt {\mathbf {A} \cdot \mathbf {A} }}={\sqrt {A_{1}^{2}+A_{2}^{2}+A_{3}^{2}}},}$

la fórmula para la longitud euclidiana del vector.

Sin referencia a los componentes de los vectores, el producto escalar de dos vectores euclidianos distintos de cero A y B se da por ^[9]

${\displaystyle \mathbf {A} \cdot \mathbf {B} =\|\mathbf {A} \|\,\|\mathbf {B} \|\cos \theta ,}$

donde θ es el ángulo entre A y B.

El producto vectorial o producto vectorial es una operación binaria sobre dos vectores en el espacio tridimensional y se denota con el símbolo ×. El producto vectorial A × B de los vectores A y B es un vector que es perpendicular a ambos y, por lo tanto, normal al plano que los contiene. Tiene muchas aplicaciones en matemáticas, física e ingeniería .

En el lenguaje funcional, el producto vectorial es una función .${\displaystyle \times :\mathbb {R} ^{3}\times \mathbb {R} ^{3}\rightarrow \mathbb {R} ^{3}}$

Los componentes del producto vectorial son , y también se pueden escribir en componentes, utilizando la convención de suma de Einstein como donde es el símbolo de Levi-Civita . Tiene la propiedad de que .${\displaystyle \mathbf {A} \times \mathbf {B} =[A_{2}B_{3}-B_{2}A_{3},A_{3}B_{1}-B_{3}A_{1},A_{1}B_{2}-B_{1}A_{2}]}$${\displaystyle (\mathbf {A} \times \mathbf {B} )_{i}=\varepsilon _{ijk}A_{j}B_{k}}$${\displaystyle \varepsilon _{ijk}}$${\displaystyle \mathbf {A} \times \mathbf {B} =-\mathbf {B} \times \mathbf {A} }$

Su magnitud está relacionada con el ángulo entre y por la identidad${\displaystyle \theta }$${\displaystyle \mathbf {A} }$${\displaystyle \mathbf {B} }$$${\displaystyle \left\|\mathbf {A} \times \mathbf {B} \right\|=\left\|\mathbf {A} \right\|\cdot \left\|\mathbf {B} \right\|\cdot \left|\sin \theta \right|.}$$

El espacio y el producto forman un álgebra sobre un cuerpo , que no es conmutativa ni asociativa , sino que es un álgebra de Lie con el producto vectorial siendo el corchete de Lie. Específicamente, el espacio junto con el producto, es isomorfo al álgebra de Lie de rotaciones tridimensionales, denotada . Para satisfacer los axiomas de un álgebra de Lie, en lugar de asociatividad el producto vectorial satisface la identidad de Jacobi . Para cualesquiera tres vectores y${\displaystyle (\mathbb {R} ^{3},\times )}$${\displaystyle {\mathfrak {so}}(3)}$${\displaystyle \mathbf {A} ,\mathbf {B} }$${\displaystyle \mathbf {C} }$

$${\displaystyle \mathbf {A} \times (\mathbf {B} \times \mathbf {C} )+\mathbf {B} \times (\mathbf {C} \times \mathbf {A} )+\mathbf {C} \times (\mathbf {A} \times \mathbf {B} )=0}$$

En n dimensiones, se puede tomar el producto de n − 1 vectores para producir un vector perpendicular a todos ellos. Pero si el producto se limita a productos binarios no triviales con resultados vectoriales, solo existe en tres y siete dimensiones . ^[10]

Puede resultar útil describir el espacio tridimensional como un espacio vectorial tridimensional sobre los números reales. Esto difiere de en un sentido sutil. Por definición, existe una base para . Esto corresponde a un isomorfismo entre y : la construcción para el isomorfismo se encuentra aquí . Sin embargo, no existe una base "preferida" o "canónica" para .${\displaystyle V}$${\displaystyle \mathbb {R} ^{3}}$${\displaystyle {\mathcal {B}}=\{e_{1},e_{2},e_{3}\}}$${\displaystyle V}$${\displaystyle V}$${\displaystyle \mathbb {R} ^{3}}$${\displaystyle V}$

Por otra parte, existe una base preferida para , que se debe a su descripción como un producto cartesiano de copias de , es decir, . Esto permite la definición de proyecciones canónicas, , donde . Por ejemplo, . Esto permite entonces la definición de la base estándar definida por donde es el delta de Kronecker . Escrita en su totalidad, la base estándar es${\displaystyle \mathbb {R} ^{3}}$${\displaystyle \mathbb {R} }$${\displaystyle \mathbb {R} ^{3}=\mathbb {R} \times \mathbb {R} \times \mathbb {R} }$${\displaystyle \pi _{i}:\mathbb {R} ^{3}\rightarrow \mathbb {R} }$${\displaystyle 1\leq i\leq 3}$${\displaystyle \pi _{1}(x_{1},x_{2},x_{3})=x}$ ${\displaystyle {\mathcal {B}}_{\text{Standard}}=\{E_{1},E_{2},E_{3}\}}$$${\displaystyle \pi _{i}(E_{j})=\delta _{ij}}$$${\displaystyle \delta _{ij}}$$${\displaystyle E_{1}={\begin{pmatrix}1\\0\\0\end{pmatrix}},E_{2}={\begin{pmatrix}0\\1\\0\end{pmatrix}},E_{3}={\begin{pmatrix}0\\0\\1\end{pmatrix}}.}$$

Por lo tanto , se puede considerar como el espacio vectorial abstracto, junto con la estructura adicional de una elección de base. A la inversa, se puede obtener comenzando con y "olvidándose" de la estructura del producto cartesiano, o equivalentemente, la elección estándar de base.${\displaystyle \mathbb {R} ^{3}}$${\displaystyle V}$${\displaystyle \mathbb {R} ^{3}}$

A diferencia de un espacio vectorial general , a veces se hace referencia al espacio como un espacio de coordenadas. ^[11]${\displaystyle V}$${\displaystyle \mathbb {R} ^{3}}$

Físicamente, es conceptualmente deseable utilizar el formalismo abstracto para suponer la menor estructura posible si no está dada por los parámetros de un problema particular. Por ejemplo, en un problema con simetría rotacional, trabajar con la descripción más concreta del espacio tridimensional supone una elección de base, correspondiente a un conjunto de ejes. Pero en la simetría rotacional, no hay razón para preferir un conjunto de ejes en lugar de, digamos, el mismo conjunto de ejes que se ha rotado arbitrariamente. Dicho de otra manera, una elección preferida de ejes rompe la simetría rotacional del espacio físico.${\displaystyle \mathbb {R} ^{3}}$

Computacionalmente, es necesario trabajar con la descripción más concreta para poder realizar cálculos concretos.${\displaystyle \mathbb {R} ^{3}}$

Una descripción aún más abstracta es modelar el espacio físico como un espacio afín tridimensional sobre los números reales. Esto es único hasta el isomorfismo afín. A veces se lo denomina espacio euclidiano tridimensional. Así como la descripción del espacio vectorial surgió de "olvidar la base preferida" de , la descripción del espacio afín surge de "olvidar el origen" del espacio vectorial. A veces, los espacios euclidianos se denominan espacios afines euclidianos para distinguirlos de los espacios vectoriales euclidianos. ^[12]${\displaystyle E(3)}$${\displaystyle \mathbb {R} ^{3}}$

Esto resulta atractivo desde el punto de vista físico, ya que pone de manifiesto la invariancia de la traducción del espacio físico. Un origen preferido rompe la invariancia de la traducción.

La discusión anterior no involucra el producto escalar . El producto escalar es un ejemplo de un producto interno . El espacio físico puede ser modelado como un espacio vectorial que además tiene la estructura de un producto interno. El producto interno define nociones de longitud y ángulo (y por lo tanto, en particular, la noción de ortogonalidad). Para cualquier producto interno, existen bases bajo las cuales el producto interno concuerda con el producto escalar, pero nuevamente, hay muchas bases posibles diferentes, ninguna de las cuales es preferida. Se diferencian entre sí por una rotación, un elemento del grupo de rotaciones SO(3) .

En un sistema de coordenadas rectangulares, el gradiente de una función (diferenciable) está dado por${\displaystyle f:\mathbb {R} ^{3}\rightarrow \mathbb {R} }$

${\displaystyle \nabla f={\frac {\partial f}{\partial x}}\mathbf {i} +{\frac {\partial f}{\partial y}}\mathbf {j} +{\frac {\partial f}{\partial z}}\mathbf {k} }$

y en notación de índice se escribe

$${\displaystyle (\nabla f)_{i}=\partial _{i}f.}$$

La divergencia de un campo vectorial (diferenciable) F = U i + V j + W k , es decir, una función , es igual a la función escalar :${\displaystyle \mathbf {F} :\mathbb {R} ^{3}\rightarrow \mathbb {R} ^{3}}$

${\displaystyle \operatorname {div} \,\mathbf {F} =\nabla \cdot \mathbf {F} ={\frac {\partial U}{\partial x}}+{\frac {\partial V}{\partial y}}+{\frac {\partial W}{\partial z}}.}$

En notación de índice, con la convención de suma de Einstein esto es $${\displaystyle \nabla \cdot \mathbf {F} =\partial _{i}F_{i}.}$$

Desarrollado en coordenadas cartesianas (ver Del en coordenadas cilíndricas y esféricas para representaciones de coordenadas esféricas y cilíndricas ), el rotacional ∇ × F es, para F compuesto de [ F _x , F _y , F _z ]:

${\displaystyle {\begin{vmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\\\{\frac {\partial }{\partial x}}&{\frac {\partial }{\partial y}}&{\frac {\partial }{\partial z}}\\\\F_{x}&F_{y}&F_{z}\end{vmatrix}}}$

donde i , j y k son los vectores unitarios de los ejes x , y y z , respectivamente. Esto se desarrolla de la siguiente manera: ^[13]

${\displaystyle \left({\frac {\partial F_{z}}{\partial y}}-{\frac {\partial F_{y}}{\partial z}}\right)\mathbf {i} +\left({\frac {\partial F_{x}}{\partial z}}-{\frac {\partial F_{z}}{\partial x}}\right)\mathbf {j} +\left({\frac {\partial F_{y}}{\partial x}}-{\frac {\partial F_{x}}{\partial y}}\right)\mathbf {k} .}$

En notación de índice, con la convención de suma de Einstein, aquí es donde está el símbolo totalmente antisimétrico, el símbolo de Levi-Civita .$${\displaystyle (\nabla \times \mathbf {F} )_{i}=\epsilon _{ijk}\partial _{j}F_{k},}$$${\displaystyle \epsilon _{ijk}}$

Para algún campo escalar f  : U ⊆ R ⁿ → R , la integral de línea a lo largo de una curva suave por partes C ⊂ U se define como

${\displaystyle \int \limits _{C}f\,ds=\int _{a}^{b}f(\mathbf {r} (t))|\mathbf {r} '(t)|\,dt.}$

donde r : [a, b] → C es una parametrización biyectiva arbitraria de la curva C tal que r ( a ) y r ( b ) dan los puntos finales de C y .${\displaystyle a<b}$

Para un campo vectorial F  : U ⊆ R ⁿ → R ⁿ , la integral de línea a lo largo de una curva suave por partes C ⊂ U , en la dirección de r , se define como

${\displaystyle \int \limits _{C}\mathbf {F} (\mathbf {r} )\cdot \,d\mathbf {r} =\int _{a}^{b}\mathbf {F} (\mathbf {r} (t))\cdot \mathbf {r} '(t)\,dt.}$

donde · es el producto escalar y r : [a, b] → C es una parametrización biyectiva de la curva C tal que r ( a ) y r ( b ) dan los puntos finales de C .

Una integral de superficie es una generalización de integrales múltiples para la integración sobre superficies . Puede considerarse como el análogo integral doble de la integral de línea. Para encontrar una fórmula explícita para la integral de superficie, necesitamos parametrizar la superficie de interés, S , considerando un sistema de coordenadas curvilíneas en S , como la latitud y la longitud en una esfera . Sea dicha parametrización x ( s , t ), donde ( s , t ) varía en alguna región T en el plano . Entonces, la integral de superficie está dada por

${\displaystyle \iint _{S}f\,\mathrm {d} S=\iint _{T}f(\mathbf {x} (s,t))\left\|{\partial \mathbf {x} \over \partial s}\times {\partial \mathbf {x} \over \partial t}\right\|\mathrm {d} s\,\mathrm {d} t}$

donde la expresión entre las barras del lado derecho es la magnitud del producto vectorial de las derivadas parciales de x ( s , t ), y se conoce como elemento de superficie . Dado un campo vectorial v en S , es decir, una función que asigna a cada x en S un vector v ( x ), la integral de superficie se puede definir componente por componente de acuerdo con la definición de la integral de superficie de un campo escalar; el resultado es un vector.

Una integral de volumen es una integral sobre un dominio o región tridimensional . Cuando el integrando es trivial (unidad), la integral de volumen es simplemente el volumen de la región . ^{[14] [1]} También puede significar una integral triple dentro de una región D en R ³ de una función y generalmente se escribe como:${\displaystyle f(x,y,z),}$

${\displaystyle \iiint \limits _{D}f(x,y,z)\,dx\,dy\,dz.}$

El teorema fundamental de las integrales de línea dice que una integral de línea a través de un campo de gradiente se puede evaluar evaluando el campo escalar original en los puntos finales de la curva.

Dejar . Entonces${\displaystyle \varphi :U\subseteq \mathbb {R} ^{n}\to \mathbb {R} }$

${\displaystyle \varphi \left(\mathbf {q} \right)-\varphi \left(\mathbf {p} \right)=\int _{\gamma [\mathbf {p} ,\,\mathbf {q} ]}\nabla \varphi (\mathbf {r} )\cdot d\mathbf {r} .}$

El teorema de Stokes relaciona la integral de superficie del rotacional de un campo vectorial F sobre una superficie Σ en el tridimensional euclidiano con la integral de línea del campo vectorial sobre su límite ∂Σ:

${\displaystyle \iint _{\Sigma }\nabla \times \mathbf {F} \cdot \mathrm {d} \mathbf {\Sigma } =\oint _{\partial \Sigma }\mathbf {F} \cdot \mathrm {d} \mathbf {r} .}$

Supóngase que V es un subconjunto de (en el caso de n = 3, V representa un volumen en el espacio 3D) que es compacto y tiene un límite liso por partes S (también indicado con ∂ V = S ). Si F es un campo vectorial continuamente diferenciable definido en un entorno de V , entonces el teorema de divergencia dice: ^[15]${\displaystyle \mathbb {R} ^{n}}$

${\displaystyle \iiint _{V}\left(\mathbf {\nabla } \cdot \mathbf {F} \right)\,dV=}$ ${\displaystyle \scriptstyle S}$ ${\displaystyle (\mathbf {F} \cdot \mathbf {n} )\,dS.}$

El lado izquierdo es una integral de volumen sobre el volumen V , el lado derecho es la integral de superficie sobre el límite del volumen V . La variedad cerrada ∂ V es, en términos bastante generales, el límite de V orientado por normales que apuntan hacia afuera , y n es el campo normal unitario que apunta hacia afuera del límite ∂ V . ( d S puede usarse como una abreviatura de n dS ).

El espacio tridimensional tiene una serie de propiedades topológicas que lo distinguen de los espacios de otras dimensiones numéricas. Por ejemplo, se requieren al menos tres dimensiones para hacer un nudo en un trozo de cuerda. ^[16]

En geometría diferencial, los espacios tridimensionales genéricos son 3-variedades , que localmente se parecen a .${\displaystyle {\mathbb {R} }^{3}}$

Muchas ideas de dimensión pueden probarse con geometría finita . El ejemplo más simple es PG(3,2) , que tiene planos de Fano como sus subespacios bidimensionales. Es un ejemplo de geometría de Galois , un estudio de geometría proyectiva que utiliza cuerpos finitos . Por lo tanto, para cualquier cuerpo de Galois GF( q ), existe un espacio proyectivo PG(3, q ) de tres dimensiones. Por ejemplo, tres líneas oblicuas cualesquiera en PG(3, q ) están contenidas en exactamente un régulo . ^[17]

• Rotación 3D
  • Formalismos de rotación en tres dimensiones
• Análisis dimensional
• Distancia de un punto a un plano
• Espacio de cuatro dimensiones
• Líneas oblicuas § Distancia
• Gráfico tridimensional
• Geometría sólida
• Términos de orientación

• Anton, Howard (1994), Álgebra lineal elemental (7.ª ed.), John Wiley & Sons, ISBN 978-0-471-58742-2
• Arfken, George B. y Hans J. Weber. Métodos matemáticos para físicos , Academic Press; 6.ª edición (21 de junio de 2005). ISBN 978-0-12-059876-2 . 
• Berger, Marcel (1987), Geometría I , Berlín: Springer, ISBN 3-540-11658-3
• Brannan, David A.; Esplen, Matthew F.; Gray, Jeremy J. (1999), Geometría , Cambridge University Press, ISBN 978-0-521-59787-6
• Lang, Serge (1987), Álgebra lineal (3.ª ed.), Springer, doi :10.1007/978-1-4757-1949-9, ISBN 978-1-4757-1949-9

Wikiquote tiene citas relacionadas con Espacio tridimensional .

Wikimedia Commons tiene medios relacionados con 3D .

• La definición del diccionario de tridimensional en Wikcionario
• Weisstein, Eric W. "Geometría de cuatro dimensiones". MathWorld .
• Álgebra lineal elemental - Capítulo 8: Geometría tridimensional Keith Matthews de la Universidad de Queensland , 1991