Coordenadas curvilíneas

En geometría , las coordenadas curvilíneas son un sistema de coordenadas para el espacio euclidiano en el que las líneas de coordenadas pueden ser curvas. Estas coordenadas pueden derivarse de un conjunto de coordenadas cartesianas mediante una transformación que es localmente invertible (una función biunívoca) en cada punto. Esto significa que se puede convertir un punto dado en un sistema de coordenadas cartesianas a sus coordenadas curvilíneas y viceversa. El nombre de coordenadas curvilíneas , acuñado por el matemático francés Lamé , deriva del hecho de que las superficies de coordenadas de los sistemas curvilíneos son curvas.

Ejemplos bien conocidos de sistemas de coordenadas curvilíneas en el espacio euclidiano tridimensional ( R ³ ) son las coordenadas cilíndricas y esféricas . Una superficie de coordenadas cartesianas en este espacio es un plano de coordenadas ; por ejemplo, z = 0 define el plano x - y . En el mismo espacio, la superficie de coordenadas r = 1 en coordenadas esféricas es la superficie de una esfera unitaria , que es curva. El formalismo de las coordenadas curvilíneas proporciona una descripción unificada y general de los sistemas de coordenadas estándar.

Las coordenadas curvilíneas se utilizan a menudo para definir la ubicación o distribución de magnitudes físicas que pueden ser, por ejemplo, escalares , vectores o tensores . Las expresiones matemáticas que involucran estas magnitudes en el cálculo vectorial y el análisis tensorial (como el gradiente , la divergencia , el rotacional y el laplaciano ) se pueden transformar de un sistema de coordenadas a otro, de acuerdo con las reglas de transformación para escalares, vectores y tensores. Dichas expresiones se vuelven entonces válidas para cualquier sistema de coordenadas curvilíneas.

Un sistema de coordenadas curvilíneas puede ser más sencillo de utilizar que el sistema de coordenadas cartesianas para algunas aplicaciones. El movimiento de partículas bajo la influencia de fuerzas centrales suele ser más fácil de resolver en coordenadas esféricas que en coordenadas cartesianas; esto es cierto para muchos problemas físicos con simetría esférica definida en R ³ . Las ecuaciones con condiciones de contorno que siguen superficies de coordenadas para un sistema de coordenadas curvilíneas particular pueden ser más fáciles de resolver en ese sistema. Si bien uno podría describir el movimiento de una partícula en una caja rectangular utilizando coordenadas cartesianas, es más fácil describir el movimiento en una esfera con coordenadas esféricas. Las coordenadas esféricas son los sistemas de coordenadas curvilíneas más comunes y se utilizan en ciencias de la Tierra , cartografía , mecánica cuántica , relatividad e ingeniería .

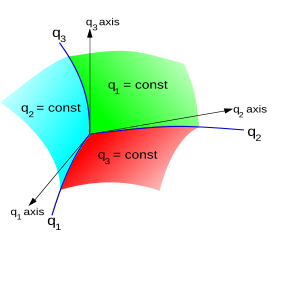
Por ahora, consideremos el espacio 3-D . Un punto P en el espacio 3-D (o su vector de posición r ) se puede definir usando coordenadas cartesianas ( x , y , z ) [escritas de manera equivalente ( x ¹ , x ² , x ³ )], por , donde e _x , e _y , e _z son los vectores base estándar .${\displaystyle \mathbf {r} =x\mathbf {e} _{x}+y\mathbf {e} _{y}+z\mathbf {e} _{z}}$

También se puede definir por sus coordenadas curvilíneas ( q ¹ , q ² , q ³ ) si este triplete de números define un único punto de forma inequívoca. La relación entre las coordenadas viene dada entonces por las funciones de transformación invertibles:

${\displaystyle x=f^{1}(q^{1},q^{2},q^{3}),\,y=f^{2}(q^{1},q^{2},q^{3}),\,z=f^{3}(q^{1},q^{2},q^{3})}$

${\displaystyle q^{1}=g^{1}(x,y,z),\,q^{2}=g^{2}(x,y,z),\,q^{3} =g^{3}(x,y,z)}$

Las superficies q ¹ = constante, q ² = constante, q ³ = constante se denominan superficies coordenadas ; y las curvas espaciales formadas por su intersección en pares se denominan curvas coordenadas . Los ejes de coordenadas están determinados por las tangentes a las curvas coordenadas en la intersección de tres superficies. En general, no son direcciones fijas en el espacio, lo que sucede en el caso de las coordenadas cartesianas simples, y por lo tanto, generalmente no existe una base global natural para las coordenadas curvilíneas.

En el sistema cartesiano, los vectores base estándar se pueden derivar de la derivada de la ubicación del punto P con respecto a la coordenada local.

${\displaystyle \mathbf {e} _{x}={\dfrac {\partial \mathbf {r} }{\partial x}};\;\mathbf {e} _{y}={\dfrac {\partial \mathbf {r} }{\partial y}};\;\mathbf {e} _{z}={\dfrac {\partial \mathbf {r} }{\partial z}}.}$

Aplicando las mismas derivadas al sistema curvilíneo localmente en el punto P se definen los vectores base naturales:

${\displaystyle \mathbf {h} _{1}={\dfrac {\partial \mathbf {r} }{\partial q^{1}}};\;\mathbf {h} _{2}={\dfrac {\partial \mathbf {r} }{\partial q^{2}}};\;\mathbf {h} _{3}={\dfrac {\partial \mathbf {r} }{\partial q^{3}}}.}$

Una base de este tipo, cuyos vectores cambian su dirección y/o magnitud de un punto a otro, se denomina base local . Todas las bases asociadas a coordenadas curvilíneas son necesariamente locales. Los vectores de base que son iguales en todos los puntos son bases globales y pueden asociarse únicamente a sistemas de coordenadas lineales o afines .

Para este artículo, e está reservado para la base estándar (cartesiana) y h o b son para la base curvilínea.

Estos pueden no tener longitud unitaria y también pueden no ser ortogonales. En el caso de que sean ortogonales en todos los puntos donde las derivadas estén bien definidas, definimos los coeficientes de Lamé.(según Gabriel Lamé ) por

${\displaystyle h_{1}=|\mathbf {h} _{1}|;\;h_{2}=|\mathbf {h} _{2}|;\;h_{3}=|\mathbf {h} _{3}|}$

y los vectores base ortonormales curvilíneos por

${\displaystyle \mathbf {b} _{1}={\dfrac {\mathbf {h} _{1}}{h_{1}}};\;\mathbf {b} _{2}={\dfrac {\mathbf {h} _{2}}{h_{2}}};\;\mathbf {b} _{3}={\dfrac {\mathbf {h} _{3}}{h_{3}}}.}$

Estos vectores base pueden depender de la posición de P ; por lo tanto, es necesario que no se suponga que son constantes en una región. (Técnicamente, forman una base para el fibrado tangente de en P , y por lo tanto son locales a P ).${\displaystyle \mathbb {R} ^{3}}$

En general, las coordenadas curvilíneas permiten que los vectores de base naturales h _i no sean todos mutuamente perpendiculares entre sí, y no se requiere que tengan una longitud unitaria: pueden tener una magnitud y dirección arbitrarias. El uso de una base ortogonal hace que las manipulaciones de vectores sean más simples que para las no ortogonales. Sin embargo, algunas áreas de la física y la ingeniería , particularmente la mecánica de fluidos y la mecánica de medios continuos , requieren bases no ortogonales para describir deformaciones y transporte de fluidos para dar cuenta de dependencias direccionales complicadas de cantidades físicas. Más adelante en esta página aparece una discusión del caso general.

En coordenadas curvilíneas ortogonales, dado que el cambio diferencial total en r es

${\displaystyle d\mathbf {r} ={\dfrac {\partial \mathbf {r} }{\partial q^{1}}}dq^{1}+{\dfrac {\partial \mathbf {r} }{\partial q^{2}}}dq^{2}+{\dfrac {\partial \mathbf {r} }{\partial q^{3}}}dq^{3}=h_{1}dq^{1}\mathbf {b} _{1}+h_{2}dq^{2}\mathbf {b} _{2}+h_{3}dq^{3}\mathbf {b} _{3}}$

Entonces los factores de escala son${\displaystyle h_{i}=\left|{\frac {\partial \mathbf {r} }{\partial q^{i}}}\right|}$

En coordenadas no ortogonales, la longitud de es la raíz cuadrada positiva de (con la convención de suma de Einstein ). Los seis productos escalares independientes g _ij = h _i . h _j de los vectores base naturales generalizan los tres factores de escala definidos anteriormente para coordenadas ortogonales. Los nueve g _ij son los componentes del tensor métrico , que tiene solo tres componentes distintos de cero en coordenadas ortogonales: g ₁₁ = h ₁ h ₁ , g ₂₂ = h ₂ h ₂ , g ₃₃ = h ₃ h ₃ .${\displaystyle d\mathbf {r} =dq^{1}\mathbf {h} _{1}+dq^{2}\mathbf {h} _{2}+dq^{3}\mathbf {h} _{3}}$${\displaystyle d\mathbf {r} \cdot d\mathbf {r} =dq^{i}dq^{j}\mathbf {h} _{i}\cdot \mathbf {h} _{j}}$

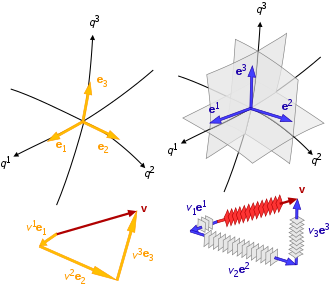
Los gradientes espaciales, las distancias, las derivadas temporales y los factores de escala están interrelacionados dentro de un sistema de coordenadas mediante dos grupos de vectores base:

1. vectores base que son localmente tangentes a su trayectoria de coordenadas asociada: son vectores contravariantes (denotados por índices reducidos), y$${\displaystyle \mathbf {b} _{i}={\dfrac {\partial \mathbf {r} }{\partial q^{i}}}}$$
2. vectores base que son localmente normales a la isosuperficie creada por las otras coordenadas: son vectores covariantes (denotados por índices elevados), ∇ es el operador del .$${\displaystyle \mathbf {b} ^{i}=\nabla q^{i}}$$

Nótese que, debido a la convención de suma de Einstein, la posición de los índices de los vectores es opuesta a la de las coordenadas.

En consecuencia, un sistema de coordenadas curvilíneas general tiene dos conjuntos de vectores base para cada punto: { b ₁ , b ₂ , b ₃ } es la base contravariante, y { b ¹ , b ² , b ³ } es la base covariante (también conocida como recíproca). Los tipos de vectores base covariantes y contravariantes tienen una dirección idéntica para los sistemas de coordenadas curvilíneas ortogonales, pero como es habitual, tienen unidades invertidas entre sí.

Tenga en cuenta la siguiente igualdad importante: donde denota el delta de Kronecker generalizado .$${\displaystyle \mathbf {b} ^{i}\cdot \mathbf {b} _{j}=\delta _{j}^{i}}$$${\displaystyle \delta _{j}^{i}}$

Un vector v se puede especificar en términos de cualquiera de las bases, es decir,

${\displaystyle \mathbf {v} =v^{1}\mathbf {b} _{1}+v^{2}\mathbf {b} _{2}+v^{3}\mathbf {b} _{3}=v_{1}\mathbf {b} ^{1}+v_{2}\mathbf {b} ^{2}+v_{3}\mathbf {b} ^{3}}$

Utilizando la convención de suma de Einstein, los vectores base se relacionan con los componentes mediante ^{[2] : 30–32}

${\displaystyle \mathbf {v} \cdot \mathbf {b} ^{i}=v^{k}\mathbf {b} _{k}\cdot \mathbf {b} ^{i}=v^{k}\delta _{k}^{i}=v^{i}}$

${\displaystyle \mathbf {v} \cdot \mathbf {b} _{i}=v_{k}\mathbf {b} ^{k}\cdot \mathbf {b} _{i}=v_{k}\delta _{i}^{k}=v_{i}}$

y

${\displaystyle \mathbf {v} \cdot \mathbf {b} _{i}=v^{k}\mathbf {b} _{k}\cdot \mathbf {b} _{i}=g_{ki}v^{k}}$

${\displaystyle \mathbf {v} \cdot \mathbf {b} ^{i}=v_{k}\mathbf {b} ^{k}\cdot \mathbf {b} ^{i}=g^{ki}v_{k}}$

donde g es el tensor métrico (ver más abajo).

Un vector puede especificarse con coordenadas covariantes (índices reducidos, escritos v _k ) o coordenadas contravariantes (índices elevados, escritos v ^k ). A partir de las sumas de vectores anteriores, se puede ver que las coordenadas contravariantes están asociadas con vectores base covariantes, y las coordenadas covariantes están asociadas con vectores base contravariantes.

Una característica clave de la representación de vectores y tensores en términos de componentes indexados y vectores base es la invariancia en el sentido de que los componentes vectoriales que se transforman de manera covariante (o contravariante) se emparejan con vectores base que se transforman de manera contravariante (o covariante).

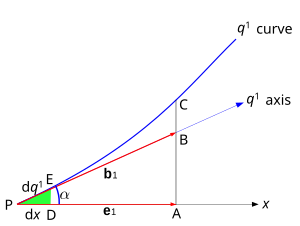
Considere la curva unidimensional que se muestra en la Fig. 3. En el punto P , tomado como origen , x es una de las coordenadas cartesianas, y q ¹ es una de las coordenadas curvilíneas. El vector base local (no unitario) es b ₁ (anotado h ₁ arriba, con b reservado para vectores unitarios) y está construido sobre el eje q ¹ que es una tangente a esa línea de coordenadas en el punto P . El eje q ¹ y por lo tanto el vector b ₁ forman un ángulo con el eje cartesiano x y el vector base cartesiano e ₁ .${\displaystyle \alpha }$

Se puede ver desde el triángulo PAB que

${\displaystyle \cos \alpha ={\cfrac {|\mathbf {e} _{1}|}{|\mathbf {b} _{1}|}}\quad \Rightarrow \quad |\mathbf {e} _{1}|=|\mathbf {b} _{1}|\cos \alpha }$

donde | e ₁ |, | b ₁ | son las magnitudes de los dos vectores base, es decir, las intersecciones escalares PB y PA . PA es también la proyección de b ₁ sobre el eje x .

Sin embargo, este método para transformaciones de vectores base utilizando cosenos direccionales no es aplicable a coordenadas curvilíneas por las siguientes razones:

1. Al aumentar la distancia desde P , el ángulo entre la línea curva q ¹ y el eje cartesiano x se desvía cada vez más de .${\displaystyle \alpha }$
2. A la distancia PB el ángulo verdadero es el que forma la tangente en el punto C con el eje x y este último ángulo es claramente distinto de .${\displaystyle \alpha }$

Los ángulos que la línea q ¹ y ese eje forman con el eje x se acercan en valor cuanto más nos acercamos al punto P y se vuelven exactamente iguales en P .

Sea el punto E situado muy cerca de P , tan cerca que la distancia PE sea infinitesimalmente pequeña. Entonces, PE medido en el eje q ¹ casi coincide con PE medido en la línea q ¹ . Al mismo tiempo, la relación PD/PE ( siendo PD la proyección de PE en el eje x ) se vuelve casi exactamente igual a .${\displaystyle \cos \alpha }$

Sean los puntos de corte infinitesimalmente pequeños PD y PE etiquetados, respectivamente, como dx y d q ¹ . Entonces

${\displaystyle \cos \alpha ={\cfrac {dx}{dq^{1}}}={\frac {|\mathbf {e} _{1}|}{|\mathbf {b} _{1}|}}}$.

De este modo, los cosenos direccionales pueden sustituirse en las transformaciones con las razones más exactas entre los puntos de corte de coordenadas infinitesimalmente pequeños. De ello se deduce que el componente (proyección) de b ₁ sobre el eje x es

${\displaystyle p^{1}=\mathbf {b} _{1}\cdot {\cfrac {\mathbf {e} _{1}}{|\mathbf {e} _{1}|}}=|\mathbf {b} _{1}|{\cfrac {|\mathbf {e} _{1}|}{|\mathbf {e} _{1}|}}\cos \alpha =|\mathbf {b} _{1}|{\cfrac {dx}{dq^{1}}}\quad \Rightarrow \quad {\cfrac {p^{1}}{|\mathbf {b} _{1}|}}={\cfrac {dx}{dq^{1}}}}$.

Si q ⁱ = q ⁱ ( x ₁ , x ₂ , x ₃ ) y x _i = x _i ( q ¹ , q ² , q ³ ) son funciones suaves (continuamente diferenciables), las razones de transformación se pueden escribir como y . Es decir, esas razones son derivadas parciales de coordenadas pertenecientes a un sistema con respecto a coordenadas pertenecientes al otro sistema.${\displaystyle {\cfrac {\partial q^{i}}{\partial x_{j}}}}$${\displaystyle {\cfrac {\partial x_{i}}{\partial q^{j}}}}$

Haciendo lo mismo para las coordenadas en las otras 2 dimensiones, b ₁ se puede expresar como:

${\displaystyle \mathbf {b} _{1}=p^{1}\mathbf {e} _{1}+p^{2}\mathbf {e} _{2}+p^{3}\mathbf {e} _{3}={\cfrac {\partial x_{1}}{\partial q^{1}}}\mathbf {e} _{1}+{\cfrac {\partial x_{2}}{\partial q^{1}}}\mathbf {e} _{2}+{\cfrac {\partial x_{3}}{\partial q^{1}}}\mathbf {e} _{3}}$

Se cumplen ecuaciones similares para b ₂ y b ₃ de modo que la base estándar { e ₁ , e ₂ , e ₃ } se transforma en una base local (ordenada y normalizada ) { b ₁ , b ₂ , b ₃ } mediante el siguiente sistema de ecuaciones:

${\displaystyle {\begin{aligned}\mathbf {b} _{1}&={\cfrac {\partial x_{1}}{\partial q^{1}}}\mathbf {e} _{1}+{\cfrac {\partial x_{2}}{\partial q^{1}}}\mathbf {e} _{2}+{\cfrac {\partial x_{3}}{\partial q^{1}}}\mathbf {e} _{3}\\\mathbf {b} _{2}&={\cfrac {\partial x_{1}}{\partial q^{2}}}\mathbf {e} _{1}+{\cfrac {\partial x_{2}}{\partial q^{2}}}\mathbf {e} _{2}+{\cfrac {\partial x_{3}}{\partial q^{2}}}\mathbf {e} _{3}\\\mathbf {b} _{3}&={\cfrac {\partial x_{1}}{\partial q^{3}}}\mathbf {e} _{1}+{\cfrac {\partial x_{2}}{\partial q^{3}}}\mathbf {e} _{2}+{\cfrac {\partial x_{3}}{\partial q^{3}}}\mathbf {e} _{3}\end{aligned}}}$

Por razonamiento análogo, se puede obtener la transformación inversa de base local a base estándar:

${\displaystyle {\begin{aligned}\mathbf {e} _{1}&={\cfrac {\partial q^{1}}{\partial x_{1}}}\mathbf {b} _{1}+{\cfrac {\partial q^{2}}{\partial x_{1}}}\mathbf {b} _{2}+{\cfrac {\partial q^{3}}{\partial x_{1}}}\mathbf {b} _{3}\\\mathbf {e} _{2}&={\cfrac {\partial q^{1}}{\partial x_{2}}}\mathbf {b} _{1}+{\cfrac {\partial q^{2}}{\partial x_{2}}}\mathbf {b} _{2}+{\cfrac {\partial q^{3}}{\partial x_{2}}}\mathbf {b} _{3}\\\mathbf {e} _{3}&={\cfrac {\partial q^{1}}{\partial x_{3}}}\mathbf {b} _{1}+{\cfrac {\partial q^{2}}{\partial x_{3}}}\mathbf {b} _{2}+{\cfrac {\partial q^{3}}{\partial x_{3}}}\mathbf {b} _{3}\end{aligned}}}$

Los sistemas de ecuaciones lineales anteriores se pueden escribir en forma matricial utilizando la convención de suma de Einstein como

${\displaystyle {\cfrac {\partial x_{i}}{\partial q^{k}}}\mathbf {e} _{i}=\mathbf {b} _{k},\quad {\cfrac {\partial q^{i}}{\partial x_{k}}}\mathbf {b} _{i}=\mathbf {e} _{k}}$.

Esta matriz de coeficientes del sistema lineal es la matriz jacobiana (y su inversa) de la transformación. Estas son las ecuaciones que se pueden utilizar para transformar una base cartesiana en una base curvilínea y viceversa.

En tres dimensiones, las formas expandidas de estas matrices son

${\displaystyle \mathbf {J} ={\begin{bmatrix}{\cfrac {\partial x_{1}}{\partial q^{1}}}&{\cfrac {\partial x_{1}}{\partial q^{2}}}&{\cfrac {\partial x_{1}}{\partial q^{3}}}\\{\cfrac {\partial x_{2}}{\partial q^{1}}}&{\cfrac {\partial x_{2}}{\partial q^{2}}}&{\cfrac {\partial x_{2}}{\partial q^{3}}}\\{\cfrac {\partial x_{3}}{\partial q^{1}}}&{\cfrac {\partial x_{3}}{\partial q^{2}}}&{\cfrac {\partial x_{3}}{\partial q^{3}}}\\\end{bmatrix}},\quad \mathbf {J} ^{-1}={\begin{bmatrix}{\cfrac {\partial q^{1}}{\partial x_{1}}}&{\cfrac {\partial q^{1}}{\partial x_{2}}}&{\cfrac {\partial q^{1}}{\partial x_{3}}}\\{\cfrac {\partial q^{2}}{\partial x_{1}}}&{\cfrac {\partial q^{2}}{\partial x_{2}}}&{\cfrac {\partial q^{2}}{\partial x_{3}}}\\{\cfrac {\partial q^{3}}{\partial x_{1}}}&{\cfrac {\partial q^{3}}{\partial x_{2}}}&{\cfrac {\partial q^{3}}{\partial x_{3}}}\\\end{bmatrix}}}$

En la transformación inversa (segundo sistema de ecuaciones), las incógnitas son los vectores base curvilíneos. Para cualquier posición específica solo puede existir un único conjunto de vectores base (de lo contrario, la base no está bien definida en ese punto). Esta condición se cumple si y solo si el sistema de ecuaciones tiene una única solución. En álgebra lineal , un sistema de ecuaciones lineales tiene una única solución (no trivial) solo si el determinante de su matriz de sistema no es cero:

${\displaystyle \det(\mathbf {J} ^{-1})\neq 0}$

lo que muestra la razón detrás del requisito anterior relativo al determinante jacobiano inverso.

El formalismo se extiende a cualquier dimensión finita de la siguiente manera.

Consideremos el espacio euclidiano real n -dimensional, es decir R ⁿ = R × R × ... × R ( n veces) donde R es el conjunto de números reales y × denota el producto cartesiano , que es un espacio vectorial .

Las coordenadas de este espacio se pueden denotar por: x = ( x ₁ , x ₂ ,..., x _n ). Como se trata de un vector (un elemento del espacio vectorial), se puede escribir como:

${\displaystyle \mathbf {x} =\sum _{i=1}^{n}x_{i}\mathbf {e} ^{i}}$

donde e ¹ = (1,0,0...,0), e ² = (0,1,0...,0), e ³ = (0,0,1...,0),..., e ⁿ = (0,0,0...,1) es el conjunto base estándar de vectores para el espacio R ⁿ , e i = 1, 2,... n es un índice que etiqueta los componentes. Cada vector tiene exactamente un componente en cada dimensión (o "eje") y son mutuamente ortogonales ( perpendiculares ) y normalizados (tienen magnitud unitaria ).

En términos más generales, podemos definir vectores base b _i de modo que dependan de q = ( q ₁ , q ₂ ,..., q _n ), es decir, que cambien de un punto a otro: b _i = b _i ( q ). En cuyo caso, para definir el mismo punto x en términos de esta base alternativa: las coordenadas con respecto a esta base v _i también dependen necesariamente de x , es decir, v _i = v _i ( x ). Entonces, un vector v en este espacio, con respecto a estas coordenadas alternativas y vectores base, se puede desarrollar como una combinación lineal en esta base (lo que simplemente significa multiplicar cada vector base e _i por un número v _i – multiplicación escalar ):

${\displaystyle \mathbf {v} =\sum _{j=1}^{n}{\bar {v}}^{j}\mathbf {b} _{j}=\sum _{j=1}^{n}{\bar {v}}^{j}(\mathbf {q} )\mathbf {b} _{j}(\mathbf {q} )}$

La suma vectorial que describe v en la nueva base está compuesta de diferentes vectores, aunque la suma en sí sigue siendo la misma.

Desde una perspectiva más general y abstracta, un sistema de coordenadas curvilíneas es simplemente un parche de coordenadas en la variedad diferenciable E ^{n (} espacio euclidiano n-dimensional ) que es difeomorfo al parche de coordenadas cartesianas en la variedad. ^[3] Dos parches de coordenadas difeomorfos en una variedad diferencial no necesitan superponerse de manera diferenciable. Con esta definición simple de un sistema de coordenadas curvilíneas, todos los resultados que siguen a continuación son simplemente aplicaciones de teoremas estándar en topología diferencial .

Las funciones de transformación son tales que existe una relación uno a uno entre los puntos en las coordenadas "antiguas" y "nuevas", es decir, esas funciones son biyecciones y cumplen los siguientes requisitos dentro de sus dominios :

El álgebra elemental de vectores y tensores en coordenadas curvilíneas se utiliza en algunas de las publicaciones científicas más antiguas sobre mecánica y física y puede ser indispensable para comprender trabajos de principios y mediados del siglo XX, por ejemplo, el texto de Green y Zerna. ^[5] En esta sección se dan algunas relaciones útiles en el álgebra de vectores y tensores de segundo orden en coordenadas curvilíneas. La notación y el contenido provienen principalmente de Ogden, ^[6] Naghdi, ^[7] Simmonds, ^[2] Green y Zerna, ^[5] Basar y Weichert, ^[8] y Ciarlet. ^[9]

Un tensor de segundo orden se puede expresar como

${\displaystyle {\boldsymbol {S}}=S^{ij}\mathbf {b} _{i}\otimes \mathbf {b} _{j}=S^{i}{}_{j}\mathbf {b} _{i}\otimes \mathbf {b} ^{j}=S_{i}{}^{j}\mathbf {b} ^{i}\otimes \mathbf {b} _{j}=S_{ij}\mathbf {b} ^{i}\otimes \mathbf {b} ^{j}}$

donde denota el producto tensorial . Los componentes S ^ij se denominan componentes contravariantes , S ⁱ _j componentes mixtos covariantes por la derecha , S _i ^j componentes mixtos covariantes por la izquierda y S _ij componentes covariantes del tensor de segundo orden. Los componentes del tensor de segundo orden están relacionados por${\displaystyle \scriptstyle \otimes }$

${\displaystyle S^{ij}=g^{ik}S_{k}{}^{j}=g^{jk}S^{i}{}_{k}=g^{ik}g^{j\ell }S_{k\ell }}$

En cada punto, se puede construir un pequeño elemento de línea d x , por lo que el cuadrado de la longitud del elemento de línea es el producto escalar d x • d x y se llama métrica del espacio , dado por:

${\displaystyle d\mathbf {x} \cdot d\mathbf {x} ={\cfrac {\partial x_{i}}{\partial q^{j}}}{\cfrac {\partial x_{i}}{\partial q^{k}}}dq^{j}dq^{k}}$.

La siguiente parte de la ecuación anterior

${\displaystyle {\cfrac {\partial x_{k}}{\partial q^{i}}}{\cfrac {\partial x_{k}}{\partial q^{j}}}=g_{ij}(q^{i},q^{j})=\mathbf {b} _{i}\cdot \mathbf {b} _{j}}$

es un tensor simétrico llamado tensor fundamental (o métrico) del espacio euclidiano en coordenadas curvilíneas.

Los índices se pueden aumentar o disminuir mediante la métrica:

${\displaystyle v^{i}=g^{ik}v_{k}}$

Definiendo los factores de escala h _i mediante

${\displaystyle h_{i}h_{j}=g_{ij}=\mathbf {b} _{i}\cdot \mathbf {b} _{j}\quad \Rightarrow \quad h_{i}={\sqrt {g_{ii}}}=\left|\mathbf {b} _{i}\right|=\left|{\cfrac {\partial \mathbf {x} }{\partial q^{i}}}\right|}$

da una relación entre el tensor métrico y los coeficientes de Lamé, y

${\displaystyle g_{ij}={\cfrac {\partial \mathbf {x} }{\partial q^{i}}}\cdot {\cfrac {\partial \mathbf {x} }{\partial q^{j}}}=\left(h_{ki}\mathbf {e} _{k}\right)\cdot \left(h_{mj}\mathbf {e} _{m}\right)=h_{ki}h_{kj}}$

donde h _ij son los coeficientes de Lamé. Para una base ortogonal también tenemos:

${\displaystyle g=g_{11}g_{22}g_{33}=h_{1}^{2}h_{2}^{2}h_{3}^{2}\quad \Rightarrow \quad {\sqrt {g}}=h_{1}h_{2}h_{3}=J}$

Si consideramos coordenadas polares para R ² ,

${\displaystyle (x,y)=(r\cos \theta ,r\sin \theta )}$

(r, θ) son las coordenadas curvilíneas, y el determinante jacobiano de la transformación ( r ,θ) → ( r cos θ, r sin θ) es r .

Los vectores de base ortogonales son b _r = (cos θ, sin θ), b _θ = (−r sin θ, r cos θ). Los factores de escala son h _r = 1 y h _θ = r . El tensor fundamental es g ₁₁ =1, g ₂₂ = r ² , g ₁₂ = g ₂₁ =0.

En una base dextrógira ortonormal, el tensor alterno de tercer orden se define como

${\displaystyle {\boldsymbol {\mathcal {E}}}=\varepsilon _{ijk}\mathbf {e} ^{i}\otimes \mathbf {e} ^{j}\otimes \mathbf {e} ^{k}}$

En una base curvilínea general el mismo tensor puede expresarse como

${\displaystyle {\boldsymbol {\mathcal {E}}}={\mathcal {E}}_{ijk}\mathbf {b} ^{i}\otimes \mathbf {b} ^{j}\otimes \mathbf {b} ^{k}={\mathcal {E}}^{ijk}\mathbf {b} _{i}\otimes \mathbf {b} _{j}\otimes \mathbf {b} _{k}}$

También se puede demostrar que

${\displaystyle {\mathcal {E}}^{ijk}={\cfrac {1}{J}}\varepsilon _{ijk}={\cfrac {1}{+{\sqrt {g}}}}\varepsilon _{ijk}}$

Símbolos de Christoffel del primer tipo${\displaystyle \Gamma _{kij}}$

${\displaystyle \mathbf {b} _{i,j}={\frac {\partial \mathbf {b} _{i}}{\partial q^{j}}}=\mathbf {b} ^{k}\Gamma _{kij}\quad \Rightarrow \quad \mathbf {b} _{k}\cdot \mathbf {b} _{i,j}=\Gamma _{kij}}$

donde la coma denota una derivada parcial (ver Cálculo de Ricci ). Para expresar Γ _kij en términos de g _ij ,

${\displaystyle {\begin{aligned}g_{ij,k}&=(\mathbf {b} _{i}\cdot \mathbf {b} _{j})_{,k}=\mathbf {b} _{i,k}\cdot \mathbf {b} _{j}+\mathbf {b} _{i}\cdot \mathbf {b} _{j,k}=\Gamma _{jik}+\Gamma _{ijk}\\g_{ik,j}&=(\mathbf {b} _{i}\cdot \mathbf {b} _{k})_{,j}=\mathbf {b} _{i,j}\cdot \mathbf {b} _{k}+\mathbf {b} _{i}\cdot \mathbf {b} _{k,j}=\Gamma _{kij}+\Gamma _{ikj}\\g_{jk,i}&=(\mathbf {b} _{j}\cdot \mathbf {b} _{k})_{,i}=\mathbf {b} _{j,i}\cdot \mathbf {b} _{k}+\mathbf {b} _{j}\cdot \mathbf {b} _{k,i}=\Gamma _{kji}+\Gamma _{jki}\end{aligned}}}$

Desde

${\displaystyle \mathbf {b} _{i,j}=\mathbf {b} _{j,i}\quad \Rightarrow \quad \Gamma _{kij}=\Gamma _{kji}}$

Al utilizarlos para reorganizar las relaciones anteriores se obtiene

${\displaystyle \Gamma _{kij}={\frac {1}{2}}(g_{ik,j}+g_{jk,i}-g_{ij,k})={\frac {1}{2}}[(\mathbf {b} _{i}\cdot \mathbf {b} _{k})_{,j}+(\mathbf {b} _{j}\cdot \mathbf {b} _{k})_{,i}-(\mathbf {b} _{i}\cdot \mathbf {b} _{j})_{,k}]}$

Símbolos de Christoffel del segundo tipo${\displaystyle \Gamma ^{k}{}_{ji}}$

${\displaystyle \Gamma ^{k}{}_{ij}=g^{kl}\Gamma _{lij}=\Gamma ^{k}{}_{ji},\quad {\cfrac {\partial \mathbf {b} _{i}}{\partial q^{j}}}=\mathbf {b} _{k}\Gamma ^{k}{}_{ij}}$

Esto implica que

${\displaystyle \Gamma ^{k}{}_{ij}={\cfrac {\partial \mathbf {b} _{i}}{\partial q^{j}}}\cdot \mathbf {b} ^{k}=-\mathbf {b} _{i}\cdot {\cfrac {\partial \mathbf {b} ^{k}}{\partial q^{j}}}\quad }$desde .${\displaystyle \quad {\cfrac {\partial }{\partial q^{j}}}(\mathbf {b} _{i}\cdot \mathbf {b} ^{k})=0}$

Otras relaciones que siguen son

${\displaystyle {\cfrac {\partial \mathbf {b} ^{i}}{\partial q^{j}}}=-\Gamma ^{i}{}_{jk}\mathbf {b} ^{k},\quad {\boldsymbol {\nabla }}\mathbf {b} _{i}=\Gamma ^{k}{}_{ij}\mathbf {b} _{k}\otimes \mathbf {b} ^{j},\quad {\boldsymbol {\nabla }}\mathbf {b} ^{i}=-\Gamma ^{i}{}_{jk}\mathbf {b} ^{k}\otimes \mathbf {b} ^{j}}$

Es necesario realizar ajustes en el cálculo de las integrales de línea , superficie y volumen . Para simplificar, lo siguiente se limita a tres dimensiones y coordenadas curvilíneas ortogonales. Sin embargo, los mismos argumentos se aplican para espacios n -dimensionales. Cuando el sistema de coordenadas no es ortogonal, hay algunos términos adicionales en las expresiones.

Simmonds, ^[2] en su libro sobre análisis tensorial , cita a Albert Einstein diciendo ^[10]

La magia de esta teoría difícilmente dejará de imponerse a cualquiera que la haya comprendido verdaderamente; representa un auténtico triunfo del método del cálculo diferencial absoluto, fundado por Gauss, Riemann, Ricci y Lévi-Civita.

El cálculo vectorial y tensorial en coordenadas curvilíneas generales se utiliza en el análisis tensorial en variedades curvilíneas de cuatro dimensiones en la relatividad general , ^[11] en la mecánica de capas curvas , ^[9] en el examen de las propiedades de invariancia de las ecuaciones de Maxwell , lo que ha sido de interés en metamateriales ^{[12] [13]} y en muchos otros campos.

En esta sección se presentan algunas relaciones útiles en el cálculo de vectores y tensores de segundo orden en coordenadas curvilíneas. La notación y el contenido provienen principalmente de Ogden, ^[14] Simmonds, ^[2] Green y Zerna, ^[5] Basar y Weichert, ^[8] y Ciarlet. ^[9]

Sea φ = φ( x ) un campo escalar bien definido y v = v ( x ) un campo vectorial bien definido, y λ ₁ , λ ₂ ... parámetros de las coordenadas

Operador	Campo escalar	Campo vectorial
Integral de línea	${\displaystyle \int _{C}\varphi (\mathbf {x} )ds=\int _{a}^{b}\varphi (\mathbf {x} (\lambda ))\left|{\partial \mathbf {x} \over \partial \lambda }\right|d\lambda }$	${\displaystyle \int _{C}\mathbf {v} (\mathbf {x} )\cdot d\mathbf {s} =\int _{a}^{b}\mathbf {v} (\mathbf {x} (\lambda ))\cdot \left({\partial \mathbf {x} \over \partial \lambda }\right)d\lambda }$
Integral de superficie	${\displaystyle \int _{S}\varphi (\mathbf {x} )dS=\iint _{T}\varphi (\mathbf {x} (\lambda _{1},\lambda _{2}))\left|{\partial \mathbf {x} \over \partial \lambda _{1}}\times {\partial \mathbf {x} \over \partial \lambda _{2}}\right|d\lambda _{1}d\lambda _{2}}$	${\displaystyle \int _{S}\mathbf {v} (\mathbf {x} )\cdot dS=\iint _{T}\mathbf {v} (\mathbf {x} (\lambda _{1},\lambda _{2}))\cdot \left({\partial \mathbf {x} \over \partial \lambda _{1}}\times {\partial \mathbf {x} \over \partial \lambda _{2}}\right)d\lambda _{1}d\lambda _{2}}$
Integral de volumen	${\displaystyle \iiint _{V}\varphi (x,y,z)dV=\iiint _{V}\chi (q_{1},q_{2},q_{3})Jdq_{1}dq_{2}dq_{3}}$	${\displaystyle \iiint _{V}\mathbf {u} (x,y,z)dV=\iiint _{V}\mathbf {v} (q_{1},q_{2},q_{3})Jdq_{1}dq_{2}dq_{3}}$

Las expresiones para el gradiente, la divergencia y el laplaciano se pueden extender directamente a n dimensiones, sin embargo el rizo solo se define en 3D.

El campo vectorial b _i es tangente a la curva de coordenadas q ⁱ y forma una base natural en cada punto de la curva. Esta base, como se explicó al principio de este artículo, también se denomina base curvilínea covariante . También podemos definir una base recíproca o base curvilínea contravariante , b ⁱ . Todas las relaciones algebraicas entre los vectores base, como se explicó en la sección sobre álgebra tensorial, se aplican a la base natural y su recíproco en cada punto x .

Operador	Campo escalar	Campo vectorial	Campo tensorial de segundo orden
Gradiente	${\displaystyle \nabla \varphi ={\cfrac {1}{h_{i}}}{\partial \varphi \over \partial q^{i}}\mathbf {b} ^{i}}$	${\displaystyle \nabla \mathbf {v} ={\cfrac {1}{h_{i}^{2}}}{\partial \mathbf {v} \over \partial q^{i}}\otimes \mathbf {b} _{i}}$	${\displaystyle {\boldsymbol {\nabla }}{\boldsymbol {S}}={\cfrac {\partial {\boldsymbol {S}}}{\partial q^{i}}}\otimes \mathbf {b} ^{i}}$
Divergencia	N / A	${\displaystyle \nabla \cdot \mathbf {v} ={\cfrac {1}{\prod _{j}h_{j}}}{\frac {\partial }{\partial q^{i}}}(v^{i}\prod _{j\neq i}h_{j})}$	${\displaystyle ({\boldsymbol {\nabla }}\cdot {\boldsymbol {S}})\cdot \mathbf {a} ={\boldsymbol {\nabla }}\cdot ({\boldsymbol {S}}\cdot \mathbf {a} )}$ donde a es un vector constante arbitrario. En coordenadas curvilíneas, ${\displaystyle {\boldsymbol {\nabla }}\cdot {\boldsymbol {S}}=\left[{\cfrac {\partial S_{ij}}{\partial q^{k}}}-\Gamma _{ki}^{l}S_{lj}-\Gamma _{kj}^{l}S_{il}\right]g^{ik}\mathbf {b} ^{j}}$
Laplaciano	${\displaystyle \nabla ^{2}\varphi ={\cfrac {1}{\prod _{j}h_{j}}}{\frac {\partial }{\partial q^{i}}}\left({\cfrac {\prod _{j}h_{j}}{h_{i}^{2}}}{\frac {\partial \varphi }{\partial q^{i}}}\right)}$	${\displaystyle \nabla ^{2}\mathbf {v} \equiv \nabla \nabla \cdot \mathbf {v} -\nabla \times \nabla \times \mathbf {v} }$ ${\displaystyle ~~~={\hat {\mathbf {x} }}\nabla ^{2}v_{x}+{\hat {\mathbf {y} }}\nabla ^{2}v_{y}+{\hat {\mathbf {z} }}\nabla ^{2}v_{z}}$(Primera igualdad solo en 3D; segunda igualdad solo en componentes cartesianos)
Rizo	N / A	Solo para campos vectoriales en 3D, ${\displaystyle \nabla \times \mathbf {v} ={\frac {1}{h_{1}h_{2}h_{3}}}\mathbf {e} _{i}\epsilon _{ijk}h_{i}{\frac {\partial (h_{k}v_{k})}{\partial q^{j}}}}$ ¿Dónde está el símbolo de Levi-Civita ?${\displaystyle \epsilon _{ijk}}$	Ver Curl de un campo tensorial