Transición de fase
Proceso físico de transición entre estados básicos de la materia.

Este diagrama muestra la nomenclatura de las diferentes transiciones de fase.

En física , química y otros campos relacionados como la biología, una transición de fase (o cambio de fase ) es el proceso físico de transición entre un estado de un medio y otro. Comúnmente, el término se usa para referirse a cambios entre los estados básicos de la materia : sólido , líquido y gas , y en casos raros, plasma . Una fase de un sistema termodinámico y los estados de la materia tienen propiedades físicas uniformes . Durante una transición de fase de un medio dado, ciertas propiedades del medio cambian como resultado del cambio de las condiciones externas, como la temperatura o la presión . Este puede ser un cambio discontinuo; por ejemplo, un líquido puede convertirse en gas al calentarse hasta su punto de ebullición , lo que resulta en un cambio abrupto en el volumen. La identificación de las condiciones externas en las que ocurre una transformación define el punto de transición de fase.

Tipos de transición de fase

Estados de la materia

Un diagrama de fases simplificado para el agua , que muestra si el hielo sólido, el agua líquida o el vapor de agua gaseoso son los más estables en diferentes combinaciones de temperatura y presión.

Las transiciones de fase se refieren comúnmente a cuando una sustancia se transforma de uno de los cuatro estados de la materia a otro. En el punto de transición de fase de una sustancia, por ejemplo el punto de ebullición , las dos fases involucradas (líquido y vapor ) tienen energías libres idénticas y, por lo tanto, es igualmente probable que existan. Por debajo del punto de ebullición, el líquido es el estado más estable de los dos, mientras que por encima del punto de ebullición, la forma gaseosa es la más estable.

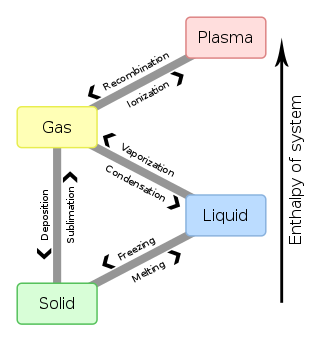
Las transiciones comunes entre las fases sólida, líquida y gaseosa de un solo componente, debido a los efectos de la temperatura y/o la presión , se identifican en la siguiente tabla:

Transiciones de fase de la materia (
)
A
De
SólidoLíquidoGasPlasma
Sólido
FusiónSublimación
LíquidoCongelación
Vaporización
GasDeclaraciónCondensación
Ionización
PlasmaRecombinación

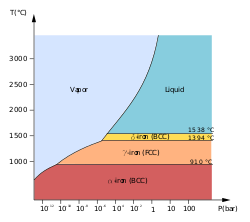
Para un solo componente, la fase más estable a diferentes temperaturas y presiones se puede mostrar en un diagrama de fases . Este tipo de diagrama suele representar estados en equilibrio. Una transición de fase suele ocurrir cuando la presión o la temperatura cambian y el sistema pasa de una región a otra, como el agua que pasa de líquido a sólido tan pronto como la temperatura cae por debajo del punto de congelación . Como excepción al caso habitual, a veces es posible cambiar el estado de un sistema diabáticamente (en lugar de adiabáticamente ) de tal manera que pueda pasar un punto de transición de fase sin sufrir una transición de fase. El estado resultante es metaestable , es decir, menos estable que la fase a la que se habría producido la transición, pero tampoco inestable. Esto ocurre en el sobrecalentamiento y el sobreenfriamiento , por ejemplo. Los estados metaestables no aparecen en los diagramas de fases habituales.

Estructural

Un diagrama de fases que muestra los alótropos del hierro , distinguiendo entre varias estructuras cristalinas diferentes, incluidas la ferrita (hierro α) y la austenita (hierro γ).

Las transiciones de fase también pueden ocurrir cuando un sólido cambia a una estructura diferente sin cambiar su composición química. En los elementos, esto se conoce como alotropía , mientras que en los compuestos se conoce como polimorfismo . El cambio de una estructura cristalina a otra, de un sólido cristalino a un sólido amorfo o de una estructura amorfa a otra ( poliamorfos ) son todos ejemplos de transiciones de fase de sólido a sólido.

La transformación martensítica se produce como una de las muchas transformaciones de fase en el acero al carbono y se erige como un modelo para las transformaciones de fase desplazativas . Transiciones de orden-desorden como en los aluminuros de titanio alfa . Al igual que con los estados de la materia, también hay una transformación de fase metaestable a equilibrio para las transiciones de fase estructurales. Un polimorfo metaestable que se forma rápidamente debido a una energía superficial menor se transformará a una fase de equilibrio si se le aplica suficiente entrada térmica para superar una barrera energética.

Magnético

Un diagrama de fases que muestra diferentes estructuras magnéticas en la misma estructura cristalina del monosiliciuro de manganeso .

Las transiciones de fase también pueden describir el cambio entre diferentes tipos de ordenamiento magnético . La más conocida es la transición entre las fases ferromagnética y paramagnética de los materiales magnéticos , que ocurre en lo que se denomina el punto de Curie . Otro ejemplo es la transición entre estructuras magnéticas conmensuradas o inconmensurables , como en el antimoniuro de cerio . Un modelo simplificado pero muy útil de las transiciones de fase magnéticas lo proporciona el modelo de Ising.

Mezclas

Un diagrama de fase binario que muestra los compuestos químicos más estables de titanio y níquel en diferentes proporciones de mezcla y temperaturas .

Las transiciones de fase que involucran soluciones y mezclas son más complicadas que las transiciones que involucran un solo compuesto. Mientras que los compuestos químicamente puros exhiben un único punto de fusión de temperatura entre las fases sólida y líquida, las mezclas pueden tener un único punto de fusión, conocido como fusión congruente , o tener diferentes temperaturas de liquidus y solidus , lo que resulta en un intervalo de temperatura donde el sólido y el líquido coexisten en equilibrio. Este suele ser el caso en soluciones sólidas , donde los dos componentes son isoestructurales.

También hay una serie de transiciones de fase que involucran tres fases: una transformación eutéctica , en la que un líquido monofásico de dos componentes se enfría y se transforma en dos fases sólidas. El mismo proceso, pero comenzando con un sólido en lugar de un líquido, se llama transformación eutectoide . Una transformación peritéctica , en la que un sólido monofásico de dos componentes se calienta y se transforma en una fase sólida y una fase líquida. Una reacción peritectoide es una reacción peritectoide, excepto que involucra solo fases sólidas. Una reacción monotéctica consiste en el cambio de un líquido a una combinación de un sólido y un segundo líquido, donde los dos líquidos muestran una brecha de miscibilidad . [1]

La separación en múltiples fases puede ocurrir a través de la descomposición espinodal , en la que una sola fase se enfría y se separa en dos composiciones diferentes.

Pueden ocurrir mezclas que no estén en equilibrio, como en la sobresaturación .

Otros ejemplos

Un pequeño trozo de argón sólido que se derrite rápidamente muestra dos cambios de fase simultáneos: la transición de sólido a líquido y de gas a líquido (mostrado por el vapor de agua condensado de color blanco).

Otros cambios de fase incluyen:

Las transiciones de fase se producen cuando la energía libre termodinámica de un sistema no es analítica para alguna elección de variables termodinámicas (cf. fases ). Esta condición generalmente se origina de las interacciones de un gran número de partículas en un sistema, y ​​no aparece en sistemas que son pequeños. Las transiciones de fase pueden ocurrir para sistemas no termodinámicos, donde la temperatura no es un parámetro. Algunos ejemplos incluyen: transiciones de fase cuánticas , transiciones de fase dinámicas y transiciones de fase topológicas (estructurales). En estos tipos de sistemas, otros parámetros toman el lugar de la temperatura. Por ejemplo, la probabilidad de conexión reemplaza a la temperatura para las redes de percolación.

Física de la materia condensada
Estados de la materia
Fenómenos de fase
Fases electrónicas
Fenómenos electrónicos
Fases magnéticas
Cuasipartículas
Materia blanda
Científicos

Clasificaciones

Clasificación de Ehrenfest

Paul Ehrenfest clasificó las transiciones de fase basándose en el comportamiento de la energía libre termodinámica como una función de otras variables termodinámicas. [5] Bajo este esquema, las transiciones de fase fueron etiquetadas por la derivada más baja de la energía libre que es discontinua en la transición. Las transiciones de fase de primer orden exhiben una discontinuidad en la primera derivada de la energía libre con respecto a alguna variable termodinámica. [6] Las diversas transiciones sólido/líquido/gas se clasifican como transiciones de primer orden porque involucran un cambio discontinuo en la densidad, que es la (inversa de la) primera derivada de la energía libre con respecto a la presión. Las transiciones de fase de segundo orden son continuas en la primera derivada (el parámetro de orden, que es la primera derivada de la energía libre con respecto al campo externo, es continuo a lo largo de la transición) pero exhiben discontinuidad en una segunda derivada de la energía libre. [6] Entre ellas se incluye la transición de fase ferromagnética en materiales como el hierro, donde la magnetización , que es la primera derivada de la energía libre con respecto a la intensidad del campo magnético aplicado, aumenta continuamente desde cero a medida que la temperatura desciende por debajo de la temperatura de Curie . La susceptibilidad magnética , la segunda derivada de la energía libre con el campo, cambia de forma discontinua. Según el esquema de clasificación de Ehrenfest, en principio podría haber transiciones de fase de tercer, cuarto y orden superior. Por ejemplo, la transición de fase de Gross-Witten-Wadia en la cromodinámica cuántica de red 2-d es una transición de fase de tercer orden. [7] [8] Los puntos de Curie de muchos ferromagnéticos también son una transición de tercer orden, como lo demuestra su calor específico que tiene un cambio repentino en la pendiente. [9] [10]

En la práctica, normalmente sólo se observan las transiciones de fase de primer y segundo orden. La transición de fase de segundo orden fue controvertida durante un tiempo, ya que parece requerir dos láminas de energía libre de Gibbs para oscilar exactamente, lo que es tan improbable que nunca ocurre en la práctica. Cornelis Gorter respondió a las críticas señalando que la superficie de energía libre de Gibbs podría tener dos láminas en un lado, pero sólo una lámina en el otro lado, creando una apariencia bifurcada. [11] ( [9] pp. 146--150)

La clasificación de Ehrenfest permite implícitamente transformaciones de fase continuas, en las que el carácter de enlace de un material cambia, pero no hay discontinuidad en ninguna derivada de energía libre. Un ejemplo de esto ocurre en los límites supercríticos entre líquido y gas .

El primer ejemplo de una transición de fase que no encajaba en la clasificación de Ehrenfest fue la solución exacta del modelo de Ising , descubierto en 1944 por Lars Onsager . El calor específico exacto difería de las aproximaciones de campo medio anteriores , que habían predicho que tiene una discontinuidad simple a la temperatura crítica. En cambio, el calor específico exacto tenía una divergencia logarítmica a la temperatura crítica. [12] En las décadas siguientes, la clasificación de Ehrenfest fue reemplazada por un esquema de clasificación simplificado que puede incorporar tales transiciones.

Clasificaciones modernas

En el esquema de clasificación moderno, las transiciones de fase se dividen en dos categorías amplias, denominadas de manera similar a las clases de Ehrenfest: [5]

Las transiciones de fase de primer orden son aquellas que implican un calor latente . Durante una transición de este tipo, un sistema absorbe o libera una cantidad fija (y normalmente grande) de energía por volumen. Durante este proceso, la temperatura del sistema se mantendrá constante a medida que se añade calor: el sistema se encuentra en un "régimen de fase mixta" en el que algunas partes del sistema han completado la transición y otras no. [13] [14]

Ejemplos conocidos son la fusión del hielo o la ebullición del agua (el agua no se convierte instantáneamente en vapor , sino que forma una mezcla turbulenta de agua líquida y burbujas de vapor). Yoseph Imry y Michael Wortis demostraron que el desorden extinguido puede ampliar una transición de primer orden. Es decir, la transformación se completa en un rango finito de temperaturas, pero los fenómenos como el sobreenfriamiento y el sobrecalentamiento sobreviven y se observa histéresis en el ciclo térmico. [15] [16] [17]

Las transiciones de fase de segundo orden también se denominan"transiciones de fase continuas". Se caracterizan por una susceptibilidad divergente, unalongitud de correlacióny undecaimiento dela ley de potenciala criticidad. Ejemplos de transiciones de fase de segundo orden son laferromagnética, la transición superconductora (para unsuperconductor de Tipo I,la transición de fase es de segundo orden en campo externo cero y para unsuperconductor de Tipo II,la transición de fase es de segundo orden tanto para las transiciones de estado normal-estado mixto como de estado mixto-estado superconductor) y lasuperfluida. A diferencia de la viscosidad, la expansión térmica y la capacidad térmica de los materiales amorfos muestran un cambio relativamente repentino en la temperatura de transición vítrea[18]que permite una detección precisa utilizandode calorimetría de barrido diferencial. Lev Landaupresentó unateoríafenomenológica de las transiciones de fase de segundo orden.

Además de transiciones de fase simples y aisladas, existen líneas de transición así como puntos multicríticos , al variar parámetros externos como el campo magnético o la composición.

Varias transiciones se conocen como transiciones de fase de orden infinito . Son continuas pero no rompen simetrías. El ejemplo más famoso es la transición de Kosterlitz-Thouless en el modelo XY bidimensional . Muchas transiciones de fase cuánticas , por ejemplo, en gases de electrones bidimensionales , pertenecen a esta clase.

La transición líquido-vítrea se observa en muchos polímeros y otros líquidos que pueden sobreenfriarse mucho por debajo del punto de fusión de la fase cristalina. Esto es atípico en varios aspectos. No es una transición entre estados fundamentales termodinámicos: se cree ampliamente que el verdadero estado fundamental es siempre cristalino. El vidrio es un estado de desorden extinguido , y su entropía, densidad, etc., dependen de la historia térmica. Por lo tanto, la transición vítrea es principalmente un fenómeno dinámico: al enfriar un líquido, los grados de libertad internos caen sucesivamente fuera del equilibrio. Algunos métodos teóricos predicen una transición de fase subyacente en el límite hipotético de tiempos de relajación infinitamente largos. [19] [20] No hay evidencia experimental directa que respalde la existencia de estas transiciones.

Propiedades características

Coexistencia de fases

Una transición de primer orden ensanchada por desorden ocurre en un rango finito de temperaturas donde la fracción de la fase de equilibrio de baja temperatura crece de cero a uno (100%) a medida que se reduce la temperatura. Esta variación continua de las fracciones coexistentes con la temperatura planteó posibilidades interesantes. Al enfriarse, algunos líquidos se vitrifican en un vidrio en lugar de transformarse en la fase cristalina de equilibrio. Esto sucede si la velocidad de enfriamiento es más rápida que una velocidad de enfriamiento crítica, y se atribuye a que los movimientos moleculares se vuelven tan lentos que las moléculas no pueden reorganizarse en las posiciones cristalinas. [21] Esta desaceleración ocurre por debajo de una temperatura de formación de vidrio T g , que puede depender de la presión aplicada. [18] [22] Si la transición de congelación de primer orden ocurre en un rango de temperaturas, y T g cae dentro de este rango, entonces existe una posibilidad interesante de que la transición se detenga cuando es parcial e incompleta. Extender estas ideas a las transiciones magnéticas de primer orden que se detienen a bajas temperaturas, resultó en la observación de transiciones magnéticas incompletas, con dos fases magnéticas coexistentes, hasta la temperatura más baja. Esta coexistencia de fases persistente, que se informó por primera vez en el caso de una transición de ferromagnético a antiferromagnético [23], ahora se ha informado en una variedad de transiciones magnéticas de primer orden. Estas incluyen materiales de manganita con magnetorresistencia colosal, [24] [25] materiales magnetocalóricos, [26] materiales con memoria de forma magnética, [27] y otros materiales. [28] La característica interesante de estas observaciones de T g dentro del rango de temperatura en el que ocurre la transición es que la transición magnética de primer orden está influenciada por el campo magnético, al igual que la transición estructural está influenciada por la presión. La relativa facilidad con la que se pueden controlar los campos magnéticos, en contraste con la presión, plantea la posibilidad de que se pueda estudiar la interacción entre T g y T c de manera exhaustiva. La coexistencia de fases en las transiciones magnéticas de primer orden permitirá entonces la resolución de problemas pendientes en la comprensión de los vidrios.

Puntos críticos

En cualquier sistema que contenga fases líquidas y gaseosas, existe una combinación especial de presión y temperatura, conocida como punto crítico , en el que la transición entre líquido y gas se convierte en una transición de segundo orden. Cerca del punto crítico, el fluido está lo suficientemente caliente y comprimido como para que la distinción entre las fases líquida y gaseosa sea casi inexistente. Esto está asociado con el fenómeno de la opalescencia crítica , una apariencia lechosa del líquido debido a las fluctuaciones de densidad en todas las longitudes de onda posibles (incluidas las de la luz visible).

Simetría

Las transiciones de fase a menudo implican un proceso de ruptura de simetría . Por ejemplo, el enfriamiento de un fluido para convertirse en un sólido cristalino rompe la simetría de traslación continua : cada punto del fluido tiene las mismas propiedades, pero cada punto de un cristal no tiene las mismas propiedades (a menos que los puntos se elijan de los puntos de la red cristalina). Por lo general, la fase de alta temperatura contiene más simetrías que la fase de baja temperatura debido a la ruptura espontánea de la simetría , con la excepción de ciertas simetrías accidentales (por ejemplo, la formación de partículas virtuales pesadas , que solo ocurre a bajas temperaturas). [29]

Parámetros del pedido

Un parámetro de orden es una medida del grado de orden a través de los límites en un sistema de transición de fase; normalmente varía entre cero en una fase (generalmente por encima del punto crítico) y distinto de cero en la otra. [30] En el punto crítico, la susceptibilidad del parámetro de orden generalmente divergirá.

Un ejemplo de parámetro de orden es la magnetización neta en un sistema ferromagnético que atraviesa una transición de fase. En el caso de las transiciones de líquido a gas, el parámetro de orden es la diferencia de densidades.

Desde una perspectiva teórica, los parámetros de orden surgen de la ruptura de la simetría. Cuando esto sucede, es necesario introducir una o más variables adicionales para describir el estado del sistema. Por ejemplo, en la fase ferromagnética , se debe proporcionar la magnetización neta , cuya dirección se eligió espontáneamente cuando el sistema se enfrió por debajo del punto de Curie . Sin embargo, tenga en cuenta que los parámetros de orden también se pueden definir para transiciones que no rompen la simetría. [ cita requerida ]

Algunas transiciones de fase, como las superconductoras y las ferromagnéticas, pueden tener parámetros de orden para más de un grado de libertad. En dichas fases, el parámetro de orden puede adoptar la forma de un número complejo, un vector o incluso un tensor, cuya magnitud tiende a cero en la transición de fase. [ cita requerida ]

También existen descripciones duales de transiciones de fase en términos de parámetros de desorden. Estos indican la presencia de excitaciones lineales, como líneas de vórtice o de defecto .

Relevancia en la cosmología

Las transiciones de fase que rompen la simetría desempeñan un papel importante en la cosmología . A medida que el universo se expandió y se enfrió, el vacío experimentó una serie de transiciones de fase que rompieron la simetría. Por ejemplo, la transición electrodébil rompió la simetría SU(2)×U(1) del campo electrodébil en la simetría U(1) del campo electromagnético actual. Esta transición es importante para explicar la asimetría entre la cantidad de materia y antimateria en el universo actual, según la teoría de la bariogénesis electrodébil .

Las transiciones de fase progresivas en un universo en expansión están implicadas en el desarrollo del orden en el universo, como lo ilustra el trabajo de Eric Chaisson [31] y David Layzer . [32]

Véase también teorías del orden relacional y orden y desorden .

Exponentes críticos y clases de universalidad

Las transiciones de fase continuas son más fáciles de estudiar que las transiciones de primer orden debido a la ausencia de calor latente , y se ha descubierto que tienen muchas propiedades interesantes. Los fenómenos asociados con las transiciones de fase continuas se denominan fenómenos críticos, debido a su asociación con puntos críticos.

Las transiciones de fase continuas se pueden caracterizar por parámetros conocidos como exponentes críticos . El más importante es quizás el exponente que describe la divergencia de la longitud de correlación térmica al acercarse a la transición. Por ejemplo, examinemos el comportamiento de la capacidad térmica cerca de una transición de este tipo. Variamos la temperatura T del sistema mientras mantenemos fijas todas las demás variables termodinámicas y descubrimos que la transición ocurre a una temperatura crítica T c . Cuando T está cerca de T c , la capacidad térmica C normalmente tiene un comportamiento de ley de potencia :

C ∝ | T c − T | − α . {\displaystyle C\propto |T_{\text{c}}-T|^{-\alpha }.}

La capacidad térmica de los materiales amorfos tiene un comportamiento tal cerca de la temperatura de transición vítrea donde el exponente crítico universal α = 0,59 [33] Un comportamiento similar, pero con el exponente ν en lugar de α , se aplica para la longitud de correlación.

El exponente ν es positivo. Esto es diferente con α . ​​Su valor real depende del tipo de transición de fase que estemos considerando.

Los exponentes críticos no son necesariamente los mismos por encima y por debajo de la temperatura crítica. Cuando una simetría continua se descompone explícitamente en una simetría discreta por anisotropías irrelevantes (en el sentido del grupo de renormalización), entonces algunos exponentes (como , el exponente de la susceptibilidad) no son idénticos. [34] γ {\displaystyle \gamma }

Para −1 < α < 0, la capacidad térmica tiene un "punto muerto" en la temperatura de transición. Este es el comportamiento del helio líquido en la transición lambda de un estado normal al estado superfluido , para el cual los experimentos han encontrado α = −0,013 ± 0,003. Al menos un experimento se realizó en las condiciones de gravedad cero de un satélite en órbita para minimizar las diferencias de presión en la muestra. [35] Este valor experimental de α concuerda con las predicciones teóricas basadas en la teoría de perturbación variacional . [36]

Para 0 < α < 1, la capacidad térmica diverge en la temperatura de transición (aunque, como α < 1, la entalpía permanece finita). Un ejemplo de este comportamiento es la transición de fase ferromagnética tridimensional. En el modelo tridimensional de Ising para imanes uniaxiales, estudios teóricos detallados han arrojado el exponente α ≈ +0,110.

Algunos sistemas modelo no obedecen a un comportamiento de ley de potencia. Por ejemplo, la teoría del campo medio predice una discontinuidad finita de la capacidad térmica a la temperatura de transición, y el modelo de Ising bidimensional tiene una divergencia logarítmica . Sin embargo, estos sistemas son casos límite y una excepción a la regla. Las transiciones de fase reales exhiben un comportamiento de ley de potencia.

Se definen otros exponentes críticos, β , γ , δ , ν y η , examinando el comportamiento de la ley de potencia de una cantidad física medible cerca de la transición de fase. Los exponentes están relacionados mediante relaciones de escala, como

β = γ / ( δ − 1 ) , ν = γ / ( 2 − η ) . {\displaystyle \beta =\gamma /(\delta -1),\quad \nu =\gamma /(2-\eta ).}

Se puede demostrar que sólo hay dos exponentes independientes, por ejemplo , ν y η .

Es un hecho notable que las transiciones de fase que surgen en diferentes sistemas a menudo poseen el mismo conjunto de exponentes críticos. Este fenómeno se conoce como universalidad . Por ejemplo, se ha descubierto que los exponentes críticos en el punto crítico líquido-gas son independientes de la composición química del fluido.

Lo que es más impresionante, pero comprensible por lo que hemos visto anteriormente, es que coinciden exactamente con los exponentes críticos de la transición de fase ferromagnética en imanes uniaxiales. Se dice que estos sistemas pertenecen a la misma clase de universalidad. La universalidad es una predicción de la teoría del grupo de renormalización de las transiciones de fase, que establece que las propiedades termodinámicas de un sistema cerca de una transición de fase dependen solo de un pequeño número de características, como la dimensionalidad y la simetría, y son insensibles a las propiedades microscópicas subyacentes del sistema. Una vez más, la divergencia de la longitud de correlación es el punto esencial.

Fenómenos críticos

Existen también otros fenómenos críticos; por ejemplo, además de las funciones estáticas, también existen dinámicas críticas . Como consecuencia, en una transición de fase se puede observar una desaceleración o aceleración crítica . Conectado al fenómeno anterior también está el fenómeno de fluctuaciones aumentadas antes de la transición de fase, como consecuencia de un menor grado de estabilidad de la fase inicial del sistema. Las grandes clases de universalidad estática de una transición de fase continua se dividen en clases de universalidad dinámica más pequeñas . Además de los exponentes críticos, también existen relaciones universales para ciertas funciones estáticas o dinámicas de los campos magnéticos y las diferencias de temperatura con respecto al valor crítico. [ cita requerida ]

Transiciones de fase en sistemas biológicos

Las transiciones de fase desempeñan muchas funciones importantes en los sistemas biológicos. Entre los ejemplos se incluyen la formación de la bicapa lipídica , la transición de espiral a glóbulo en el proceso de plegamiento de proteínas y fusión del ADN , las transiciones similares a cristales líquidos en el proceso de condensación del ADN y la unión cooperativa de ligandos al ADN y las proteínas con el carácter de transición de fase. [37]

En las membranas biológicas , las transiciones de fase de gel a líquido cristalino desempeñan un papel crítico en el funcionamiento fisiológico de las biomembranas. En la fase de gel, debido a la baja fluidez de las cadenas de acilo graso de los lípidos de la membrana, las proteínas de membrana tienen un movimiento restringido y, por lo tanto, están restringidas en el ejercicio de su función fisiológica. Las plantas dependen críticamente de la fotosíntesis de las membranas tilacoides de los cloroplastos que están expuestas a temperaturas ambientales frías. Las membranas tilacoides conservan la fluidez innata incluso a temperaturas relativamente bajas debido al alto grado de desorden de acilo graso permitido por su alto contenido de ácido linolénico , cadena de 18 carbonos con 3 enlaces dobles. [38] La temperatura de transición de fase de gel a líquido cristalino de las membranas biológicas se puede determinar mediante muchas técnicas, incluidas la calorimetría, la fluorescencia, la resonancia paramagnética electrónica de etiqueta de espín y la RMN registrando las mediciones del parámetro en cuestión en una serie de temperaturas de muestra. También se ha propuesto un método simple para su determinación a partir de las intensidades de línea de RMN de 13-C. [39]

Se ha propuesto que algunos sistemas biológicos podrían encontrarse cerca de puntos críticos. Los ejemplos incluyen redes neuronales en la retina de la salamandra, [40] bandadas de pájaros [41] redes de expresión génica en Drosophila, [42] y plegamiento de proteínas. [43] Sin embargo, no está claro si razones alternativas podrían explicar algunos de los fenómenos que apoyan los argumentos de criticidad. [44] También se ha sugerido que los organismos biológicos comparten dos propiedades clave de las transiciones de fase: el cambio de comportamiento macroscópico y la coherencia de un sistema en un punto crítico. [45] Las transiciones de fase son una característica destacada del comportamiento motor en los sistemas biológicos. [46] Las transiciones espontáneas de la marcha, [47] así como las desvinculaciones de tareas motoras inducidas por la fatiga, [48] muestran un comportamiento crítico típico como una insinuación del cambio cualitativo repentino del patrón de comportamiento motor previamente estable.

La característica característica de las transiciones de fase de segundo orden es la aparición de fractales en algunas propiedades sin escala . Se sabe desde hace mucho tiempo que los glóbulos de proteínas se forman mediante interacciones con el agua. Hay 20 aminoácidos que forman grupos laterales en las cadenas de péptidos de proteínas que van desde hidrófilos a hidrófobos, lo que hace que los primeros se encuentren cerca de la superficie globular, mientras que los segundos se encuentran más cerca del centro globular. Se descubrieron veinte fractales en áreas de superficie asociadas a solventes de > 5000 segmentos de proteínas. [49] La existencia de estos fractales demuestra que las proteínas funcionan cerca de puntos críticos de transiciones de fase de segundo orden.

En grupos de organismos sometidos a estrés (cuando se acercan a transiciones críticas), las correlaciones tienden a aumentar, mientras que, al mismo tiempo, las fluctuaciones también aumentan. Este efecto está respaldado por muchos experimentos y observaciones de grupos de personas, ratones, árboles y plantas herbáceas. [50]

Transiciones de fase en los sistemas sociales

Se ha planteado la hipótesis de que las transiciones de fase se producen en sistemas sociales considerados como sistemas dinámicos. Una hipótesis propuesta en los años 1990 y 2000 en el contexto de la paz y los conflictos armados es que cuando un conflicto que no es violento pasa a una fase de conflicto armado, se trata de una transición de fase latente a fase manifiesta dentro del sistema dinámico. [51] : 49 

Experimental

Se aplican diversos métodos para estudiar los distintos efectos. Algunos ejemplos seleccionados son:

Véase también

Referencias

  1. ^ Askeland, Donald R.; Haddleton, Frank; Green, Phil; Robertson, Howard (1996). La ciencia y la ingeniería de los materiales . Chapman & Hall. pág. 286. ISBN 978-0-412-53910-7.
  2. ^ Rybin, MV; et al. (2015). "Diagrama de fase para la transición de cristales fotónicos a metamateriales dieléctricos". Nature Communications . 6 : 10102. arXiv : 1507.08901 . Bibcode :2015NatCo...610102R. doi :10.1038/ncomms10102. PMC 4686770 . PMID  26626302. 
  3. ^ Eds. Zhou, W., y Fan. S., Semiconductores y semimetales. Vol 100. Optoelectrónica de metasuperficies de cristales fotónicos , Elsevier, 2019
  4. ^ Carol Kendall (2004). "Fundamentos de la geoquímica de isótopos estables". USGS . Consultado el 10 de abril de 2014 .
  5. ^ ab Jaeger, Gregg (1 de mayo de 1998). «La clasificación de Ehrenfest de las transiciones de fase: introducción y evolución». Archivo de Historia de las Ciencias Exactas . 53 (1): 51–81. doi :10.1007/s004070050021. S2CID  121525126.
  6. ^ ab Blundell, Stephen J.; Katherine M. Blundell (2008). Conceptos de física térmica . Oxford University Press. ISBN 978-0-19-856770-7.
  7. ^ Gross, David J. (1980), "Posible transición de fase de tercer orden en la teoría de calibración de red N grande", Physical Review D , 21 (2): 446–453, doi :10.1103/PhysRevD.21.446
  8. ^ Majumdar, Satya N; Schehr, Grégory (31 de enero de 2014). "Valor propio superior de una matriz aleatoria: grandes desviaciones y transición de fase de tercer orden". Journal of Statistical Mechanics: Theory and Experiment . 2014 (1): P01012. arXiv : 1311.0580 . Bibcode :2014JSMTE..01..012M. doi :10.1088/1742-5468/2014/01/P01012. ISSN  1742-5468. S2CID  119122520.
  9. ^ ab Pippard, Alfred B. (1981). Elementos de termodinámica clásica: para estudiantes avanzados de física (edición revisada). Cambridge: Univ. Pr. pp. 140–141. ISBN 978-0-521-09101-5.
  10. ^ Austin, JB (noviembre de 1932). "Capacidad térmica del hierro: una revisión". Química industrial e ingeniería . 24 (11): 1225–1235. doi :10.1021/ie50275a006. ISSN  0019-7866.
  11. ^ Jaeger, Gregg (1 de mayo de 1998). «La clasificación de Ehrenfest de las transiciones de fase: introducción y evolución». Archivo de Historia de las Ciencias Exactas . 53 (1): 51–81. doi :10.1007/s004070050021. ISSN  1432-0657.
  12. ^ Stanley, H. Eugene (1971). Introducción a las transiciones de fase y fenómenos críticos . Oxford: Clarendon Press.
  13. ^ Faghri, A., y Zhang, Y., Fenómenos de transporte en sistemas multifásicos, Elsevier, Burlington, MA, 2006,
  14. ^ Faghri, A. y Zhang, Y., Fundamentos de la transferencia y el flujo de calor multifásico, Springer, Nueva York, NY, 2020
  15. ^ Imry, Y.; Wortis, M. (1979). "Influencia de impurezas extinguidas en transiciones de fase de primer orden". Phys. Rev. B . 19 (7): 3580–3585. Código Bibliográfico :1979PhRvB..19.3580I. doi :10.1103/physrevb.19.3580.
  16. ^ Kumar, Kranti; Pramanik, AK; Banerjee, A.; Chaddah, P.; Roy, SB; Park, S.; Zhang, CL; Cheong, S.-W. (2006). "Relacionar el sobreenfriamiento y el arresto de la cinética similar al vidrio para sistemas separados en fases: DopedCeFe2and(La,Pr,Ca)MnO3". Physical Review B . 73 (18): 184435. arXiv : cond-mat/0602627 . Código Bibliográfico :2006PhRvB..73r4435K. doi :10.1103/PhysRevB.73.184435. ISSN  1098-0121. S2CID  117080049.
  17. ^ Pasquini, G.; Daroca, D. Pérez; Chiliotte, C.; Lozano, GS; Bekeris, V. (2008). "Redes de vórtices estables ordenadas, desordenadas y coexistentes en monocristales de NbSe2". Physical Review Letters . 100 (24): 247003. arXiv : 0803.0307 . Código Bibliográfico :2008PhRvL.100x7003P. doi :10.1103/PhysRevLett.100.247003. ISSN  0031-9007. PMID  18643617. S2CID  1568288.
  18. ^ ab Ojovan, MI (2013). "Ordenamiento y cambios estructurales en la transición vidrio-líquido". J. Non-Cryst. Solids . 382 : 79–86. Bibcode :2013JNCS..382...79O. doi :10.1016/j.jnoncrysol.2013.10.016.
  19. ^ Gotze, Wolfgang. "Dinámica compleja de líquidos formadores de vidrio: una teoría de acoplamiento de modos".
  20. ^ Lubchenko, V. Wolynes; Wolynes, Peter G. (2007). "Teoría de vidrios estructurales y líquidos superenfriados". Revista anual de química física . 58 : 235–266. arXiv : cond-mat/0607349 . Código Bibliográfico :2007ARPC...58..235L. doi :10.1146/annurev.physchem.58.032806.104653. PMID  17067282. S2CID  46089564.
  21. ^ Greer, AL (1995). "Gafas metálicas". Science . 267 (5206): 1947–1953. Bibcode :1995Sci...267.1947G. doi :10.1126/science.267.5206.1947. PMID  17770105. S2CID  220105648.
  22. ^ Tarjus, G. (2007). «Ciencia de los materiales: metal convertido en vidrio». Nature . 448 (7155): 758–759. Bibcode :2007Natur.448..758T. doi : 10.1038/448758a . PMID  17700684. S2CID  4410586.
  23. ^ Manekar, MA; Chaudhary, S.; Chattopadhyay, MK; Singh, KJ; Roy, SB; Chaddah, P. (2001). "Transición de primer orden del antiferromagnetismo al ferromagnetismo en Ce(Fe 0.96 Al 0.04 ) 2 ". Physical Review B . 64 (10): 104416. arXiv : cond-mat/0012472 . Bibcode :2001PhRvB..64j4416M. doi :10.1103/PhysRevB.64.104416. ISSN  0163-1829. S2CID  16851501.
  24. ^ Banerjee, A.; Pramanik, AK; Kumar, Kranti; Chaddah, P. (2006). "Fracciones ajustables coexistentes de fases vítreas y de equilibrio de orden de largo alcance en manganitas". Journal of Physics: Condensed Matter . 18 (49): L605. arXiv : cond-mat/0611152 . Bibcode :2006JPCM...18L.605B. doi :10.1088/0953-8984/18/49/L02. S2CID  98145553.
  25. ^ Wu W.; Israel C.; Hur N.; Park S.; Cheong SW; de Lozanne A. (2006). "Imágenes magnéticas de una transición vítrea de superenfriamiento en un ferroimán débilmente desordenado". Nature Materials . 5 (11): 881–886. Bibcode :2006NatMa...5..881W. doi :10.1038/nmat1743. PMID  17028576. S2CID  9036412.
  26. ^ Roy, SB; Chattopadhyay, MK; Chaddah, P.; Moore, JD; Perkins, GK; Cohen, LF; Gschneidner, KA; Pecharsky, VK (2006). "Evidencia de un estado de vidrio magnético en el material magnetocalórico Gd 5 Ge 4 ". Physical Review B . 74 (1): 012403. Bibcode :2006PhRvB..74a2403R. doi :10.1103/PhysRevB.74.012403. ISSN  1098-0121.
  27. ^ Lakhani, Archana; Banerjee, A.; Chaddah, P.; Chen, X.; Ramanujan, RV (2012). "Vidrio magnético en aleación con memoria de forma: Ni 45 Co 5 Mn 38 Sn 12 ". Journal of Physics: Condensed Matter . 24 (38): 386004. arXiv : 1206.2024 . Bibcode :2012JPCM...24L6004L. doi :10.1088/0953-8984/24/38/386004. ISSN  0953-8984. PMID  22927562. S2CID  206037831.
  28. ^ Kushwaha, Pallavi; Lakhani, Archana; Rawat, R.; Chaddah, P. (2009). "Estudio a baja temperatura de la transición antiferromagnética-ferromagnética inducida por campo en Fe-Rh dopado con Pd". Physical Review B . 80 (17): 174413. arXiv : 0911.4552 . Código Bibliográfico :2009PhRvB..80q4413K. doi :10.1103/PhysRevB.80.174413. ISSN  1098-0121. S2CID  119165221.
  29. ^ Ivancevic, Vladimir G.; Ivancevic, Tijiana, T. (2008). No linealidad compleja. Berlín: Springer. pp. 176–177. ISBN 978-3-540-79357-1. Recuperado el 12 de octubre de 2014 .{{cite book}}: CS1 maint: multiple names: authors list (link)
  30. ^ Clark, JB; Hastie, JW; Kihlborg, LHE; Metselaar, R.; Thackeray, MM (1994). "Definiciones de términos relacionados con las transiciones de fase del estado sólido". Química pura y aplicada . 66 (3): 577–594. doi : 10.1351/pac199466030577 . S2CID  95616565.
  31. ^ Chaisson, Eric J. (2001). Evolución cósmica . Harvard University Press. ISBN 978-0-674-00342-2.
  32. ^ David Layzer, Cosmogénesis, el desarrollo del orden en el universo , Oxford Univ. Press, 1991
  33. ^ Ojovan, Michael I.; Lee, William E. (2006). "Sistemas topológicamente desordenados en la transición vítrea" (PDF) . Journal of Physics: Condensed Matter . 18 (50): 11507–11520. Bibcode :2006JPCM...1811507O. doi :10.1088/0953-8984/18/50/007. S2CID  96326822.
  34. ^ Leonard, F.; Delamotte, B. (2015). "Los exponentes críticos pueden ser diferentes en los dos lados de una transición". Phys. Rev. Lett . 115 (20): 200601. arXiv : 1508.07852 . Bibcode :2015PhRvL.115t0601L. doi :10.1103/PhysRevLett.115.200601. PMID  26613426. S2CID  22181730.
  35. ^ Lipa, J.; Nissen, J.; Stricker, D.; Swanson, D.; Chui, T. (2003). "Calor específico del helio líquido en gravedad cero muy cerca del punto lambda". Physical Review B . 68 (17): 174518. arXiv : cond-mat/0310163 . Código Bibliográfico :2003PhRvB..68q4518L. doi :10.1103/PhysRevB.68.174518. S2CID  55646571.
  36. ^ Kleinert, Hagen (1999). "Exponentes críticos de la teoría de φ4 de acoplamiento fuerte de siete bucles en tres dimensiones". Physical Review D . 60 (8): 085001. arXiv : hep-th/9812197 . Código Bibliográfico :1999PhRvD..60h5001K. doi :10.1103/PhysRevD.60.085001. S2CID  117436273.
  37. ^ DY Lando y VB Teif (2000). "Las interacciones de largo alcance entre ligandos unidos a una molécula de ADN dan lugar a una adsorción con el carácter de una transición de fase del primer tipo". J. Biomol. Struct. Dyn . 17 (5): 903–911. doi :10.1080/07391102.2000.10506578. PMID  10798534. S2CID  23837885.
  38. ^ Yashroy RC (1987). "Estudios de RMN de 13C de cadenas de acilo graso lipídico de membranas de cloroplastos". Indian Journal of Biochemistry and Biophysics . 24 (6): 177–178. doi :10.1016/0165-022X(91)90019-S. PMID  3428918.
  39. ^ YashRoy, RC (1990). "Determinación de la temperatura de transición de fase de lípidos de membrana a partir de intensidades de RMN de 13-C". Journal of Biochemical and Biophysical Methods . 20 (4): 353–356. doi :10.1016/0165-022X(90)90097-V. PMID  2365951.
  40. ^ Tkacik, Gasper; Mora, Thierry; Marre, Olivier; Amodei, Dario; Berry II, Michael J.; Bialek, William (2014). "Termodinámica para una red de neuronas: Firmas de criticidad". arXiv : 1407.5946 [q-bio.NC].
  41. ^ Bialek, W; Cavagna, A; Giardina, I (2014). "Las interacciones sociales dominan el control de la velocidad en el equilibrio de bandadas naturales cerca de la criticidad". PNAS . 111 (20): 7212–7217. arXiv : 1307.5563 . Bibcode :2014PNAS..111.7212B. doi : 10.1073/pnas.1324045111 . PMC 4034227 . PMID  24785504. 
  42. ^ Krotov, D; Dubuis, JO; Gregor, T; Bialek, W (2014). "Morfogénesis en criticidad". PNAS . 111 (10): 3683–3688. arXiv : 1309.2614 . Bibcode :2014PNAS..111.3683K. doi : 10.1073/pnas.1324186111 . PMC 3956198 . PMID  24516161. 
  43. ^ Mora, Thierry; Bialek, William (2011). "¿Están los sistemas biológicos preparados para la criticidad?". Journal of Statistical Physics . 144 (2): 268–302. arXiv : 1012.2242 . Bibcode :2011JSP...144..268M. doi :10.1007/s10955-011-0229-4. S2CID  703231.
  44. ^ Schwab, David J; Nemenman, Ilya; Mehta, Pankaj (2014). "Ley de Zipf y criticidad en datos multivariados sin ajuste fino". Physical Review Letters . 113 (6): 068102. arXiv : 1310.0448 . Bibcode :2014PhRvL.113f8102S. doi :10.1103/PhysRevLett.113.068102. PMC 5142845 . PMID  25148352. 
  45. ^ Longo, G.; Montévil, M. (1 de agosto de 2011). "De la física a la biología mediante la extensión de la criticidad y las rupturas de simetría". Progreso en biofísica y biología molecular . Biología de sistemas y cáncer. 106 (2): 340–347. arXiv : 1103.1833 . doi :10.1016/j.pbiomolbio.2011.03.005. PMID  21419157. S2CID  723820.
  46. ^ Kelso, JA Scott (1995). Patrones dinámicos: la autoorganización del cerebro y la conducta (sistemas adaptativos complejos) . MIT Press. ISBN 978-0-262-61131-2.
  47. ^ Diedrich, FJ; Warren, WH Jr. (1995). "¿Por qué cambiar la marcha? Dinámica de la transición de caminar a correr". Revista de Psicología Experimental. Percepción y rendimiento humanos . 21 (1): 183–202. doi :10.1037/0096-1523.21.1.183. PMID  7707029.
  48. ^ Hristovski, R.; Balagué, N. (2010). "Punto de terminación espontánea inducido por fatiga: transiciones de fase de no equilibrio y comportamiento crítico en el esfuerzo cuasi-isométrico". Human Movement Science . 29 (4): 483–493. doi :10.1016/j.humov.2010.05.004. PMID  20619908.
  49. ^ Moret, Marcelo; Zebende, Gilney (enero de 2007). "Hidrofobicidad de aminoácidos y área superficial accesible". Physical Review E . 75 (1): 011920. Bibcode :2007PhRvE..75a1920M. doi :10.1103/PhysRevE.75.011920. PMID  17358197.
  50. ^ Gorban, AN; Smirnova, EV; Tyukina, TA (agosto de 2010). "Correlaciones, riesgo y crisis: de la fisiología a las finanzas". Physica A: Mecánica estadística y sus aplicaciones . 389 (16): 3193–3217. arXiv : 0905.0129 . Código Bibliográfico :2010PhyA..389.3193G. doi :10.1016/j.physa.2010.03.035. S2CID  276956.
  51. ^ Diane Hendrick (junio de 2009), Teoría de la complejidad y transformación de conflictos: una exploración del potencial y las implicaciones (PDF) , Departamento de Estudios para la Paz, Universidad de Bradford , Wikidata  Q126669745, archivado (PDF) desde el original el 26 de noviembre de 2022

Lectura adicional

  • Anderson, PW , Nociones básicas de física de la materia condensada , Perseus Publishing (1997).
  • Faghri, A. y Zhang, Y. , Fundamentos de transferencia y flujo de calor multifásico, Springer Nature Switzerland AG, 2020.
  • Fisher, ME (1974). "El grupo de renormalización en la teoría del comportamiento crítico". Rev. Mod. Phys . 46 (4): 597–616. Bibcode :1974RvMP...46..597F. doi :10.1103/revmodphys.46.597.
  • Goldenfeld, N., Conferencias sobre transiciones de fase y el grupo de renormalización , Perseus Publishing (1992).
  • Ivancevic, Vladimir G; Ivancevic, Tijana T (2008), Caos, transiciones de fase, cambios de topología e integrales de trayectoria, Berlín: Springer, ISBN 978-3-540-79356-4, consultado el 14 de marzo de 2013
  • MR Khoshbin-e-Khoshnazar, La transición de fase del hielo como ejemplo de transición de fase de un sistema finito (Physics Education (India), volumen 32, n.º 2, abril-junio de 2016)
  • Kleinert, H. , Gauge Fields in Condensed Matter , Vol. I, " Superfluidity and Vortex lines ; Disorder Fields, Phase Transitions ", págs. 1–742, World Scientific (Singapur, 1989); ISBN de tapa blanda 9971-5-0210-0 (physik.fu-berlin.de, legible en línea) 
  • Kleinert, Hagen ; Verena Schulte-Frohlinde. Propiedades críticas de las teorías φ4. ISBN 981-02-4659-5Archivado desde el original el 26 de febrero de 2008.(legible en línea).
  • Kogut, J.; Wilson, K (1974). "El grupo de renormalización y la expansión épsilon". Phys. Rep . 12 (2): 75–199. Bibcode :1974PhR....12...75W. doi :10.1016/0370-1573(74)90023-4.
  • Krieger, Martin H. , Constituciones de la materia: modelado matemático de los fenómenos físicos más cotidianos , University of Chicago Press , 1996. Contiene una discusión pedagógica detallada de la solución de Onsager del modelo de Ising 2-D.
  • Landau, LD y Lifshitz, EM , Física estadística parte 1 , vol. 5 del Curso de física teórica , Pergamon Press, 3.ª ed. (1994).
  • Mussardo G., "Teoría estadística de campos. Una introducción a los modelos exactamente resueltos de física estadística", Oxford University Press, 2010.
  • Schroeder, Manfred R. , Fractals, chaos, power laws : minutes from an infinite paradise , Nueva York: WH Freeman , 1991. Un libro muy bien escrito en un estilo "semipopular" (no es un libro de texto) dirigido a un público con cierta formación en matemáticas y ciencias físicas. Explica, entre otras cosas, en qué consiste el escalamiento en las transiciones de fase.
  • HE Stanley , Introducción a las transiciones de fase y fenómenos críticos (Oxford University Press, Oxford y Nueva York 1971).
  • Yeomans JM , Mecánica estadística de transiciones de fase , Oxford University Press, 1992.

Medios relacionados con Cambios de fase en Wikimedia Commons

  • Transiciones de fase interactivas en redes con applets de Java
  • Clases de universalidad de Sklogwiki
Retrieved from "https://en.wikipedia.org/w/index.php?title=Phase_transition&oldid=1238491506"