Función de correlación (mecánica estadística)

En mecánica estadística , la función de correlación es una medida del orden en un sistema, tal como se caracteriza por una función de correlación matemática . Las funciones de correlación describen cómo se relacionan las variables microscópicas, como el espín y la densidad, en diferentes posiciones. Más específicamente, las funciones de correlación miden cuantitativamente el grado en que las variables microscópicas fluctúan juntas, en promedio, a través del espacio y/o el tiempo. Tenga en cuenta que la correlación no equivale automáticamente a causalidad. Por lo tanto, incluso si hay una correlación distinta de cero entre dos puntos en el espacio o el tiempo, no significa que haya un vínculo causal directo entre ellos. A veces, puede existir una correlación sin ninguna relación causal. Esto podría ser pura coincidencia o deberse a otros factores subyacentes, conocidos como variables de confusión, que hacen que ambos puntos covaríen (estadísticamente).

Un ejemplo clásico de correlación espacial se puede observar en los materiales ferromagnéticos y antiferromagnéticos. En estos materiales, los espines atómicos tienden a alinearse en configuraciones paralelas y antiparalelas con sus contrapartes adyacentes, respectivamente. La figura de la derecha representa visualmente esta correlación espacial entre los espines en dichos materiales.

La definición más común de una función de correlación es el promedio canónico del conjunto (térmico) del producto escalar de dos variables aleatorias, y , en las posiciones y y tiempos y :$estilo de visualización s_{1}$$estilo de visualización s_{2}$${\estilo de visualización R}$${\estilo de visualización R+r}$${\estilo de visualización t}$${\estilo de visualización t+\tau}$$${\displaystyle C(r,\tau )=\langle \mathbf {s_{1}} (R,t)\cdot \mathbf {s_{2}} (R+r,t+\tau )\rangle \ -\ langle \mathbf {s_{1}} (R,t)\rangle \langle \mathbf {s_{2}} (R+r,t+\tau )\rangle \,.}$$

Aquí los corchetes, , indican el promedio térmico mencionado anteriormente. Sin embargo, es importante señalar aquí que, si bien los corchetes se denominan promedio, se calculan como un valor esperado , no como un valor promedio. Es una cuestión de convención si uno resta el producto promedio no correlacionado de y , del producto correlacionado, , y la convención difiere entre campos. Los usos más comunes de las funciones de correlación son cuando y describen la misma variable, como una función de correlación de espín-espín, o una función de correlación de posición-posición de partículas en un líquido elemental o un sólido (a menudo llamada función de distribución radial o función de correlación de pares). Las funciones de correlación entre la misma variable aleatoria son funciones de autocorrelación . Sin embargo, en mecánica estadística, no todas las funciones de correlación son funciones de autocorrelación. Por ejemplo, en fases condensadas multicomponentes, la función de correlación de pares entre diferentes elementos suele ser de interés. Tales funciones de correlación de pares de elementos mixtos son un ejemplo de funciones de correlación cruzada , ya que las variables aleatorias y representan las variaciones promedio en la densidad como una posición de función para dos elementos distintos.${\displaystyle \langle \cdot \rangle }$$estilo de visualización s_{1}$$estilo de visualización s_{2}$${\displaystyle \langle \mathbf {s_{1}} (R,t)\rangle \langle \mathbf {s_{2}} (R+r,t+\tau )\rangle }$${\displaystyle \langle \mathbf {s_{1}} (R,t)\cdot \mathbf {s_{2}} (R+r,t+\tau )\rangle }$$estilo de visualización s_{1}$$estilo de visualización s_{2}$$estilo de visualización s_{1}$$estilo de visualización s_{2}$

A menudo, uno se interesa únicamente por la influencia espacial de una variable aleatoria dada, digamos la dirección de un giro, en su entorno local, sin considerar tiempos posteriores, . En este caso, ignoramos la evolución temporal del sistema, por lo que la definición anterior se reescribe con . Esto define la función de correlación de tiempo igual , . Se escribe como:${\estilo de visualización \tau}$${\displaystyle \tau = 0}$${\displaystyle C(r,0)}$$${\displaystyle C(r,0)=\langle \mathbf {s_{1}} (R,t)\cdot \mathbf {s_{2}} (R+r,t)\rangle \ -\langle \mathbf {s_{1}} (R,t)\rangle \langle \mathbf {s_{2}} (R+r,t)\rangle \,.}$$

A menudo, se omite el tiempo de referencia, , y el radio de referencia, , al suponer el equilibrio (y, por lo tanto, la invariancia temporal del conjunto) y promediar todas las posiciones de la muestra, lo que da como resultado: donde, nuevamente, la elección de si restar o no las variables no correlacionadas difiere entre los campos. La función de distribución radial es un ejemplo de una función de correlación de tiempo igual donde la referencia no correlacionada generalmente no se resta. En esta página se muestran otras funciones de correlación de espín-espín de tiempo igual para una variedad de materiales y condiciones.${\estilo de visualización t}$${\estilo de visualización R}$$${\displaystyle C(r)=\langle \mathbf {s_{1}} (0)\cdot \mathbf {s_{2}} (r)\rangle \ -\langle \mathbf {s_{1}} (0 )\rangle \langle \mathbf {s_ {2}} (r)\rangle }$$

También puede interesarnos la evolución temporal de las variables microscópicas. En otras palabras, cómo el valor de una variable microscópica en una posición y tiempo determinados, y , influye en el valor de la misma variable microscópica en un tiempo posterior, (y normalmente en la misma posición). Estas correlaciones temporales se cuantifican mediante funciones de correlación de posición igual , . Se definen de forma análoga a las funciones de correlación de tiempo igual anteriores, pero ahora ignoramos las dependencias espaciales estableciendo , lo que da como resultado:${\estilo de visualización R}$${\estilo de visualización t}$${\estilo de visualización t+\tau}$${\displaystyle C(0,\tau )}$${\displaystyle r=0}$$${\displaystyle C(0,\tau )=\langle \mathbf {s_{1}} (R,t)\cdot \mathbf {s_{2}} (R,t+\tau )\rangle \ -\langle \ mathbf {s_{1}} (R,t)\rangle \langle \mathbf {s_{2}} (R,t+\tau )\rangle \,.}$$

Suponiendo el equilibrio (y por lo tanto la invariancia temporal del conjunto) y haciendo un promedio de todos los sitios de la muestra, se obtiene una expresión más simple para la función de correlación de posición igual que para la función de correlación de tiempo igual:$${\displaystyle C(\tau )=\langle \mathbf {s_{1}} (0)\cdot \mathbf {s_{2}} (\tau )\rangle \ -\langle \mathbf {s_{1}} (0)\rangle \langle \mathbf {s_{2}} (\tau )\rangle \,.}$$

La suposición anterior puede parecer poco intuitiva al principio: ¿cómo puede un conjunto que es invariante en el tiempo tener una función de correlación temporal no uniforme? Las correlaciones temporales siguen siendo relevantes para hablar de ellas en sistemas de equilibrio porque un conjunto macroscópico invariante en el tiempo puede tener dinámicas temporales no triviales a nivel microscópico . Un ejemplo es la difusión. Un sistema monofásico en equilibrio tiene una composición homogénea a nivel macroscópico. Sin embargo, si uno observa el movimiento microscópico de cada átomo, se producen fluctuaciones en la composición constantemente debido a los paseos cuasialeatorios que toman los átomos individuales. La mecánica estadística permite hacer afirmaciones perspicaces sobre el comportamiento temporal de tales fluctuaciones de los sistemas de equilibrio. Esto se analiza más adelante en la sección sobre la evolución temporal de las funciones de correlación y la hipótesis de regresión de Onsager.

Todas las funciones de correlación anteriores se han definido en el contexto de la mecánica estadística del equilibrio. Sin embargo, es posible definir funciones de correlación para sistemas alejados del equilibrio. Al examinar la definición general de , queda claro que se pueden definir las variables aleatorias utilizadas en estas funciones de correlación, como las posiciones atómicas y los espines, alejados del equilibrio. Como tal, su producto escalar está bien definido alejado del equilibrio. La operación que ya no está bien definida alejado del equilibrio es el promedio sobre el conjunto de equilibrio. Este proceso de promediado para sistemas que no están en equilibrio se reemplaza típicamente por el promedio del producto escalar en toda la muestra. Esto es típico en experimentos de dispersión y simulaciones por computadora, y se usa a menudo para medir las funciones de distribución radial de vidrios.${\displaystyle C(r,\tau )}$

También se pueden definir promedios sobre estados para sistemas ligeramente perturbados respecto del equilibrio. Véase, por ejemplo, http://xbeams.chem.yale.edu/~batista/vaa/node56.html Archivado el 25 de diciembre de 2018 en Wayback Machine.

Las funciones de correlación se miden típicamente con experimentos de dispersión. Por ejemplo, los experimentos de dispersión de rayos X miden directamente las correlaciones electrón-electrón en el mismo tiempo. ^[1] A partir del conocimiento de los factores de estructura elemental, también se pueden medir las funciones de correlación de pares elementales. Consulte Función de distribución radial para obtener más información. Las funciones de correlación espín-espín en el mismo tiempo se miden con dispersión de neutrones en lugar de dispersión de rayos X. La dispersión de neutrones también puede brindar información sobre las correlaciones de pares. Para sistemas compuestos por partículas más grandes que aproximadamente un micrómetro, se puede utilizar la microscopía óptica para medir funciones de correlación en el mismo tiempo y en la misma posición. Por lo tanto, la microscopía óptica es común para suspensiones coloidales, especialmente en dos dimensiones.

En 1931, Lars Onsager propuso que la regresión de las fluctuaciones térmicas microscópicas en equilibrio sigue la ley macroscópica de relajación de pequeñas perturbaciones de no equilibrio. ^[2] Esto se conoce como la hipótesis de regresión de Onsager . Como los valores de las variables microscópicas separadas por grandes escalas de tiempo, , deberían estar descorrelacionados más allá de lo que esperaríamos del equilibrio termodinámico, la evolución en el tiempo de una función de correlación puede verse desde un punto de vista físico como el sistema que gradualmente "olvida" las condiciones iniciales que se le impusieron a través de la especificación de alguna variable microscópica. En realidad, existe una conexión intuitiva entre la evolución temporal de las funciones de correlación y la evolución temporal de los sistemas macroscópicos: en promedio, la función de correlación evoluciona en el tiempo de la misma manera que si un sistema se preparara en las condiciones especificadas por el valor inicial de la función de correlación y se le permitiera evolucionar. ^[1]${\displaystyle \tau }$

Las fluctuaciones de equilibrio del sistema pueden relacionarse con su respuesta a perturbaciones externas a través del teorema de fluctuación-disipación .

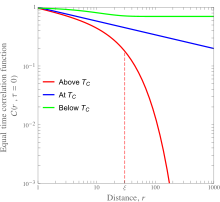
Las transiciones de fase continuas, como las transiciones de orden-desorden en aleaciones metálicas y las transiciones ferromagnéticas-paramagnéticas, implican una transición de un estado ordenado a uno desordenado. En términos de funciones de correlación, la función de correlación de tiempo igual no es cero para todos los puntos de la red por debajo de la temperatura crítica, y no es despreciable solo para un radio bastante pequeño por encima de la temperatura crítica. Como la transición de fase es continua, la longitud sobre la que se correlacionan las variables microscópicas, , debe pasar continuamente de ser infinita a finita cuando el material se calienta hasta su temperatura crítica. Esto da lugar a una dependencia de la ley de potencia de la función de correlación como una función de la distancia en el punto crítico. Esto se muestra en la figura de la izquierda para el caso de un material ferromagnético, con los detalles cuantitativos enumerados en la sección sobre magnetismo.${\displaystyle \xi }$

En un sistema de espín , la función de correlación de tiempo igual está especialmente bien estudiada. Describe el promedio (térmico) del conjunto canónico del producto escalar de los espines en dos puntos de la red sobre todos los ordenamientos posibles: Aquí los corchetes significan el promedio térmico mencionado anteriormente. Se muestran gráficos esquemáticos de esta función para un material ferromagnético por debajo, en y por encima de su temperatura de Curie a la izquierda.${\displaystyle C(r)=\langle \mathbf {s} (R)\cdot \mathbf {s} (R+r)\rangle \ -\langle \mathbf {s} (R)\rangle \langle \mathbf {s} (R+r)\rangle \,.}$

Incluso en una fase magnéticamente desordenada, los espines en diferentes posiciones están correlacionados, es decir, si la distancia r es muy pequeña (en comparación con una escala de longitud ), la interacción entre los espines hará que estén correlacionados. La alineación que surgiría naturalmente como resultado de la interacción entre espines se destruye por efectos térmicos. A altas temperaturas, se observan correlaciones que decaen exponencialmente con el aumento de la distancia, y la función de correlación viene dada asintóticamente por${\displaystyle \xi }$

${\displaystyle C(r)\approx {\frac {1}{r^{\vartheta }}}\exp {\left(-{\frac {r}{d}}\right)}\,,}$

donde r es la distancia entre espines, y d es la dimensión del sistema, y ​​es un exponente, cuyo valor depende de si el sistema está en la fase desordenada (es decir, por encima del punto crítico), o en la fase ordenada (es decir, por debajo del punto crítico). A altas temperaturas, la correlación decae a cero exponencialmente con la distancia entre los espines. El mismo decaimiento exponencial en función de la distancia radial también se observa por debajo de , pero con el límite a grandes distancias siendo la magnetización media . Precisamente en el punto crítico, se ve un comportamiento algebraico. ${\displaystyle \vartheta }$${\displaystyle T_{c}}$${\displaystyle \langle M^{2}\rangle }$

${\displaystyle C(r)\approx {\frac {1}{r^{(d-2+\eta )}}}\,,}$

donde es un exponente crítico , que no tiene ninguna relación simple con el exponente no crítico introducido anteriormente. Por ejemplo, la solución exacta del modelo de Ising bidimensional (con interacciones ferromagnéticas de corto alcance) da precisamente en criticidad , pero por encima de la criticidad y por debajo de la criticidad . ^{[3] [4]}${\displaystyle \eta }$${\displaystyle \vartheta }$${\displaystyle \eta ={\frac {1}{4}}}$${\displaystyle \vartheta ={\frac {1}{2}}}$${\displaystyle \vartheta =2}$

A medida que se reduce la temperatura, se reduce el desorden térmico y, en una transición de fase continua , la longitud de correlación diverge, ya que la longitud de correlación debe realizar una transición continua desde un valor finito por encima de la transición de fase a infinito por debajo de la transición de fase:

${\displaystyle \xi \propto |T-T_{c}|^{-\nu }\,,}$

con otro exponente crítico .${\displaystyle \nu }$

Esta correlación de ley de potencia es responsable del escalamiento que se observa en estas transiciones. Todos los exponentes mencionados son independientes de la temperatura. De hecho, son universales , es decir, se ha comprobado que son los mismos en una amplia variedad de sistemas.

Una función de correlación común es la función de distribución radial que se ve a menudo en mecánica estadística y mecánica de fluidos . La función de correlación se puede calcular en modelos exactamente solucionables (gas de Bose unidimensional, cadenas de espín, modelo de Hubbard) por medio del método de dispersión inversa cuántica y el ansatz de Bethe . En un modelo XY isotrópico, Its, Korepin, Izergin y Slavnov evaluaron las correlaciones de tiempo y temperatura. ^[5]

Las funciones de correlación de orden superior involucran múltiples puntos de referencia y se definen a través de una generalización de la función de correlación anterior tomando el valor esperado del producto de más de dos variables aleatorias:

${\displaystyle C_{i_{1}i_{2}\cdots i_{n}}(s_{1},s_{2},\cdots ,s_{n})=\langle X_{i_{1}}(s_{1})X_{i_{2}}(s_{2})\cdots X_{i_{n}}(s_{n})\rangle .}$

Sin embargo, estas funciones de correlación de orden superior son relativamente difíciles de interpretar y medir. Por ejemplo, para medir los análogos de orden superior de las funciones de distribución de pares, se necesitan fuentes de rayos X coherentes. Tanto la teoría de este tipo de análisis ^{[6] [7]} como la medición experimental de las funciones de correlación cruzada de rayos X necesarias ^[8] son ​​áreas de investigación activa.

• Ecuación de Ornstein-Zernike

• Sethna, James P. (2006). "Capítulo 10: Correlaciones, respuesta y disipación". Mecánica estadística: entropía, parámetros de orden y complejidad . Oxford University Press. ISBN 978-0198566779.
• Función de distribución radial
• Yeomans, JM (1992). Mecánica estadística de transiciones de fase . Oxford Science Publications. ISBN 978-0-19-851730-6.
• Fisher, ME (1974). "Grupo de renormalización en la teoría del comportamiento crítico". Reseñas de física moderna . 46 (4): 597–616. Bibcode :1974RvMP...46..597F. doi :10.1103/RevModPhys.46.597.
• C. Domb , MS Green , JL Lebowitz editores, Transiciones de fase y fenómenos críticos , vol. 1-20 (1972–2001), Academic Press.