Prueba de raíz

Parte de una serie de artículos sobre
Cálculo
${\displaystyle \int _{a}^{b}f'(t)\,dt=f(b)-f(a)}$
Teorema fundamental Límites Continuidad Teorema de Rolle Teorema del valor medio Teorema de la función inversa
Diferencial Definiciones Derivada  ( generalizaciones ) Diferencial infinitesimal de una función total Conceptos Notación de diferenciación Segunda derivada Diferenciación implícita Diferenciación logarítmica Tarifas relacionadas Teorema de Taylor Reglas e identidades Suma Producto Cadena Fuerza Cociente La regla del Hospital Inverso General Leibniz La fórmula de Faà di Bruno Reynolds
Integral Listas de integrales Transformada integral Regla integral de Leibniz Definiciones Antiderivada Integral  ( impropia ) Integral de Riemann Integración de Lebesgue Integración de contornos Integral de funciones inversas Integración por Regiones Discos Conchas cilíndricas Sustitución  ( trigonométrica , tangente de semiángulo , Euler ) Fórmula de Euler Fracciones parciales ( método de Heaviside ) Cambiar orden Fórmulas de reducción Derivando bajo el signo integral Algoritmo de riesgo
Serie Geométrico  ( aritmético-geométrico ) Armónico Alterno Fuerza Binomio Taylor Pruebas de convergencia Límite de sumando (prueba de término) Relación Raíz Integral Comparación directa Comparación de límites Serie alternada Condensación de Cauchy Dirichlet Abel
Vector Gradiente Divergencia Rizo Laplaciano Derivada direccional Identidades Teoremas Gradiente Verduras De Stokes Divergencia Stokes generalizado Descomposición de Helmholtz
Multivariable Formalismos Matriz Tensor Exterior Geométrico Definiciones Derivada parcial Integral múltiple Integral de línea Integral de superficie Integral de volumen Jacobiano arpillera
Avanzado Cálculo en el espacio euclidiano Funciones generalizadas Límite de distribuciones
Especializado Fraccionario Malliavin Estocástico Variaciones
Miscelánea Precálculo Historia Glosario Lista de temas Abeja de integración Análisis matemático Análisis no estándar
en a mi

En matemáticas , la prueba de la raíz es un criterio para la convergencia (una prueba de convergencia ) de una serie infinita . Depende de la cantidad

${\displaystyle \limsup _{n\rightarrow \infty }{\sqrt[{n}]{|a_{n}|}},}$

donde están los términos de la serie, y establece que la serie converge absolutamente si esta cantidad es menor que uno, pero diverge si es mayor que uno. Es particularmente útil en relación con las series de potencias .${\displaystyle a_{n}}$

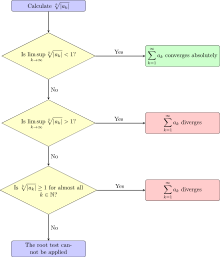
La prueba de la raíz fue desarrollada por primera vez por Augustin-Louis Cauchy , quien la publicó en su libro de texto Cours d'analyse (1821). ^[1] Por lo tanto, a veces se la conoce como prueba de la raíz de Cauchy o prueba radical de Cauchy . Para una serie

${\displaystyle \sum _{n=1}^{\infty }a_{n}}$

La prueba de raíz utiliza el número

${\displaystyle C=\limsup _{n\rightarrow \infty }{\sqrt[{n}]{|a_{n}|}},}$

donde "lim sup" denota el límite superior , posiblemente +∞. Nótese que si

${\displaystyle \lim _{n\rightarrow \infty }{\sqrt[{n}]{|a_{n}|}},}$

converge, entonces es igual a C y puede usarse en la prueba de raíz.

La prueba raíz establece que:

• si C < 1 entonces la serie converge absolutamente ,
• si C > 1 entonces la serie diverge ,
• Si C = 1 y el límite se aproxima estrictamente desde arriba, entonces la serie diverge,
• de lo contrario la prueba no es concluyente (la serie puede divergir, converger absolutamente o converger condicionalmente ).

Hay algunas series para las cuales C = 1 y la serie converge, por ejemplo , y hay otras para las cuales C = 1 y la serie diverge, por ejemplo .${\displaystyle \textstyle \sum 1/{n^{2}}}$${\displaystyle \textstyle \sum 1/n}$

Esta prueba se puede utilizar con una serie de potencias.

${\displaystyle f(z)=\sum _{n=0}^{\infty }c_{n}(z-p)^{n}}$

donde los coeficientes c _n y el centro p son números complejos y el argumento z es una variable compleja.

Los términos de esta serie vendrían dados por a _n = c _n ( z − p ) ⁿ . A continuación, se aplica la prueba de la raíz a a n _como se indicó anteriormente. Nótese que a veces una serie como esta se denomina serie de potencias "alrededor de p ", porque el radio de convergencia es el radio R del intervalo o disco más grande centrado en p tal que la serie convergerá para todos los puntos z estrictamente en el interior (la convergencia en el límite del intervalo o disco generalmente debe comprobarse por separado).

Un corolario de la prueba de la raíz aplicada a una serie de potencias es el teorema de Cauchy-Hadamard : el radio de convergencia es exactamente el que garantiza que realmente queremos decir ∞ si el denominador es 0.${\displaystyle 1/\limsup _{n\rightarrow \infty }{\sqrt[{n}]{|c_{n}|}},}$

La prueba de la convergencia de una serie Σ a _n es una aplicación de la prueba de comparación .

Si para todo n ≥ N ( N algún número natural fijo ) tenemos , entonces . Como la serie geométrica converge, también lo hace según la prueba de comparación. Por lo tanto, Σ a _n converge de manera absoluta. ${\displaystyle {\sqrt[{n}]{|a_{n}|}}\leq k<1}$${\displaystyle |a_{n}|\leq k^{n}<1}$ ${\displaystyle \sum _{n=N}^{\infty }k^{n}}$${\displaystyle \sum _{n=N}^{\infty }|a_{n}|}$

Si para un número infinito de n , entonces a _n no converge a 0, por lo tanto la serie es divergente.${\displaystyle {\sqrt[{n}]{|a_{n}|}}>1}$

Demostración del corolario : Para una serie de potencias Σ a _n = Σ c _n ( z  −  p ) ⁿ , vemos por lo anterior que la serie converge si existe una N tal que para todo n ≥ N tenemos

${\displaystyle {\sqrt[{n}]{|a_{n}|}}={\sqrt[{n}]{|c_{n}(z-p)^{n}|}}<1,}$

equivalente a

${\displaystyle {\sqrt[{n}]{|c_{n}|}}\cdot |z-p|<1}$

para todo n ≥ N , lo que implica que para que la serie converja debemos tener para todo n suficientemente grande . Esto es equivalente a decir${\displaystyle |z-p|<1/{\sqrt[{n}]{|c_{n}|}}}$

${\displaystyle |z-p|<1/\limsup _{n\rightarrow \infty }{\sqrt[{n}]{|c_{n}|}},}$

Así que ahora el único otro lugar donde la convergencia es posible es cuando${\displaystyle R\leq 1/\limsup _{n\rightarrow \infty }{\sqrt[{n}]{|c_{n}|}}.}$

${\displaystyle {\sqrt[{n}]{|a_{n}|}}={\sqrt[{n}]{|c_{n}(z-p)^{n}|}}=1,}$

(ya que los puntos > 1 divergirán) y esto no cambiará el radio de convergencia ya que estos son solo los puntos que se encuentran en el límite del intervalo o disco, por lo que

${\displaystyle R=1/\limsup _{n\rightarrow \infty }{\sqrt[{n}]{|c_{n}|}}.}$

Ejemplo 1:

${\displaystyle \sum _{i=1}^{\infty }{\frac {2^{i}}{i^{9}}}}$

Aplicando la prueba de la raíz y utilizando el hecho de que${\displaystyle \lim _{n\to \infty }n^{1/n}=1,}$

${\displaystyle C=\lim _{n\to \infty }{\sqrt[{n}]{\left|{\frac {2^{n}}{n^{9}}}\right|}}=\lim _{n\to \infty }{\frac {\sqrt[{n}]{2^{n}}}{\sqrt[{n}]{n^{9}}}}=\lim _{n\to \infty }{\frac {2}{(n^{1/n})^{9}}}=2}$

Dado que la serie diverge. ^[2]${\displaystyle C=2>1,}$

Ejemplo 2:

${\displaystyle \sum _{n=0}^{\infty }{\frac {1}{2^{\lfloor n/2\rfloor }}}=1+1+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{4}}+{\frac {1}{8}}+{\frac {1}{8}}+\ldots }$

La prueba de raíz muestra convergencia porque

${\displaystyle r=\limsup _{n\to \infty }{\sqrt[{n}]{|a_{n}|}}=\limsup _{n\to \infty }{\sqrt[{2n}]{|a_{2n}|}}=\limsup _{n\to \infty }{\sqrt[{2n}]{|1/2^{n}|}}={\frac {1}{\sqrt {2}}}<1.}$

Este ejemplo muestra cómo la prueba de la raíz es más sólida que la prueba de la razón . La prueba de la razón no es concluyente para esta serie, ya que si es par, mientras que si es impar, , por lo tanto, el límite no existe.${\displaystyle n}$${\displaystyle a_{n+1}/a_{n}=1}$${\displaystyle n}$${\displaystyle a_{n+1}/a_{n}=1/2}$${\displaystyle \lim _{n\to \infty }|a_{n+1}/a_{n}|}$

La jerarquía de pruebas de raíz ^{[3] [4]} se construye de manera similar a la jerarquía de pruebas de razón (ver Sección 4.1 de prueba de razón , y más específicamente la Subsección 4.1.4 allí).

Para una serie con términos positivos tenemos las siguientes pruebas de convergencia/divergencia.${\displaystyle \sum _{n=1}^{\infty }a_{n}}$

Sea un número entero, y sea el iterador número uno del logaritmo natural , es decir, y para cualquier , .${\displaystyle K\geq 1}$${\displaystyle \ln _{(K)}(x)}$${\displaystyle K}$${\displaystyle \ln _{(1)}(x)=\ln(x)}$${\displaystyle 2\leq k\leq K}$${\displaystyle \ln _{(k)}(x)=\ln _{(k-1)}(\ln(x))}$

Supongamos que , cuando es grande, se puede presentar en la forma${\displaystyle {\sqrt[{-n}]{a_{n}}}}$${\displaystyle n}$

${\displaystyle {\sqrt[{-n}]{a_{n}}}=1+{\frac {1}{n}}+{\frac {1}{n}}\sum _{i=1}^{K-1}{\frac {1}{\prod _{k=1}^{i}\ln _{(k)}(n)}}+{\frac {\rho _{n}}{n\prod _{k=1}^{K}\ln _{(k)}(n)}}.}$

(Se supone que la suma vacía es 0).

• La serie converge, si${\displaystyle \liminf _{n\to \infty }\rho _{n}>1}$
• La serie diverge, si${\displaystyle \limsup _{n\to \infty }\rho _{n}<1}$
• De lo contrario, la prueba no es concluyente.

Desde entonces tenemos${\displaystyle {\sqrt[{-n}]{a_{n}}}=\mathrm {e} ^{-{\frac {1}{n}}\ln a_{n}}}$

${\displaystyle \mathrm {e} ^{-{\frac {1}{n}}\ln a_{n}}=1+{\frac {1}{n}}+{\frac {1}{n}}\sum _{i=1}^{K-1}{\frac {1}{\prod _{k=1}^{i}\ln _{(k)}(n)}}+{\frac {\rho _{n}}{n\prod _{k=1}^{K}\ln _{(k)}(n)}}.}$

De esto,

${\displaystyle \ln a_{n}=-n\ln \left(1+{\frac {1}{n}}+{\frac {1}{n}}\sum _{i=1}^{K-1}{\frac {1}{\prod _{k=1}^{i}\ln _{(k)}(n)}}+{\frac {\rho _{n}}{n\prod _{k=1}^{K}\ln _{(k)}(n)}}\right).}$

De la expansión de Taylor aplicada al lado derecho, obtenemos:

${\displaystyle \ln a_{n}=-1-\sum _{i=1}^{K-1}{\frac {1}{\prod _{k=1}^{i}\ln _{(k)}(n)}}-{\frac {\rho _{n}}{\prod _{k=1}^{K}\ln _{(k)}(n)}}+O\left({\frac {1}{n}}\right).}$

Por eso,

${\displaystyle a_{n}={\begin{cases}\mathrm {e} ^{-1+O(1/n)}{\frac {1}{(n\prod _{k=1}^{K-2}\ln _{(k)}n)\ln _{(K-1)}^{\rho _{n}}n}},&K\geq 2,\\\mathrm {e} ^{-1+O(1/n)}{\frac {1}{n^{\rho _{n}}}},&K=1.\end{cases}}}$

(El producto vacío se establece en 1.)

El resultado final se desprende de la prueba integral de convergencia .

• Prueba de proporción
• Serie convergente

• Knopp, Konrad (1956). "§ 3.2". Sucesiones y series infinitas . Dover publications, Inc., Nueva York. ISBN 0-486-60153-6.
• Whittaker, ET y Watson, GN (1963). "§ 2.35". Un curso de análisis moderno (cuarta edición). Cambridge University Press. ISBN 0-521-58807-3.

Este artículo incorpora material de la prueba de la raíz de Cauchy en PlanetMath , que se encuentra bajo la licencia Creative Commons Attribution/Share-Alike License .