Tarifas relacionadas

‹ Se está considerando la posibilidad de fusionar la plantilla Manual .› 

Este artículo está escrito como un manual o una guía . Por favor, ayude a reescribir este artículo y elimine consejos o instrucciones. ( Octubre de 2015 )

Parte de una serie de artículos sobre
Cálculo
${\displaystyle \int _{a}^{b}f'(t)\,dt=f(b)-f(a)}$
Teorema fundamental Límites Continuidad Teorema de Rolle Teorema del valor medio Teorema de la función inversa
Diferencial Definiciones Derivada  ( generalizaciones ) Diferencial infinitesimal de una función total Conceptos Notación de diferenciación Segunda derivada Diferenciación implícita Diferenciación logarítmica Tarifas relacionadas Teorema de Taylor Reglas e identidades Suma Producto Cadena Fuerza Cociente La regla del Hospital Inverso El general Leibniz La fórmula de Faà di Bruno Reynolds
Integral Listas de integrales Transformada integral Regla integral de Leibniz Definiciones Antiderivada Integral  ( impropia ) Integral de Riemann Integración de Lebesgue Integración de contornos Integral de funciones inversas Integración por Regiones Discos Conchas cilíndricas Sustitución  ( trigonométrica , tangente de semiángulo , Euler ) Fórmula de Euler Fracciones parciales ( método de Heaviside ) Cambiar orden Fórmulas de reducción Derivando bajo el signo integral Algoritmo de riesgo
Serie Geométrico  ( aritmético-geométrico ) Armónico Alterno Fuerza Binomio Taylor Pruebas de convergencia Límite de sumando (prueba de término) Relación Raíz Integral Comparación directa Comparación de límites Serie alternada Condensación de Cauchy Dirichlet Abel
Vector Gradient Divergence Curl Laplacian Directional derivative Identities Theorems Gradient Green's Stokes' Divergence generalized Stokes Helmholtz decomposition
Multivariable Formalisms Matrix Tensor Exterior Geometric Definitions Partial derivative Multiple integral Line integral Surface integral Volume integral Jacobian Hessian
Advanced Calculus on Euclidean space Generalized functions Limit of distributions
Specialized Fractional Malliavin Stochastic Variations
Miscellanea Precalculus History Glossary List of topics Integration Bee Mathematical analysis Nonstandard analysis
v t e

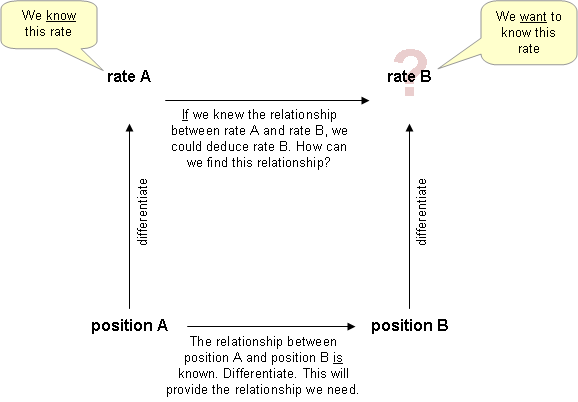
En el cálculo diferencial , los problemas de tasas relacionadas implican encontrar una tasa a la que cambia una cantidad relacionando esa cantidad con otras cantidades cuyas tasas de cambio son conocidas. La tasa de cambio suele ser con respecto al tiempo . Debido a que la ciencia y la ingeniería a menudo relacionan cantidades entre sí, los métodos de tasas relacionadas tienen amplias aplicaciones en estos campos. La diferenciación con respecto al tiempo o una de las otras variables requiere la aplicación de la regla de la cadena , ^[1] ya que la mayoría de los problemas involucran varias variables.

Fundamentalmente, si una función se define de manera que , entonces la derivada de la función se puede tomar con respecto a otra variable. Suponemos que es una función de , es decir . Entonces , entonces ${\displaystyle F}$${\displaystyle F=f(x)}$${\displaystyle F}$${\displaystyle x}$${\displaystyle t}$${\displaystyle x=g(t)}$${\displaystyle F=f(g(t))}$

${\displaystyle F'(t)=f'(g(t))\cdot g'(t)}$

Escrito en notación Leibniz, esto es:

${\displaystyle {\frac {dF}{dt}}={\frac {df}{dx}}\cdot {\frac {dx}{dt}}.}$

Así, si se sabe cómo cambia con respecto a , entonces podemos determinar cómo cambia con respecto a y viceversa. Podemos extender esta aplicación de la regla de la cadena con las reglas de suma, diferencia, producto y cociente del cálculo, etc.${\displaystyle x}$${\displaystyle t}$${\displaystyle F}$${\displaystyle t}$

Por ejemplo, si entonces${\displaystyle F(x)=G(y)+H(z)}$

${\displaystyle {\frac {dF}{dx}}\cdot {\frac {dx}{dt}}={\frac {dG}{dy}}\cdot {\frac {dy}{dt}}+{\frac {dH}{dz}}\cdot {\frac {dz}{dt}}.}$

La forma más común de abordar los problemas de tasas relacionadas es la siguiente: ^[2]

1. Identificar las variables conocidas , incluidas las tasas de cambio y la tasa de cambio que se debe encontrar. (Dibujar una imagen o representación del problema puede ayudar a mantener todo en orden)
2. Construya una ecuación que relacione las cantidades cuyas tasas de cambio se conocen con la cantidad cuya tasa de cambio se desea encontrar.
3. Derivar ambos lados de la ecuación con respecto al tiempo (u otra tasa de cambio). En este paso, a menudo se emplea la regla de la cadena .
4. Sustituya las tasas de cambio conocidas y las cantidades conocidas en la ecuación.
5. Resuelva la tasa de cambio deseada.

Los errores en este procedimiento suelen deberse a que se introducen los valores conocidos de las variables antes (en lugar de después) de hallar la derivada con respecto al tiempo. Si se hace así, se obtendrá un resultado incorrecto, ya que si se sustituyen esos valores por las variables antes de la diferenciación, esas variables se convertirán en constantes y, cuando se deriva la ecuación, aparecen ceros en los lugares de todas las variables para las que se han introducido los valores.

Una escalera de 10 metros está apoyada contra la pared de un edificio y la base de la escalera se desliza alejándose del edificio a una velocidad de 3 metros por segundo. ¿A qué velocidad se desliza la parte superior de la escalera por la pared cuando la base de la escalera está a 6 metros de la pared?

La distancia entre la base de la escalera y la pared, x , y la altura de la escalera sobre la pared, y , representan los lados de un triángulo rectángulo con la escalera como hipotenusa, h . El objetivo es encontrar dy / dt , la tasa de cambio de y con respecto al tiempo, t , cuando se conocen h , x y dx / dt , la tasa de cambio de x .

Paso 1:

• ${\displaystyle x=6}$
• ${\displaystyle h=10}$
• ${\displaystyle {\frac {dx}{dt}}=3}$
• ${\displaystyle {\frac {dh}{dt}}=0}$
• ${\displaystyle {\frac {dy}{dt}}={\text{?}}}$

Paso 2: Del teorema de Pitágoras , la ecuación

${\displaystyle x^{2}+y^{2}=h^{2},}$

describe la relación entre x , y y h para un triángulo rectángulo. Derivando ambos lados de esta ecuación con respecto al tiempo, t , se obtiene

${\displaystyle {\frac {d}{dt}}\left(x^{2}+y^{2}\right)={\frac {d}{dt}}\left(h^{2}\right)}$

Paso 3: Cuando se resuelve para la tasa de cambio deseada, dy / dt , obtenemos

${\displaystyle {\frac {d}{dt}}\left(x^{2}\right)+{\frac {d}{dt}}\left(y^{2}\right)={\frac {d}{dt}}\left(h^{2}\right)}$

${\displaystyle (2x){\frac {dx}{dt}}+(2y){\frac {dy}{dt}}=(2h){\frac {dh}{dt}}}$

${\displaystyle x{\frac {dx}{dt}}+y{\frac {dy}{dt}}=h{\frac {dh}{dt}}}$

${\displaystyle {\frac {dy}{dt}}={\frac {h{\frac {dh}{dt}}-x{\frac {dx}{dt}}}{y}}.}$

Paso 4 y 5: Utilizando las variables del paso 1 obtenemos:

${\displaystyle {\frac {dy}{dt}}={\frac {h{\frac {dh}{dt}}-x{\frac {dx}{dt}}}{y}}.}$

${\displaystyle {\frac {dy}{dt}}={\frac {10\times 0-6\times 3}{y}}=-{\frac {18}{y}}.}$

Resolviendo y usando el Teorema de Pitágoras obtenemos:

${\displaystyle x^{2}+y^{2}=h^{2}}$

${\displaystyle 6^{2}+y^{2}=10^{2}}$

${\displaystyle y=8}$

Sustituyendo 8 en la ecuación:

${\displaystyle -{\frac {18}{y}}=-{\frac {18}{8}}=-{\frac {9}{4}}}$

Generalmente se supone que los valores negativos representan la dirección descendente. De esta manera, la parte superior de la escalera se desliza por la pared a una velocidad de ⁠9/4⁠ metros por segundo.

Debido a que una cantidad física a menudo depende de otra, que a su vez depende de otras, como el tiempo, los métodos de velocidades relacionadas tienen amplias aplicaciones en Física. Esta sección presenta un ejemplo de cinemática de velocidades relacionadas y de inducción electromagnética .

Por ejemplo, se puede considerar el problema cinemático en el que un vehículo se dirige hacia el oeste en dirección a una intersección a 80 millas por hora, mientras que otro se dirige hacia el norte alejándose de la intersección a 60 millas por hora. Se puede preguntar si los vehículos se están acercando o alejando y a qué velocidad en el momento en que el vehículo que se dirige hacia el norte se encuentra a 3 millas al norte de la intersección y el vehículo que se dirige hacia el oeste se encuentra a 4 millas al este de la intersección.

Gran idea: utilizar la regla de la cadena para calcular la tasa de cambio de la distancia entre dos vehículos.

Plan:

1. Elija el sistema de coordenadas
2. Identificar variables
3. Dibujar imagen
4. Gran idea: utilizar la regla de la cadena para calcular la tasa de cambio de la distancia entre dos vehículos
5. Expresar c en términos de x e y mediante el teorema de Pitágoras
6. Expresar dc / dt utilizando la regla de la cadena en términos de dx / dt y dy / dt
7. Sustituir en x , y , dx / dt , dy / dt
8. Simplificar.

Elija el sistema de coordenadas: Deje que el eje y apunte al norte y el eje x apunte al este.

Identificar las variables: Defina y ( t ) como la distancia del vehículo que se dirige al norte desde el origen y x ( t ) como la distancia del vehículo que se dirige al oeste desde el origen.

Expresar c en términos de x e y mediante el teorema de Pitágoras:

${\displaystyle c=\left(x^{2}+y^{2}\right)^{1/2}}$

Expresar dc / dt utilizando la regla de la cadena en términos de dx / dt y dy/dt:

${\displaystyle {\frac {dc}{dt}}={\frac {d}{dt}}\left(x^{2}+y^{2}\right)^{1/2}}$	Aplicar el operador derivado a toda la función
${\displaystyle ={\frac {1}{2}}\left(x^{2}+y^{2}\right)^{-1/2}{\frac {d}{dt}}\left(x^{2}+y^{2}\right)}$	La raíz cuadrada está fuera de la función; la suma de los cuadrados está dentro de la función
${\displaystyle ={\frac {1}{2}}\left(x^{2}+y^{2}\right)^{-1/2}\left[{\frac {d}{dt}}(x^{2})+{\frac {d}{dt}}(y^{2})\right]}$	Operador de diferenciación distribuida
${\displaystyle ={\frac {1}{2}}\left(x^{2}+y^{2}\right)^{-1/2}\left[2x{\frac {dx}{dt}}+2y{\frac {dy}{dt}}\right]}$	Aplicar la regla de la cadena a x ( t ) e y ( t )}
${\displaystyle ={\frac {x{\frac {dx}{dt}}+y{\frac {dy}{dt}}}{\sqrt {x^{2}+y^{2}}}}}$	Simplificar.

Sustituya en x = 4 mi, y = 3 mi, dx / dt = −80 mi/hr, dy / dt = 60 mi/hr y simplifique

${\displaystyle {\begin{aligned}{\frac {dc}{dt}}&={\frac {4{\text{ mi}}\cdot (-80{\text{ mi}}/{\text{hr}})+3{\text{ mi}}\cdot (60){\text{mi}}/{\text{hr}}}{\sqrt {(4{\text{ mi}})^{2}+(3{\text{ mi}})^{2}}}}\\&={\frac {-320{\text{ mi}}^{2}/{\text{hr}}+180{\text{ mi}}^{2}/{\text{hr}}}{5{\text{ mi}}}}\\&={\frac {-140{\text{ mi}}^{2}/{\text{hr}}}{5{\text{ mi}}}}\\&=-28{\text{ mi}}/{\text{hr}}\end{aligned}}}$

En consecuencia, los dos vehículos se acercan entre sí a una velocidad de 45 km/h.

El flujo magnético a través de un bucle de área A cuya normal forma un ángulo θ con respecto a un campo magnético de intensidad B es

${\displaystyle \Phi _{B}=BA\cos(\theta ),}$

La ley de inducción electromagnética de Faraday establece que la fuerza electromotriz inducida es la tasa negativa de cambio del flujo magnético a través de un bucle conductor.${\displaystyle {\mathcal {E}}}$${\displaystyle \Phi _{B}}$

${\displaystyle {\mathcal {E}}=-{\frac {d\Phi _{B}}{dt}},}$

Si el área del bucle A y el campo magnético B se mantienen constantes, pero el bucle se gira de modo que el ángulo θ sea una función conocida del tiempo, la tasa de cambio de θ se puede relacionar con la tasa de cambio de (y, por lo tanto, la fuerza electromotriz) tomando la derivada temporal de la relación de flujo.${\displaystyle \Phi _{B}}$

${\displaystyle {\mathcal {E}}=-{\frac {d\Phi _{B}}{dt}}=BA\sin \theta {\frac {d\theta }{dt}}}$

Si, por ejemplo, el bucle gira a una velocidad angular constante ω , de modo que θ  =  ωt , entonces

${\displaystyle {\mathcal {E}}=\omega BA\sin \omega t}$