Relatividad especial

| Special relativity |
|---|
 |
En física , la teoría especial de la relatividad , o relatividad especial para abreviar, es una teoría científica de la relación entre el espacio y el tiempo . En el artículo de Albert Einstein de 1905, Sobre la electrodinámica de los cuerpos en movimiento , la teoría se presenta como basada en solo dos postulados : [p 1] [1] [2]
- Las leyes de la física son invariantes (idénticas) en todos los marcos de referencia inerciales (es decir, marcos de referencia sin aceleración ). Esto se conoce como el principio de relatividad .
- La velocidad de la luz en el vacío es la misma para todos los observadores, independientemente del movimiento de la fuente de luz o del observador. Esto se conoce como el principio de constancia de la luz o el principio de invariancia de la velocidad de la luz.
El primer postulado fue formulado por primera vez por Galileo Galilei (véase Invariancia galileana ).
Orígenes y significado
La relatividad especial fue descrita por Albert Einstein en un artículo publicado el 26 de septiembre de 1905 titulado "Sobre la electrodinámica de los cuerpos en movimiento". [p 1] Las ecuaciones de Maxwell del electromagnetismo parecían ser incompatibles con la mecánica newtoniana , y el experimento de Michelson-Morley no logró detectar el movimiento de la Tierra frente al hipotético éter luminífero . Esto condujo al desarrollo de las transformaciones de Lorentz , por Hendrik Lorentz , que ajustan las distancias y los tiempos para los objetos en movimiento. La relatividad especial corrige las leyes de la mecánica hasta entonces vigentes para manejar situaciones que involucran todos los movimientos y especialmente aquellos a una velocidad cercana a la de la luz (conocida comovelocidades relativistas ). Hoy en día, se ha demostrado que la relatividad especial es el modelo más preciso del movimiento a cualquier velocidad cuando los efectos gravitacionales y cuánticos son insignificantes.[3][4]Aun así, el modelo newtoniano sigue siendo válido como una aproximación simple y precisa a bajas velocidades (en relación con la velocidad de la luz), por ejemplo, los movimientos cotidianos en la Tierra.
La relatividad especial tiene una amplia gama de consecuencias que han sido verificadas experimentalmente. [5] Incluyen la relatividad de la simultaneidad , la contracción de la longitud , la dilatación del tiempo , la fórmula relativista de adición de velocidad, el efecto Doppler relativista , la masa relativista , un límite de velocidad universal , la equivalencia masa-energía , la velocidad de causalidad y la precesión de Thomas . [1] [2] Por ejemplo, ha reemplazado la noción convencional de un tiempo universal absoluto con la noción de un tiempo que depende del marco de referencia y la posición espacial . En lugar de un intervalo de tiempo invariante entre dos eventos, hay un intervalo de espacio-tiempo invariante . Combinados con otras leyes de la física, los dos postulados de la relatividad especial predicen la equivalencia de masa y energía , como se expresa en la fórmula de equivalencia masa-energía , donde es la velocidad de la luz en el vacío. [6] [7] También explica cómo se relacionan los fenómenos de la electricidad y el magnetismo. [1] [2]
Una característica definitoria de la relatividad especial es la sustitución de las transformaciones galileanas de la mecánica newtoniana por las transformaciones de Lorentz . El tiempo y el espacio no pueden definirse por separado (como se creía anteriormente). Más bien, el espacio y el tiempo están entrelazados en un único continuo conocido como "espacio-tiempo" . Los acontecimientos que ocurren al mismo tiempo para un observador pueden ocurrir en momentos diferentes para otro.
Hasta varios años después, cuando Einstein desarrolló la relatividad general , que introdujo un espacio-tiempo curvado para incorporar la gravedad, no se utilizó la frase "relatividad especial". Una traducción que a veces se utiliza es "relatividad restringida"; "especial" en realidad significa "caso especial". [p 2] [p 3] [p 4] [nota 1] Parte del trabajo de Albert Einstein en relatividad especial se basa en el trabajo anterior de Hendrik Lorentz y Henri Poincaré . La teoría se completó esencialmente en 1907, con los artículos de Hermann Minkowski sobre el espacio-tiempo. [4]
La teoría es "especial" en el sentido de que sólo se aplica en el caso especial en el que el espacio-tiempo es "plano", es decir, donde la curvatura del espacio-tiempo (una consecuencia del tensor de energía-momento y que representa la gravedad ) es despreciable. [8] [nota 2] Para dar cabida correctamente a la gravedad, Einstein formuló la relatividad general en 1915. La relatividad especial, al contrario de algunas descripciones históricas, da cabida tanto a las aceleraciones como a los marcos de referencia acelerados . [9] [10]
Así como ahora se acepta que la relatividad galileana es una aproximación de la relatividad especial que es válida para velocidades bajas, la relatividad especial se considera una aproximación de la relatividad general que es válida para campos gravitatorios débiles , es decir, a una escala suficientemente pequeña (por ejemplo, cuando las fuerzas de marea son despreciables) y en condiciones de caída libre . Pero la relatividad general incorpora geometría no euclidiana para representar los efectos gravitatorios como la curvatura geométrica del espacio-tiempo. La relatividad especial está restringida al espacio-tiempo plano conocido como espacio de Minkowski . Mientras el universo pueda modelarse como una variedad pseudo-riemanniana , se puede definir un marco invariante de Lorentz que respete la relatividad especial para una vecindad suficientemente pequeña de cada punto en este espacio-tiempo curvado .
Galileo Galilei ya había postulado que no existe un estado de reposo absoluto y bien definido (no hay marcos de referencia privilegiados ), un principio que ahora se denomina principio de relatividad de Galileo . Einstein amplió este principio de modo que explicara la velocidad constante de la luz, [11] un fenómeno que se había observado en el experimento de Michelson-Morley. También postuló que se cumple para todas las leyes de la física , incluidas tanto las leyes de la mecánica como las de la electrodinámica . [12]
El enfoque tradicional de los "dos postulados" para la relatividad especial
"Reflexiones de este tipo me hicieron comprender, ya poco después de 1900, es decir, poco después del trabajo pionero de Planck, que ni la mecánica ni la electrodinámica podían (salvo en casos limitados) reivindicar una validez exacta. Poco a poco fui perdiendo la esperanza de poder descubrir las leyes verdaderas mediante esfuerzos constructivos basados en hechos conocidos. Cuanto más lo intentaba y más desesperadamente, más llegaba a la convicción de que sólo el descubrimiento de un principio formal universal podía llevarnos a resultados seguros... ¿Cómo, entonces, podría encontrarse un principio tan universal?"
Albert Einstein: Notas autobiográficas [p 5]
Einstein distinguió dos proposiciones fundamentales que parecían ser las más seguras, independientemente de la validez exacta de las leyes (entonces) conocidas de la mecánica o la electrodinámica. Estas proposiciones eran la constancia de la velocidad de la luz en el vacío y la independencia de las leyes físicas (especialmente la constancia de la velocidad de la luz) de la elección del sistema inercial. En su presentación inicial de la relatividad especial en 1905, expresó estos postulados como: [p 1]
- El principio de relatividad : las leyes por las cuales los estados de los sistemas físicos experimentan cambios no se ven afectadas, ya sea que estos cambios de estado se refieran a uno u otro de dos sistemas en movimiento de traslación uniforme uno con respecto al otro. [p 1]
- Principio de invariabilidad de la velocidad de la luz: "... la luz se propaga siempre en el espacio vacío con una velocidad definida [rapidez] c , que es independiente del estado de movimiento del cuerpo emisor" (del prefacio). [p. 1] Es decir, la luz en el vacío se propaga con la velocidad c (una constante fija, independiente de la dirección) en al menos un sistema de coordenadas inerciales (el "sistema estacionario"), independientemente del estado de movimiento de la fuente de luz.
La constancia de la velocidad de la luz fue motivada por la teoría del electromagnetismo de Maxwell [13] y la falta de evidencia del éter luminífero . [14] Hay evidencia contradictoria sobre el grado en que Einstein fue influenciado por el resultado nulo del experimento de Michelson-Morley. [15] [16] En cualquier caso, el resultado nulo del experimento de Michelson-Morley ayudó a que la noción de la constancia de la velocidad de la luz ganara una aceptación generalizada y rápida.
La derivación de la relatividad especial depende no sólo de estos dos postulados explícitos, sino también de varias suposiciones tácitas ( hechas en casi todas las teorías de la física ), incluyendo la isotropía y homogeneidad del espacio y la independencia de las varas de medición y los relojes de su historia pasada. [p 6]
Tras la presentación original de la relatividad especial por parte de Einstein en 1905, se han propuesto muchos conjuntos diferentes de postulados en diversas derivaciones alternativas. [17] Pero el conjunto de postulados más común sigue siendo el empleado por Einstein en su artículo original. Una declaración más matemática del principio de relatividad hecha posteriormente por Einstein, que introduce el concepto de simplicidad no mencionado anteriormente, es:
Principio especial de relatividad : Si se elige un sistema de coordenadas K de modo que, en relación con él, las leyes físicas se cumplan en su forma más simple, las mismas leyes se cumplen en relación con cualquier otro sistema de coordenadas K ′ que se mueva en traslación uniforme con respecto a K . [18]
Henri Poincaré proporcionó el marco matemático para la teoría de la relatividad al demostrar que las transformaciones de Lorentz son un subconjunto de su grupo de Poincaré de transformaciones de simetría. Einstein derivó posteriormente estas transformaciones a partir de sus axiomas.
Muchos de los artículos de Einstein presentan derivaciones de la transformación de Lorentz basadas en estos dos principios. [p 7]
Principio de relatividad
Marcos de referencia y movimiento relativo

Los marcos de referencia desempeñan un papel crucial en la teoría de la relatividad. El término marco de referencia tal como se utiliza aquí es una perspectiva de observación en el espacio que no sufre ningún cambio de movimiento (aceleración), desde el que se puede medir una posición a lo largo de tres ejes espaciales (es decir, en reposo o a velocidad constante). Además, un marco de referencia tiene la capacidad de determinar mediciones del tiempo de los acontecimientos utilizando un "reloj" (cualquier dispositivo de referencia con periodicidad uniforme).
Un evento es un suceso al que se le puede asignar un único momento y ubicación en el espacio en relación con un marco de referencia: es un "punto" en el espacio-tiempo . Dado que la velocidad de la luz es constante en relatividad independientemente del marco de referencia, los pulsos de luz se pueden utilizar para medir distancias de forma inequívoca y hacer referencia al reloj a los momentos en que ocurrieron los eventos, aunque la luz tarda en llegar al reloj después de que el evento haya ocurrido.
Por ejemplo, la explosión de un petardo puede considerarse un "acontecimiento". Podemos especificar completamente un acontecimiento mediante sus cuatro coordenadas espacio-temporales: el momento en que se produce y su ubicación espacial tridimensional definen un punto de referencia. Llamemos a este marco de referencia S .
En la teoría de la relatividad, a menudo queremos calcular las coordenadas de un evento a partir de diferentes sistemas de referencia. Las ecuaciones que relacionan las mediciones realizadas en diferentes sistemas se denominan ecuaciones de transformación .
Configuración estándar
Para comprender mejor cómo se comparan entre sí las coordenadas del espacio-tiempo medidas por observadores en diferentes marcos de referencia , es útil trabajar con una configuración simplificada con marcos en una configuración estándar . [19] : 107 Con cuidado, esto permite simplificar las matemáticas sin pérdida de generalidad en las conclusiones a las que se llega. En la Fig. 2-1, se muestran dos marcos de referencia galileanos (es decir, marcos convencionales de 3 espacios) en movimiento relativo. El marco S pertenece a un primer observador O , y el marco S ′ (pronunciado "S prima" o "S guión") pertenece a un segundo observador O ′ .
- Los ejes x , y , z del marco S están orientados paralelos a los respectivos ejes primos del marco S ′ .
- El marco S ′ se mueve, para simplificar, en una sola dirección: la dirección x del marco S con una velocidad constante v medida en el marco S .
- Los orígenes de los marcos S y S ′ son coincidentes cuando el tiempo t = 0 para el marco S y t ′ = 0 para el marco S ′ .
Como no existe un sistema de referencia absoluto en la teoría de la relatividad, no existe estrictamente el concepto de "movimiento", ya que todo puede estar moviéndose con respecto a algún otro sistema de referencia. En cambio, se dice que dos sistemas cualesquiera que se muevan a la misma velocidad en la misma dirección están en co-movimiento . Por lo tanto, S y S ′ no están en co-movimiento .
Falta de un marco de referencia absoluto
El principio de relatividad , que establece que las leyes físicas tienen la misma forma en cada sistema de referencia inercial , se remonta a Galileo y fue incorporado a la física newtoniana. Pero a finales del siglo XIX, la existencia de ondas electromagnéticas llevó a algunos físicos a sugerir que el universo estaba lleno de una sustancia que llamaron " éter ", que, según postularon, actuaría como el medio a través del cual se propagarían estas ondas o vibraciones (en muchos aspectos de manera similar a la forma en que el sonido se propaga a través del aire). Se pensaba que el éter era un sistema de referencia absoluto contra el cual se podían medir todas las velocidades, y podía considerarse fijo e inmóvil en relación con la Tierra o algún otro punto de referencia fijo. Se suponía que el éter era lo suficientemente elástico como para soportar ondas electromagnéticas, mientras que esas ondas podían interactuar con la materia, pero no ofrecer resistencia a los cuerpos que pasaban a través de él (su única propiedad era que permitía que las ondas electromagnéticas se propagaran). Los resultados de varios experimentos, incluido el experimento de Michelson-Morley en 1887 (posteriormente verificado con experimentos más precisos e innovadores), condujeron a la teoría de la relatividad especial, al demostrar que el éter no existía. [20] La solución de Einstein fue descartar la noción de éter y el estado de reposo absoluto. En relatividad, cualquier sistema de referencia que se mueva con un movimiento uniforme observará las mismas leyes de la física. En particular, la velocidad de la luz en el vacío siempre se mide como c , incluso cuando se mide por múltiples sistemas que se mueven a velocidades diferentes (pero constantes).
Relatividad sin el segundo postulado
A partir del principio de relatividad únicamente y sin asumir la constancia de la velocidad de la luz (es decir, utilizando la isotropía del espacio y la simetría implícita en el principio de relatividad especial), se puede demostrar que las transformaciones del espacio-tiempo entre sistemas inerciales son euclidianas, galileanas o lorentzianas. En el caso lorentziano, se puede obtener la conservación del intervalo relativista y una cierta velocidad límite finita. Los experimentos sugieren que esta velocidad es la velocidad de la luz en el vacío. [p 8] [21]
La invariancia de Lorentz como núcleo esencial de la relatividad especial
Enfoques alternativos a la relatividad especial
Einstein basó sistemáticamente la derivación de la invariancia de Lorentz (el núcleo esencial de la relatividad especial) únicamente en los dos principios básicos de la relatividad y la invariancia de la velocidad de la luz. Escribió:
La idea fundamental de la teoría especial de la relatividad es la siguiente: los supuestos de relatividad e invariancia de la velocidad de la luz son compatibles si se postulan relaciones de un nuevo tipo ("transformación de Lorentz") para la conversión de coordenadas y tiempos de eventos... El principio universal de la teoría especial de la relatividad está contenido en el postulado: las leyes de la física son invariantes con respecto a las transformaciones de Lorentz (para la transición de un sistema inercial a cualquier otro sistema inercial elegido arbitrariamente). Este es un principio restrictivo para las leyes naturales... [p 5]
Por ello, muchos tratamientos modernos de la relatividad especial la basan en el postulado único de la covariancia universal de Lorentz o, equivalentemente, en el postulado único del espacio-tiempo de Minkowski . [p 9] [p 10]
En lugar de considerar la covariancia universal de Lorentz como un principio derivado, este artículo la considera como el postulado fundamental de la relatividad especial. El enfoque tradicional de dos postulados para la relatividad especial se presenta en innumerables libros de texto universitarios y presentaciones populares. [22] Los libros de texto que comienzan con el postulado único del espacio-tiempo de Minkowski incluyen los de Taylor y Wheeler [11] y los de Callahan. [23] Este es también el enfoque seguido por los artículos de Wikipedia Espacio-tiempo y Diagrama de Minkowski .
Transformación de Lorentz y su inversa
Definamos un evento con coordenadas espaciotemporales ( t , x , y , z ) en el sistema S y ( t ′ , x ′ , y ′ , z ′ ) en un marco de referencia que se mueve a una velocidad v en el eje x con respecto a ese marco, S ′ . Luego, la transformación de Lorentz especifica que estas coordenadas están relacionadas de la siguiente manera: donde es el factor de Lorentz y c es la velocidad de la luz en el vacío, y la velocidad v de S ′ , relativa a S , es paralela al eje x . Para simplificar, las coordenadas y y z no se ven afectadas; solo se transforman las coordenadas x y t . Estas transformaciones de Lorentz forman un grupo de un parámetro de aplicaciones lineales , cuyo parámetro se denomina rapidez .
Resolviendo las cuatro ecuaciones de transformación anteriores para las coordenadas no primas se obtiene la transformación de Lorentz inversa:
Esto demuestra que el marco no preparado se mueve con la velocidad − v , medida en el marco preparado. [24]
El eje x no tiene nada de especial . La transformación se puede aplicar al eje y o al eje z , o incluso en cualquier dirección paralela al movimiento (que se deforma por el factor γ ) y perpendicular; consulte el artículo Transformación de Lorentz para obtener más detalles.
Una cantidad invariante bajo las transformaciones de Lorentz se conoce como escalar de Lorentz .
Escribiendo la transformación de Lorentz y su inversa en términos de diferencias de coordenadas, donde un evento tiene coordenadas ( x 1 , t 1 ) y ( x ′ 1 , t ′ 1 ) , otro evento tiene coordenadas ( x 2 , t 2 ) y ( x ′ 2 , t ′ 2 ) , y las diferencias se definen como
- Ecuación 1:
- Ecuación 2:
Nosotros conseguimos
- Ecuación 3:
- Ecuación 4:
Si tomamos diferenciales en lugar de tomar diferencias, obtenemos
- Ecuación 5:
- Ecuación 6:
Representación gráfica de la transformación de Lorentz
Los diagramas de espacio-tiempo ( diagramas de Minkowski ) son una ayuda extremadamente útil para visualizar cómo se transforman las coordenadas entre diferentes sistemas de referencia. Aunque no es tan fácil realizar cálculos exactos utilizándolos como invocando directamente las transformaciones de Lorentz, su principal poder es su capacidad de proporcionar una comprensión intuitiva de los resultados de un escenario relativista. [21]
Para dibujar un diagrama de espacio-tiempo, comience por considerar dos marcos de referencia galileanos, S y S', en configuración estándar, como se muestra en la figura 2-1. [21] [25] : 155–199
Fig. 3-1a . Dibuje los ejes y del marco S. El eje es horizontal y el eje (en realidad ) es vertical, lo que es lo opuesto a la convención habitual en cinemática. El eje está escalado por un factor de de modo que ambos ejes tienen unidades de longitud comunes. En el diagrama mostrado, las líneas de cuadrícula están espaciadas una unidad de distancia. Las líneas diagonales de 45° representan las líneas de mundo de dos fotones que pasan por el origen en el tiempo La pendiente de estas líneas de mundo es 1 porque los fotones avanzan una unidad en el espacio por unidad de tiempo. Se han trazado dos eventos y en este gráfico de modo que sus coordenadas se puedan comparar en los marcos S y S'.
Fig. 3-1b . Dibuje los ejes y del marco S'. El eje representa la línea de mundo del origen del sistema de coordenadas S' medido en el marco S. En esta figura, los ejes y están inclinados con respecto a los ejes no primarios en un ángulo donde Los ejes primarios y no primarios comparten un origen común porque los marcos S y S' se habían configurado en la configuración estándar, de modo que cuando
Fig. 3-1c . Las unidades en los ejes con cebadores tienen una escala diferente a las unidades en los ejes sin cebadores. A partir de las transformaciones de Lorentz, observamos que las coordenadas de en el sistema de coordenadas con cebadores se transforman a en el sistema de coordenadas sin cebadores. Asimismo, las coordenadas de en el sistema de coordenadas con cebadores se transforman a en el sistema sin cebadores. Dibuje líneas de cuadrícula paralelas al eje a través de los puntos medidos en el marco sin cebadores, donde es un entero. Asimismo, dibuje líneas de cuadrícula paralelas al eje a través de los puntos medidos en el marco sin cebadores. Utilizando el teorema de Pitágoras, observamos que el espaciado entre unidades es igual a veces el espaciado entre unidades, medido en el marco S. Esta relación siempre es mayor que 1 y, en última instancia, se acerca al infinito como
Fig. 3-1d . Puesto que la velocidad de la luz es invariante, las líneas de mundo de dos fotones que pasan por el origen en el tiempo todavía se trazan como líneas diagonales de 45°. Las coordenadas primadas de y están relacionadas con las coordenadas no primadas a través de las transformaciones de Lorentz y podrían medirse aproximadamente a partir del gráfico (suponiendo que se haya trazado con la suficiente precisión), pero el verdadero mérito de un diagrama de Minkowski es que nos otorga una vista geométrica del escenario. Por ejemplo, en esta figura, observamos que los dos eventos separados en el tiempo que tenían diferentes coordenadas x en el marco no primado ahora están en la misma posición en el espacio.
Mientras que el marco sin primar está dibujado con ejes de espacio y tiempo que se encuentran en ángulos rectos, el marco primar está dibujado con ejes que se encuentran en ángulos agudos u obtusos. Esta asimetría se debe a distorsiones inevitables en la forma en que las coordenadas del espacio-tiempo se asignan a un plano cartesiano , pero los marcos son en realidad equivalentes.
Consecuencias derivadas de la transformación de Lorentz
Las consecuencias de la relatividad especial pueden derivarse de las ecuaciones de transformación de Lorentz . [26] Estas transformaciones, y por lo tanto la relatividad especial, conducen a predicciones físicas diferentes a las de la mecánica newtoniana en todas las velocidades relativas, y más pronunciadas cuando las velocidades relativas se vuelven comparables a la velocidad de la luz. La velocidad de la luz es mucho mayor que cualquier cosa que la mayoría de los humanos encuentren, por lo que algunos de los efectos predichos por la relatividad son inicialmente contraintuitivos .
Intervalo invariante
En la relatividad galileana, la longitud de un objeto ( ) [nota 3] y la separación temporal entre dos eventos ( ) son invariantes independientes, cuyos valores no cambian cuando se observan desde diferentes marcos de referencia. [nota 4] [nota 5]
Sin embargo, en relatividad especial, el entrelazamiento de coordenadas espaciales y temporales genera el concepto de intervalo invariante , denotado como : [nota 6]
El entrelazamiento del espacio y el tiempo revoca los conceptos implícitos de simultaneidad absoluta y sincronización a través de marcos no comóviles.
La forma de ser la diferencia del cuadrado del lapso de tiempo y la distancia espacial al cuadrado, demuestra una discrepancia fundamental entre las distancias euclidianas y del espacio-tiempo. [nota 7] La invariancia de este intervalo es una propiedad de la transformada general de Lorentz (también llamada transformación de Poincaré ), lo que la convierte en una isometría del espacio-tiempo. La transformada general de Lorentz extiende la transformada de Lorentz estándar (que trata con traslaciones sin rotación, es decir, impulsos de Lorentz , en la dirección x) con todas las demás traslaciones , reflexiones y rotaciones entre cualquier marco inercial cartesiano. [30] : 33–34
En el análisis de escenarios simplificados, como los diagramas de espacio-tiempo, a menudo se emplea una forma de dimensionalidad reducida del intervalo invariante:
Demostrar que el intervalo es invariante es sencillo para el caso de dimensionalidad reducida y con marcos en configuración estándar: [21]
El valor de es por tanto independiente del marco en el que se mide.
Al considerar el significado físico de , hay tres casos a tener en cuenta: [21] [31] : 25–39
- Δs 2 > 0: En este caso, los dos eventos están separados por más tiempo que espacio, y por lo tanto se dice que están separados temporalmente . Esto implica que y dada la transformación de Lorentz es evidente que existe un menor que para el cual (en particular, ). En otras palabras, dados dos eventos que están separados temporalmente, es posible encontrar un marco en el que los dos eventos ocurren en el mismo lugar. En este marco, la separación en el tiempo se llama tiempo propio .
- Δs 2 < 0: En este caso, los dos eventos están separados por más espacio que tiempo, y por lo tanto se dice que están separados espacialmente . Esto implica que y dada la transformación de Lorentz existe un menor que para el cual (en particular, ). En otras palabras, dados dos eventos que están separados espacialmente, es posible encontrar un marco en el que los dos eventos ocurren al mismo tiempo. En este marco, la separación en el espacio se llama distancia propia o longitud propia . Para valores de mayor que y menor que el signo de cambia, lo que significa que el orden temporal de los eventos separados espacialmente cambia dependiendo del marco en el que se vean los eventos. Pero el orden temporal de los eventos separados temporalmente es absoluto, ya que la única forma en que podría ser mayor que sería si
- Δs 2 = 0: En este caso, se dice que los dos eventos están separados por la luz . Esto implica que y esta relación es independiente del marco debido a la invariancia de A partir de esto, observamos que la velocidad de la luz es en cada marco inercial. En otras palabras, a partir del supuesto de la covarianza universal de Lorentz, la velocidad constante de la luz es un resultado derivado, en lugar de un postulado como en la formulación de dos postulados de la teoría especial.
Relatividad de la simultaneidad

Consideremos dos eventos que suceden en dos lugares diferentes y que ocurren simultáneamente en el marco de referencia de un observador inercial. Pueden ocurrir de manera no simultánea en el marco de referencia de otro observador inercial (falta de simultaneidad absoluta ).
De la ecuación 3 (la transformación de Lorentz hacia adelante en términos de diferencias de coordenadas)
Es evidente que los dos eventos que son simultáneos en el marco S (satisfaciendo Δ t = 0 ), no son necesariamente simultáneos en otro marco inercial S ′ (satisfaciendo Δ t ′ = 0 ). Sólo si estos eventos son además co-locales en el marco S (satisfaciendo Δ x = 0 ), serán simultáneos en otro marco S ′ .
El efecto Sagnac puede considerarse una manifestación de la relatividad de la simultaneidad. [32] Dado que la relatividad de la simultaneidad es un efecto de primer orden en , [21] los instrumentos basados en el efecto Sagnac para su funcionamiento, como los giroscopios láser de anillo y los giroscopios de fibra óptica , son capaces de alcanzar niveles extremos de sensibilidad. [p 14]
Dilatación del tiempo
El lapso de tiempo entre dos eventos no es invariable de un observador a otro, sino que depende de las velocidades relativas de los marcos de referencia de los observadores.
Supongamos que un reloj está en reposo en el sistema no primo S . La posición del reloj en dos tics diferentes se caracteriza entonces por Δ x = 0 . Para encontrar la relación entre los tiempos entre estos tics medidos en ambos sistemas, se puede utilizar la ecuación 3 para encontrar:
- Para eventos que satisfagan
Esto demuestra que el tiempo (Δ t ′ ) entre los dos tics, como se ve en el marco en el que se mueve el reloj ( S ′ ), es más largo que el tiempo (Δ t ) entre estos tics, medido en el marco de reposo del reloj ( S ). La dilatación del tiempo explica una serie de fenómenos físicos; por ejemplo, la vida útil de los muones de alta velocidad creados por la colisión de rayos cósmicos con partículas en la atmósfera exterior de la Tierra y que se mueven hacia la superficie es mayor que la vida útil de los muones que se mueven lentamente, creados y decayendo en un laboratorio. [33]

Siempre que se oye una afirmación del tipo "los relojes en movimiento van más despacio", hay que imaginarse un sistema de referencia inercial poblado de relojes idénticos y sincronizados. A medida que un reloj en movimiento recorre este sistema, su lectura en cualquier punto concreto se compara con la de un reloj estacionario en el mismo punto. [34] : 149–152
Las mediciones que obtendríamos si miráramos un reloj en movimiento no serían, en general, en absoluto las mismas, porque el tiempo que veríamos estaría retrasado por la velocidad finita de la luz, es decir, los tiempos que veríamos estarían distorsionados por el efecto Doppler . Las mediciones de los efectos relativistas siempre deben entenderse como realizadas después de que se hayan descartado los efectos de la velocidad finita de la luz. [34] : 149–152
El reloj de luz de Langevin

Paul Langevin , uno de los primeros defensores de la teoría de la relatividad, hizo mucho por popularizar la teoría frente a la resistencia de muchos físicos a los conceptos revolucionarios de Einstein. Entre sus numerosas contribuciones a los fundamentos de la relatividad especial se encuentran trabajos independientes sobre la relación masa-energía, un examen exhaustivo de la paradoja de los gemelos e investigaciones sobre sistemas de coordenadas rotatorios. Su nombre se asocia con frecuencia a un concepto hipotético llamado "reloj de luz" (desarrollado originalmente por Lewis y Tolman en 1909 [35] ) que utilizó para realizar una novedosa derivación de la transformación de Lorentz. [36]
Se considera que un reloj de luz es una caja de paredes perfectamente reflectantes en la que una señal luminosa se refleja de un lado a otro desde caras opuestas. El concepto de dilatación del tiempo se enseña con frecuencia utilizando un reloj de luz que se desplaza en un movimiento inercial uniforme perpendicular a una línea que conecta los dos espejos. [37] [38] [39] [40] (El propio Langevin utilizó un reloj de luz orientado en paralelo a su línea de movimiento. [36] )
Consideremos el escenario ilustrado en la Fig. 4-3A. El observador A sostiene un reloj de luz de longitud así como un cronómetro electrónico con el que mide cuánto tarda un pulso en hacer un viaje de ida y vuelta a lo largo del reloj de luz. Aunque el observador A viaja rápidamente a lo largo de un tren, desde su punto de vista la emisión y recepción del pulso ocurren en el mismo lugar, y mide el intervalo utilizando un solo reloj ubicado en la posición precisa de estos dos eventos. Para el intervalo entre estos dos eventos, el observador A encuentra Un intervalo de tiempo medido utilizando un solo reloj que está inmóvil en un marco de referencia particular se llama intervalo de tiempo propio . [41]
La figura 4-3B ilustra estos mismos dos eventos desde el punto de vista del observador B, que está estacionado junto a las vías mientras el tren pasa a una velocidad de En lugar de hacer movimientos rectos hacia arriba y hacia abajo, el observador B ve los pulsos moviéndose a lo largo de una línea en zigzag. Sin embargo, debido al postulado de la constancia de la velocidad de la luz, la velocidad de los pulsos a lo largo de estas líneas diagonales es la misma que la que el observador A vio para sus pulsos hacia arriba y hacia abajo. B mide la velocidad del componente vertical de estos pulsos como de modo que el tiempo total de ida y vuelta de los pulsos es Nótese que para el observador B, la emisión y recepción del pulso de luz ocurrieron en diferentes lugares, y midió el intervalo utilizando dos relojes estacionarios y sincronizados ubicados en dos posiciones diferentes en su marco de referencia. El intervalo que B midió, por lo tanto, no fue un intervalo de tiempo propio porque no lo midió con un solo reloj en reposo. [41]
Dilatación recíproca del tiempo
En la descripción anterior del reloj de luz de Langevin, la clasificación de un observador como estacionario y del otro como en movimiento fue completamente arbitraria. También podría suceder que el observador B llevara el reloj de luz y se moviera a una velocidad de hacia la izquierda, en cuyo caso el observador A percibiría que el reloj de B funcionaba más lento que su reloj local.
No hay ninguna paradoja aquí, porque no hay un observador independiente C que esté de acuerdo con A y B. El observador C necesariamente hace sus mediciones a partir de su propio marco de referencia. Si ese marco de referencia coincide con el marco de referencia de A, entonces C estará de acuerdo con la medición del tiempo de A. Si el marco de referencia de C coincide con el marco de referencia de B, entonces C estará de acuerdo con la medición del tiempo de B. Si el marco de referencia de C no coincide ni con el marco de A ni con el de B, entonces la medición del tiempo de C estará en desacuerdo con la medición del tiempo de A y de B. [42]
Paradoja de los gemelos
La reciprocidad de la dilatación del tiempo entre dos observadores en sistemas inerciales separados conduce a la llamada paradoja de los gemelos , articulada en su forma actual por Langevin en 1911. [43] Langevin imaginó a un aventurero que desea explorar el futuro de la Tierra. Este viajero se sube a un proyectil capaz de viajar al 99,995% de la velocidad de la luz. Después de hacer un viaje de ida y vuelta hacia y desde una estrella cercana que dura solo dos años de su propia vida, regresa a una Tierra que es doscientos años más vieja.
Este resultado parece desconcertante porque tanto el viajero como un observador terrestre verían al otro en movimiento y, por lo tanto, debido a la reciprocidad de la dilatación del tiempo, uno podría esperar inicialmente que cada uno hubiera encontrado que el otro había envejecido menos. En realidad, no hay ninguna paradoja, porque para que los dos observadores comparen sus tiempos propios, la simetría de la situación debe romperse: al menos uno de los dos observadores debe cambiar su estado de movimiento para coincidir con el del otro. [44]

Sin embargo, conocer la resolución general de la paradoja no permite calcular inmediatamente resultados cuantitativos correctos. En la literatura se han proporcionado muchas soluciones a este problema y se han analizado en el artículo sobre la paradoja de los gemelos . A continuación, examinaremos una de esas soluciones a la paradoja.
Nuestro objetivo básico será demostrar que, después del viaje, ambos gemelos están en perfecto acuerdo sobre quién envejeció cuánto, independientemente de sus diferentes experiencias. La figura 4-4 ilustra un escenario donde el gemelo viajero vuela a 0,6 c hacia y desde una estrella a 3 años luz de distancia. Durante el viaje, cada gemelo envía señales de tiempo anuales (medidas en sus propios tiempos propios) al otro. Después del viaje, se comparan los recuentos acumulativos. En la fase de ida del viaje, cada gemelo recibe las señales del otro a la tasa reducida de Inicialmente, la situación es perfectamente simétrica: observe que cada gemelo recibe la señal de un año del otro a los dos años medidos en su propio reloj. La simetría se rompe cuando el gemelo viajero se da la vuelta en la marca de los cuatro años medidos por su reloj. Durante los cuatro años restantes de su viaje, recibe señales a la tasa mejorada de La situación es bastante diferente con el gemelo estacionario. Debido al retraso de la velocidad de la luz, no ve a su hermana darse la vuelta hasta que hayan pasado ocho años en su propio reloj. Por lo tanto, recibe señales de frecuencia aumentada de su hermana durante un período relativamente breve. Aunque los gemelos no están de acuerdo en sus respectivas medidas del tiempo total, vemos en la siguiente tabla, así como por simple observación del diagrama de Minkowski, que cada gemelo está totalmente de acuerdo con el otro en cuanto al número total de señales enviadas de uno al otro. Por lo tanto, no hay ninguna paradoja. [34] : 152–159
| Artículo | Medido por el quedarse en casa | Figura 4-4 | Medido por el viajero | Figura 4-4 |
|---|---|---|---|---|
| Tiempo total del viaje | 10 años | 8 años | ||
| Número total de pulsos enviados | 10 | 8 | ||
| Hora en que se detecta el cambio de rumbo del viajero | 8 años | 4 años | ||
| Número de pulsos recibidos a la velocidad inicial | | 4 | | 2 |
| Tiempo para el resto del viaje. | 2 años | 4 años | ||
| Número de señales recibidas a velocidad final | 4 | 8 | ||
| Número total de pulsos recibidos | 8 | 10 | ||
| Cálculo del gemelo sobre cuánto debería haber envejecido el otro gemelo | 8 años | 10 años |
Contracción de longitud
Las dimensiones (por ejemplo, la longitud) de un objeto medidas por un observador pueden ser menores que los resultados de las mediciones del mismo objeto realizadas por otro observador (por ejemplo, la paradoja de la escalera implica una escalera larga que viaja casi a la velocidad de la luz y está contenida dentro de un garaje más pequeño).
De manera similar, supongamos que una varilla de medición está en reposo y alineada a lo largo del eje x en el sistema no primo S . En este sistema, la longitud de esta varilla se escribe como Δ x . Para medir la longitud de esta varilla en el sistema S ′ , en el que la varilla se está moviendo, las distancias x ′ a los puntos finales de la varilla deben medirse simultáneamente en ese sistema S ′ . En otras palabras, la medición se caracteriza por Δ t ′ = 0 , que se puede combinar con la Ecuación 4 para encontrar la relación entre las longitudes Δ x y Δ x ′ :
- Para eventos que satisfagan
Esto demuestra que la longitud (Δ x ′ ) de la varilla medida en el marco en el que se mueve ( S ′ ), es más corta que su longitud (Δ x ) en su propio marco de reposo ( S ).
La dilatación del tiempo y la contracción de la longitud no son meras apariencias. La dilatación del tiempo está explícitamente relacionada con nuestra forma de medir los intervalos de tiempo entre eventos que ocurren en el mismo lugar en un sistema de coordenadas dado (llamados eventos "co-locales"). Estos intervalos de tiempo (que pueden ser, y son, medidos experimentalmente por observadores relevantes) son diferentes en otro sistema de coordenadas que se mueve con respecto al primero, a menos que los eventos, además de ser co-locales, también sean simultáneos. De manera similar, la contracción de la longitud se relaciona con nuestras distancias medidas entre eventos separados pero simultáneos en un sistema de coordenadas dado de elección. Si estos eventos no son co-locales, sino que están separados por la distancia (espacio), no ocurrirán a la misma distancia espacial entre sí cuando se los observe desde otro sistema de coordenadas en movimiento.
Transformación de velocidades de Lorentz
Consideremos dos marcos S y S ′ en configuración estándar. Una partícula en S se mueve en la dirección x con el vector de velocidad ¿Cuál es su velocidad en el marco S ′ ?
Podemos escribir
| ( 7 ) |
| ( 8 ) |
Sustituyendo expresiones para y de la ecuación 5 en la ecuación 8 , seguido de manipulaciones matemáticas sencillas y sustitución inversa de la ecuación 7, se obtiene la transformación de Lorentz de la velocidad en :
| ( 9 ) |
La relación inversa se obtiene intercambiando los símbolos primados y no primados y reemplazando con
| ( 10 ) |
Para no alineado a lo largo del eje x, escribimos: [12] : 47–49
| ( 11 ) |
| ( 12 ) |
Las transformaciones directa e inversa para este caso son:
| ( 13 ) |
| ( 14 ) |
La ecuación 10 y la ecuación 14 pueden interpretarse como la resultante de las dos velocidades y y reemplazan la fórmula que es válida en la relatividad galileana. Interpretadas de esa manera, se las conoce comúnmente como fórmulas relativistas de adición (o composición) de velocidades , válidas para los tres ejes de S y S ′ alineados entre sí (aunque no necesariamente en la configuración estándar). [12] : 47–49
Tomamos nota de los siguientes puntos:
- Si un objeto (por ejemplo, un fotón ) se moviera a la velocidad de la luz en un marco (es decir, u = ± c o u ′ = ± c ) , entonces también se movería a la velocidad de la luz en cualquier otro marco, moviéndose a | v | < c .
- La velocidad resultante de dos velocidades con magnitud menor que c es siempre una velocidad con magnitud menor que c .
- Si tanto | u | como | v | (y entonces también | u ′ | y | v ′ |) son pequeños con respecto a la velocidad de la luz (es decir, por ejemplo, | tú/do | ≪ 1 ), entonces las transformaciones galileanas intuitivas se recuperan de las ecuaciones de transformación para la relatividad especial
- Unir un marco a un fotón ( que viaja sobre un haz de luz , como considera Einstein) requiere un tratamiento especial de las transformaciones.
No hay nada especial en la dirección x en la configuración estándar. El formalismo anterior se aplica a cualquier dirección; y tres direcciones ortogonales permiten tratar con todas las direcciones en el espacio descomponiendo los vectores de velocidad en sus componentes en estas direcciones. Consulte la fórmula de adición de velocidad para obtener más detalles.
Rotación de Thomas
La composición de dos impulsos de Lorentz no colineales (es decir, dos transformaciones de Lorentz no colineales, ninguna de las cuales implica rotación) da como resultado una transformación de Lorentz que no es un impulso puro, sino que es la composición de un impulso y una rotación.
La rotación de Thomas resulta de la relatividad de la simultaneidad. En la figura 4-5a, una varilla de longitud en su sistema de referencia en reposo (es decir, que tiene una longitud propia de ) se eleva verticalmente a lo largo del eje y en el sistema de referencia en el suelo.
En la figura 4-5b, se observa la misma varilla desde el marco de un cohete que se mueve a gran velocidad hacia la derecha. Si imaginamos dos relojes situados en los extremos izquierdo y derecho de la varilla que están sincronizados en el marco de la varilla , la relatividad de la simultaneidad hace que el observador en el marco del cohete observe (no vea) el reloj en el extremo derecho de la varilla como si estuviera adelantado en el tiempo y la varilla se observe correspondientemente como inclinada. [31] : 98–99
A diferencia de los efectos relativistas de segundo orden, como la contracción de la longitud o la dilatación del tiempo, este efecto se vuelve bastante significativo incluso a velocidades bastante bajas. Por ejemplo, esto se puede ver en el espín de partículas en movimiento , donde la precesión de Thomas es una corrección relativista que se aplica al espín de una partícula elemental o la rotación de un giroscopio macroscópico , relacionando la velocidad angular del espín de una partícula que sigue una órbita curvilínea con la velocidad angular del movimiento orbital. [31] : 169–174
La rotación de Thomas proporciona la solución a la conocida "paradoja del metro y el agujero". [p 15] [31] : 98–99
Causalidad y prohibición del movimiento más rápido que la luz

En la figura 4-6, el intervalo de tiempo entre los eventos A (la "causa") y B (el "efecto") es "temporal"; es decir, hay un marco de referencia en el que los eventos A y B ocurren en el mismo lugar en el espacio , separados solo por ocurrir en diferentes momentos. Si A precede a B en ese marco, entonces A precede a B en todos los marcos accesibles por una transformación de Lorentz. Es posible que la materia (o información) viaje (por debajo de la velocidad de la luz) desde el lugar de A, comenzando en el momento de A, hasta el lugar de B, llegando al momento de B, por lo que puede haber una relación causal (siendo A la causa y B el efecto).
El intervalo AC del diagrama es "similar al espacio", es decir, hay un marco de referencia en el que los eventos A y C ocurren simultáneamente, separados solo en el espacio. También hay marcos en los que A precede a C (como se muestra) y marcos en los que C precede a A. Pero no hay marcos accesibles mediante una transformación de Lorentz, en la que los eventos A y C ocurran en el mismo lugar. Si fuera posible que existiera una relación de causa y efecto entre los eventos A y C, se producirían paradojas de causalidad.
Por ejemplo, si las señales pudieran enviarse más rápido que la luz, entonces podrían enviarse señales al pasado del remitente (el observador B en los diagramas). [45] [p 16] Se podrían construir entonces una variedad de paradojas causales.
"comunicadores instantáneos" ficticios
Considere los diagramas de espacio-tiempo de la figura 4-7. A y B se encuentran junto a una vía férrea cuando pasa un tren de alta velocidad, con C viajando en el último vagón del tren y D viajando en el vagón delantero. Las líneas de universo de A y B son verticales ( ct ), lo que distingue la posición estacionaria de estos observadores en el suelo, mientras que las líneas de universo de C y D están inclinadas hacia delante ( ct ′ ), lo que refleja el movimiento rápido de los observadores C y D estacionarios en su tren, tal como se observa desde el suelo.
- Fig. 4-7a. El evento de "B pasando un mensaje a D", mientras el vagón que va delante pasa, está en el origen del marco de D. D envía el mensaje a lo largo del tren a C en el vagón trasero, utilizando un "comunicador instantáneo" ficticio. La línea de tiempo de este mensaje es la flecha roja gruesa a lo largo del eje, que es una línea de simultaneidad en los marcos preparados de C y D. En el marco de tierra (no preparado) la señal llega antes de lo que fue enviada.
- Fig. 4-7b. El evento de "C pasando el mensaje a A", que está de pie junto a las vías del tren, está en el origen de sus tramas. Ahora A envía el mensaje a lo largo de las vías a B mediante un "comunicador instantáneo". La línea de tiempo de este mensaje es la flecha gruesa azul, a lo largo del eje, que es una línea de simultaneidad para las tramas de A y B. Como se ve en el diagrama del espacio-tiempo, B recibirá el mensaje antes de haberlo enviado, una violación de la causalidad. [46]
No es necesario que las señales sean instantáneas para violar la causalidad. Incluso si la señal de D a C fuera ligeramente más superficial que el eje (y la señal de A a B ligeramente más inclinada que el eje), aún sería posible que B recibiera su mensaje antes de haberlo enviado. Al aumentar la velocidad del tren a velocidades cercanas a la de la luz, los ejes y pueden comprimirse muy cerca de la línea discontinua que representa la velocidad de la luz. Con esta configuración modificada, se puede demostrar que incluso señales solo ligeramente más rápidas que la velocidad de la luz darán como resultado una violación de la causalidad. [47]
Por lo tanto, si se quiere preservar la causalidad , una de las consecuencias de la relatividad especial es que ninguna señal de información ni ningún objeto material puede viajar más rápido que la luz en el vacío.
Esto no quiere decir que todas las velocidades superiores a la de la luz sean imposibles. Se pueden describir varias situaciones triviales en las que algunas "cosas" (no materia ni energía reales) se mueven más rápido que la luz. [48] Por ejemplo, el lugar donde el haz de luz de un reflector incide en la parte inferior de una nube puede moverse más rápido que la luz cuando el reflector se gira rápidamente (aunque esto no viola la causalidad ni ningún otro fenómeno relativista). [49] [50]
Efectos ópticos
Efectos de arrastre

En 1850, Hippolyte Fizeau y Léon Foucault establecieron de forma independiente que la luz viaja más lentamente en el agua que en el aire, validando así una predicción de la teoría ondulatoria de la luz de Fresnel e invalidando la predicción correspondiente de la teoría corpuscular de Newton . [51] La velocidad de la luz se midió en agua en calma. ¿Cuál sería la velocidad de la luz en agua en movimiento?
En 1851, Fizeau realizó un experimento para responder a esta pregunta, cuya representación simplificada se ilustra en la figura 5-1. Un divisor de haz divide un haz de luz y los haces divididos pasan en direcciones opuestas a través de un tubo de agua en movimiento. Se recombinan para formar franjas de interferencia, que indican una diferencia en la longitud del recorrido óptico, que un observador puede ver. El experimento demostró que el arrastre de la luz por el agua en movimiento provocó un desplazamiento de las franjas, lo que demuestra que el movimiento del agua había afectado a la velocidad de la luz.
Según las teorías que prevalecían en ese momento, la luz que viaja a través de un medio en movimiento sería una simple suma de su velocidad a través del medio más la velocidad del medio. Contrariamente a lo esperado, Fizeau descubrió que, aunque la luz parecía ser arrastrada por el agua, la magnitud del arrastre era mucho menor de lo esperado. Si es la velocidad de la luz en agua quieta, y es la velocidad del agua, y es la velocidad de la luz transportada por el agua en el marco de referencia del laboratorio con el flujo de agua sumando o restando a la velocidad de la luz, entonces
Los resultados de Fizeau, aunque consistentes con la hipótesis anterior de Fresnel sobre el arrastre parcial del éter , fueron extremadamente desconcertantes para los físicos de la época. Entre otras cosas, la presencia de un término de índice de refracción significaba que, dado que depende de la longitud de onda, el éter debe ser capaz de sostener diferentes movimientos al mismo tiempo . [nota 8] Se propusieron diversas explicaciones teóricas para explicar el coeficiente de arrastre de Fresnel , que eran completamente contradictorias entre sí. Incluso antes del experimento de Michelson-Morley, los resultados experimentales de Fizeau se encontraban entre una serie de observaciones que crearon una situación crítica para explicar la óptica de los cuerpos en movimiento. [52]
Desde el punto de vista de la relatividad especial, el resultado de Fizeau no es más que una aproximación a la ecuación 10 , la fórmula relativista para la composición de velocidades. [30]
Aberración relativista de la luz

Debido a la velocidad finita de la luz, si los movimientos relativos de una fuente y un receptor incluyen un componente transversal, entonces la dirección desde la cual la luz llega al receptor se desplazará con respecto a la posición geométrica en el espacio de la fuente con respecto al receptor. El cálculo clásico del desplazamiento adopta dos formas y realiza predicciones diferentes dependiendo de si el receptor, la fuente o ambos están en movimiento con respecto al medio. (1) Si el receptor está en movimiento, el desplazamiento sería consecuencia de la aberración de la luz . El ángulo de incidencia del haz con respecto al receptor se podría calcular a partir de la suma vectorial de los movimientos del receptor y la velocidad de la luz incidente. [53] (2) Si la fuente está en movimiento, el desplazamiento sería consecuencia de la corrección del tiempo de luz . El desplazamiento de la posición aparente de la fuente con respecto a su posición geométrica sería el resultado del movimiento de la fuente durante el tiempo que tarda su luz en llegar al receptor. [54]
La explicación clásica no superó la prueba experimental. Dado que el ángulo de aberración depende de la relación entre la velocidad del receptor y la velocidad de la luz incidente, el paso de la luz incidente a través de un medio refractivo debería cambiar el ángulo de aberración. En 1810, Arago utilizó este fenómeno esperado en un intento fallido de medir la velocidad de la luz, [55] y en 1870, George Airy probó la hipótesis utilizando un telescopio lleno de agua, encontrando que, contra lo esperado, la aberración medida era idéntica a la aberración medida con un telescopio lleno de aire. [56] Un intento "engorroso" de explicar estos resultados utilizó la hipótesis del arrastre parcial del éter, [57] pero era incompatible con los resultados del experimento de Michelson-Morley, que aparentemente exigía un arrastre completo del éter. [58]
Suponiendo sistemas inerciales, la expresión relativista para la aberración de la luz es aplicable tanto a los casos de receptor en movimiento como a los de fuente en movimiento. Se han publicado diversas fórmulas trigonométricamente equivalentes. Expresadas en términos de las variables de la figura 5-2, estas incluyen [30] : 57–60
- O O
Efecto Doppler relativista
Efecto Doppler longitudinal relativista
El efecto Doppler clásico depende de si la fuente, el receptor o ambos están en movimiento con respecto al medio. El efecto Doppler relativista es independiente de cualquier medio. Sin embargo, el desplazamiento Doppler relativista para el caso longitudinal, con la fuente y el receptor moviéndose directamente uno hacia el otro o alejándose uno del otro, se puede derivar como si fuera el fenómeno clásico, pero modificado mediante la adición de un término de dilatación del tiempo , y ese es el tratamiento que se describe aquí. [59] [60]
Suponga que el receptor y la fuente se alejan entre sí con una velocidad relativa medida por un observador en el receptor o la fuente (la convención de signos adoptada aquí es que es negativa si el receptor y la fuente se mueven uno hacia el otro). Suponga que la fuente está estacionaria en el medio. Entonces, ¿dónde es la velocidad del sonido?
En el caso de la luz, y con el receptor moviéndose a velocidades relativistas, los relojes del receptor están dilatados en el tiempo en relación con los relojes de la fuente. El receptor medirá la frecuencia recibida para que esté donde
- y
- es el factor de Lorentz .
Se obtiene una expresión idéntica para el desplazamiento Doppler relativista cuando se realiza el análisis en el marco de referencia del receptor con una fuente en movimiento. [61] [21]
Efecto Doppler transversal

El efecto Doppler transversal es una de las principales predicciones novedosas de la teoría especial de la relatividad.
Clásicamente, uno podría esperar que si la fuente y el receptor se mueven transversalmente uno con respecto al otro sin ningún componente longitudinal en sus movimientos relativos, no debería haber ningún desplazamiento Doppler en la luz que llega al receptor.
La relatividad especial predice lo contrario. La figura 5-3 ilustra dos variantes comunes de este escenario. Ambas variantes pueden analizarse utilizando argumentos simples de dilatación del tiempo. [21] En la figura 5-3a, el receptor observa que la luz de la fuente se desplaza hacia el azul por un factor de . En la figura 5-3b, la luz se desplaza hacia el rojo por el mismo factor.
Medición versus apariencia visual

La dilatación del tiempo y la contracción de la longitud no son ilusiones ópticas, sino efectos genuinos. Las mediciones de estos efectos no son un artefacto del efecto Doppler , ni son el resultado de no tener en cuenta el tiempo que tarda la luz en viajar desde un evento hasta un observador.
Los científicos hacen una distinción fundamental entre la medición u observación , por un lado, y la apariencia visual , o lo que uno ve . La forma medida de un objeto es una instantánea hipotética de todos los puntos del objeto tal como existen en un momento determinado en el tiempo. Pero la apariencia visual de un objeto se ve afectada por los diferentes tiempos que tarda la luz en viajar desde diferentes puntos del objeto hasta el ojo.

Durante muchos años, la distinción entre ambos no había sido apreciada en general, y se había pensado en general que un objeto con una longitud contraída que pasara por un observador, de hecho, sería visto como una longitud contraída. En 1959, James Terrell y Roger Penrose señalaron de forma independiente que los efectos de desfase temporal diferencial en las señales que llegan al observador desde las diferentes partes de un objeto en movimiento dan como resultado que la apariencia visual de un objeto en movimiento rápido sea bastante diferente de su forma medida. Por ejemplo, un objeto que se aleja parecería contraído , un objeto que se acerca parecería alargado y un objeto que pasa tendría una apariencia torcida que se ha comparado con una rotación. [p 19] [p 20] [62] [63] Una esfera en movimiento conserva el contorno circular para todas las velocidades, para cualquier distancia y para todos los ángulos de visión, aunque la superficie de la esfera y las imágenes en ella aparecerán distorsionadas. [64] [65]
.jpg/440px-M87_jet_(1).jpg)
Tanto la figura 5-4 como la figura 5-5 ilustran objetos que se mueven transversalmente a la línea de visión. En la figura 5-4, se observa un cubo desde una distancia de cuatro veces la longitud de sus lados. A altas velocidades, los lados del cubo que son perpendiculares a la dirección del movimiento parecen tener forma hiperbólica. El cubo en realidad no está rotado. Más bien, la luz de la parte trasera del cubo tarda más en llegar a los ojos en comparación con la luz de la parte delantera, tiempo durante el cual el cubo se ha movido hacia la derecha. A altas velocidades, la esfera de la figura 5-5 adquiere la apariencia de un disco aplanado inclinado hasta 45° con respecto a la línea de visión. Si los movimientos de los objetos no son estrictamente transversales sino que incluyen un componente longitudinal, se pueden ver distorsiones exageradas en la perspectiva. [66] Esta ilusión se conoce como rotación de Terrell o efecto Terrell-Penrose . [nota 9]
Otro ejemplo en el que la apariencia visual está en desacuerdo con la medición proviene de la observación del aparente movimiento superlumínico en varias radiogalaxias , objetos BL Lac , cuásares y otros objetos astronómicos que expulsan chorros de materia a velocidad relativista en ángulos estrechos con respecto al observador. Se produce una aparente ilusión óptica que da la apariencia de viajar más rápido que la luz. [67] [68] [69] En la Fig. 5-6, la galaxia M87 expulsa un chorro de partículas subatómicas a alta velocidad casi directamente hacia nosotros, pero la rotación de Penrose-Terrell hace que el chorro parezca moverse lateralmente de la misma manera que se ha estirado la apariencia del cubo en la Fig. 5-4. [70]
Dinámica
La sección Consecuencias derivadas de la transformación de Lorentz se ocupa estrictamente de la cinemática , el estudio del movimiento de puntos, cuerpos y sistemas de cuerpos sin considerar las fuerzas que causan el movimiento. Esta sección analiza las masas, las fuerzas, la energía, etc. y, como tal, requiere la consideración de efectos físicos más allá de los abarcados por la propia transformación de Lorentz.
Equivalencia de masa y energía
A medida que la velocidad de un objeto se aproxima a la velocidad de la luz desde el punto de vista de un observador, su masa relativista aumenta, lo que hace cada vez más difícil acelerarlo desde dentro del marco de referencia del observador.
El contenido energético de un objeto en reposo con masa m es igual a mc2 . La conservación de la energía implica que, en cualquier reacción, una disminución de la suma de las masas de las partículas debe ir acompañada de un aumento de las energías cinéticas de las partículas después de la reacción. De manera similar, la masa de un objeto puede aumentarse al absorber energías cinéticas.
Además de los artículos mencionados anteriormente, que proporcionan derivaciones de la transformación de Lorentz y describen los fundamentos de la relatividad especial, Einstein también escribió al menos cuatro artículos que ofrecen argumentos heurísticos para la equivalencia (y transmutabilidad) de la masa y la energía, para E = mc 2 .
La equivalencia masa-energía es una consecuencia de la relatividad especial. La energía y el momento, que están separados en la mecánica newtoniana, forman un cuatrivector en la relatividad, y esto relaciona el componente temporal (la energía) con los componentes espaciales (el momento) de una manera no trivial. Para un objeto en reposo, el cuatrivector energía-momento es ( E / c , 0, 0, 0) : tiene un componente temporal que es la energía, y tres componentes espaciales que son cero. Al cambiar los sistemas de referencia con una transformación de Lorentz en la dirección x con un valor pequeño de la velocidad v, el cuatrivector energía-momento se convierte en ( E / c , Ev / c 2 , 0, 0) . El momento es igual a la energía multiplicada por la velocidad dividida por c 2 . Como tal, la masa newtoniana de un objeto, que es la relación entre el momento y la velocidad para velocidades lentas, es igual a E / c 2 .
La energía y el momento son propiedades de la materia y la radiación, y es imposible deducir que forman un cuatrivector sólo a partir de los dos postulados básicos de la relatividad especial, porque éstos no hablan de materia ni radiación, sólo hablan de espacio y tiempo. Por tanto, la derivación requiere un razonamiento físico adicional. En su artículo de 1905, Einstein utilizó los principios adicionales que la mecánica newtoniana debería cumplir para velocidades lentas, de modo que hay un escalar de energía y un momento trivectorial a velocidades lentas, y que la ley de conservación de la energía y el momento es exactamente cierta en la relatividad. Además, supuso que la energía de la luz se transforma por el mismo factor de desplazamiento Doppler que su frecuencia, lo que previamente había demostrado que era cierto basándose en las ecuaciones de Maxwell. [p 1] El primero de los artículos de Einstein sobre este tema fue "¿Depende la inercia de un cuerpo de su contenido energético?" en 1905. [p 21] Aunque el argumento de Einstein en este artículo es aceptado casi universalmente por los físicos como correcto, incluso evidente, muchos autores a lo largo de los años han sugerido que es erróneo. [71] Otros autores sugieren que el argumento era simplemente inconcluyente porque se basaba en algunas suposiciones implícitas. [72]
Einstein reconoció la controversia sobre su derivación en su artículo de 1907 sobre la relatividad especial. Allí señala que es problemático confiar en las ecuaciones de Maxwell para el argumento heurístico de masa-energía. El argumento en su artículo de 1905 se puede llevar a cabo con la emisión de cualquier partícula sin masa, pero las ecuaciones de Maxwell se utilizan implícitamente para hacer obvio que la emisión de luz en particular solo se puede lograr realizando trabajo. Para emitir ondas electromagnéticas, todo lo que hay que hacer es agitar una partícula cargada, y esto claramente está realizando trabajo, por lo que la emisión es de energía. [p 22] [nota 10]
La demostración de Einstein en 1905mi=mc2
En su cuarto artículo de 1905 titulado Annus mirabilis , [p. 21] Einstein presentó un argumento heurístico a favor de la equivalencia de masa y energía. Aunque, como se ha comentado anteriormente, estudios posteriores han establecido que sus argumentos no alcanzaban a constituir una prueba ampliamente definitiva, las conclusiones a las que llegó en este artículo han resistido la prueba del tiempo.
Einstein tomó como supuestos de partida su recientemente descubierta fórmula para el efecto Doppler relativista , las leyes de conservación de la energía y de la conservación del momento , y la relación entre la frecuencia de la luz y su energía tal como se desprende de las ecuaciones de Maxwell .
Fig. 6-1 (arriba). Consideremos un sistema de ondas planas de luz que tienen una frecuencia que viaja en dirección relativa al eje x del marco de referencia S . La frecuencia (y por lo tanto la energía) de las ondas, medida en el marco S ′ que se mueve a lo largo del eje x a velocidad, está dada por la fórmula relativista del desplazamiento Doppler que Einstein había desarrollado en su artículo de 1905 sobre la relatividad especial: [p 1]
Fig. 6-1 (abajo). Considere un cuerpo arbitrario que está estacionario en el marco de referencia S . Sea que este cuerpo emita un par de pulsos de luz de igual energía en direcciones opuestas en un ángulo con respecto al eje x. Cada pulso tiene energía . Debido a la conservación del momento, el cuerpo permanece estacionario en S después de la emisión de los dos pulsos. Sea la energía del cuerpo antes de la emisión de los dos pulsos y después de su emisión.
A continuación, considere el mismo sistema observado desde el marco S ′ que se mueve a lo largo del eje x a velocidad relativa al marco S . En este marco, la luz de los pulsos de ida y vuelta se desplazará Doppler de manera relativista. Sea la energía del cuerpo medida en el marco de referencia S ′ antes de la emisión de los dos pulsos y después de su emisión. Obtenemos las siguientes relaciones: [p 21]
De las ecuaciones anteriores, obtenemos lo siguiente:
| ( 6-1 ) |
Las dos diferencias de forma que se observan en la ecuación anterior tienen una interpretación física sencilla. Puesto que y son las energías del cuerpo arbitrario en los sistemas de referencia móviles y estacionarios, y representan las energías cinéticas de los cuerpos antes y después de la emisión de luz (excepto una constante aditiva que fija el punto cero de energía y se establece convencionalmente en cero). Por lo tanto,
| ( 6-2 ) |
Tomando una expansión en serie de Taylor y descuidando los términos de orden superior, obtuvo
| ( 6-3 ) |
Comparando la expresión anterior con la expresión clásica para la energía cinética, EC = 1/2 mv 2 , Einstein observó entonces: "Si un cuerpo emite energía L en forma de radiación, su masa disminuye en L / c 2 ."
Rindler ha observado que el argumento heurístico de Einstein sugería simplemente que la energía contribuye a la masa. En 1905, la expresión cautelosa de Einstein de la relación masa-energía permitía la posibilidad de que pudiera existir una masa "dormida" que permanecería después de que se eliminara toda la energía de un cuerpo. Sin embargo, en 1907, Einstein estaba listo para afirmar que toda la masa inercial representaba una reserva de energía. "Igualar toda la masa con la energía requería un acto de fe estética, muy característico de Einstein". [12] : 81–84 La audaz hipótesis de Einstein ha sido ampliamente confirmada en los años posteriores a su propuesta original.
Por diversas razones, actualmente rara vez se enseña la derivación original de Einstein. Además del intenso debate que continúa hasta el día de hoy sobre la corrección formal de su derivación original, el reconocimiento de la relatividad especial como lo que Einstein llamó una "teoría de principios" ha llevado a un cambio de la dependencia de los fenómenos electromagnéticos hacia métodos de prueba puramente dinámicos. [73]
¿Hasta dónde puedes viajar desde la Tierra?
Puesto que nada puede viajar más rápido que la luz, se podría concluir que un ser humano nunca puede viajar más lejos de la Tierra que ~100 años luz. Fácilmente pensarías que un viajero nunca sería capaz de alcanzar más que los pocos sistemas solares que existen dentro del límite de 100 años luz de la Tierra. Sin embargo, debido a la dilatación del tiempo, una nave espacial hipotética puede viajar miles de años luz durante la vida de un pasajero. Si se pudiera construir una nave espacial que acelerara a una constante de 1 g , después de un año, viajaría casi a la velocidad de la luz vista desde la Tierra. Esto se describe por: donde v ( t ) es la velocidad en un tiempo t , a es la aceleración de la nave espacial y t es el tiempo de coordenadas medido por personas en la Tierra. [p 23] Por lo tanto, después de un año de acelerar a 9,81 m/s 2 , la nave espacial viajará a v = 0,712 c y 0,946 c después de tres años, en relación con la Tierra. Después de tres años de esta aceleración, con la nave espacial alcanzando una velocidad del 94,6% de la velocidad de la luz relativa a la Tierra, la dilatación del tiempo dará como resultado que cada segundo experimentado en la nave espacial corresponda a 3,1 segundos en la Tierra. Durante su viaje, las personas en la Tierra experimentarán más tiempo del que experimentan, ya que sus relojes (todos los fenómenos físicos) en realidad estarían funcionando 3,1 veces más rápido que los de la nave espacial. Un viaje de ida y vuelta de 5 años para el viajero tomará 6,5 años terrestres y cubrirá una distancia de más de 6 años luz. Un viaje de ida y vuelta de 20 años para ellos (5 años acelerando, 5 desacelerando, dos veces cada uno) los aterrizará de regreso en la Tierra después de haber viajado durante 335 años terrestres y una distancia de 331 años luz. [74] Un viaje completo de 40 años a 1 g parecerá en la Tierra durar 58.000 años y cubrir una distancia de 55.000 años luz. Un viaje de 40 años a 1,1 g durará 148.000 años terrestres y cubrirá unos 140.000 años luz. Un viaje de ida de 28 años (14 años acelerando, 14 desacelerando, según las mediciones del reloj del astronauta) a 1 g de aceleración podría alcanzar los 2.000.000 de años luz hasta la galaxia de Andrómeda. [74] Esta misma dilatación del tiempo es la razón por la que se observa que un muón que viaja cerca de c recorre una distancia mucho mayor que c multiplicada por su vida media (cuando está en reposo). [75]
Colisiones elásticas
El estudio de los productos de colisión generados por los aceleradores de partículas de todo el mundo proporciona a los científicos pruebas de la estructura del mundo subatómico y de las leyes naturales que lo gobiernan. El análisis de los productos de colisión, cuya suma de masas puede superar ampliamente las masas de las partículas incidentes, requiere la relatividad especial. [76]
En la mecánica newtoniana, el análisis de las colisiones implica el uso de las leyes de conservación de la masa , el momento y la energía . En la mecánica relativista, la masa no se conserva de forma independiente, porque ha sido subsumida en la energía relativista total. Ilustramos las diferencias que surgen entre los tratamientos newtonianos y relativistas de las colisiones de partículas examinando el caso simple de dos partículas perfectamente elásticas en colisión de igual masa. ( Las colisiones inelásticas se analizan en Espacio-tiempo#Leyes de conservación . La desintegración radiactiva puede considerarse una especie de colisión inelástica invertida en el tiempo. [76] )
La dispersión elástica de partículas elementales cargadas se desvía de la idealidad debido a la producción de radiación de frenado . [77] [78]
Análisis newtoniano

La figura 6-2 proporciona una demostración del resultado, familiar para los jugadores de billar, de que si una bola estacionaria es golpeada elásticamente por otra de la misma masa (suponiendo que no hay efecto lateral o "inglés"), entonces después de la colisión, las trayectorias divergentes de las dos bolas subtenderán un ángulo recto. (a) En el marco estacionario, una esfera incidente que viaja a 2 v golpea una esfera estacionaria. (b) En el marco del centro del momento, las dos esferas se aproximan simétricamente a ± v . Después de la colisión elástica, las dos esferas rebotan una de la otra con velocidades iguales y opuestas ± u . La conservación de la energía requiere que | u | = | v |. (c) Volviendo al marco estacionario, las velocidades de rebote son v ± u . El producto escalar ( v + u ) ⋅ ( v − u ) = v 2 − u 2 = 0 , indicando que los vectores son ortogonales. [12] : 26–27
Análisis relativista

Consideremos el escenario de colisión elástica de la figura 6-3 entre una partícula en movimiento que choca con una partícula estacionaria de igual masa. A diferencia del caso newtoniano, el ángulo entre las dos partículas después de la colisión es menor a 90°, depende del ángulo de dispersión y se vuelve cada vez más pequeño a medida que la velocidad de la partícula incidente se acerca a la velocidad de la luz:
El momento relativista y la energía relativista total de una partícula están dados por
| ( 6-4 ) |
La conservación del momento dicta que la suma de los momentos de la partícula entrante y de la partícula estacionaria (que inicialmente tiene momento = 0) es igual a la suma de los momentos de las partículas emergentes:
| ( 6-5 ) |
De la misma manera, la suma de las energías relativistas totales de la partícula entrante y la partícula estacionaria (que inicialmente tiene energía total mc 2 ) es igual a la suma de las energías totales de las partículas emergentes:
| ( 6-6 ) |
Al descomponer ( 6-5 ) en sus componentes, reemplazar con el adimensional y factorizar los términos comunes de ( 6-5 ) y ( 6-6 ) se obtiene lo siguiente: [p 24]
| ( 6-7 ) |
| ( 6-8 ) |
| ( 6-9 ) |
De aquí obtenemos las siguientes relaciones: [p 24]
| ( 6-10 ) |
| ( 6-11 ) |
| ( 6-12 ) |
Para el caso simétrico en el que y ( 6-12 ) toma la forma más simple: [p 24]
| ( 6-13 ) |
Más allá de lo básico
Rapidez
Las transformaciones de Lorentz relacionan las coordenadas de los eventos en un sistema de referencia con las de otro sistema. La composición relativista de velocidades se utiliza para sumar dos velocidades. Las fórmulas para realizar estos últimos cálculos no son lineales, lo que las hace más complejas que las fórmulas galileanas correspondientes.
Esta no linealidad es un artefacto de nuestra elección de parámetros. [11] : 47–59 Hemos observado anteriormente que en un diagrama de espacio-tiempo x–ct , los puntos en algún intervalo de espacio-tiempo constante desde el origen forman una hipérbola invariante. También hemos observado que los sistemas de coordenadas de dos marcos de referencia de espacio-tiempo en configuración estándar están rotados hiperbólicamente uno con respecto al otro.
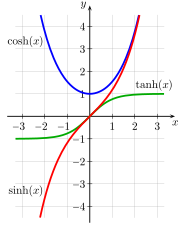
Las funciones naturales para expresar estas relaciones son los análogos hiperbólicos de las funciones trigonométricas . La figura 7-1a muestra un círculo unitario con sin( a ) y cos( a ), la única diferencia entre este diagrama y el círculo unitario familiar de la trigonometría elemental es que a se interpreta, no como el ángulo entre el rayo y el eje x , sino como el doble del área del sector barrido por el rayo desde el eje x . Numéricamente, las medidas del ángulo y del área 2 × para el círculo unitario son idénticas. La figura 7-1b muestra una hipérbola unitaria con sinh( a ) y cosh( a ), donde a se interpreta igualmente como el doble del área teñida. [79] La figura 7-2 presenta gráficos de las funciones sinh, cosh y tanh.
Para el círculo unitario, la pendiente del rayo está dada por
En el plano cartesiano, la rotación del punto ( x , y ) al punto ( x ' , y ' ) por un ángulo θ está dada por
En un diagrama de espacio-tiempo, el parámetro de velocidad es el análogo de la pendiente. La rapidez , φ , se define mediante [21] : 96–99
dónde
La rapidez definida anteriormente es muy útil en relatividad especial porque muchas expresiones adoptan una forma considerablemente más simple cuando se expresan en términos de ella. Por ejemplo, la rapidez es simplemente aditiva en la fórmula de adición de velocidad colineal; [11] : 47–59
o en otras palabras,
Las transformaciones de Lorentz adoptan una forma simple cuando se expresan en términos de rapidez. El factor γ se puede escribir como
Las transformaciones que describen un movimiento relativo con velocidad uniforme y sin rotación de los ejes de coordenadas espaciales se denominan " boosts" .
Sustituyendo γ y γβ en las transformaciones presentadas previamente y reescribiendo en forma matricial, el impulso de Lorentz en la dirección x se puede escribir como
y el impulso de Lorentz inverso en la dirección x puede escribirse como
En otras palabras, los impulsos de Lorentz representan rotaciones hiperbólicas en el espacio-tiempo de Minkowski. [21] : 96–99
Las ventajas de utilizar funciones hiperbólicas son tales que algunos libros de texto como los clásicos de Taylor y Wheeler introducen su uso en una etapa muy temprana. [11] [nota 11]
4-vectores
Los cuatro vectores se han mencionado anteriormente en el contexto del 4-vector de energía-momento , pero sin mucho énfasis. De hecho, ninguna de las derivaciones elementales de la relatividad especial los requiere. Pero una vez entendidos, los 4-vectores , y más generalmente los tensores , simplifican enormemente las matemáticas y la comprensión conceptual de la relatividad especial. Trabajar exclusivamente con tales objetos conduce a fórmulas que son manifiestamente relativísticamente invariantes, lo que es una ventaja considerable en contextos no triviales. Por ejemplo, demostrar la invariancia relativista de las ecuaciones de Maxwell en su forma habitual no es trivial, mientras que es meramente un cálculo rutinario, realmente no más que una observación, utilizando la formulación del tensor de intensidad de campo . [80]
Por otra parte, la relatividad general, desde el principio, se basa en gran medida en 4-vectores y, más generalmente, en tensores que representan entidades físicamente relevantes. Relacionarlos mediante ecuaciones que no dependen de coordenadas específicas requiere tensores capaces de conectar dichos 4-vectores incluso dentro de un espacio-tiempo curvo , y no solo dentro de uno plano como en la relatividad especial. El estudio de los tensores queda fuera del alcance de este artículo, que solo proporciona una discusión básica del espacio-tiempo.
Definición de 4-vectores
Una 4-tupla, es un "4-vector" si su componente A i se transforma entre marcos de acuerdo con la transformación de Lorentz.
Si se utilizan coordenadas , A es un 4–vector si se transforma (en la dirección x ) de acuerdo con
que proviene simplemente de reemplazar ct con A 0 y x con A 1 en la presentación anterior de la transformación de Lorentz.
Como es habitual, cuando escribimos x , t , etc. generalmente queremos decir Δx , Δt , etc.
Los últimos tres componentes de un 4–vector deben ser un vector estándar en el espacio tridimensional. Por lo tanto, un 4–vector debe transformarse como bajo transformaciones de Lorentz y rotaciones. [81] : 36–59
Propiedades de los 4-vectores
- Cierre bajo combinación lineal: Si A y B son 4-vectores , entonces también es un 4-vector .
- Invariancia del producto interno: si A y B son 4-vectores , entonces su producto interno (producto escalar) es invariante, es decir, su producto interno es independiente del marco en el que se calcula. Observe cómo el cálculo del producto interno difiere del cálculo del producto interno de un 3-vector . A continuación, y son 3-vectores :
- Además de ser invariante bajo la transformación de Lorentz, el producto interno anterior también es invariante bajo la rotación en el espacio tridimensional .
- Se dice que dos vectores son ortogonales si A diferencia del caso de los 3-vectores, los 4-vectores ortogonales no necesariamente forman ángulos rectos entre sí. La regla es que dos 4-vectores son ortogonales si están desplazados por ángulos iguales y opuestos con respecto a la línea de 45°, que es la línea del universo de un rayo de luz. Esto implica que un 4-vector similar a la luz es ortogonal consigo mismo .
- Invariancia de la magnitud de un vector: La magnitud de un vector es el producto interno de un 4-vector consigo mismo, y es una propiedad independiente del marco. Al igual que con los intervalos, la magnitud puede ser positiva, negativa o cero, de modo que los vectores se denominan temporales, espaciales o nulos (lumínicos). Nótese que un vector nulo no es lo mismo que un vector cero. Un vector nulo es uno para el cual mientras que un vector cero es uno cuyos componentes son todos cero. Los casos especiales que ilustran la invariancia de la norma incluyen el intervalo invariante y la longitud invariante del vector de momento relativista [21] : 178–181 [81] : 36–59
Ejemplos de 4-vectores
- Desplazamiento de 4 vectores: También conocido como separación espacio-temporal , es ( Δt, Δx, Δy, Δz ), o para separaciones infinitesimales, ( dt, dx, dy, dz ) .
- 4-vector de velocidad: Esto resulta cuando el 4-vector de desplazamiento se divide por , donde es el tiempo apropiado entre los dos eventos que producen dt, dx, dy y dz .
- La velocidad 4 es tangente a la línea del mundo de una partícula y tiene una longitud igual a una unidad de tiempo en el marco de la partícula.
- Una partícula acelerada no tiene un sistema inercial en el que se encuentre siempre en reposo. Sin embargo, siempre se puede encontrar un sistema inercial que se mueva momentáneamente con la partícula. Este sistema, el sistema de referencia que se mueve momentáneamente con ella (MCRF), permite aplicar la relatividad especial al análisis de partículas aceleradas.
- Dado que los fotones se mueven sobre líneas nulas, para un fotón no se puede definir una velocidad de 4. No existe un marco en el que un fotón esté en reposo y no se puede establecer una MCRF a lo largo de la trayectoria de un fotón.
- 4-vectores de energía-momento:
- Como se indicó anteriormente, existen diversos tratamientos para el 4-vector de energía-momento , de modo que también se lo puede ver expresado como o El primer componente es la energía total (incluida la masa) de la partícula (o sistema de partículas) en un marco dado, mientras que los componentes restantes son su momento espacial. El 4-vector de energía-momento es una cantidad conservada.
- Aceleración 4-vector: Resulta de tomar la derivada del 4-vector velocidad con respecto a
- Fuerza 4-vector: Es la derivada del 4-vector momento con respecto a
Como se esperaba, los componentes finales de los 4 vectores anteriores son todos 3 vectores estándar correspondientes a 3-momentos espaciales , 3-fuerzas , etc. [21] : 178–181 [81] : 36–59
4-vectores y ley física
El primer postulado de la relatividad especial declara la equivalencia de todos los sistemas inerciales. Una ley física que se cumple en un sistema debe aplicarse en todos los sistemas, ya que de lo contrario sería posible diferenciar entre sistemas. Los momentos newtonianos no se comportan adecuadamente bajo la transformación de Lorentz, y Einstein prefirió cambiar la definición de momento a una que incluyera 4 vectores en lugar de renunciar a la conservación del momento.
Las leyes físicas deben basarse en construcciones que sean independientes del marco. Esto significa que las leyes físicas pueden tomar la forma de ecuaciones que conectan escalares, que siempre son independientes del marco. Sin embargo, las ecuaciones que involucran 4-vectores requieren el uso de tensores con el rango apropiado, que a su vez pueden considerarse como construidos a partir de 4-vectores . [21] : 186
Aceleración
Es un error muy común pensar que la relatividad especial es aplicable únicamente a sistemas inerciales y que no puede manejar objetos en aceleración ni sistemas de referencia en aceleración. En realidad, los objetos en aceleración pueden analizarse generalmente sin necesidad de manejar sistemas en aceleración. La relatividad general sólo es necesaria cuando la gravitación es significativa. [82]
Sin embargo, el manejo adecuado de los sistemas de referencia acelerados requiere cierto cuidado. La diferencia entre la relatividad especial y la general es que (1) en la relatividad especial, todas las velocidades son relativas, pero la aceleración es absoluta. (2) en la relatividad general, todo movimiento es relativo, ya sea inercial, acelerado o rotatorio. Para compensar esta diferencia, la relatividad general utiliza el espacio-tiempo curvo. [82]
En esta sección analizamos varios escenarios que involucran marcos de referencia acelerados.
Paradoja de la nave espacial Dewan-Beran-Bell
La paradoja de la nave espacial Dewan-Beran-Bell ( paradoja de la nave espacial de Bell ) es un buen ejemplo de un problema en el que el razonamiento intuitivo sin la ayuda de la percepción geométrica del enfoque espaciotemporal puede generar problemas.

En la figura 7-4, dos naves espaciales idénticas flotan en el espacio y se encuentran en reposo una respecto de la otra. Están conectadas por una cuerda que solo puede estirarse un poco antes de romperse. En un instante dado en nuestro sistema de referencia, el sistema del observador, ambas naves espaciales aceleran en la misma dirección a lo largo de la línea que las une con la misma aceleración propia constante. [nota 12] ¿Se romperá la cuerda?
Cuando la paradoja era nueva y relativamente desconocida, incluso los físicos profesionales tenían dificultades para encontrar la solución. Dos líneas de razonamiento conducen a conclusiones opuestas. Ambos argumentos, que se presentan a continuación, son defectuosos, aunque uno de ellos ofrece la respuesta correcta. [21] : 106, 120–122
- Para los observadores en el sistema de referencia en reposo, las naves espaciales parten de una distancia L y permanecen separadas durante la aceleración. Durante la aceleración, L es una distancia contraída en longitud de la distancia L ' = γL en el sistema de referencia de las naves espaciales en aceleración. Después de un tiempo suficientemente largo, γ aumentará hasta un factor suficientemente grande como para que la cuerda se rompa.
- Sean A y B las naves espaciales delantera y trasera. En el marco de las naves espaciales, cada nave espacial ve a la otra nave espacial haciendo lo mismo que ella. A dice que B tiene la misma aceleración que él, y B ve que A imita cada uno de sus movimientos. De modo que las naves espaciales permanecen a la misma distancia entre sí y la cuerda no se rompe. [21] : 106, 120–122
El problema con el primer argumento es que no existe un "marco de referencia de las naves espaciales". No puede haberlo, porque las dos naves espaciales miden una distancia creciente entre sí. Como no existe un marco de referencia común de las naves espaciales, la longitud de la cuerda está mal definida. No obstante, la conclusión es correcta y el argumento es en gran parte correcto. El segundo argumento, sin embargo, ignora por completo la relatividad de la simultaneidad. [21] : 106, 120–122
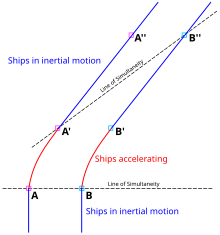
Un diagrama de espacio-tiempo (Fig. 7-5) hace que la solución correcta a esta paradoja sea evidente casi inmediatamente. Dos observadores en el espacio-tiempo de Minkowski aceleran con aceleración de magnitud constante durante un tiempo propio (la aceleración y el tiempo transcurrido los miden los propios observadores, no algún observador inercial). Son comóviles e inerciales antes y después de esta fase. En la geometría de Minkowski, la longitud a lo largo de la línea de simultaneidad resulta ser mayor que la longitud a lo largo de la línea de simultaneidad .
El aumento de longitud se puede calcular con la ayuda de la transformación de Lorentz. Si, como se ilustra en la figura 7-5, se termina la aceleración, los barcos permanecerán con un desplazamiento constante en algún sistema de referencia. Si y son las posiciones de los barcos en las posiciones en el sistema de referencia : [83]
La "paradoja", por así decirlo, proviene de la forma en que Bell construyó su ejemplo. En la discusión habitual de la contracción de Lorentz, la longitud en reposo es fija y la longitud en movimiento se acorta según se mide en el marco . Como se muestra en la Figura 7-5, el ejemplo de Bell afirma que las longitudes en movimiento y medidas en el marco son fijas, lo que obliga a que la longitud en reposo en el marco aumente.
Observador acelerado con horizonte
Ciertas configuraciones de problemas de relatividad especial pueden llevar a comprender fenómenos normalmente asociados con la relatividad general, como los horizontes de eventos . En el texto que acompaña la sección "Hipérbola invariante" del artículo Espacio-tiempo , las hipérbolas magenta representan trayectorias reales que sigue un viajero en constante aceleración en el espacio-tiempo. Durante los períodos de aceleración positiva, la velocidad del viajero apenas se acerca a la velocidad de la luz, mientras que, medida en nuestro marco, la aceleración del viajero disminuye constantemente.
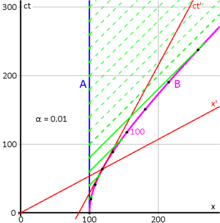
La figura 7-6 detalla con más detalle diversas características de los movimientos del viajero. En cualquier momento dado, su eje espacial está formado por una línea que pasa por el origen y su posición actual en la hipérbola, mientras que su eje temporal es la tangente a la hipérbola en su posición. El parámetro de velocidad se acerca a un límite de uno a medida que aumenta. Asimismo, tiende al infinito.
La forma de la hipérbola invariante corresponde a una trayectoria de aceleración propia constante. Esto se puede demostrar de la siguiente manera:
- Recordamos que
- Puesto que concluimos que
- De la ley de fuerza relativista,
- Sustituyendo del paso 2 y la expresión del paso 3 se obtiene que es una expresión constante. [84] : 110–113
La figura 7-6 ilustra un escenario calculado específico. Terence (A) y Stella (B) se encuentran inicialmente juntos a 100 horas luz del origen. Stella despega en el tiempo 0, su nave espacial acelera a 0,01 c por hora. Cada veinte horas, Terence envía actualizaciones por radio a Stella sobre la situación en casa (líneas verdes continuas). Stella recibe estas transmisiones regulares, pero la distancia creciente (compensada en parte por la dilatación del tiempo) hace que reciba las comunicaciones de Terence cada vez más tarde, según lo medido en su reloj, y nunca recibe ninguna comunicación de Terence después de 100 horas en su reloj (líneas verdes discontinuas). [84] : 110–113
Después de 100 horas según el reloj de Terence, Stella entra en una región oscura. Ha viajado fuera del futuro temporal de Terence. Por otro lado, Terence puede seguir recibiendo los mensajes de Stella indefinidamente. Solo tiene que esperar lo suficiente. El espacio-tiempo se ha dividido en regiones distintas separadas por un aparente horizonte de sucesos. Mientras Stella siga acelerando, nunca podrá saber qué ocurre detrás de este horizonte. [84] : 110–113
Relatividad y electromagnetismo unificador
La investigación teórica en electromagnetismo clásico condujo al descubrimiento de la propagación de ondas. Las ecuaciones que generalizan los efectos electromagnéticos descubrieron que la velocidad finita de propagación de los campos E y B requería ciertos comportamientos en partículas cargadas. El estudio general de cargas en movimiento forma el potencial de Liénard-Wiechert , que es un paso hacia la relatividad especial.
La transformación de Lorentz del campo eléctrico de una carga en movimiento en el marco de referencia de un observador inmóvil da como resultado la aparición de un término matemático comúnmente llamado campo magnético . Por el contrario, el campo magnético generado por una carga en movimiento desaparece y se convierte en un campo puramente electrostático en un marco de referencia comóvil. Las ecuaciones de Maxwell son, por lo tanto, simplemente un ajuste empírico a los efectos relativistas especiales en un modelo clásico del Universo. Como los campos eléctricos y magnéticos dependen del marco de referencia y, por lo tanto, están entrelazados, se habla de campos electromagnéticos . La relatividad especial proporciona las reglas de transformación de cómo un campo electromagnético en un marco inercial aparece en otro marco inercial.
Las ecuaciones de Maxwell en forma 3D ya son consistentes con el contenido físico de la relatividad especial, aunque son más fáciles de manipular en una forma manifiestamente covariante , es decir, en el lenguaje del cálculo tensorial . [80]
Teorías de la relatividad y la mecánica cuántica
La relatividad especial puede combinarse con la mecánica cuántica para formar la mecánica cuántica relativista y la electrodinámica cuántica . Cómo se pueden unificar la relatividad general y la mecánica cuántica es uno de los problemas no resueltos de la física ; la gravedad cuántica y una " teoría del todo ", que requieren una unificación que incluya también la relatividad general, son áreas activas y en curso en la investigación teórica.
El primer modelo atómico de Bohr-Sommerfeld explicaba la estructura fina de los átomos de metales alcalinos utilizando tanto la relatividad especial como el conocimiento preliminar sobre mecánica cuántica de la época. [85]
En 1928, Paul Dirac construyó una influyente ecuación de onda relativista , ahora conocida como la ecuación de Dirac en su honor, [p 25] que es totalmente compatible tanto con la relatividad especial como con la versión final de la teoría cuántica existente después de 1926. Esta ecuación no solo describía el momento angular intrínseco de los electrones llamado espín , sino que también condujo a la predicción de la antipartícula del electrón (el positrón ), [p 25] [p 26] y la estructura fina solo podía explicarse completamente con la relatividad especial. Fue el primer fundamento de la mecánica cuántica relativista .
Por otra parte, la existencia de antipartículas lleva a la conclusión de que la mecánica cuántica relativista no es suficiente para una teoría más precisa y completa de las interacciones entre partículas, sino que se hace necesaria una teoría de partículas interpretadas como campos cuantizados, llamada teoría cuántica de campos ; en la que las partículas pueden crearse y destruirse a lo largo del espacio y del tiempo.
Estado
La relatividad especial en su espacio-tiempo de Minkowski es precisa solo cuando el valor absoluto del potencial gravitatorio es mucho menor que c 2 en la región de interés. [86] En un campo gravitatorio fuerte, se debe utilizar la relatividad general . La relatividad general se convierte en relatividad especial en el límite de un campo débil. A escalas muy pequeñas, como en la longitud de Planck y menores, se deben tener en cuenta los efectos cuánticos, lo que da como resultado la gravedad cuántica . Pero a escalas macroscópicas y en ausencia de campos gravitatorios fuertes, la relatividad especial se prueba experimentalmente con un grado extremadamente alto de precisión (10 −20 ) [87] y, por lo tanto, es aceptada por la comunidad de físicos. Los resultados experimentales que parecen contradecirla no son reproducibles y, por lo tanto, se cree ampliamente que se deben a errores experimentales. [88]
La relatividad especial es matemáticamente autoconsistente y es una parte orgánica de todas las teorías físicas modernas, más notablemente la teoría cuántica de campos , la teoría de cuerdas y la relatividad general (en el caso límite de campos gravitacionales despreciables).
La mecánica newtoniana se deduce matemáticamente de la relatividad especial a velocidades pequeñas (en comparación con la velocidad de la luz), por lo que se puede considerar la mecánica newtoniana como una relatividad especial de cuerpos que se mueven lentamente. Véase mecánica clásica para una explicación más detallada.
Varios experimentos anteriores al artículo de Einstein de 1905 se interpretan ahora como evidencia de la relatividad. De ellos, se sabe que Einstein conocía el experimento de Fizeau antes de 1905, [89] y los historiadores han llegado a la conclusión de que Einstein conocía al menos el experimento de Michelson-Morley ya en 1899, a pesar de las afirmaciones que hizo en sus últimos años de que no jugó ningún papel en su desarrollo de la teoría. [16]
- El experimento de Fizeau (1851, repetido por Michelson y Morley en 1886) midió la velocidad de la luz en medios en movimiento, con resultados que son consistentes con la adición relativista de velocidades colineales.
- El famoso experimento de Michelson-Morley (1881, 1887) dio más respaldo al postulado de que no era posible detectar una velocidad de referencia absoluta. Cabe señalar aquí que, contrariamente a muchas afirmaciones alternativas, dijo poco sobre la invariancia de la velocidad de la luz con respecto a la velocidad de la fuente y del observador, ya que tanto la fuente como el observador viajaban juntos a la misma velocidad en todo momento.
- El experimento de Trouton-Noble (1903) demostró que el torque en un capacitor es independiente de la posición y del marco de referencia inercial.
- Los experimentos de Rayleigh y Brace (1902, 1904) demostraron que la contracción de la longitud no conduce a la birrefringencia para un observador en movimiento conjunto, de acuerdo con el principio de relatividad.
Los aceleradores de partículas aceleran y miden las propiedades de partículas que se mueven a una velocidad cercana a la de la luz, donde su comportamiento es consistente con la teoría de la relatividad e incompatible con la mecánica newtoniana anterior . Estas máquinas simplemente no funcionarían si no estuvieran diseñadas de acuerdo con los principios relativistas. Además, se han realizado una cantidad considerable de experimentos modernos para probar la relatividad especial. Algunos ejemplos:
- Pruebas de energía y momento relativistas : prueba de la velocidad límite de las partículas
- Experimento de Ives-Stilwell : prueba del efecto Doppler relativista y la dilatación del tiempo
- Prueba experimental de la dilatación del tiempo : efectos relativistas sobre la vida media de una partícula de rápido movimiento
- Experimento de Kennedy-Thorndike : dilatación del tiempo según las transformaciones de Lorentz
- Experimento Hughes-Drever : prueba de la isotropía del espacio y la masa
- Búsquedas modernas de violación de Lorentz : diversas pruebas modernas
- Los experimentos para probar la teoría de la emisión demostraron que la velocidad de la luz es independiente de la velocidad del emisor.
- Experimentos para probar la hipótesis del arrastre del éter : no hay "obstrucción del flujo del éter".
Discusión técnica del espacio-tiempo
Geometría del espacio-tiempo
Comparación entre el espacio euclidiano plano y el espacio de Minkowski

La relatividad especial utiliza un espacio de Minkowski "plano" de cuatro dimensiones, un ejemplo de espacio-tiempo . El espacio-tiempo de Minkowski parece ser muy similar al espacio euclidiano tridimensional estándar , pero hay una diferencia crucial con respecto al tiempo.
En el espacio 3D, el diferencial de distancia (elemento de línea) ds se define por donde d x = ( dx 1 , dx 2 , dx 3 ) son los diferenciales de las tres dimensiones espaciales. En la geometría de Minkowski, hay una dimensión extra con coordenada X 0 derivada del tiempo, de modo que el diferencial de distancia cumple donde d X = ( dX 0 , dX 1 , dX 2 , dX 3 ) son los diferenciales de las cuatro dimensiones del espacio-tiempo. Esto sugiere una profunda visión teórica: la relatividad especial es simplemente una simetría rotacional de nuestro espacio-tiempo, análoga a la simetría rotacional del espacio euclidiano (véase la figura 10-1). [91] Así como el espacio euclidiano utiliza una métrica euclidiana , el espacio-tiempo utiliza una métrica de Minkowski .Básicamente, la relatividad especial puede enunciarse como la invariancia de cualquier intervalo de espacio-tiempo (es decir, la distancia 4D entre dos eventos cualesquiera) cuando se observa desde cualquier sistema de referencia inercial . Todas las ecuaciones y efectos de la relatividad especial pueden derivarse de esta simetría rotacional (el grupo de Poincaré ) del espacio-tiempo de Minkowski.
La forma real de ds anterior depende de la métrica y de las opciones para la coordenada X 0 . Para que la coordenada temporal se parezca a las coordenadas espaciales, se puede tratar como imaginaria : X 0 = ict (esto se llama rotación de Wick ). Según Misner, Thorne y Wheeler (1971, §2.3), en última instancia, la comprensión más profunda de la relatividad especial y general provendrá del estudio de la métrica de Minkowski (descrita a continuación) y de tomar X 0 = ct , en lugar de una métrica euclidiana "disfrazada" que use ict como la coordenada temporal.
Algunos autores utilizan X 0 = t , con factores de c en otros lugares para compensar; por ejemplo, las coordenadas espaciales se dividen por c o se incluyen factores de c ±2 en el tensor métrico. [92] Estas numerosas convenciones se pueden reemplazar mediante el uso de unidades naturales donde c = 1 . Entonces el espacio y el tiempo tienen unidades equivalentes, y no aparecen factores de c en ninguna parte.
Espacio-tiempo 3D

Si reducimos las dimensiones espaciales a 2, de modo que podamos representar la física en un espacio 3D, vemos que las geodésicas nulas se encuentran a lo largo de un cono dual (ver Fig. 10-2) definido por la ecuación; o simplemente que es la ecuación de un círculo de radio c dt .
Espacio-tiempo 4D
Si extendemos esto a tres dimensiones espaciales, las geodésicas nulas son el cono de 4 dimensiones: entonces

Como se ilustra en la figura 10-3, las geodésicas nulas se pueden visualizar como un conjunto de esferas concéntricas continuas con radios = c dt .
Este doble cono nulo representa la "línea de visión" de un punto en el espacio. Es decir, cuando miramos las estrellas y decimos "La luz de esa estrella que estoy recibiendo tiene X años", estamos mirando hacia abajo por esta línea de visión: una geodésica nula. Estamos mirando un evento a una distancia lejana y en un tiempo d/c en el pasado. Por esta razón, el doble cono nulo también se conoce como "cono de luz". (El punto en la parte inferior izquierda de la Fig. 10-2 representa la estrella, el origen representa al observador y la línea representa la "línea de visión" de la geodésica nula).
El cono en la región − t es la información que el punto está "recibiendo", mientras que el cono en la sección + t es la información que el punto está "enviando".
La geometría del espacio de Minkowski se puede representar utilizando diagramas de Minkowski , que también son útiles para comprender muchos de los experimentos mentales en relatividad especial.
Física en el espacio-tiempo
Transformaciones de magnitudes físicas entre sistemas de referencia
Arriba, la transformación de Lorentz para la coordenada temporal y tres coordenadas espaciales ilustra que están entrelazadas. Esto es cierto en términos más generales: ciertos pares de magnitudes "temporales" y "espaciales" se combinan naturalmente en igualdad de condiciones bajo la misma transformación de Lorentz.
La transformación de Lorentz en la configuración estándar anterior, es decir, para un impulso en la dirección x , se puede reformular en forma matricial de la siguiente manera:
En la mecánica newtoniana, las cantidades que tienen magnitud y dirección se describen matemáticamente como vectores 3d en el espacio euclidiano y, en general, están parametrizadas por el tiempo. En la relatividad especial, esta noción se extiende añadiendo la cantidad temporal apropiada a una cantidad vectorial espacial, y tenemos vectores 4d, o " cuatro vectores ", en el espacio-tiempo de Minkowski. Los componentes de los vectores se escriben utilizando la notación de índice tensorial , ya que esto tiene numerosas ventajas. La notación deja claro que las ecuaciones son manifiestamente covariantes bajo el grupo de Poincaré , evitando así los tediosos cálculos para comprobar este hecho. Al construir tales ecuaciones, a menudo encontramos que ecuaciones que antes se pensaba que no estaban relacionadas están, de hecho, estrechamente conectadas al ser parte de la misma ecuación tensorial. Reconocer otras cantidades físicas como tensores simplifica sus leyes de transformación. En todo el texto, los índices superiores (superíndices) son índices contravariantes en lugar de exponentes, excepto cuando indican un cuadrado (esto debería quedar claro en el contexto), y los índices inferiores (subíndices) son índices covariantes. Para simplificar y mantener la coherencia con las ecuaciones anteriores, se utilizarán coordenadas cartesianas.
El ejemplo más simple de un cuatri-vector es la posición de un evento en el espacio-tiempo, que constituye un componente temporal ct y un componente espacial x = ( x , y , z ) , en un cuatri-vector de posición contravariante con componentes: donde definimos X 0 = ct de modo que la coordenada de tiempo tiene la misma dimensión de distancia que las otras dimensiones espaciales; de modo que el espacio y el tiempo son tratados por igual. [93] [94] [95] Ahora la transformación de los componentes contravariantes del 4-vector de posición se puede escribir de forma compacta como: donde hay una suma implícita en de 0 a 3, y es una matriz .
De manera más general, todos los componentes contravariantes de un sistema de cuatro vectores se transforman de un marco a otro mediante una transformación de Lorentz :
Ejemplos de otros 4-vectores incluyen el 4-velocidad definido como la derivada del 4-vector de posición con respecto al tiempo propio : donde el factor de Lorentz es:
La energía relativista y el momento relativista de un objeto son respectivamente los componentes temporales y espaciales de un vector de cuatro momentos contravariante : donde m es la masa invariante .
La cuatri-aceleración es la derivada temporal propia de la cuatri-velocidad:
Las reglas de transformación para velocidades y aceleraciones tridimensionales son muy complicadas; incluso en la configuración estándar, las ecuaciones de velocidad son bastante complicadas debido a su no linealidad. Por otro lado, la transformación de cuatro velocidades y cuatro aceleraciones es más sencilla mediante la matriz de transformación de Lorentz.
El cuadrigrado de un campo escalar φ se transforma de manera covariante en lugar de contravariante: que es la transpuesta de: solo en coordenadas cartesianas. Es la derivada covariante la que se transforma en covariancia manifiesta, en coordenadas cartesianas esto sucede para reducirse a las derivadas parciales, pero no en otras coordenadas.
De manera más general, los componentes covariantes de una transformación de 4 vectores se transforman de acuerdo con la transformación de Lorentz inversa : donde es la matriz recíproca de .
Los postulados de la relatividad especial restringen la forma exacta que adoptan las matrices de transformación de Lorentz.
En términos más generales, la mayoría de las cantidades físicas se describen mejor como (componentes de) tensores . Por lo tanto, para transformar de un marco a otro, utilizamos la conocida ley de transformación de tensores [96] donde es la matriz recíproca de . Todos los tensores se transforman mediante esta regla.
Un ejemplo de tensor antisimétrico de segundo orden de cuatro dimensiones es el momento angular relativista , que tiene seis componentes: tres son el momento angular clásico y los otros tres están relacionados con el impulso del centro de masas del sistema. La derivada del momento angular relativista con respecto al tiempo propio es el par relativista, también tensor antisimétrico de segundo orden .
El tensor de campo electromagnético es otro campo tensor antisimétrico de segundo orden , con seis componentes: tres para el campo eléctrico y otras tres para el campo magnético . También existe el tensor de tensión-energía para el campo electromagnético, es decir, el tensor de tensión-energía electromagnética .
Métrico
El tensor métrico permite definir el producto interno de dos vectores, lo que a su vez permite asignar una magnitud al vector. Dada la naturaleza cuatridimensional del espacio-tiempo, la métrica de Minkowski η tiene componentes (válidos con coordenadas elegidas adecuadamente) que se pueden organizar en una matriz de 4 × 4 : que es igual a su recíproco, , en esos marcos. En todo momento usamos los signos como se indica arriba, diferentes autores usan diferentes convenciones – ver signos alternativos de la métrica de Minkowski .
El grupo de Poincaré es el grupo más general de transformaciones que preserva la métrica de Minkowski: y ésta es la simetría física que subyace a la relatividad especial.
La métrica se puede utilizar para aumentar y disminuir los índices de vectores y tensores. Se pueden construir invariantes utilizando la métrica; el producto interno de un cuadrivector T con otro cuadrivector S es:
Invariante significa que toma el mismo valor en todos los sistemas inerciales, porque es un escalar (tensor de rango 0), y por lo tanto no aparece Λ en su transformación trivial. La magnitud del 4-vector T es la raíz cuadrada positiva del producto interno consigo mismo:
Se puede extender esta idea a tensores de orden superior; para un tensor de segundo orden, podemos formar los invariantes; lo mismo ocurre con los tensores de orden superior. Las expresiones invariantes, en particular los productos internos de 4-vectores consigo mismos, proporcionan ecuaciones que son útiles para los cálculos, porque no es necesario realizar transformaciones de Lorentz para determinar los invariantes.
Cinemática relativista e invariancia
Las diferenciales de coordenadas también se transforman contravariantemente: por lo que la longitud al cuadrado de la diferencial del cuadrivector de posición dX μ construido utilizando es un invariante. Nótese que cuando el elemento de línea d X 2 es negativo, √ − d X 2 es la diferencial del tiempo propio , mientras que cuando d X 2 es positivo, √ d X 2 es la diferencial de la distancia propia .
La 4-velocidad U μ tiene una forma invariante: lo que significa que todos los 4-vectores de velocidad tienen una magnitud de c . Esto es una expresión del hecho de que no existe tal cosa como estar en reposo de coordenadas en relatividad: al menos, siempre te estás moviendo hacia adelante a través del tiempo. Diferenciando la ecuación anterior por τ se obtiene: Entonces, en relatividad especial, el 4-vector de aceleración y el 4-vector de velocidad son ortogonales.
Dinámica relativista e invariancia
La magnitud invariante del 4-vector de momento genera la relación energía-momento :
Podemos determinar qué es este invariante argumentando primero que, dado que es un escalar, no importa en qué marco de referencia lo calculemos, y luego transformando a un marco donde el momento total es cero.
Vemos que la energía en reposo es una invariante independiente. La energía en reposo se puede calcular incluso para partículas y sistemas en movimiento, traduciéndola a un sistema en el que el momento es cero.
La energía en reposo está relacionada con la masa según la célebre ecuación comentada anteriormente:
La masa de los sistemas medida en su sistema de referencia central (donde el momento total es cero) está dada por la energía total del sistema en este sistema. Puede no ser igual a la suma de las masas de los sistemas individuales medidas en otros sistemas.
Para utilizar la tercera ley de Newton del movimiento , ambas fuerzas deben definirse como la tasa de cambio del momento con respecto a la misma coordenada temporal. Es decir, se requiere la fuerza 3D definida anteriormente. Desafortunadamente, no existe ningún tensor en 4D que contenga los componentes del vector de fuerza 3D entre sus componentes.
Si una partícula no se desplaza en c , se puede transformar la fuerza 3D del marco de referencia de la partícula que se mueve en paralelo al marco de referencia del observador. Esto produce un vector de cuatro fuerzas llamado cuatrifuerza . Es la tasa de cambio del vector de cuatro fuerzas de energía anterior con respecto al tiempo propio. La versión covariante de la cuatrifuerza es:
En el marco de reposo del objeto, el componente temporal de la fuerza cuaternaria es cero a menos que la " masa invariante " del objeto esté cambiando (esto requiere un sistema no cerrado en el que se esté añadiendo o quitando directamente energía/masa del objeto), en cuyo caso es el negativo de esa tasa de cambio de masa, multiplicado por c . Sin embargo, en general, los componentes de la fuerza cuaternaria no son iguales a los componentes de la fuerza cuaternaria, porque la fuerza cuaternaria se define por la tasa de cambio de momento con respecto al tiempo coordinado, es decir, dp / dt, mientras que la fuerza cuaternaria se define por la tasa de cambio de momento con respecto al tiempo propio, es decir, dp / dτ .
En un medio continuo, la densidad de fuerza 3D se combina con la densidad de potencia para formar un 4-vector covariante. La parte espacial es el resultado de dividir la fuerza sobre una célula pequeña (en el espacio tridimensional) por el volumen de esa célula. El componente temporal es −1/ c multiplicado por la potencia transferida a esa célula dividido por el volumen de la célula. Esto se utilizará más adelante en la sección sobre electromagnetismo.
Véase también
- Gente
- Relatividad
- Historia de la relatividad especial
- Relatividad doblemente especial
- Cálculo k de Bondi
- Sincronización de Einstein
- Argumento de Rietdijk-Putnam
- Relatividad especial (formulaciones alternativas)
- Disputa sobre la prioridad de la relatividad
- Física
- Los experimentos mentales de Einstein
- cosmología física
- Ecuaciones relativistas de Euler
- Teoría del éter de Lorentz
- Problema del imán móvil y del conductor
- Ondas de forma
- Conducción de calor relativista
- Disco relativista
- Rigidez innata
- Coordenadas de nacimiento
- Matemáticas
- Filosofía
- Paradojas
- Paradoja de Ehrenfest
- La paradoja de la nave espacial de Bell
- Paradoja de la composición de la velocidad
- Paradoja del faro
Notas
- ^ El propio Einstein, en The Foundations of the General Theory of Relativity, Ann. Phys. 49 (1916), escribe: "La palabra 'especial' pretende dar a entender que el principio está restringido al caso...". Véase la pág. 111 de The Principle of Relativity, A. Einstein, HA Lorentz, H. Weyl, H. Minkowski, reimpresión en Dover de la traducción de 1923 de Methuen and Company.]
- ^ Wald, Relatividad general, p. 60: "... la teoría especial de la relatividad afirma que el espacio-tiempo es una variedad con una métrica plana de signatura de Lorentz definida en ella. A la inversa, todo el contenido de la relatividad especial... está contenido en esta afirmación..."
- ^ En un contexto espaciotemporal, la longitud de un objeto rígido en movimiento es la distancia espacial entre los extremos del objeto medidos al mismo tiempo. En el marco de referencia en reposo del objeto, no se requiere simultaneidad.
- ^ Los resultados del experimento de Michelson-Morley llevaron a George Francis FitzGerald y Hendrik Lorentz a proponer de forma independiente el fenómeno de la contracción de la longitud . Lorentz creía que la contracción de la longitud representaba una contracción física de los átomos que formaban un objeto. No previó ningún cambio fundamental en la naturaleza del espacio y el tiempo. [27] : 62–68
Lorentz esperaba que la contracción de la longitud resultara en tensiones de compresión en un objeto que deberían dar lugar a efectos mensurables. Tales efectos incluirían efectos ópticos en medios transparentes, como la rotación óptica [p. 11] y la inducción de doble refracción, [p. 12] y la inducción de pares en condensadores cargados que se mueven en un ángulo con respecto al éter. [p. 12] Lorentz estaba perplejo por experimentos como el experimento de Trouton-Noble y los experimentos de Rayleigh y Brace que no lograron validar sus expectativas teóricas. [27] - ^ Para lograr coherencia matemática, Lorentz propuso una nueva variable temporal, la "hora local", llamada así porque dependía de la posición de un cuerpo en movimiento, siguiendo la relación t ′ = t − vx / c 2 . [p 13] Lorentz consideraba que la hora local no era "real"; más bien, representaba un cambio ad hoc de variable. [28] : 51, 80
Impresionado por la "idea más ingeniosa" de Lorentz, Poincaré vio en la hora local más que un mero truco matemático. Representaba la hora real que se mostraría en los relojes de un observador en movimiento. Por otro lado, Poincaré no consideró que este tiempo medido fuera la "hora verdadera" que exhibirían los relojes en reposo en el éter. Poincaré no intentó redefinir los conceptos de espacio y tiempo. Para Poincaré, la transformación de Lorentz describía los estados aparentes del campo para un observador en movimiento. Los estados verdaderos seguían siendo los definidos con respecto al éter. [29] - ^ Este concepto es contraintuitivo al menos por el hecho de que, en contraste con los conceptos usuales de distancia , puede asumir valores negativos (no es definida positiva para eventos no coincidentes), y que la denotación cuadrada es engañosa. Este cuadrado negativo conduce a conceptos, ahora no ampliamente utilizados, de tiempo imaginario . Es inmediato que el negativo de Δ s 2 es también un invariante, generado por una variante de la firma métrica del espacio-tiempo.
- ^ La invariancia de Δ s 2 bajo la transformación estándar de Lorentz es análoga a la invariancia de las distancias al cuadrado Δ r 2 bajo rotaciones en el espacio euclidiano. Aunque el espacio y el tiempo tienen un pie de igualdad en la relatividad, el signo menos delante de los términos espaciales marca el espacio y el tiempo como de carácter esencialmente diferente. No son lo mismo. Debido a que trata el tiempo de manera diferente a las 3 dimensiones espaciales, el espacio de Minkowski difiere del espacio euclidiano de cuatro dimensiones .
- ^ La dependencia del índice de refracción del arrastre parcial del éter fue finalmente confirmada por Pieter Zeeman en 1914-1915, mucho después de que la teoría de la relatividad especial hubiera sido aceptada por la mayoría. Utilizando una versión ampliada del aparato de Michelson conectada directamente al conducto principal de agua de Ámsterdam , Zeeman pudo realizar mediciones extendidas utilizando luz monocromática que abarcaba desde el violeta (4358 Å) hasta el rojo (6870 Å). [p 17] [p 18]
- ^ Aunque han pasado muchas décadas desde que Terrell y Penrose publicaron sus observaciones, los escritos populares siguen confundiendo la medición con la apariencia. Por ejemplo, Michio Kaku escribió en Einstein's Cosmos (WW Norton & Company, 2004, p. 65): "... imaginemos que la velocidad de la luz es de sólo 32 kilómetros por hora. Si un coche fuera por la calle, podría parecer comprimido en la dirección del movimiento, como si estuviera comprimido como un acordeón hasta quedar tal vez a 2,5 centímetros de longitud".
- ^ En una carta a Carl Seelig en 1955, Einstein escribió: "Ya había descubierto previamente que la teoría de Maxwell no tenía en cuenta la microestructura de la radiación y, por lo tanto, no podía tener validez general". Carta de Einstein a Carl Seelig, 1955.
- ^ La rapidez surge naturalmente como coordenadas en los generadores de impulsos puros dentro del álgebra de Lie del grupo de Lorentz. Del mismo modo, los ángulos de rotación surgen naturalmente como coordenadas (módulo 2 π ) en los generadores de rotación pura en el álgebra de Lie. (Juntos coordinan toda el álgebra de Lie). Una diferencia notable es que las rotaciones resultantes son periódicas en el ángulo de rotación, mientras que los impulsos resultantes no son periódicos en rapidez (sino más bien uno a uno). La similitud entre impulsos y rotaciones es el parecido formal.
- ^ En la teoría de la relatividad, la aceleración propia es la aceleración física (es decir, la aceleración medible mediante un acelerómetro) que experimenta un objeto. Por lo tanto, es la aceleración relativa a un observador en caída libre o inercial que se encuentra momentáneamente en reposo con respecto al objeto que se mide.
Fuentes primarias
- ^ abcdefg Albert Einstein (1905) "Zur Elektrodynamik bewegter Körper", Annalen der Physik 17: 891; traducción al inglés Sobre la electrodinámica de los cuerpos en movimiento de George Barker Jeffery y Wilfrid Perrett (1923); Otra traducción al inglés Sobre la electrodinámica de los cuerpos en movimiento de Megh Nad Saha (1920).
- ^ "Ciencia y sentido común", PW Bridgman, The Scientific Monthly , vol. 79, núm. 1 (julio de 1954), págs. 32-39.
- ^ La masa electromagnética y el momento de un electrón giratorio, G. Breit, Actas de la Academia Nacional de Ciencias, vol. 12, pág. 451, 1926
- ^ Cinemática de un electrón con eje. Phil. Mag. 3:1-22. LH Thomas.]
- ^ ab Einstein, Notas autobiográficas, 1949.
- ^ Einstein, "Ideas y métodos fundamentales de la teoría de la relatividad", 1920
- ^ Einstein, Sobre el principio de relatividad y las conclusiones que de él se derivan, 1907; "El principio de relatividad y sus consecuencias en la física moderna", 1910; "La teoría de la relatividad", 1911; Manuscrito sobre la teoría especial de la relatividad, 1912; Teoría de la relatividad, 1913; Einstein, Relatividad, teoría especial y general, 1916; Las ideas principales de la teoría de la relatividad, 1916; ¿Qué es la teoría de la relatividad?, 1919; El principio de relatividad (Conferencias de Princeton), 1921; Física y realidad, 1936; La teoría de la relatividad, 1949.
- ^ Yaakov Friedman (2004). Aplicaciones físicas de esferas homogéneas . Progreso en física matemática. Vol. 40. Págs. 1–21. ISBN. 978-0-8176-3339-4.
- ^ Das, A. (1993) La teoría especial de la relatividad, una exposición matemática , Springer, ISBN 0-387-94042-1 .
- ^ Schutz, J. (1997) Axiomas independientes para el espacio-tiempo de Minkowski, Addison Wesley Longman Limited, ISBN 0-582-31760-6 .
- ^ Lorentz, HA (1902). "La rotación del plano de polarización en medios en movimiento" (PDF) . Instituto Huygens - Real Academia de las Artes y las Ciencias de los Países Bajos (KNAW) . 4 : 669–678. Código Bibliográfico :1901KNAB....4..669L . Consultado el 15 de noviembre de 2018 .
- ^ ab Lorentz, HA (1904). "Fenómenos electromagnéticos en un sistema que se mueve con una velocidad menor que la de la luz" (PDF) . Instituto Huygens - Real Academia de las Artes y las Ciencias de los Países Bajos (KNAW) . 6 : 809–831. Código Bibliográfico :1903KNAB....6..809L . Consultado el 15 de noviembre de 2018 .
- ^ Lorentz, Hendrik (1895). "Investigación de oscilaciones excitadas por iones oscilantes". Intento de teoría de los fenómenos eléctricos y ópticos de los cuerpos en movimiento (Versuch einer Theorie der electrischen und optischen Erscheinungen in bewegten Körpern). Leiden: EJ Brill. (inciso § 31).
- ^ Lin, Shih-Chun; Giallorenzi, Thomas G. (1979). "Análisis de sensibilidad del interferómetro de anillo de fibra óptica de efecto Sagnac". Óptica Aplicada . 18 (6): 915–931. Código Bibliográfico :1979ApOpt..18..915L. doi :10.1364/AO.18.000915. PMID 20208844. S2CID 5343180.
- ^ Shaw, R. (1962). "Paradoja de la contracción de la longitud". American Journal of Physics . 30 (1): 72. Bibcode :1962AmJPh..30...72S. doi :10.1119/1.1941907. S2CID 119855914.
- ^ GA Benford; DL Book y WA Newcomb (1970). "El antiteléfono taquiónico". Physical Review D . 2 (2): 263–265. Código Bibliográfico :1970PhRvD...2..263B. doi :10.1103/PhysRevD.2.263. S2CID 121124132.
- ^ Zeeman, Pieter (1914). "Coeficiente de Fresnel para luz de diferentes colores. (Primera parte)". Proc. Kon. Acad. Van Weten . 17 : 445–451. Código bibliográfico : 1914KNAB...17..445Z.
- ^ Zeeman, Pieter (1915). "Coeficiente de Fresnel para luz de diferentes colores. (Segunda parte)". Proc. Kon. Acad. Van Weten . 18 : 398–408. Código bibliográfico : 1915KNAB...18..398Z.
- ^ Terrell, James (15 de noviembre de 1959). "Invisibilidad de la contracción de Lorentz". Physical Review . 116 (4): 1041–1045. Código Bibliográfico :1959PhRv..116.1041T. doi :10.1103/PhysRev.116.1041.
- ^ Penrose, Roger (24 de octubre de 2008). "La forma aparente de una esfera que se mueve de manera relativista". Actas matemáticas de la Sociedad filosófica de Cambridge . 55 (1): 137–139. Bibcode :1959PCPS...55..137P. doi :10.1017/S0305004100033776. S2CID 123023118.
- ^ abc ¿Depende la inercia de un cuerpo de su contenido energético? A. Einstein, Annalen der Physik . 18 :639, 1905 (traducción al inglés de W. Perrett y GB Jeffery)
- ^ Sobre la inercia de la energía requerida por el principio de relatividad, A. Einstein, Annalen der Physik 23 (1907): 371–384
- ^ Baglio, Julien (26 de mayo de 2007). «Aceleración en relatividad especial: ¿qué significa «movimiento uniformemente acelerado»?» (PDF) . Departamento de Física, ENS Cachan . Consultado el 22 de enero de 2016 .
- ^ abc Champion, Frank Clive (1932). "Sobre algunas colisiones cercanas de partículas β rápidas con electrones, fotografiadas por el método de expansión". Actas de la Royal Society de Londres. Serie A, que contiene artículos de carácter matemático y físico . 136 (830). The Royal Society Publishing: 630–637. Bibcode :1932RSPSA.136..630C. doi : 10.1098/rspa.1932.0108 . S2CID 123018629.
- ^ ab PAM Dirac (1930). "Una teoría de electrones y protones". Actas de la Royal Society . A126 (801): 360–365. Bibcode :1930RSPSA.126..360D. doi : 10.1098/rspa.1930.0013 . JSTOR 95359.
- ^ CD Anderson (1933). "El electrón positivo". Phys. Rev . 43 (6): 491–494. Código Bibliográfico :1933PhRv...43..491A. doi : 10.1103/PhysRev.43.491 .
Referencias
- ^ abc Griffiths, David J. (2013). "Electrodinámica y relatividad". Introducción a la electrodinámica (4.ª ed.). Pearson. Capítulo 12. ISBN 978-0-321-85656-2.
- ^ abc Jackson, John D. (1999). "Teoría especial de la relatividad". Electrodinámica clásica (3.ª ed.). John Wiley & Sons. Capítulo 11. ISBN 0-471-30932-X.
- ^ Goldstein, Herbert (1980). "Capítulo 7: Relatividad especial en la mecánica clásica". Mecánica clásica (2.ª ed.). Addison-Wesley Publishing Company. ISBN 0-201-02918-9.
- ^ ab Lanczos, Cornelius (1970). "Capítulo IX: Mecánica relativista". Los principios variacionales de la mecánica (4.ª ed.). Publicaciones de Dover. ISBN 978-0-486-65067-8.
- ^ Tom Roberts y Siegmar Schleif (octubre de 2007). "¿Cuál es la base experimental de la relatividad especial?". Usenet Physics FAQ . Consultado el 17 de septiembre de 2008 .
- ^ Albert Einstein (2001). Relatividad: teoría especial y teoría general (reimpresión de la traducción de 1920 de Robert W. Lawson, ed.). Routledge. pág. 48. ISBN 978-0-415-25384-0.
- ^ Las conferencias de física de Feynman, vol. I, cap. 15-9: Equivalencia de masa y energía
- ^ Sean Carroll, Notas de clase sobre relatividad general, cap. 1, "Relatividad especial y espacio-tiempo plano", http://ned.ipac.caltech.edu/level5/March01/Carroll3/Carroll1.html
- ^ Koks, Don (2006). Exploraciones en física matemática: los conceptos detrás de un lenguaje elegante (edición ilustrada). Springer Science & Business Media. pág. 234. ISBN 978-0-387-32793-8.Extracto de la página 234
- ^ Steane, Andrew M. (2012). Relativity Made Relatively Easy (edición ilustrada). OUP Oxford. pág. 226. ISBN 978-0-19-966286-9.Extracto de la página 226
- ^ abcde Taylor, Edwin F.; Wheeler, John Archibald (1992). Física del espacio-tiempo (2.ª ed.). WH Freeman. ISBN 0-7167-2327-1.
- ^ abcde Rindler, Wolfgang (1977). Relatividad esencial: especial, general y cosmológica (edición ilustrada). Springer Science & Business Media. pág. §1,11 pág. 7. ISBN 978-3-540-07970-5.
- ^ "James Clerk Maxwell: una fuerza para la física". Physics World . 2006-12-01 . Consultado el 2024-03-22 .
- ↑ «Noviembre de 1887: Michelson y Morley informan de su fracaso en la detección del éter luminífero». www.aps.org . Consultado el 22 de marzo de 2024 .
- ^ Michael Polanyi (1974) Personal Knowledge: Towards a Post-Critical Philosophy , ISBN 0-226-67288-3 , nota al pie página 10-11: Einstein informa, a través del Dr. N. Balzas en respuesta a la pregunta de Polanyi, que "el experimento de Michelson-Morley no tuvo ningún papel en la fundación de la teoría" y "... la teoría de la relatividad no fue fundada para explicar su resultado en absoluto". [1]
- ^ por Jeroen van Dongen (2009). "Sobre el papel del experimento de Michelson-Morley: Einstein en Chicago". Archivo de Historia de las Ciencias Exactas . 63 (6): 655–663. arXiv : 0908.1545 . Bibcode :2009arXiv0908.1545V. doi :10.1007/s00407-009-0050-5. S2CID 119220040.
- ^ Para un estudio de dichas derivaciones, véase Lucas y Hodgson, Spacetime and Electromagnetism, 1990.
- ^ Einstein, A., Lorentz, H. A., Minkowski, H., y Weyl, H. (1952). El principio de la relatividad: una colección de memorias originales sobre la teoría especial y general de la relatividad. Courier Dover Publications. pág. 111. ISBN 978-0-486-60081-9.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ^ Collier, Peter (2017). Una cosa sumamente incomprensible: notas para una introducción muy amable a las matemáticas de la relatividad (3.ª ed.). Libros incomprensibles. ISBN 9780957389465.
- ^ Staley, Richard (2009), "Albert Michelson, la velocidad de la luz y la deriva del éter", La generación de Einstein. Los orígenes de la revolución de la relatividad , Chicago: University of Chicago Press, ISBN 0-226-77057-5
- ^ abcdefghijklmnop David Morin (2007) Introducción a la mecánica clásica , Cambridge University Press, Cambridge, capítulo 11, Apéndice I, ISBN 1-139-46837-5 .
- ^ Miller, DJ (2010). "Un enfoque constructivo de la teoría especial de la relatividad". American Journal of Physics . 78 (6): 633–638. arXiv : 0907.0902 . Código Bibliográfico :2010AmJPh..78..633M. doi :10.1119/1.3298908. S2CID 20444859.
- ^ Callahan, James J. (2011). La geometría del espacio-tiempo: una introducción a la relatividad especial y general . Nueva York: Springer. ISBN 9781441931429.
- ^ PG Bergmann (1976) Introducción a la teoría de la relatividad , edición Dover, Capítulo IV, página 36 ISBN 0-486-63282-2 .
- ^ Mermin, N. David (1968). Espacio y tiempo en la relatividad especial . McGraw-Hill. ISBN 978-0881334203.
- ^ Robert Resnick (1968). Introducción a la relatividad especial. Wiley. pp. 62-63. ISBN 9780471717249.
- ^ ab Miller, Arthur I. (1998). La teoría especial de la relatividad de Albert Einstein: surgimiento (1905) e interpretación temprana (1905-1911) . Nueva York: Springer-Verlag. ISBN 978-0-387-94870-6.
- ^ Bernstein, Jeremy (2006). Secretos del Antiguo: Einstein, 1905. Copernicus Books (sello editorial de Springer Science + Business Media). ISBN 978-0387-26005-1.
- ^ Darrigol, Olivier (2005). «La génesis de la teoría de la relatividad» (PDF) . Séminaire Poincaré . 1 : 1–22. Bibcode :2006eins.book....1D . Consultado el 15 de noviembre de 2018 .
- ^ abc Rindler, Wolfgang (1977). Relatividad esencial (2.ª ed.). Nueva York: Springer-Verlag. ISBN 978-0-387-10090-6.
- ^ abcd Taylor, Edwin F.; Wheeler, John Archibald (1966). Física del espacio-tiempo (1.ª ed.). San Francisco: WH Freeman and Company.
- ^ Ashby, Neil (2003). "Relatividad en el Sistema de Posicionamiento Global". Living Reviews in Relativity . 6 (1): 1. Bibcode :2003LRR.....6....1A. doi : 10.12942/lrr-2003-1 . PMC 5253894 . PMID 28163638.
- ^ Daniel Kleppner y David Kolenkow (1973). Introducción a la mecánica. McGraw-Hill. pp. 468-70. ISBN 978-0-07-035048-9.
- ^ abc French, AP (1968). Relatividad especial . Nueva York: WW Norton & Company. ISBN 0-393-09793-5.
- ^ Lewis, Gilbert Newton; Tolman, Richard Chase (1909). "El principio de relatividad y la mecánica no newtoniana". Actas de la Academia Estadounidense de Artes y Ciencias . 44 (25): 709–726. doi :10.2307/20022495. JSTOR 20022495 . Consultado el 22 de agosto de 2023 .
- ^ ab Cuvaj, Camillo (1971). "Paul Langeyin y la teoría de la relatividad" (PDF) . Estudios japoneses en la historia de la ciencia . 10 : 113–142 . Consultado el 12 de junio de 2023 .
- ^ Cassidy, David C.; Holton, Gerald James; Rutherford, Floyd James (2002). Understanding Physics. Springer-Verlag. p. 422. ISBN 978-0-387-98756-9.
- ^ Cutner, Mark Leslie (2003). Astronomy, A Physical Perspective. Cambridge University Press. p. 128. ISBN 978-0-521-82196-4.
- ^ Ellis, George F. R.; Williams, Ruth M. (2000). Flat and Curved Space-times (2n ed.). Oxford University Press. pp. 28–29. ISBN 978-0-19-850657-7.
- ^ Feynman, Richard P.; Leighton, Robert B.; Sands, Matthew (2011). The feynman lectures on physics; vol I: The new millennium edition. Basic Books. p. 15-5. ISBN 978-0-465-02414-8. Retrieved 12 June 2023.
- ^ a b Halliday, David; Resnick, Robert (1988). Fundamental Physics: Extended Third Edition. New York: John Wiley & sons. pp. 958–959. ISBN 0-471-81995-6.
- ^ Adams, Steve (1997). Relativity: An introduction to space-time physics. CRC Press. p. 54. ISBN 978-0-7484-0621-0.
- ^ Langevin, Paul (1911). "L'Évolution de l'espace et du temps". Scientia. 10: 31–54. Retrieved 20 June 2023.
- ^ Debs, Talal A.; Redhead, Michael L.G. (1996). "The twin "paradox" and the conventionality of simultaneity". American Journal of Physics. 64 (4): 384–392. Bibcode:1996AmJPh..64..384D. doi:10.1119/1.18252.
- ^ Tolman, Richard C. (1917). The Theory of the Relativity of Motion. Berkeley: University of California Press. p. 54.
- ^ Takeuchi, Tatsu. "Special Relativity Lecture Notes – Section 10". Virginia Tech. Retrieved 31 October 2018.
- ^ Morin, David (2017). Special Relativity for the Enthusiastic Beginner. CreateSpace Independent Publishing Platform. pp. 90–92. ISBN 9781542323512.
- ^ Gibbs, Philip. "Is Faster-Than-Light Travel or Communication Possible?". Physics FAQ. Department of Mathematics, University of California, Riverside. Retrieved 31 October 2018.
- ^ Ginsburg, David (1989). Applications of Electrodynamics in Theoretical Physics and Astrophysics (illustrated ed.). CRC Press. p. 206. Bibcode:1989aetp.book.....G. ISBN 978-2-88124-719-4. Extract of page 206
- ^ Wesley C. Salmon (2006). Four Decades of Scientific Explanation. University of Pittsburgh. p. 107. ISBN 978-0-8229-5926-7., Section 3.7 page 107
- ^ Lauginie, P. (2004). "Measuring Speed of Light: Why? Speed of what?" (PDF). Proceedings of the Fifth International Conference for History of Science in Science Education. Archived from the original (PDF) on 4 July 2015. Retrieved 3 July 2015.
- ^ Stachel, J. (2005). "Fresnel's (dragging) coefficient as a challenge to 19th century optics of moving bodies". In Kox, A.J.; Eisenstaedt, J (eds.). The universe of general relativity. Boston: Birkhäuser. pp. 1–13. ISBN 978-0-8176-4380-5. Retrieved 17 April 2012.
- ^ Richard A. Mould (2001). Basic Relativity (2nd ed.). Springer. p. 8. ISBN 978-0-387-95210-9.
- ^ Seidelmann, P. Kenneth, ed. (1992). Explanatory Supplement to the Astronomical Almanac. ill Valley, Calif.: University Science Books. p. 393. ISBN 978-0-935702-68-2.
- ^ Ferraro, Rafael; Sforza, Daniel M. (2005). "European Physical Society logo Arago (1810): the first experimental result against the ether". European Journal of Physics. 26 (1): 195–204. arXiv:physics/0412055. Bibcode:2005EJPh...26..195F. doi:10.1088/0143-0807/26/1/020. S2CID 119528074.
- ^ Dolan, Graham. "Airy's Water Telescope (1870)". The Royal Observatory Greenwich. Retrieved 20 November 2018.
- ^ Hollis, H. P. (1937). "Airy's water telescope". The Observatory. 60: 103–107. Bibcode:1937Obs....60..103H. Retrieved 20 November 2018.
- ^ Janssen, Michel; Stachel, John (2004). "The Optics and Electrodynamics of Moving Bodies" (PDF). In Stachel, John (ed.). Going Critical. Springer. ISBN 978-1-4020-1308-9.
- ^ Sher, D. (1968). "The Relativistic Doppler Effect". Journal of the Royal Astronomical Society of Canada. 62: 105–111. Bibcode:1968JRASC..62..105S. Retrieved 11 October 2018.
- ^ Gill, T. P. (1965). The Doppler Effect. London: Logos Press Limited. pp. 6–9. OL 5947329M.
- ^ Feynman, Richard P.; Leighton, Robert B.; Sands, Matthew (February 1977). "Relativistic Effects in Radiation". The Feynman Lectures on Physics: Volume 1. Reading, Massachusetts: Addison-Wesley. pp. 34–7 f. ISBN 9780201021165. LCCN 2010938208.
- ^ Cook, Helen. "Relativistic Distortion". Mathematics Department, University of British Columbia. Retrieved 12 April 2017.
- ^ Signell, Peter. "Appearances at Relativistic Speeds" (PDF). Project PHYSNET. Michigan State University, East Lansing, MI. Archived from the original (PDF) on 13 April 2017. Retrieved 12 April 2017.
- ^ Kraus, Ute. "The Ball is Round". Space Time Travel: Relativity visualized. Institut für Physik Universität Hildesheim. Archived from the original on 12 May 2017. Retrieved 16 April 2017.
- ^ Boas, Mary L. (1961). "Apparent Shape of Large Objects at Relativistic Speeds". American Journal of Physics. 29 (5): 283. Bibcode:1961AmJPh..29..283B. doi:10.1119/1.1937751.
- ^ Müller, Thomas; Boblest, Sebastian (2014). "Visual appearance of wireframe objects in special relativity". European Journal of Physics. 35 (6): 065025. arXiv:1410.4583. Bibcode:2014EJPh...35f5025M. doi:10.1088/0143-0807/35/6/065025. S2CID 118498333.
- ^ Zensus, J. Anton; Pearson, Timothy J. (1987). Superluminal Radio Sources (1st ed.). Cambridge, New York: Cambridge University Press. p. 3. ISBN 9780521345606.
- ^ Chase, Scott I. "Apparent Superluminal Velocity of Galaxies". The Original Usenet Physics FAQ. Department of Mathematics, University of California, Riverside. Retrieved 12 April 2017.
- ^ Richmond, Michael. ""Superluminal" motions in astronomical sources". Physics 200 Lecture Notes. School of Physics and Astronomy, Rochester Institute of Technology. Archived from the original on 16 February 2017. Retrieved 20 April 2017.
- ^ Keel, Bill. "Jets, Superluminal Motion, and Gamma-Ray Bursts". Galaxies and the Universe - WWW Course Notes. Department of Physics and Astronomy, University of Alabama. Archived from the original on 1 March 2017. Retrieved 29 April 2017.
- ^ Max Jammer (1997). Concepts of Mass in Classical and Modern Physics. Courier Dover Publications. pp. 177–178. ISBN 978-0-486-29998-3.
- ^ John J. Stachel (2002). Einstein from B to Z. Springer. p. 221. ISBN 978-0-8176-4143-6.
- ^ Fernflores, Francisco (2018). Einstein's Mass-Energy Equation, Volume I: Early History and Philosophical Foundations. New York: Momentum Pres. ISBN 978-1-60650-857-2.
- ^ a b Philip Gibbs & Don Koks. "The Relativistic Rocket". Retrieved 30 August 2012.
- ^ The special theory of relativity shows that time and space are affected by motion Archived 2012-10-21 at the Wayback Machine. Library.thinkquest.org. Retrieved on 2013-04-24.
- ^ a b Idema, Timon (17 April 2019). "Mechanics and Relativity. Chapter 14: Relativistic Collisions". LibreTexts Physics. California State University Affordable Learning Solutions Program. Retrieved 2 January 2023.
- ^ Nakel, Werner (1994). "The elementary process of bremsstrahlung". Physics Reports. 243 (6): 317–353. Bibcode:1994PhR...243..317N. doi:10.1016/0370-1573(94)00068-9.
- ^ Halbert, M.L. (1972). "Review of Experiments on Nucleon-Nucleon Bremsstrahlung". In Austin, S.M.; Crawley, G.M. (eds.). The Two-Body Force in Nuclei. Boston, MA.: Springer.
- ^ Thomas, George B.; Weir, Maurice D.; Hass, Joel; Giordano, Frank R. (2008). Thomas' Calculus: Early Transcendentals (Eleventh ed.). Boston: Pearson Education, Inc. p. 533. ISBN 978-0-321-49575-4.
- ^ a b E. J. Post (1962). Formal Structure of Electromagnetics: General Covariance and Electromagnetics. Dover Publications Inc. ISBN 978-0-486-65427-0.
- ^ a b c Schutz, Bernard F. (1985). A first course in general relativity. Cambridge, UK: Cambridge University Press. p. 26. ISBN 0521277035.
- ^ a b Gibbs, Philip. "Can Special Relativity Handle Acceleration?". The Physics and Relativity FAQ. math.ucr.edu. Archived from the original on 7 June 2017. Retrieved 28 May 2017.
- ^ Franklin, Jerrold (2010). "Lorentz contraction, Bell's spaceships, and rigid body motion in special relativity". European Journal of Physics. 31 (2): 291–298. arXiv:0906.1919. Bibcode:2010EJPh...31..291F. doi:10.1088/0143-0807/31/2/006. S2CID 18059490.
- ^ a b c Bais, Sander (2007). Very Special Relativity: An Illustrated Guide. Cambridge, Massachusetts: Harvard University Press. ISBN 978-0-674-02611-7.
- ^ R. Resnick; R. Eisberg (1985). Quantum Physics of Atoms, Molecules, Solids, Nuclei and Particles (2nd ed.). John Wiley & Sons. pp. 114–116. ISBN 978-0-471-87373-0.
- ^ Øyvind Grøn & Sigbjørn Hervik (2007). Einstein's general theory of relativity: with modern applications in cosmology. Springer. p. 195. ISBN 978-0-387-69199-2. Extract of page 195 (with units where c = 1)
- ^ The number of works is vast, see as example:
Sidney Coleman; Sheldon L. Glashow (1997). "Cosmic Ray and Neutrino Tests of Special Relativity". Physics Letters B. 405 (3–4): 249–252. arXiv:hep-ph/9703240. Bibcode:1997PhLB..405..249C. doi:10.1016/S0370-2693(97)00638-2. S2CID 17286330.
An overview can be found on this page - ^ Roberts, Tom; Schleif, Siegmar. "Experiments that Apparently are NOT Consistent with SR/GR". What is the experimental basis of Special Relativity?. University of California at Riverside. Retrieved 10 July 2024.
- ^ John D. Norton, John D. (2004). "Einstein's Investigations of Galilean Covariant Electrodynamics prior to 1905". Archive for History of Exact Sciences. 59 (1): 45–105. Bibcode:2004AHES...59...45N. doi:10.1007/s00407-004-0085-6. S2CID 17459755.
- ^ J.A. Wheeler; C. Misner; K.S. Thorne (1973). Gravitation. W.H. Freeman & Co. p. 58. ISBN 978-0-7167-0344-0.
- ^ J.R. Forshaw; A.G. Smith (2009). Dynamics and Relativity. Wiley. p. 247. ISBN 978-0-470-01460-8.
- ^ R. Penrose (2007). The Road to Reality. Vintage books. ISBN 978-0-679-77631-4.
- ^ Jean-Bernard Zuber & Claude Itzykson, Quantum Field Theory, pg 5, ISBN 0-07-032071-3
- ^ Charles W. Misner, Kip S. Thorne & John A. Wheeler, Gravitation, pg 51, ISBN 0-7167-0344-0
- ^ George Sterman, An Introduction to Quantum Field Theory, pg 4, ISBN 0-521-31132-2
- ^ Sean M. Carroll (2004). Spacetime and Geometry: An Introduction to General Relativity. Addison Wesley. p. 22. ISBN 978-0-8053-8732-2.
Further reading
Texts by Einstein and text about history of special relativity
- Einstein, Albert (1920). Relativity: The Special and General Theory.
- Einstein, Albert (1996). The Meaning of Relativity. Fine Communications. ISBN 1-56731-136-9
- Logunov, Anatoly A. (2005). Henri Poincaré and the Relativity Theory (transl. from Russian by G. Pontocorvo and V. O. Soloviev, edited by V. A. Petrov). Nauka, Moscow.
Textbooks
- Charles Misner, Kip Thorne, and John Archibald Wheeler (1971) Gravitation. W. H. Freeman & Co. ISBN 0-7167-0334-3
- Post, E.J., 1997 (1962) Formal Structure of Electromagnetics: General Covariance and Electromagnetics. Dover Publications.
- Wolfgang Rindler (1991). Introduction to Special Relativity (2nd ed.), Oxford University Press. ISBN 978-0-19-853952-0; ISBN 0-19-853952-5
- Harvey R. Brown (2005). Physical relativity: space–time structure from a dynamical perspective, Oxford University Press, ISBN 0-19-927583-1; ISBN 978-0-19-927583-0
- Qadir, Asghar (1989). Relativity: An Introduction to the Special Theory. Singapore: World Scientific Publications. p. 128. Bibcode:1989rist.book.....Q. ISBN 978-9971-5-0612-4.
- French, A. P. (1968). Special Relativity (M.I.T. Introductory Physics) (1st ed.). W. W. Norton & Company. ISBN 978-0393097931.
- Silberstein, Ludwik (1914). The Theory of Relativity.
- Lawrence Sklar (1977). Space, Time and Spacetime. University of California Press. ISBN 978-0-520-03174-6.
- Lawrence Sklar (1992). Philosophy of Physics. Westview Press. ISBN 978-0-8133-0625-4.
- Sergey Stepanov (2018). Relativistic World. De Gruyter. ISBN 9783110515879.
- Taylor, Edwin, and John Archibald Wheeler (1992). Spacetime Physics (2nd ed.). W. H. Freeman & Co. ISBN 0-7167-2327-1.
- Tipler, Paul, and Llewellyn, Ralph (2002). Modern Physics (4th ed.). W. H. Freeman & Co. ISBN 0-7167-4345-0.
Journal articles
- Alvager, T.; Farley, F. J. M.; Kjellman, J.; Wallin, L.; et al. (1964). "Test of the Second Postulate of Special Relativity in the GeV region". Physics Letters. 12 (3): 260–262. Bibcode:1964PhL....12..260A. doi:10.1016/0031-9163(64)91095-9.
- Darrigol, Olivier (2004). "The Mystery of the Poincaré–Einstein Connection". Isis. 95 (4): 614–26. doi:10.1086/430652. PMID 16011297. S2CID 26997100.
- Wolf, Peter; Petit, Gerard (1997). "Satellite test of Special Relativity using the Global Positioning System". Physical Review A. 56 (6): 4405–09. Bibcode:1997PhRvA..56.4405W. doi:10.1103/PhysRevA.56.4405.
- Special Relativity Scholarpedia
- Rindler, Wolfgang (2011). "Special relativity: Kinematics". Scholarpedia. 6 (2): 8520. Bibcode:2011SchpJ...6.8520R. doi:10.4249/scholarpedia.8520.
External links
Original works
- Zur Elektrodynamik bewegter Körper Einstein's original work in German, Annalen der Physik, Bern 1905
- On the Electrodynamics of Moving Bodies English Translation as published in the 1923 book The Principle of Relativity.
Special relativity for a general audience (no mathematical knowledge required)
- Einstein Light An award-winning, non-technical introduction (film clips and demonstrations) supported by dozens of pages of further explanations and animations, at levels with or without mathematics.
- Einstein Online Archived 2010-02-01 at the Wayback Machine Introduction to relativity theory, from the Max Planck Institute for Gravitational Physics.
- Audio: Cain/Gay (2006) – Astronomy Cast. Einstein's Theory of Special Relativity
Special relativity explained (using simple or more advanced mathematics)
- Bondi K-Calculus – A simple introduction to the special theory of relativity.
- Greg Egan's Foundations Archived 2013-04-25 at the Wayback Machine.
- The Hogg Notes on Special Relativity A good introduction to special relativity at the undergraduate level, using calculus.
- Relativity Calculator: Special Relativity Archived 2013-03-21 at the Wayback Machine – An algebraic and integral calculus derivation for E = mc2.
- MathPages – Reflections on Relativity A complete online book on relativity with an extensive bibliography.
- Special Relativity An introduction to special relativity at the undergraduate level.
- Relativity: the Special and General Theory at Project Gutenberg, by Albert Einstein
- Special Relativity Lecture Notes is a standard introduction to special relativity containing illustrative explanations based on drawings and spacetime diagrams from Virginia Polytechnic Institute and State University.
- Understanding Special Relativity The theory of special relativity in an easily understandable way.
- An Introduction to the Special Theory of Relativity (1964) by Robert Katz, "an introduction ... that is accessible to any student who has had an introduction to general physics and some slight acquaintance with the calculus" (130 pp; pdf format).
- Lecture Notes on Special Relativity by J D Cresser Department of Physics Macquarie University.
- SpecialRelativity.net – An overview with visualizations and minimal mathematics.
- Relativity 4-ever? The problem of superluminal motion is discussed in an entertaining manner.
Visualization
- Raytracing Special Relativity Software visualizing several scenarios under the influence of special relativity.
- Real Time Relativity Archived 2013-05-08 at the Wayback Machine The Australian National University. Relativistic visual effects experienced through an interactive program.
- Spacetime travel A variety of visualizations of relativistic effects, from relativistic motion to black holes.
- Through Einstein's Eyes Archived 2013-05-14 at the Wayback Machine The Australian National University. Relativistic visual effects explained with movies and images.
- Warp Special Relativity Simulator A computer program to show the effects of traveling close to the speed of light.
- Animation clip on YouTube visualizing the Lorentz transformation.
- Original interactive FLASH Animations from John de Pillis illustrating Lorentz and Galilean frames, Train and Tunnel Paradox, the Twin Paradox, Wave Propagation, Clock Synchronization, etc.
- lightspeed An OpenGL-based program developed to illustrate the effects of special relativity on the appearance of moving objects.
- Animation showing the stars near Earth, as seen from a spacecraft accelerating rapidly to light speed.






































































































































![{\displaystyle \sin \theta '={\frac {\sin \theta }{\gamma [1+(v/c)\cos \theta ]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04b1d959a5aa9840f249611011e804cba5079e53)
















![{\displaystyle {\begin{aligned}E_{0}&=E_{1}+{\frac {1}{2}}L+{\frac {1}{2}}L=E_{1}+L\\[5mu]H_{0}&=H_{1}+{\frac {1}{2}}L{\frac {1-(v/c)\cos {\phi }}{\sqrt {1-v^{2}/c^{2}}}}+{\frac {1}{2}}L{\frac {1+(v/c)\cos {\phi }}{\sqrt {1-v^{2}/c^{2}}}}=H_{1}+{\frac {L}{\sqrt {1-v^{2}/c^{2}}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/343ffb26e1d6fe9149832c6e8b3f2ef79fecad0c)











































































































































