Escalar de Lorentz

En una teoría relativista de la física , un escalar de Lorentz es una expresión escalar cuyo valor es invariante bajo cualquier transformación de Lorentz . Un escalar de Lorentz puede generarse a partir, por ejemplo, del producto escalar de vectores o contrayendo tensores. Si bien los componentes de las cantidades contraídas pueden cambiar bajo transformaciones de Lorentz, los escalares de Lorentz permanecen inalterados.

Un escalar de Lorentz simple en el espacio-tiempo de Minkowski es la distancia espacio-temporal ("longitud" de su diferencia) de dos eventos fijos en el espacio-tiempo. Mientras que los 4 vectores de "posición" de los eventos cambian entre diferentes sistemas inerciales, su distancia espacio-temporal permanece invariable bajo la transformación de Lorentz correspondiente. Otros ejemplos de escalares de Lorentz son la "longitud" de las 4 velocidades (ver abajo), o la curvatura de Ricci en un punto en el espacio-tiempo de la relatividad general , que es una contracción del tensor de curvatura de Riemann .

En relatividad especial, la ubicación de una partícula en el espacio-tiempo de 4 dimensiones está dada por donde es la posición en el espacio tridimensional de la partícula, es la velocidad en el espacio tridimensional y es la velocidad de la luz .$${\displaystyle x^{\mu}=(ct,\mathbf {x})}$$${\displaystyle \mathbf {x} =\mathbf {v} t}$${\displaystyle \mathbf {v}}$${\estilo de visualización c}$

La "longitud" del vector es un escalar de Lorentz y está dada por donde es el tiempo propio medido por un reloj en el marco de reposo de la partícula y la métrica de Minkowski está dada por Esta es una métrica similar al tiempo.$${\displaystyle x_{\mu }x^{\mu }=\eta _{\mu \nu }x^{\mu }x^{\nu }=(ct)^{2}-\mathbf {x} \cdot \mathbf {x} \ {\stackrel {\mathrm {def} }{=}}\ (c\tau )^{2}}$$${\estilo de visualización \tau}$$${\displaystyle \eta ^{\mu \nu }=\eta _{\mu \nu }={\begin{pmatrix}1&0&0&0\\0&-1&0&0\\0&0&-1&0\\0&0&0&-1\end{pmatrix} }.}$$

A menudo se utiliza la firma alternativa de la métrica de Minkowski, en la que los signos de los unos están invertidos. Se trata de una métrica de tipo espacial.$${\displaystyle \eta ^{\mu \nu }=\eta _{\mu \nu }={\begin{pmatrix}-1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{pmatrix}}.}$$

En la métrica de Minkowski el intervalo espacial se define como${\estilo de visualización s}$$${\displaystyle x_{\mu }x^{\mu }=\eta _{\mu \nu }x^{\mu }x^{\nu }=\mathbf {x} \cdot \mathbf {x} -(ct)^{2}\ {\stackrel {\mathrm {def} }{=}}\ s^{2}.}$$

En el resto de este artículo utilizamos la métrica de Minkowski, de tipo espacial.

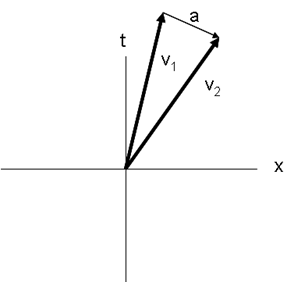
La velocidad en el espacio-tiempo se define como donde$${\displaystyle v^{\mu }\ {\stackrel {\mathrm {def} }{=}}\ {dx^{\mu } \over d\tau }=\left(c{dt \over d\tau },{dt \over d\tau }{d\mathbf {x} \over dt}\right)=\left(\gamma c,\gamma {\mathbf {v} }\right)=\gamma \left(c,{\mathbf {v} }\right)}$$$${\displaystyle \gamma \ {\stackrel {\mathrm {def} }{=}}\ {1 \over {\sqrt {1-{{\mathbf {v} \cdot \mathbf {v} } \over c^{2}}}}}.}$$

La magnitud de la 4-velocidad es un escalar de Lorentz,$${\displaystyle v_{\mu }v^{\mu }=-c^{2}\,.}$$

Por lo tanto, ⁠ ⁠${\displaystyle c}$ es un escalar de Lorentz.

La 4-aceleración viene dada por$${\displaystyle a^{\mu }\ {\stackrel {\mathrm {def} }{=}}\ {dv^{\mu } \over d\tau }.}$$

La 4-aceleración es siempre perpendicular a la 4-velocidad$${\displaystyle 0={1 \over 2}{d \over d\tau }\left(v_{\mu }v^{\mu }\right)={dv_{\mu } \over d\tau }v^{\mu }=a_{\mu }v^{\mu }.}$$

Por lo tanto, podemos considerar la aceleración en el espacio-tiempo como una simple rotación de la 4-velocidad. El producto interno de la aceleración y la velocidad es un escalar de Lorentz y es cero. Esta rotación es simplemente una expresión de conservación de la energía: donde es la energía de una partícula y es la 3-fuerza sobre la partícula.$${\displaystyle {dE \over d\tau }=\mathbf {F} \cdot \mathbf {v} }$$${\displaystyle E}$${\displaystyle \mathbf {F} }$

El 4-momento de una partícula es donde es la masa en reposo de la partícula, es el momento en el 3-espacio y es la energía de la partícula.$${\displaystyle p^{\mu }=mv^{\mu }=\left(\gamma mc,\gamma m\mathbf {v} \right)=\left(\gamma mc,\mathbf {p} \right)=\left({\frac {E}{c}},\mathbf {p} \right)}$$${\displaystyle m}$${\displaystyle \mathbf {p} }$$${\displaystyle E=\gamma mc^{2}}$$

Consideremos una segunda partícula con velocidad 4 y una velocidad 3. En el marco de reposo de la segunda partícula, el producto interno de con es proporcional a la energía de la primera partícula, donde el subíndice 1 indica la primera partícula.${\displaystyle u}$${\displaystyle \mathbf {u} _{2}}$${\displaystyle u}$${\displaystyle p}$$${\displaystyle p_{\mu }u^{\mu }=-E_{1}}$$

Dado que la relación es verdadera en el marco de referencia en reposo de la segunda partícula, es verdadera en cualquier marco de referencia. , la energía de la primera partícula en el marco de referencia de la segunda partícula, es un escalar de Lorentz. Por lo tanto, en cualquier marco de referencia inercial, donde sigue siendo la energía de la primera partícula en el marco de referencia de la segunda partícula.${\displaystyle E_{1}}$$${\displaystyle E_{1}=\gamma _{1}\gamma _{2}m_{1}c^{2}-\gamma _{2}\mathbf {p} _{1}\cdot \mathbf {u} _{2}}$$${\displaystyle E_{1}}$

En el marco de reposo de la partícula, el producto interno del momento es$${\displaystyle p_{\mu }p^{\mu }=-(mc)^{2}\,.}$$

Por lo tanto, la masa en reposo ( m ) es un escalar de Lorentz. La relación sigue siendo cierta independientemente del marco en el que se calcule el producto interno. En muchos casos, la masa en reposo se escribe como para evitar confusiones con la masa relativista, que es .${\displaystyle m_{0}}$${\displaystyle \gamma m_{0}}$

Tenga en cuenta que$${\displaystyle \left({\frac {p_{\mu }u^{\mu }}{c}}\right)^{2}+p_{\mu }p^{\mu }={E_{1}^{2} \over c^{2}}-(mc)^{2}=\left(\gamma _{1}^{2}-1\right)(mc)^{2}=\gamma _{1}^{2}{\mathbf {v} _{1}\cdot \mathbf {v} _{1}}m^{2}=\mathbf {p} _{1}\cdot \mathbf {p} _{1}.}$$

El cuadrado de la magnitud del momento 3-momento de la partícula medido en el marco de la segunda partícula es un escalar de Lorentz.

La velocidad 3, en el marco de la segunda partícula, se puede construir a partir de dos escalares de Lorentz$${\displaystyle v_{1}^{2}=\mathbf {v} _{1}\cdot \mathbf {v} _{1}={\frac {\mathbf {p} _{1}\cdot \mathbf {p} _{1}}{E_{1}^{2}}}c^{4}.}$$

Los escalares también pueden construirse a partir de tensores y vectores, a partir de la contracción de tensores (como ), o de combinaciones de contracciones de tensores y vectores (como ).${\displaystyle F_{\mu \nu }F^{\mu \nu }}$${\displaystyle g_{\mu \nu }x^{\mu }x^{\nu }}$

• Misner, Charles; Thorne, Kip S. y Wheeler, John Archibald (1973). Gravitación . San Francisco: WH Freeman. ISBN 0-7167-0344-0.
• Landau, LD y Lifshitz, EM (1975). Teoría clásica de campos (cuarta edición revisada en inglés). Oxford: Pergamon. ISBN 0-08-018176-7.

• Medios relacionados con el escalar de Lorentz en Wikimedia Commons