Posición (geometría)

En geometría , un vector de posición o posición , también conocido como vector de localización o vector de radio , es un vector euclidiano que representa un punto P en el espacio . Su longitud representa la distancia en relación con un origen de referencia arbitrario O , y su dirección representa la orientación angular con respecto a ejes de referencia dados. Generalmente denotado x , r o s , corresponde al segmento de línea recta de O a P. En otras palabras, es el desplazamiento o traslación que mapea el origen a P : ^[1]

${\displaystyle \mathbf {r} ={\overrightarrow {OP}}.}$

El término vector de posición se utiliza principalmente en los campos de la geometría diferencial , la mecánica y, ocasionalmente, el cálculo vectorial . Con frecuencia se utiliza en espacios bidimensionales o tridimensionales , pero se puede generalizar fácilmente a espacios euclidianos y espacios afines de cualquier dimensión . ^[2]

La posición relativa de un punto Q con respecto al punto P es el vector euclidiano resultante de la resta de los dos vectores de posición absoluta (cada uno con respecto al origen):

${\displaystyle \Delta \mathbf {r} =\mathbf {s} -\mathbf {r} ={\overrightarrow {PQ}},}$

donde . La dirección relativa entre dos puntos es su posición relativa normalizada como un vector unitario${\displaystyle \mathbf {s} ={\overrightarrow {OQ}}}$

En tres dimensiones , se puede utilizar cualquier conjunto de coordenadas tridimensionales y sus vectores base correspondientes para definir la ubicación de un punto en el espacio; se puede utilizar el que sea más simple para la tarea en cuestión.

Comúnmente se utiliza el conocido sistema de coordenadas cartesianas , o a veces coordenadas polares esféricas , o coordenadas cilíndricas :

${\displaystyle {\begin{aligned}\mathbf {r} (t)&\equiv \mathbf {r} (x,y,z)\equiv x(t)\mathbf {\hat {e}} _ {x }+y(t)\mathbf {\hat {e}} _{y}+z(t)\mathbf {\hat {e}} _{z}\\&\equiv \mathbf {r} (r, \theta ,\phi )\equiv r(t)\mathbf {\hat {e}} _{r}{\big (}\theta (t),\phi (t){\big )}\\&\ equiv \mathbf {r} (r,\phi ,z)\equiv r(t)\mathbf {\hat {e}} _{r}{\big (}\phi (t){\big )}+z (t)\mathbf {\sombrero {e}} _{z},\\\end{alineado}}}$

donde t es un parámetro , debido a su simetría rectangular o circular. Estas diferentes coordenadas y los vectores base correspondientes representan el mismo vector de posición. Se podrían utilizar en su lugar coordenadas curvilíneas más generales, que se encuentran en contextos como la mecánica de medios continuos y la relatividad general (en este último caso se necesita una coordenada de tiempo adicional).

El álgebra lineal permite la abstracción de un vector de posición n -dimensional. Un vector de posición puede expresarse como una combinación lineal de vectores base : ^{[3] [4]}

${\displaystyle \mathbf {r} =\sum _{i=1}^{n}x_{i}\mathbf {e} _{i}=x_{1}\mathbf {e} _{1}+x_ {2}\mathbf {e} _{2}+\dotsb +x_{n}\mathbf {e} _{n}.}$

El conjunto de todos los vectores de posición forma el espacio de posición (un espacio vectorial cuyos elementos son los vectores de posición), ya que las posiciones se pueden sumar ( suma vectorial ) y escalar en longitud ( multiplicación escalar ) para obtener otro vector de posición en el espacio. La noción de "espacio" es intuitiva, ya que cada x _i ( i = 1, 2, …, n ) puede tener cualquier valor, la colección de valores define un punto en el espacio.

La dimensión del espacio de posición es n (también denotada dim( R ) = n ). Las coordenadas del vector r con respecto a los vectores base e _i son x _i . El vector de coordenadas forma el vector de coordenadas o n - tupla ( x ₁ , x ₂ , …, x _n ).

Cada coordenada x _i puede parametrizarse con una serie de parámetros t . Un parámetro x _i ( t ) describiría una trayectoria curva 1D, dos parámetros x _i ( t ₁ , t ₂ ) describirían una superficie curva 2D, tres x _i ( t ₁ , t ₂ , t ₃ ) describirían un volumen de espacio curvado 3D, y así sucesivamente.

El espacio lineal de un conjunto base B = { e ₁ , e ₂ , …, e _n } es igual al espacio de posición R , denotado span( B ) = R .

Los campos vectoriales de posición se utilizan para describir curvas espaciales continuas y diferenciables, en cuyo caso el parámetro independiente no necesita ser el tiempo, sino que puede ser (por ejemplo) la longitud del arco de la curva.

En cualquier ecuación de movimiento , el vector de posición r ( t ) suele ser la cantidad más buscada porque esta función define el movimiento de una partícula (es decir, una masa puntual ): su ubicación relativa a un sistema de coordenadas dado en algún momento t .

Para definir el movimiento en términos de posición, cada coordenada puede ser parametrizada por el tiempo; dado que cada valor sucesivo del tiempo corresponde a una secuencia de ubicaciones espaciales sucesivas dadas por las coordenadas, el límite continuo de muchas ubicaciones sucesivas es una trayectoria que traza la partícula.

En el caso de una dimensión, la posición tiene un solo componente, por lo que efectivamente degenera en una coordenada escalar. Podría ser, por ejemplo, un vector en la dirección x o en la dirección radial r . Las notaciones equivalentes incluyen

${\displaystyle \mathbf {x} \equiv x\equiv x(t),\cuadrado r\equiv r(t),\cuadrado s\equiv s(t).}$

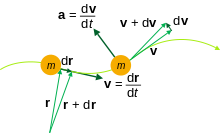
Para un vector de posición r que es una función del tiempo t , las derivadas temporales se pueden calcular con respecto a t . Estas derivadas tienen una utilidad común en el estudio de la cinemática , la teoría de control , la ingeniería y otras ciencias.

Velocidad

${\displaystyle \mathbf {v} ={\frac {\mathrm {d} \mathbf {r} }{\mathrm {d} t}},}$

donde d r es un desplazamiento infinitesimalmente pequeño (vector) .

Aceleración

${\displaystyle \mathbf {a} ={\frac {\mathrm {d} \mathbf {v} }{\mathrm {d} t}}={\frac {\mathrm {d} ^{2}\mathbf { r} }{\mathrm {d} t^{2}}}.}$

Idiota

${\displaystyle \mathbf {j} ={\frac {\mathrm {d} \mathbf {a} }{\mathrm {d} t}}={\frac {\mathrm {d} ^{2}\mathbf { v} }{\mathrm {d} t^{2}}}={\frac {\mathrm {d} ^{3}\mathbf {r} }{\mathrm {d} t^{3}}}. }$

Estos nombres para la primera, segunda y tercera derivada de la posición se utilizan comúnmente en cinemática básica. ^[5] Por extensión, las derivadas de orden superior se pueden calcular de manera similar. El estudio de estas derivadas de orden superior puede mejorar las aproximaciones de la función de desplazamiento original. Dichos términos de orden superior son necesarios para representar con precisión la función de desplazamiento como una suma de una secuencia infinita , lo que permite varias técnicas analíticas en ingeniería y física.

• Espacio afín
• Sistema de coordenadas
• Posición horizontal
• Elemento de línea
• Superficie paramétrica
• Fijación de posición
• Posición cuatro-vectorial
• Seis grados de libertad
• Posición vertical

• Keller, FJ, Gettys, WE et al. (1993). "Física: clásica y moderna", 2.ª ed. McGraw Hill Publishing.

• Medios relacionados con Posición (geometría) en Wikimedia Commons