Historia de la trigonometría
| Trigonometría |
|---|
 |
| Referencia |
| Leyes y teoremas |
| Cálculo |
| Matemáticos |
Los primeros estudios de los triángulos se remontan al segundo milenio a. C. , en las matemáticas egipcias ( Papiro matemático de Rhind ) y las matemáticas babilónicas . La trigonometría también prevaleció en las matemáticas kushitas . [1] El estudio sistemático de las funciones trigonométricas comenzó en las matemáticas helenísticas , llegando a la India como parte de la astronomía helenística . [2] En la astronomía india , el estudio de las funciones trigonométricas floreció en el período Gupta , especialmente debido a Aryabhata (siglo VI d. C.), quien descubrió la función seno, la función coseno y la función verseno.
Durante la Edad Media , el estudio de la trigonometría continuó en las matemáticas islámicas , por matemáticos como Al-Khwarizmi y Abu al-Wafa . Se convirtió en una disciplina independiente en el mundo islámico , donde se conocían las seis funciones trigonométricas . Las traducciones de textos árabes y griegos llevaron a que la trigonometría se adoptara como materia en el Occidente latino a partir del Renacimiento con Regiomontano .
El desarrollo de la trigonometría moderna cambió durante la Era de la Ilustración occidental , comenzando con las matemáticas del siglo XVII ( Isaac Newton y James Stirling ) y alcanzando su forma moderna con Leonhard Euler (1748).
Etimología
El término "trigonometría" se deriva del griego τρίγωνον trigōnon , "triángulo" y μέτρον metron , "medida". [3]
Las palabras modernas "seno" y "coseno" derivan de la palabra latina sinus por una traducción errónea del árabe (véase Seno y coseno#Etimología ). En particular, el seno recto del arco de Fibonacci influyó en el establecimiento del término. [4]
La palabra tangente proviene del latín tangens , que significa "tocar", ya que la línea toca el círculo de radio unitario, mientras que secante proviene del latín secans, "cortar", ya que la línea corta el círculo. [5]
El prefijo " co- " (en "coseno", "cotangente", "cosecante") se encuentra en el Canon triangulorum (1620) de Edmund Gunter , que define el coseno como una abreviatura del seno complementario (seno del ángulo complementario ) y procede a definir las cotangentes de manera similar. [6] [7]
Las palabras "minuto" y "segundo" se derivan de las frases latinas partes minutae primae y partes minutae secundae . [8] Estas se traducen aproximadamente como "primeras partes pequeñas" y "segundas partes pequeñas".
Antiguo
Antiguo Cercano Oriente
Los antiguos egipcios y babilonios conocían desde hacía siglos teoremas sobre las proporciones de los lados de triángulos semejantes. Sin embargo, como las sociedades prehelénicas carecían del concepto de medida de ángulos, se limitaban a estudiar los lados de los triángulos. [9]
Los astrónomos babilónicos llevaban registros detallados de la salida y puesta de las estrellas , el movimiento de los planetas y los eclipses solares y lunares , todo lo cual requería familiaridad con las distancias angulares medidas en la esfera celeste . [10] Basándose en una interpretación de la tablilla cuneiforme Plimpton 322 (c. 1900 a. C.), algunos incluso han afirmado que los antiguos babilonios tenían una tabla de secantes pero que no funciona en este contexto ya que sin el uso de círculos y ángulos en la situación las notaciones trigonométricas modernas no se aplicarán. [11] Sin embargo, existe mucho debate sobre si se trata de una tabla de ternas pitagóricas , una solución de ecuaciones cuadráticas o una tabla trigonométrica . [12]
Los egipcios, por otra parte, utilizaron una forma primitiva de trigonometría para construir pirámides en el segundo milenio a. C. [10] El Papiro matemático de Rhind , escrito por el escriba egipcio Ahmes (c. 1680-1620 a. C.), contiene el siguiente problema relacionado con la trigonometría: [10]
"Si una pirámide tiene 250 codos de altura y el lado de su base 360 codos de largo, ¿cuál es su seked ?"
La solución de Ahmes al problema es la relación entre la mitad del lado de la base de la pirámide y su altura, o la relación entre la longitud de la cara y la altura de la misma. En otras palabras, la cantidad que halló para el seked es la cotangente del ángulo entre la base de la pirámide y su cara. [10]
Antigüedad clásica
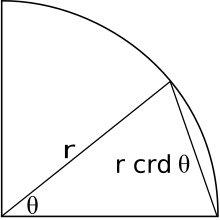
Los matemáticos griegos y helenísticos de la antigüedad utilizaron la cuerda . Dado un círculo y un arco en el círculo, la cuerda es la línea que subtiende el arco. La mediatriz de una cuerda pasa por el centro del círculo y biseca el ángulo. La mitad de la cuerda bisecada es el seno de la mitad del ángulo bisecado, es decir, [13]
y, en consecuencia, la función seno también se conoce como semicuerda . Debido a esta relación, una serie de identidades y teoremas trigonométricos que se conocen hoy en día también eran conocidos por los matemáticos helenísticos , pero en su forma de cuerda equivalente. [14] [15]
Aunque no hay trigonometría en las obras de Euclides y Arquímedes , en el sentido estricto de la palabra, hay teoremas presentados de forma geométrica (en lugar de trigonométrica) que son equivalentes a leyes o fórmulas trigonométricas específicas. [9] Por ejemplo, las proposiciones doce y trece del libro dos de los Elementos son las leyes de los cosenos para ángulos obtusos y agudos, respectivamente. Los teoremas sobre las longitudes de las cuerdas son aplicaciones de la ley de los senos . Y el teorema de Arquímedes sobre las cuerdas rotas es equivalente a las fórmulas para los senos de las sumas y diferencias de ángulos. [9] Para compensar la falta de una tabla de acordes , los matemáticos de la época de Aristarco utilizaban a veces la afirmación de que, en la notación moderna, sin α /sin β < α / β < tan α /tan β siempre que 0° < β < α < 90°, ahora conocida como la desigualdad de Aristarco . [16]
La primera tabla trigonométrica fue aparentemente compilada por Hiparco de Nicea (180 – 125 a. C.), a quien ahora se lo conoce como "el padre de la trigonometría". [17] Hiparco fue el primero en tabular los valores correspondientes de arco y cuerda para una serie de ángulos. [4] [17]
Aunque no se sabe cuándo entró en uso sistemático el círculo de 360° en las matemáticas, se sabe que la introducción sistemática del círculo de 360° se produjo poco después de que Aristarco de Samos compusiera Sobre los tamaños y distancias del Sol y la Luna (c. 260 a. C.), ya que midió un ángulo en términos de una fracción de un cuadrante. [16] Parece que el uso sistemático del círculo de 360° se debe en gran medida a Hiparco y su tabla de cuerdas . Hiparco puede haber tomado la idea de esta división de Hipsícles , quien anteriormente había dividido el día en 360 partes, una división del día que puede haber sido sugerida por la astronomía babilónica. [18] En la astronomía antigua, el zodíaco se había dividido en doce "signos" o treinta y seis "decanos". Un ciclo estacional de aproximadamente 360 días podría haberse correspondido con los signos y decanos del zodíaco dividiendo cada signo en treinta partes y cada decano en diez partes. [8] Es debido al sistema de numeración sexagesimal babilónico que cada grado se divide en sesenta minutos y cada minuto se divide en sesenta segundos. [8]
Menelao de Alejandría (c. 100 d. C.) escribió en tres libros su Sphaerica . En el Libro I, estableció una base para los triángulos esféricos análoga a la base euclidiana para los triángulos planos. [15] Estableció un teorema que no tiene análogo euclidiano, según el cual dos triángulos esféricos son congruentes si los ángulos correspondientes son iguales, pero no distinguió entre triángulos esféricos congruentes y simétricos. [15] Otro teorema que estableció es que la suma de los ángulos de un triángulo esférico es mayor que 180°. [15] El Libro II de Sphaerica aplica la geometría esférica a la astronomía. Y el Libro III contiene el "teorema de Menelao". [15] Además, dio su famosa "regla de las seis cantidades". [19]
Más tarde, Claudio Ptolomeo (c. 90 – c. 168 d. C.) amplió las Cuerdas en un círculo de Hiparco en su Almagesto , o Sintaxis matemática . El Almagesto es principalmente una obra sobre astronomía, y la astronomía se basa en la trigonometría. La tabla de cuerdas de Ptolomeo da las longitudes de las cuerdas de un círculo de diámetro 120 en función del número de grados n en el arco correspondiente del círculo, para n que varía de 1/2 a 180 en incrementos de 1/2. [20] Los trece libros del Almagesto son la obra trigonométrica más influyente y significativa de toda la antigüedad. [21] Un teorema que fue central para el cálculo de cuerdas de Ptolomeo fue lo que todavía hoy se conoce como el teorema de Ptolomeo , que dice que la suma de los productos de los lados opuestos de un cuadrilátero cíclico es igual al producto de las diagonales. Un caso especial del teorema de Ptolomeo apareció como proposición 93 en Datos de Euclides . El teorema de Ptolomeo conduce al equivalente de las cuatro fórmulas de suma y diferencia para seno y coseno que hoy se conocen como fórmulas de Ptolomeo, aunque el propio Ptolomeo utilizó cuerdas en lugar de seno y coseno. [21] Ptolomeo derivó además el equivalente de la fórmula del medio ángulo.
- [21]
Ptolomeo utilizó estos resultados para crear sus tablas trigonométricas, pero no se puede determinar si estas tablas se derivaron del trabajo de Hiparco. [21]
Ni las tablas de Hiparco ni las de Ptolomeo han sobrevivido hasta nuestros días, aunque las descripciones de otros autores antiguos dejan pocas dudas de que alguna vez existieron. [22]
Matemáticas indias
Algunos de los primeros y más significativos desarrollos de la trigonometría se produjeron en la India . Obras influyentes del siglo IV-V d. C., conocidas como Siddhantas (de las cuales hubo cinco, la más importante de las cuales es la Surya Siddhanta [23] ) definieron por primera vez el seno como la relación moderna entre la mitad de un ángulo y la mitad de una cuerda, al tiempo que definieron el coseno, el verseno y el seno inverso . [24] Poco después, otro matemático y astrónomo indio , Aryabhata (476-550 d. C.), recopiló y amplió los desarrollos de los Siddhantas en una obra importante llamada Aryabhatiya . [25] Los Siddhantas y el Aryabhatiya contienen las tablas supervivientes más antiguas de valores de seno y verseno (1 − coseno), en intervalos de 3,75° desde 0° hasta 90°, con una precisión de 4 decimales. [26] Utilizaron las palabras jya para seno, kojya para coseno, utkrama-jya para versino y otkram jya para seno inverso. Las palabras jya y kojya finalmente se convirtieron en seno y coseno respectivamente después de una traducción errónea descrita anteriormente.
En el siglo VII, Bhaskara I elaboró una fórmula para calcular el seno de un ángulo agudo sin utilizar una tabla. También proporcionó la siguiente fórmula de aproximación para sen( x ), que tenía un error relativo de menos del 1,9 %:
Más tarde, en el siglo VII, Brahmagupta rediseñó la fórmula.
(también derivada anteriormente, como se mencionó anteriormente) y la fórmula de interpolación de Brahmagupta para calcular valores de seno. [11]
Otro autor indio posterior sobre trigonometría fue Bhaskara II, en el siglo XII. Bhaskara II desarrolló la trigonometría esférica y descubrió muchos resultados trigonométricos.
Bhaskara II fue uno de los primeros en descubrir resultados trigonométricos como:
Madhava (c. 1400) hizo avances tempranos en el análisis de funciones trigonométricas y sus expansiones en series infinitas . Desarrolló los conceptos de serie de potencias y serie de Taylor , y produjo las expansiones en series de potencias de seno, coseno, tangente y arcotangente. [27] [28] Utilizando las aproximaciones de la serie de Taylor de seno y coseno, produjo una tabla de senos con 12 decimales de precisión y una tabla de cosenos con 9 decimales de precisión. También proporcionó la serie de potencias de π y el ángulo , radio , diámetro y circunferencia de un círculo en términos de funciones trigonométricas. Sus seguidores de la Escuela de Kerala ampliaron sus obras hasta el siglo XVI. [27] [28]
| No. | Serie | Nombre | Descubridores occidentales de la serie y fechas aproximadas de descubrimiento [29] |
|---|---|---|---|
| 1 | sen x = x − x 3 / 3! + x 5 / 5! − x 7 / 7! + ... | Serie de senos de Madhava | Isaac Newton (1670) y Wilhelm Leibniz (1676) |
| 2 | cos x = 1 − x 2 / 2! + x 4 / 4! − x 6 / 6! + ... | Serie de cosenos de Madhava | Isaac Newton (1670) y Wilhelm Leibniz (1676) |
| 3 | tan −1 x = x − x 3 / 3 + x 5 / 5 − x 7 / 7 + ... | Serie arcangente de Madhava | James Gregory (1671) y Wilhelm Leibniz (1676) |
El texto indio Yuktibhāṣā contiene pruebas para la expansión de las funciones seno y coseno y la derivación y prueba de la serie de potencias para la tangente inversa , descubierta por Madhava. El Yuktibhāṣā también contiene reglas para hallar los senos y los cosenos de la suma y la diferencia de dos ángulos.
Matemáticas chinas

En China , la tabla de senos de Aryabhata se tradujo al libro matemático chino de Kaiyuan Zhanjing , compilado en 718 d. C. durante la dinastía Tang . [30] Aunque los chinos sobresalieron en otros campos de las matemáticas, como la geometría sólida, el teorema del binomio y las fórmulas algebraicas complejas, las primeras formas de trigonometría no fueron tan ampliamente apreciadas como en los mundos griego, helenístico, indio e islámico anteriores. [31] En cambio, los primeros chinos utilizaron un sustituto empírico conocido como chong cha , mientras que se conocía el uso práctico de la trigonometría plana al utilizar el seno, la tangente y la secante. [30] Sin embargo, este estado embrionario de la trigonometría en China comenzó a cambiar y avanzar lentamente durante la dinastía Song (960-1279), donde los matemáticos chinos comenzaron a expresar un mayor énfasis en la necesidad de la trigonometría esférica en la ciencia calendárica y los cálculos astronómicos. [30] El científico, matemático y funcionario chino Shen Kuo (1031-1095) utilizó funciones trigonométricas para resolver problemas matemáticos de cuerdas y arcos. [30] Victor J. Katz escribe que en la fórmula de Shen "técnica de intersección de círculos", creó una aproximación del arco s de un círculo dado el diámetro d , la sagitta v y la longitud c de la cuerda que subtiende el arco, cuya longitud aproximó como [32]
Sal Restivo escribe que el trabajo de Shen en las longitudes de los arcos de círculo proporcionó la base para la trigonometría esférica desarrollada en el siglo XIII por el matemático y astrónomo Guo Shoujing (1231-1316). [33] Como afirman los historiadores L. Gauchet y Joseph Needham, Guo Shoujing utilizó la trigonometría esférica en sus cálculos para mejorar el sistema de calendario y la astronomía china . [30] [34] Junto con una ilustración china posterior del siglo XVII de las pruebas matemáticas de Guo, Needham afirma que:
Guo utilizó una pirámide esférica cuadrangular, cuyo cuadrilátero basal consistía en un arco ecuatorial y uno eclíptico, junto con dos arcos meridianos , uno de los cuales pasaba por el punto del solsticio de verano ... Mediante estos métodos pudo obtener el du lü (grados del ecuador correspondientes a grados de la eclíptica), el ji cha (valores de las cuerdas para arcos eclípticos dados) y el cha lü (diferencia entre cuerdas de arcos que difieren en 1 grado). [35]
A pesar de los logros del trabajo de Shen y Guo en trigonometría, otro trabajo sustancial en trigonometría china no se publicaría nuevamente hasta 1607, con la publicación doble de los Elementos de Euclides por el funcionario y astrónomo chino Xu Guangqi (1562-1633) y el jesuita italiano Matteo Ricci (1552-1610). [36]
Mundo islámico medieval

Las obras anteriores fueron traducidas y ampliadas posteriormente en el mundo islámico medieval por matemáticos musulmanes de ascendencia mayoritariamente persa y árabe , quienes enunciaron una gran cantidad de teoremas que liberaron al tema de la trigonometría de la dependencia del cuadrilátero completo , como era el caso en las matemáticas helenísticas debido a la aplicación del teorema de Menelao . Según E. S. Kennedy, fue después de este desarrollo en las matemáticas islámicas que "surgió la primera trigonometría real, en el sentido de que solo entonces el objeto de estudio pasó a ser el triángulo esférico o plano , sus lados y ángulos ". [37]
También se conocían métodos para tratar con triángulos esféricos, en particular el método de Menelao de Alejandría , que desarrolló el "teorema de Menelao" para tratar problemas esféricos. [15] [38] Sin embargo, ES Kennedy señala que, si bien en las matemáticas preislámicas era posible calcular las magnitudes de una figura esférica, en principio, mediante el uso de la tabla de cuerdas y el teorema de Menelao, la aplicación del teorema a problemas esféricos era muy difícil en la práctica. [39] Para observar los días sagrados en el calendario islámico en el que los tiempos se determinaban por las fases de la luna , los astrónomos utilizaron inicialmente el método de Menelao para calcular el lugar de la luna y las estrellas , aunque este método resultó ser torpe y difícil. Implicaba establecer dos triángulos rectángulos que se intersecaban ; al aplicar el teorema de Menelao era posible resolver uno de los seis lados, pero solo si se conocían los otros cinco lados. Para saber la hora a partir de la altura del sol , por ejemplo, se requerían repetidas aplicaciones del teorema de Menelao. Para los astrónomos islámicos medievales , era un desafío obvio encontrar un método trigonométrico más simple. [40]
A principios del siglo IX d. C., Muhammad ibn Mūsā al-Khwārizmī produjo tablas precisas de senos y cosenos, y la primera tabla de tangentes. También fue pionero en trigonometría esférica . En 830 d. C., Habash al-Hasib al-Marwazi produjo la primera tabla de cotangentes. [41] [42] Muhammad ibn Jābir al-Harrānī al-Battānī (Albatenius) (853–929 d. C.) descubrió las funciones recíprocas de secante y cosecante, y produjo la primera tabla de cosecantes para cada grado desde 1° hasta 90°. [43]
En el siglo X d. C., en la obra de Abū al-Wafā' al-Būzjānī , se utilizaban las seis funciones trigonométricas . [44] Abu al-Wafa tenía tablas de senos en incrementos de 0,25°, con una precisión de 8 decimales, y tablas precisas de valores de tangente. [44] También desarrolló la siguiente fórmula trigonométrica: [45]
- (un caso especial de la fórmula de adición de ángulos de Ptolomeo; ver arriba)
En su texto original, Abū al-Wafā' afirma: "Si queremos eso, multiplicamos el seno dado por el coseno minutos , y el resultado es la mitad del seno del doble". [45] Abū al-Wafā también estableció las identidades de suma y diferencia de ángulos presentadas con pruebas completas: [45]
Para el segundo, el texto dice: “Multiplicamos el seno de cada uno de los dos arcos por el coseno de los otros minutos . Si queremos el seno de la suma, sumamos los productos, si queremos el seno de la diferencia, tomamos su diferencia”. [45]
También descubrió la ley de los senos para la trigonometría esférica: [41]
También a finales del siglo X y principios del XI d.C., el astrónomo egipcio Ibn Yunus realizó muchos cálculos trigonométricos cuidadosos y demostró la siguiente identidad trigonométrica : [46]
Al-Jayyani (989-1079) de al-Ándalus escribió El libro de los arcos desconocidos de una esfera , que se considera «el primer tratado sobre trigonometría esférica ». [47] «Contiene fórmulas para triángulos rectos , la ley general de los senos y la solución de un triángulo esférico por medio del triángulo polar». Este tratado tuvo posteriormente una «fuerte influencia en las matemáticas europeas», y es probable que su «definición de las proporciones como números» y su «método de resolver un triángulo esférico cuando todos los lados son desconocidos» hayan influido en Regiomontano . [47]
El método de triangulación fue desarrollado por primera vez por matemáticos musulmanes, quienes lo aplicaron a usos prácticos como la topografía [48] y la geografía islámica , como lo describió Abu Rayhan Biruni a principios del siglo XI. El propio Biruni introdujo técnicas de triangulación para medir el tamaño de la Tierra y las distancias entre varios lugares. [49] A fines del siglo XI, Omar Khayyám (1048-1131) resolvió ecuaciones cúbicas utilizando soluciones numéricas aproximadas encontradas por interpolación en tablas trigonométricas. En el siglo XIII, Nasīr al-Dīn al-Tūsī fue el primero en tratar la trigonometría como una disciplina matemática independiente de la astronomía, y desarrolló la trigonometría esférica en su forma actual. [42] Enumeró los seis casos distintos de un triángulo rectángulo en trigonometría esférica, y en su obra Sobre la figura del sector , enunció la ley de los senos para triángulos planos y esféricos, descubrió la ley de las tangentes para triángulos esféricos y proporcionó pruebas para ambas leyes. [50] Nasir al-Din al-Tusi ha sido descrito como el creador de la trigonometría como una disciplina matemática por derecho propio. [51] [52] [53]
En el siglo XV, Jamshīd al-Kāshī proporcionó la primera declaración explícita de la ley de los cosenos en una forma adecuada para la triangulación . [ cita requerida ] En Francia , la ley de los cosenos todavía se conoce como el teorema de Al-Kashi . También proporcionó tablas trigonométricas de valores de la función seno con cuatro dígitos sexagesimales (equivalentes a 8 decimales) para cada 1° de argumento con diferencias que se deben agregar por cada 1/60 de 1°. [ cita requerida ] Ulugh Beg también proporciona tablas precisas de senos y tangentes correctas a 8 decimales aproximadamente en la misma época. [ cita requerida ]
Moderno
![[icon]](http://upload.wikimedia.org/wikipedia/commons/thumb/1/1c/Wiki_letter_w_cropped.svg/20px-Wiki_letter_w_cropped.svg.png) | This section needs expansion. You can help by adding to it. (March 2024) |
El renacimiento europeo y más allá
En 1342, Levi ben Gershon, conocido como Gersonides , escribió Sobre senos, cuerdas y arcos , en particular demostrando la ley del seno para triángulos planos y dando tablas de senos de cinco cifras . [54]
Los navegantes del Mediterráneo durante los siglos XIV y XV utilizaban una tabla trigonométrica simplificada, la " toleta de marteloio ", para calcular los rumbos de la navegación . Fue descrita por Ramon Llull de Mallorca en 1295 y plasmada en el atlas de 1436 del capitán veneciano Andrea Bianco .
Regiomontanus fue quizás el primer matemático en Europa en tratar la trigonometría como una disciplina matemática distinta, [55] en su De triangulis omnimodis escrito en 1464, así como en su posterior Tabulae directionum que incluía la función tangente, sin nombre. El Opus palatinum de triangulis de Georg Joachim Rheticus , un estudiante de Copérnico , fue probablemente el primero en Europa en definir funciones trigonométricas directamente en términos de triángulos rectángulos en lugar de círculos, con tablas para las seis funciones trigonométricas; este trabajo fue terminado por el estudiante de Rheticus, Valentin Otho, en 1596.
En el siglo XVII, Isaac Newton y James Stirling desarrollaron la fórmula general de interpolación de Newton-Stirling para funciones trigonométricas.
En el siglo XVIII, la Introducción al análisis infinitorum (1748) de Leonhard Euler fue la principal responsable de establecer el tratamiento analítico de las funciones trigonométricas en Europa, derivando sus series infinitas y presentando la " fórmula de Euler " e ix = cos x + i sen x . Euler utilizó las abreviaturas casi modernas sen. , cos. , tang. , cot. , sec. y cosec. Antes de esto, Roger Cotes había calculado la derivada del seno en su Harmonia Mensurarum (1722). [56] También en el siglo XVIII, Brook Taylor definió la serie general de Taylor y dio las expansiones y aproximaciones de la serie para las seis funciones trigonométricas. Los trabajos de James Gregory en el siglo XVII y de Colin Maclaurin en el siglo XVIII también fueron muy influyentes en el desarrollo de las series trigonométricas.
Véase también
- Matemáticas griegas
- Historia de las matemáticas
- Funciones trigonométricas
- Trigonometría
- Tabla de acordes de Ptolomeo
- Tabla de senos de Aryabhata
- Trigonometría racional
Citas y notas a pie de página
- ^ Otto Neugebauer (1975). Una historia de la astronomía matemática antigua. 1. Springer-Verlag. pag. 744.ISBN 978-3-540-06995-9.
- ^ Katz 1998, pág. 212.
- ^ "trigonometría". Diccionario Etimológico en Línea .
- ^ ab O'Connor, JJ; Robertson, EF (1996). "Funciones trigonométricas". Archivo de Historia de las Matemáticas de MacTutor . Archivado desde el original el 4 de junio de 2007.
- ^ Diccionario Oxford de inglés
- ^ Gunter, Edmund (1620). Canon triangulorum .
- ^ Roegel, Denis, ed. (6 de diciembre de 2010). "A recreation of Gunter's Canon triangulorum (1620)" (Informe de investigación). HAL. inria-00543938. Archivado desde el original el 28 de julio de 2017. Consultado el 28 de julio de 2017 .
- ^ abc Boyer 1991, pp. 166–167, Trigonometría y medición griegas: "Debe recordarse que desde los días de Hiparco hasta los tiempos modernos no existían razones trigonométricas . Los griegos, y después de ellos los hindúes y los árabes, usaban líneas trigonométricas . Estas al principio tomaron la forma, como hemos visto, de cuerdas en un círculo, y a Ptolomeo le correspondió asociar valores numéricos (o aproximaciones) con las cuerdas. [...] No es improbable que la medida de 260 grados fuera heredada de la astronomía, donde el zodíaco había sido dividido en doce "signos" o 36 "decanos". Un ciclo de las estaciones de aproximadamente 360 días podría fácilmente corresponderse con el sistema de signos y decanos zodiacales subdividiendo cada signo en treinta partes y cada decano en diez partes. Nuestro sistema común de medición de ángulos puede derivar de esta correspondencia. Además, dado que el sistema de posición babilónico "Como las fracciones eran tan obviamente superiores a las fracciones unitarias egipcias y a las fracciones comunes griegas, era natural que Ptolomeo subdividiera sus grados en sesenta partes minutae primae , cada una de estas últimas en sesenta partes minutae secundae , y así sucesivamente. Es de las frases latinas que los traductores usaron en este sentido de donde se han derivado nuestras palabras "minuto" y "segundo". Sin duda fue el sistema sexagesimal lo que llevó a Ptolomeo a subdividir el diámetro de su círculo trigonométrico en 120 partes; cada una de estas a su vez subdividió en sesenta minutos y cada minuto de duración en sesenta segundos".
- ^ abc Boyer 1991, pp. 158-159, Trigonometría y medición griegas: "La trigonometría, como otras ramas de las matemáticas, no fue obra de un solo hombre o nación. Los antiguos egipcios y babilonios conocían y utilizaban teoremas sobre las proporciones de los lados de triángulos semejantes. En vista de la falta prehelénica del concepto de medida de ángulos, un estudio de este tipo podría llamarse mejor "trilaterometría", o la medida de polígonos de tres lados (triláteros), que "trigonometría", la medida de las partes de un triángulo. Con los griegos encontramos primero un estudio sistemático de las relaciones entre los ángulos (o arcos) en un círculo y las longitudes de las cuerdas que los subtienden. Las propiedades de las cuerdas, como medidas de ángulos centrales e inscritos en círculos, eran familiares para los griegos de la época de Hipócrates, y es probable que Eudoxo hubiera utilizado proporciones y medidas de ángulos para determinar el tamaño de la Tierra y la distancias del sol y la luna. En las obras de Euclides no hay trigonometría en el sentido estricto de la palabra, pero sí teoremas equivalentes a leyes o fórmulas trigonométricas específicas. Las proposiciones II.12 y 13 de los Elementos , por ejemplo, son las leyes de los cosenos para ángulos obtusos y agudos respectivamente, enunciadas en lenguaje geométrico en lugar de trigonométrico y demostradas mediante un método similar al utilizado por Euclides en relación con el teorema de Pitágoras. Los teoremas sobre las longitudes de las cuerdas son esencialmente aplicaciones de la ley moderna de los senos. Hemos visto que el teorema de Arquímedes sobre la cuerda rota puede traducirse fácilmente a lenguaje trigonométrico de manera análoga a las fórmulas para los senos de las sumas y diferencias de ángulos.
- ^ abcd Maor, Eli (1998). Delicias trigonométricas . Princeton University Press . pág. 20. ISBN 978-0-691-09541-7.
- ^ por Joseph 2000, págs. 383–384.
- ^ Mansfield, Daniel F.; Wildberger, NJ (noviembre de 2017). "Plimpton 322 es trigonometría sexagesimal exacta babilónica". Historia Mathematica . 44 (4): 395–419. doi :10.1016/j.hm.2017.08.001.
- ^ Katz 1998, pág. 143.
- ^ Como estos cálculos históricos no utilizaban un círculo unitario, era necesario incluir la longitud del radio en la fórmula. Comparemos esto con el uso moderno de la función crd , que supone un círculo unitario en su definición.
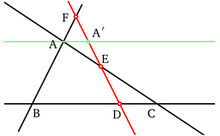
- ^ abcdef Boyer 1991, pág. 163, Trigonometría y medición griegas: "En el Libro I de este tratado, Menelao establece una base para los triángulos esféricos análoga a la de Euclides I para los triángulos planos. Se incluye un teorema sin análogo euclidiano: que dos triángulos esféricos son congruentes si los ángulos correspondientes son iguales (Menelao no distinguió entre triángulos esféricos congruentes y simétricos); y se establece el teorema A + B + C > 180°. El segundo libro de la Sphaerica describe la aplicación de la geometría esférica a los fenómenos astronómicos y es de poco interés matemático. El Libro III, el último, contiene el conocido "teorema de Menelao" como parte de lo que es esencialmente trigonometría esférica en la forma griega típica: una geometría o trigonometría de cuerdas en un círculo. En el círculo de la Fig. 10.4 deberíamos escribir que la cuerda AB es el doble del seno de la mitad del ángulo central AOB (multiplicado por el radio del círculo). Menelao y sus sucesores griegos en cambio se refirieron a AB simplemente como la cuerda correspondiente al arco AB. Si BOB' es un diámetro del círculo, entonces la cuerda A' es el doble del coseno de la mitad del ángulo AOB (multiplicado por el radio del círculo).
- ^ desde Boyer 1991, pág. 159, Trigonometría y medición griegas: "En cambio, tenemos un tratado, compuesto quizás antes (ca. 260 a. C.), Sobre los tamaños y distancias del Sol y la Luna , que supone un universo geocéntrico. En esta obra, Aristarco hizo la observación de que cuando la luna está justo en la mitad de su fase llena, el ángulo entre las líneas de visión del sol y la luna es menor que un ángulo recto en un trigésimo de un cuadrante. (La introducción sistemática del círculo de 360° llegó un poco más tarde. En el lenguaje trigonométrico de hoy, esto significaría que la relación entre la distancia de la luna y la del sol (la relación ME a SE en la figura 10.1) es sen(3°). Como las tablas trigonométricas aún no se habían desarrollado, Aristarco recurrió a un teorema geométrico bien conocido de la época que ahora se expresaría en las desigualdades sen α/ sen β < α/β < tan α/ tan β, para 0° " < β < α < 90°.)"
- ^ ab Boyer 1991, p. 162, Trigonometría y medición griegas: "Durante unos dos siglos y medio, desde Hipócrates hasta Eratóstenes, los matemáticos griegos habían estudiado las relaciones entre líneas y círculos y las habían aplicado en una variedad de problemas astronómicos, pero no se había producido ninguna trigonometría sistemática. Luego, presumiblemente durante la segunda mitad del siglo II a. C., la primera tabla trigonométrica aparentemente fue compilada por el astrónomo Hiparco de Nicea (ca. 180–ca. 125 a. C.), quien así se ganó el derecho a ser conocido como "el padre de la trigonometría". Aristarco sabía que en un círculo dado la relación entre el arco y la cuerda disminuye a medida que el arco disminuye de 180° a 0°, tendiendo hacia un límite de 1. Sin embargo, parece que hasta que Hiparco no emprendió la tarea, nadie había tabulado los valores correspondientes de arco y cuerda para una serie completa de ángulos".
- ^ Boyer 1991, p. 162, Trigonometría y medición griegas: "No se sabe exactamente cuándo se introdujo el uso sistemático del círculo de 360° en las matemáticas, pero parece deberse en gran medida a Hiparco en relación con su tabla de cuerdas. Es posible que haya tomado el relevo de Hipsícles, que antes había dividido el día en partes, una subdivisión que puede haber sido sugerida por la astronomía babilónica".
- ^ Needham 1986, pág. 108.
- ^ Toomer, Gerald J. (1998). Almagesto de Ptolomeo . Princeton University Press. ISBN 978-0-691-00260-6.
- ^ abcd Boyer 1991, pp. 164–166, Trigonometría y medición griegas: "El teorema de Menelao desempeñó un papel fundamental en la trigonometría esférica y la astronomía, pero, con mucho, la obra trigonométrica más influyente y significativa de toda la antigüedad fue compuesta por Ptolomeo de Alejandría aproximadamente medio siglo después de Menelao. [...] De la vida del autor estamos tan poco informados como de la del autor de los Elementos. No sabemos cuándo ni dónde nacieron Euclides y Ptolomeo. Sabemos que Ptolomeo hizo observaciones en Alejandría desde el 127 d. C. hasta el 151 d. C. y, por lo tanto, suponemos que nació a fines del siglo I. Suidas, un escritor que vivió en el siglo X, informó que Ptolomeo estaba vivo bajo Marco Aurelio (emperador desde el 161 al 180 d. C.). Se presume que el Almagesto
de Ptolomeo está en gran parte en deuda con sus métodos a las Cuerdas en un Círculo de Hiparco, pero no se puede evaluar de manera fiable el alcance de la deuda. Está claro que en astronomía Ptolomeo hizo uso del catálogo de posiciones de las estrellas legado por Hiparco, pero no se puede determinar si las tablas trigonométricas de Ptolomeo se derivaron en gran parte de su distinguido predecesor. [...] Central para el cálculo de las cuerdas de Ptolomeo fue una proposición geométrica todavía conocida como "teorema de Ptolomeo": [...] es decir, la suma de los productos de los lados opuestos de un cuadrilátero cíclico es igual al producto de las diagonales. [...] Un caso especial del teorema de Ptolomeo había aparecido en los Datos de Euclides (Proposición 93): [...] El teorema de Ptolomeo, por lo tanto, conduce al resultado sen( α − β ) = sen α cos β − cos α sen Β . Un razonamiento similar conduce a la fórmula [...] Estas cuatro fórmulas de suma y diferencia se conocen hoy en día como fórmulas de Ptolomeo. La fórmula del seno de la diferencia –o, más exactamente, la cuerda de la diferencia– fue la que Ptolomeo encontró especialmente útil para construir sus tablas. Otra fórmula que le resultó eficaz fue el equivalente de nuestra fórmula del medio ángulo. - ^ Boyer 1991, págs. 158-168.
- ^ Boyer 1991, pág. 208.
- ^ Boyer 1991, pág. 209.
- ^ Boyer 1991, pág. 210.
- ^ Boyer 1991, pág. 215.
- ^ ab O'Connor, JJ; Robertson, EF (2000). "Madhava de Sangamagramma". Archivo de Historia de las Matemáticas de MacTutor .
- ^ ab Pearce, Ian G. (2002). "Madhava de Sangamagramma". Archivo de Historia de las Matemáticas de MacTutor .
- ^ Charles Henry Edwards (1994). El desarrollo histórico del cálculo . Springer Study Edition Series (3.ª ed.). Springer. pág. 205. ISBN 978-0-387-94313-8.
- ^ abcde Needham 1986, pág. 109.
- ^ Needham 1986, págs. 108-109.
- ^ Katz 2007, pág. 308.
- ^ Restivo 1992, pág. 32.
- ^ Gauchet, L. (1917). Note Sur La Trigonométrie Sphérique de Kouo Cheou-King . pag. 151.
- ^ Needham 1986, págs. 109-110.
- ^ Needham 1986, pág. 110.
- ^ Kennedy, ES (1969). "La historia de la trigonometría". 31.° anuario . Washington DC: Consejo Nacional de Profesores de Matemáticas.( cf. Haq, Syed Nomanul (1996). "El contexto indio y persa". En Seyyed Hossein Nasr ; Oliver Leaman (eds.). Historia de la filosofía islámica . Routledge . Págs. 52-70 [60-63]. ISBN. 978-0-415-13159-9.)
- ^ O'Connor, John J.; Robertson, Edmund F. , "Menelao de Alejandría", Archivo de Historia de las Matemáticas MacTutor , Universidad de St Andrews"El libro 3 trata de la trigonometría esférica e incluye el teorema de Menelao".
- ^ Kennedy, ES (1969). "La historia de la trigonometría". 31.° anuario . Washington DC: Consejo Nacional de Profesores de Matemáticas: 337.( cf. Haq, Syed Nomanul (1996). "El contexto indio y persa". En Seyyed Hossein Nasr ; Oliver Leaman (eds.). Historia de la filosofía islámica . Routledge . Págs. 52-70 [68]. ISBN 978-0-415-13159-9.)
- ^ Gingerich, Owen (abril de 1986). "Astronomía islámica". Scientific American . 254 (10): 74. Bibcode :1986SciAm.254d..74G. doi :10.1038/scientificamerican0486-74. Archivado desde el original el 2011-01-01 . Consultado el 2008-05-18 .
- ^ ab Jacques Sesiano, "Matemáticas islámicas", pág. 157, en Selin, Helaine ; D'Ambrosio, Ubiratan , eds. (2000). Matemáticas en distintas culturas: la historia de las matemáticas no occidentales . Springer Science+Business Media . ISBN 978-1-4020-0260-1.
- ^ ab "trigonometría". Encyclopædia Britannica . Consultado el 21 de julio de 2008 .
- ^ Maor, Eli (1998). Delicias trigonométricas . Princeton: Princeton University Press. pág. 38. ISBN 978-0-691-15820-4.
- ^Ab Boyer 1991, pág. 238.
- ^ abcd Moussa, Ali (2011). "Métodos matemáticos en el Almagesto de Abū al-Wafāʾ y las determinaciones de la qibla". Ciencias y filosofía árabes . 21 (1). Cambridge University Press : 1–56. doi :10.1017/S095742391000007X. S2CID 171015175.
- ^ William Charles Brice, 'Atlas histórico del Islam', pág. 413
- ^ ab O'Connor, John J.; Robertson, Edmund F. , "Abu Abd Allah Muhammad ibn Muadh Al-Jayyani", Archivo de Historia de las Matemáticas de MacTutor , Universidad de St Andrews
- ^ Donald Routledge Hill (1996), "Ingeniería", en Roshdi Rashed, Enciclopedia de la historia de la ciencia árabe , vol. 3, pág. 751–795 [769].
- ^ O'Connor, John J.; Robertson, Edmund F. , "Abu Arrayhan Muhammad ibn Ahmad al-Biruni", Archivo MacTutor de Historia de las Matemáticas , Universidad de St Andrews
- ^ Berggren, J. Lennart (2007). "Matemáticas en el Islam medieval". Las matemáticas de Egipto, Mesopotamia, China, India y el Islam: un libro de consulta . Princeton University Press. pág. 518. ISBN 978-0-691-11485-9.
- ^ "Biografía de Al-Tusi_Nasir". www-history.mcs.st-andrews.ac.uk . Consultado el 5 de agosto de 2018 .
Una de las contribuciones matemáticas más importantes de Al-Tusi fue la creación de la trigonometría como disciplina matemática por derecho propio, en lugar de como una simple herramienta para aplicaciones astronómicas. En su Tratado sobre el cuadrilátero, Al-Tusi realizó la primera exposición existente de todo el sistema de trigonometría plana y esférica. Esta obra es realmente la primera en la historia sobre la trigonometría como una rama independiente de las matemáticas puras y la primera en la que se exponen los seis casos de un triángulo esférico rectángulo.
- ^ Berggren, JL (octubre de 2013). "Matemáticas islámicas" . Historia de la ciencia de Cambridge . Cambridge University Press. págs. 62-83. doi :10.1017/CHO9780511974007.004. ISBN . 978-0-511-97400-7.
- ^ electricpulp.com. "ṬUSI, NAṢIR-AL-DIN i. Biografía – Enciclopedia Iranica". www.iranicaonline.org . Consultado el 5 de agosto de 2018 .
Se dice que su principal contribución en matemáticas (Nasr, 1996, pp. 208-214) fue en trigonometría, que por primera vez fue compilada por él como una nueva disciplina por derecho propio. La trigonometría esférica también debe su desarrollo a sus esfuerzos, y esto incluye el concepto de las seis fórmulas fundamentales para la solución de triángulos rectángulos esféricos.
- ^ Charles G. Simonson (invierno de 2000). "Las matemáticas de Levi ben Gershon, el Ralbag" (PDF) . Bekhol Derakhekha Daehu . 10. Bar-Ilan University Press: 5–21.
- ^ Boyer 1991, pág. 274.
- ^ Katz, Victor J. (noviembre de 1987). "El cálculo de las funciones trigonométricas". Historia Mathematica . 14 (4): 311–324. doi : 10.1016/0315-0860(87)90064-4 .La prueba de Cotes se menciona en la pág. 315.
Referencias
- Boyer, Carl Benjamin (1991). Una historia de las matemáticas (2.ª ed.). John Wiley & Sons, Inc. ISBN 978-0-471-54397-8.
- Joseph, George G. (2000). La cresta del pavo real: raíces no europeas de las matemáticas (2.ª ed.). Londres: Penguin Books . ISBN 978-0-691-00659-8.
- Katz, Victor J. (1998). Una historia de las matemáticas / Una introducción (2.ª ed.). Addison Wesley. ISBN 978-0-321-01618-8.
- Katz, Victor J. (2007). Las matemáticas de Egipto, Mesopotamia, China, India y el Islam: un libro de consulta . Princeton: Princeton University Press. ISBN 978-0-691-11485-9.
- Needham, Joseph (1986). Ciencia y civilización en China: Volumen 3, Matemáticas y ciencias de los cielos y la tierra . Taipei: Caves Books, Ltd.
- Restivo, Sal (1992). Matemáticas en la sociedad y la historia: investigaciones sociológicas . Dordrecht: Kluwer Academic Publishers. ISBN 1-4020-0039-1.
Lectura adicional
- Braunmuhl, Anton von (1900-1903). Vorlesungen über Geschichte der Trigonometrie [ Conferencias sobre la historia de la trigonometría ] (en alemán). BG Teubner.
- Kennedy, Edward S. (1969). "La historia de la trigonometría" . Temas históricos para el aula de matemáticas . Anuarios del NCTM. Vol. 31. Consejo Nacional de Profesores de Matemáticas. págs. 333–375.
- Maor, Eli (1998). Delicias trigonométricas. Princeton University Press. doi :10.1515/9780691202204. ISBN 0691057540. Archivado desde el original el 11 de julio de 2003.
- Ostermann, Alexander; Wanner, Gerhard (2012). "Trigonometría". Geometría por su historia . Textos de pregrado en matemáticas. Springer. págs. 113-155. doi :10.1007/978-3-642-29163-0. ISBN 978-3-642-29162-3.
- Van Brummelen, Glen (2009). Las matemáticas de los cielos y la tierra: la historia temprana de la trigonometría . Princeton University Press.
- Van Brummelen, Glen (2021). La doctrina de los triángulos: una historia de la trigonometría moderna . Princeton University Press.















