Serie trigonométrica

Trigonometría
Describir Historia Uso Funciones  ( sin , cos , tan , inversa ) Trigonometría generalizada
Referencia
Identidades Constantes exactas Tablas Círculo unitario
Leyes y teoremas
Senos Cosenos Tangentes Cotangentes Teorema de Pitágoras
Cálculo
Sustitución trigonométrica Integrales  ( funciones inversas ) Derivados Serie trigonométrica
Matemáticos
Hiparco Ptolomeo Brahma-upta Al-Hasib Al-Battani Regiomontano Viète de Moivre Euler Fourier
en a mi

En matemáticas, una serie trigonométrica es una serie infinita de la forma

${\displaystyle A_{0}+\sum _ {n=1}^{\infty }A_{n}\cos {(nx)}+B_{n}\sin {(nx)},}$

donde es la variable y y son coeficientes . Es una versión infinita de un polinomio trigonométrico .${\estilo de visualización x}$$Estilo de visualización: {A_{n}\}}$$Estilo de visualización: Bn$

Una serie trigonométrica se denomina serie de Fourier de la función integrable si los coeficientes tienen la forma:${\textstyle f}$

${\displaystyle A_{n}={\frac {1}{\pi }}\int _{0}^{2\pi }\!f(x)\cos {(nx)}\,dx}$

${\displaystyle B_{n}={\frac {1}{\pi }}\displaystyle \int _{0}^{2\pi }\!f(x)\sin {(nx)}\,dx}$

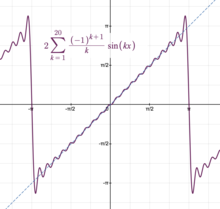
Toda serie de Fourier da un ejemplo de una serie trigonométrica. Supongamos que la función en se extiende periódicamente (véase onda de diente de sierra ). Entonces sus coeficientes de Fourier son:${\displaystyle f(x)=x}$${\estilo de visualización [-\pi ,\pi ]}$

${\displaystyle {\begin{aligned}A_{n}&={\frac {1}{\pi }}\int _{-\pi }^{\pi }x\cos {(nx)}\,dx =0,\quad n\geq 0.\\[4pt]B_{n}&={\frac {1}{\pi }}\int _{-\pi }^{\pi }x\sin {( nx)}\,dx\\[4pt]&=-{\frac {x}{n\pi }}\cos {(nx)}+{\frac {1}{n^{2}\pi }} \sin {(nx)}{\Bigg \vert }_{x=-\pi }^{\pi }\\[5mu]&={\frac {2\,(-1)^{n+1} }{n}},\quad n\geq 1.\end{alineado}}}$

Lo que da un ejemplo de una serie trigonométrica:

${\displaystyle 2\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}\sin {(nx)}=2\sin {(x)}-{\frac {2}{2}}\sin {(2x)}+{\frac {2}{3}}\sin {(3x)}-{\frac {2}{4}}\sin {(4x)}+\cdots }$

Sin embargo, lo contrario es falso, no todas las series trigonométricas son series de Fourier. La serie

${\displaystyle \sum _{n=2}^{\infty }{\frac {\sin {(nx)}}{\log {n}}}={\frac {\sin {(2x)}}{\log {2}}}+{\frac {\sin {(3x)}}{\log {3}}}+{\frac {\sin {(4x)}}{\log {4}}}+\cdots }$

es una serie trigonométrica que converge para todos pero no es una serie de Fourier . ^[1] Aquí para y todos los demás coeficientes son cero.${\estilo de visualización x}$${\displaystyle B_{n}={\frac {1}{\log(n)}}}$${\displaystyle n\geq 2}$

La unicidad y los ceros de las series trigonométricas fue un área activa de investigación en la Europa del siglo XIX. En primer lugar, Georg Cantor demostró que si una serie trigonométrica es convergente a una función en el intervalo , que es idénticamente cero, o más generalmente, es distinta de cero en un número finito de puntos, entonces los coeficientes de la serie son todos cero. ^[2]${\estilo de visualización f(x)}$${\displaystyle [0,2\pi ]}$

Más tarde, Cantor demostró que incluso si el conjunto S en el que S es distinto de cero es infinito, pero el conjunto derivado S' de S es finito, entonces los coeficientes son todos cero. De hecho, demostró un resultado más general. Sea S ₀ = S y sea S _k+1 el conjunto derivado de S _k . Si hay un número finito n para el que S _n es finito, entonces todos los coeficientes son cero. Más tarde, Lebesgue demostró que si hay un ordinal infinito numerable α tal que S _α es finito, entonces los coeficientes de la serie son todos cero. El trabajo de Cantor sobre el problema de unicidad lo llevó a inventar los números ordinales transfinitos , que aparecían como los subíndices α en S _α . ^[3]${\estilo de visualización f}$

• Bari, Nina Karlovna (1964). Tratado sobre series trigonométricas . Vol. 1. Traducido por Mullins, Margaret F. Pergamon.
• Zygmund, Antoni (1968). Series trigonométricas . Vol. 1 y 2 (2.ª edición reimpresa). Cambridge University Press. MR  0236587.

• Teorema de Denjoy-Luzin