Ley de los cosenos

En trigonometría , la ley de los cosenos (también conocida como fórmula del coseno o regla del coseno ) relaciona las longitudes de los lados de un triángulo con el coseno de uno de sus ángulos . Para un triángulo con lados y ángulos respectivos opuestos y (ver Fig. 1), la ley de los cosenos establece:${\estilo de visualización a,}$ ${\estilo de visualización b,}$${\estilo de visualización c,}$${\estilo de visualización \alfa ,}$ ${\estilo de visualización \beta ,}$${\estilo de visualización \gamma}$

${\displaystyle {\begin{aligned}c^{2}&=a^{2}+b^{2}-2ab\cos \gamma ,\\[3mu]a^{2}&=b^{2 }+c^{2}-2bc\cos \alpha ,\\[3mu]b^{2}&=a^{2}+c^{2}-2ac\cos \beta .\end{aligned}} }$

La ley de los cosenos generaliza el teorema de Pitágoras , que sólo es válido para triángulos rectángulos : si es un ángulo recto entonces y la ley de los cosenos se reduce a${\estilo de visualización \gamma}$${\displaystyle \cos \gamma =0,}$ ${\displaystyle c^{2}=a^{2}+b^{2}.}$

La ley de los cosenos es útil para resolver un triángulo cuando se dan los tres lados o dos lados y su ángulo incluido.

El teorema se utiliza en la solución de triángulos , es decir, para encontrar (ver Figura 3):

• el tercer lado de un triangulo si se conocen dos lados y el ángulo entre ellos:$${\displaystyle c={\sqrt {a^{2}+b^{2}-2ab\cos \gamma }}\,;}$$
• los ángulos de un triangulo si se conocen los tres lados:$${\displaystyle \gamma =\arccos \left({\frac {a^{2}+b^{2}-c^{2}}{2ab}}\right)\,;}$$
• el tercer lado de un triángulo si se conocen dos lados y un ángulo opuesto a uno de ellos (este lado también se puede encontrar mediante dos aplicaciones de la ley de los senos ): ^[a] $${\displaystyle a=b\cos\gamma\pm {\sqrt {c^{2}-b^{2}\sin ^{2}\gamma }}\,.}$$

Estas fórmulas producen altos errores de redondeo en los cálculos de punto flotante si el triángulo es muy agudo, es decir, si c es pequeño en relación con a y b o γ es pequeño en comparación con 1. Incluso es posible obtener un resultado ligeramente mayor que uno para el coseno de un ángulo.

La tercera fórmula que se muestra es el resultado de resolver a en la ecuación cuadrática a ² − 2 ab cos γ + b ² − c ² = 0 . Esta ecuación puede tener 2, 1 o 0 soluciones positivas correspondientes al número de triángulos posibles dados los datos. Tendrá dos soluciones positivas si b sin γ < c < b , solo una solución positiva si c = b sin γ y ninguna solución si c < b sin γ . Estos diferentes casos también se explican por la ambigüedad de congruencia lado-lado-ángulo .

El Libro II de los Elementos de Euclides , compilado alrededor del 300 a. C. a partir de material hasta un siglo o dos más antiguo, contiene un teorema geométrico correspondiente a la ley de los cosenos pero expresado en el lenguaje contemporáneo de áreas rectangulares; la trigonometría helenística se desarrolló más tarde, y el seno y el coseno per se aparecieron por primera vez siglos después en la India.

Los casos de triángulos obtusos y triángulos agudos (correspondientes a los dos casos de coseno negativo o positivo) se tratan por separado, en las Proposiciones II.12 y II.13: ^[1]

Proposición 12.
En los triángulos obtusángulos, el cuadrado del lado que subtiende el ángulo obtuso es mayor que los cuadrados de los lados que contienen el ángulo obtuso en el doble del rectángulo contenido por uno de los lados que rodean al ángulo obtuso, es decir, aquel sobre el cual cae la perpendicular, y la recta cortada por fuera por la perpendicular hacia el ángulo obtuso.

—  Elementos de Euclides , traducción de Thomas L. Heath . ^[1]

La proposición 13 contiene una afirmación análoga para los triángulos agudos. En su comentario (hoy perdido y preservado sólo a través de citas fragmentarias), Herón de Alejandría proporcionó pruebas de las inversas de II.12 y II.13. ^[2]

Usando una notación como la de la Figura 2, la declaración de Euclides de la proposición II.12 se puede representar de manera más concisa (aunque anacrónica) mediante la fórmula

${\displaystyle AB^{2}=CA^{2}+CB^{2}+2(CA)(CH).}$

Para transformar esto en la expresión familiar para la ley de los cosenos, sustituya y${\estilo de visualización AB=c,}$ ${\displaystyle CA=b,}$ ${\displaystyle CB=a,}$${\displaystyle CH=a\cos(\pi -\gamma )\ }$${\displaystyle =-a\cos \gamma .}$

La Proposición II.13 no fue utilizada en la época de Euclides para la solución de triángulos , pero más tarde fue utilizada de esa manera en el curso de la resolución de problemas astronómicos por al-Bīrūnī (siglo XI) y Johannes de Muris (siglo XIV). ^[3] Algo equivalente a la ley esférica de los cosenos fue utilizado (pero no establecido en general) por al-Khwārizmī (siglo IX), al-Battānī (siglo IX) y Nīlakaṇṭha (siglo XV). ^[4]

El matemático persa del siglo XIII Naṣīr al-Dīn al-Ṭūsī , en su Kitāb al-Shakl al-qattāʴ ( Libro sobre el cuadrilátero completo , c. 1250), dio un método para hallar el tercer lado de un triángulo escaleno general dados dos lados y el ángulo incluido, trazando una perpendicular desde el vértice de uno de los ángulos desconocidos hasta la base opuesta, reduciendo el problema a la solución de un triángulo rectángulo mediante el teorema de Pitágoras. Si se escribe utilizando la notación matemática moderna, la relación resultante se puede manipular algebraicamente para obtener la ley moderna de los cosenos. ^[5]

Aproximadamente dos siglos después, otro matemático persa, Jamshīd al-Kāshī , que calculó las tablas trigonométricas más precisas de su época, escribió sobre varios métodos para resolver triángulos en su Miftāḥ al-ḥisāb ( Clave de aritmética , 1427), y repitió esencialmente el método de al-Ṭūsī, incluyendo detalles más explícitos, de la siguiente manera: ^[6]

Otro caso es cuando se conocen dos lados y el ángulo que forman y el resto son desconocidos. Multiplicamos uno de los lados por el seno del ángulo [conocido] una vez y por el seno de su complemento la otra vez convertido y restamos el segundo resultado del otro lado si el ángulo es agudo y lo sumamos si el ángulo es obtuso. Luego elevamos al cuadrado el resultado y le sumamos el cuadrado del primer resultado. Tomamos la raíz cuadrada de la suma para obtener el lado restante.

—  Miftāḥ al-ḥisāb de Al-Kāshī ,      traducción de Nuh Aydin, Lakhdar Hammoudi y Ghada Bakbouk ^[7]

Usando la notación y las convenciones algebraicas modernas esto podría escribirse

${\displaystyle c={\sqrt {(ba\cos \gamma )^{2}+(a\sin \gamma )^{2}}}}$

¿Cuándo es agudo o${\estilo de visualización \gamma}$

${\displaystyle c={\sqrt {\left(b+a\left|\cos \gamma \right|\right)^{2}+\left(a\sin \gamma \right)^{2}}}}$

cuando es obtuso. (Cuando es obtuso, la convención moderna es que es negativo y es positivo; históricamente, se consideraba que los senos y cosenos eran segmentos de línea con longitudes no negativas). Al elevar al cuadrado ambos lados, desarrollar el binomio al cuadrado y luego aplicar la identidad trigonométrica pitagórica, obtenemos la conocida ley de los cosenos:${\estilo de visualización \gamma}$${\estilo de visualización \gamma}$${\displaystyle \cos \gamma}$${\displaystyle \cos(\pi -\gamma )=-\cos \gamma }$${\displaystyle \cos ^{2}\gamma +\sin ^{2}\gamma =1,}$

${\displaystyle {\begin{aligned}c^{2}&=b^{2}-2ba\cos \gamma +a^{2}\cos ^{2}\gamma +a^{2}\sin ^{2}\gamma \\[5mu]&=a^{2}+b^{2}-2ab\cos \gamma .\end{aligned}}}$

En Francia , la ley de los cosenos a veces se denomina " teorema de Al-Kashi" . ^{[8] [9]}

El teorema fue escrito por primera vez en notación algebraica por François Viète en el siglo XVI. A principios del siglo XIX, la notación algebraica moderna permitió escribir la ley de los cosenos en su forma simbólica actual. ^[10]

Euclides demostró este teorema aplicando el teorema de Pitágoras a cada uno de los dos triángulos rectángulos de la figura 2 ( AHB y CHB ). Utilizando d para denotar el segmento de línea CH y h para la altura BH , el triángulo AHB nos da

${\displaystyle c^{2}=(b+d)^{2}+h^{2},}$

y el triangulo CHB da

${\displaystyle d^{2}+h^{2}=a^{2}.}$

Desarrollando la primera ecuación obtenemos

${\displaystyle c^{2}=b^{2}+2bd+d^{2}+h^{2}.}$

Sustituyendo la segunda ecuación en esta, se puede obtener lo siguiente:

${\displaystyle c^{2}=a^{2}+b^{2}+2bd.}$

Esta es la Proposición 12 de Euclides del Libro 2 de los Elementos . ^[11] Para transformarla en la forma moderna de la ley de los cosenos, observe que

${\displaystyle d=a\cos(\pi -\gamma )=-a\cos \gamma .}$

La prueba de Euclides de su Proposición 13 sigue la misma línea que su prueba de la Proposición 12: aplica el teorema de Pitágoras a ambos triángulos rectángulos formados al dejar caer la perpendicular sobre uno de los lados que encierra el ángulo γ y utiliza el cuadrado de una diferencia para simplificar.

Utilizando más trigonometría, la ley de los cosenos se puede deducir utilizando el teorema de Pitágoras sólo una vez. De hecho, utilizando el triángulo rectángulo del lado izquierdo de la figura 6 se puede demostrar que:

${\displaystyle {\begin{aligned}c^{2}&=(ba\cos \gamma )^{2}+(a\sin \gamma )^{2}\\&=b^{2}-2ab \cos \gamma +a^{2}\cos ^{2}\gamma +a^{2}\sin ^{2}\gamma \\&=b^{2}+a^{2}-2ab\ porque \gamma ,\end{alineado}}}$

utilizando la identidad trigonométrica ${\displaystyle \cos ^{2}\gamma +\sin ^{2}\gamma =1.}$

Esta prueba necesita una ligera modificación si b < a cos( γ ) . En este caso, el triángulo rectángulo al que se aplica el teorema de Pitágoras se mueve fuera del triángulo ABC . El único efecto que esto tiene en el cálculo es que la cantidad b − a cos( γ ) se reemplaza por a cos( γ ) − b . Como esta cantidad entra en el cálculo solo a través de su cuadrado, el resto de la prueba no se ve afectado. Sin embargo, este problema solo ocurre cuando β es obtuso y se puede evitar reflejando el triángulo sobre la bisectriz de γ .

En referencia a la Figura 6, vale la pena señalar que si el ángulo opuesto al lado a es α entonces:

${\displaystyle \tan \alpha ={\frac {a\sin \gamma }{ba\cos \gamma }}.}$

Esto es útil para el cálculo directo de un segundo ángulo cuando se dan dos lados y un ángulo incluido.

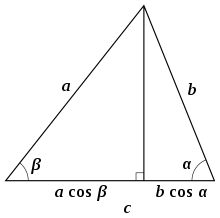
La altura que pasa por el vértice C es un segmento perpendicular al lado c . La distancia desde el pie de la altura hasta el vértice A más la distancia desde el pie de la altura hasta el vértice B es igual a la longitud del lado c (véase la figura 5). Cada una de estas distancias se puede escribir como uno de los otros lados multiplicado por el coseno del ángulo adyacente, ^[12]

${\displaystyle c=a\cos \beta +b\cos \alpha .}$

(Esto sigue siendo cierto si α o β son obtusos, en cuyo caso la perpendicular cae fuera del triángulo). Multiplicar ambos lados por c da como resultado

${\displaystyle c^{2}=ac\cos \beta +bc\cos \alpha .}$

Los mismos pasos funcionan igual de bien cuando se trata cualquiera de los otros lados como base del triángulo:

${\displaystyle {\begin{aligned}a^{2}&=ac\cos \beta +ab\cos \gamma ,\\[3mu]b^{2}&=bc\cos \alpha +ab\cos \gamma .\end{aligned}}}$

Tomando la ecuación para y restando las ecuaciones para y$Estilo de visualización c^{2}}$$Estilo de visualización b^{2}}$${\estilo de visualización a^{2},}$

${\displaystyle {\begin{aligned}c^{2}-a^{2}-b^{2}&={\color {AzulVerde}{\cancel {\color {Negro}ac\cos \beta }}}+{\color {Melocotón}{\cancel {\color {Negro}bc\cos \alpha }}}-{\color {AzulVerde}{\cancel {\color {Negro}ac\cos \beta }}}-{\color {Melocotón}{\cancel {\color {Negro}bc\cos \alpha }}}-2ab\cos \gamma \\c^{2}&=a^{2}+b^{2}-2ab\cos \gamma .\end{aligned}}}$

Esta prueba es independiente del teorema de Pitágoras , en la medida en que se basa únicamente en la definición de coseno en un triángulo rectángulo y obtiene las longitudes de los lados algebraicamente al cuadrado. Otras pruebas suelen invocar el teorema de Pitágoras de forma explícita y son más geométricas, ya que tratan un  cos γ como una etiqueta para la longitud de un determinado segmento de línea. ^[12]

A diferencia de muchas pruebas, ésta maneja los casos de ángulos obtusos y agudos γ de manera unificada.

Consideremos un triángulo cuyos lados miden a , b , c , donde θ es la medida del ángulo opuesto al lado de longitud c . Este triángulo se puede colocar en el sistema de coordenadas cartesianas con el lado a alineado a lo largo del eje x y el ángulo θ colocado en el origen, trazando los componentes de los 3 puntos del triángulo como se muestra en la figura 4:

${\displaystyle A=(b\cos \theta ,b\sin \theta ),B=(a,0),{\text{ y }}C=(0,0).}$

Por la fórmula de la distancia , ^[13]

${\displaystyle c={\sqrt {(a-b\cos \theta )^{2}+(0-b\sin \theta )^{2}}}.}$

Elevando al cuadrado ambos lados y simplificando

${\displaystyle {\begin{aligned}c^{2}&=(a-b\cos \theta )^{2}+(-b\sin \theta )^{2}\\&=a^{2}-2ab\cos \theta +b^{2}\cos ^{2}\theta +b^{2}\sin ^{2}\theta \\&=a^{2}+b^{2}(\sin ^{2}\theta +\cos ^{2}\theta )-2ab\cos \theta \\&=a^{2}+b^{2}-2ab\cos \theta .\end{aligned}}}$

Una ventaja de esta demostración es que no requiere la consideración de casos separados dependiendo de si el ángulo γ es agudo, recto u obtuso. Sin embargo, los casos tratados por separado en Elementos II.12-13 y posteriormente por al-Ṭūsī, al-Kāshī y otros podrían combinarse mediante el uso de conceptos de longitudes y áreas con signo y un concepto de coseno con signo, sin necesidad de un sistema de coordenadas cartesianas completo.

En referencia al diagrama, el triángulo ABC con lados AB = c , BC = a y AC = b se dibuja dentro de su circunferencia circunscrita como se muestra. El triángulo ABD se construye congruente con el triángulo ABC con AD = BC y BD = AC . Las perpendiculares desde D y C se encuentran con la base AB en E y F respectivamente. Entonces:

${\displaystyle {\begin{aligned}&BF=AE=BC\cos {\hat {B}}=a\cos {\hat {B}}\\\Rightarrow \ &DC=EF=AB-2BF=c-2a\cos {\hat {B}}.\end{aligned}}}$

Ahora la ley de los cosenos se obtiene mediante una aplicación directa del teorema de Ptolomeo al cuadrilátero cíclico ABCD :

${\displaystyle {\begin{aligned}&AD\times BC+AB\times DC=AC\times BD\\\Rightarrow \ &a^{2}+c(c-2a\cos {\hat {B}})=b^{2}\\\Rightarrow \ &a^{2}+c^{2}-2ac\cos {\hat {B}}=b^{2}.\end{aligned}}}$

Es claro que si el ángulo B es recto , entonces ABCD es un rectángulo y la aplicación del teorema de Ptolomeo da como resultado el teorema de Pitágoras :

${\displaystyle a^{2}+c^{2}=b^{2}.\quad }$

También se puede demostrar la ley de los cosenos calculando áreas . El cambio de signo cuando el ángulo γ se vuelve obtuso hace necesaria una distinción entre casos.

Recuerde que

• a ² , b ² y c ² son las áreas de los cuadrados con lados a , b y c , respectivamente;
• Si γ es agudo, entonces ab cos γ es el área del paralelogramo cuyos lados a y b forman un ángulo de γ′ = ⁠π/2⁠ − γ ;
• Si γ es obtuso, y por lo tanto cos γ es negativo, entonces − ab cos γ es el área del paralelogramo cuyos lados a y b forman un ángulo de γ′ = γ −π/2⁠ .

Caso agudo. La figura 7a muestra un heptágono cortado en trozos más pequeños (de dos maneras diferentes) para obtener una prueba de la ley de los cosenos. Los distintos trozos son

• en rosa, las áreas a ² , b ² a la izquierda y las áreas 2 ab cos γ y c ² a la derecha;
• en azul, el triángulo ABC , a la izquierda y a la derecha;
• en gris, triángulos auxiliares, todos congruentes con ABC , un número igual (es decir, 2) tanto a la izquierda como a la derecha.

La igualdad de áreas a la izquierda y a la derecha da

${\displaystyle \,a^{2}+b^{2}=c^{2}+2ab\cos \gamma \,.}$

Caso obtuso. La figura 7b corta un hexágono de dos maneras diferentes en trozos más pequeños, lo que da una prueba de la ley de los cosenos en el caso de que el ángulo γ sea obtuso. Tenemos

• en rosa, las áreas a ² , b ² y −2 ab cos γ a la izquierda y c ² a la derecha;
• En azul, el triángulo ABC dos veces, a la izquierda, así como a la derecha.

La igualdad de áreas a la izquierda y a la derecha da

${\displaystyle \,a^{2}+b^{2}-2ab\cos(\gamma )=c^{2}.}$

La prueba rigurosa deberá incluir pruebas de que varias formas son congruentes y, por lo tanto, tienen áreas iguales. Para ello se utilizará la teoría de triángulos congruentes .

Utilizando la geometría del círculo , es posible dar una demostración más geométrica que utilizando únicamente el teorema de Pitágoras . Se evitan las manipulaciones algebraicas (en particular, el teorema del binomio ).

Caso de ángulo agudo γ , donde a > 2 b cos γ . Traza la perpendicular desde A sobre a = BC , creando un segmento de línea de longitud b cos γ . Duplica el triángulo rectángulo para formar el triángulo isósceles ACP . Construye el círculo con centro A y radio b , y su tangente h = BH a través de B . La tangente h forma un ángulo recto con el radio b ( Elementos de Euclides : Libro 3, Proposición 18; o ver aquí ), por lo que el triángulo amarillo en la Figura 8 es recto. Aplica el teorema de Pitágoras para obtener

${\displaystyle c^{2}=b^{2}+h^{2}.}$

Luego, utilice el teorema de la secante tangente ( Elementos de Euclides : Libro 3, Proposición 36), que dice que el cuadrado de la tangente que pasa por un punto B fuera del círculo es igual al producto de los dos segmentos de línea (desde B ) creados por cualquier secante del círculo que pasa por B. En el presente caso: BH ² = BC · BP , o

${\displaystyle h^{2}=a(a-2b\cos \gamma ).}$

Sustituyendo en la ecuación anterior se obtiene la ley de los cosenos:

${\displaystyle c^{2}=b^{2}+a(a-2b\cos \gamma ).}$

Nótese que h ² es la potencia del punto B con respecto al círculo. El uso del teorema de Pitágoras y del teorema de la tangente secante se puede reemplazar por una única aplicación del teorema de la potencia de un punto .

Caso de ángulo agudo γ , donde a < 2 b cos γ . Traza la perpendicular desde A sobre a = BC , creando un segmento de línea de longitud b cos γ . Duplica el triángulo rectángulo para formar el triángulo isósceles ACP . Construye el círculo con centro A y radio b , y una cuerda a través de B perpendicular a c = AB , la mitad de la cual es h = BH . Aplica el teorema de Pitágoras para obtener

${\displaystyle b^{2}=c^{2}+h^{2}.}$

Ahora utilicemos el teorema de las cuerdas ( Elementos de Euclides : Libro 3, Proposición 35), que dice que si dos cuerdas se intersecan, el producto de los dos segmentos de línea obtenidos en una cuerda es igual al producto de los dos segmentos de línea obtenidos en la otra cuerda. En el presente caso: BH ² = BC · BP , o

${\displaystyle h^{2}=a(2b\cos \gamma -a).}$

Sustituyendo en la ecuación anterior se obtiene la ley de los cosenos:

${\displaystyle b^{2}=c^{2}+a(2b\cos \gamma -a)\,.}$

Nótese que la potencia del punto B con respecto al círculo tiene el valor negativo − h ² .

Caso del ángulo obtuso γ . Esta demostración utiliza el teorema de la potencia de un punto directamente, sin los triángulos auxiliares obtenidos mediante la construcción de una tangente o una cuerda. Construya un círculo con centro B y radio a (ver Figura 9), que interseca la secante a través de A y C en C y K . La potencia del punto A con respecto al círculo es igual tanto a AB ² − BC ² como a AC · AK . Por lo tanto,

${\displaystyle {\begin{aligned}c^{2}-a^{2}&{}=b(b+2a\cos(\pi -\gamma ))\\&{}=b(b-2a\cos \gamma ),\end{aligned}}}$

que es la ley de los cosenos.

Utilizando medidas algebraicas para segmentos de línea (permitiendo números negativos como longitudes de segmentos) el caso del ángulo obtuso ( CK > 0 ) y del ángulo agudo ( CK < 0 ) se pueden tratar simultáneamente.

La ley de los cosenos se puede demostrar algebraicamente a partir de la ley de los senos y algunas identidades trigonométricas estándar. ^[14] Para empezar, tres ángulos de un triángulo suman un ángulo recto ( radianes). Por lo tanto, por las identidades de suma de ángulos para el seno y el coseno,${\displaystyle \alpha +\beta +\gamma =\pi }$

${\displaystyle {\begin{alignedat}{3}\sin \gamma &={\phantom {-}}\sin(\pi -\gamma )&&={\phantom {-}}\sin(\alpha +\beta )&&=\sin \alpha \,\cos \beta +\cos \alpha \,\sin \beta ,\\[5mu]\cos \gamma &=-\cos(\pi -\gamma )&&=-\cos(\alpha +\beta )&&=\sin \alpha \,\sin \beta -\cos \alpha \,\cos \beta .\end{alignedat}}}$

Elevando al cuadrado la primera de estas identidades, luego sustituyendo a partir de la segunda y finalmente reemplazando la identidad trigonométrica pitagórica , tenemos:${\displaystyle \cos \alpha \,\cos \beta ={}}$${\displaystyle \sin \alpha \,\sin \beta -\cos \gamma }$${\displaystyle \cos ^{2}\alpha +\sin ^{2}\alpha ={}}$${\displaystyle \cos ^{2}\beta +\sin ^{2}\beta =1,}$

${\displaystyle {\begin{aligned}\sin ^{2}\gamma &=(\sin \alpha \,\cos \beta +\cos \alpha \,\sin \beta )^{2}\\[3mu]&=\sin ^{2}\alpha \,\cos ^{2}\beta +2\sin \alpha \,\sin \beta \,\cos \alpha \,\cos \beta +\cos ^{2}\alpha \,\sin ^{2}\beta \\[3mu]&=\sin ^{2}\alpha \,\cos ^{2}\beta +2\sin \alpha \,\sin \beta (\sin \alpha \,\sin \beta -\cos \gamma )+\cos ^{2}\alpha \,\sin ^{2}\beta \\[3mu]&=\sin ^{2}\alpha (\cos ^{2}\beta +\sin ^{2}\beta )+\sin ^{2}\beta (\cos ^{2}\alpha +\sin ^{2}\alpha )-2\sin \alpha \,\sin \beta \,\cos \gamma \\[3mu]&=\sin ^{2}\alpha +\sin ^{2}\beta -2\sin \alpha \,\sin \beta \,\cos \gamma .\end{aligned}}}$

La ley de los senos sostiene que

${\displaystyle {\frac {a}{\sin \alpha {\vphantom {\beta }}}}={\frac {b}{\sin \beta }}={\frac {c}{\sin \gamma {\vphantom {\beta }}}}=k,}$

Entonces, para demostrar la ley de los cosenos, multiplicamos ambos lados de nuestra identidad anterior por${\displaystyle k^{2}\colon }$

${\displaystyle {\begin{aligned}\sin ^{2}\gamma {\frac {c^{2}}{\sin ^{2}\gamma }}&=\sin ^{2}\alpha {\frac {a^{2}}{\sin ^{2}\alpha }}+\sin ^{2}\beta {\frac {b^{2}}{\sin ^{2}\beta }}-2\sin \alpha \,\sin \beta \,\cos \gamma {\frac {ab}{\sin \alpha \,\sin \beta {\vphantom {\sin ^{2}}}}}\\[10mu]c^{2}&=a^{2}+b^{2}-2ab\cos \gamma .\end{aligned}}}$

Con esto concluye la prueba.

Denotar

${\displaystyle {\overrightarrow {CB}}={\vec {a}},\ {\overrightarrow {CA}}={\vec {b}},\ {\overrightarrow {AB}}={\vec {c}}}$

Por lo tanto,

${\displaystyle {\vec {c}}={\vec {a}}-{\vec {b}}}$

Tomando el producto escalar de cada lado consigo mismo:

${\displaystyle {\vec {c}}\cdot {\vec {c}}=({\vec {a}}-{\vec {b}})\cdot ({\vec {a}}-{\vec {b}})}$

${\displaystyle \Vert {\vec {c}}\Vert ^{2}=\Vert {\vec {a}}\Vert ^{2}+\Vert {\vec {b}}\Vert ^{2}-2\,{\vec {a}}\cdot {\vec {b}}}$

Usando la identidad

${\displaystyle {\vec {u}}\cdot {\vec {v}}=\Vert {\vec {u}}\Vert \,\Vert {\vec {v}}\Vert \cos \angle ({\vec {u}},\ {\vec {v}})}$

conduce a

${\displaystyle \Vert {\vec {c}}\Vert ^{2}=\Vert {\vec {a}}\Vert ^{2}+{\Vert {\vec {b}}\Vert }^{2}-2\,\Vert {\vec {a}}\Vert \!\;\Vert {\vec {b}}\Vert \cos \angle ({\vec {a}},\ {\vec {b}})}$

El resultado es el siguiente:

Cuando a = b , es decir, cuando el triángulo es isósceles con los dos lados incidentes al ángulo γ iguales, la ley de los cosenos se simplifica significativamente. Es decir, como a ² + b ² = 2 a ² = 2 ab , la ley de los cosenos se convierte en

${\displaystyle \cos \gamma =1-{\frac {c^{2}}{2a^{2}}}}$

o

${\displaystyle c^{2}=2a^{2}(1-\cos \gamma ).}$

Dado un tetraedro arbitrario cuyas cuatro caras tienen áreas A , B , C y D , con un ángulo diedro entre las caras A y B , etc., un análogo de dimensión superior de la ley de los cosenos es: ^[15]${\displaystyle \varphi _{ab}}$

${\displaystyle A^{2}=B^{2}+C^{2}+D^{2}-2\left(BC\cos \varphi _{bc}+CD\cos \varphi _{cd}+DB\cos \varphi _{db}\right).}$

Cuando el ángulo γ es pequeño y los lados adyacentes a y b tienen una longitud similar, el lado derecho de la forma estándar de la ley de los cosenos está sujeto a una cancelación catastrófica en las aproximaciones numéricas. En situaciones en las que esto es una preocupación importante, una versión matemáticamente equivalente de la ley de los cosenos, similar a la fórmula de Haversine , puede resultar útil:

${\displaystyle {\begin{aligned}c^{2}&=(a-b)^{2}+4ab\sin ^{2}\left({\frac {\gamma }{2}}\right)\\&=(a-b)^{2}+4ab\operatorname {haversin} (\gamma ).\end{aligned}}}$

En el límite de un ángulo infinitesimal, la ley de los cosenos degenera en la fórmula de la longitud del arco circular , c = a γ .

Versiones similares a la ley de los cosenos para el plano euclidiano también se cumplen en una esfera unitaria y en un plano hiperbólico. En geometría esférica , un triángulo se define por tres puntos u , v y w en la esfera unitaria y los arcos de círculos máximos que conectan esos puntos. Si estos círculos máximos forman ángulos A , B y C con lados opuestos a , b , c, entonces la ley esférica de los cosenos afirma que se cumplen las dos relaciones siguientes:

${\displaystyle {\begin{aligned}\cos a&=\cos b\cos c+\sin b\sin c\cos A\\\cos A&=-\cos B\cos C+\sin B\sin C\cos a.\end{aligned}}}$

En geometría hiperbólica , un par de ecuaciones se conocen colectivamente como la ley hiperbólica de los cosenos . La primera es

${\displaystyle \cosh a=\cosh b\cosh c-\sinh b\sinh c\cos A}$

donde sinh y cosh son el seno y el coseno hiperbólicos , y el segundo es

${\displaystyle \cos A=-\cos B\cos C+\sin B\sin C\cosh a.}$

Al igual que en la geometría euclidiana, se puede utilizar la ley de los cosenos para determinar los ángulos A , B , C a partir del conocimiento de los lados a , b , c . A diferencia de la geometría euclidiana, lo inverso también es posible en ambos modelos no euclidianos: los ángulos A , B , C determinan los lados a , b , c .

La Ley de los Cosenos se puede generalizar a todos los poliedros considerando cualquier poliedro con lados vectoriales e invocando el Teorema de Divergencia . ^[16]

• Fórmula de la mitad del lado
• Ley de senos
• Ley de las tangentes
• Ley de cotangentes
• Lista de identidades trigonométricas
• Fórmula de Mollweide

Wikimedia Commons tiene medios relacionados con Ley de los cosenos .

• "Teorema del coseno", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• Varias derivaciones de la Ley del Coseno, incluida la de Euclides en el momento del corte del nudo
• Aplicación interactiva de la Ley de los cosenos