Grupo de puntos

Grupo de simetrías geométricas con al menos un punto fijo

La flor Bauhinia blakeana en la bandera de la región de Hong Kong tiene simetría C ₅ ; la estrella en cada pétalo tiene simetría D ₅ .	El símbolo del Yin y el Yang tiene simetría geométrica C _{2 con colores invertidos.}

En geometría , un grupo de puntos es un grupo matemático de operaciones de simetría ( isometrías en un espacio euclidiano ) que tienen un punto fijo en común. El origen de coordenadas del espacio euclidiano se toma convencionalmente como un punto fijo, y cada grupo de puntos en dimensión d es entonces un subgrupo del grupo ortogonal O( d ). Los grupos de puntos se utilizan para describir las simetrías de figuras geométricas y objetos físicos como las moléculas .

Cada grupo de puntos puede representarse como un conjunto de matrices ortogonales M que transforman el punto x en el punto y según y = Mx . Cada elemento de un grupo de puntos es una rotación ( determinante de M = 1 ), o bien es una reflexión o rotación impropia (determinante de M = −1 ).

Las simetrías geométricas de los cristales se describen mediante grupos espaciales , que permiten traslaciones y contienen grupos puntuales como subgrupos. Los grupos puntuales discretos en más de una dimensión se presentan en familias infinitas, pero a partir del teorema de restricción cristalográfico y de uno de los teoremas de Bieberbach , cada número de dimensiones tiene solo un número finito de grupos puntuales que son simétricos sobre alguna red o rejilla con ese número de dimensiones. Estos son los grupos puntuales cristalográficos .

Grupos puntuales quirales y aquirales, grupos de reflexión

Los grupos puntuales se pueden clasificar en grupos quirales (o puramente rotacionales) y grupos aquirales . ^[1] Los grupos quirales son subgrupos del grupo ortogonal especial SO( d ): contienen solo transformaciones ortogonales que preservan la orientación, es decir, aquellas de determinante +1. Los grupos aquirales contienen también transformaciones de determinante −1. En un grupo aquiral, las transformaciones que preservan la orientación forman un subgrupo (quiral) de índice 2.

Los grupos de Coxeter finitos o grupos de reflexión son aquellos grupos puntuales que se generan puramente mediante un conjunto de espejos de reflexión que pasan por el mismo punto. Un grupo de Coxeter de rango n tiene n espejos y se representa mediante un diagrama de Coxeter-Dynkin . La notación de Coxeter ofrece una notación entre corchetes equivalente al diagrama de Coxeter, con símbolos de marcado para grupos puntuales de subsimetría rotacional y de otro tipo. Los grupos de reflexión son necesariamente aquirales (excepto el grupo trivial que contiene solo el elemento identidad).

Lista de grupos de puntos

Una dimensión

Sólo hay dos grupos de puntos unidimensionales: el grupo identidad y el grupo de reflexión.

Grupo	Coxeter	Diagrama de Coxeter	Orden	Descripción
C ₁	[ ] ⁺		1	identidad
D1	[ ]		2	grupo de reflexión

Dos dimensiones

Grupos de puntos en dos dimensiones , a veces llamados grupos roseta .

Vienen en dos familias infinitas:

Grupos cíclicos C _n de grupos de rotación de n pliegues
Grupos diedros D _n de rotación n -fold y grupos de reflexión

La aplicación del teorema de restricción cristalográfica restringe n a los valores 1, 2, 3, 4 y 6 para ambas familias, lo que produce 10 grupos.

Grupo	Internacional	Plegado orbi	Coxeter	Orden	Descripción
C _n	norte	en •	[ n ] ⁺	norte	cíclico: rotaciones de n pliegues; grupo abstracto Z _n , el grupo de números enteros bajo adición módulo n
Dn	nuevo	* y •	[ n ]	2 n	diedro: cíclico con reflexiones; grupo abstracto Dih _n , el grupo diedro

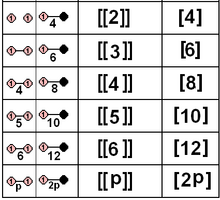
El subconjunto de grupos puntuales de reflexión pura, definido por 1 o 2 espejos, también puede estar dado por su grupo de Coxeter y polígonos relacionados. Estos incluyen 5 grupos cristalográficos. La simetría de los grupos de reflexión se puede duplicar mediante un isomorfismo , mapeando ambos espejos entre sí mediante un espejo bisectriz, duplicando el orden de simetría.

Pensativo						Rotacional			Polígonos relacionados
Grupo	Grupo Coxeter		Diagrama de Coxeter		Orden	Subgrupo	Coxeter	Orden	Polígonos relacionados
D1	Un ₁	[ ]			2	C ₁	[] ⁺	1	Digón
D2	Un ₁²	[2]			4	C ₂	[2] ⁺	2	rectángulo
D3	Un ₂	[3]			6	C ₃	[3] ⁺	3	triángulo equilátero
D4	₂ antes de Cristo	[4]			8	C ₄	[4] ⁺	4	cuadrado
D5	H2	[5]			10	C ₅	[5] ⁺	5	pentágono regular
D6	G2	[6]			12	C ₆	[6] ⁺	6	hexágono regular
Dn	Yo ₂ ( n )	[ n ]			2 n	C _n	[ n ] ⁺	norte	polígono regular
D2 × ₂	Un ₁² × 2	[[2]] = [4]		=	8
D3 _× 2	Un ₂ ×2	[[3]] = [6]		=	12
D4 _× 2	B.C. ₂ × 2	[[4]] = [8]		=	16
D5 _× 2	Alto ₂ × 2	[[5]] = [10]		=	20
D6 _× 2	sol ₂ × 2	[[6]] = [12]		=	24
D _n × 2	yo ₂ ( n )×2	[[ n ]] = [2 n ]		=	4 n

Tres dimensiones

Grupos puntuales en tres dimensiones , a veces llamados grupos puntuales moleculares debido a su amplio uso en el estudio de las simetrías de las moléculas .

Se presentan en 7 familias infinitas de grupos axiales (también llamados prismáticos) y 7 grupos poliédricos adicionales (también llamados platónicos). En la notación de Schönflies ,

Grupos axiales: C _n , S _{2 n} , C _{n h} , C _{n v} , D _n , D _{n d} , D _{n h}
Grupos poliédricos : T, T _d , T _h , O, Oh _h , I, I _h

Aplicando el teorema de restricción cristalográfica a estos grupos se obtienen los 32 grupos puntuales cristalográficos .

Dominios fundamentales de los grupos reflexivos de colores pares e impares
C _1v Orden 2	C _2v Orden 4	C _3v Orden 6	C _4v Orden 8	C _5v Orden 10	C _6v Orden 12	...

D _1h Orden 4	D _2h Orden 8	D _3h Orden 12	D _4h Orden 16	D _5h Orden 20	D _6h Orden 24	...

Orden T _d 24	Oh _Orden 48	Yo _ordeno 120

Internacional ^*	Geo ^[2]	Plegado orbi	Moscas de Schön	Coxeter	Orden
1	1	1	C ₁	[ ] ⁺	1
1	22	×1	C _i = S ₂	[2 ⁺ ,2 ⁺ ]	2
2 = m	1	*1	Cs = _C1v = _C1h	[ ]	2
2 3 4 5 6 n	2 3 4 5 6 n	22 33 44 55 66 n	C2C3C4C5C6Cn	[2] ⁺ [3] ⁺ [4] ⁺ [5] ⁺ [6] ⁺ [n] ⁺	2 3 4 5 6 n
mm2 3 m 4 mm 5 m 6 mm n mm n m	2 3 4 5 6 n	22 33 44 55 66 nn	C2v _C3v_C4v C5v _C6v Cnv	[2] [3] [4] [5] [6] [ n ]	4 6 8 10 12 2 n
2 / m6 4 / m10 6 / m2n	2 2 3 2 4 2 5 2 6 2 n 2	2* 3* 4* 5* 6* n *	C2hC3hC4hC5hC6hCnh	[2,2 ⁺ ] [2,3 ⁺ ] [2,4 ⁺ ] [2,5 ⁺ ] [2,6 ⁺ ] [2,n ⁺ ]	4 6 8 10 12 2 n
4 3 8 5 12 2 n n	4 2 6 2 8 2 10 2 12 2 2 n 2	2× 3× 4× 5× 6× n ×	S ₄ S ₆ S ₈ S ₁₀ S ₁₂ S _{2 n}	[2 ⁺ ,4 ⁺ ] [2 ⁺ ,6 ⁺ ] [2 ⁺ ,8 ⁺ ] [ 2 ⁺ ,10 ⁺ ] [2 ⁺ ,12 ⁺ ] [2 ⁺ ,2 n ⁺ ]	4 6 8 10 12 2 n

Internacional	Geo	Plegado orbi	Moscas de Schön	Coxeter	Orden
222 32 422 52 622 22 2	2 2 3 2 4 2 5 2 6 2 n 2	222 223 224 225 226 22 n	D2D3D4D5D6Dn	[2,2] ⁺ [2,3] ⁺ [2,4] ⁺ [2,5] ⁺ [2,6] ⁺ [2, n ] ⁺	4 6 8 10 12 2 n
mmm 6 m2 4/mmm 10 m2 6/mmm n /mmm 2 n m2	2 2 3 2 4 2 5 2 6 2 n 2	222 223 224 225 226 22 n	D _2h D _3h D _4h D _5h D _6h D _{n h}	[2,2] [2,3] [2,4] [2,5] [2,6] [2, n ]	8 12 16 20 24 4 n
4,2 m 3,8 m 8,2 m 5,1 m 12,2 m 2 , n 2 , m n m	4 2 6 2 8 2 10 2 12 2 n 2	22 23 24 25 26 2 n	D _2d D _3d D _4d D _5d D _6d D _{n d}	[2 ⁺ ,4] [2 ⁺ ,6] [2 ⁺ ,8] [2 ⁺ ,10] [2 ⁺ ,12] [2 ⁺ ,2 n ]	8 12 16 20 24 4 n
23	3 3	332	yo	[3,3] ⁺	12
metros 3	4 3	3*2	El	[3 ⁺ ,4]	24
4 3 m	3 3	*332	T.D.	[3,3]	24
432	4 3	432	Oh	[3,4] ⁺	24
metros cúbicos	4 3	*432	Oh	[3,4]	48
532	5 3	532	I	[3,5] ⁺	60
5 3 m	5 3	*532	Yo _soy	[3,5]	120

(*) Cuando las entradas Intl están duplicadas, la primera es para n par, la segunda para n impar .

Grupos de reflexión

Los grupos de puntos de reflexión, definidos por 1 a 3 planos de simetría, también pueden estar dados por su grupo de Coxeter y poliedros relacionados. El grupo [3,3] puede duplicarse, escribiéndose como [[3,3]], mapeando el primer y el último espejo entre sí, duplicando la simetría a 48 y siendo isomorfo al grupo [4,3].

Moscas de Schön	Grupo Coxeter			Orden	Poliedros regulares y prismáticos relacionados
T.D.	Un ₃	[3,3]		24	tetraedro
T _d × Dih ₁ = _Oh	A ₃ × 2 = BC ₃	[[3,3]] = [4,3]	=	48	octaedro estrellado
Oh	₃ antes de Cristo	[4,3]		48	cubo , octaedro
Yo _soy	H3	[5,3]		120	icosaedro , dodecaedro
D 3 _horas	Un ₂ × Un ₁	[3,2]		12	prisma triangular
D3h × _Dih1 = _D6h	Un ₂ × Un ₁ × 2	[[3],2]	=	24	prisma hexagonal
D _{4 horas}	BC2 × _A1	[4,2]		16	prisma cuadrado
D _{4 h} × Di h ₁ = D _{8 h}	antes de Cristo ₂ × A ₁ × 2	[[4],2] = [8,2]	=	32	prisma octogonal
D _{5 horas}	H2 × _A1	[5,2]		20	prisma pentagonal
D _{6 horas}	sol ₂ × la ₁	[6,2]		24	prisma hexagonal
D _{y H}	Yo ₂ ( n )×A ₁	[ n ,2]		4 n	prisma n -gonal
D _{n h} × Dih ₁ = D _{2 n h}	yo ₂ ( n )×A ₁ ×2	[[ n ],2]	=	8 n
D 2 _horas	Un ₁³	[2,2]		8	cuboides
D2h × _Dih1	Un ₁³ × 2	[[2],2] = [4,2]	=	16
D _2h × Dih ₃ = _Oh	Un ₁³ × 6	[3[2,2]] = [4,3]	=	48
C _3v	Un ₂	[1,3]		6	hosoedro
C _4v	₂ antes de Cristo	[1,4]		8
C _5v	H2	[1,5]		10
C _6v	G2	[1,6]		12
C- _nv	Yo ₂ ( n )	[1, n ]		2 n
C _{n v} × Dih ₁ = C _{2 n v}	yo ₂ ( n )×2	[1,[ n ]] = [1,2 n ]	=	4 n
C _2v	Un ₁²	[1,2]		4
C _2v × Dih ₁	Un ₁² × 2	[1,[2]]	=	8
C _s	Un ₁	[1,1]		2

Cuatro dimensiones

Los grupos puntuales de cuatro dimensiones (tanto quirales como aquirales) se enumeran en Conway y Smith, ^[1] Sección 4, Tablas 4.1–4.3.

La siguiente lista proporciona los grupos de reflexión de cuatro dimensiones (excluyendo aquellos que dejan un subespacio fijo y que, por lo tanto, son grupos de reflexión de dimensión inferior). Cada grupo se especifica como un grupo de Coxeter y, al igual que los grupos poliédricos de 3D, se puede nombrar por su 4-politopo regular convexo relacionado . Existen grupos rotacionales puros relacionados para cada uno con la mitad del orden, y se pueden representar mediante la notación de Coxeter entre corchetes con un exponente '+', por ejemplo, [3,3,3] ⁺ tiene tres puntos de giro triples y un orden de simetría de 60. Los grupos simétricos frontales-posteriores como [3,3,3] y [3,4,3] se pueden duplicar, se muestran como corchetes dobles en la notación de Coxeter, por ejemplo, [[3,3,3]] con su orden duplicado a 240.

Grupo de Coxeter / notación			Orden	Politopos relacionados
Un ₄	[3,3,3]		120	5 celdas
Un ₄ ×2	[[3,3,3]]		240	Compuesto dual de 5 celdas
₄ antes de Cristo	[4,3,3]		384	16 celdas / teseracto
D4	[3 ^1,1,1 ]		192	demitesseractic
D ₄ × 2 = BC ₄	<[3,3 ^1,1 ]> = [4,3,3]	=	384
D4 _× 6 = _F4	[3[3 ^1,1,1 ]] = [3,4,3]	=	1152
F4	[3,4,3]		1152	24 celdas
F4 _× 2	[[3,4,3]]		2304	Compuesto dual de 24 celdas
H4	[5,3,3]		14400	120 celdas / 600 celdas
Un ₃ × Un ₁	[3,3,2]		48	prisma tetraédrico
Un ₃ × Un ₁ × 2	[[3,3],2] = [4,3,2]	=	96	prisma octaédrico
BC3 × _A1	[4,3,2]		96	prisma octaédrico
H3 × _A1	[5,3,2]		240	prisma icosaédrico
Un ₂ ×Un ₂	[3,2,3]		36	duoprisma
Un ₂ × BC ₂	[3,2,4]		48
Un ₂ ×H ₂	[3,2,5]		60
Un ₂ × G ₂	[3,2,6]		72
BC2 × _BC2	[4,2,4]		64
2 ² × ₂	[[4,2,4]]		128
B.C. ₂ × H. ₂	[4,2,5]		80
BC ₂ × G ₂	[4,2,6]		96
Alto ₂ × Alto ₂	[5,2,5]		100
H2 × _G2	[5,2,6]		120
Sol ₂ × Sol ₂	[6,2,6]		144
Yo ₂ ( p )×Yo ₂ ( q )	[ p ,2, q ]		4 piezas
Yo ₂ (2 p )×Yo ₂ ( q )	[[ p ],2, q ] = [2 p ,2, q ]	=	8 piezas
Yo ₂ (2 p )×Yo ₂ (2 q )	[[ p ]],2,[[ q ]] = [2 p ,2,2 q ]	=	16 piezas
yo ₂ ( p ) ² × 2	[[ pág . 2, pág. ]]		8 pág. ²
Yo ₂ (2 págs. ) ² × 2	[[[ p ]],2,[ p ]]] = [[2 p ,2,2 p ]]	=	32 pág. ²
Un ₂ × Un ₁ × Un ₁	[3,2,2]		24
antes de Cristo ₂ × A ₁ × A ₁	[4,2,2]		32
H2 × _A1 × _A1	[5,2,2]		40
G ₂ × A ₁ × A ₁	[6,2,2]		48
yo ₂ ( p )×A ₁ ×A ₁	[ pág . 2,2]		8 p
yo ₂ (2 p )×A ₁ ×A ₁ ×2	[[ p ],2,2] = [2 p ,2,2]	=	16 p
yo ₂ ( p )×A ₁² ×2	[ p ,2,[2]] = [ p ,2,4]	=	16 p
Yo ₂ (2 p )×A ₁² ×4	[[ p ]],2,[[2]] = [2 p ,2,4]	=	32 p
Un ₁ ×Un ₁ ×Un ₁ ×Un ₁	[2,2,2]		16	4- ortotopo
Un ₁² × Un ₁ × Un ₁ × 2	[[2],2,2] = [4,2,2]	=	32
Un ₁² × Un ₁² × 4	[[2]],2,[[2]] = [4,2,4]	=	64
Un ₁³ × Un ₁ × 6	[3[2,2],2] = [4,3,2]	=	96
Un ₁⁴ × 24	[3,3[2,2,2]] = [4,3,3]	=	384

Cinco dimensiones

La siguiente tabla muestra los grupos de reflexión de cinco dimensiones (excluyendo aquellos que son grupos de reflexión de dimensiones inferiores), enumerándolos como grupos de Coxeter . Existen grupos quirales relacionados para cada uno con la mitad del orden, y pueden representarse mediante la notación de Coxeter entre corchetes con un exponente '+', por ejemplo [3,3,3,3] ⁺ tiene cuatro puntos de giro triples y un orden de simetría de 360.

Grupo de Coxeter / notación			Orden	Politopos regulares y prismáticos relacionados
Un ₅	[3,3,3,3]		720	5-símplex
Un ₅ × 2	[[3,3,3,3]]		1440	Compuesto dual 5-simplex
₅ antes de Cristo	[4,3,3,3]		3840	5-cubo , 5-ortoplex
D5	[3 ^2,1,1 ]		1920	5-demicubes
D5 _× 2	<[3,3,3 ^1,1 ]>	=	3840
Un ₄ ×Un ₁	[3,3,3,2]		240	Prisma de 5 celdas
Un ₄ ×Un ₁ ×2	[[3,3,3],2]		480
₄ × A ₁	[4,3,3,2]		768	prisma teseracto
F4 × _A1	[3,4,3,2]		2304	Prisma de 24 celdas
F ₄ × A ₁ × 2	[[3,4,3],2]		4608	Prisma de 24 celdas
Alto ₄ × Alto ₁	[5,3,3,2]		28800	Prisma de 600 o 120 celdas
D4 × _A1	[3 ^1,1,1 ,2]		384	prisma demitesseract
Un ₃ × Un ₂	[3,3,2,3]		144	duoprisma
Un ₃ × Un ₂ × 2	[[3,3],2,3]		288
Un ₃ × BC ₂	[3,3,2,4]		192
Un ₃ × Alto ₂	[3,3,2,5]		240
Un ₃ × G ₂	[3,3,2,6]		288
A ₃ × I ₂ ( p )	[3,3,2,pág.]		48 p
BC3 × _A2	[4,3,2,3]		288
BC3 × _BC2	[4,3,2,4]		384
B.C. ₃ × H. ₂	[4,3,2,5]		480
BC3 × _G2	[4,3,2,6]		576
BC3 × _I2 ( p )	[4,3,2,pág.]		96 p
H3 × _A2	[5,3,2,3]		720
H3 × _BC2	[5,3,2,4]		960
Alto ₃ × Alto ₂	[5,3,2,5]		1200
Alto ₃ × Sol ₂	[5,3,2,6]		1440
H3 × _I2 ( p )	[5,3,2, pág .]		240 p
Un ₃ × Un ₁²	[3,3,2,2]		96
antes de Cristo ₃ × A ₁²	[4,3,2,2]		192
H3 × _A12	[5,3,2,2]		480
Un ₂² × Un ₁	[3,2,3,2]		72	prisma duoprisma
A ₂ × BC ₂ × A ₁	[3,2,4,2]		96
A ₂ × Alto ₂ × A ₁	[3,2,5,2]		120
Un ₂ × Sol ₂ × Un ₁	[3,2,6,2]		144
antes de Cristo ₂² × A ₁	[4,2,4,2]		128
B.C. ₂ × H. ₂ × A. ₁	[4,2,5,2]		160
BC2 × _G2 × _A1	[4,2,6,2]		192
H22 × _A1	[5,2,5,2]		200
H2 × _G2 × _A1	[5,2,6,2]		240
G ₂² × A ₁	[6,2,6,2]		288
Yo ₂ ( p ) × Yo ₂ ( q ) × A ₁	[ p ,2, q ,2]		8 piezas
Un ₂ × Un ₁³	[3,2,2,2]		48
antes de Cristo ₂ × A ₁³	[4,2,2,2]		64
H2 × _A13	[5,2,2,2]		80
G ₂ × A ₁³	[6,2,2,2]		96
yo ₂ ( p )×A ₁³	[ pág . 2,2,2]		16 p
Un ₁⁵	[2,2,2,2]		32	5- ortotopo
Un ₁⁵ ×(2 ! )	[[2],2,2,2]	=	64
Un ₁⁵ ×(2!×2 ! )	[[2]],2,[2],2]	=	128
Un ₁⁵ ×(3 ! )	[3[2,2],2,2]	=	192
Un ₁⁵ ×(3!×2 ! )	[3[2,2],2,[[2]]	=	384
Un ₁⁵ ×(4 ! )	[3,3[2,2,2],2]]	=	768
Un ₁⁵ ×(5 ! )	[3,3,3[2,2,2,2]]	=	3840

Seis dimensiones

La siguiente tabla muestra los grupos de reflexión de seis dimensiones (excluidos aquellos que son grupos de reflexión de dimensiones inferiores), enumerándolos como grupos de Coxeter . Existen grupos rotacionales puros relacionados para cada uno con la mitad del orden, y pueden representarse mediante la notación de Coxeter entre corchetes con un exponente '+', por ejemplo [3,3,3,3,3] ⁺ tiene cinco puntos de giro triples y un orden de simetría de 2520.

Grupo Coxeter		Orden	Politopos regulares y prismáticos relacionados
Un ₆	[3,3,3,3,3]	5040 (7!)	6-símplex
Un ₆ × 2	[[3,3,3,3,3]]	10080 (¡2×7!)	Compuesto dual 6-simplex
₆ antes de Cristo	[4,3,3,3,3]	46080 (2 ⁶ × 6!)	6-cubo , 6-ortoplex
D6	[3,3,3,3 ^1,1 ]	23040 (2 ⁵ × 6!)	6-demicubes
E6	[3,3 ^2,2 ]	51840 (72×6!)	1 ₂₂ , 2 ₂₁
Un ₅ × Un ₁	[3,3,3,3,2]	1440 (2×6!)	Prisma 5-símplex
₅ aC × ₁	[4,3,3,3,2]	7680 (2 ⁶ × 5!)	Prisma de 5 cubos
D5 × _A1	[3,3,3 ^1,1 ,2]	3840 (2 ⁵ × 5!)	Prisma de 5 demicubes
Un ₄ ×I2 ₍ pág . 1 )	[3,3,3,2, pág. ]	240 p	duoprisma
BC ₄ × 1 ₂ ( p )	[4,3,3,2, pág. ]	768 p
F ₄ × I ₂ ( p )	[3,4,3,2, pág. ]	2304 p
H ₄ × I ₂ ( p )	[5,3,3,2, pág. ]	28800 p
D ₄ × I ₂ ( p )	[3,3 ^1,1 ,2, pág ]	384 p
Un ₄ ×Un ₁²	[3,3,3,2,2]	480
antes de Cristo ₄ × A ₁²	[4,3,3,2,2]	1536
F ₄ × A ₁²	[3,4,3,2,2]	4608
Alto ₄ × A ₁²	[5,3,3,2,2]	57600
D4 × _A12	[3,3 ^1,1 ,2,2]	768
Un ₃²	[3,3,2,3,3]	576
Un ₃ × BC ₃	[3,3,2,4,3]	1152
Un ₃ × Alto ₃	[3,3,2,5,3]	2880
antes de Cristo ₃²	[4,3,2,4,3]	2304
₃ × ₃ de BC	[4,3,2,5,3]	5760
H32	[5,3,2,5,3]	14400
A ₃ × I ₂ ( p ) × A ₁	[3,3,2, pág . 2]	96 p	prisma duoprisma
BC3 × _I2 ( _p) × _A1	[4,3,2, pág . 2]	192 p
H3 × _I2₍p ) × _A1	[5,3,2, pág . 2]	480 p
Un ₃ × Un ₁³	[3,3,2,2,2]	192
antes de Cristo ₃ × A ₁³	[4,3,2,2,2]	384
H3 × _A13	[5,3,2,2,2]	960
Yo ₂ ( p ) × Yo ₂ ( q ) × Yo ₂ ( r )	[ p ,2, q ,2, r ]	8 pqr	triaprisma
Yo ₂ ( p ) × Yo ₂ ( q ) × A ₁²	[ p ,2, q ,2,2]	16 piezas
yo ₂ ( p )×A ₁⁴	[ pág . 2,2,2,2]	32 p
Un ₁⁶	[2,2,2,2,2]	64	6- ortotopo

Siete dimensiones

La siguiente tabla muestra los grupos de reflexión de siete dimensiones (excluyendo aquellos que son grupos de reflexión de dimensiones inferiores), enumerándolos como grupos de Coxeter . Existen grupos quirales relacionados para cada uno con la mitad del orden, definidos por un número par de reflexiones, y pueden representarse mediante la notación de Coxeter entre corchetes con un exponente '+', por ejemplo [3,3,3,3,3,3] ⁺ tiene seis puntos de giro triples y un orden de simetría de 20160.

Grupo Coxeter		Orden	Politopos relacionados
Un ₇	[3,3,3,3,3,3]	40320 (8!)	7-símplex
Un ₇ × 2	[[3,3,3,3,3,3]]	80640 (2×8!)	Compuesto dual 7-simplex
₇ antes de Cristo	[4,3,3,3,3,3]	645120 (2 ⁷ × 7!)	7-cubo , 7-ortoplex
D7	[3,3,3,3,3 ^1,1 ]	322560 (2 ⁶ × 7!)	7-demicube
E7	[3,3,3,3 ^2,1 ]	2903040 (¡8×9!)	3 ₂₁ , 2 ₃₁ , 1 ₃₂
Un ₆ × Un ₁	[3,3,3,3,3,2]	10080 (¡2×7!)
₆ aC × ₁	[4,3,3,3,3,2]	92160 (2 ⁷ × 6!)
D6 × _A1	[3,3,3,3 ^1,1 ,2]	46080 (2 ⁶ × 6!)
E6 × _A1	[3,3,3 ^2,1 ,2]	103680 (144×6!)
A ₅ × 1 ₂ ( p )	[3,3,3,3,2, pág .]	1440 p
BC ₅ × 1 ₂ ( p )	[4,3,3,3,2, pág .]	7680 p
D ₅ × I ₂ ( p )	[3,3,3 ^1,1 ,2, pág ]	3840 p
Un ₅ × Un ₁²	[3,3,3,3,2,2]	2880
antes de Cristo ₅ × A ₁²	[4,3,3,3,2,2]	15360
D ₅ × A ₁²	[3,3,3 ^1,1 ,2,2]	7680
Un ₄ ×Un ₃	[3,3,3,2,3,3]	2880
Un ₄ × BC ₃	[3,3,3,2,4,3]	5760
Un ₄ × Alto ₃	[3,3,3,2,5,3]	14400
BC ₄ × A ₃	[4,3,3,2,3,3]	9216
4 a. C. ₃ x _{4 a. C.}	[4,3,3,2,4,3]	18432
4 _×₃ de alto	[4,3,3,2,5,3]	46080
Alto ₄ × Alto ₃	[5,3,3,2,3,3]	345600
H4 × _BC3	[5,3,3,2,4,3]	691200
Alto ₄ × Alto ₃	[5,3,3,2,5,3]	1728000
F ₄ × A ₃	[3,4,3,2,3,3]	27648
F ₄ × BC ₃	[3,4,3,2,4,3]	55296
F4 × _Al3	[3,4,3,2,5,3]	138240
D4 × _A3	[3 ^1,1,1 ,2,3,3]	4608
D ₄ × BC ₃	[3,3 ^1,1 ,2,4,3]	9216
Profundidad ₄ × altura ₃	[3,3 ^1,1 ,2,5,3]	23040
A ₄ × I ₂ ( p ) × A ₁	[3,3,3,2, pág . 2]	480 p
B C ₄ × I ₂ ( p ) × A ₁	[4,3,3,2, pág . 2]	1536 p
D ₄ × I ₂ ( p ) × A ₁	[3,3 ^1,1 ,2, pág ,2]	768 p
F ₄ × I ₂ ( p ) × A ₁	[3,4,3,2, pág . 2]	4608 p
H ₄ × I ₂ ( p ) × A ₁	[5,3,3,2, pág . 2]	57600 p
Un ₄ ×Un ₁³	[3,3,3,2,2,2]	960
antes de Cristo ₄ × A ₁³	[4,3,3,2,2,2]	3072
F ₄ × A ₁³	[3,4,3,2,2,2]	9216
Alto ₄ × Alto ₁³	[5,3,3,2,2,2]	115200
D4 × _A13	[3,3 ^1,1 ,2,2,2]	1536
Un ₃² × Un ₁	[3,3,2,3,3,2]	1152
A ₃ × BC ₃ × A ₁	[3,3,2,4,3,2]	2304
A ₃ × Alto ₃ × A ₁	[3,3,2,5,3,2]	5760
B.C. ₃² × A ₁	[4,3,2,4,3,2]	4608
B.C. ₃ × H. ₃ × A. ₁	[4,3,2,5,3,2]	11520
H32 × _A1	[5,3,2,5,3,2]	28800
A ₃ × I ₂ ( p ) × I ₂ ( q )	[3,3,2, p ,2, q ]	96 piezas
B C ₃ × I ₂ ( p ) × I ₂ ( q )	[4,3,2, p ,2, q ]	192 piezas
H3 × _I2 ( _p ) × _I2 ( q )	[5,3,2, p ,2, q ]	480 piezas
A ₃ × I ₂ ( p ) × A ₁²	[3,3,2, pág . 2,2]	192 p
BC ₃ × I ₂ ( p ) × A ₁²	[4,3,2, pág . 2,2]	384 p
H ₃ × I ₂ ( p ) × A ₁²	[5,3,2, pág . 2,2]	960 p
Un ₃ × Un ₁⁴	[3,3,2,2,2,2]	384
antes de Cristo ₃ × A ₁⁴	[4,3,2,2,2,2]	768
H3 × _A14	[5,3,2,2,2,2]	1920
Yo ₂ ( p ) × Yo ₂ ( q ) × Yo ₂ ( r ) × A ₁	[ p ,2, q ,2, r ,2]	16 pqr
Yo ₂ ( p ) × Yo ₂ ( q ) × A ₁³	[ p ,2, q ,2,2,2]	32 piezas
yo ₂ ( p )×A ₁⁵	[ pág . 2,2,2,2,2]	64 p
Un ₁⁷	[2,2,2,2,2,2]	128

Ocho dimensiones

La siguiente tabla muestra los grupos de reflexión de ocho dimensiones (excluyendo aquellos que son grupos de reflexión de dimensiones inferiores), enumerándolos como grupos de Coxeter . Existen grupos quirales relacionados para cada uno con la mitad del orden, definidos por un número par de reflexiones, y pueden representarse mediante la notación de Coxeter entre corchetes con un exponente '+', por ejemplo [3,3,3,3,3,3,3] ⁺ tiene siete puntos de giro triples y un orden de simetría de 181440.

Grupo Coxeter		Orden	Politopos relacionados
Un ₈	[3,3,3,3,3,3,3]	362880 (9!)	8-símplex
Un ₈ × 2	[[3,3,3,3,3,3,3]]	725760 (2×9!)	Compuesto dual 8-simplex
₈ antes de Cristo	[4,3,3,3,3,3,3]	10321920 (288 ^! )	8-cubo , 8-ortoplex
D8	[3,3,3,3,3,3 ^1,1 ]	5160960 (278 ^! )	8-demicubes
E8	[3,3,3,3,3 ^2,1 ]	696729600 (192×10!)	4 ₂₁ , 2 ₄₁ , 1 ₄₂
Un ₇ × Un ₁	[3,3,3,3,3,3,2]	80640	Prisma 7-simplex
₇ aC × ₁	[4,3,3,3,3,3,2]	645120	Prisma de siete cubos
D7 × _A1	[3,3,3,3,3 ^1,1 ,2]	322560	Prisma de 7 demicubes
E7 × _A1	[3,3,3,3 ^2,1 ,2]	5806080	Prisma 3 _{21 , prisma 2}₃₁ , prisma 1 ₄₂
A ₆ × 1 ₂ ( p )	[3,3,3,3,3,2, pág .]	10080p	duoprisma
BC ₆ × 1 ₂ ( p )	[4,3,3,3,3,2, pág .]	92160 p
D ₆ × I ₂ ( pág )	[3,3,3,3 ^1,1 ,2, pág ]	46080 p
E6 _× I2 ( _pág. )	[3,3,3 ^2,1 ,2, p ]	103680 p
Un ₆ × Un ₁²	[3,3,3,3,3,2,2]	20160
antes de Cristo ₆ × A ₁²	[4,3,3,3,3,2,2]	184320
D6 × _A12	[3 ^3,1,1 ,2,2]	92160
E6 × _A12	[3,3,3 ^2,1 ,2,2]	207360
Un ₅ × Un ₃	[3,3,3,3,2,3,3]	17280
₅ aC × ₃	[4,3,3,3,2,3,3]	92160
D5 × _A3	[3 ^2,1,1 ,2,3,3]	46080
Un ₅ × BC ₃	[3,3,3,3,2,4,3]	34560
₅ a. C. 3 x _{5 a. C.}	[4,3,3,3,2,4,3]	184320
D ₅ × BC ₃	[3 ^2,1,1 ,2,4,3]	92160
Un ₅ × Alto ₃	[3,3,3,3,2,5,3]
5 _×₃ de alto	[4,3,3,3,2,5,3]
Profundidad ₅ × altura ₃	[3 ^2,1,1 ,2,5,3]
A ₅ × I ₂ ( p ) × A ₁	[3,3,3,3,2, pág . 2]
BC ₅ × I ₂ ( p ) × A ₁	[4,3,3,3,2, pág . 2]
D ₅ × I ₂ ( p ) × A ₁	[3 ^2,1,1 ,2, pág ,2]
Un ₅ × Un ₁³	[3,3,3,3,2,2,2]
antes de Cristo ₅ × A ₁³	[4,3,3,3,2,2,2]
D5 × _A13	[3 ^2,1,1 ,2,2,2]
Un ₄ ×Un ₄	[3,3,3,2,3,3,3]
₄ × ₄ antes de Cristo	[4,3,3,2,3,3,3]
D4 × _A4	[3 ^1,1,1 ,2,3,3,3]
F ₄ × A ₄	[3,4,3,2,3,3,3]
Alto ₄ × Alto ₄	[5,3,3,2,3,3,3]
₄ antes de Cristo × _{4 antes de Cristo}	[4,3,3,2,4,3,3]
D ₄ × BC ₄	[3 ^1,1,1 ,2,4,3,3]
F ₄ × BC ₄	[3,4,3,2,4,3,3]
H4 × _BC4	[5,3,3,2,4,3,3]
D4 × _D4	[3 ^1,1,1 ,2,3 ^1,1,1 ]
F4 × _D4	[3,4,3,2,3 ^1,1,1 ]
Alto ₄ × Profundidad ₄	[5,3,3,2,3 ^1,1,1 ]
F4 × _F4	[3,4,3,2,3,4,3]
Alto ₄ × Fondo ₄	[5,3,3,2,3,4,3]
Alto ₄ × Alto ₄	[5,3,3,2,5,3,3]
Un ₄ ×Un ₃ ×Un ₁	[3,3,3,2,3,3,2]		prismas de duoprisma
A ₄ × BC ₃ × A ₁	[3,3,3,2,4,3,2]
A ₄ × Alto ₃ × A ₁	[3,3,3,2,5,3,2]
B.C. ₄ × A. ₃ × A. ₁	[4,3,3,2,3,3,2]
BC4 × _BC3 × _A1	[4,3,3,2,4,3,2]
B.C. ₄ × Alto ₃ × Ancho ₁	[4,3,3,2,5,3,2]
H4 × _A3 × _A1	[5,3,3,2,3,3,2]
H4 × _BC3 × _A1	[5,3,3,2,4,3,2]
Alto ₄ × Alto ₃ × Ancho ₁	[5,3,3,2,5,3,2]
F ₄ × A ₃ × A ₁	[3,4,3,2,3,3,2]
F ₄ × BC ₃ × A ₁	[3,4,3,2,4,3,2]
F4 × _Al3 × _A1	[3,4,2,3,5,3,2]
D ₄ × A ₃ × A ₁	[3 ^1,1,1 ,2,3,3,2]
D ₄ × BC ₃ × A ₁	[3 ^1,1,1 ,2,4,3,2]
Re ₄ × Alto ₃ × Ancho ₁	[3 ^1,1,1 ,2,5,3,2]
A ₄ × I ₂ ( p ) × I ₂ ( q )	[3,3,3,2, p ,2, q ]		triaprisma
B C ₄ × I ₂ ( p ) × I ₂ ( q )	[4,3,3,2, p ,2,q]
F ₄ × I ₂ ( p ) × I ₂ ( q )	[3,4,3,2, p ,2,q]
H ₄ × I ₂ ( p ) × I ₂ ( q )	[5,3,3,2, p ,2,q]
D ₄ × I ₂ ( p ) × I ₂ ( q )	[3 ^1,1,1 ,2, p ,2, q ]
A ₄ × I ₂ ( p ) × A ₁²	[3,3,3,2, pág . 2,2]
B C ₄ × I ₂ ( p ) × A ₁²	[4,3,3,2, pág . 2,2]
F ₄ × I ₂ ( p ) × A ₁²	[3,4,3,2, pág . 2,2]
H ₄ × I ₂ ( p ) × A ₁²	[5,3,3,2, pág . 2,2]
D ₄ × I ₂ ( p ) × A ₁²	[3 ^1,1,1 ,2, pág ,2,2]
Un ₄ ×Un ₁⁴	[3,3,3,2,2,2,2]
antes de Cristo ₄ × A ₁⁴	[4,3,3,2,2,2,2]
F ₄ × A ₁⁴	[3,4,3,2,2,2,2]
Alto ₄ × Alto ₁⁴	[5,3,3,2,2,2,2]
D4 × _A14	[3 ^1,1,1 ,2,2,2,2]
A3 × _A3_× I2 ( pág . ₎	[3,3,2,3,3,2, pág .]
BC3 × _A3_× I2 ( _pág. )	[4,3,2,3,3,2, pág .]
H3 × _A3 × _I2 ( p )	[5,3,2,3,3,2, pág .]
BC3 × _BC3 × _I2 ( p )	[4,3,2,4,3,2, pág .]
H3 × _BC3 × _I2 ( p )	[5,3,2,4,3,2, pág .]
H3 × _H3 × _I2 ( p )	[5,3,2,5,3,2, pág .]
Un ₃ × Un ₃ × Un ₁²	[3,3,2,3,3,2,2]
B C ₃ × A ₃ × A ₁²	[4,3,2,3,3,2,2]
H3 × _A3 × _A12	[5,3,2,3,3,2,2]
BC3 × _BC3 × _A12	[4,3,2,4,3,2,2]
H3 × _BC3 × _A12	[5,3,2,4,3,2,2]
Alto ₃ × Alto ₃ × Un ₁²	[5,3,2,5,3,2,2]
A ₃ × I ₂ ( p ) × I ₂ ( q ) × A ₁	[3,3,2, p ,2, q ,2]
BC3 × _I2 ( _p )× I2 ₍ q ) × _A1	[4,3,2, p ,2, q ,2]
H ₃ × I ₂ ( p ) × I ₂ ( q ) × A ₁	[5,3,2, p ,2, q ,2]
A ₃ × I ₂ ( p ) × A ₁³	[3,3,2, pág . 2,2,2]
BC ₃ × I ₂ ( p ) × A ₁³	[4,3,2, pág . 2,2,2]
H3 × _I2 ( p ⁾ × _A13	[5,3,2, pág . 2,2,2]
Un ₃ × Un ₁⁵	[3,3,2,2,2,2,2]
antes de Cristo ₃ × A ₁⁵	[4,3,2,2,2,2,2]
H3 × _A15	[5,3,2,2,2,2,2]
Yo ₂ ( p ) × Yo ₂ ( q ) × Yo ₂ ( r ) × Yo ₂ ( s )	[ p ,2, q ,2, r ,2, s ]	16 pqrs
Yo ₂ ( p ) × Yo ₂ ( q ) × Yo ₂ ( r ) × A ₁²	[ p ,2, q ,2, r ,2,2]	32 pqr
Yo ₂ ( p ) × Yo ₂ ( q ) × A ₁⁴	[ p ,2, q ,2,2,2,2]	64 piezas
Yo ₂ ( p )×A ₁⁶	[ pág ,2,2,2,2,2,2]	128 p
Un ₁⁸	[2,2,2,2,2,2,2]	256

Véase también

Referencias

^ ab Conway, John H. ; Smith, Derek A. (2003). Sobre cuaterniones y octoniones: su geometría, aritmética y simetría . AK Peters. ISBN 978-1-56881-134-5.
^ Los grupos del espacio cristalográfico en el álgebra geométrica, D. Hestenes y J. Holt, Journal of Mathematical Physics. 48, 023514 (2007) (22 páginas)

Lectura adicional

HSM Coxeter (1995), F. Arthur Sherk; Peter McMullen; Anthony C. Thompson; Asia Ivic Weiss (eds.), Caleidoscopios: escritos seleccionados de HSM Coxeter, Wiley-Interscience Publication, ISBN 978-0-471-01003-6
- (Artículo 23) HSM Coxeter, Politopos regulares y semirregulares II , [Math. Zeit. 188 (1985) 559–591]
HSM Coxeter ; WOJ Moser (1980), Generadores y relaciones para grupos discretos (4.ª ed.), Nueva York: Springer-Verlag
NW Johnson (2018), "Capítulo 11: Grupos de simetría finitos", Geometrías y transformaciones

Enlaces externos

Tutorial de grupos de puntos basado en la Web (requiere Java y Flash)
Enumeración de subgrupos (requiere Java)
El Centro de Geometría: 2.1 Fórmulas para Simetrías en Coordenadas Cartesianas (dos dimensiones)
El Centro de Geometría: 10.1 Fórmulas para Simetrías en Coordenadas Cartesianas (tres dimensiones)

[Conway-Smith-1] Conway, John H. ; Smith, Derek A. (2003). Sobre cuaterniones y octoniones: su geometría, aritmética y simetría . AK Peters. ISBN 978-1-56881-134-5.

[2] Los grupos del espacio cristalográfico en el álgebra geométrica, D. Hestenes y J. Holt, Journal of Mathematical Physics. 48, 023514 (2007) (22 páginas)