Economía matemática

Parte de una serie sobre
Ciencias económicas
Historia Describir Índice
Ramas y clasificaciones Aplicado Econometría Heterodoxo Internacional Micro / Macro Corriente principal Matemático Metodología Político Códigos de clasificación JEL
Conceptos, teoría y técnicas Sistemas económicos Crecimiento económico Mercado Contabilidad nacional Economía experimental Economía computacional Teoría de juegos Operations research Middle income trap Industrial complex
By application Agricultural Behavioral Business Cultural Democracy Demographic Development Digitization Ecological Education Engineering Environmental Evolutionary Expeditionary Feminist Financial Geographical Happiness Health Historical Humanistic Industrial organization Information Institutional Knowledge Labour Law Managerial Monetary Natural resource Organizational Participation Personnel Planning Policy Public Public choice / Social choice theory Regional Rural Service Socio Sociological Solidarity Statistics Urban Welfare
Notable economists de Mandeville Quesnay Smith Malthus Say Ricardo von Thünen List Bastiat Cournot Mill Gossen Marx Walras Jevons George Menger Marshall Edgeworth Clark Pareto von Böhm-Bawerk von Wieser Veblen Fisher Pigou Heckscher von Mises Schumpeter Keynes Knight Polanyi Frisch Sraffa Myrdal Hayek Kalecki Röpke Kuznets Tinbergen Robinson von Neumann Hicks Lange Leontief Galbraith Koopmans Schumacher Friedman Samuelson Simon Buchanan Arrow Baumol Solow Rothbard Greenspan Sowell Becker Ostrom Sen Lucas Stiglitz Thaler Hoppe Krugman Piketty more
Lists Glossary Economists Publications (journals) Schools
Business portal Money portal
v t e

Part of a series on
Mathematics
History Index
Areas Number theory Geometry Algebra Calculus and Analysis Discrete mathematics Logic and Set theory Probability Statistics and Decision theory Relationship with sciences Physics Chemistry Geosciences Computation Biology Linguistics Economics Philosophy Education
Mathematics Portal
v t e

La economía matemática es la aplicación de métodos matemáticos para representar teorías y analizar problemas en economía . A menudo, estos métodos aplicados van más allá de la geometría simple y pueden incluir cálculo diferencial e integral , ecuaciones diferenciales y de diferencias , álgebra matricial , programación matemática u otros métodos computacionales . ^{[1] [2]} Los defensores de este enfoque afirman que permite la formulación de relaciones teóricas con rigor, generalidad y simplicidad. ^[3]

Las matemáticas permiten a los economistas formular proposiciones significativas y comprobables sobre temas amplios y complejos que no podrían expresarse fácilmente de manera informal. Además, el lenguaje de las matemáticas permite a los economistas hacer afirmaciones específicas y positivas sobre temas controvertidos o polémicos que serían imposibles sin las matemáticas. ^[4] Gran parte de la teoría económica se presenta actualmente en términos de modelos económicos matemáticos , un conjunto de relaciones matemáticas estilizadas y simplificadas que se afirman para aclarar supuestos e implicaciones. ^[5]

Las aplicaciones amplias incluyen:

• Problemas de optimización en cuanto al equilibrio de objetivos, ya sea de un hogar, una empresa o un responsable de políticas.
• Análisis estático (o de equilibrio ) en el que la unidad económica (como un hogar) o el sistema económico (como un mercado o la economía ) se modela como si no cambiara.
• estática comparativa en cuanto a un cambio de un equilibrio a otro inducido por un cambio en uno o más factores
• análisis dinámico , que rastrea los cambios en un sistema económico a lo largo del tiempo, por ejemplo, el crecimiento económico . ^{[2] [6] [7]}

El modelado económico formal comenzó en el siglo XIX con el uso del cálculo diferencial para representar y explicar el comportamiento económico, como la maximización de la utilidad , una aplicación económica temprana de la optimización matemática . La economía se volvió más matemática como disciplina a lo largo de la primera mitad del siglo XX, pero la introducción de técnicas nuevas y generalizadas en el período en torno a la Segunda Guerra Mundial , como en la teoría de juegos , ampliaría enormemente el uso de formulaciones matemáticas en economía. ^{[8] [7]}

Esta rápida sistematización de la economía alarmó a los críticos de la disciplina, así como a algunos economistas destacados. John Maynard Keynes , Robert Heilbroner , Friedrich Hayek y otros han criticado el uso generalizado de modelos matemáticos para el comportamiento humano, argumentando que algunas decisiones humanas son irreductibles a las matemáticas.

El uso de las matemáticas al servicio del análisis social y económico se remonta al siglo XVII. Entonces, principalmente en las universidades alemanas , surgió un estilo de instrucción que trataba específicamente de la presentación detallada de datos relacionados con la administración pública. Gottfried Achenwall daba clases de esta manera, acuñando el término estadística . Al mismo tiempo, un pequeño grupo de profesores en Inglaterra estableció un método de "razonamiento mediante cifras sobre cuestiones relacionadas con el gobierno" y se refirió a esta práctica como Aritmética Política . ^[9] Sir William Petty escribió extensamente sobre temas que más tarde preocuparían a los economistas, como los impuestos, la velocidad del dinero y el ingreso nacional , pero aunque su análisis era numérico, rechazó la metodología matemática abstracta. El uso de datos numéricos detallados por parte de Petty (junto con John Graunt ) influiría en los estadísticos y economistas durante algún tiempo, aunque los trabajos de Petty fueron en gran medida ignorados por los académicos ingleses. ^[10]

La matematización de la economía comenzó en serio en el siglo XIX. La mayor parte del análisis económico de la época era lo que más tarde se llamaría economía clásica . Los temas se discutían y se eliminaban por medios algebraicos , pero no se utilizaba el cálculo. Más importante aún, hasta El Estado aislado de Johann Heinrich von Thünen en 1826, los economistas no desarrollaron modelos explícitos y abstractos para el comportamiento con el fin de aplicar las herramientas de las matemáticas. El modelo de Thünen sobre el uso de las tierras agrícolas representa el primer ejemplo de análisis marginal. ^[11] El trabajo de Thünen fue en gran parte teórico, pero también extrajo datos empíricos para intentar respaldar sus generalizaciones. En comparación con sus contemporáneos, Thünen construyó modelos y herramientas económicas, en lugar de aplicar herramientas anteriores a nuevos problemas. ^[12]

Mientras tanto, una nueva cohorte de académicos formados en los métodos matemáticos de las ciencias físicas gravitó hacia la economía, defendiendo y aplicando esos métodos a su materia, ^[13] y descrita hoy como pasando de la geometría a la mecánica . ^[14] Entre ellos se encontraba WS Jevons , que presentó un artículo sobre una "teoría matemática general de la economía política" en 1862, proporcionando un esquema para el uso de la teoría de la utilidad marginal en la economía política. ^[15] En 1871, publicó Los principios de la economía política , declarando que la materia como ciencia "debe ser matemática simplemente porque trata con cantidades". Jevons esperaba que sólo la recopilación de estadísticas de precios y cantidades permitiría que la materia tal como se presentaba se convirtiera en una ciencia exacta. ^[16] Otros precedieron y siguieron en la expansión de las representaciones matemáticas de los problemas económicos . ^[17]

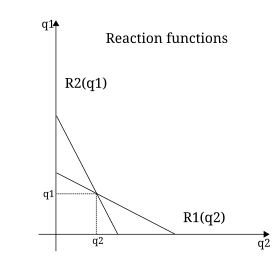
Augustin Cournot y Léon Walras construyeron las herramientas de la disciplina axiomáticamente en torno a la utilidad, argumentando que los individuos buscaban maximizar su utilidad a través de elecciones de una manera que pudiera describirse matemáticamente. ^[18] En ese momento, se pensaba que la utilidad era cuantificable, en unidades conocidas como utils . ^[19] Cournot, Walras y Francis Ysidro Edgeworth son considerados los precursores de la economía matemática moderna. ^[20]

Cournot, profesor de matemáticas, desarrolló en 1838 un tratamiento matemático para el duopolio , una condición de mercado definida por la competencia entre dos vendedores. ^[20] Este tratamiento de la competencia, publicado por primera vez en Investigaciones sobre los principios matemáticos de la riqueza , ^[21] se conoce como duopolio de Cournot . Se supone que ambos vendedores tenían igual acceso al mercado y podían producir sus bienes sin costo. Además, suponía que ambos bienes eran homogéneos . Cada vendedor variaría su producción en función de la producción del otro y el precio de mercado estaría determinado por la cantidad total suministrada. La ganancia de cada empresa se determinaría multiplicando su producción por el precio de mercado por unidad . La diferenciación de la función de ganancia con respecto a la cantidad suministrada por cada empresa dejó un sistema de ecuaciones lineales, cuya solución simultánea dio la cantidad, el precio y las ganancias de equilibrio. ^[22] Las contribuciones de Cournot a la matematización de la economía serían ignoradas durante décadas, pero finalmente influyeron en muchos de los marginalistas . ^{[22] [23] Los modelos de duopolio y} oligopolio de Cournot también representan una de las primeras formulaciones de juegos no cooperativos . Hoy en día, la solución puede darse como un equilibrio de Nash , pero el trabajo de Cournot precedió a la teoría de juegos moderna en más de 100 años. ^[24]

Mientras que Cournot proporcionó una solución para lo que más tarde se llamaría equilibrio parcial, Léon Walras intentó formalizar el análisis de la economía en su conjunto a través de una teoría del equilibrio competitivo general . El comportamiento de cada actor económico se consideraría tanto del lado de la producción como del lado del consumo. Walras presentó originalmente cuatro modelos separados de intercambio, cada uno incluido recursivamente en el siguiente. La solución del sistema de ecuaciones resultante (tanto lineal como no lineal) es el equilibrio general. ^[25] En ese momento, no se podía expresar una solución general para un sistema de un número arbitrario de ecuaciones, pero los intentos de Walras produjeron dos resultados famosos en economía. El primero es la ley de Walras y el segundo es el principio de tâtonnement . El método de Walras se consideró altamente matemático para la época y Edgeworth comentó extensamente sobre este hecho en su revisión de Éléments d'économie politique pure (Elementos de economía pura). ^[26]

La ley de Walras se introdujo como una respuesta teórica al problema de determinar las soluciones en equilibrio general. Su notación es diferente de la notación moderna, pero se puede construir utilizando una notación de suma más moderna. Walras supuso que en equilibrio, todo el dinero se gastaría en todos los bienes: cada bien se vendería al precio de mercado para ese bien y cada comprador gastaría su último dólar en una canasta de bienes. Partiendo de esta suposición, Walras pudo demostrar que si había n mercados y n-1 mercados se vaciaban (alcanzaban condiciones de equilibrio), el n-ésimo mercado también se vaciaría. Esto es más fácil de visualizar con dos mercados (considerados en la mayoría de los textos como un mercado de bienes y un mercado de dinero). Si uno de los dos mercados ha alcanzado un estado de equilibrio, ningún bien adicional (o, por el contrario, dinero) puede entrar o salir del segundo mercado, por lo que también debe estar en un estado de equilibrio. Walras utilizó esta afirmación para avanzar hacia una prueba de la existencia de soluciones al equilibrio general, pero hoy en día se utiliza comúnmente para ilustrar el vaciado del mercado en los mercados monetarios a nivel de pregrado. ^[27]

El término tâtonnement (que en francés significa, aproximadamente, tantear hacia ) tenía como objetivo servir como expresión práctica del equilibrio general walrasiano. Walras abstrajo el mercado como una subasta de bienes donde el subastador anunciaría los precios y los participantes del mercado esperarían hasta que cada uno pudiera satisfacer sus precios de reserva personales para la cantidad deseada (recordando aquí que se trata de una subasta de todos los bienes, por lo que todos tienen un precio de reserva para su canasta de bienes deseada). ^[28]

Sólo cuando todos los compradores estén satisfechos con el precio de mercado dado se producirán las transacciones. El mercado se "limpiará" a ese precio, no existirá excedente ni escasez. La palabra tâtonnement se utiliza para describir las direcciones que toma el mercado en su búsqueda del equilibrio, estableciendo precios altos o bajos para diferentes bienes hasta que se acuerde un precio para todos los bienes. Si bien el proceso parece dinámico, Walras sólo presentó un modelo estático, ya que no se producirán transacciones hasta que todos los mercados estén en equilibrio. En la práctica, muy pocos mercados funcionan de esta manera. ^[29]

Edgeworth introdujo elementos matemáticos en la economía explícitamente en Mathematical Psychics: An Essay on the Application of Mathematics to the Moral Sciences , publicado en 1881. ^[30] Adoptó el cálculo felicífico de Jeremy Bentham para el comportamiento económico, permitiendo que el resultado de cada decisión se convierta en un cambio en la utilidad. ^[31] Utilizando este supuesto, Edgeworth construyó un modelo de intercambio sobre tres supuestos: los individuos son egoístas, los individuos actúan para maximizar la utilidad y los individuos son "libres de recontratar con otro independientemente de... cualquier tercero". ^[32]

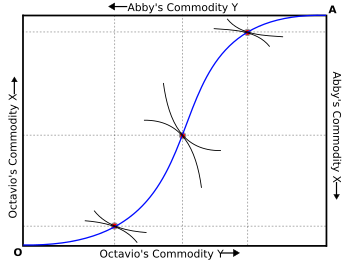
Dados dos individuos, el conjunto de soluciones en el que ambos individuos pueden maximizar la utilidad se describe mediante la curva de contrato en lo que ahora se conoce como la Caja de Edgeworth . Técnicamente, la construcción de la solución de dos personas al problema de Edgeworth no fue desarrollada gráficamente hasta 1924 por Arthur Lyon Bowley . ^[34] La curva de contrato de la caja de Edgeworth (o, de manera más general, de cualquier conjunto de soluciones al problema de Edgeworth para más actores) se conoce como el núcleo de una economía. ^[35]

Edgeworth dedicó un esfuerzo considerable a insistir en que las pruebas matemáticas eran apropiadas para todas las escuelas de pensamiento en economía. Mientras estaba al frente de The Economic Journal , publicó varios artículos criticando el rigor matemático de investigadores rivales, incluido Edwin Robert Anderson Seligman , un conocido escéptico de la economía matemática. ^[36] Los artículos se centraron en un ida y vuelta sobre la incidencia de los impuestos y las respuestas de los productores. Edgeworth se dio cuenta de que un monopolio que produce un bien que tiene una oferta conjunta pero no una demanda conjunta (como primera clase y clase económica en un avión, si el avión vuela, ambos juegos de asientos vuelan con él) podría en realidad reducir el precio visto por el consumidor por uno de los dos productos si se aplicara un impuesto. El sentido común y el análisis numérico más tradicional parecían indicar que esto era absurdo. Seligman insistió en que los resultados que Edgeworth logró fueron una peculiaridad de su formulación matemática. Sugirió que el supuesto de una función de demanda continua y un cambio infinitesimal en el impuesto resultó en las predicciones paradójicas. Harold Hotelling demostró posteriormente que Edgeworth tenía razón y que el mismo resultado (una "disminución del precio como resultado del impuesto") podría ocurrir con una función de demanda discontinua y grandes cambios en la tasa impositiva. ^[37]

A partir de finales de la década de 1930, se implementaron una serie de nuevas herramientas matemáticas del cálculo diferencial y las ecuaciones diferenciales, los conjuntos convexos y la teoría de grafos para avanzar en la teoría económica de una manera similar a los nuevos métodos matemáticos aplicados anteriormente a la física. ^{[8] [38]} El proceso se describió más tarde como un paso de la mecánica a la axiomática . ^[39]

Vilfredo Pareto analizó la microeconomía al tratar las decisiones de los actores económicos como intentos de cambiar una asignación dada de bienes por otra asignación más preferida. Los conjuntos de asignaciones podrían entonces ser tratados como eficientes en el sentido de Pareto (el término equivalente es óptimo en el sentido de Pareto) cuando no pudieran ocurrir intercambios entre actores que pudieran mejorar la situación de al menos un individuo sin empeorar la de ningún otro. ^[40] La prueba de Pareto se confunde comúnmente con el equilibrio walrassiano o se atribuye informalmente a la hipótesis de la mano invisible de Adam Smith . ^[41] Más bien, la declaración de Pareto fue la primera afirmación formal de lo que se conocería como el primer teorema fundamental de la economía del bienestar . ^[42] Estos modelos carecían de las desigualdades de la siguiente generación de economía matemática.

En el tratado de referencia Fundamentos del análisis económico (1947), Paul Samuelson identificó un paradigma común y una estructura matemática en múltiples campos de la materia, basándose en el trabajo previo de Alfred Marshall . Fundamentos tomó conceptos matemáticos de la física y los aplicó a problemas económicos. Esta visión amplia (por ejemplo, comparando el principio de Le Chatelier con el tâtonnement ) impulsa la premisa fundamental de la economía matemática: los sistemas de actores económicos pueden modelarse y su comportamiento puede describirse de manera muy similar a cualquier otro sistema. Esta extensión siguió el trabajo de los marginalistas del siglo anterior y lo extendió significativamente. Samuelson abordó los problemas de aplicar la maximización de la utilidad individual sobre grupos agregados con estática comparativa , que compara dos estados de equilibrio diferentes después de un cambio exógeno en una variable. Este y otros métodos en el libro proporcionaron la base para la economía matemática en el siglo XX. ^{[7] [43]}

Los modelos restringidos de equilibrio general fueron formulados por John von Neumann en 1937. ^[44] A diferencia de las versiones anteriores, los modelos de von Neumann tenían restricciones de desigualdad. Para su modelo de una economía en expansión, von Neumann demostró la existencia y unicidad de un equilibrio utilizando su generalización del teorema del punto fijo de Brouwer . El modelo de von Neumann de una economía en expansión consideró la matriz lápiz  A - λ B con matrices no negativas  A y B ; von Neumann buscó vectores de probabilidad p y  q y un número positivo  λ que resolviera la ecuación de complementariedad .  

p ^T  ( A − λ  B )  q = 0,

junto con dos sistemas de desigualdad que expresan la eficiencia económica. En este modelo, el vector de probabilidad ( transpuesto ) p representa los precios de los bienes mientras que el vector de probabilidad q representa la "intensidad" a la que se ejecutaría el proceso de producción. La solución única λ representa la tasa de crecimiento de la economía, que es igual a la tasa de interés . Probar la existencia de una tasa de crecimiento positiva y demostrar que la tasa de crecimiento es igual a la tasa de interés fueron logros notables, incluso para von Neumann. ^{[45] [46] [47]} Los resultados de von Neumann han sido vistos como un caso especial de programación lineal , donde el modelo de von Neumann usa solo matrices no negativas. ^[48] El estudio del modelo de von Neumann de una economía en expansión continúa interesando a los economistas matemáticos con intereses en la economía computacional. ^{[49] [50] [51]}

En 1936, el economista nacido en Rusia Wassily Leontief construyó su modelo de análisis de insumo-producto a partir de las tablas de "balance de materiales" construidas por los economistas soviéticos, que a su vez siguieron el trabajo anterior de los fisiócratas . Con su modelo, que describía un sistema de procesos de producción y demanda, Leontief describió cómo los cambios en la demanda en un sector económico influirían en la producción en otro. ^[52] En la práctica, Leontief estimó los coeficientes de sus modelos simples, para abordar cuestiones económicamente interesantes. En la economía de la producción , las "tecnologías de Leontief" producen resultados utilizando proporciones constantes de insumos, independientemente del precio de los insumos, lo que reduce el valor de los modelos de Leontief para comprender las economías pero permite estimar sus parámetros con relativa facilidad. En contraste, el modelo de von Neumann de una economía en expansión permite la elección de técnicas , pero los coeficientes deben estimarse para cada tecnología. ^{[53] [54]}

En matemáticas, la optimización matemática (u optimización o programación matemática) se refiere a la selección de un mejor elemento de un conjunto de alternativas disponibles. ^[55] En el caso más simple, un problema de optimización implica maximizar o minimizar una función real seleccionando valores de entrada de la función y calculando los valores correspondientes de la función. El proceso de solución incluye satisfacer las condiciones generales necesarias y suficientes para la optimalidad . Para los problemas de optimización, se puede utilizar una notación especializada en cuanto a la función y su(s) entrada(s). De manera más general, la optimización incluye encontrar el mejor elemento disponible de alguna función dado un dominio definido y puede utilizar una variedad de diferentes técnicas de optimización computacional . ^[56]

La economía está tan estrechamente vinculada a la optimización por parte de los agentes en una economía que una definición influyente describe a la economía como ciencia como el "estudio del comportamiento humano como una relación entre fines y medios escasos " con usos alternativos. ^[57] Los problemas de optimización atraviesan la economía moderna, muchos de ellos con restricciones económicas o técnicas explícitas. En microeconomía, el problema de maximización de la utilidad y su problema dual , el problema de minimización del gasto para un nivel dado de utilidad, son problemas de optimización económica. ^[58] La teoría postula que los consumidores maximizan su utilidad , sujetos a sus restricciones presupuestarias y que las empresas maximizan sus ganancias , sujetos a sus funciones de producción , costos de insumos y demanda del mercado . ^[59]

El equilibrio económico se estudia en la teoría de la optimización como un ingrediente clave de los teoremas económicos que, en principio, podrían probarse con datos empíricos. ^{[7] [60]} Se han producido desarrollos más recientes en la programación dinámica y la optimización de modelos con riesgo e incertidumbre , incluidas aplicaciones a la teoría de carteras , la economía de la información y la teoría de la búsqueda . ^[59]

Las propiedades de optimalidad de un sistema de mercado completo pueden enunciarse en términos matemáticos, como en la formulación de los dos teoremas fundamentales de la economía del bienestar ^[61] y en el modelo de equilibrio general de Arrow-Debreu (que también se analiza más adelante). ^[62] Más concretamente, muchos problemas se pueden resolver mediante métodos analíticos (formulativos). Muchos otros pueden ser lo suficientemente complejos como para requerir métodos numéricos de solución, con la ayuda de software. ^[56] Otros son complejos pero lo suficientemente manejables como para permitir métodos computables de solución, en particular modelos computables de equilibrio general para toda la economía. ^[63]

La programación lineal y no lineal ha afectado profundamente a la microeconomía, que anteriormente solo había considerado restricciones de igualdad. ^[64] Muchos de los economistas matemáticos que recibieron premios Nobel de Economía habían realizado investigaciones notables utilizando programación lineal: Leonid Kantorovich , Leonid Hurwicz , Tjalling Koopmans , Kenneth J. Arrow , Robert Dorfman , Paul Samuelson y Robert Solow . ^[65] Tanto Kantorovich como Koopmans reconocieron que George B. Dantzig merecía compartir su Premio Nobel de programación lineal. Los economistas que realizaron investigaciones en programación no lineal también han ganado el premio Nobel, en particular Ragnar Frisch además de Kantorovich, Hurwicz, Koopmans, Arrow y Samuelson.

La programación lineal se desarrolló para facilitar la asignación de recursos en empresas e industrias durante la década de 1930 en Rusia y durante la década de 1940 en los Estados Unidos. Durante el puente aéreo de Berlín (1948) , se utilizó la programación lineal para planificar el envío de suministros para evitar que Berlín muriera de hambre después del bloqueo soviético. ^{[66] [67]}

En 1951, Albert W. Tucker y Harold Kuhn lograron extensiones a la optimización no lineal con restricciones de desigualdad , quienes consideraron el problema de optimización no lineal :

Minimizar sujeto a y donde${\displaystyle f(x)}$${\displaystyle g_{i}(x)\leq 0}$${\displaystyle h_{j}(x)=0}$

${\displaystyle f(\cdot )}$¿Es la función a minimizar?

${\displaystyle g_{i}(\cdot )}$son las funciones de las restricciones de desigualdad donde${\displaystyle m}$ ${\displaystyle i=1,\dots ,m}$

${\displaystyle h_{j}(\cdot )}$son las funciones de las restricciones de igualdad donde .${\displaystyle l}$${\displaystyle j=1,\dots ,l}$

Al permitir restricciones de desigualdad, el enfoque de Kuhn-Tucker generalizó el método clásico de multiplicadores de Lagrange , que (hasta entonces) solo había permitido restricciones de igualdad. ^[68] El enfoque de Kuhn-Tucker inspiró más investigaciones sobre la dualidad lagrangiana, incluido el tratamiento de las restricciones de desigualdad. ^{[69] [70]} La teoría de dualidad de la programación no lineal es particularmente satisfactoria cuando se aplica a problemas de minimización convexa , que disfrutan de la teoría de dualidad convexo-analítica de Fenchel y Rockafellar ; esta dualidad convexa es particularmente fuerte para funciones convexas poliédricas , como las que surgen en la programación lineal . La dualidad lagrangiana y el análisis convexo se utilizan a diario en la investigación de operaciones , en la programación de plantas de energía, la planificación de programas de producción para fábricas y el enrutamiento de aerolíneas (rutas, vuelos, aviones, tripulaciones). ^[70]

La dinámica económica permite cambios en las variables económicas a lo largo del tiempo, incluso en sistemas dinámicos . El problema de encontrar funciones óptimas para tales cambios se estudia en el cálculo variacional y en la teoría del control óptimo . Antes de la Segunda Guerra Mundial, Frank Ramsey y Harold Hotelling utilizaron el cálculo de variaciones con ese fin.

Tras el trabajo de Richard Bellman sobre programación dinámica y la traducción al inglés de 1962 del trabajo anterior de L. Pontryagin et al ., ^[71] la teoría del control óptimo se utilizó más ampliamente en economía para abordar problemas dinámicos, especialmente en lo que respecta al equilibrio del crecimiento económico y la estabilidad de los sistemas económicos, ^[72] de los cuales un ejemplo clásico es el consumo y el ahorro óptimos . ^[73] Una distinción crucial es entre modelos de control deterministas y estocásticos. ^[74] Otras aplicaciones de la teoría del control óptimo incluyen aquellas en finanzas, inventarios y producción, por ejemplo. ^[75]

Fue en el curso de la prueba de la existencia de un equilibrio óptimo en su modelo de crecimiento económico de 1937 que John von Neumann introdujo métodos analíticos funcionales para incluir la topología en la teoría económica, en particular, la teoría del punto fijo a través de su generalización del teorema del punto fijo de Brouwer . ^{[8] [44] [76]} Siguiendo el programa de von Neumann, Kenneth Arrow y Gérard Debreu formularon modelos abstractos de equilibrios económicos utilizando conjuntos convexos y la teoría del punto fijo. Al introducir el modelo Arrow-Debreu en 1954, demostraron la existencia (pero no la unicidad) de un equilibrio y también demostraron que todo equilibrio de Walras es eficiente en el sentido de Pareto ; en general, los equilibrios no necesitan ser únicos. ^[77] En sus modelos, el espacio vectorial ("primario") representaba cantidades mientras que el espacio vectorial "dual" representaba precios . ^[78]

En Rusia, el matemático Leonid Kantorovich desarrolló modelos económicos en espacios vectoriales parcialmente ordenados , que enfatizaban la dualidad entre cantidades y precios. ^[79] Kantorovich renombró los precios como "valoraciones determinadas objetivamente" que se abreviaron en ruso como "o. o. o.", en alusión a la dificultad de discutir precios en la Unión Soviética. ^{[78] [80] [81]}

Incluso en dimensiones finitas, los conceptos de análisis funcional han iluminado la teoría económica, en particular al aclarar el papel de los precios como vectores normales a un hiperplano que soporta un conjunto convexo, que representa las posibilidades de producción o consumo. Sin embargo, los problemas de descripción de la optimización en el tiempo o bajo incertidumbre requieren el uso de espacios de funciones de dimensión infinita, porque los agentes eligen entre funciones o procesos estocásticos . ^{[78] [82] [83] [84]}

El trabajo de John von Neumann sobre el análisis funcional y la topología abrió nuevos caminos en las matemáticas y la teoría económica. ^{[44] [85]} También dejó a la economía matemática avanzada con menos aplicaciones del cálculo diferencial. En particular, los teóricos del equilibrio general utilizaron la topología general , la geometría convexa y la teoría de la optimización más que el cálculo diferencial, porque el enfoque del cálculo diferencial no había logrado establecer la existencia de un equilibrio.

Sin embargo, no se debe exagerar el declive del cálculo diferencial, porque el cálculo diferencial siempre se ha utilizado en la formación de posgrado y en aplicaciones. Además, el cálculo diferencial ha regresado a los niveles más altos de la economía matemática, la teoría del equilibrio general (GET), tal como se practica por el " conjunto GET " (la designación humorística debida a Jacques H. Drèze ). Sin embargo, en las décadas de 1960 y 1970, Gérard Debreu y Stephen Smale lideraron un renacimiento del uso del cálculo diferencial en la economía matemática. En particular, pudieron demostrar la existencia de un equilibrio general, donde los escritores anteriores habían fracasado, debido a sus matemáticas novedosas: la categoría de Baire a partir de la topología general y el lema de Sard a partir de la topología diferencial . Otros economistas asociados con el uso del análisis diferencial incluyen a Egbert Dierker, Andreu Mas-Colell e Yves Balasko . ^{[86] [87]} Estos avances han cambiado la narrativa tradicional de la historia de la economía matemática, siguiendo a von Neumann, que celebró el abandono del cálculo diferencial.

John von Neumann, trabajando con Oskar Morgenstern en la teoría de juegos , abrió nuevos caminos matemáticos en 1944 al extender los métodos analíticos funcionales relacionados con los conjuntos convexos y la teoría topológica del punto fijo al análisis económico. ^{[8] [85] De este modo, su trabajo evitó el} cálculo diferencial tradicional , para el cual el operador máximo no se aplicaba a funciones no diferenciables. Continuando el trabajo de von Neumann en la teoría de juegos cooperativos , los teóricos de juegos Lloyd S. Shapley , Martin Shubik , Hervé Moulin , Nimrod Megiddo y Bezalel Peleg influyeron en la investigación económica en política y economía. Por ejemplo, la investigación sobre los precios justos en los juegos cooperativos y los valores justos para los juegos de votación condujo a un cambio en las reglas para votar en las legislaturas y para contabilizar los costos en los proyectos de obras públicas. Por ejemplo, la teoría de juegos cooperativos se utilizó para diseñar el sistema de distribución de agua del sur de Suecia y para establecer tarifas para líneas telefónicas dedicadas en los EE. UU.

La teoría neoclásica anterior había limitado sólo el rango de resultados de negociación y en casos especiales, por ejemplo, monopolio bilateral o a lo largo de la curva de contrato de la caja de Edgeworth . ^[88] Los resultados de von Neumann y Morgenstern fueron igualmente débiles. Sin embargo, siguiendo el programa de von Neumann, John Nash utilizó la teoría del punto fijo para demostrar las condiciones bajo las cuales el problema de negociación y los juegos no cooperativos pueden generar una solución de equilibrio única . ^[89] La teoría de juegos no cooperativos ha sido adoptada como un aspecto fundamental de la economía experimental , ^[90] economía del comportamiento , ^[91] economía de la información , ^[92] organización industrial , ^[93] y economía política . ^[94] También ha dado lugar al tema del diseño de mecanismos (a veces llamado teoría de juegos inversos), que tiene aplicaciones de política pública y privada en cuanto a formas de mejorar la eficiencia económica a través de incentivos para compartir información. ^[95]

En 1994, Nash, John Harsanyi y Reinhard Selten recibieron el Premio Nobel de Economía por su trabajo sobre juegos no cooperativos. Harsanyi y Selten fueron premiados por su trabajo sobre juegos repetidos . Trabajos posteriores extendieron sus resultados a métodos computacionales de modelado. ^[96]

La economía computacional basada en agentes (ACE, por sus siglas en inglés) es un campo relativamente reciente, que data de alrededor de la década de 1990 en cuanto a trabajos publicados. Estudia los procesos económicos, incluidas las economías completas , como sistemas dinámicos de agentes que interactúan a lo largo del tiempo. Como tal, cae en el paradigma de los sistemas adaptativos complejos . ^[97] En los modelos basados ​​en agentes correspondientes , los agentes no son personas reales sino "objetos computacionales modelados como interactuando de acuerdo con reglas" ... "cuyas interacciones de nivel micro crean patrones emergentes" en el espacio y el tiempo. ^[98] Las reglas se formulan para predecir el comportamiento y las interacciones sociales basadas en incentivos e información. El supuesto teórico de optimización matemática por parte de los agentes en los mercados se reemplaza por el postulado menos restrictivo de agentes con racionalidad limitada que se adaptan a las fuerzas del mercado. ^[99]

Los modelos ACE aplican métodos numéricos de análisis a simulaciones basadas en computadora de problemas dinámicos complejos para los cuales los métodos más convencionales, como la formulación de teoremas, pueden no ser de fácil uso. ^[100] Partiendo de condiciones iniciales específicas, el sistema económico computacional se modela como evolucionando con el tiempo a medida que sus agentes constituyentes interactúan repetidamente entre sí. En estos aspectos, ACE se ha caracterizado como un enfoque de abajo hacia arriba de cultivo de cultura para el estudio de la economía. ^[101] A diferencia de otros métodos de modelado estándar, los eventos ACE son impulsados ​​únicamente por condiciones iniciales, ya sea que existan o no equilibrios o sean computacionalmente manejables. El modelado ACE, sin embargo, incluye la adaptación, autonomía y aprendizaje de los agentes. ^[102] Tiene una similitud y superposición con la teoría de juegos como un método basado en agentes para modelar interacciones sociales. ^[96] Otras dimensiones del enfoque incluyen temas económicos estándar como la competencia y la colaboración , ^[103] la estructura del mercado y la organización industrial , ^[104] los costos de transacción , ^[105] la economía del bienestar , ^[106] y el diseño de mecanismos , ^[95] la información y la incertidumbre , ^[107] y la macroeconomía . ^{[108] [109]}

Se dice que el método se beneficia de las mejoras continuas en las técnicas de modelado de la ciencia informática y del aumento de las capacidades informáticas. Entre los problemas se incluyen los que son comunes a la economía experimental en general ^[110] y por comparación ^[111] y al desarrollo de un marco común para la validación empírica y la resolución de cuestiones abiertas en el modelado basado en agentes. ^[112] El objetivo científico último del método se ha descrito como "probar los hallazgos teóricos frente a datos del mundo real de formas que permitan que las teorías sustentadas empíricamente se acumulen con el tiempo, y que el trabajo de cada investigador se base adecuadamente en el trabajo anterior". ^[113]

A lo largo del siglo XX, los artículos en las "revistas fundamentales" ^[115] de economía han sido escritos casi exclusivamente por economistas académicos . Como resultado, gran parte del material transmitido en esas revistas se relaciona con la teoría económica, y "la teoría económica en sí misma ha sido cada vez más abstracta y matemática". ^[116] Una evaluación subjetiva de las técnicas matemáticas ^[117] empleadas en estas revistas fundamentales mostró una disminución en los artículos que no utilizan ni representaciones geométricas ni notación matemática del 95% en 1892 al 5,3% en 1990. ^[118] Una encuesta de 2007 de diez de las principales revistas económicas encuentra que solo el 5,8% de los artículos publicados en 2003 y 2004 carecían de análisis estadístico de los datos y de expresiones matemáticas mostradas que estuvieran indexadas con números en el margen de la página. ^[119]

Entre las dos guerras mundiales, los avances en las estadísticas matemáticas y un grupo de economistas con formación matemática dieron lugar a la econometría , que fue el nombre propuesto para la disciplina que se ocupa del avance de la economía mediante el uso de las matemáticas y la estadística. En el campo de la economía, el término "econometría" se ha utilizado a menudo para referirse a los métodos estadísticos en economía, en lugar de a la economía matemática. La econometría estadística se caracteriza por la aplicación de la regresión lineal y el análisis de series temporales a los datos económicos.

Ragnar Frisch acuñó la palabra "econometría" y ayudó a fundar tanto la Econometric Society en 1930 como la revista Econometrica en 1933. ^{[120] [121]} Un estudiante de Frisch, Trygve Haavelmo publicó The Probability Approach in Econometrics en 1944, donde afirmó que el análisis estadístico preciso podría usarse como una herramienta para validar teorías matemáticas sobre actores económicos con datos de fuentes complejas. ^[122] Esta vinculación del análisis estadístico de sistemas a la teoría económica también fue promulgada por la Comisión Cowles (ahora la Fundación Cowles ) a lo largo de los años 1930 y 1940. ^[123]

Las raíces de la econometría moderna se remontan al economista estadounidense Henry L. Moore, que estudió la productividad agrícola e intentó ajustar los valores cambiantes de productividad de las parcelas de maíz y otros cultivos a una curva utilizando diferentes valores de elasticidad. Moore cometió varios errores en su trabajo, algunos de ellos debido a su elección de modelos y otros a las limitaciones en su uso de las matemáticas. La precisión de los modelos de Moore también se vio limitada por la escasez de datos de las cuentas nacionales en los Estados Unidos en ese momento. Si bien sus primeros modelos de producción eran estáticos, en 1925 publicó un modelo dinámico de "equilibrio móvil" diseñado para explicar los ciclos económicos; esta variación periódica a partir de la sobrecorrección en las curvas de oferta y demanda se conoce ahora como el modelo de la telaraña . Una derivación más formal de este modelo fue realizada más tarde por Nicholas Kaldor , a quien se le atribuye en gran medida su exposición. ^[124]

Gran parte de la economía clásica puede presentarse en términos geométricos simples o en notación matemática elemental. Sin embargo, la economía matemática convencionalmente hace uso del cálculo y del álgebra matricial en el análisis económico para hacer afirmaciones poderosas que serían más difíciles sin esas herramientas matemáticas. Estas herramientas son prerrequisitos para el estudio formal, no sólo en la economía matemática sino en la teoría económica contemporánea en general. Los problemas económicos a menudo involucran tantas variables que las matemáticas son la única manera práctica de abordarlos y resolverlos. Alfred Marshall sostuvo que todo problema económico que pueda cuantificarse, expresarse analíticamente y resolverse, debe tratarse por medio del trabajo matemático. ^[126]

La economía se ha vuelto cada vez más dependiente de los métodos matemáticos y las herramientas matemáticas que emplea se han vuelto más sofisticadas. Como resultado, las matemáticas se han vuelto considerablemente más importantes para los profesionales de la economía y las finanzas. Los programas de posgrado tanto en economía como en finanzas requieren una sólida preparación universitaria en matemáticas para la admisión y, por esta razón, atraen a un número cada vez mayor de matemáticos . Los matemáticos aplicados aplican principios matemáticos a problemas prácticos, como el análisis económico y otras cuestiones relacionadas con la economía, y muchos problemas económicos a menudo se definen como integrados en el ámbito de las matemáticas aplicadas. ^[18]

Esta integración resulta de la formulación de los problemas económicos como modelos estilizados con supuestos claros y predicciones refutables. Esta modelización puede ser informal o prosaica, como en La riqueza de las naciones de Adam Smith , o puede ser formal, rigurosa y matemática.

En términos generales, los modelos económicos formales pueden clasificarse como estocásticos o deterministas y como discretos o continuos. En la práctica, el modelado cuantitativo se aplica a muchas áreas de la economía y varias metodologías han evolucionado de manera más o menos independiente unas de otras. ^[127]

• Los modelos estocásticos se formulan utilizando procesos estocásticos . Modelan valores observables económicamente a lo largo del tiempo. La mayor parte de la econometría se basa en estadísticas para formular y probar hipótesis sobre estos procesos o estimar parámetros para ellos. Entre las dos guerras mundiales, Herman Wold desarrolló una representación de los procesos estocásticos estacionarios en términos de modelos autorregresivos y una tendencia determinista. Wold y Jan Tinbergen aplicaron el análisis de series temporales a los datos económicos. La investigación contemporánea sobre las estadísticas de series temporales considera formulaciones adicionales de procesos estacionarios, como los modelos autorregresivos de promedio móvil . Los modelos más generales incluyen los modelos autorregresivos de heterocedasticidad condicional (ARCH) y los modelos ARCH generalizados ( GARCH ).
• Los modelos matemáticos no estocásticos pueden ser puramente cualitativos (por ejemplo, los modelos que intervienen en algún aspecto de la teoría de la elección social ) o cuantitativos (que implican la racionalización de variables financieras, por ejemplo, con coordenadas hiperbólicas , y/o formas específicas de relaciones funcionales entre variables). En algunos casos, las predicciones económicas de un modelo simplemente afirman la dirección del movimiento de las variables económicas, por lo que las relaciones funcionales se utilizan solo en un sentido cualitativo: por ejemplo, si el precio de un artículo aumenta, entonces la demanda de ese artículo disminuirá. Para tales modelos, los economistas a menudo utilizan gráficos bidimensionales en lugar de funciones.
• En ocasiones se utilizan modelos cualitativos . Un ejemplo es la planificación de escenarios cualitativos en los que se representan posibles eventos futuros. Otro ejemplo es el análisis de árboles de decisión no numéricos. Los modelos cualitativos suelen adolecer de falta de precisión.

El gran atractivo de la economía matemática es que aporta un grado de rigor al pensamiento económico, en particular en torno a temas políticos delicados. Por ejemplo, durante el debate sobre la eficacia de un recorte de impuestos corporativos para aumentar los salarios de los trabajadores, un modelo matemático simple resultó beneficioso para comprender los problemas en cuestión.

Como ejercicio intelectual, el profesor Greg Mankiw de la Universidad de Harvard planteó el siguiente problema : ^[128]

Una economía abierta tiene la función de producción , donde es la producción por trabajador y es el capital por trabajador. El stock de capital se ajusta de modo que el producto marginal del capital después de impuestos sea igual a la tasa de interés mundial dada exógenamente ... ¿Cuánto aumentarán los salarios con la reducción de impuestos?${\textstyle y=f(k)}$${\textstyle y}$${\textstyle k}$${\textstyle r}$

Para responder a esta pregunta, seguimos a John H. Cochrane de la Hoover Institution . ^[129] Supongamos que una economía abierta tiene la función de producción : Donde las variables en esta ecuación son:$${\displaystyle Y=F(K,L)=f(k)L,\quad k=K/L}$$

• ${\textstyle Y}$es la producción total
• ${\textstyle F(K,L)}$es la función de producción
• ${\textstyle K}$es el capital social total
• ${\textstyle L}$es el stock total de mano de obra

La opción estándar para la función de producción es la función de producción Cobb-Douglas : donde es el factor de productividad , asumido como constante. Un recorte de impuestos corporativos en este modelo es equivalente a un impuesto al capital. Con los impuestos, las empresas buscan maximizar: donde es la tasa de impuesto al capital, son los salarios por trabajador y es la tasa de interés exógena. Entonces las condiciones de optimalidad de primer orden se convierten en: Por lo tanto, las condiciones de optimalidad implican que: Defina los impuestos totales . Esto implica que los impuestos por trabajador son: Entonces el cambio en los impuestos por trabajador, dada la tasa de impuesto, es: Para encontrar el cambio en los salarios, diferenciamos la segunda condición de optimalidad para los salarios por trabajador para obtener: Suponiendo que la tasa de interés está fija en , de modo que , podemos diferenciar la primera condición de optimalidad para la tasa de interés para encontrar: Por el momento, centrémonos solo en el efecto estático de un recorte de impuestos al capital, de modo que . Si sustituimos esta ecuación en la ecuación para los cambios salariales con respecto a la tasa impositiva, entonces encontramos que: Por lo tanto, el efecto estático de un recorte de impuestos al capital sobre los salarios es: Con base en el modelo, parece posible que podamos lograr un aumento en el salario de un trabajador mayor que el monto del recorte de impuestos. Pero eso solo considera el efecto estático, y sabemos que el efecto dinámico debe tenerse en cuenta. En el modelo dinámico, podemos reescribir la ecuación para los cambios en los impuestos por trabajador con respecto a la tasa impositiva como: Recordando que , tenemos que: Usando la función de producción Cobb-Douglas, tenemos que: Por lo tanto, el efecto dinámico de un recorte de impuestos al capital sobre los salarios es: Si tomamos , entonces el efecto dinámico de reducir los impuestos al capital sobre los salarios será incluso mayor que el efecto estático. Además, si hay externalidades positivas para la acumulación de capital , el efecto del recorte de impuestos sobre los salarios sería mayor que en el modelo que acabamos de derivar. Es importante notar que el resultado es una combinación de:$${\displaystyle Y=AK^{\alpha }L^{1-\alpha }=Ak^{\alpha }L,\quad \alpha \in [0,1]}$$${\textstyle A}$$${\displaystyle J=\max _{K,L}\;(1-\tau )\left[F(K,L)-wL\right]-rK\equiv \max _{K,L}\;(1-\tau )\left[f(k)-w\right]L-rK}$$${\textstyle \tau }$${\textstyle w}$${\textstyle r}$$${\displaystyle {\begin{aligned}{\frac {\partial J}{\partial K}}&=(1-\tau )f'(k)-r\\{\frac {\partial J}{\partial L}}&=(1-\tau )\left[f(k)-f'(k)k-w\right]\end{aligned}}}$$$${\displaystyle r=(1-\tau )f'(k),\quad w=f(k)-f'(k)k}$$${\textstyle X=\tau [F(K,L)-wL]}$${\textstyle x}$$${\displaystyle x=\tau [f(k)-w]=\tau f'(k)k}$$$${\displaystyle {dx \over {d\tau }}=\underbrace {f'(k)k} _{\text{Static}}+\underbrace {\tau \left[f'(k)+f''(k)k\right]{dk \over {d\tau }}} _{\text{Dynamic}}}$$$${\displaystyle {\frac {dw}{d\tau }}=\left[f'(k)-f'(k)-f''(k)k\right]{\frac {dk}{d\tau }}=-f''(k)k{\frac {dk}{d\tau }}}$$${\textstyle r}$${\textstyle dr/d\tau =0}$$${\displaystyle {dk \over {d\tau }}={f'(k) \over {(1-\tau )f''(k)}}}$$${\textstyle dx/d\tau =f'(k)k}$$${\displaystyle {dw \over {d\tau }}=-{\frac {f'(k)k}{1-\tau }}=-{1 \over {1-\tau }}{\frac {dx}{d\tau }}}$$$${\displaystyle {dw \over {dx}}=-{1 \over {1-\tau }}}$$$${\displaystyle {\begin{aligned}{dx \over {d\tau }}&=f'(k)k+\tau \left[f'(k)+f''(k)k\right]{dk \over {d\tau }}\\&=f'(k)k+{\tau \over {1-\tau }}{[f'(k)]^{2}+f'(k)f''(k)k \over {f''(k)}}\\&={\tau \over {1-\tau }}{f'(k)^{2} \over {f''(k)}}+{1 \over {1-\tau }}f'(k)k\\&={f'(k) \over {1-\tau }}\left[\tau {f'(k) \over {f''(k)}}+k\right]\end{aligned}}}$$${\textstyle dw/d\tau =-f'(k)k/(1-\tau )}$$${\displaystyle {\frac {dw}{dx}}=-{{\frac {f'(k)k}{1-\tau }} \over {{\frac {f'(k)}{1-\tau }}\left[\tau {\frac {f'(k)}{f''(k)}}+k\right]}}=-{\frac {1}{\tau {\frac {f'(k)}{kf''(k)}}+1}}}$$$${\displaystyle {f'(k) \over {kf''(k)}}=-{1 \over {1-\alpha }}}$$$${\displaystyle {dw \over {dx}}=-{1-\alpha \over {1-\tau -\alpha }}}$$${\textstyle \alpha =\tau =1/3}$

1. El resultado estándar de que en una economía pequeña y abierta el trabajo soporta el 100% del impuesto sobre la renta del capital pequeño
2. El hecho de que, a partir de una tasa impositiva positiva, la carga de un aumento de impuestos exceda la recaudación de ingresos debido a la pérdida irrecuperable de primer orden.

Este resultado, que muestra que, en determinadas hipótesis, un recorte de impuestos a las empresas puede aumentar los salarios de los trabajadores en una cantidad mayor que la pérdida de ingresos, no implica que la magnitud sea correcta. Más bien, sugiere una base para el análisis de políticas que no se basa en vaguedades. Si las hipótesis son razonables, entonces el modelo es una aproximación aceptable a la realidad; si no lo son, entonces se deberían desarrollar modelos mejores.

Ahora supongamos que en lugar de la función de producción Cobb-Douglas tenemos una función de producción de elasticidad constante de sustitución (CES) más general : donde ; es la elasticidad de sustitución entre capital y trabajo. La cantidad relevante que queremos calcular es , que puede derivarse como: Por lo tanto, podemos usar esto para encontrar que: Por lo tanto, bajo un modelo CES general, el efecto dinámico de un recorte de impuestos al capital sobre los salarios es: Recuperamos la solución Cobb-Douglas cuando . Cuando , que es el caso cuando existen sustitutos perfectos, encontramos que - no hay efecto de cambios en los impuestos al capital sobre los salarios. Y cuando , que es el caso cuando existen complementos perfectos, encontramos que - un recorte en los impuestos al capital aumenta los salarios en exactamente un dólar.$${\displaystyle f(k)=A\left[\alpha k^{\rho }+(1-\alpha )\right]^{1/\rho }}$$${\textstyle \rho =1-\sigma ^{-1}}$${\textstyle \sigma }$${\textstyle f'/kf''}$$${\displaystyle {f' \over {kf''}}=-{1 \over {1-\rho -{\alpha (1-\rho ) \over {\alpha +(1-\alpha )k^{-\rho }}}}}}$$$${\displaystyle {\begin{aligned}1+\tau {f' \over {kf''}}&=1-{\tau [\alpha +(1-\alpha )k^{-\rho }] \over {(1-\rho )[\alpha +(1-\alpha )k^{-\rho }]-\alpha (1-\rho )}}\\[6pt]&={(1-\rho -\tau )[\alpha +(1-\alpha )k^{-\rho }]-\alpha (1-\rho ) \over {(1-\rho )[\alpha +(1-\alpha )k^{-\rho }]-\alpha (1-\rho )}}\end{aligned}}}$$$${\displaystyle {dw \over {dx}}=-{(1-\rho )[\alpha +(1-\alpha )k^{-\rho }]-\alpha (1-\rho ) \over {(1-\rho -\tau )[\alpha +(1-\alpha )k^{-\rho }]-\alpha (1-\rho )}}}$$${\textstyle \rho =0}$${\textstyle \rho =1}$${\textstyle dw/dx=0}$${\textstyle \rho =-\infty }$${\textstyle dw/dx=-1}$

La escuela austriaca —si bien utiliza muchos de los mismos argumentos económicos normativos que los economistas convencionales de tradiciones marginalistas, como la escuela de Chicago— difiere metodológicamente de las escuelas neoclásicas de economía convencionales, en particular en sus agudas críticas a la matematización de la economía. ^[130] Friedrich Hayek sostuvo que el uso de técnicas formales proyecta una exactitud científica que no da cuenta apropiadamente de las limitaciones informativas que enfrentan los agentes económicos reales. ^[131]

En una entrevista de 1999, el historiador económico Robert Heilbroner afirmó: ^[132]

Supongo que el enfoque científico empezó a penetrar y pronto dominó la profesión en los últimos veinte o treinta años. Esto se produjo en parte debido a la "invención" de análisis matemáticos de diversos tipos y, de hecho, a mejoras considerables en él. Esta es la era en la que no sólo tenemos más datos sino un uso más sofisticado de los mismos. Por lo tanto, existe una fuerte sensación de que se trata de una ciencia cargada de datos y una tarea cargada de datos, que, en virtud de los números puros, las ecuaciones puras y el aspecto puro de una página de revista, tiene cierta semejanza con la ciencia... Esa actividad central parece científica. Lo entiendo. Creo que es genuino. Se acerca a ser una ley universal. Pero parecerse a una ciencia es diferente a ser una ciencia.

Heilbroner afirmó que "una parte o gran parte de la economía no es naturalmente cuantitativa y, por lo tanto, no se presta a la exposición matemática". ^[133]

El filósofo Karl Popper analizó la posición científica de la economía en los años 1940 y 1950. Sostuvo que la economía matemática adolecía de ser tautológica. En otras palabras, en la medida en que la economía se convirtió en una teoría matemática, dejó de depender de la refutación empírica para pasar a depender de pruebas y refutaciones matemáticas. ^[134] Según Popper, los supuestos refutables pueden comprobarse mediante experimentos y observaciones, mientras que los supuestos infalsables pueden explorarse matemáticamente para determinar sus consecuencias y su coherencia con otros supuestos. ^[135]

Milton Friedman, que compartía las preocupaciones de Popper sobre los supuestos en la economía en general, y no sólo en la economía matemática, declaró que "todos los supuestos son irreales". Friedman propuso juzgar los modelos económicos por su desempeño predictivo en lugar de por la correspondencia entre sus supuestos y la realidad. ^[136]

Considerando la economía matemática, JM Keynes escribió en La teoría general : ^[137]

Un gran defecto de los métodos pseudomatemáticos simbólicos para formalizar un sistema de análisis económico es que presuponen expresamente una estricta independencia entre los factores implicados y pierden su coherencia y autoridad si se rechaza esta hipótesis; mientras que en el discurso ordinario, en el que no manipulamos ciegamente y sabemos todo el tiempo lo que hacemos y lo que significan las palabras, podemos guardar "en el fondo de la cabeza" las reservas y calificaciones necesarias y los ajustes que tendremos que hacer más adelante, de un modo en que no podemos guardar complicadas derivadas parciales "en el fondo" de varias páginas de álgebra que suponen que todas desaparecen. Una proporción demasiado grande de la economía "matemática" reciente son meras invenciones, tan imprecisas como las suposiciones iniciales en las que se basan, que permiten al autor perder de vista las complejidades e interdependencias del mundo real en un laberinto de símbolos pretenciosos e inútiles.

En respuesta a estas críticas, Paul Samuelson sostuvo que las matemáticas son un lenguaje, repitiendo una tesis de Josiah Willard Gibbs . En economía, el lenguaje de las matemáticas es a veces necesario para representar problemas sustantivos. Además, la economía matemática ha llevado a avances conceptuales en economía. ^[138] En particular, Samuelson dio el ejemplo de la microeconomía , escribiendo que "pocas personas son lo suficientemente ingeniosas como para comprender [sus] partes más complejas... sin recurrir al lenguaje de las matemáticas, mientras que la mayoría de las personas comunes pueden hacerlo con bastante facilidad con la ayuda de las matemáticas". ^[139]

Algunos economistas afirman que la economía matemática merece apoyo al igual que otras formas de matemáticas, particularmente sus vecinas en la optimización matemática y la estadística matemática y cada vez más en la informática teórica . La economía matemática y otras ciencias matemáticas tienen una historia en la que los avances teóricos han contribuido regularmente a la reforma de las ramas más aplicadas de la economía. En particular, siguiendo el programa de John von Neumann , la teoría de juegos ahora proporciona las bases para describir gran parte de la economía aplicada, desde la teoría de la decisión estadística (como "juegos contra la naturaleza") y la econometría hasta la teoría del equilibrio general y la organización industrial. En la última década, con el auge de Internet, los economistas matemáticos y los expertos en optimización y los científicos informáticos han trabajado en problemas de fijación de precios para servicios en línea --- sus contribuciones utilizando matemáticas de la teoría de juegos cooperativos, la optimización no diferenciable y los juegos combinatorios.

Robert M. Solow concluyó que la economía matemática era la " infraestructura " central de la economía contemporánea:

La economía ya no es un tema de conversación apropiado para damas y caballeros. Se ha convertido en un tema técnico. Como cualquier tema técnico, atrae a algunas personas que están más interesadas en la técnica que en el tema. Es una lástima, pero puede ser inevitable. En cualquier caso, no se engañe: el núcleo técnico de la economía es una infraestructura indispensable para la economía política. Por eso, si consulta [una referencia en economía contemporánea] buscando información sobre el mundo de hoy, se encontrará con economía técnica, o con historia, o con nada en absoluto. ^[140]

Entre los economistas matemáticos destacados se incluyen los siguientes:

• Econofísica
• Finanzas matemáticas

• Alpha C. Chiang y Kevin Wainwright, [1967] 2005. Métodos fundamentales de economía matemática , McGraw-Hill Irwin. Contenido.
• E. Roy Weintraub , 1982. Matemáticas para economistas , Cambridge. Contenido.
• Stephen Glaister , 1984. Métodos matemáticos para economistas , 3.ª ed., Blackwell. Contenido.
• Akira Takayama, 1985. Economía matemática , 2.ª ed. Cambridge. Contenido.
• Nancy L. Stokey y Robert E. Lucas con Edward Prescott , 1989. Métodos recursivos en dinámica económica , Harvard University Press. Descripción y enlaces a vistas previas de capítulos.
• AK Dixit , [1976] 1990. Optimization in Economic Theory , 2.ª ed., Oxford. Descripción y vista previa de contenidos.
• Kenneth L. Judd , 1998. Métodos numéricos en economía , MIT Press. Descripción y enlaces a vistas previas de capítulos.
• Michael Carter, 2001. Fundamentos de economía matemática , MIT Press. Contenido.
• Ferenc Szidarovszky y Sándor Molnár, 2002. Introducción a la teoría de matrices: con aplicaciones a los negocios y la economía , World Scientific Publishing. Descripción y vista previa.
• D. Wade Hands, 2004. Introducción a la economía matemática , 2.ª ed. Oxford. Contenido.
• Giancarlo Gandolfo, [1997] 2009. Economic Dynamics , 4ª ed., Springer. Descripción y avance.
• John Stachurski, 2009. Economic Dynamics: Theory and Computation , MIT Press. Descripción y vista previa.

Wikiquote tiene citas relacionadas con Economía matemática .

Busque economía matemática en Wikcionario, el diccionario libre.

• Revista de Economía Matemática Objetivos y alcance
• Máster Erasmus Mundus QEM - Modelos y métodos de economía cuantitativa, Los modelos y métodos de la economía cuantitativa - QEM