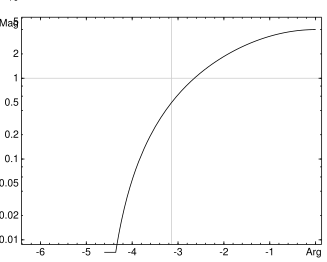
Diagrama de Bode

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Bode plot" – news · newspapers · books · scholar · JSTOR (December 2011) (Learn how and when to remove this message)

En ingeniería eléctrica y teoría de control , un diagrama de Bode ( / ˈb oʊ d i / BOH - dee ) es un gráfico de la respuesta de frecuencia de un sistema. Suele ser una combinación de un diagrama de magnitud de Bode , que expresa la magnitud (normalmente en decibelios ) de la respuesta de frecuencia, y un diagrama de fase de Bode , que expresa el desplazamiento de fase .

Tal como lo concibió originalmente Hendrik Wade Bode en la década de 1930, el gráfico es una aproximación asintótica de la respuesta de frecuencia, utilizando segmentos de línea recta . ^[1]

Entre sus varias contribuciones importantes a la teoría de circuitos y la teoría de control , el ingeniero Hendrik Wade Bode , mientras trabajaba en Bell Labs en la década de 1930, ideó un método simple pero preciso para graficar gráficos de ganancia y desplazamiento de fase. Estos llevan su nombre, diagrama de ganancia de Bode y diagrama de fase de Bode . "Bode" a menudo se pronuncia / ˈb oʊ d i / BOH -dee , aunque la pronunciación holandesa es [ ˈboːdə] , más cercana al inglés / ˈb oʊ d ə / BOH -də . ^{[2] [3]}

Bode se enfrentó al problema de diseñar amplificadores estables con retroalimentación para su uso en redes telefónicas. Desarrolló la técnica de diseño gráfico de los diagramas de Bode para mostrar el margen de ganancia y el margen de fase necesarios para mantener la estabilidad ante variaciones en las características del circuito causadas durante la fabricación o durante el funcionamiento. ^[4] Los principios desarrollados se aplicaron a problemas de diseño de servomecanismos y otros sistemas de control con retroalimentación. El diagrama de Bode es un ejemplo de análisis en el dominio de la frecuencia .

El diagrama de Bode para un sistema lineal, invariante en el tiempo con función de transferencia ( siendo la frecuencia compleja en el dominio de Laplace ) consta de un diagrama de magnitud y un diagrama de fase.${\displaystyle H(s)}$${\displaystyle s}$

El diagrama de magnitud de Bode es el gráfico de la función de frecuencia ( siendo la unidad imaginaria ). El eje del diagrama de magnitud es logarítmico y la magnitud se expresa en decibeles , es decir, se traza un valor para la magnitud en el eje en .${\displaystyle |H(s=j\omega )|}$${\displaystyle \omega }$${\displaystyle j}$${\displaystyle \omega }$${\displaystyle |H|}$${\displaystyle 20\log _{10}|H|}$

El diagrama de fase de Bode es el gráfico de la fase , comúnmente expresada en grados, de la función de transferencia en función de . La fase se representa en el mismo eje logarítmico que el diagrama de magnitud, pero el valor de la fase se representa en un eje vertical lineal.${\displaystyle \arg \left(H(s=j\omega )\right)}$${\displaystyle \omega }$${\displaystyle \omega }$

Esta sección ilustra que un diagrama de Bode es una visualización de la respuesta de frecuencia de un sistema.

Consideremos un sistema lineal invariante en el tiempo con función de transferencia . Supongamos que el sistema está sujeto a una entrada sinusoidal con frecuencia ,${\displaystyle H(s)}$${\displaystyle \omega }$

${\displaystyle u(t)=\sin(\omega t),}$

que se aplica de forma persistente, es decir, de vez en cuando . La respuesta será de la forma${\displaystyle -\infty }$${\displaystyle t}$

${\displaystyle y(t)=y_{0}\sin(\omega t+\varphi ),}$

es decir, también una señal sinusoidal con amplitud desplazada por una fase con respecto a la entrada.${\displaystyle y_{0}}$${\displaystyle \varphi }$

Se puede demostrar ^[5] que la magnitud de la respuesta es

${\displaystyle y_{0}=|H(\mathrm {j} \omega )|}$

( 1 )

y que el cambio de fase es

${\displaystyle \varphi =\arg H(\mathrm {j} \omega ).}$

( 2 )

En resumen, sometido a una entrada con frecuencia , el sistema responde a la misma frecuencia con una salida amplificada por un factor y desfasada por . Estas cantidades, por tanto, caracterizan la respuesta en frecuencia y se muestran en el diagrama de Bode.${\displaystyle \omega }$${\displaystyle |H(\mathrm {j} \omega )|}$${\displaystyle \arg H(\mathrm {j} \omega )}$

Para muchos problemas prácticos, los diagramas de Bode detallados se pueden aproximar con segmentos de línea recta que son asíntotas de la respuesta precisa. El efecto de cada uno de los términos de una función de transferencia de múltiples elementos se puede aproximar mediante un conjunto de líneas rectas en un diagrama de Bode. Esto permite una solución gráfica de la función de respuesta de frecuencia general. Antes de la disponibilidad generalizada de las computadoras digitales, se utilizaban ampliamente métodos gráficos para reducir la necesidad de cálculos tediosos; se podía utilizar una solución gráfica para identificar rangos factibles de parámetros para un nuevo diseño.

La premisa de un diagrama de Bode es que se puede considerar el logaritmo de una función en la forma

${\displaystyle f(x)=A\prod (x-c_{n})^{a_{n}}}$

como suma de los logaritmos de sus ceros y polos :

${\displaystyle \log(f(x))=\log(A)+\sum a_{n}\log(x-c_{n}).}$

Esta idea se utiliza explícitamente en el método para dibujar diagramas de fase. El método para dibujar gráficos de amplitud utiliza implícitamente esta idea, pero como el logaritmo de la amplitud de cada polo o cero siempre comienza en cero y solo tiene un cambio de asíntota (las líneas rectas), el método se puede simplificar.

La amplitud de decibeles se suele definir utilizando para ello. Dada una función de transferencia en la forma${\displaystyle {\text{dB}}=20\log _{10}(X)}$

${\displaystyle H(s)=A\prod {\frac {(s-x_{n})^{a_{n}}}{(s-y_{n})^{b_{n}}}},}$

donde y son constantes, , , y es la función de transferencia:${\displaystyle x_{n}}$${\displaystyle y_{n}}$${\displaystyle s=\mathrm {j} \omega }$${\displaystyle a_{n},b_{n}>0}$${\displaystyle H}$

• En cada valor de s donde (un cero), aumenta la pendiente de la línea en por década .${\displaystyle \omega =x_{n}}$${\displaystyle 20a_{n}\ {\text{dB}}}$
• En cada valor de s donde (un polo), disminuye la pendiente de la línea en por década.${\displaystyle \omega =y_{n}}$${\displaystyle 20b_{n}\ {\text{dB}}}$
• El valor inicial del gráfico depende de los límites. El punto inicial se encuentra introduciendo la frecuencia angular inicial en la función y hallando .${\displaystyle \omega }$${\displaystyle |H(\mathrm {j} \omega )|}$
• La pendiente inicial de la función en el valor inicial depende del número y orden de ceros y polos que estén en valores inferiores al valor inicial, y se encuentra utilizando las dos primeras reglas.

Para manejar polinomios irreducibles de segundo orden, puede, en muchos casos, aproximarse como .${\displaystyle ax^{2}+bx+c}$${\displaystyle ({\sqrt {a}}x+{\sqrt {c}})^{2}}$

Nótese que los ceros y los polos aparecen cuando es igual a un cierto valor o . Esto se debe a que la función en cuestión es la magnitud de , y dado que es una función compleja, . Por lo tanto, en cualquier lugar donde haya un cero o un polo que involucre al término , la magnitud de ese término es .${\displaystyle \omega }$${\displaystyle x_{n}}$${\displaystyle y_{n}}$${\displaystyle H(\mathrm {j} \omega )}$${\displaystyle |H(\mathrm {j} \omega )|={\sqrt {H\cdot H^{*}}}}$${\displaystyle (s+x_{n})}$${\displaystyle {\sqrt {(x_{n}+\mathrm {j} \omega )(x_{n}-\mathrm {j} \omega )}}={\sqrt {x_{n}^{2}+\omega ^{2}}}}$

Para corregir un gráfico de amplitud en línea recta:

• En cada cero, coloque un punto encima de la línea.${\displaystyle 3a_{n}\ {\text{dB}}}$
• En cada polo, coloque un punto debajo de la línea.${\displaystyle 3b_{n}\ {\text{dB}}}$
• Dibuje una curva suave a través de esos puntos usando las líneas rectas como asíntotas (líneas a las que se aproxima la curva).

Tenga en cuenta que este método de corrección no incorpora cómo manejar valores complejos de o . En el caso de un polinomio irreducible, la mejor manera de corregir el gráfico es calcular la magnitud de la función de transferencia en el polo o cero correspondiente al polinomio irreducible y colocar ese punto sobre o debajo de la línea en ese polo o cero.${\displaystyle x_{n}}$${\displaystyle y_{n}}$

Dada una función de transferencia en la misma forma que la anterior,

${\displaystyle H(s)=A\prod {\frac {(s-x_{n})^{a_{n}}}{(s-y_{n})^{b_{n}}}},}$

La idea es dibujar gráficos separados para cada polo y cero, y luego sumarlos. La curva de fase real está dada por

${\displaystyle \varphi (s)=-\arctan {\frac {\operatorname {Im} [H(s)]}{\operatorname {Re} [H(s)]}}.}$

Para dibujar el diagrama de fase, para cada polo y cero:

• Si es positivo, la línea de inicio (con pendiente cero) está en 0°.${\displaystyle A}$
• Si es negativo, la línea de inicio (con pendiente cero) está en -180°.${\displaystyle A}$
• Si la suma del número de ceros y polos inestables es impar, agregue 180° a esa base.
• En cada (para ceros estables ), aumente la pendiente en grados por década, comenzando una década antes (por ejemplo, ).${\displaystyle \omega =|x_{n}|}$${\displaystyle -\operatorname {Re} (z)<0}$${\displaystyle 45a_{n}}$${\displaystyle \omega =|x_{n}|}$${\displaystyle |x_{n}|/10}$
• En cada (para polos estables ), disminuya la pendiente en grados por década, comenzando una década antes (por ejemplo, ).${\displaystyle \omega =|y_{n}|}$${\displaystyle -\operatorname {Re} (p)<0}$${\displaystyle 45b_{n}}$${\displaystyle \omega =|y_{n}|}$${\displaystyle |y_{n}|/10}$
• Los polos y ceros "inestables" (semiplano derecho) ( ) tienen un comportamiento opuesto.${\displaystyle \operatorname {Re} (s)>0}$
• Aplana la pendiente nuevamente cuando la fase haya cambiado en grados (para un cero) o grados (para un polo).${\displaystyle 90a_{n}}$${\displaystyle 90b_{n}}$
• Después de trazar una línea para cada polo o cero, sume las líneas para obtener el gráfico de fase final; es decir, el gráfico de fase final es la superposición de cada gráfico de fase anterior.

Para crear un gráfico de línea recta para un filtro de paso bajo de primer orden (unipolar), se considera la forma normalizada de la función de transferencia en términos de la frecuencia angular:

${\displaystyle H_{\text{lp}}(\mathrm {j} \omega )={\frac {1}{1+\mathrm {j} {\frac {\omega }{\omega _{\text{c}}}}}}.}$

El diagrama de Bode se muestra en la Figura 1(b) anterior, y a continuación se analiza la construcción de la aproximación en línea recta.

La magnitud (en decibeles ) de la función de transferencia anterior (normalizada y convertida a forma de frecuencia angular), dada por la expresión de ganancia en decibeles :${\displaystyle A_{\text{vdB}}}$

${\displaystyle {\begin{aligned}A_{\text{vdB}}&=20\log |H_{\text{lp}}(\mathrm {j} \omega )|\\&=20\log {\frac {1}{\left|1+\mathrm {j} {\frac {\omega }{\omega _{\text{c}}}}\right|}}\\&=-20\log \left|1+\mathrm {j} {\frac {\omega }{\omega _{\text{c}}}}\right|\\&=-10\log \left(1+{\frac {\omega ^{2}}{\omega _{\text{c}}^{2}}}\right).\end{aligned}}}$

Luego, graficado versus la frecuencia de entrada en una escala logarítmica, se puede aproximar mediante dos líneas , formando el diagrama de Bode de magnitud asintótica (aproximada) de la función de transferencia:${\displaystyle \omega }$

• La primera línea para frecuencias angulares a continuación es una línea horizontal a 0 dB, ya que a frecuencias bajas el término es pequeño y se puede descuidar, lo que hace que la ecuación de ganancia de decibeles anterior sea igual a cero.${\displaystyle \omega _{\text{c}}}$${\displaystyle \omega /\omega _{\text{c}}}$
• La segunda línea para frecuencias angulares anterior es una línea con una pendiente de −20 dB por década, ya que en frecuencias altas el término domina y la expresión de ganancia de decibeles anterior se simplifica a , que es una línea recta con una pendiente de −20 dB por década.${\displaystyle \omega _{\text{c}}}$${\displaystyle \omega /\omega _{\text{c}}}$${\displaystyle -20\log(\omega /\omega _{\text{c}})}$

Estas dos líneas se encuentran en la frecuencia de corte . En el gráfico se puede ver que para frecuencias muy por debajo de la frecuencia de corte, el circuito tiene una atenuación de 0 dB, que corresponde a una ganancia de banda de paso unitaria, es decir, la amplitud de la salida del filtro es igual a la amplitud de la entrada. Las frecuencias por encima de la frecuencia de corte se atenúan: cuanto mayor sea la frecuencia, mayor será la atenuación .${\displaystyle \omega _{\text{c}}}$

El diagrama de fase de Bode se obtiene trazando el ángulo de fase de la función de transferencia dada por

${\displaystyle \arg H_{\text{lp}}(\mathrm {j} \omega )=-\tan ^{-1}{\frac {\omega }{\omega _{\text{c}}}}}$

versus , donde y son las frecuencias angulares de entrada y de corte respectivamente. Para frecuencias de entrada mucho más bajas que la frecuencia de corte, la relación es pequeña y, por lo tanto, el ángulo de fase es cercano a cero. A medida que aumenta la relación, el valor absoluto de la fase aumenta y se convierte en −45° cuando . A medida que aumenta la relación para frecuencias de entrada mucho mayores que la frecuencia de corte, el ángulo de fase se acerca asintóticamente a −90°. La escala de frecuencia para el gráfico de fase es logarítmica.${\displaystyle \omega }$${\displaystyle \omega }$${\displaystyle \omega _{\text{c}}}$${\displaystyle \omega /\omega _{\text{c}}}$${\displaystyle \omega =\omega _{\text{c}}}$

El eje de frecuencia horizontal, tanto en los gráficos de magnitud como de fase, se puede reemplazar por la relación de frecuencia normalizada (adimensional) . En tal caso, se dice que el gráfico está normalizado y ya no se utilizan unidades de frecuencia, ya que todas las frecuencias de entrada se expresan ahora como múltiplos de la frecuencia de corte .${\displaystyle \omega /\omega _{\text{c}}}$${\displaystyle \omega _{\text{c}}}$

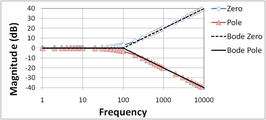
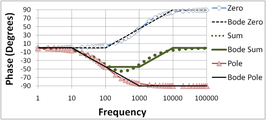
Las figuras 2 a 5 ilustran con más detalle la construcción de diagramas de Bode. Este ejemplo con un polo y un cero muestra cómo utilizar la superposición. Para comenzar, los componentes se presentan por separado.

La Figura 2 muestra el diagrama de magnitud de Bode para un polo cero y uno de paso bajo, y compara ambos con los diagramas de línea recta de Bode. Los diagramas de línea recta son horizontales hasta la ubicación del polo (cero) y luego caen (suben) a 20 dB/década. La segunda Figura 3 hace lo mismo para la fase. Los diagramas de fase son horizontales hasta un factor de frecuencia de diez por debajo de la ubicación del polo (cero) y luego caen (suben) a 45°/década hasta que la frecuencia es diez veces mayor que la ubicación del polo (cero). Luego, los diagramas son nuevamente horizontales a frecuencias más altas en un cambio de fase total final de 90°.

Las figuras 4 y 5 muestran cómo se realiza la superposición (simple adición) de un gráfico de polo y cero. Los gráficos de línea recta de Bode se comparan nuevamente con los gráficos exactos. El cero se ha movido a una frecuencia más alta que el polo para hacer un ejemplo más interesante. Observe en la figura 4 que la caída de 20 dB/década del polo se detiene por el aumento de 20 dB/década del cero, lo que da como resultado un gráfico de magnitud horizontal para frecuencias por encima de la ubicación del cero. Observe en la figura 5 en el gráfico de fase que la aproximación en línea recta es bastante aproximada en la región donde tanto el polo como el cero afectan la fase. Observe también en la figura 5 que el rango de frecuencias donde la fase cambia en el gráfico de línea recta está limitado a frecuencias un factor de diez por encima y por debajo de la ubicación del polo (cero). Cuando la fase del polo y del cero están presentes, el gráfico de fase en línea recta es horizontal porque la caída de 45°/década del polo se detiene por el aumento superpuesto de 45°/década del cero en el rango limitado de frecuencias donde ambos son contribuyentes activos a la fase.

• Ejemplo con polo y cero
• 
  Figura 2: Diagrama de magnitud de Bode para polos cero y de paso bajo; las curvas etiquetadas como "Bode" son los diagramas de Bode de línea recta
• 
  Figura 3: Diagrama de fase de Bode para polos cero y de paso bajo; las curvas etiquetadas como "Bode" son los diagramas de Bode de línea recta
• 
  Figura 4: Diagrama de magnitud de Bode para la combinación polo-cero; la ubicación del cero es diez veces más alta que en las figuras 2 y 3; las curvas etiquetadas como "Bode" son los diagramas de Bode de línea recta
• 
  Figura 5: Diagrama de fase de Bode para la combinación polo-cero; la ubicación del cero es diez veces más alta que en las figuras 2 y 3; las curvas etiquetadas como "Bode" son los diagramas de Bode de línea recta

Los diagramas de Bode se utilizan para evaluar la estabilidad de los amplificadores de retroalimentación negativa al encontrar los márgenes de ganancia y fase de un amplificador. La noción de ganancia y margen de fase se basa en la expresión de ganancia para un amplificador de retroalimentación negativa dada por

${\displaystyle A_{\text{FB}}={\frac {A_{\text{OL}}}{1+\beta A_{\text{OL}}}},}$

donde A _FB es la ganancia del amplificador con retroalimentación (la ganancia de lazo cerrado ), β es el factor de retroalimentación y A _OL es la ganancia sin retroalimentación (la ganancia de lazo abierto ). La ganancia A _OL es una función compleja de la frecuencia, con magnitud y fase. ^{[nota 1]} El examen de esta relación muestra la posibilidad de ganancia infinita (interpretada como inestabilidad) si el producto β A _OL = −1 (es decir, la magnitud de β A _OL es la unidad y su fase es −180°, el llamado criterio de estabilidad de Barkhausen ). Los diagramas de Bode se utilizan para determinar qué tan cerca está un amplificador de satisfacer esta condición.

La clave para esta determinación son dos frecuencias. La primera, denominada aquí f ₁₈₀ , es la frecuencia en la que la ganancia de lazo abierto cambia de signo. La segunda, denominada aquí f _{0 dB} , es la frecuencia en la que la magnitud del producto |β A _OL | = 1 = 0 dB. Es decir, la frecuencia f ₁₈₀ está determinada por la condición

${\displaystyle \beta A_{\text{OL}}(f_{180})=-|\beta A_{\text{OL}}(f_{180})|=-|\beta A_{\text{OL}}|_{180},}$

donde las barras verticales indican la magnitud de un número complejo y la frecuencia f _{0 dB} está determinada por la condición

${\displaystyle |\beta A_{\text{OL}}(f_{\text{0 dB}})|=1.}$

Una medida de proximidad a la inestabilidad es el margen de ganancia . El diagrama de fase de Bode ubica la frecuencia donde la fase de β A _OL alcanza −180°, denotada aquí como frecuencia f _180. Usando esta frecuencia, el diagrama de magnitud de Bode encuentra la magnitud de β A _OL . Si |β A _OL | ₁₈₀ ≥ 1, el amplificador es inestable, como se mencionó. Si |β A _OL | ₁₈₀ < 1, no ocurre inestabilidad, y la separación en dB de la magnitud de |β A _OL | ₁₈₀ de |β A _OL | = 1 se llama margen de ganancia . Debido a que una magnitud de 1 es 0 dB, el margen de ganancia es simplemente una de las formas equivalentes: .${\displaystyle 20\log _{10}|\beta A_{\text{OL}}|_{180}=20\log _{10}|A_{\text{OL}}|-20\log _{10}\beta ^{-1}}$

Otra medida equivalente de proximidad a la inestabilidad es el margen de fase . El diagrama de magnitud de Bode ubica la frecuencia donde la magnitud de |β A _OL | alcanza la unidad, denotada aquí como frecuencia f _{0 dB} . Usando esta frecuencia, el diagrama de fase de Bode encuentra la fase de β A _OL . Si la fase de β A _OL ( f _{0 dB} ) > −180°, la condición de inestabilidad no se puede cumplir en ninguna frecuencia (porque su magnitud va a ser < 1 cuando f = f ₁₈₀ ), y la distancia de la fase en f _{0 dB} en grados por encima de −180° se llama margen de fase .

Si todo lo que se necesita es una respuesta simple sí o no a la cuestión de la estabilidad, el amplificador es estable si f _{0 dB} < f ₁₈₀ . Este criterio es suficiente para predecir la estabilidad solo para amplificadores que satisfacen algunas restricciones en sus posiciones de polo y cero ( sistemas de fase mínima ). Aunque estas restricciones generalmente se cumplen, si no es así, se debe utilizar otro método, como el diagrama de Nyquist . ^{[6] [7]} Los márgenes óptimos de ganancia y fase se pueden calcular utilizando la teoría de interpolación de Nevanlinna-Pick . ^[8]

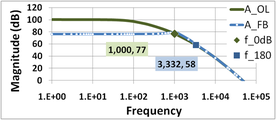
Las figuras 6 y 7 ilustran el comportamiento y la terminología de la ganancia. Para un amplificador de tres polos, la figura 6 compara el diagrama de Bode para la ganancia sin retroalimentación ( ganancia de lazo abierto ) A _OL con la ganancia con retroalimentación A _FB ( ganancia de lazo cerrado ). Consulte el amplificador con retroalimentación negativa para obtener más detalles.

En este ejemplo, A _OL = 100 dB a bajas frecuencias y 1 / β = 58 dB. A bajas frecuencias, A _FB ≈ 58 dB también.

Como se representa gráficamente la ganancia de lazo abierto A _{OL y no el producto β} A _OL , la condición A _OL = 1 / β determina que f _{0 dB . La ganancia de retroalimentación a frecuencias bajas y para} A _OL grande es A _FB ≈ 1 / β (observe la fórmula para la ganancia de retroalimentación al comienzo de esta sección para el caso de ganancia grande A _OL ), por lo que una forma equivalente de encontrar f _{0 dB} es mirar dónde la ganancia de retroalimentación se cruza con la ganancia de lazo abierto. (La frecuencia f _{0 dB} se necesita más adelante para encontrar el margen de fase).

Cerca de este cruce de las dos ganancias en f _{0 dB} , los criterios de Barkhausen casi se satisfacen en este ejemplo, y el amplificador de realimentación exhibe un pico masivo en ganancia (sería infinito si β A _OL = −1). Más allá de la frecuencia de ganancia unitaria f _{0 dB} , la ganancia de lazo abierto es suficientemente pequeña como para que A _FB ≈ A _OL (examine la fórmula al comienzo de esta sección para el caso de A _OL pequeño ).

La figura 7 muestra la comparación de fases correspondiente: la fase del amplificador de retroalimentación es casi cero hasta la frecuencia f ₁₈₀ , donde la ganancia de lazo abierto tiene una fase de −180°. En esta zona, la fase del amplificador de retroalimentación cae abruptamente hacia abajo para volverse casi igual a la fase del amplificador de lazo abierto. (Recuerde, A _FB ≈ A _{OL para} A _OL pequeño ).

Al comparar los puntos marcados en la Figura 6 y la Figura 7, se observa que la frecuencia de ganancia unitaria f _{0 dB} y la frecuencia de inversión de fase f ₁₈₀ son casi iguales en este amplificador, f ₁₈₀ ≈ f _{0 dB} ≈ 3,332 kHz, lo que significa que el margen de ganancia y el margen de fase son casi cero. El amplificador está al borde de la estabilidad.

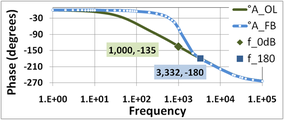
Las figuras 8 y 9 ilustran el margen de ganancia y el margen de fase para una cantidad diferente de retroalimentación β. El factor de retroalimentación se elige más pequeño que en la figura 6 o 7, lo que hace que la condición | β A _OL | = 1 pase a una frecuencia más baja. En este ejemplo, 1 / β = 77 dB, y a frecuencias bajas A _FB ≈ 77 dB también.

La figura 8 muestra el gráfico de ganancia. En la figura 8, la intersección de 1 / β y A _OL se produce en f _{0 dB} = 1 kHz. Observe que el pico en la ganancia A _FB cerca de f _{0 dB} casi ha desaparecido. ^{[nota 2] [9]}

La figura 9 es el diagrama de fase. Si se utiliza el valor de f _{0 dB} = 1 kHz que se encontró anteriormente en el diagrama de magnitud de la figura 8, la fase de bucle abierto en f _{0 dB} es −135°, lo que representa un margen de fase de 45° por encima de −180°.

Utilizando la Figura 9, para una fase de −180° el valor de f ₁₈₀ = 3,332 kHz (el mismo resultado que se encontró anteriormente, por supuesto ^{[nota 3]} ). La ganancia de lazo abierto de la Figura 8 en f ₁₈₀ es 58 dB, y 1 / β = 77 dB, por lo que el margen de ganancia es 19 dB.

La estabilidad no es el único criterio para la respuesta del amplificador y, en muchas aplicaciones, una exigencia más estricta que la estabilidad es una buena respuesta al escalón . Como regla general , una buena respuesta al escalón requiere un margen de fase de al menos 45° y, a menudo, se recomienda un margen de más de 70°, en particular cuando la variación de los componentes debido a las tolerancias de fabricación es un problema. ^[9] Véase también la discusión del margen de fase en el artículo sobre la respuesta al escalón .

• Ejemplos
• 
  Figura 6: Ganancia del amplificador de realimentación A _FB en dB y del amplificador de lazo abierto correspondiente A _OL . Parámetro 1/β = 58 dB, y a bajas frecuencias A _FB ≈ 58 dB también. El margen de ganancia en este amplificador es casi cero porque | β A _OL | = 1 ocurre a casi f = f _180° .
• 
  Figura 7: Fase del amplificador de realimentación °A _FB en grados y amplificador de lazo abierto correspondiente °A _OL . El margen de fase en este amplificador es casi cero porque el cambio de fase se produce casi en la frecuencia de ganancia unitaria f = f _{0 dB} donde | β A _OL | = 1.
• 
  Figura 8: Ganancia del amplificador de realimentación A _FB en dB y del amplificador de lazo abierto correspondiente A _OL . En este ejemplo, 1 / β = 77 dB. El margen de ganancia en este amplificador es de 19 dB.
• 
  Figura 9: Fase del amplificador de realimentación A _FB en grados y amplificador de lazo abierto correspondiente A _OL . El margen de fase en este amplificador es de 45°.

El trazador de Bode es un instrumento electrónico parecido a un osciloscopio , que produce un diagrama de Bode, o un gráfico, de la ganancia de voltaje o el desplazamiento de fase de un circuito graficado en función de la frecuencia en un sistema de control de retroalimentación o un filtro. Un ejemplo de esto se muestra en la Figura 10. Es extremadamente útil para analizar y probar filtros y la estabilidad de los sistemas de control de retroalimentación , a través de la medición de frecuencias de corte y márgenes de ganancia y fase.

Esto es idéntico a la función realizada por un analizador de red vectorial , pero el analizador de red normalmente se utiliza en frecuencias mucho más altas.

Para fines educativos y de investigación, trazar diagramas de Bode para funciones de transferencia dadas facilita una mejor comprensión y la obtención de resultados más rápidos (ver enlaces externos).

Dos gráficos relacionados que muestran los mismos datos en diferentes sistemas de coordenadas son el gráfico de Nyquist y el gráfico de Nichols . Estos son gráficos paramétricos , con la frecuencia como entrada y la magnitud y la fase de la respuesta de frecuencia como salida. El gráfico de Nyquist los muestra en coordenadas polares , con la magnitud asignada al radio y la fase al argumento (ángulo). El gráfico de Nichols los muestra en coordenadas rectangulares, en la escala logarítmica .

• 
  Figura 11: Un diagrama de Nyquist .
• 
  Figura 12: Un gráfico de Nichols de la misma respuesta de la Figura 11.

• Procesamiento de señales analógicas
• Margen de fase
• Integral de sensibilidad de Bode
• Relación magnitud (ganancia)-fase de Bode
• Espectroscopia de impedancia electroquímica

Wikimedia Commons alberga una categoría multimedia sobre Diagramas de Bode .

• Cómo dibujar diagramas de Bode asintóticos por partes
• Código Gnuplot para generar diagramas de Bode: Plantilla de impresión DIN-A4 (pdf)