Análisis de redes (circuitos eléctricos)
| Análisis de red lineal | |
|---|---|
| Elementos | |
| Componentes | |
| Circuitos en serie y en paralelo | |
| Transformadas de impedancia | |
| Teoremas generadores | Teoremas de redes |
| Métodos de análisis de redes | |
| Parámetros de dos puertos | |
En ingeniería eléctrica y electrónica , una red es una colección de componentes interconectados . El análisis de redes es el proceso de encontrar los voltajes y las corrientes a través de todos los componentes de la red. Existen muchas técnicas para calcular estos valores; sin embargo, en su mayoría, las técnicas suponen componentes lineales . Salvo que se indique lo contrario, los métodos descritos en este artículo solo son aplicables al análisis de redes lineales .
Definiciones
| Componente | Un dispositivo con dos o más terminales hacia dentro o hacia fuera del cual puede fluir corriente. |
| Nodo | Punto en el que se unen los terminales de más de dos componentes. Un conductor con una resistencia prácticamente nula se considera un nodo a efectos de análisis. |
| Rama | Los componentes que unen dos nodos. |
| Malla | Un grupo de ramas dentro de una red unidas para formar un bucle completo tal que no hay ningún otro bucle dentro de él. |
| Puerto | Dos terminales donde la corriente que entra en uno es idéntica a la corriente que sale del otro. |
| Circuito | Corriente que va desde un terminal de un generador a través de uno o más componentes de carga y de regreso al otro terminal. Un circuito es, en este sentido, una red de un solo puerto y es un caso trivial de analizar. Si hay alguna conexión con cualquier otro circuito, se ha formado una red no trivial y deben existir al menos dos puertos. A menudo, "circuito" y "red" se usan indistintamente, pero muchos analistas reservan el término "red" para referirse a un modelo idealizado que consta de componentes ideales. [1] |
| Función de transferencia | Relación de las corrientes y/o voltajes entre dos puertos. En la mayoría de los casos, se habla de un puerto de entrada y un puerto de salida y la función de transferencia se describe como ganancia o atenuación. |
| Función de transferencia de componentes | En el caso de un componente de dos terminales (es decir, un componente de un puerto), la corriente y el voltaje se toman como entrada y salida y la función de transferencia tendrá unidades de impedancia o admitancia (normalmente es una cuestión de conveniencia arbitraria si se considera la entrada el voltaje o la corriente). Un componente de tres (o más) terminales tiene efectivamente dos (o más) puertos y la función de transferencia no se puede expresar como una única impedancia. El enfoque habitual es expresar la función de transferencia como una matriz de parámetros. Estos parámetros pueden ser impedancias, pero hay una gran cantidad de otros enfoques (consulte la red de dos puertos ). |
Circuitos equivalentes

Un procedimiento útil en el análisis de redes consiste en simplificar la red reduciendo el número de componentes. Esto se puede hacer sustituyendo los componentes físicos por otros componentes teóricos que tengan el mismo efecto. Una técnica concreta puede reducir directamente el número de componentes, por ejemplo combinando impedancias en serie. Por otra parte, puede simplemente cambiar la forma a una en la que los componentes se puedan reducir en una operación posterior. Por ejemplo, se puede transformar un generador de tensión en un generador de corriente utilizando el teorema de Norton para poder combinar posteriormente la resistencia interna del generador con una carga de impedancia paralela.
Un circuito resistivo es un circuito que contiene solo resistencias , fuentes de corriente ideales y fuentes de voltaje ideales . Si las fuentes son fuentes constantes ( CC ), el resultado es un circuito de CC . El análisis de un circuito consiste en resolver los voltajes y las corrientes presentes en el circuito. Los principios de solución que se describen aquí también se aplican al análisis fasorial de circuitos de CA.
Se dice que dos circuitos son equivalentes con respecto a un par de terminales si el voltaje a través de los terminales y la corriente a través de los terminales de una red tienen la misma relación que el voltaje y la corriente en los terminales de la otra red.
Si esto implica para todos los valores (reales) de V 1 , entonces con respecto a los terminales ab y xy , el circuito 1 y el circuito 2 son equivalentes.
La definición anterior es suficiente para una red de un solo puerto . Para más de un puerto, se debe definir que las corrientes y voltajes entre todos los pares de puertos correspondientes deben guardar la misma relación. Por ejemplo, las redes en estrella y en triángulo son efectivamente redes de tres puertos y, por lo tanto, requieren tres ecuaciones simultáneas para especificar completamente su equivalencia.
Impedancias en serie y en paralelo
Algunas redes de impedancias de dos terminales pueden eventualmente reducirse a una única impedancia mediante aplicaciones sucesivas de impedancias en serie o impedancias en paralelo.
- Impedancias en serie :
- Impedancias en paralelo :
- Lo anterior simplificado para solo dos impedancias en paralelo:
Transformación delta-estrella

Una red de impedancias con más de dos terminales no se puede reducir a un circuito equivalente de una sola impedancia. Una red de n terminales se puede reducir, en el mejor de los casos, a n impedancias (en el peor de los casos , ). Para una red de tres terminales, las tres impedancias se pueden expresar como una red delta de tres nodos (Δ) o una red estrella de cuatro nodos (Y). Estas dos redes son equivalentes y las transformaciones entre ellas se dan a continuación. Una red general con un número arbitrario de nodos no se puede reducir al número mínimo de impedancias utilizando solo combinaciones en serie y en paralelo. En general, también se deben utilizar las transformaciones Y-Δ y Δ-Y. Para algunas redes, también puede ser necesaria la extensión de Y-Δ a transformaciones estrella-polígono.
Para que haya equivalencia, las impedancias entre cualquier par de terminales deben ser las mismas para ambas redes, lo que da como resultado un conjunto de tres ecuaciones simultáneas. Las ecuaciones que se muestran a continuación se expresan como resistencias, pero se aplican igualmente al caso general con impedancias.
Ecuaciones de transformación de delta a estrella
Ecuaciones de transformación de estrella a delta
Forma general de eliminación de nodos de red
Las transformaciones de estrella a triángulo y de resistencia en serie son casos especiales del algoritmo general de eliminación de nodos de la red de resistencias. Cualquier nodo conectado por N resistencias ( R 1 … R N ) a los nodos 1 … N puede reemplazarse por resistencias que interconecten los N nodos restantes. La resistencia entre dos nodos cualesquiera x, y está dada por:
Para una relación estrella-delta ( N = 3 ) esto se reduce a:
Para una reducción en serie ( N = 2 ) esto se reduce a:
Para una resistencia colgante ( N = 1 ) el resultado es la eliminación de la resistencia porque .
Transformación de la fuente

Un generador con una impedancia interna (es decir, un generador no ideal) se puede representar como un generador de voltaje ideal o como un generador de corriente ideal más la impedancia. Estas dos formas son equivalentes y las transformaciones se dan a continuación. Si las dos redes son equivalentes con respecto a los terminales ab, entonces V e I deben ser idénticos para ambas redes. Por lo tanto,
- o
- El teorema de Norton establece que cualquier red lineal de dos terminales puede reducirse a un generador de corriente ideal y una impedancia paralela.
- El teorema de Thévenin establece que cualquier red lineal de dos terminales puede reducirse a un generador de tensión ideal más una impedancia en serie.
Redes simples
Algunas redes muy simples pueden analizarse sin necesidad de aplicar enfoques más sistemáticos.
División de tensión de componentes en serie
Considere n impedancias que están conectadas en serie . El voltaje a través de cualquier impedancia es
División actual de componentes paralelos
Considere n admitancias que están conectadas en paralelo . La corriente a través de cualquier admitancia es
para
Caso especial: División de corriente de dos componentes paralelas
Análisis nodal
This section contains instructions, advice, or how-to content. (October 2022) |
El análisis nodal utiliza el concepto de voltaje de nodo y considera que los voltajes de nodo son las variables desconocidas. [2] : 2-8 - 2-9 Para todos los nodos, excepto un nodo de referencia elegido, el voltaje de nodo se define como la caída de voltaje desde el nodo hasta el nodo de referencia. Por lo tanto, hay N-1 voltajes de nodo para un circuito con N nodos. [2] : 2-10
En principio, el análisis nodal utiliza la ley de corrientes de Kirchhoff (LKC) en N-1 nodos para obtener N-1 ecuaciones independientes. Dado que las ecuaciones generadas con la KCL se expresan en términos de corrientes que entran y salen de los nodos, estas corrientes, si no se conocen sus valores, deben representarse mediante las variables desconocidas (voltajes de nodo). Para algunos elementos (como resistencias y capacitores), obtener las corrientes de los elementos en términos de voltajes de nodo es trivial.
Para algunos elementos comunes en los que esto no es posible, se desarrollan métodos especializados. Por ejemplo, se utiliza un concepto llamado supernodo para circuitos con fuentes de tensión independientes. [2] : 2-12 - 2-13
- Etiquete todos los nodos del circuito. Seleccione arbitrariamente cualquier nodo como referencia.
- Definir una variable de tensión desde cada nodo restante hasta la referencia. Estas variables de tensión deben definirse a medida que aumenta la tensión con respecto al nodo de referencia.
- Escriba una ecuación KCL para cada nodo excepto la referencia.
- Resolver el sistema de ecuaciones resultante.
Análisis de malla
This section contains instructions, advice, or how-to content. (October 2022) |
Malla : un bucle que no contiene un bucle interior.
- Cuente la cantidad de “cristales” del circuito. Asigne una corriente de malla a cada cristal de la ventana.
- Escriba una ecuación KVL para cada malla cuya corriente sea desconocida.
- Resolver las ecuaciones resultantes
Superposición
En este método, se calcula el efecto de cada generador por turno. Se eliminan todos los generadores excepto el que se está considerando y se los pone en cortocircuito en el caso de los generadores de tensión o en circuito abierto en el caso de los generadores de corriente. A continuación, se calcula la corriente total o el voltaje total a través de una rama en particular sumando todas las corrientes o voltajes individuales.
Este método parte de la premisa de que la corriente o el voltaje total es una superposición lineal de sus partes. Por lo tanto, el método no se puede utilizar si hay componentes no lineales. [2] : 6–14 La superposición de potencias no se puede utilizar para encontrar la potencia total consumida por los elementos, incluso en circuitos lineales. La potencia varía según el cuadrado del voltaje o la corriente totales y el cuadrado de la suma no suele ser igual a la suma de los cuadrados. La potencia total de un elemento se puede encontrar aplicando la superposición a los voltajes y la corriente de forma independiente y luego calculando la potencia a partir del voltaje y la corriente totales.
Elección del método
La elección del método [3] : 112–113 es hasta cierto punto una cuestión de gusto. Si la red es particularmente simple o solo se requiere una corriente o voltaje específico, la aplicación ad hoc de algunos circuitos equivalentes simples puede dar la respuesta sin recurrir a métodos más sistemáticos.
- Análisis nodal : el número de variables de tensión y, por lo tanto, de ecuaciones simultáneas para resolver, es igual al número de nodos menos uno. Cada fuente de tensión conectada al nodo de referencia reduce el número de incógnitas y ecuaciones en uno.
- Análisis de mallas : el número de variables de corriente y, por lo tanto, de ecuaciones simultáneas para resolver, es igual al número de mallas. Cada fuente de corriente en una malla reduce el número de incógnitas en uno. El análisis de mallas solo se puede utilizar con redes que se pueden dibujar como una red plana , es decir, sin componentes cruzados. [3] : 94
- La superposición es posiblemente el método conceptualmente más simple, pero rápidamente conduce a una gran cantidad de ecuaciones y combinaciones de impedancia desordenadas a medida que la red se hace más grande.
- Aproximaciones de medio efectivo : para una red que consta de una alta densidad de resistencias aleatorias, una solución exacta para cada elemento individual puede resultar poco práctica o imposible. En cambio, las propiedades de distribución de corriente y resistencia efectiva se pueden modelar en términos de medidas gráficas y propiedades geométricas de las redes. [4]
Función de transferencia
Una función de transferencia expresa la relación entre una entrada y una salida de una red. Para redes resistivas, esto siempre será un número real simple o una expresión que se reduce a un número real. Las redes resistivas se representan mediante un sistema de ecuaciones algebraicas simultáneas. Sin embargo, en el caso general de redes lineales, la red se representa mediante un sistema de ecuaciones diferenciales lineales simultáneas. En el análisis de redes, en lugar de utilizar las ecuaciones diferenciales directamente, es una práctica habitual realizar primero una transformada de Laplace sobre ellas y luego expresar el resultado en términos del parámetro de Laplace s, que en general es complejo . Esto se describe como trabajar en el dominio s . Trabajar con las ecuaciones directamente se describiría como trabajar en el dominio del tiempo (o t) porque los resultados se expresarían como cantidades que varían con el tiempo. La transformada de Laplace es el método matemático de transformación entre el dominio s y el dominio t.
Este enfoque es estándar en la teoría de control y es útil para determinar la estabilidad de un sistema, por ejemplo, en un amplificador con retroalimentación.
Funciones de transferencia de componentes de dos terminales
Para dos componentes terminales, la función de transferencia, o más generalmente para elementos no lineales, la ecuación constitutiva , es la relación entre la entrada de corriente al dispositivo y el voltaje resultante a través de él. La función de transferencia, Z(s), tendrá por lo tanto unidades de impedancia, ohmios. Para los tres componentes pasivos que se encuentran en las redes eléctricas, las funciones de transferencia son:
| Resistor | |
| Inductor | |
| Condensador |
Para una red a la que solo se aplican señales de CA constantes, s se reemplaza por jω y resultan los valores más familiares de la teoría de redes de CA.
| Resistor | |
| Inductor | |
| Condensador |
Finalmente, para una red a la que solo se aplica corriente continua constante, s se reemplaza por cero y se aplica la teoría de redes de corriente continua.
| Resistor | |
| Inductor | |
| Condensador |
Función de transferencia de red de dos puertos
En general, las funciones de transferencia en la teoría de control se simbolizan con el símbolo H(s). En electrónica, la función de transferencia se define como la relación entre el voltaje de salida y el voltaje de entrada y se simboliza con el símbolo A(s), o más comúnmente (porque el análisis se realiza invariablemente en términos de respuesta de onda sinusoidal), A ( jω ), de modo que:
La A representa atenuación o amplificación, según el contexto. En general, será una función compleja de jω , que se puede derivar de un análisis de las impedancias en la red y sus funciones de transferencia individuales. A veces, al analista solo le interesa la magnitud de la ganancia y no el ángulo de fase. En este caso, los números complejos se pueden eliminar de la función de transferencia y, en ese caso, se podría escribir como:
Dos parámetros de puerto
El concepto de una red de dos puertos puede ser útil en el análisis de redes como un enfoque de caja negra para el análisis. El comportamiento de la red de dos puertos en una red más grande se puede caracterizar completamente sin necesariamente indicar nada sobre la estructura interna. Sin embargo, para hacer esto es necesario tener más información que solo la A(jω) descrita anteriormente. Se puede demostrar que se requieren cuatro de estos parámetros para caracterizar completamente la red de dos puertos. Estos podrían ser la función de transferencia directa, la impedancia de entrada, la función de transferencia inversa (es decir, el voltaje que aparece en la entrada cuando se aplica un voltaje a la salida) y la impedancia de salida. Hay muchos otros (consulte el artículo principal para obtener una lista completa), uno de ellos expresa los cuatro parámetros como impedancias. Es habitual expresar los cuatro parámetros como una matriz;
La matriz puede abreviarse a un elemento representativo;
o simplemente
Estos conceptos se pueden extender a redes de más de dos puertos. Sin embargo, esto rara vez se hace en la realidad porque, en muchos casos prácticos, los puertos se consideran puramente de entrada o puramente de salida. Si se ignoran las funciones de transferencia de dirección inversa, una red multipuerto siempre se puede descomponer en varias redes de dos puertos.
Componentes distribuidos
Cuando una red está compuesta por componentes discretos, el análisis mediante redes de dos puertos es una cuestión de elección, no esencial. La red siempre se puede analizar alternativamente en términos de sus funciones de transferencia de componentes individuales. Sin embargo, si una red contiene componentes distribuidos , como en el caso de una línea de transmisión , entonces no es posible analizar en términos de componentes individuales ya que no existen. El enfoque más común para esto es modelar la línea como una red de dos puertos y caracterizarla utilizando parámetros de dos puertos (o algo equivalente a ellos). Otro ejemplo de esta técnica es modelar las portadoras que cruzan la región base en un transistor de alta frecuencia. La región base tiene que modelarse como resistencia y capacitancia distribuidas en lugar de componentes agrupados .
Análisis de imágenes
Las líneas de transmisión y algunos tipos de diseño de filtros utilizan el método de la imagen para determinar sus parámetros de transferencia. En este método, se considera el comportamiento de una cadena infinitamente larga de redes idénticas conectadas en cascada. A continuación, se calculan las impedancias de entrada y salida y las funciones de transmisión directa e inversa para esta cadena infinitamente larga. Aunque los valores teóricos así obtenidos nunca pueden realizarse exactamente en la práctica, en muchos casos sirven como una muy buena aproximación para el comportamiento de una cadena finita, siempre que no sea demasiado corta.
Análisis de red basado en el tiempo con simulación
La mayoría de los métodos de análisis calculan los valores de voltaje y corriente para redes estáticas, que son circuitos que consisten únicamente en componentes sin memoria pero que tienen dificultades con redes dinámicas complejas. En general, las ecuaciones que describen el comportamiento de un circuito dinámico están en forma de un sistema de ecuaciones diferenciales-algebraicas (DAE). Las DAE son difíciles de resolver y los métodos para hacerlo aún no se comprenden ni se desarrollan por completo (a fecha de 2010). Además, no existe un teorema general que garantice que las soluciones a las DAE existirán y serán únicas. [5] : 204–205 En casos especiales, las ecuaciones del circuito dinámico estarán en forma de ecuaciones diferenciales ordinarias (EDO), que son más fáciles de resolver, ya que los métodos numéricos para resolver EDO tienen una rica historia, que se remonta a fines del siglo XIX. Una estrategia para adaptar los métodos de solución de EDO a las DAE se llama discretización directa y es el método de elección en la simulación de circuitos. [5] : 204-205
Los métodos basados en simulación para el análisis de redes basado en el tiempo resuelven un circuito que se plantea como un problema de valor inicial (IVP). Es decir, los valores de los componentes con memorias (por ejemplo, los voltajes en los capacitores y las corrientes a través de los inductores) se dan en un punto inicial de tiempo t 0 , y el análisis se realiza para el tiempo . [5] : 206-207 Dado que no es posible encontrar resultados numéricos para el número infinito de puntos de tiempo desde t 0 hasta t f , este período de tiempo se discretiza en instancias de tiempo discretas, y la solución numérica se encuentra para cada instancia. El tiempo entre las instancias de tiempo se llama paso de tiempo y puede ser fijo a lo largo de toda la simulación o puede ser adaptativo .
En un método de ecuaciones diferenciales inverso, al buscar una solución para el tiempo t n+1 , ya se conoce la solución para el tiempo t n . Luego, se utiliza la discretización temporal para reemplazar las derivadas con diferencias, como en el caso del método de Euler inverso , donde h n+1 es el paso de tiempo. [5] : 266
Si todos los componentes del circuito fueran lineales o el circuito se hubiera linealizado de antemano, el sistema de ecuaciones en este punto es un sistema de ecuaciones lineales y se resuelve con métodos numéricos de álgebra lineal . De lo contrario, es un sistema de ecuaciones algebraicas no lineales y se resuelve con métodos numéricos no lineales como los algoritmos de búsqueda de raíces .
Comparación con otros métodos
Los métodos de simulación son mucho más aplicables que los métodos basados en la transformada de Laplace , como las funciones de transferencia, que solo funcionan para redes dinámicas simples con capacitores e inductores. Además, las señales de entrada a la red no se pueden definir de manera arbitraria para los métodos basados en la transformada de Laplace.
Redes no lineales
La mayoría de los diseños electrónicos son, en realidad, no lineales. Son muy pocos los que no incluyen algunos dispositivos semiconductores. Estos son invariablemente no lineales, la función de transferencia de una unión pn semiconductora ideal está dada por la misma relación no lineal;
dónde;
- i y v son la corriente y el voltaje instantáneos.
- I o es un parámetro arbitrario llamado corriente de fuga inversa cuyo valor depende de la construcción del dispositivo.
- V T es un parámetro proporcional a la temperatura llamado voltaje térmico e igual a aproximadamente 25 mV a temperatura ambiente.
Existen muchas otras formas en las que puede aparecer la no linealidad en una red. Todos los métodos que utilizan la superposición lineal fallarán cuando existan componentes no lineales. Existen varias opciones para abordar la no linealidad según el tipo de circuito y la información que el analista desee obtener.
Ecuaciones constitutivas
La ecuación del diodo anterior es un ejemplo de una ecuación constitutiva de elementos de la forma general,
Esto puede considerarse como una resistencia no lineal. Las ecuaciones constitutivas correspondientes para inductores y capacitores no lineales son respectivamente:
donde f es cualquier función arbitraria, φ es el flujo magnético almacenado y q es la carga almacenada.
Existencia, singularidad y estabilidad
Una consideración importante en el análisis no lineal es la cuestión de la unicidad. Para una red compuesta de componentes lineales siempre habrá una, y sólo una, solución única para un conjunto dado de condiciones de contorno. Esto no siempre es así en los circuitos no lineales. Por ejemplo, una resistencia lineal con una corriente fija aplicada a ella tiene sólo una solución para el voltaje a través de ella. Por otro lado, el diodo túnel no lineal tiene hasta tres soluciones para el voltaje para una corriente dada. Es decir, una solución particular para la corriente a través del diodo no es única, puede haber otras, igualmente válidas. En algunos casos puede que no haya ninguna solución en absoluto: debe considerarse la cuestión de la existencia de soluciones.
Otra consideración importante es la cuestión de la estabilidad. Puede existir una solución particular, pero puede no ser estable y alejarse rápidamente de ese punto ante el menor estímulo. Se puede demostrar que una red que sea absolutamente estable para todas las condiciones debe tener una, y sólo una, solución para cada conjunto de condiciones. [6]
Métodos
Análisis booleano de redes de conmutación
Un dispositivo de conmutación es aquel en el que se utiliza la no linealidad para producir dos estados opuestos. Los dispositivos CMOS en circuitos digitales, por ejemplo, tienen su salida conectada al riel de alimentación positivo o negativo y nunca se encuentran en ningún punto intermedio, excepto durante un período transitorio cuando el dispositivo está conmutando. En este caso, la no linealidad está diseñada para ser extrema y el analista puede aprovechar ese hecho. Este tipo de redes se pueden analizar utilizando álgebra booleana asignando los dos estados ("encendido"/"apagado", "positivo"/"negativo" o cualquier estado que se esté utilizando) a las constantes booleanas "0" y "1".
En este análisis se ignoran los transitorios, junto con cualquier ligera discrepancia entre el estado del dispositivo y el estado nominal asignado a un valor booleano. Por ejemplo, el valor booleano "1" puede asignarse al estado de +5 V. La salida del dispositivo puede ser de +4,5 V, pero el analista sigue considerando que es el valor booleano "1". Los fabricantes de dispositivos suelen especificar un rango de valores en sus hojas de datos que se considerarán indefinidos (es decir, el resultado será impredecible).
Los transitorios no son del todo carentes de interés para el analista. La tasa máxima de conmutación está determinada por la velocidad de transición de un estado a otro. Afortunadamente para el analista, para muchos dispositivos la mayor parte de la transición ocurre en la parte lineal de la función de transferencia del dispositivo y se puede aplicar el análisis lineal para obtener al menos una respuesta aproximada.
Es matemáticamente posible derivar álgebras de Boole que tengan más de dos estados. No se les ha encontrado demasiada utilidad en electrónica, aunque los dispositivos de tres estados son relativamente comunes.
Separación de análisis de sesgo y señal
Esta técnica se utiliza cuando el funcionamiento del circuito debe ser esencialmente lineal, pero los dispositivos utilizados para implementarlo no son lineales. Un amplificador de transistores es un ejemplo de este tipo de red. La esencia de esta técnica es separar el análisis en dos partes. En primer lugar, se analizan las polarizaciones de CC utilizando algún método no lineal. Esto establece el punto de funcionamiento en reposo del circuito. En segundo lugar, se analizan las características de pequeña señal del circuito utilizando el análisis de red lineal. A continuación se ofrecen ejemplos de métodos que se pueden utilizar para ambas etapas.
Método gráfico de análisis de corriente continua
En muchos diseños de circuitos, la polarización de CC se aplica a un componente no lineal a través de una resistencia (o posiblemente una red de resistencias). Dado que las resistencias son componentes lineales, es particularmente fácil determinar el punto de funcionamiento en reposo del dispositivo no lineal a partir de un gráfico de su función de transferencia. El método es el siguiente: a partir del análisis de la red lineal, se calcula la función de transferencia de salida (es decir, el voltaje de salida contra la corriente de salida) para la red de resistencias y el generador que las impulsa. Esta será una línea recta (llamada línea de carga ) y se puede superponer fácilmente en el gráfico de la función de transferencia del dispositivo no lineal. El punto donde se cruzan las líneas es el punto de funcionamiento en reposo.
Quizás el método práctico más sencillo sea calcular la tensión de circuito abierto y la corriente de cortocircuito de la red (lineal) y representarlas gráficamente en la función de transferencia del dispositivo no lineal. La línea recta que une estos dos puntos es la función de transferencia de la red.
En realidad, el diseñador del circuito procedería en sentido inverso al descrito. Partiendo de un gráfico proporcionado en la hoja de datos del fabricante del dispositivo no lineal, el diseñador elegiría el punto de funcionamiento deseado y luego calcularía los valores de los componentes lineales necesarios para alcanzarlo.
Todavía es posible utilizar este método si el dispositivo que se va a polarizar recibe su polarización a través de otro dispositivo que no es lineal, por ejemplo un diodo. En este caso, sin embargo, el gráfico de la función de transferencia de red sobre el dispositivo que se va a polarizar ya no sería una línea recta y, en consecuencia, sería más tedioso de realizar.
Circuito equivalente de pequeña señal
Este método se puede utilizar cuando la desviación de las señales de entrada y salida en una red se mantiene dentro de una porción sustancialmente lineal de la función de transferencia de dispositivos no lineales, o bien son tan pequeñas que la curva de la función de transferencia se puede considerar lineal. Bajo un conjunto de estas condiciones específicas, el dispositivo no lineal se puede representar mediante una red lineal equivalente. Debe recordarse que este circuito equivalente es completamente nocional y solo válido para las pequeñas desviaciones de señal. Es completamente inaplicable a la polarización de CC del dispositivo.
En el caso de un dispositivo simple de dos terminales, el circuito equivalente de señal pequeña puede tener como máximo dos componentes: una resistencia igual a la pendiente de la curva v/i en el punto de funcionamiento (llamada resistencia dinámica) y tangente a la curva; y un generador, ya que esta tangente, en general, no pasa por el origen. Con más terminales, se requieren circuitos equivalentes más complicados.
Una forma popular de especificar el circuito equivalente de pequeña señal entre los fabricantes de transistores es utilizar los parámetros de red de dos puertos conocidos como parámetros [h] . Estos son una matriz de cuatro parámetros como los parámetros [z] pero en el caso de los parámetros [h] son una mezcla híbrida de impedancias, admitancias, ganancias de corriente y ganancias de voltaje. En este modelo, el transistor de tres terminales se considera una red de dos puertos, siendo uno de sus terminales común a ambos puertos. Los parámetros [h] son bastante diferentes según qué terminal se elija como común. El parámetro más importante para los transistores suele ser la ganancia de corriente directa, h 21 , en la configuración de emisor común. Esto se designa h fe en las hojas de datos.
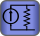
El circuito equivalente de señal pequeña en términos de parámetros de dos puertos conduce al concepto de generadores dependientes. Es decir, el valor de un generador de voltaje o corriente depende linealmente de un voltaje o corriente en otra parte del circuito. Por ejemplo, el modelo del parámetro [z] conduce a generadores de voltaje dependientes como se muestra en este diagrama;

En un circuito equivalente de parámetros de dos puertos siempre habrá generadores dependientes. Esto se aplica tanto a los parámetros [h] como a los [z] y de cualquier otro tipo. Estas dependencias deben conservarse al desarrollar las ecuaciones en un análisis de red lineal más amplio.
Método lineal por partes
En este método, la función de transferencia del dispositivo no lineal se divide en regiones. Cada una de estas regiones se aproxima mediante una línea recta. Por lo tanto, la función de transferencia será lineal hasta un punto particular en el que habrá una discontinuidad. Más allá de este punto, la función de transferencia volverá a ser lineal, pero con una pendiente diferente.
Una aplicación bien conocida de este método es la aproximación de la función de transferencia de un diodo de unión pn. La función de transferencia de un diodo ideal se ha dado en la parte superior de esta sección (no lineal). Sin embargo, esta fórmula rara vez se utiliza en el análisis de redes, en su lugar se utiliza una aproximación por partes. Se puede ver que la corriente del diodo disminuye rápidamente a -I o a medida que cae el voltaje. Esta corriente, para la mayoría de los propósitos, es tan pequeña que se puede ignorar. Al aumentar el voltaje, la corriente aumenta exponencialmente. El diodo se modela como un circuito abierto hasta el punto de inflexión de la curva exponencial, luego más allá de este punto como una resistencia igual a la resistencia volumétrica del material semiconductor.
Los valores comúnmente aceptados para el voltaje del punto de transición son 0,7 V para dispositivos de silicio y 0,3 V para dispositivos de germanio. Un modelo aún más simple del diodo, que a veces se utiliza en aplicaciones de conmutación, es el de cortocircuito para voltajes directos y el de circuito abierto para voltajes inversos.
El modelo de una unión pn polarizada directamente que tiene una tensión aproximadamente constante de 0,7 V también es una aproximación muy utilizada para el voltaje de la unión base-emisor del transistor en el diseño de amplificadores.
El método por partes es similar al método de señal pequeña en el sentido de que las técnicas de análisis de redes lineales solo se pueden aplicar si la señal se mantiene dentro de ciertos límites. Si la señal cruza un punto de discontinuidad, el modelo ya no es válido para fines de análisis lineal. Sin embargo, el modelo tiene la ventaja sobre la señal pequeña de que es igualmente aplicable a la señal y a la polarización de CC. Por lo tanto, ambos se pueden analizar en las mismas operaciones y serán superponibles linealmente.
Componentes que varían con el tiempo
En el análisis lineal, se supone que los componentes de la red no cambian, pero en algunos circuitos esto no se aplica, como los osciladores de barrido, los amplificadores controlados por voltaje y los ecualizadores variables . En muchas circunstancias, el cambio en el valor del componente es periódico. Un componente no lineal excitado con una señal periódica, por ejemplo, puede representarse como un componente lineal que varía periódicamente. Sidney Darlington reveló un método para analizar dichos circuitos periódicos que varían en el tiempo. Desarrolló formas de circuito canónico que son análogas a las formas canónicas de Ronald M. Foster y Wilhelm Cauer utilizadas para analizar circuitos lineales. [7]
Teoría de circuitos vectoriales
La generalización de la teoría de circuitos basada en magnitudes escalares a corrientes vectoriales es una necesidad para los circuitos de nueva evolución, como los circuitos de espín. [ aclaración necesaria ] Las variables de circuito generalizadas constan de cuatro componentes: corriente escalar y corriente de espín vectorial en las direcciones x, y y z. Los voltajes y las corrientes se convierten en magnitudes vectoriales con conductancia descrita como una matriz de conductancia de espín 4x4. [ cita requerida ]
Véase también
- Teorema de bisección de Bartlett
- Leyes de circuitos de Kirchhoff
- Teorema de Millman
- Análisis nodal modificado
- Ley de Ohm
- Reciprocidad (redes eléctricas)
- Teorema de Tellegen
- Análisis de circuitos simbólicos
Referencias
- ^ Belevitch V (mayo de 1962). "Resumen de la historia de la teoría de circuitos". Actas del IRE . 50 (5): 849. doi :10.1109/JRPROC.1962.288301. S2CID 51666316.cita "Normas IRE sobre circuitos: definiciones de términos para redes lineales pasivas recíprocas invariantes en el tiempo, 1960". Actas del IRE . 48 (9): 1609. Septiembre de 1960. doi :10.1109/JRPROC.1960.287676.para justificar esta definición.
Sidney Darlington Darlington S (1984). "Una historia de la síntesis de redes y la teoría de filtros para circuitos compuestos de resistencias, inductores y condensadores". IEEE Transactions on Circuits and Systems . 31 (1): 4. doi :10.1109/TCS.1984.1085415.
Sigue a Belevitch pero señala que ahora también hay muchos usos coloquiales de "red". - ^ abcd Chen, Wai-Kai (2005). Análisis de circuitos y teoría de amplificadores de realimentación . CRC Press. ISBN 1420037277.
- ^ ab Nilsson, James W.; Riedel, Susan A. (2007). Circuitos eléctricos (8.ª ed.). Pearson Prentice Hall. ISBN 978-0-13-198925-2.
- ^ Kumar, Ankush; Vidhyadhiraja, NS; Kulkarni, G. U. (2017). "Distribución de corriente en redes de nanocables conductores". Journal of Applied Physics . 122 (4): 045101. Bibcode :2017JAP...122d5101K. doi :10.1063/1.4985792.
- ^ abcd Najm, Farid N. (2010). Simulación de circuitos . John Wiley & Sons. ISBN 9780470538715.
- ^ Ljiljana Trajković, "Circuitos no lineales", The Electrical Engineering Handbook (Ed: Wai-Kai Chen), págs. 79-81, Academic Press, 2005 ISBN 0-12-170960-4
- ^ Patente estadounidense 3265973, Sidney Darlington, Irwin W. Sandberg, "Síntesis de redes de dos puertos con elementos que varían periódicamente en el tiempo", publicada el 9 de agosto de 1966
Enlaces externos
- Las conferencias de física de Feynman, vol. II, cap. 22: circuitos de corriente alterna







































































![{\displaystyle \left[z(j\omega )\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10811182bc24215e2eb8f5675f205548a9dc10a4)
![{\displaystyle \izquierda[z\derecha]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1602ad8f429c7bdd31909a2c96547ada8d4d3f36)





