Coeficiente de Gini

- Más de 50
- Entre 45 y 50
- Entre 40 y 45
- Entre 35 y 40
- Entre 30 y 35
- Menos de 30
- Sin datos


| Parte de una serie sobre |
| Ciencias económicas |
|---|
 |
En economía , el coeficiente de Gini ( / ˈdʒiːn i / JEE -nee ), también conocido como índice de Gini o ratio de Gini , es una medida de dispersión estadística destinada a representar la desigualdad de ingresos , la desigualdad de riqueza o la desigualdad de consumo [ 3] dentro de una nación o un grupo social . Fue desarrollado por el estadístico y sociólogo italiano Corrado Gini .
El coeficiente de Gini mide la desigualdad entre los valores de una distribución de frecuencias , como los niveles de ingresos . Un coeficiente de Gini de 0 refleja una igualdad perfecta, donde todos los valores de ingresos o riqueza son iguales, mientras que un coeficiente de Gini de 1 (o 100%) refleja una desigualdad máxima entre valores, una situación en la que un solo individuo tiene todos los ingresos mientras que todos los demás no tienen ninguno. [4] [5]
El coeficiente de Gini fue propuesto por Corrado Gini como una medida de la desigualdad de ingresos o riqueza . [6] Para los países de la OCDE a finales del siglo XX, considerando el efecto de los impuestos y los pagos de transferencias , el coeficiente de Gini de ingresos osciló entre 0,24 y 0,49, siendo Eslovaquia el más bajo y México el más alto. [7] Los países africanos tuvieron los coeficientes de Gini antes de impuestos más altos en 2008-2009, siendo Sudáfrica el más alto del mundo, estimado entre 0,63 y 0,7. [8] [9] Sin embargo, esta cifra cae a 0,52 después de que se tiene en cuenta la asistencia social, y cae nuevamente a 0,47 después de los impuestos. [10] El país con el coeficiente de Gini más bajo es Eslovaquia, con un coeficiente de Gini de 0,232. [11] Varias fuentes han estimado que el coeficiente de Gini del ingreso global en 2005 estaba entre 0,61 y 0,68. [12] [13]
La interpretación del coeficiente de Gini plantea algunos problemas, ya que el mismo valor puede resultar de muchas curvas de distribución diferentes. Para mitigar este problema, se debe tener en cuenta la estructura demográfica. Los países con una población que envejece o aquellos con una tasa de natalidad mayor experimentan un aumento del coeficiente de Gini antes de impuestos, incluso si la distribución del ingreso real para los adultos que trabajan se mantiene constante. Muchos investigadores han ideado más de una docena de variantes del coeficiente de Gini. [14] [15] [16]
Historia
El coeficiente de Gini fue desarrollado por el estadístico italiano Corrado Gini y publicado en su artículo de 1912 Variabilità e mutabilità (en español: variabilidad y mutabilidad ). [17] [18] Basándose en el trabajo del economista estadounidense Max Lorenz , Gini propuso que la diferencia entre la línea recta hipotética que representa la igualdad perfecta y la línea real que representa los ingresos de las personas se utilizara como una medida de desigualdad. [19] En este artículo, introdujo el concepto de diferencia de medias simple como medida de variabilidad.
En su obra On the measurement of concentrate and variability of characters (Sobre la medición de la concentración y la variabilidad de los caracteres) , de 1914 , aplicó la simple diferencia de medias de las variables observadas a la desigualdad de ingresos y riqueza. En ella, presentó el coeficiente de concentración , que luego desarrolló en el coeficiente de Gini que se utiliza en la actualidad. En segundo lugar, Gini observó que el coeficiente que propuso también se puede lograr mejorando los métodos ya introducidos por Lorenz, Chatelain o Séailles.
En 1915, Gaetano Pietra introdujo una interpretación geométrica entre el coeficiente de Gini propuesto y el cociente entre el área de concentración observada y la concentración máxima. Esta versión modificada del coeficiente de Gini se convirtió en el índice de desigualdad más utilizado en los años siguientes. [20]
Según datos de la OCDE , el coeficiente de Gini se utilizó oficialmente por primera vez en todo el país en Canadá en la década de 1970. El índice canadiense de desigualdad de ingresos osciló entre 0,303 y 0,284 desde 1976 hasta finales de la década de 1980. La OCDE comenzó a publicar datos de más países desde principios del siglo XXI. Los países de Europa central Eslovenia , Chequia y Eslovaquia han tenido el índice de desigualdad más bajo de todos los países de la OCDE desde la década de 2000. Los países escandinavos también aparecieron con frecuencia en la parte superior de la lista de igualdad en las últimas décadas. [21]
Definición
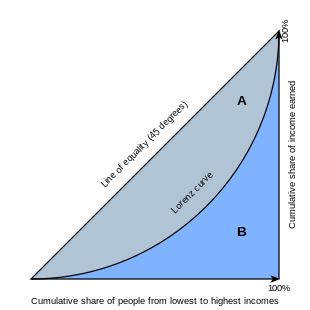
El coeficiente de Gini es un índice del grado de desigualdad en la distribución del ingreso/riqueza, utilizado para estimar en qué medida la distribución de la riqueza o el ingreso de un país se desvía de una distribución equitativa. [22]
El coeficiente de Gini se define generalmente matemáticamente basándose en la curva de Lorenz , que traza la proporción del ingreso total de la población (eje y) que gana acumulativamente el extremo inferior x de la población (ver diagrama). [23] La línea a 45 grados representa así la igualdad perfecta de ingresos. El coeficiente de Gini puede entonces considerarse como la relación entre el área que se encuentra entre la línea de igualdad y la curva de Lorenz (marcada A en el diagrama) sobre el área total bajo la línea de igualdad (marcada A y B en el diagrama); es decir, G = A /( A + B ) . Si no hay ingresos negativos, también es igual a 2 A y 1 − 2 B debido al hecho de que A + B = 0,5 . [24]
Suponiendo que los ingresos o la riqueza de todos no sean negativos, el rango teórico del coeficiente de Gini va de 0 (igualdad total) a 1 (desigualdad absoluta). Esta medida suele expresarse como un porcentaje que abarca de 0 a 100. Sin embargo, si se tienen en cuenta valores negativos, como en los casos de deuda, el índice de Gini podría superar 1. Normalmente, presuponemos una media o un total positivo, lo que excluye un coeficiente de Gini inferior a cero. [25]
Un enfoque alternativo es definir el coeficiente de Gini como la mitad de la diferencia absoluta media relativa , que es equivalente a la definición basada en la curva de Lorenz . [26] La diferencia absoluta media es la diferencia absoluta promedio de todos los pares de elementos de la población, y la diferencia absoluta media relativa es la diferencia absoluta media dividida por el promedio , , para normalizar la escala. Si x i es la riqueza o los ingresos de la persona i , y hay n personas, entonces el coeficiente de Gini G viene dado por:
Cuando la distribución del ingreso (o riqueza) se da como una función de densidad de probabilidad continua p ( x ), el coeficiente de Gini es nuevamente la mitad de la diferencia absoluta media relativa:
donde es la media de la distribución, y los límites inferiores de integración pueden reemplazarse por cero cuando todos los ingresos son positivos. [27]
Cálculo

Si bien la distribución del ingreso de un país en particular no se corresponderá perfectamente con los modelos teóricos , estos modelos pueden proporcionar una explicación cualitativa de la distribución del ingreso en una nación dado el coeficiente de Gini.
Ejemplo: Dos niveles de ingresos
Los casos extremos están representados por la sociedad más igualitaria posible en la que cada persona recibe el mismo ingreso ( G = 0 ), y la sociedad más desigual (con N individuos) donde una sola persona recibe el 100% del ingreso total y las N − 1 personas restantes no reciben nada ( G = 1 − 1/ N ).
Un caso sencillo supone sólo dos niveles de ingresos, bajo y alto. Si el grupo de altos ingresos es una proporción u de la población y gana una proporción f de todos los ingresos, entonces el coeficiente de Gini es f − u . Una distribución más graduada con estos mismos valores u y f siempre tendrá un coeficiente de Gini más alto que f − u .
Por ejemplo, si el más rico u = 20% de la población tiene f = 80% de todos los ingresos (véase el principio de Pareto ), el coeficiente de Gini de los ingresos es al menos del 60%. En otro ejemplo, [28] si u = 1% de la población mundial posee f = 50% de toda la riqueza, el coeficiente de Gini de la riqueza es al menos del 49%.
Expresiones alternativas
En algunos casos, esta ecuación se puede aplicar para calcular el coeficiente de Gini sin referencia directa a la curva de Lorenz . Por ejemplo, (tomando y para indicar el ingreso o la riqueza de una persona o un hogar):
- Para una población de n individuos con valores , [29]
- Esto se puede simplificar así:
El coeficiente de Gini también puede considerarse como la mitad de la diferencia absoluta de la media relativa . Para una muestra aleatoria S con valores , el coeficiente de Gini de la muestra
es un estimador consistente del coeficiente de Gini de la población, pero en general no es insesgado . En forma simplificada:
No existe una estadística muestral que sea siempre un estimador imparcial del coeficiente de Gini de la población.
Distribución de probabilidad discreta
Para una distribución de probabilidad discreta con función de masa de probabilidad i = 1 , … , n {\displaystyle i=1,\ldots ,n} , donde es la fracción de la población con ingresos o riqueza , el coeficiente de Gini es:
dónde
Si los puntos con probabilidades distintas de cero están indexados en orden creciente , entonces:
dónde
- y Estas fórmulas también son aplicables en el límite, ya que
Distribución de probabilidad continua
Cuando la población es grande, la distribución del ingreso puede representarse mediante una función de densidad de probabilidad continua f ( x ) donde f ( x ) dx es la fracción de la población con riqueza o ingreso en el intervalo dx en torno a x . Si F ( x ) es la función de distribución acumulativa para f ( x ):
y L ( x ) es la función de Lorenz:
Entonces la curva de Lorenz L ( F ) puede representarse como una función paramétrica en L ( x ) y F ( x ) y el valor de B puede encontrarse por integración :
El coeficiente de Gini también se puede calcular directamente a partir de la función de distribución acumulativa de la distribución F ( y ). Si se define μ como la media de la distribución y se especifica que F ( y ) es cero para todos los valores negativos, el coeficiente de Gini viene dado por:
El último resultado proviene de la integración por partes . (Tenga en cuenta que esta fórmula se puede aplicar cuando hay valores negativos si la integración se toma de menos infinito a más infinito).
El coeficiente de Gini puede expresarse en términos de la función cuantil Q ( F ) (inversa de la función de distribución acumulativa: Q(F(x)) = x)
Dado que el coeficiente de Gini es independiente de la escala , si la función de distribución se puede expresar en la forma f(x,φ,a,b,c...) donde φ es un factor de escala y a, b, c... son parámetros adimensionales, entonces el coeficiente de Gini será una función solo de a, b, c... . [30] Por ejemplo, para la distribución exponencial , que es una función solo de x y un parámetro de escala, el coeficiente de Gini es una constante, igual a 1/2.
Para algunas formas funcionales, el índice de Gini se puede calcular explícitamente. Por ejemplo, si y sigue una distribución log-normal con la desviación estándar de logs igual a , entonces donde es la función de error ( ya que , donde es la función de distribución acumulativa de una distribución normal estándar). [31] En la siguiente tabla, se muestran algunos ejemplos de funciones de densidad de probabilidad con soporte en . La distribución delta de Dirac representa el caso en el que todos tienen la misma riqueza (o ingresos); implica que no hay variaciones entre los ingresos. [32]
Función de distribución del ingreso PDF(x) Coeficiente de Gini Función delta de Dirac 0 Distribución uniforme [33] Distribución exponencial [34] Distribución log-normal [31] [35] Distribución de Pareto [36] Distribución Chi [36] Distribución de chi-cuadrado [37] Distribución gamma [30] Distribución de Weibull [38] Distribución beta [39] Distribución log-logística [40]
- es la función Gamma
- es la función Beta
- es la función beta incompleta regularizada
Otros enfoques
En ocasiones no se conoce la curva de Lorenz completa y solo se dan valores en ciertos intervalos. En ese caso, el coeficiente de Gini se puede aproximar utilizando varias técnicas para interpolar los valores faltantes de la curva de Lorenz. Si ( X k , Y k ) son los puntos conocidos en la curva de Lorenz, con los X k indexados en orden creciente ( X k – 1 < X k ), de modo que:
- X k es la proporción acumulada de la variable población, para k = 0,..., n , con X 0 = 0, X n = 1.
- Y k es la proporción acumulada de la variable ingreso, para k = 0,..., n , con Y 0 = 0, Y n = 1.
- Y k debe indexarse en orden no decreciente ( Y k > Y k – 1 )
Si la curva de Lorenz se aproxima en cada intervalo como una línea entre puntos consecutivos, entonces el área B se puede aproximar con trapecios y:
es la aproximación resultante para G. Se pueden obtener resultados más precisos utilizando otros métodos para aproximar el área B, como aproximar la curva de Lorenz con una función cuadrática a través de pares de intervalos o construir una aproximación apropiadamente suave a la función de distribución subyacente que coincida con los datos conocidos. Si también se conocen la media de la población y los valores límite para cada intervalo, estos también se pueden utilizar a menudo para mejorar la precisión de la aproximación.
El coeficiente de Gini calculado a partir de una muestra es una estadística, y se debe informar su error estándar, o intervalos de confianza para el coeficiente de Gini de la población. Estos pueden calcularse utilizando técnicas bootstrap , matemáticamente complicadas y computacionalmente exigentes incluso en una era de computadoras rápidas. [41] El economista Tomson Ogwang hizo que el proceso fuera más eficiente al establecer un "modelo de regresión con truco" en el que se clasifican las respectivas variables de ingresos en la muestra, y se asigna el rango 1 al ingreso más bajo. Luego, el modelo expresa el rango (variable dependiente) como la suma de una constante A y un término de error normal cuya varianza es inversamente proporcional a y k :
Por lo tanto, G puede expresarse como una función de la estimación de mínimos cuadrados ponderados de la constante A y esto puede utilizarse para acelerar el cálculo de la estimación de la navaja para el error estándar. El economista David Giles argumentó que el error estándar de la estimación de A puede utilizarse para derivar la estimación de G directamente sin utilizar una navaja. Este método solo requiere utilizar la regresión de mínimos cuadrados ordinarios después de ordenar los datos de la muestra. Los resultados se comparan favorablemente con las estimaciones de la navaja y la concordancia mejora a medida que aumenta el tamaño de la muestra. [42]
Sin embargo, se ha argumentado que esto depende de los supuestos del modelo sobre las distribuciones de error y la independencia de los términos de error. Estos supuestos a menudo no son válidos para conjuntos de datos reales. Todavía hay un debate en curso en torno a este tema.
Guillermina Jasso [43] y Angus Deaton [44] propusieron independientemente la siguiente fórmula para el coeficiente de Gini:
donde es el ingreso medio de la población, P i es el rango de ingreso P de la persona i, con un ingreso X, de modo que la persona más rica recibe un rango de 1 y la más pobre un rango de N . Esto efectivamente otorga mayor peso a las personas más pobres en la distribución del ingreso, lo que permite que el Gini cumpla con el Principio de Transferencia . Nótese que la fórmula de Jasso-Deaton reescala el coeficiente de modo que su valor sea uno si todos los son cero excepto uno. Nótese, sin embargo, la respuesta de Allison sobre la necesidad de dividir por N² en su lugar. [45]
La FAO explica otra versión de la fórmula. [46]
Índices de desigualdad generalizados
El coeficiente de Gini y otros índices de desigualdad estándar se reducen a una forma común. La igualdad perfecta —la ausencia de desigualdad— existe cuando y sólo cuando la razón de desigualdad, , es igual a 1 para todas las j unidades en alguna población (por ejemplo, hay una igualdad perfecta de ingresos cuando el ingreso de todos es igual al ingreso medio , de modo que para todos). Las medidas de desigualdad, entonces, son medidas de las desviaciones promedio de 1; cuanto mayor sea la desviación promedio, mayor será la desigualdad. Con base en estas observaciones, los índices de desigualdad tienen esta forma común: [47]
donde p j pondera las unidades según su proporción poblacional y f ( r j ) es una función de la desviación de r j de cada unidad respecto de 1, el punto de igualdad. La idea de este índice de desigualdad generalizado es que los índices de desigualdad difieren porque emplean diferentes funciones de la distancia de las razones de desigualdad ( r j ) respecto de 1.
De las distribuciones de ingresos

Los coeficientes de Gini de los ingresos se calculan sobre la base de los ingresos de mercado y de los ingresos disponibles. El coeficiente de Gini sobre los ingresos de mercado, a veces denominado coeficiente de Gini antes de impuestos, se calcula sobre los ingresos antes de impuestos y transferencias. Mide la desigualdad en los ingresos sin tener en cuenta el efecto de los impuestos y el gasto social ya establecidos en un país. El coeficiente de Gini sobre los ingresos disponibles, a veces denominado coeficiente de Gini después de impuestos, se calcula sobre los ingresos después de impuestos y transferencias. Mide la desigualdad en los ingresos después de tener en cuenta el efecto de los impuestos y el gasto social ya establecidos en un país. [7] [48] [49]
En el caso de los países de la OCDE , durante el período 2008-2009, el coeficiente de Gini (antes de impuestos y transferencias) para una población total osciló entre 0,34 y 0,53; Corea del Sur fue el más bajo e Italia el más alto. El coeficiente de Gini (después de impuestos y transferencias) para una población total osciló entre 0,25 y 0,48; Dinamarca fue el más bajo y México el más alto. En el caso de los Estados Unidos, el país con la mayor población entre los países de la OCDE, el índice de Gini antes de impuestos fue de 0,49 y el índice de Gini después de impuestos fue de 0,38 en 2008-2009. El promedio de la OCDE para las poblaciones totales en los países de la OCDE fue de 0,46 para el índice de Gini de ingresos antes de impuestos y de 0,31 para el índice de Gini de ingresos después de impuestos. [7] [50] Los impuestos y el gasto social que se implementaron en el período 2008-2009 en los países de la OCDE redujeron significativamente la desigualdad de ingresos efectiva y, en general, "los países europeos, especialmente los estados de bienestar nórdicos y continentales , logran niveles más bajos de desigualdad de ingresos que otros países". [51]
El uso del coeficiente de Gini puede ayudar a cuantificar las diferencias en las políticas y filosofías de bienestar y compensación . Sin embargo, debe tenerse en cuenta que el coeficiente de Gini puede ser engañoso cuando se utiliza para hacer comparaciones políticas entre países grandes y pequeños o entre aquellos con diferentes políticas de inmigración (véase la sección de limitaciones).
El coeficiente de Gini para todo el mundo ha sido estimado por diversos actores entre 0,61 y 0,68. [12] [13] [52] El gráfico muestra los valores expresados como porcentaje de su evolución histórica para varios países.
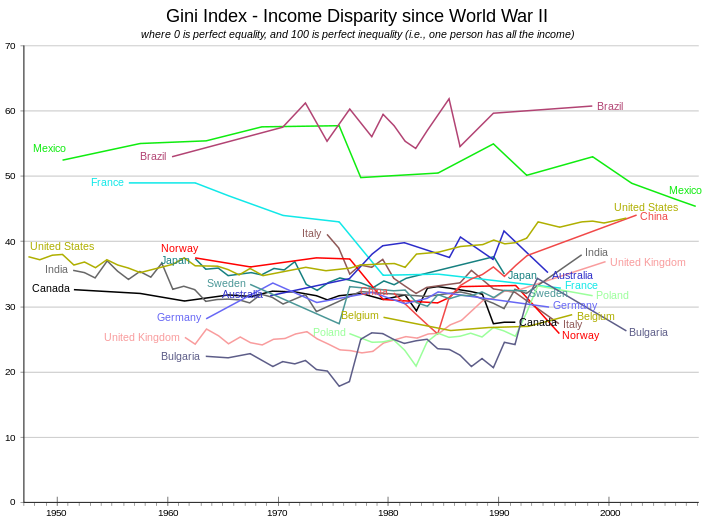
Índices de Gini de ingresos regionales
Según UNICEF, la región de América Latina y el Caribe tuvo el índice de Gini de ingresos netos más alto del mundo, con un promedio no ponderado de 48,3 en 2008. Los promedios regionales restantes fueron: África subsahariana (44,2), Asia (40,4), Oriente Medio y África del Norte (39,2), Europa oriental y Asia central (35,4) y países de altos ingresos (30,9). Utilizando el mismo método, se afirma que Estados Unidos tiene un índice de Gini de 36, mientras que Sudáfrica tuvo el puntaje más alto en el índice de Gini de ingresos, 67,8. [53]
Índice de Gini del ingreso mundial desde el siglo XIX
Si se considera la distribución del ingreso de todos los seres humanos, la desigualdad de ingresos a nivel mundial ha aumentado constantemente desde principios del siglo XIX (y seguirá aumentando con el paso de los años). El índice de Gini de la desigualdad de ingresos a nivel mundial aumentó de manera constante entre 1820 y 2002, con un aumento significativo entre 1980 y 2002. Esta tendencia parece haber alcanzado su punto máximo y haber comenzado a revertirse con el rápido crecimiento económico de las economías emergentes, en particular en las grandes poblaciones de los países BRIC . [54]
La siguiente tabla presenta los coeficientes de Gini del ingreso mundial estimados durante los últimos 200 años, según cálculos de Milanovic. [55]
| Año | Coeficientes de Gini mundiales [12] [53] [56] |
|---|---|
| 1820 | 0,43 |
| 1850 | 0,53 |
| 1870 | 0,56 |
| 1913 | 0,61 |
| 1929 | 0,62 |
| 1950 | 0,64 |
| 1960 | 0,64 |
| 1980 | 0,66 |
| 2002 | 0,71 |
| 2005 | 0,68 |
Datos más detallados de fuentes similares muestran una caída continua desde 1988. Esto se atribuye a que la globalización ha aumentado los ingresos de miles de millones de personas pobres, principalmente en países como China y la India. Países en desarrollo como Brasil también han mejorado los servicios básicos como la atención de la salud, la educación y el saneamiento; otros, como Chile y México, han promulgado políticas fiscales más progresistas . [57]
| Año | Coeficientes de Gini mundiales [58] |
|---|---|
| 1988 | 0,80 |
| 1993 | 0,76 |
| 1998 | 0,74 |
| 2003 | 0,72 |
| 2008 | 0,70 |
| 2013 | 0,65 |
Del desarrollo social
El coeficiente de Gini se utiliza ampliamente en campos tan diversos como la sociología, la economía, las ciencias de la salud, la ecología, la ingeniería y la agricultura. [59] Por ejemplo, en las ciencias sociales y la economía, además de los coeficientes de Gini de ingresos, los académicos han publicado coeficientes de Gini de educación y coeficientes de Gini de oportunidad.
Educación
El índice de Gini de la educación estima la desigualdad en la educación para una población dada. [60] Se utiliza para discernir tendencias en el desarrollo social a través del logro educativo a lo largo del tiempo. Un estudio en 85 países realizado por tres economistas del Banco Mundial , Vinod Thomas, Yan Wang y Xibo Fan, estimó que Malí tenía el índice de Gini de educación más alto de 0,92 en 1990 (lo que implica una desigualdad muy alta en el logro educativo entre la población), mientras que Estados Unidos tenía el índice de Gini de desigualdad educativa más bajo de 0,14. Entre 1960 y 1990, China, India y Corea del Sur tuvieron la caída más rápida en el índice de Gini de desigualdad educativa. También afirman que el índice de Gini de educación para Estados Unidos aumentó ligeramente durante el período 1980-1990.
Aunque el índice de Gini de la educación en la India ha estado cayendo entre 1960 y 1990, la mayor parte de la población todavía no ha recibido educación alguna, mientras que el 10 por ciento de la población recibió más del 40 por ciento del total de horas de educación en el país. Esto significa que una gran parte de los niños capaces del país no están recibiendo el apoyo necesario para permitirles convertirse en contribuyentes positivos a la sociedad. Esto conducirá a una pérdida irrecuperable para la sociedad nacional porque hay muchas personas que están subdesarrolladas y subutilizadas. [61]
Oportunidad
Similar en concepto al coeficiente de ingresos de Gini, el coeficiente de oportunidad de Gini mide la desigualdad de oportunidades. [62] [63] [64] El concepto se basa en la sugerencia de Amartya Sen [65] de que los coeficientes de desigualdad del desarrollo social deberían basarse en el proceso de ampliar las opciones de las personas y mejorar sus capacidades, en lugar de en el proceso de reducir la desigualdad de ingresos. Kovacevic, en una revisión del coeficiente de oportunidad de Gini, explicó que el coeficiente estima qué tan bien una sociedad permite a sus ciudadanos lograr el éxito en la vida donde el éxito se basa en las elecciones, esfuerzos y talentos de una persona, no en sus antecedentes definidos por un conjunto de circunstancias predeterminadas al nacer, como género, raza, lugar de nacimiento, ingresos de los padres y circunstancias fuera del control de ese individuo.
En 2003, Roemer [62] [66] informó que Italia y España exhibían el índice de Gini de desigualdad de oportunidades más grande entre las economías avanzadas.
Movilidad de ingresos
En 1978, Anthony Shorrocks introdujo una medida basada en los coeficientes de Gini de ingresos para estimar la movilidad del ingreso. [67] Esta medida, generalizada por Maasoumi y Zandvakili, [68] ahora se conoce generalmente como índice de Shorrocks , a veces como índice de movilidad de Shorrocks o índice de rigidez de Shorrocks. Intenta estimar si el coeficiente de Gini de la desigualdad de ingresos es permanente o temporal y en qué medida un país o región permite la movilidad económica a su gente para que puedan pasar de un cuartil de ingresos (por ejemplo, el 20% inferior) a otro (por ejemplo, el 20% medio) a lo largo del tiempo. En otras palabras, el índice de Shorrocks compara la desigualdad de los ingresos a corto plazo, como el ingreso anual de los hogares, con la desigualdad de los ingresos a largo plazo, como el ingreso total de 5 o 10 años para los mismos hogares.
El índice de Shorrock se calcula de varias maneras diferentes, siendo un enfoque común el de la relación entre los coeficientes de Gini de ingresos a corto y largo plazo para la misma región o país. [69]
Un estudio de 2010 que utilizó datos de ingresos de la seguridad social para los Estados Unidos desde 1937 y los índices de Shorrock basados en el coeficiente de Gini concluye que la movilidad del ingreso en los Estados Unidos ha tenido una historia complicada, principalmente debido a la afluencia masiva de mujeres a la fuerza laboral estadounidense después de la Segunda Guerra Mundial. Las tendencias de la desigualdad de ingresos y la movilidad del ingreso han sido diferentes para los trabajadores hombres y mujeres entre 1937 y la década de 2000. Cuando se consideran a hombres y mujeres juntos, las tendencias del índice de Shorrock basado en el coeficiente de Gini implican que la desigualdad de ingresos a largo plazo se ha reducido sustancialmente entre todos los trabajadores, en las últimas décadas para los Estados Unidos. [69] Otros académicos, utilizando solo datos de la década de 1990 u otros períodos cortos, han llegado a conclusiones diferentes. [70] Por ejemplo, Sastre y Ayala concluyen de su estudio de los datos del coeficiente de Gini de ingresos entre 1993 y 1998 para seis economías desarrolladas que Francia tuvo la menor movilidad de ingresos, Italia la más alta y Estados Unidos y Alemania niveles intermedios de movilidad de ingresos durante esos cinco años. [71]
Características
![[icon]](http://upload.wikimedia.org/wikipedia/commons/thumb/1/1c/Wiki_letter_w_cropped.svg/20px-Wiki_letter_w_cropped.svg.png) | This section needs expansion. You can help by adding to it. (March 2023) |
El coeficiente de Gini tiene características que lo hacen útil como medida de dispersión en una población, y de desigualdades en particular. [46] El coeficiente varía de 0, para una igualdad perfecta, a 1, que indica una desigualdad perfecta. El Gini se basa en la comparación de las proporciones acumuladas de la población con las proporciones acumuladas de los ingresos que recibe. [72]
Limitaciones
Relativo, no absoluto
El coeficiente de Gini es una medida relativa. El coeficiente de Gini de un país en desarrollo puede aumentar (debido a la creciente desigualdad de ingresos) incluso cuando disminuye el número de personas en situación de pobreza absoluta. [73] Esto se debe a que el coeficiente de Gini mide la riqueza relativa, no absoluta.
Los coeficientes de Gini son simples, y esta simplicidad puede llevar a descuidos y puede confundir la comparación de diferentes poblaciones; por ejemplo, mientras que tanto Bangladesh (renta per cápita de $1,693) como los Países Bajos (renta per cápita de $42,183) tenían un coeficiente de Gini de ingresos de 0,31 en 2010, [74] la calidad de vida, las oportunidades económicas y los ingresos absolutos en estos países son muy diferentes, es decir, los países pueden tener coeficientes de Gini idénticos, pero diferir mucho en riqueza. Las necesidades básicas pueden estar disponibles para todos en una economía desarrollada, mientras que en una economía subdesarrollada con el mismo coeficiente de Gini, las necesidades básicas pueden no estar disponibles para la mayoría o estar disponibles de manera desigual debido a una riqueza absoluta menor.
Limitaciones matemáticas
El coeficiente de Gini también tiene algunas limitaciones matemáticas. No es aditivo y no es posible promediar distintos conjuntos de personas para obtener el coeficiente de Gini de todas las personas de los conjuntos.
| Grupo de hogares | Ingreso anual del país A ($) | Ingresos anuales del país B ($) |
|---|---|---|
| 1 | 20.000 | 9.000 |
| 2 | 30.000 | 40.000 |
| 3 | 40.000 | 48.000 |
| 4 | 50.000 | 48.000 |
| 5 | 60.000 | 55.000 |
| Ingresos totales | $200,000 | $200,000 |
| Gini del país | 0,2 | 0,2 |
Incluso cuando el ingreso total de una población es el mismo, en ciertas situaciones dos países con diferentes distribuciones de ingresos pueden tener el mismo índice de Gini (por ejemplo, casos en que las curvas de Lorenz de ingresos se cruzan). [46] La Tabla A ilustra una de esas situaciones. Ambos países tienen un coeficiente de Gini de 0,2, pero las distribuciones de ingresos promedio para los grupos de hogares son diferentes. Como otro ejemplo, en una población donde el 50% más bajo de las personas no tiene ingresos, y el otro 50% tiene ingresos iguales, el coeficiente de Gini es 0,5; mientras que para otra población donde el 75% más bajo de las personas tiene el 25% de los ingresos y el 25% más alto tiene el 75% de los ingresos, el índice de Gini también es 0,5. Las economías con ingresos similares y coeficientes de Gini pueden tener distribuciones de ingresos muy diferentes. Bellù y Liberati afirman que la clasificación de la desigualdad de ingresos entre dos poblaciones no siempre es posible en función de sus índices de Gini. [75] De manera similar, el científico social computacional Fabian Stephany ilustra que la desigualdad de ingresos dentro de la población, por ejemplo, en grupos socioeconómicos específicos de la misma edad y educación, también permanece sin ser detectada por los índices de Gini convencionales. [76]
El índice de Gini sobre el ingreso puede ocultar la desigualdad de la riqueza
Un índice de Gini no contiene información sobre los ingresos nacionales o personales absolutos. Las poblaciones pueden tener simultáneamente índices de Gini de ingresos muy bajos e índices de Gini de riqueza muy altos. Al medir la desigualdad en los ingresos, el Gini ignora la eficiencia diferencial del uso de los ingresos de los hogares. Al ignorar la riqueza (excepto en la medida en que contribuye al ingreso), el Gini puede crear la apariencia de desigualdad cuando las personas comparadas se encuentran en diferentes etapas de su vida. Los países ricos como Suecia pueden mostrar un coeficiente de Gini bajo para el ingreso disponible de 0,31, lo que parece igual, pero tienen un coeficiente de Gini muy alto para la riqueza de 0,79 a 0,86, lo que sugiere una distribución de la riqueza extremadamente desigual en su sociedad. [77] [78] Estos factores no se evalúan en el Gini basado en el ingreso.
Sesgo de granularidad y tamaño del país
El índice de Gini tiene un sesgo a la baja para poblaciones pequeñas. [79] Los condados, estados o países con poblaciones pequeñas y economías menos diversas tenderán a reportar coeficientes de Gini pequeños. Para grupos de población grandes económicamente diversos, se espera un coeficiente mucho más alto que para cada una de sus regiones. Por ejemplo, tomando la economía mundial como un todo y la distribución del ingreso para todos los seres humanos, diferentes académicos estiman que el índice de Gini global oscila entre 0,61 y 0,68. [12] [13] Al igual que con otros coeficientes de desigualdad, el coeficiente de Gini está influenciado por la granularidad de las mediciones. Por ejemplo, cinco cuantiles del 20% (granularidad baja) generalmente arrojarán un coeficiente de Gini más bajo que veinte cuantiles del 5% (granularidad alta) para la misma distribución. Philippe Monfort ha demostrado que el uso de granularidad inconsistente o no especificada limita la utilidad de las mediciones del coeficiente de Gini. [80]
Cambios en la población
El cambio en la desigualdad de ingresos, medida por los coeficientes de Gini, puede deberse a cambios estructurales en una sociedad, como el crecimiento de la población (aumento de las tasas de natalidad, envejecimiento de la población, emigración, inmigración) y la movilidad de los ingresos. [81]
Otra limitación del coeficiente de Gini es que no es una medida adecuada del igualitarismo , ya que solo mide la dispersión del ingreso. Por ejemplo, supongamos que dos países igualmente igualitarios aplican políticas de inmigración diferentes . En ese caso, el país que acepta una mayor proporción de inmigrantes de bajos ingresos o empobrecidos registrará un coeficiente de Gini más alto y, por lo tanto, puede exhibir una mayor desigualdad de ingresos.
Hogar vs. individuo
| Número de hogar | Ingreso anual del país ($) | Número combinado de hogares | Ingreso anual combinado del país A ($) |
|---|---|---|---|
| 1 | 20.000 | 1 y 2 | 50.000 |
| 2 | 30.000 | ||
| 3 | 40.000 | 3 y 4 | 90.000 |
| 4 | 50.000 | ||
| 5 | 60.000 | 5 y 6 | 130.000 |
| 6 | 70.000 | ||
| 7 | 80.000 | 7 y 8 | 170.000 |
| 8 | 90.000 | ||
| 9 | 120.000 | 9 y 10 | 270.000 |
| 10 | 150.000 | ||
| Ingresos totales | $710,000 | $710,000 | |
| Gini del país | 0,303 | 0,293 |
El coeficiente de Gini arroja resultados diferentes cuando se aplica a individuos en lugar de a hogares, para la misma economía y las mismas distribuciones de ingresos. Si se utilizan datos de hogares, el valor medido del coeficiente de Gini de ingresos depende de cómo se defina el hogar. La comparación no es significativa cuando no se miden diferentes poblaciones con definiciones consistentes. Además, los cambios en el coeficiente de Gini de ingresos de los hogares pueden estar impulsados por cambios en la formación de hogares, como el aumento de las tasas de divorcio o la división de hogares de familias extensas en familias nucleares .
Deininger y Squire (1996) muestran que el coeficiente de Gini basado en el ingreso individual es diferente al del ingreso familiar. Por ejemplo, en el caso de los Estados Unidos, encontraron que el índice de Gini basado en el ingreso individual era de 0,35, mientras que en el de Francia era de 0,43. Según su método centrado en el individuo, en los 108 países que estudiaron, Sudáfrica tenía el coeficiente de Gini más alto del mundo (0,62), Malasia tenía el coeficiente de Gini más alto de Asia (0,5), Brasil el más alto de América Latina y el Caribe (0,57) y Turquía el más alto de los países de la OCDE (0,5). [82]
El multimillonario Thomas Kwok afirmó que el coeficiente de Gini de ingresos para Hong Kong ha sido alto (0,434 en 2010 [74] ), en parte debido a cambios estructurales en su población. En las últimas décadas, Hong Kong ha sido testigo de un número creciente de hogares pequeños, hogares de ancianos y ancianos que viven solos. El ingreso combinado ahora se divide en más hogares. Muchas personas mayores viven separadas de sus hijos en Hong Kong. Estos cambios sociales han causado cambios sustanciales en la distribución del ingreso de los hogares. El coeficiente de Gini de ingresos, afirma Kwok, no discierne estos cambios estructurales en su sociedad. [81] La distribución del ingreso monetario de los hogares para los Estados Unidos, resumida en la Tabla C de esta sección, confirma que este problema no se limita solo a Hong Kong. Según la Oficina del Censo de los Estados Unidos, entre 1979 y 2010, la población de los Estados Unidos experimentó cambios estructurales en los hogares en general; el ingreso para todos los tramos de ingresos aumentó en términos ajustados por inflación, las distribuciones de ingresos de los hogares se trasladaron a tramos de ingresos más altos con el tiempo, mientras que el coeficiente de Gini de ingresos aumentó. [83] [84]
| Nivel de ingresos (en dólares ajustados de 2010) | % de la población 1979 | % de la población 2010 |
|---|---|---|
| Menos de $15,000 | 14,6% | 13,7% |
| $15,000 – $24,999 | 11,9% | 12,0% |
| $25,000 – $34,999 | 12,1% | 10,9% |
| $35,000 – $49,999 | 15,4% | 13,9% |
| $50,000 – $74,999 | 22,1% | 17,7% |
| $75,000 – $99,999 | 12,4% | 11,4% |
| $100,000 – $149,999 | 8,3% | 12,1% |
| $150,000 – $199,999 | 2,0% | 4,5% |
| $200,000 y más | 1,2% | 3,9% |
| Total de hogares | 80.776.000 | 118.682.000 |
| Índice de Gini de Estados Unidos antes de impuestos | 0,404 | 0,469 |
Desigualdad instantánea vs desigualdad a lo largo de la vida
El coeficiente de Gini no es capaz de discernir los efectos de los cambios estructurales en las poblaciones. [81] Ampliando la importancia de las medidas de la expectativa de vida, el coeficiente de Gini como una estimación puntual de la igualdad en un momento determinado ignora los cambios en la expectativa de vida en los ingresos. Normalmente, los aumentos en la proporción de miembros jóvenes o viejos de una sociedad impulsarán cambios aparentes en la igualdad simplemente porque las personas generalmente tienen ingresos y riqueza menores cuando son jóvenes que cuando son mayores. Debido a esto, factores como la distribución por edades dentro de una población y la movilidad dentro de las clases de ingresos pueden crear la apariencia de desigualdad cuando no existe ninguna, teniendo en cuenta los efectos demográficos. Así, una economía dada puede tener un coeficiente de Gini más alto en cualquier momento en comparación con otra, mientras que el coeficiente de Gini calculado sobre los ingresos de por vida de los individuos es menor que el de la economía aparentemente más igualitaria (en un momento dado en el tiempo). [ aclaración necesaria ] [16] Esencialmente, lo que importa no es solo la desigualdad en un año particular sino la composición de la distribución a lo largo del tiempo.
Prestaciones e ingresos en especie
Las imprecisiones en la asignación del valor monetario al ingreso en especie reducen la precisión del coeficiente de Gini como medida de la desigualdad real.
Si bien los impuestos y las transferencias de efectivo son relativamente fáciles de contabilizar, otros beneficios gubernamentales pueden ser difíciles de valorar. Beneficios como la vivienda subsidiada, la atención médica y la educación son difíciles de valorar objetivamente, ya que depende de la calidad y el alcance del beneficio. En ausencia de un mercado libre, la valoración de estas transferencias de ingresos como ingresos de los hogares es subjetiva. El modelo teórico del coeficiente de Gini se limita a aceptar supuestos subjetivos correctos o incorrectos.
En las economías informales y de subsistencia , las personas pueden tener ingresos significativos en otras formas que no sean dinero, por ejemplo, a través de la agricultura de subsistencia o el trueque . Estas formas de ingresos tienden a acumularse en segmentos pobres de las poblaciones en países con economías emergentes y en transición, como los de África subsahariana, América Latina, Asia y Europa del Este. La economía informal representa más de la mitad del empleo mundial y hasta el 90 por ciento del empleo en algunos de los países subsaharianos más pobres con altos coeficientes oficiales de desigualdad de Gini. Schneider et al., en su estudio de 2010 de 162 países, [85] informan que alrededor del 31,2%, o alrededor de $ 20 billones, del PIB mundial es informal. En los países en desarrollo, la economía informal predomina para todos los niveles de ingresos, excepto las poblaciones más ricas y urbanas de ingresos altos. Incluso en las economías desarrolladas, entre el 8% (Estados Unidos) y el 27% (Italia) del PIB de cada nación es informal. Los ingresos informales resultantes predominan como actividad de subsistencia para aquellos en los tramos de ingresos más bajos. [86] El valor y la distribución de los ingresos de la economía informal o subterránea son difíciles de cuantificar, lo que dificulta las estimaciones de los coeficientes de Gini de los ingresos reales. [87] [88] Diferentes supuestos y cuantificaciones de estos ingresos producirán diferentes coeficientes de Gini. [89] [90] [91]
Alternativas
Dadas las limitaciones del coeficiente de Gini, se utilizan otros métodos estadísticos en combinación o como medida alternativa de la dispersión de la población. Por ejemplo, se utilizan con frecuencia medidas de entropía (p. ej., el índice de Atkinson o el índice de Theil y la desviación logarítmica media como casos especiales del índice de entropía generalizado ). Estas medidas intentan comparar la distribución de recursos por parte de agentes inteligentes en el mercado con una distribución aleatoria de máxima entropía , que se produciría si estos agentes actuaran como partículas no interactuantes en un sistema cerrado siguiendo las leyes de la física estadística.
Relación con otras medidas estadísticas
Existe una medida resumen de la capacidad diagnóstica de un sistema clasificador binario que también se denomina coeficiente de Gini , que se define como el doble del área entre la curva ROC (curva característica operativa del receptor ) y su diagonal. Está relacionado con la medida de rendimiento AUC ( área bajo la curva ROC) dada por [92] y con la U de Mann–Whitney . Aunque ambos coeficientes de Gini se definen como áreas entre ciertas curvas y comparten ciertas propiedades, no existe una relación directa simple entre el coeficiente de Gini de dispersión estadística y el coeficiente de Gini de un clasificador.
El índice de Gini también está relacionado con el índice de Pietra, ambos miden la heterogeneidad estadística y se derivan de la curva de Lorenz y la línea diagonal. [93] [94] [30]
En ciertos campos como la ecología, se utiliza el índice de Simpson inverso para cuantificar la diversidad, y no debe confundirse con el índice de Simpson . Estos indicadores están relacionados con el Gini. El índice de Simpson inverso aumenta con la diversidad, a diferencia del índice de Simpson y el coeficiente de Gini, que disminuyen con la diversidad. El índice de Simpson está en el rango [0, 1], donde 0 significa máxima y 1 significa mínima diversidad (o heterogeneidad). Dado que los índices de diversidad normalmente aumentan con el aumento de la heterogeneidad, el índice de Simpson a menudo se transforma en Simpson inverso, o utilizando el complemento , conocido como el índice de Gini-Simpson. [95]
La curva de Lorenz es otro método de representación gráfica de la distribución de la riqueza. Fue desarrollada nueve años antes que el coeficiente de Gini, que cuantifica el grado en que la curva de Lorenz se desvía de la línea de igualdad perfecta (con pendiente de 1). El índice de Hoover (también conocido como índice de Robin Hood) presenta el porcentaje del ingreso total de la población que debería redistribuirse para que el coeficiente de Gini fuera igual a 0 (igualdad perfecta). [96]
Coeficientes de Gini para sociedades premodernas
En las últimas décadas, los investigadores han intentado estimar los coeficientes de Gini para las sociedades anteriores al siglo XX. En ausencia de encuestas sobre los ingresos de los hogares y de impuestos sobre la renta, los académicos han recurrido a variables sustitutivas, como los impuestos sobre el patrimonio en las ciudades-estado europeas medievales, los patrones de propiedad de la tierra en el Egipto romano , la variación del tamaño de las casas en sociedades desde la antigua Grecia hasta el México azteca, y la herencia y las dotes en la sociedad babilónica. Otros datos no documentan directamente las variaciones en la riqueza o los ingresos, pero se sabe que reflejan la desigualdad, como la relación entre las rentas y los salarios o entre el trabajo y el capital. [97]
Otros usos
Aunque el coeficiente de Gini es más popular en economía, en teoría puede aplicarse en cualquier campo de la ciencia que estudie una distribución. Por ejemplo, en ecología, el coeficiente de Gini se ha utilizado como una medida de la biodiversidad , donde la proporción acumulada de especies se representa gráficamente frente a la proporción acumulada de individuos. [98] En salud, se ha utilizado como una medida de la desigualdad de la calidad de vida relacionada con la salud en una población. [99] En educación, se ha utilizado como una medida de la desigualdad de las universidades. [100] En química se ha utilizado para expresar la selectividad de los inhibidores de la proteína quinasa frente a un panel de quinasas. [101] En ingeniería, se ha utilizado para evaluar la imparcialidad lograda por los enrutadores de Internet al programar transmisiones de paquetes de diferentes flujos de tráfico. [102]
El coeficiente de Gini se utiliza a veces para medir el poder discriminatorio de los sistemas de calificación en la gestión del riesgo crediticio . [103]
Un estudio de 2005 utilizó datos del censo de Estados Unidos para medir la posesión de computadoras en el hogar y utilizó el coeficiente de Gini para medir las desigualdades entre blancos y afroamericanos. Los resultados indicaron que, si bien la desigualdad en la posesión de computadoras en el hogar estaba disminuyendo en general, era sustancialmente menor entre los hogares blancos. [104]
Un estudio revisado por pares de 2016 titulado Empleo del coeficiente de Gini para medir la desigualdad de participación en redes sociales de salud digital centradas en el tratamiento [105] ilustró que el coeficiente de Gini era útil y preciso para medir los cambios en la desigualdad, sin embargo, como métrica independiente no incorporaba el tamaño general de la red.
El poder discriminatorio se refiere a la capacidad de un modelo de riesgo crediticio para diferenciar entre clientes morosos y no morosos. La fórmula , en la sección de cálculo anterior, se puede utilizar para el modelo final y a nivel de factor individual del modelo para cuantificar el poder discriminatorio de los factores individuales. Está relacionada con el índice de precisión en los modelos de evaluación de la población.
El coeficiente de Gini también se ha aplicado para analizar la desigualdad en las aplicaciones de citas . [106] [107]
Kaminskiy y Krivtsov [108] extendieron el concepto del coeficiente de Gini de la economía a la teoría de la confiabilidad y propusieron un coeficiente de tipo Gini que ayuda a evaluar el grado de envejecimiento de los sistemas no reparables o el envejecimiento y rejuvenecimiento de los sistemas reparables. El coeficiente se define entre −1 y 1 y se puede utilizar tanto en distribuciones de vida empíricas como paramétricas. Toma valores negativos para la clase de distribuciones de tasa de falla decreciente y procesos puntuales con tasa de intensidad de falla decreciente y es positivo para las distribuciones de tasa de falla creciente y procesos puntuales con tasa de intensidad de falla creciente. El valor de cero corresponde a la distribución de vida exponencial o al Proceso de Poisson Homogéneo .
Véase también
- Índice de diversidad
- Desigualdad económica
- La curva del Gran Gatsby
- Índice de Herfindahl-Hirschman
- Índice Hoover (también conocido como índice Robin Hood)
- Índice de pobreza humana
- Indicadores de desigualdad de ingresos
- Curva de Kuznets
- Lista de países según igualdad de ingresos
- Lista de países según índice de desarrollo humano ajustado por desigualdad
- Lista de países según la desigualdad de la riqueza
- Lista de estados de EE.UU. según coeficiente de Gini
- Curva de Lorenz
- Efecto Mateo
- Distribución de Pareto
- Análisis ROC
- Índice de trajes
- La curva del elefante
- utopía
- Bienestar
- Economía del bienestar
Referencias
- ^ "Índice de Gini (estimación del Banco Mundial)". Datos abiertos del Banco Mundial . Consultado el 23 de abril de 2022 .
- ^ "Libro de datos sobre la riqueza mundial 2019" (PDF) . Credit Suisse . Archivado (PDF) del original el 23 de octubre de 2019.
- ^ "Glosario | Banco de datos".
- ^ "Encuesta de población actual (CPS): definiciones y explicaciones". Oficina del Censo de Estados Unidos.
- ^ Nota: El coeficiente de Gini podría ser cercano a uno sólo en una población grande donde unas pocas personas tienen todos los ingresos. En el caso especial de sólo dos personas, donde una no tiene ingresos y la otra tiene todos los ingresos, el coeficiente de Gini es 0,5. Para cinco personas, donde cuatro no tienen ingresos y la quinta tiene todos los ingresos, el coeficiente de Gini es 0,8. Véase: Bellù, LG y Liberati, P. 2006. Análisis de la desigualdad: el índice de Gini. EASYPol: Recursos para la formulación de políticas. Roma, FAO.
- ^ Gini, Corrado (1936). "Sobre la medida de la concentración con especial referencia a los ingresos y las estadísticas", Colorado College Publication, General Series No. 208, 73–79.
- ^ abc «Distribución del ingreso – Desigualdad: Distribución del ingreso – Desigualdad – Tablas por países». OCDE. 2012. Archivado desde el original el 9 de noviembre de 2014.
- ^ "Panorama de Sudáfrica, cuarto trimestre de 2013" (PDF) . KPMG. 2013. Archivado desde el original (PDF) el 2 de abril de 2016.
- ^ "Coeficiente de Gini". Programa de las Naciones Unidas para el Desarrollo. 2012. Archivado desde el original el 12 de julio de 2014.
- ^ Schüssler, Mike (16 de julio de 2014). "El coeficiente de Gini todavía está en la botella". Money Web . Consultado el 24 de noviembre de 2014 .
- ^ "Datos abiertos del Banco Mundial". Datos abiertos del Banco Mundial . Consultado el 9 de mayo de 2023 .
- ^ abcd Hillebrand, Evan (junio de 2009). "Pobreza, crecimiento y desigualdad en los próximos 50 años" (PDF) . FAO, Naciones Unidas – Departamento de Desarrollo Económico y Social. Archivado desde el original (PDF) el 20 de octubre de 2017.
- ^ abc Naciones Unidas (2011). La verdadera riqueza de las naciones: caminos hacia el desarrollo humano, 2010 (PDF) . Programa de las Naciones Unidas para el Desarrollo. pp. 72–74. ISBN 978-0-230-28445-6. Archivado desde el original (PDF) el 29 de abril de 2011.
- ^ Yitzhaki, Shlomo (1998). "Más de una docena de formas alternativas de escribir el índice de Gini" (PDF) . Desigualdad económica . 8 : 13–30. Archivado (PDF) desde el original el 3 de agosto de 2012.
- ^ Sung, Myung Jae (agosto de 2010). "Envejecimiento de la población, movilidad de los ingresos trimestrales y desigualdad del ingreso anual: análisis teórico y hallazgos empíricos". Instituto Coreano de Finanzas Públicas. CiteSeerX 10.1.1.365.4156 .
- ^ ab Blomquist, N. (1981). "Una comparación de las distribuciones de los ingresos anuales y a lo largo de la vida: Suecia alrededor de 1970". Revista de ingresos y riqueza . 27 (3): 243–264. doi :10.1111/j.1475-4991.1981.tb00227.x. S2CID 154519005.
- ^ Gini, C. (1909). "Ratios de concentración y dependencia" (en italiano). Traducción al inglés en Rivista di Politica Economica , 87 (1997), 769–789.
- ^ Gini, C (1912). Variabilidad y mutabilidad. Contributo allo Studio delle Distribuzioni e delle Relazioni Statistiche . Bolonia: C. Cuppini.
- ^ "Quién, qué, por qué: ¿Qué es el coeficiente de Gini?". BBC News . 12 de marzo de 2015 . Consultado el 30 de marzo de 2022 .
- ^ Pellegrino, Simone (2020). "EL COEFICIENTE DE GINI: SUS ORÍGENES" (PDF) .
- ^ "Desigualdad - Desigualdad de ingresos - Datos de la OCDE". theOECD . Consultado el 28 de abril de 2024 .
- ^ "Glosario | DataBank". databank.worldbank.org . Consultado el 13 de abril de 2023 .
- ^ Weisstein, Eric W. "Coeficiente de Gini". mathworld.wolfram.com . Consultado el 13 de abril de 2023 .
- ^ "5. Medición de la desigualdad: curvas de Lorenz y coeficientes de Gini – Trabajando en Excel". www.core-econ.org . Consultado el 26 de abril de 2023 .
- ^ "función de distribución acumulativa - ¿Cómo calcular la curva de riqueza de Lorenz con valores negativos?". Validación cruzada . Consultado el 30 de noviembre de 2022 .
- ^ Sen, Amartya (1977), Sobre la desigualdad económica (2.ª ed.), Oxford: Oxford University Press
- ^ Dorfman, Robert. “Una fórmula para el coeficiente de Gini”. The Review of Economics and Statistics , vol. 61, núm. 1, 1979, págs. 146-49. JSTOR , doi :10.2307/1924845. Consultado el 2 de enero de 2023.
- ^ Treanor, Jill (13 de octubre de 2015). «La mitad de la riqueza mundial está ahora en manos del 1% de la población». The Guardian .
- ^ "Coeficiente de Gini". Wolfram Mathworld.
- ^ abc McDonald, James B; Jensen, Bartell C. (diciembre de 1979). "Análisis de algunas propiedades de medidas alternativas de desigualdad de ingresos basadas en la función de distribución gamma". Journal of the American Statistical Association . 74 (368): 856–860. doi :10.1080/01621459.1979.10481042.
- ^ ab Crow, EL, y Shimizu, K. (Eds.). (1988). Distribuciones lognormales: teoría y aplicaciones (Vol. 88). Nueva York: M. Dekker, página 11.
- ^ "Función delta de Dirac: descripción general | Temas de ScienceDirect" www.sciencedirect.com . Consultado el 30 de noviembre de 2022 .
- ^ Weisstein, Eric W. "Distribución uniforme". mathworld.wolfram.com . Consultado el 30 de noviembre de 2022 .
- ^ "Distribución exponencial | Definición | Variable aleatoria sin memoria". www.probabilitycourse.com . Consultado el 30 de noviembre de 2022 .
- ^ Para el log-normal con = 0, = 0; = 0.
- ^ ab "Wolfram MathWorld: el recurso de matemáticas más completo de la Web". mathworld.wolfram.com . Consultado el 30 de noviembre de 2022 .
- ^ "Distribución de chi-cuadrado - de Wolfram MathWorld". mathworld.wolfram.com . Consultado el 11 de enero de 2023 .
- ^ "Distribución de Weibull: características de la distribución de Weibull". www.weibull.com . Consultado el 30 de noviembre de 2022 .
- ^ Weisstein, Eric W. "Distribución beta". mathworld.wolfram.com . Consultado el 30 de noviembre de 2022 .
- ^ "La distribución log-logística". www.randomservices.org . Consultado el 30 de noviembre de 2022 .
- ^ Abdon, Mitch (23 de mayo de 2011). "Bootstrapping Gini". Statadaily: Unsolicited advice for the interested (Asesoramiento no solicitado para los interesados ). Consultado el 12 de noviembre de 2022 .
- ^ Gales (2004).
- ^ Jasso, Guillermina (1979). "Sobre la diferencia de medias de Gini y el índice de concentración de Gini". American Sociological Review . 44 (5): 867–870. doi :10.2307/2094535. JSTOR 2094535.
- ^ Deaton (1997), pág. 139.
- ^ Allison, Paul D. (1979). "Respuesta a Jasso". American Sociological Review . 44 (5): 870–872. doi :10.2307/2094536. JSTOR 2094536.
- ^ abcd Bellù, Lorenzo Giovanni; Liberati, Paolo (2006). «Análisis de la desigualdad: el índice de Gini» (PDF) . Organización de las Naciones Unidas para la Alimentación y la Agricultura. Archivado desde el original (PDF) el 13 de julio de 2017. Consultado el 31 de julio de 2012 .
- ^ Firebaugh, Glenn (1999). "Estudios empíricos de la desigualdad del ingreso mundial". Revista estadounidense de sociología . 104 (6): 1597–1630. doi :10.1086/210218. S2CID 154973184.Véase también ——— (2003). "Desigualdad: qué es y cómo se mide". La nueva geografía de la desigualdad global del ingreso . Cambridge, MA: Harvard University Press. ISBN 978-0-674-01067-3.
- ^ Kakwani, NC (abril de 1977). "Aplicaciones de las curvas de Lorenz en el análisis económico". Econometrica . 45 (3): 719–728. doi :10.2307/1911684. JSTOR 1911684.
- ^ Chu, Ke-young; Davoodi, Hamid; Gupta, Sanjeev (marzo de 2000). "Income Distribution and Tax and Government Social Spending Policies in Developing Countries" (PDF) . Fondo Monetario Internacional. Archivado (PDF) desde el original el 30 de agosto de 2000.
- ^ "Seguimiento de la calidad de vida en Europa: índice de Gini". Eurofound . 26 de agosto de 2009. Archivado desde el original el 1 de diciembre de 2008.
- ^ Wang, Chen; Caminada, Koen; Goudswaard, Kees (2012). "El efecto redistributivo de los programas de transferencias sociales y los impuestos: una descomposición entre países". Revista Internacional de Seguridad Social . 65 (3): 27–48. doi :10.1111/j.1468-246X.2012.01435.x. hdl : 1887/3207160 . S2CID 154029963.
- ^ Sutcliffe, Bob (abril de 2007). «Postscriptum to the article 'World inequality and globalization' (Oxford Review of Economic Policy, primavera de 2004)» (PDF) . Archivado (PDF) desde el original el 21 de junio de 2007. Consultado el 13 de diciembre de 2007 .
- ^ ab Ortiz, Isabel; Cummins, Matthew (abril de 2011). "Global Inequality: Beyond the Bottom Billion" (PDF) . UNICEF. pág. 26. Archivado desde el original (PDF) el 12 de agosto de 2012 . Consultado el 30 de julio de 2012 .
- ^ Milanovic, Branko (septiembre de 2011). "Más o menos". Finanzas y Desarrollo . 48 (3).
- ^ Milanovic, Branko (2009). "Global Inequality and the Global Inequality Extraction Ratio" (PDF) . Banco Mundial. Archivado (PDF) del original el 11 de noviembre de 2013.
- ^ Berry, Albert; Serieux, John (septiembre de 2006). "Riding the Elephants: The Evolution of World Economic Growth and Income Distribution at the End of the Twentieth Century (1980–2000)" (PDF) . Naciones Unidas (Documento de trabajo del Departamento de Asuntos Económicos y Sociales de los Estados Unidos, Nº 27). Archivado (PDF) desde el original el 17 de febrero de 2009.
- ^ Gharib, Malaka (25 de enero de 2017). "Lo que las estadísticas sobre los ocho hombres más ricos no nos dicen sobre la desigualdad". NPR .
- ^ Banco Mundial . «Pobreza y prosperidad 2016: cómo afrontar la desigualdad» (PDF) . Archivado (PDF) del original el 15 de noviembre de 2016.Figura O.10 Desigualdad global, 1988-2013
- ^ Sadras, VO; Bongiovanni, R. (2004). "Uso de curvas de Lorenz y coeficientes de Gini para evaluar la desigualdad de rendimiento dentro de los potreros". Investigación de cultivos de campo . 90 (2–3): 303–310. doi :10.1016/j.fcr.2004.04.003.
- ^ Thomas, Vinod; Wang, Yan; Fan, Xibo (enero de 2001). Medición de la desigualdad en la educación: coeficientes de Gini de la educación (PDF) . Documentos de trabajo sobre investigación de políticas. Banco Mundial. CiteSeerX 10.1.1.608.6919 . doi :10.1596/1813-9450-2525. hdl :10986/19738. S2CID 6069811. Archivado desde el original (PDF) el 5 de junio de 2013.
- ^ Thomas, Vinod; Wang, Yan; Fan, Xibo (2001). Medición de la desigualdad educativa: coeficientes de Gini de la educación. Publicaciones del Banco Mundial.
- ^ ab Roemer, John E. (septiembre de 2006). El desarrollo económico como igualación de oportunidades (informe). Universidad de Yale. CiteSeerX 10.1.1.403.4725 . SSRN 931479.
- ^ Weymark, John (2003). "Índices de Gini generalizados de igualdad de oportunidades". Journal of Economic Inequality . 1 (1): 5–24. doi :10.1023/A:1023923807503. S2CID 133596675.
- ^ Kovacevic, Milorad (noviembre de 2010). "Medición de la desigualdad en el desarrollo humano: una revisión" (PDF) . Programa de las Naciones Unidas para el Desarrollo. Archivado desde el original (PDF) el 23 de septiembre de 2011.
- ^ Atkinson, Anthony B. (1999). "Las contribuciones de Amartya Sen a la economía del bienestar" (PDF) . The Scandinavian Journal of Economics . 101 (2): 173–190. doi :10.1111/1467-9442.00151. JSTOR 3440691. Archivado desde el original (PDF) el 13 de mayo de 2014.
- ^ Roemer, John E.; et al. (marzo de 2003). "¿En qué medida los regímenes fiscales igualan las oportunidades de adquisición de ingresos entre los ciudadanos?". Journal of Public Economics . 87 (3–4): 539–565. CiteSeerX 10.1.1.414.6220 . doi :10.1016/S0047-2727(01)00145-1.
- ^ Shorrocks, Anthony (diciembre de 1978). "Desigualdad de ingresos y movilidad del ingreso". Journal of Economic Theory . 19 (2): 376–393. doi :10.1016/0022-0531(78)90101-1.
- ^ Maasoumi, Esfandiar; Zandvakili, Sourushe (1986). "Una clase de medidas generalizadas de movilidad con aplicaciones". Economics Letters . 22 (1): 97–102. doi :10.1016/0165-1765(86)90150-3.
- ^ ab Kopczuk, Wojciech; Saez, Emmanuel; Song, Jae (2010). "Desigualdad de ingresos y movilidad en los Estados Unidos: evidencia de los datos de la seguridad social desde 1937" (PDF) . The Quarterly Journal of Economics . 125 (1): 91–128. doi :10.1162/qjec.2010.125.1.91. JSTOR 40506278. Archivado (PDF) desde el original el 13 de mayo de 2013.
- ^ Chen, Wen-Hao (marzo de 2009). "Diferencias transnacionales en la movilidad del ingreso: evidencia de Canadá, Estados Unidos, Gran Bretaña y Alemania". Revista de ingresos y riqueza . 55 (1): 75–100. doi :10.1111/j.1475-4991.2008.00307.x. S2CID 62886186.
- ^ Sastre, Mercedes; Ayala, Luis (2002). "Europa vs. Estados Unidos: ¿Existe una disyuntiva entre movilidad y desigualdad?" (PDF) . Instituto de Investigación Social y Económica, Universidad de Essex. Archivado (PDF) desde el original el 12 de junio de 2006.
- ^ "Desigualdad - Desigualdad de ingresos - Datos de la OCDE". theOECD . Consultado el 2 de junio de 2023 .
- ^ Mellor, John W. (2 de junio de 1989). "Reducción drástica de la pobreza en el Tercer Mundo: perspectivas y medidas necesarias" (PDF) . Instituto Internacional de Investigación sobre Políticas Alimentarias. pp. 18-20. Archivado (PDF) desde el original el 3 de agosto de 2012.
- ^ ab "La verdadera riqueza de las naciones: caminos hacia el desarrollo humano (Informe sobre Desarrollo Humano 2010 – véanse los cuadros estadísticos)". Programa de las Naciones Unidas para el Desarrollo. 2011. págs. 152-156.
- ^ De Maio, Fernando G. (2007). "Medidas de desigualdad de ingresos". Revista de Epidemiología y Salud Comunitaria . 61 (10): 849–852. doi :10.1136/jech.2006.052969. PMC 2652960 . PMID 17873219.
- ^ Stephany, Fabian (1 de diciembre de 2017). "¿Quiénes son tus Joneses? Desigualdad de ingresos socioespecífica y confianza". Investigación de indicadores sociales . 134 (3): 877–898. doi :10.1007/s11205-016-1460-9. ISSN 1573-0921. PMC 5684274. PMID 29187771 .
- ^ Domeij, David; Flodén, Martin (2010). "Tendencias de la desigualdad en Suecia 1978-2004". Revista de dinámica económica . 13 (1): 179–208. CiteSeerX 10.1.1.629.9417 . doi :10.1016/j.red.2009.10.005.
- ^ Domeij, David; Klein, Paul (enero de 2000). "Accounting for Swedish wealth inequality" (PDF) . Archivado desde el original (PDF) el 19 de mayo de 2003.
- ^ Deltas, George (febrero de 2003). "El sesgo de muestra pequeña del coeficiente de Gini: resultados e implicaciones para la investigación empírica". The Review of Economics and Statistics . 85 (1): 226–234. doi :10.1162/rest.2003.85.1.226. JSTOR 3211637. S2CID 57572560.
- ^ Monfort, Philippe (2008). «Convergencia de las regiones de la UE: medidas y evolución» (PDF) . Unión Europea – Europa. p. 6. Archivado (PDF) desde el original el 3 de agosto de 2012.
- ^ abc KWOK Kwok Chuen (2010). "Distribución del ingreso en Hong Kong y el coeficiente de Gini" (PDF) . Gobierno de Hong Kong, China. Archivado desde el original (PDF) el 27 de diciembre de 2010.
- ^ Deininger, Klaus; Squire, Lyn (1996). "Un nuevo conjunto de datos para medir la desigualdad del ingreso" (PDF) . Revista Económica del Banco Mundial . 10 (3): 565–591. CiteSeerX 10.1.1.314.5610 . doi :10.1093/wber/10.3.565. Archivado (PDF) desde el original el 16 de julio de 2007.
- ^ ab "Ingresos, pobreza y cobertura de seguro médico en los Estados Unidos: 2010 (véase la Tabla A-2)" (PDF) . Oficina del Censo, Departamento de Comercio, Estados Unidos. Septiembre de 2011. Archivado (PDF) desde el original el 23 de septiembre de 2011.
- ^ Oficina de Presupuesto del Congreso: Tendencias en la distribución del ingreso familiar entre 1979 y 2007. Octubre de 2011. Véanse las páginas i–x, con definiciones en ii–iii.
- ^ Schneider, Friedrich; Buehn, Andreas; Montenegro, Claudio E. (2010). "Nuevas estimaciones para las economías sumergidas en todo el mundo". Revista económica internacional . 24 (4): 443–461. doi :10.1080/10168737.2010.525974. hdl :10986/4929. S2CID 56060172.
- ^ La economía informal (PDF) . Instituto Internacional para el Medio Ambiente y el Desarrollo, Reino Unido. 2011. ISBN 978-1-84369-822-7. Archivado (PDF) del original el 3 de agosto de 2012.
- ^ Feldstein, Martin (agosto de 1998). "¿Es la desigualdad de ingresos realmente el problema? (Descripción general)" (PDF) . Reserva Federal de Estados Unidos. Archivado desde el original (PDF) el 3 de agosto de 2012. Consultado el 2 de agosto de 2012 .
- ^ Taylor, John; Weerapana, Akila (2009). Principios de microeconomía: edición de la crisis financiera mundial . Cengage Learning. págs. 416–418. ISBN 978-1-4390-7821-1.
- ^ Rosser, J. Barkley Jr.; Rosser, Marina V.; Ahmed, Ehsan (marzo de 2000). "Desigualdad de ingresos y economía informal en economías en transición". Journal of Comparative Economics . 28 (1): 156–171. doi :10.1006/jcec.2000.1645. S2CID 49552052.
- ^ Krstić, Gorana; Sanfey, Peter (febrero de 2010). "La desigualdad de ingresos y la economía informal: datos de Serbia" (PDF) . Banco Europeo de Reconstrucción y Desarrollo. Archivado (PDF) desde el original el 3 de agosto de 2012.
- ^ Schneider, Friedrich (diciembre de 2004). El tamaño de las economías sumergidas de 145 países de todo el mundo: primeros resultados para el período 1999-2003 (informe). hdl :10419/20729. SSRN 636661.
- ^ Hand, David J.; Till, Robert J. (2001). "Una generalización simple del área bajo la curva ROC para problemas de clasificación de clases múltiples" (PDF) . Machine Learning . 45 (2): 171–186. doi : 10.1023/A:1010920819831 . S2CID 43144161. Archivado (PDF) desde el original el 10 de agosto de 2013.
- ^ Eliazar, Iddo I.; Sokolov, Igor M. (2010). "Medición de la heterogeneidad estadística: el índice de Pietra". Physica A: Mecánica estadística y sus aplicaciones . 389 (1): 117–125. Bibcode :2010PhyA..389..117E. doi :10.1016/j.physa.2009.08.006.
- ^ Lee, Wen-Chung (1999). "Análisis probabilístico de los resultados globales de las pruebas diagnósticas: interpretación de las medidas de resumen basadas en la curva de Lorenz" (PDF) . Estadística en medicina . 18 (4): 455–471. doi :10.1002/(SICI)1097-0258(19990228)18:4<455::AID-SIM44>3.0.CO;2-A. PMID 10070686. Archivado desde el original (PDF) el 3 de agosto de 2012 . Consultado el 1 de agosto de 2012 .
- ^ Peet, Robert K. (1974). "La medición de la diversidad de especies". Revista Anual de Ecología y Sistemática . 5 : 285–307. doi :10.1146/annurev.es.05.110174.001441. JSTOR 2096890. S2CID 83517584.
- ^ "Índice Hoover". Instituto de Finanzas Corporativas . Consultado el 28 de abril de 2024 .
- ^ Walter Scheidel (2017). El gran nivelador: violencia e historia de la desigualdad desde la Edad de Piedra hasta el siglo XXI . Princeton University Press. pp. 15-16. ISBN 978-0-691-16502-8.
- ^ Wittebolle, Lieven; Marzorati, Massimo; et al. (2009). "La uniformidad inicial de la comunidad favorece la funcionalidad bajo estrés selectivo". Nature . 458 (7238): 623–626. Bibcode :2009Natur.458..623W. doi :10.1038/nature07840. PMID 19270679. S2CID 4419280.
- ^ Asada, Yukiko (2005). "Evaluación de la salud de los estadounidenses: la calidad de vida relacionada con la salud promedio y su desigualdad entre individuos y grupos". Métricas de salud de la población . 3 : 7. doi : 10.1186/1478-7954-3-7 . PMC 1192818 . PMID 16014174.
- ^ Halffman, Willem; Leydesdorff, Loet (2010). "¿Está aumentando la desigualdad entre las universidades? Los coeficientes de Gini y el elusivo ascenso de las universidades de élite". Minerva . 48 (1): 55–72. arXiv : 1001.2921 . doi :10.1007/s11024-010-9141-3. PMC 2850525 . PMID 20401157.
- ^ Graczyk, Piotr (2007). "Coeficiente de Gini: una nueva forma de expresar la selectividad de los inhibidores de quinasas contra una familia de quinasas". Journal of Medicinal Chemistry . 50 (23): 5773–5779. doi :10.1021/jm070562u. PMID 17948979.
- ^ Shi, Hongyuan; Sethu, Harish (2003). "Colas justas y codiciosas: una estrategia orientada a objetivos para la programación justa de paquetes en tiempo real". Actas del 24.º Simposio de sistemas en tiempo real del IEEE . IEEE Computer Society . págs. 345–356. ISBN 978-0-7695-2044-5.
- ^ Christodoulakis, George A.; Satchell, Stephen, eds. (noviembre de 2007). The Analytics of Risk Model Validation (Finanzas cuantitativas) . Academic Press. ISBN 978-0-7506-8158-2.
- ^ Chakraborty, J; Bosman, MM (2005). "Medición de la brecha digital en los Estados Unidos: raza, ingresos y posesión de computadoras personales". Prof Geogr . 57 (3): 395–410. doi :10.1111/j.0033-0124.2005.00486.x. S2CID 154401826.
- ^ van Mierlo, T; Hyatt, D; Ching, A (2016). "Uso del coeficiente de Gini para medir la desigualdad de participación en redes sociales de salud digital centradas en el tratamiento". Netw Model Anal Health Inform Bioinforma . 5 (32): 32. doi :10.1007/s13721-016-0140-7. PMC 5082574 . PMID 27840788.
- ^ worst-online-dater (25 de marzo de 2015). "Experimentos de Tinder II: Chicos, a menos que seáis realmente atractivos, probablemente sea mejor que no desperdiciéis vuestras…". Medium . Consultado el 28 de abril de 2021 .
- ^ Kopf, Dan (15 de agosto de 2017). «Estas estadísticas muestran por qué es tan difícil ser un hombre promedio en las aplicaciones de citas». Quartz . Consultado el 28 de abril de 2021 .
- ^ Kaminskiy, MP; Krivtsov, VV (2011). "Un índice de tipo Gini para objetos envejecidos/rejuvenecidos". Modelos y métodos matemáticos y estadísticos en confiabilidad. Birkhäuser Boston: Springer. págs. 133–140. ISBN 978-0-8176-4970-8.
Lectura adicional
- Amiel, Y.; Cowell, F. A. (1999). Pensando en la desigualdad . Cambridge. ISBN 978-0-521-46696-7.
- Anand, Sudhir (1983). Desigualdad y pobreza en Malasia . Nueva York: Oxford University Press. ISBN 978-0-19-520153-6.
- Brown, Malcolm (1994). "Uso de índices de estilo Gini para evaluar los patrones espaciales de los profesionales de la salud: consideraciones teóricas y una aplicación basada en datos de Alberta". Ciencias sociales y medicina . 38 (9): 1243–1256. doi :10.1016/0277-9536(94)90189-9. PMID 8016689.
- Chakravarty, S. R. (1990). Números del índice social ético . Nueva York: Springer-Verlag. ISBN 978-0-387-52274-6.
- Deaton, Angus (1997). Análisis de encuestas de hogares . Baltimore, MD: Johns Hopkins University Press. ISBN 978-0-585-23787-9.
- Dixon, Philip M.; Weiner, Jacob; Mitchell-Olds, Thomas; Woodley, Robert (1987). "Bootstrapping del coeficiente de Gini de desigualdad". Ecología . 68 (5): 1548–1551. doi :10.2307/1939238. JSTOR 1939238. S2CID 84940050.
- Dorfman, Robert (1979). "Una fórmula para el coeficiente de Gini". The Review of Economics and Statistics . 61 (1): 146–149. doi :10.2307/1924845. JSTOR 1924845.
- Firebaugh, Glenn (2003). La nueva geografía de la desigualdad del ingreso global . Cambridge, Massachusetts: Harvard University Press. ISBN 978-0-674-01067-3.
- Gastwirth, Joseph L. (1972). "La estimación de la curva de Lorenz y el índice de Gini". The Review of Economics and Statistics . 54 (3): 306–316. doi :10.2307/1937992. JSTOR 1937992.
- Giles, David (2004). "Cálculo del error estándar para el coeficiente de Gini: algunos resultados adicionales" (PDF) . Oxford Bulletin of Economics and Statistics . 66 (3): 425–433. CiteSeerX 10.1.1.202.6462 . doi :10.1111/j.1468-0084.2004.00086.x. S2CID 16972099. Archivado desde el original (PDF) el 5 de mayo de 2004.
- Gini, Corrado (1912). Variabilidad y mutabilidad . Código bibliográfico : 1912vamu.book.....G.Reimpreso en Pizetti, E.; Salvemini, T., eds. (1955). Memoria de estadística metodológica . Roma: Librería Eredi Virgilio Veschi.
- Gini, Corrado (1921). "Medición de la desigualdad de ingresos". The Economic Journal . 31 (121): 124–126. doi :10.2307/2223319. JSTOR 2223319.
- Giorgi, Giovanni Maria (1990). "Retrato bibliográfico del índice de concentración de Gini" (PDF) . Metron . 48 : 183–231. Archivado desde el original (PDF) el 4 de agosto de 2016.
- Karagiannis, E.; Kovacevic, M. (2000). "Un método para calcular el estimador de varianza Jackknife para el coeficiente de Gini". Oxford Bulletin of Economics and Statistics . 62 : 119–122. doi :10.1111/1468-0084.00163.
- Mills, Jeffrey A.; Zandvakili, Sourushe (1997). "Inferencia estadística mediante bootstrapping para medidas de desigualdad" (PDF) . Journal of Applied Econometrics . 12 (2): 133–150. CiteSeerX 10.1.1.172.5003 . doi :10.1002/(SICI)1099-1255(199703)12:2<133::AID-JAE433>3.0.CO;2-H. hdl :10419/186818. JSTOR 2284908. Archivado (PDF) desde el original el 18 de julio de 2012.
- Modarres, Reza; Gastwirth, Joseph L. (2006). "Una nota de advertencia sobre la estimación del error estándar del índice de desigualdad de Gini". Oxford Bulletin of Economics and Statistics . 68 (3): 385–390. doi :10.1111/j.1468-0084.2006.00167.x. S2CID 122716409.
- Morgan, James (1962). "La anatomía de la distribución del ingreso". Revista de Economía y Estadística . 44 (3): 270–283. doi :10.2307/1926398. JSTOR 1926398.
- Ogwang, Tomson (2000). "Un método conveniente para calcular el índice de Gini y su error estándar". Oxford Bulletin of Economics and Statistics . 62 : 123–129. doi :10.1111/1468-0084.00164.
- Ogwang, Tomson (2004). "Cálculo de un error estándar para el coeficiente de Gini: algunos resultados adicionales: Respuesta". Oxford Bulletin of Economics and Statistics . 66 (3): 435–437. doi :10.1111/j.1468-0084.2004.00087.x. S2CID 122160535.
- Xu, Kuan (enero de 2004). "¿Cómo ha evolucionado la literatura sobre el índice de Gini en los últimos 80 años?" (PDF) . Revista electrónica SSRN . Documento de trabajo sobre economía. Universidad de Dalhousie . doi :10.2139/ssrn.423200. Archivado desde el original (PDF) el 28 de septiembre de 2006. Consultado el 1 de junio de 2006 .La versión china de este artículo se publicó como Xu, Kuan (2003). "¿Cómo ha evolucionado la literatura sobre el índice de Gini en los últimos 80 años?". China Economic Quarterly . 2 : 757–778.
- Yitzhaki, Shlomo (1991). "Cálculo de estimadores de varianza Jackknife para parámetros del método de Gini". Journal of Business and Economic Statistics . 9 (2): 235–239. doi :10.2307/1391792. JSTOR 1391792.
Enlaces externos
- Deutsche Bundesbank: ¿Diversifican los bancos sus carteras de préstamos?, 2005 (sobre el uso, por ejemplo, del coeficiente de Gini para la evaluación del riesgo de las carteras de préstamos)
- Forbes: Elogio de la desigualdad
- Medición del riesgo de un proyecto de software con el coeficiente de Gini, una aplicación del coeficiente de Gini al software
- El Banco Mundial: medición de la desigualdad
- Travis Hale, Proyecto de desigualdad de la Universidad de Texas: Fundamentos teóricos de las medidas de desigualdad más populares, cálculo en línea de los ejemplos: 1A, 1B
- Artículo de The Guardian que analiza la desigualdad en el Reino Unido entre 1974 y 2006
- Base de datos sobre desigualdad de ingresos en el mundo
- BBC News: ¿Qué es el coeficiente de Gini?
- Distribución del ingreso y pobreza en los países de la OCDE
- Distribución del ingreso en Estados Unidos: ¿Cuán desigual es?












































































