Indicadores de desigualdad de ingresos
Los científicos sociales utilizan las métricas de desigualdad de ingresos o métricas de distribución de ingresos para medir la distribución de los ingresos y la desigualdad económica entre los participantes de una economía en particular, como la de un país específico o la del mundo en general. Si bien diferentes teorías pueden intentar explicar cómo se produce la desigualdad de ingresos, las métricas de desigualdad de ingresos simplemente proporcionan un sistema de medición utilizado para determinar la dispersión de los ingresos. El concepto de desigualdad es distinto de la pobreza [Nota 1] y la equidad .
La distribución del ingreso siempre ha sido una preocupación central de la teoría económica y la política económica . Los economistas clásicos como Adam Smith , Thomas Malthus y David Ricardo se preocuparon principalmente por la distribución del ingreso de los factores, es decir, la distribución del ingreso entre los principales factores de producción , tierra, trabajo y capital. A menudo se relaciona con la distribución de la riqueza , aunque factores separados influyen en la desigualdad de la riqueza .
Los economistas modernos también han abordado esta cuestión, pero se han preocupado más por la distribución del ingreso entre individuos y hogares. Entre las preocupaciones teóricas y políticas importantes se encuentra la relación entre la desigualdad del ingreso y el crecimiento económico . En el artículo Desigualdad económica se analizan los aspectos sociales y de política de las cuestiones de distribución del ingreso.
Definición de ingresos
Todas las métricas descritas a continuación son aplicables para evaluar la desigualdad distributiva de diversos tipos de recursos. En este caso, el enfoque se centra en el ingreso como recurso. Como existen diversas formas de "ingreso", el tipo de ingreso investigado debe describirse claramente.
Una forma de ingreso es la cantidad total de bienes y servicios que una persona recibe, y por lo tanto no necesariamente hay dinero en juego. Si un agricultor de subsistencia en Uganda cultiva su propio grano, esto contará como ingreso. También se contabilizan servicios como la salud pública y la educación. A menudo, el gasto o el consumo (que es lo mismo en un sentido económico) se utilizan para medir el ingreso. El Banco Mundial utiliza las llamadas "encuestas de medición del nivel de vida" [1] para medir los ingresos. Estas consisten en cuestionarios con más de 200 preguntas. Se han completado encuestas en la mayoría de los países en desarrollo .
En el análisis de la desigualdad de ingresos dentro de los países, el término "ingreso" suele hacer referencia a los ingresos gravados por persona o por hogar. En este caso, las medidas de desigualdad de ingresos también pueden utilizarse para comparar las distribuciones de ingresos antes y después de los impuestos, a fin de medir los efectos de las tasas impositivas progresivas.
Propiedades de las métricas de desigualdad
En el caso discreto, un índice de desigualdad económica puede representarse mediante una función I(x) , donde x es un conjunto de n valores económicos (por ejemplo, riqueza o ingresos) x={x 1 ,x 2 ,...,x n }, siendo x i el valor económico asociado con el "agente económico" i .
En la literatura económica sobre la desigualdad generalmente se postulan cuatro propiedades que cualquier medida de desigualdad debe satisfacer:
- Anonimato o simetría
- Este supuesto establece que una métrica de desigualdad no depende de la "clasificación" de los individuos en una economía y que lo único que importa es la distribución del ingreso. Por ejemplo, en una economía compuesta por dos personas, el Sr. Smith y la Sra. Jones, donde uno de ellos tiene el 60% del ingreso y el otro el 40%, la métrica de desigualdad debería ser la misma independientemente de que sea el Sr. Smith o la Sra. Jones quien tenga el 40% de los ingresos. Esta propiedad distingue el concepto de desigualdad del de justicia, donde es de importancia central quién posee un nivel particular de ingresos y cómo lo ha adquirido. Una métrica de desigualdad es simplemente una declaración sobre cómo se distribuye el ingreso, no sobre quiénes son las personas particulares en la economía o qué tipo de ingresos "merecen".
- Generalmente esto se expresa matemáticamente como:
- donde P(x) es cualquier permutación de x ;
- Independencia u homogeneidad de escala
- Esta propiedad indica que las economías más ricas no deberían considerarse automáticamente más desiguales por construcción. En otras palabras, si el ingreso de cada persona en una economía se duplica (o se multiplica por cualquier constante positiva), entonces la métrica general de desigualdad no debería cambiar. Por supuesto, lo mismo se aplica a las economías más pobres. La métrica de desigualdad del ingreso debería ser independiente del nivel agregado de ingresos. Esto puede expresarse como:
- donde α es un número real positivo.
- Independencia de la población
- De manera similar, la métrica de la desigualdad de ingresos no debería depender de si una economía tiene una población grande o pequeña. Una economía con sólo unas pocas personas no debería ser juzgada automáticamente por la métrica como más igualitaria que una economía grande con muchas personas. Esto significa que la métrica debería ser independiente del nivel de población. Esto generalmente se escribe:
- donde es la unión de x con (una copia de) sí mismo.
- Principio de transferencia
- El principio de Pigou-Dalton , o principio de transferencia, es el supuesto que convierte una métrica de desigualdad en una medida de la desigualdad. En su forma débil, dice que si se transfiere una parte del ingreso de una persona rica a una persona pobre, mientras se conserva el orden de los rangos de ingresos, entonces la desigualdad medida no debería aumentar. En su forma fuerte, el nivel medido de desigualdad debería disminuir.
Otras propiedades útiles pero no obligatorias incluyen:
- No negatividad
- El índice I(x) es mayor o igual a cero.
- Cero igualitario
- El índice I(x) es cero en el caso igualitario, cuando todos los valores x i son iguales.
- Limitado arriba por la máxima desigualdad
- El índice I(x) alcanza su valor máximo para la máxima desigualdad. (todos los x i son cero excepto uno). Este valor suele ser la unidad a medida que el número de agentes n se acerca al infinito.
- Descomponibilidad de subgrupos [2]
- Esta propiedad establece que si un conjunto de agentes x se divide en dos subconjuntos disjuntos ( y y z ), entonces I(x) se puede expresar como:
- donde μ(x) y μ(y) son los ingresos medios de x e y .
- y las funciones w son funciones de ponderación escalar de los conjuntos y y z . En una afirmación más fuerte, w y = μ y / μ x y w z = μ z / μ x .
Métricas comunes de desigualdad de ingresos
Entre las métricas más comunes que se utilizan para medir la desigualdad se encuentran el índice de Gini (también conocido como coeficiente de Gini ), el índice de Theil y el índice de Hoover . Todos ellos tienen las cuatro propiedades descritas anteriormente.
Una propiedad adicional de una métrica de desigualdad que puede ser deseable desde un punto de vista empírico es la de la "descomponibilidad". Esto significa que si una economía particular se divide en subregiones y se calcula una métrica de desigualdad para cada subregión por separado, entonces la medida de desigualdad para la economía en su conjunto debería ser un promedio ponderado de las desigualdades regionales más un término proporcional a la desigualdad en los promedios de las regiones (en una forma más débil, significa que debería ser una función explícita de las desigualdades subregionales, aunque no necesariamente lineal). De los índices anteriores, solo el índice de Theil tiene esta propiedad.
Dado que estas métricas de desigualdad de ingresos son estadísticas resumidas que buscan agregar una distribución completa de ingresos en un único índice, la información sobre la desigualdad medida se reduce. Esta reducción de información es, por supuesto, el objetivo de calcular las medidas de desigualdad, ya que reduce la complejidad.
Se logra una reducción más débil de la complejidad si las distribuciones de ingresos se describen como porcentajes del ingreso total. En lugar de indicar una única medida, la sociedad en estudio se divide en segmentos, como por ejemplo en quintiles (o cualquier otro porcentaje de la población). Por lo general, cada segmento contiene la misma proporción de personas que perciben ingresos. En caso de una distribución desigual del ingreso, las proporciones del ingreso disponibles en cada segmento son diferentes.
En muchos casos, los índices de desigualdad mencionados anteriormente se calculan a partir de datos de segmentos sin evaluar las desigualdades dentro de los segmentos. Cuanto mayor sea el número de segmentos (por ejemplo, decilos en lugar de quintiles), más se acerca la desigualdad de distribución medida a la desigualdad real. (Si se conoce la desigualdad dentro de los segmentos, la desigualdad total se puede determinar mediante aquellas métricas de desigualdad que tienen la propiedad de ser "descomponibles").
Las medidas de desigualdad por quintiles satisfacen el principio de transferencia sólo en su forma débil porque los cambios en la distribución del ingreso fuera de los quintiles relevantes no son detectados por estas medidas; sólo importa la distribución del ingreso entre los muy ricos y los muy pobres, mientras que la desigualdad en el medio no juega ningún papel.
Los detalles de las tres medidas de desigualdad se describen en los respectivos artículos de Wikipedia. Las siguientes subsecciones las cubren sólo brevemente.
Índice de Gini

El índice de Gini es una estadística resumida que mide la equidad con que se distribuye un recurso en una población ; el ingreso es un ejemplo principal. Además de una presentación completa del índice de Gini, ofrecemos dos formas equivalentes de interpretar esta estadística resumida: primero en términos del nivel percentil de la persona que gana el dólar promedio , y segundo en términos de cómo el menor de dos ingresos elegidos al azar se compara, en promedio, con el ingreso medio. [3]
El Gini es la suma, sobre todos los percentiles de población ordenados por ingresos, del déficit, a partir de una proporción igual, del ingreso acumulado hasta cada percentil de población, con ese déficit sumado dividido por el mayor valor que podría tener, con completa desigualdad.
El rango del índice de Gini está entre 0 y 1 (0% y 100%), donde 0 indica igualdad perfecta y 1 (100%) indica máxima desigualdad.
El índice de Gini es el índice de desigualdad más utilizado. La razón de su popularidad es que es fácil entender cómo calcular el índice de Gini como una relación de dos áreas en los diagramas de curvas de Lorenz . Esta medida intenta capturar la dispersión general del ingreso; sin embargo, tiende a asignar diferentes niveles de importancia a los extremos inferior, medio y superior de la distribución. Como desventaja, el índice de Gini solo asigna un número a las propiedades de un diagrama, pero el diagrama en sí no se basa en ningún modelo de un proceso de distribución. El "significado" del índice de Gini solo se puede entender empíricamente. Además, el índice de Gini no captura en qué parte de la distribución se produce la desigualdad. Como resultado, dos distribuciones de ingresos muy diferentes pueden tener el mismo índice de Gini.
Relación 20:20

La proporción 20:20 o 20/20 compara cuánto más rico es el 20% más rico de las poblaciones en comparación con el 20% más pobre de una población dada. Esto puede ser más revelador del impacto real de la desigualdad en una población, ya que reduce el efecto en las estadísticas de los valores atípicos en la parte superior e inferior y evita que el 60% medio oculte estadísticamente la desigualdad que de otro modo sería obvia en el campo. La medida se utiliza para los Indicadores de Desarrollo Humano del Programa de las Naciones Unidas para el Desarrollo. [4] [5] La proporción 20:20, por ejemplo, muestra que Japón y Suecia tienen una brecha de desigualdad baja, donde el 20% más rico solo gana 4 veces más que el 20% más pobre, mientras que en el Reino Unido la proporción es 7 veces y en los EE. UU. 8 veces. Algunos creen que la proporción 20:20 es una medida más útil ya que se correlaciona bien con las medidas de desarrollo humano y estabilidad social, incluyendo el índice de bienestar infantil, [6] el índice de salud y problemas sociales, [7] la población en prisión, [8] la salud física, [9] la salud mental [10] y muchos otros. [11]
Relación de palma

El índice de Palma se define como la relación entre la participación del 10% más rico de la población en el ingreso nacional bruto dividido por la participación del 40% más pobre. [12] Se basa en el trabajo del economista chileno Gabriel Palma, quien descubrió que los ingresos de la clase media casi siempre representan aproximadamente la mitad del ingreso nacional bruto, mientras que la otra mitad se divide entre el 10% más rico y el 40% más pobre, pero la participación de esos dos grupos varía considerablemente entre países. [13]
El índice de Palma aborda la hipersensibilidad del índice de Gini a los cambios en la parte media de la distribución y su insensibilidad a los cambios en los niveles superior e inferior [14] , y por lo tanto refleja con mayor precisión los impactos económicos de la desigualdad de ingresos en la sociedad en su conjunto. Palma ha sugerido que la política distributiva se relaciona principalmente con la lucha entre ricos y pobres, y con quién se pone de parte la clase media [13] .
El índice de Palma de carbono, que se deriva del índice de Palma de ingresos y se describe como la relación entre las emisiones totales del 10% superior de los emisores y las del 40% inferior, se propone como un nuevo indicador para informar a la comunidad internacional y al público en general sobre la desigualdad en la distribución de las emisiones de carbono entre los individuos. El índice se calcula tanto dentro de los países como entre ellos utilizando una relación elástica entre las emisiones individuales y los ingresos. Los resultados muestran que los índices de Palma de carbono en la mayoría de los países en desarrollo son generalmente altos, lo que implica que deberían concentrarse más en coordinar las desigualdades regionales y de ingresos y principalmente alentar a los grandes emisores a reducir para mejorar las emisiones y la equidad de ingresos al mismo tiempo. Los índices de Palma de carbono en los países desarrollados son comparativamente más bajos; sin embargo, sus mayores obligaciones históricas con el calentamiento indican que reducen significativamente las emisiones de todas las personas, con el fin de aumentar sistemáticamente las contribuciones nacionales a la mitigación. A escala mundial, el índice de Palma de carbono actual es notablemente más alto que dentro de cualquier país, lo que indica una desigualdad extremadamente grave cuando se consideran las emisiones individuales fuera de los límites territoriales. [15]
Índice Hoover
El índice Hoover es la medida de desigualdad más sencilla de calcular: es la proporción de todo el ingreso que debería redistribuirse para alcanzar un estado de perfecta igualdad.
En un mundo perfectamente igualitario, no sería necesario redistribuir recursos para lograr una distribución equitativa: un índice de Hoover de 0. En un mundo en el que todos los ingresos fueran recibidos por una sola familia, casi el 100% de esos ingresos tendrían que ser redistribuidos (es decir, tomados y entregados a otras familias) para lograr la igualdad. El índice de Hoover oscila entonces entre 0 y 1 (0% y 100%), donde 0 indica una igualdad perfecta y 1 (100%) indica una desigualdad máxima.
Puntuación de Galt
La puntuación Galt es una simple relación entre el salario del director ejecutivo de una empresa y el salario del trabajador medio de esa empresa . Una empresa que paga a su director ejecutivo muchas veces más que a su empleado medio tendrá una puntuación Galt alta.
Recibe su nombre del personaje ficticio John Galt de la novela La rebelión de Atlas (1957) de Ayn Rand .
La puntuación se calcula utilizando la compensación total del CEO, incluyendo el salario, las bonificaciones, el valor de las adjudicaciones de acciones y las opciones sobre acciones de los empleados , así como la compensación del plan de incentivos no accionario y la compensación diferida no calificada .
Coeficiente de variación
El coeficiente de variación (CV) utilizado como medida de la desigualdad de ingresos se obtiene dividiendo la desviación típica de los ingresos (raíz cuadrada de la varianza de los ingresos) por la media de los ingresos. Por lo tanto, el coeficiente de variación será menor en los países con desviaciones típicas menores, lo que implica una distribución más equitativa de los ingresos.
Tiene la ventaja de ser matemáticamente manejable y su cuadrado es descomponible en subgrupos, pero no está acotado desde arriba. Esta forma simple de medición no se usa comúnmente, principalmente por sus dos limitaciones considerables. La primera podría atribuirse a que el CV no tiene un límite superior, a diferencia del coeficiente de Gini, lo que causa dificultades con la interpretación y la comparación. En segundo lugar, como la media y la desviación estándar pueden verse muy afectadas por valores límite anómalos, el coeficiente no sería una opción apropiada para medir la desigualdad de ingresos en un caso de distribución de datos anormal. [16]
En comparación con el coeficiente de Gini, en la práctica el coeficiente de variación otorga un mayor peso a la cola derecha de la escala, lo que lo hace sensible a los ricos. El coeficiente de variación puede ser una opción adecuada de medida si el objetivo de un estudio es analizar la concentración de la riqueza en la parte superior de la distribución. [17] [18]
Varianza del logaritmo natural del ingreso
La varianza del logaritmo del ingreso se describe como la varianza aplicada a la distribución del logaritmo del ingreso. [19] Esta medida invariante de escala de la desigualdad relativa es sensible a la cola izquierda, lo que la hace ideal para usarla cuando se estudian los niveles de pobreza de la mitad de ingresos más bajos (los pobres). [16]
Participación salarial
La participación salarial es la relación entre la remuneración de los empleados y el PIB. En otras palabras, es el total de los ingresos de los empleados dividido por el ingreso nacional.
Medida de pobreza de Sen
El índice de pobreza de Sen combina el coeficiente de Gini para las personas que viven por debajo de la línea de pobreza con el índice de recuento de la pobreza y el ingreso promedio de quienes viven por debajo de la línea de pobreza. [20] Esta medida fue desarrollada por el ganador del Premio Nobel Amartya Sen, pero aún no se ha utilizado en el campo de la hipótesis de la desigualdad de ingresos. Aunque ha sido recibido con entusiasmo, el índice de pobreza de Sen no cumple con varias condiciones ideales, por ejemplo, no satisface el axioma de transferencia, no es descomponible ni consistente con subgrupos. [21]
Índice de Theil
Como se describe en una sección más adelante, Theil-L es la desentropía de una distribución de ingresos por persona, medida con respecto a la entropía máxima (que se logra con igualdad completa). (En una interpretación alternativa, Theil-L es el logaritmo natural de la media geométrica de la relación: (ingreso medio)/(ingreso i), sobre todos los ingresos. El Atkinson(1) relacionado es simplemente 1 menos la media geométrica de (ingreso i)/(ingreso medio), sobre la distribución de ingresos).
Dado que una transferencia entre un ingreso mayor y uno menor cambiará la relación del ingreso menor más de lo que cambia la relación del ingreso mayor, el principio de transferencia se satisface con este índice.
Un índice de Theil de 0 indica una igualdad perfecta. Un índice de Theil de 1 indica que la entropía distributiva del sistema bajo investigación es casi similar a la de un sistema con una distribución de 82:18. [22] Esto es ligeramente más desigual que la desigualdad en un sistema al que se aplica el " principio de Pareto 80:20 ". [Nota 2] El índice de Theil se puede transformar en un índice de Atkinson , que tiene un rango entre 0 y 1 (0% y 100%), donde 0 indica una igualdad perfecta y 1 (100%) indica una desigualdad máxima. (Véase el índice de entropía generalizado para la transformación).
El índice de Theil es una medida de entropía. Como ocurre con cualquier distribución de recursos y en relación con la teoría de la información, la "máxima entropía" se produce cuando no es posible distinguir a los perceptores de ingresos por sus recursos, es decir, cuando existe una igualdad perfecta. En las sociedades reales, las personas pueden distinguirse por sus diferentes recursos, siendo los recursos los ingresos. Cuanto más "distinguibles" sean, menor será la "entropía real" de un sistema formado por ingresos y perceptores de ingresos. También en base a la teoría de la información, la brecha entre estas dos entropías puede denominarse " redundancia ". [23] Se comporta como una entropía negativa .
Para el índice de Theil también se ha utilizado el término "entropía de Theil". Esto causó confusión. Como ejemplo, Amartya Sen comentó sobre el índice de Theil: "dada la asociación de la fatalidad con la entropía en el contexto de la termodinámica, puede llevar un poco de tiempo acostumbrarse a la entropía como algo bueno". [24] Es importante entender que un índice de Theil creciente no indica un aumento de la entropía, sino que indica un aumento de la redundancia (disminución de la entropía).
Una alta desigualdad produce altas redundancias de Theil. Una alta redundancia significa una baja entropía. Pero esto no implica necesariamente que una desigualdad muy alta sea "buena", porque las entropías muy bajas también pueden conducir a procesos de compensación explosivos. El uso del índice de Theil tampoco implica necesariamente que una desigualdad muy baja (baja redundancia, alta entropía) sea "buena", porque una alta entropía se asocia con procesos de asignación de recursos lentos, débiles e ineficientes.
Existen tres variantes del índice de Theil. Cuando se aplica a la distribución de ingresos, el primer índice de Theil (Theil-L) se relaciona con la forma en que se distribuyen los ingresos entre quienes perciben ingresos, mientras que el segundo índice de Theil (Theil-T) se relaciona con la forma en que los ingresos se distribuyen entre quienes perciben ingresos.
Un tercer índice de Theil "simetrizado" (Theil-S) es la media aritmética de los dos índices anteriores. La fórmula del tercer índice de Theil tiene cierta similitud con el índice de Hoover (como se explica en los artículos relacionados). Al igual que en el caso del índice de Hoover, el índice de Theil simetrizado no cambia al intercambiar los ingresos con los perceptores de ingresos. A continuación se muestra cómo generar ese tercer índice de Theil mediante un cálculo en una hoja de cálculo directamente a partir de los datos de distribución.
Una propiedad importante del índice de Theil que hace popular su aplicación es su descomponibilidad en el componente intergrupal y dentro del grupo. Por ejemplo, el índice de Theil de la desigualdad de ingresos general se puede descomponer en los componentes interregionales y dentro de las regiones de la desigualdad, mientras que la proporción relativa atribuible al componente interregional sugiere la importancia relativa de la dimensión espacial de la desigualdad de ingresos. [25]
Comparación del índice de Theil y el índice de Hoover

El índice de Theil indica la redundancia distributiva de un sistema en el que los ingresos se asignan a los perceptores de ingresos mediante un proceso estocástico. En comparación, el índice de Hoover indica el tamaño mínimo de la participación en el ingreso de una sociedad que debería redistribuirse para alcanzar la entropía máxima. Para no superar ese tamaño mínimo se requeriría una redistribución perfectamente planificada. Por lo tanto, el índice de Hoover es la contraparte "no estocástica" del índice "estocástico" de Theil.
La aplicación del índice de Theil a los procesos de asignación en el mundo real no implica que estos procesos sean estocásticos: el índice de Theil arroja la distancia entre una distribución ordenada de recursos en un sistema observado y la etapa final de una distribución estocástica de recursos en un sistema cerrado. De manera similar, la aplicación del índice de Hoover no implica que los procesos de asignación ocurran en una economía perfectamente planificada: el índice de Hoover arroja la distancia entre la distribución de recursos en un sistema observado y la etapa final de una "igualación" planificada de la distribución de recursos. Para ambos índices, dicha igualación sólo sirve como referencia, no como objetivo.
Para una distribución dada, el índice de Theil puede ser mayor que el índice de Hoover o menor que el índice de Hoover:
- En el caso de desigualdades elevadas , el índice de Theil es mayor que el índice de Hoover. Esto significa que para alcanzar el equilibrio (máxima entropía) en un sistema cerrado, se deberían reasignar más recursos que en el caso de un proceso de reasignación planificado y optimizado, en el que solo se debería reasignar la proporción mínima necesaria de recursos. En un sistema abierto, la exportación de entropía (importación de redundancia) permitiría mantener la dinámica de distribución impulsada por una alta desigualdad.
- En el caso de desigualdades bajas , el índice de Theil es menor que el índice de Hoover. En este caso, en el camino hacia el equilibrio, una reasignación planificada y optimizada de los recursos contribuiría más a la dinámica de la redistribución que una redistribución estocástica. Esto también es intuitivamente comprensible, ya que las desigualdades bajas también debilitan la necesidad de redistribuir los recursos. Las personas en un sistema de este tipo pueden tolerar o incluso fomentar un aumento de la desigualdad. Como esto sería un aumento de la redundancia (una disminución de la entropía), la redundancia tendría que ser importada a la sociedad (la entropía tendría que ser exportada de ella). En ese caso, la sociedad debe ser un sistema abierto. Para aumentar la redundancia en la categoría de distribución de una sociedad como sistema cerrado, la entropía debe ser exportada desde el subsistema que opera en esa categoría económica a otros subsistemas con otras categorías de entropía en la sociedad. Por ejemplo, la entropía social puede aumentar. Sin embargo, en el mundo real, las sociedades son sistemas abiertos, pero la apertura está restringida por las capacidades de intercambio de entropía de las interfaces entre la sociedad y el medio ambiente de esa sociedad. Para las sociedades con una distribución de recursos que, en términos de entropía, es similar a la distribución de recursos de una sociedad de referencia con una división 73:27 (el 73% de los recursos pertenecen al 27% de la población y viceversa), [Nota 3] el punto en el que el índice de Hoover y el índice de Theil son iguales, se encuentra en un valor de alrededor del 46% (0,46) para el índice de Hoover y el índice de Theil.
Índice de Atkinson
El índice de Atkinson (también conocido como medida de Atkinson o medida de desigualdad de Atkinson) es una medida útil para determinar qué extremo de la distribución contribuyó más a la desigualdad observada.
El parámetro ε de Atkinson suele denominarse "parámetro de aversión a la desigualdad", ya que regula la sensibilidad de las pérdidas de bienestar social implícitas de la desigualdad a la desigualdad de ingresos, medida mediante un índice de entropía generalizado correspondiente. El índice de Atkinson se define en referencia a una función de bienestar social correspondiente, donde el ingreso medio multiplicado por uno menos el índice de Atkinson da como resultado el equivalente de bienestar: un ingreso distribuido equitativamente.
El índice puede convertirse en una medida normativa imponiendo un coeficiente ε para ponderar los ingresos. Se puede dar mayor peso a los cambios en una porción dada de la distribución del ingreso eligiendo ε, el nivel de "aversión a la desigualdad", de manera apropiada. El índice de Atkinson se vuelve más sensible a los cambios en el extremo inferior de la distribución del ingreso a medida que ε aumenta. Por el contrario, a medida que el nivel de aversión a la desigualdad cae (es decir, cuando ε se acerca a 0), el índice de Atkinson se vuelve menos sensible a los cambios en el extremo inferior de la distribución. El índice de Atkinson no es muy sensible a los ingresos más altos para ningún valor de ε debido a la restricción común de que ε es no negativo.
Proporciones
Otra clase común de métricas es la que toma la proporción de los ingresos de dos grupos diferentes, generalmente "los más altos sobre los más bajos". Esto compara dos partes de la distribución del ingreso, en lugar de la distribución en su conjunto; la igualdad entre estas partes corresponde a 1:1, mientras que cuanto más desiguales sean las partes, mayor será la proporción. Estas estadísticas son fáciles de interpretar y comunicar, porque son relativas (esta población gana el doble que esta otra), pero, como no caen en una escala absoluta, no proporcionan una medida absoluta de la desigualdad.
Relación de percentiles

Es particularmente común comparar un percentil dado con la mediana, como en el primer gráfico aquí; compare el resumen de siete números , que resume una distribución por ciertos percentiles. Si bien estas proporciones no representan el nivel general de desigualdad en la población en su conjunto, proporcionan medidas de la forma de la distribución del ingreso. Por ejemplo, el gráfico adjunto muestra que en el período 1967-2003, la proporción del ingreso estadounidense entre la mediana y los percentiles 10 y 20 no cambió significativamente, mientras que la proporción entre la mediana y los percentiles 80, 90 y 95 aumentó. Esto refleja que el aumento en el coeficiente de Gini de los EE. UU. en este período de tiempo se debe a ganancias de los asalariados de ingresos superiores (en relación con la mediana), en lugar de pérdidas de los asalariados de ingresos inferiores (en relación con la mediana).

Porcentaje de ingresos
Una clase relacionada de proporciones es la "participación en el ingreso", el porcentaje del ingreso nacional que recibe un segmento porcentual específico, más rico o más pobre, de la población.
La población, pero la curva de Lorenz (discutida en la sección de Gini) grafica el ingreso acumulado del x % de la población con ingresos más bajos, para todos los x de 0 a 100. Sin embargo, al comentar los datos, se puede expresar como la inversa, mostrando el porcentaje de ingresos del x % más rico.
Una propiedad importante y obvia de la curva de Lorenz es que, si el país A tiene una mayor participación en el ingreso nacional acumulado para (digamos) el 1% más pobre, en comparación con el país B, entonces:
- Si las curvas de Lorenz de ambos países no se cruzan, entonces la curva de Lorenz del país A es en todas partes más alta que la del país B, lo que significa que, para cualquier X de 0 a 100, el X% más pobre de la población tiene una mayor participación en el ingreso nacional en el país A que en el país B.
- Si las curvas de Lorenz de dos países se cruzan, entonces es casi seguro que, en el lado pobre del punto de cruce, el país A tiene una curva de Lorenz más alta, lo que significa que, para cualquier X% más pobre de la población hasta el punto de cruce, la población del país A tiene una mayor participación en el ingreso nacional.
Cuando la desigualdad causa daño, lo hace sobre todo en el extremo más pobre de la población. En cualquier percentil de ingresos, una mayor participación en el ingreso nacional significa un mayor porcentaje recibido de la participación igualitaria (el ingreso medio nacional).
De modo que el país con una mayor participación acumulada en el ingreso nacional para el 1% más pobre tendrá un mayor porcentaje acumulado recibido de participación igual para el X% más pobre, ya sea para cada percentil X, o (si las curvas de Lorenz se cruzan), para los percentiles del lado más pobre del punto de cruce.
Algunas fuentes [¿ cuáles? ] informan varios puntos de datos de la curva de Lorenz (participaciones acumuladas del ingreso nacional hasta varios percentiles).
Como se mencionó anteriormente, tomar la relación entre la participación en el ingreso y el tamaño de la subpoblación corresponde a una relación entre el ingreso medio de la subpoblación y el ingreso medio .
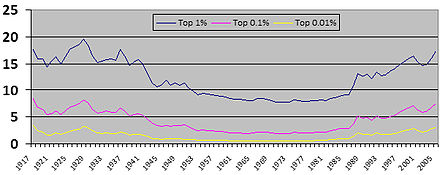
Como la distribución del ingreso generalmente está sesgada positivamente , la media es mayor que la mediana, por lo que las razones con respecto a la media son menores que las razones con respecto a la mediana. Esto se utiliza particularmente para medir la fracción del ingreso que corresponde a los que más ganan (el 10%, el 1%, el 0,1%, el 0,01% y también los que más ganan, o similares; en los EE. UU., los 400 que más ganan son el 0,0002% de los que ganan (2 en 1.000.000)) para estudiar la concentración del ingreso ( condensación de la riqueza o, más bien, condensación del ingreso). Por ejemplo, en el gráfico de la derecha, la proporción del ingreso de los que más ganan en los EE. UU. se mantuvo aproximadamente constante desde mediados de la década de 1950 hasta mediados de la de 1980, y luego aumentó desde mediados de la década de 1980 hasta la década de 2000; esta mayor desigualdad se reflejó en el coeficiente de Gini.
Por ejemplo, en 2007 el decil superior (10%) de los asalariados estadounidenses representaba el 49,7% de los salarios totales ( fracción multiplicada por 600 en igualdad de condiciones), y el 0,01% superior de los asalariados estadounidenses representaba el 6% de los salarios totales (fracción multiplicada por 600 en igualdad de condiciones). [30]
Aproches
Enfoque normativo
La interpretación normativa de la desigualdad a través de índices de desigualdad significa que existe una relación entre un índice de desigualdad y un orden de evaluación social definido en función de los ingresos (nominales o reales) de los miembros de la sociedad. Los ingresos se asignan típicamente a individuos en lugar de a hogares utilizando una escala de equivalencia de adultos. [31]
El enfoque normativo ha sido analizado por Charles Blackorby, Walter Bossert y David Donaldson en el trabajo "Medición de la desigualdad de ingresos: el enfoque normativo".
Enfoque estadístico
La interpretación estadística de la desigualdad se basa en datos fiscales y en el parámetro α del modelo de Pareto (1895) como medida de la desigualdad del ingreso . [32] Este enfoque se analiza con más detalle en el trabajo "Income Inequality Measurement: The Statistical Approach" de Giovanni M. Giorgi.
Cálculos en hojas de cálculo
El coeficiente de Gini, el índice de Hoover y el índice de Theil, así como las funciones de bienestar relacionadas [33], se pueden calcular juntos en una hoja de cálculo. [Nota 5] Las funciones de bienestar sirven como alternativas al ingreso medio .
| Grupo | Miembros por grupo | Ingresos por grupo | Ingresos por persona | Desviación relativa | Ingresos acumulados | coeficiente de gin | Aspiradora | Teil |
|---|---|---|---|---|---|---|---|---|
| 1 | Un 1 | Y 1 | E 1 = E 1 / A 1 | D 1 = E 1 /ΣE - A 1 /ΣA | K1 = E1 | G 1 = (2 * K 1 - E 1 ) * A 1 | H 1 = abs(D 1 ) | T 1 = ln(Ē 1 ) * D 1 |
| 2 | Un 2 | Y 2 | E2 = E2 / A2 | D2 = E2 / ΣE- A2 / ΣA | K2 = E2 + K1 | G 2 = (2 * K 2 - E 2 ) * A 2 | H2 = abs( D2 ) | T 2 = ln(E 2 ) * D 2 |
| 3 | Un 3 | Y 3 | E3 = E3 / A3 | D3 = E3 / ΣE- A3 / ΣA | K3 = E3 + K2 | G3 = ( 2 * K3 - E3 ) * A3 | H3 = abs( D3 ) | T 3 = ln(E 3 ) * D 3 |
| 4 | Un 4 | E4 | E 4 = E 4 / A 4 | D 4 = E 4 / Σ E - A 4 / Σ A | K 4 = E 4 + K 3 | G 4 = (2 * K 4 - E 4 ) * A 4 | H 4 = abs(D 4 ) | T 4 = ln(E 4 ) * D 4 |
| Totales | ΣA | ΣE | Ē = ΣE/ΣA | ΣG | ΣH | ΣT | ||
| Medidas de desigualdad | Gini = 1 - ΣG/ΣA/ΣE | Aspiradora = ΣH / 2 | Teil = ΣT / 2 | |||||
| Función de bienestar | W G = Ē * (1 - Gini) | W H = Ē * (1 - Hoover) | W T = Ē * (1 - Theil) |
En la tabla, los campos con fondo amarillo se utilizan para la entrada de datos. A partir de estos datos, se calculan las medidas de desigualdad, así como las funciones de bienestar relacionadas, y se muestran en los campos con fondo verde.
En el ejemplo que se da aquí, el "índice de Theil" representa la media aritmética de un índice de Theil calculado para la distribución de los ingresos dentro de una sociedad entre los individuos (u hogares) de esa sociedad y un índice de Theil calculado para la distribución de los individuos (u hogares) de la sociedad entre los ingresos de esa sociedad. La diferencia entre el índice de Theil y el índice de Hoover es la ponderación de la desviación relativa D. En el caso del índice de Hoover, la desviación relativa D por grupo se pondera con su propio signo. En el caso del índice de Theil, la desviación relativa D por grupo se pondera con el tamaño de la información proporcionada por los ingresos por individuo en ese grupo.
Para realizar el cálculo, la sociedad suele dividirse en grupos de ingresos. A menudo hay cuatro o cinco grupos que constan de un número similar de individuos en cada grupo. En otros casos, los grupos se crean en función de los rangos de ingresos, lo que lleva a tener diferentes números de individuos en los diferentes grupos. La tabla anterior muestra un cálculo de los índices de desigualdad para cuatro grupos. Para cada grupo se especifica el número de individuos (u hogares) por grupo A y el ingreso total en ese grupo E.
Para calcular el coeficiente de Gini es necesario ordenar los pares de parámetros A y E (para el índice de Theil y el índice de Hoover no es necesario ordenarlos). A y E deben ordenarse de modo que los valores de la columna "Ingresos por persona" estén alineados en orden ascendente.
Uso adecuado
- Al utilizar indicadores de ingresos, es necesario aclarar cómo se deben definir los ingresos. ¿Deben incluir las ganancias de capital , los alquileres imputados de la vivienda propia y las donaciones? Si se ignoran (como suele ocurrir) estas fuentes de ingresos o las supuestas fuentes de ingresos (en el caso de los " alquileres imputados "), ¿cómo podría esto sesgar el análisis? ¿Cómo debería manejarse el trabajo no remunerado (como el cuidado de los hijos por parte de los padres o cocinar en lugar de contratar a un chef para cada comida)? La riqueza o el consumo pueden ser indicadores más apropiados en algunas situaciones. Podrían ser útiles indicadores más amplios de la calidad de vida .
- La comparación de medidas de desigualdad requiere que la segmentación de los grupos comparados (sociedades, etc.) en quintiles sea similar.
- Distinga adecuadamente si la unidad básica de medida son los hogares o los individuos. El valor de Gini para los hogares siempre es menor que para los individuos debido a la agrupación de ingresos y las transferencias intrafamiliares. Además, los hogares tienen un número variable de miembros. Las métricas se verán influidas al alza o a la baja según la unidad de medida que se utilice.
- Consideremos los efectos del ciclo de vida. En la mayoría de las sociedades occidentales, una persona tiende a comenzar su vida con poco o ningún ingreso, y gradualmente aumenta su ingreso hasta aproximadamente los 50 años, después de lo cual los ingresos disminuyen y finalmente se vuelven negativos. Esto afecta las conclusiones que se pueden extraer de una desigualdad medida. Se ha estimado (por AS Blinder en The Decomposition of Inequality , MIT press) que el 30% de la desigualdad de ingresos medida se debe a la desigualdad que experimenta una persona a medida que pasa por las distintas etapas de la vida.
- Aclarar si se deben utilizar distribuciones de ingresos reales o nominales. ¿Qué efecto tendrá la inflación sobre las medidas absolutas? ¿Algunos grupos (por ejemplo, los jubilados) sienten el efecto de la inflación más que otros?
- Al extraer conclusiones de las mediciones de desigualdad, ¿hay que pensar en cómo debemos asignar los beneficios del gasto público? ¿Cómo influye la existencia de una red de seguridad social en la definición de las mediciones absolutas de pobreza? ¿Los programas públicos apoyan a algunos grupos de ingresos más que a otros?
- Las métricas de desigualdad miden la desigualdad, pero no miden las posibles causas de la desigualdad de ingresos. Algunas de las supuestas causas son: los efectos del ciclo de vida (edad), las características heredadas (coeficiente intelectual, talento), la disposición a asumir riesgos (aversión al riesgo), la elección entre ocio y trabajo, la riqueza heredada, las circunstancias económicas, la educación y la formación, la discriminación y las imperfecciones del mercado.
- Las métricas de desigualdad son anónimas. Ignoran ciertos efectos de la movilidad del ingreso , en los que se considera la identidad de "quién es rico" y "quién es pobre". Por ejemplo, en un momento determinado, Alice puede tener $10 y Bob puede tener $2. En algún momento posterior, Bob puede tener $10 y Alice puede tener $2. El índice de desigualdad será el mismo en ambos casos y bastante alto. Sin embargo, la desigualdad del promedio será cero, ya que las tenencias promedio de Alice y Bob son iguales ($6). Los $8 que han cambiado de manos son una medida de la movilidad de la riqueza y la desigualdad promedio es generalmente mayor que la desigualdad del promedio.
Tener presentes estos puntos ayuda a comprender los problemas que genera el uso inadecuado de las medidas de desigualdad. Sin embargo, no invalidan los coeficientes de desigualdad. Si las medidas de desigualdad se calculan de una manera bien explicada y coherente , pueden proporcionar una buena herramienta para las comparaciones cuantitativas de desigualdades.
Desigualdad, crecimiento y progreso
La evidencia de un amplio panel de estudios académicos recientes muestra que existe una relación no lineal entre la desigualdad de ingresos y la tasa de crecimiento e inversión. Una desigualdad muy alta desacelera el crecimiento; una desigualdad moderada lo estimula. Los estudios difieren sobre el efecto de una desigualdad muy baja.
Robert J. Barro , de la Universidad de Harvard , encontró en su estudio "Desigualdad y crecimiento en un panel de países" que una mayor desigualdad tiende a retardar el crecimiento en los países pobres y a alentar el crecimiento en las regiones bien desarrolladas. [34] Subrayando la necesidad de iniciativas como el Objetivo de Desarrollo Sostenible 10 de las Naciones Unidas , que apunten a reducir la desigualdad. [35] Según Pak Hung Mo, la desigualdad de ingresos tiene un efecto negativo significativo en la tasa de crecimiento del PIB . En su trabajo "Desigualdad de ingresos y crecimiento económico", descubrieron que el más importante es el canal de transferencia, mientras que el menos importante es el canal de capital humano. Sin embargo, el impacto directo de la desigualdad de ingresos en la tasa de crecimiento de la productividad representa más del 55 por ciento de su efecto total general. Esto indica que los efectos de la desigualdad de ingresos en el crecimiento económico son mucho más complicados de lo que hemos percibido o modelado. [36]
En su estudio para el Instituto Mundial de Investigación en Economía del Desarrollo, Giovanni Andrea Cornia y Julius Court (2001) llegan a conclusiones ligeramente diferentes. [37] [38] Por lo tanto, los autores recomiendan buscar la moderación también en lo que respecta a la distribución de la riqueza y, en particular, evitar los extremos. Tanto un igualitarismo muy alto como una desigualdad muy alta causan un crecimiento lento. Considerando las desigualdades en los países económicamente bien desarrollados, la política pública debería apuntar a un "rango de desigualdad eficiente". Los autores afirman que ese rango de eficiencia se encuentra aproximadamente entre los valores de los coeficientes de Gini de 0,25 (desigualdad cercana a los países europeos menos desiguales) y 0,40 (cerca del nivel de desigualdad de Estados Unidos).
Según el trabajo “Desigualdad de oportunidades, desigualdad de ingresos y crecimiento económico”, la relación entre la desigualdad de ingresos y el crecimiento económico está mediada por el nivel de igualdad de oportunidades, identificado por la movilidad intergeneracional. Después de una serie de medidas de movilidad intergeneracional comparables a nivel internacional desarrolladas recientemente, se confirmó que el impacto negativo de la desigualdad de ingresos sobre el crecimiento aumenta a medida que disminuye la movilidad intergeneracional. Los hallazgos implican que excluir la movilidad intergeneracional conduce a una especificación errónea, lo que explica por qué la literatura empírica sobre la desigualdad de ingresos y el crecimiento ha sido tan poco concluyente. [39]
Otro investigador ha demostrado que en los mercados perfectos la desigualdad no influye en el crecimiento. [40]
La forma precisa de la curva de desigualdad-crecimiento obviamente varía entre países dependiendo de su dotación de recursos, su historia, los niveles restantes de pobreza absoluta y el stock disponible de programas sociales, así como de la distribución del capital físico y humano.
Véase también
- Lista de países por igualdad de ingresos
- Lista de países según la igualdad de riqueza
- Desigualdad de ingresos en Estados Unidos
- Déficit de ingresos
- Desigualdad internacional
- Curva de Kuznets
- Umbral de pobreza
- Socioeconomía
- Objetivos de Desarrollo Sostenible
- " Los ricos se hacen más ricos y los pobres más pobres "
- Justicia distributiva : ideal político dedicado a una mayor igualdad de ingresos
- Índice de diversidad
- La curva del Gran Gatsby
- Índice de desarrollo humano
- Índice de trajes
- Índice de Gini
- Curva de Lorenz
- La curva del elefante
Notas
- ^ Para la pobreza, consulte las métricas del FGT .
- ^ Un índice de Theil de 0,5 caracteriza a los sistemas que se aproximan a una distribución 74:26. Una distribución 92:8 daría un índice de Theil de 2 y una 98:2 daría un índice de Theil de 4. Algunas observaciones especiales: para una distribución 80:20 (principio de Pareto), el índice de Theil es 0,83. Para 73:27, el índice de Theil y el índice de Hoover son idénticos: ambos son 0,46. Para 62:38, la diferencia entre el índice de Theil (que representa una distribución estocástica) y el índice de Hoover (que representa una distribución perfectamente planificada) alcanza un mínimo de −0,12.
- ^ En estas sociedades, que se dividen en dos denominados "a-fractiles", el índice de Hoover y el coeficiente de Gini siempre son similares.
- ^ Las diferencias entre los datos del Censo y del Servicio de Impuestos Internos se pueden ver más fácilmente en el percentil 95, presente en ambos conjuntos de datos. Para obtener más detalles, consulte el archivo de ayuda para los datos "incomeInequality" en el paquete Ecdat disponible en la Red Integral de Archivos R (CRAN; consulte r-project.org).
- ^ Como alternativa a los cálculos en hojas de cálculo, también se puede utilizar un script de Python.
Referencias
- ^ "Unidad de Encuesta – surveyunit". BancoMundial.org . Consultado el 8 de septiembre de 2018 .
- ^ "Conceptos básicos y grupos completamente descomponibles", Grupos casi completamente descomponibles , CRC Press, págs. 37-72, 9 de marzo de 2000, doi : 10.1201/9781482287486-8, ISBN 978-0-429-07843-9, consultado el 30 de abril de 2021
- ^ "Figura 5.8. Coeficientes de Gini de diferentes medidas de desigualdad interprovincial". doi :10.1787/778454437583 . Consultado el 30 de abril de 2021 .
{{cite journal}}: Requiere citar revista|journal=( ayuda ) - ^ "Notas sobre fuentes y métodos estadísticos – The Equality Trust". Equalitytrust.org.uk . Archivado desde el original el 16 de enero de 2014 . Consultado el 8 de septiembre de 2018 .
- ^ Econometría de datos de panel: contribuciones teóricas y aplicaciones empíricas editado por Badi Hani Baltag
- ^ "Radiografía". Br Med J . 2 (4157): 321. 7 de septiembre de 1940. doi :10.1136/bmj.2.4157.321-a. S2CID 214960331 . Consultado el 8 de septiembre de 2018 en www.bmj.com.
- ^ "La desigualdad económica es mala para la salud". Archivado desde el original el 25 de mayo de 2013. Consultado el 18 de mayo de 2013 .
- ^ "Encarcelamiento – The Equality Trust". Equalitytrust.org.uk . Consultado el 8 de septiembre de 2018 .
- ^ "Salud física: The Equality Trust". Equalitytrust.org.uk . Consultado el 8 de septiembre de 2018 .
- ^ "Salud mental: The Equality Trust". Equalitytrust.org.uk . Consultado el 8 de septiembre de 2018 .
- ^ "Investigación externa – Página 2 – The Equality Trust". Equalitytrust.org.uk . Consultado el 8 de septiembre de 2018 .
- ^ Alex Cobham; Andy Sumner (15 de marzo de 2013). "Putting the Gini Back in the Bottle? 'The Palma' as a Policy-Relevant Measure of Inequality" (PDF) . King's International Development Institute . King's College London. Archivado desde el original (PDF) el 23 de abril de 2013. Consultado el 14 de enero de 2019 .
- ^ ab Palma, José Gabriel (enero de 2011). «Grupos homogéneos de clase media frente a grupos heterogéneos de clase media, y el fin de la «U invertida»: lo importante es la proporción de los ricos» (PDF) . Cambridge Working Papers in Economics (CWPE) 1111. Cambridge University . Consultado el 19 de marzo de 2013 .
- ^ Atkinson, Anthony (1970). "Sobre la medición de la desigualdad" (PDF) . Journal of Economic Theory . 2 (3): 244–63. doi :10.1016/0022-0531(70)90039-6 . Consultado el 19 de marzo de 2013 .
- ^ Pan, Xunzhang; Wang, Hailin; Wang, Ziwei; Lin, Lu; Zhang, Qi; Zheng, Xinzhu; Chen, Wenying (diciembre de 2019). "Ratio de palma de carbono: un nuevo indicador para medir la desigualdad de distribución de las emisiones de carbono entre individuos". Journal of Cleaner Production . 241 : 118418. doi :10.1016/j.jclepro.2019.118418. ISSN 0959-6526. S2CID 203452007.
- ^ ab Trapeznikova, Ija (17 de julio de 2019). "Medición de la desigualdad de ingresos". IZA World of Labor . doi : 10.15185/izawol.462 .
- ^ Renaud, B.; Buda, M.; Lewis, BD; Pujol, JF (1975-09-15). "Efectos de la 5,6-dihidroxitriptamina sobre la actividad de la tirosina-hidroxilasa en neuronas catecolaminérgicas centrales de la rata". Farmacología bioquímica . 24 (18): 1739–1742. doi :10.1016/0006-2952(75)90018-0. ISSN 0006-2952. PMID 17.
- ^ Ris, MM; Deitrich, RA; Von Wartburg, JP (15 de octubre de 1975). "Inhibición de las isoenzimas de la aldehído reductasa en el cerebro humano y de rata". Farmacología bioquímica . 24 (20): 1865–1869. doi :10.1016/0006-2952(75)90405-0. ISSN 0006-2952. PMID 18.
- ^ Foster, James E.; Ok, Efe A. (julio de 1999). "Dominancia de Lorenz y varianza de logaritmos". Econometrica . 67 (4): 901–907. doi :10.1111/1468-0262.00057. ISSN 0012-9682.
- ^ Fahnestock, SR (2 de diciembre de 1975). "Evidencia de la participación de una proteína ribosomal 50S en varios sitios activos". Bioquímica . 14 (24): 5321–5327. doi :10.1021/bi00695a016. ISSN 0006-2960. PMID 52.
- ^ Shorrocks, Anthony F. (septiembre de 1995). "Revisitando el índice de pobreza de Sen". Econometrica . 63 (5): 1225–1230. doi :10.2307/2171728. JSTOR 2171728.
- ^ "Calculadora en línea: desigualdad". Poorcity.richcity.org . Consultado el 8 de septiembre de 2018 .
- ^ ISO/IEC DIS 2382-16:1996 ( Teoría de la información )
- ^ pp. 35, capítulo 2.11 en Amartya Sen y James E. Foster: On Economic Inequality , Oxford University Press, 1996 (script de Python archivado el 19 de julio de 2011 en Wayback Machine para una selección de fórmulas en el libro).
- ^ Novotny, J. (2007). "Sobre la medición de la desigualdad regional: ¿Importa la dimensión espacial de la desigualdad de ingresos?" (PDF) . Annals of Regional Science . 41, 3 (3): 563–80. doi :10.1007/s00168-007-0113-y. S2CID 51753883.
- ^ "Tabla F-1. Límites de ingresos para cada quinto y el 5 por ciento superior de las familias (todas las razas): 1947 a 2010". Encuesta de población actual, suplementos económicos y sociales anuales . Oficina del censo de los Estados Unidos . Consultado el 24 de enero de 2012.
La mediana se calcula como la media geométrica de los percentiles 20 y 40
. - ^ Piketty, Thomas ; Saez, Emmanuel , "Income Inequality in the United States, 1913–2002", en Atkinson, AB; Piketty, Thomas (eds.), Los ingresos más altos durante el siglo XX : un contraste entre los países de Europa continental y los países de habla inglesa , consultado el 8 de febrero de 2012
- ^ Saez, E. y Piketty, T. (2003). "Desigualdad de ingresos en Estados Unidos: 1913-1998". Quarterly Journal of Economics , 118(1), 1–39.
- ^ "Saez, E. (octubre de 2007). Tabla A1: Participación en el ingreso de los fractiles superiores (excluidas las ganancias de capital) en los EE. UU., 1913-2005". Elsa.berkeley.edu . Consultado el 17 de enero de 2008 .
- ^ "Haciéndose más rico: La evolución de los ingresos más altos en Estados Unidos", actualizado en agosto de 2009, Emmanuel Saez, resumen del trabajo para el público en general.
- ^ Charles., Blackorby (1999). Medición de la desigualdad de ingresos: el enfoque normativo. [sn] OCLC 848679839.
- ^ Maria., Giorgi, Giovanni (1999). Medición de la desigualdad de ingresos: el enfoque estadístico. [sn] OCLC 848679881.
{{cite book}}: CS1 maint: varios nombres: lista de autores ( enlace ) - ^ James E. Foster y Amartya Sen, 1997, On Economic Inequality, edición ampliada con un anexo sustancial , ISBN 0-19-828193-5 . Para calcular la función de bienestar, Sen dio un ejemplo utilizando el coeficiente de Gini, mientras que Foster utilizó una medida de entropía. El índice de Theil es una de esas medidas de entropía.
- ^ "Desigualdad y crecimiento en un panel de países" (PDF) . Scholar.harvard.edu . Consultado el 8 de septiembre de 2018 .
- ^ "Metas del Objetivo 10". PNUD . Archivado desde el original el 2020-11-27 . Consultado el 2020-09-23 .
- ^ Mo, Pak Hung (2000). "Desigualdad de ingresos y crecimiento económico". Revista Internacional de Ciencias Sociales . 53 (3): 293–315. doi :10.1111/1467-6435.00122.
- ^ "Desigualdad, crecimiento y pobreza en la era de la liberalización y la globalización". UNU-WIDER . 2015-08-18 . Consultado el 2019-05-25 .
- ^ "UNU-WIDER : Publicaciones" (PDF) . UNU-WIDER . Archivado desde el original (PDF) el 14 de julio de 2020 . Consultado el 8 de septiembre de 2018 .
- ^ Aiyar, Shekhar; Ebeke, Christian (diciembre de 2020). «Desigualdad de oportunidades, desigualdad de ingresos y crecimiento económico». Desarrollo mundial . 136 : 105115. doi :10.1016/j.worlddev.2020.105115. ISSN 0305-750X. S2CID 224891145.
- ^ Wolfgang Kitterer: ¿Mehr Wachstum durch Umverteilung? Archivado el 27 de septiembre de 2007 en Wayback Machine (¿Más crecimiento mediante la redistribución?) , 2006
Literatura
- AB Atkinson y F. Bourguignon, ed. (2000). Handbook of Income Distribution , v. 1. Elsevier.Índice
- _____", Enciclopedia Internacional de las Ciencias Sociales y del Comportamiento (2001), págs. 7265–7271. Resumen.
- Yoram Amiel (autor), Frank A. Cowell: Reflexiones sobre la desigualdad: juicio personal y distribución del ingreso , 2000
- Philip B. Coulter: Medición de la desigualdad , 1989
Enlaces externos
- Travis Hale, Universidad de Texas Proyecto de desigualdad: Fundamentos teóricos de las medidas de desigualdad más populares; cálculo en línea de ejemplos: 1A, 1B
- Samuel Murray Matheson: Medidas de equidad distributiva para la selección de proyectos sostenibles, 1997
- Luxembourg Income Study realiza una investigación comparativa sobre la desigualdad de ingresos
- Dos Américas: ¿una rica y otra pobre? Cómo entender la desigualdad de ingresos en Estados Unidos
- ¿Ha aumentado realmente la desigualdad del ingreso en Estados Unidos?
- Un sitio web dedicado al tema de la desigualdad de ingresos.
- WIID – Base de datos sobre desigualdad de ingresos en el mundo, Instituto Mundial de Investigaciones sobre Economía del Desarrollo de la Universidad de las Naciones Unidas
- Software:
- La calculadora en línea calcula el coeficiente de Gini, traza la curva de Lorenz y calcula muchas otras medidas de concentración para cualquier conjunto de datos.
- Calculadora en línea: Calculadora en línea (ejemplo para procesar datos de la Tabla HINC-06 [ enlace muerto permanente ] , Oficina del Censo de EE. UU., 2007: Distribución de ingresos de $250 000 o más para hogares) y scripts descargables ( Python y Lua ) para las desigualdades de Atkinson, Gini y Hoover
- Script de Python archivado el 10 de julio de 2011 en Wayback Machine que utiliza fórmulas en Sobre la desigualdad económica de Amartya Sen
- Los usuarios del software de análisis de datos R pueden instalar el paquete ineq que permite calcular una variedad de índices de desigualdad, incluidos Gini, Atkinson y Theil.
- Un paquete de desigualdades de MATLAB archivado el 4 de octubre de 2008 en Wayback Machine , que incluye código para calcular los índices de Gini, Atkinson y Theil y para trazar la curva de Lorenz. Hay muchos ejemplos disponibles.








