Espacio de Hilbert

En matemáticas , los espacios de Hilbert (llamados así por David Hilbert ) permiten que los métodos del álgebra lineal y el cálculo se generalicen desde espacios vectoriales euclidianos (de dimensión finita) a espacios que pueden ser de dimensión infinita . Los espacios de Hilbert surgen de forma natural y frecuente en matemáticas y física , típicamente como espacios de funciones . Formalmente, un espacio de Hilbert es un espacio vectorial equipado con un producto interno que induce una función de distancia para la cual el espacio es un espacio métrico completo . Un espacio de Hilbert es un caso especial de un espacio de Banach .
Los primeros espacios de Hilbert fueron estudiados desde este punto de vista en la primera década del siglo XX por David Hilbert , Erhard Schmidt y Frigyes Riesz . Son herramientas indispensables en las teorías de ecuaciones diferenciales parciales , mecánica cuántica , análisis de Fourier (que incluye aplicaciones al procesamiento de señales y transferencia de calor ) y teoría ergódica (que forma la base matemática de la termodinámica ). John von Neumann acuñó el término espacio de Hilbert para el concepto abstracto que subyace a muchas de estas diversas aplicaciones. El éxito de los métodos del espacio de Hilbert marcó el comienzo de una era muy fructífera para el análisis funcional . Aparte de los espacios vectoriales euclidianos clásicos, los ejemplos de espacios de Hilbert incluyen espacios de funciones integrables al cuadrado , espacios de secuencias , espacios de Sobolev que consisten en funciones generalizadas y espacios de Hardy de funciones holomorfas .
La intuición geométrica desempeña un papel importante en muchos aspectos de la teoría del espacio de Hilbert. En un espacio de Hilbert se cumplen analogías exactas del teorema de Pitágoras y la ley del paralelogramo . En un nivel más profundo, la proyección perpendicular sobre un subespacio lineal desempeña un papel importante en los problemas de optimización y otros aspectos de la teoría. Un elemento de un espacio de Hilbert se puede especificar de forma única por sus coordenadas con respecto a una base ortonormal , en analogía con las coordenadas cartesianas en la geometría clásica. Cuando esta base es infinitamente numerable , permite identificar el espacio de Hilbert con el espacio de las secuencias infinitas que son sumables al cuadrado . Este último espacio se suele denominar en la literatura más antigua espacio de Hilbert.
Definición e ilustración
Ejemplo motivador: espacio vectorial euclidiano
Uno de los ejemplos más conocidos de un espacio de Hilbert es el espacio vectorial euclidiano que consta de vectores tridimensionales , denotados por R 3 , y equipados con el producto escalar . El producto escalar toma dos vectores x e y , y produce un número real x ⋅ y . Si x e y se representan en coordenadas cartesianas , entonces el producto escalar se define por
El producto escalar satisface las propiedades [1]
- Es simétrico en x e y : x ⋅ y = y ⋅ x .
- Es lineal en su primer argumento: ( a x 1 + b x 2 ) ⋅ y = a ( x 1 ⋅ y ) + b ( x 2 ⋅ y ) para cualquier escalar a , b , y vectores x 1 , x 2 , e y .
- Es definida positiva : para todos los vectores x , x ⋅ x ≥ 0 , con igualdad si y sólo si x = 0 .
Una operación sobre pares de vectores que, como el producto escalar, satisface estas tres propiedades se conoce como producto interno (real) . Un espacio vectorial equipado con un producto interno de este tipo se conoce como espacio de producto interno (real) . Todo espacio de producto interno de dimensión finita es también un espacio de Hilbert. [2] La característica básica del producto escalar que lo conecta con la geometría euclidiana es que está relacionado tanto con la longitud (o norma ) de un vector, denotada ‖ x ‖ , como con el ángulo θ entre dos vectores x e y mediante la fórmula
El cálculo multivariable en el espacio euclidiano se basa en la capacidad de calcular límites y de disponer de criterios útiles para concluir que existen límites. Una serie matemática formada por vectores en R 3 es absolutamente convergente siempre que la suma de las longitudes converja como una serie ordinaria de números reales: [3]
Al igual que una serie de escalares, una serie de vectores que converge absolutamente también converge a algún vector límite L en el espacio euclidiano, en el sentido de que
Esta propiedad expresa la completitud del espacio euclidiano: una serie que converge de manera absoluta también converge en el sentido ordinario.
Los espacios de Hilbert se utilizan a menudo para los números complejos . El plano complejo denotado por C está dotado de una noción de magnitud, el módulo complejo | z | , que se define como la raíz cuadrada del producto de z por su conjugado complejo :
Si z = x + iy es una descomposición de z en sus partes real e imaginaria, entonces el módulo es la longitud bidimensional euclidiana habitual:
El producto interno de un par de números complejos z y w es el producto de z con el conjugado complejo de w :
Esto tiene un valor complejo. La parte real de ⟨ z , w ⟩ da el producto escalar euclidiano bidimensional habitual .
Un segundo ejemplo es el espacio C 2 cuyos elementos son pares de números complejos z = ( z 1 , z 2 ) . Entonces el producto interno de z con otro vector de ese tipo w = ( w 1 , w 2 ) está dado por
La parte real de ⟨ z , w ⟩ es entonces el producto escalar euclidiano bidimensional. Este producto interno es simétrico hermítico , lo que significa que el resultado de intercambiar z y w es el conjugado complejo:
Definición
Un espacio de Hilbert es un espacio de producto interno real o complejo que también es un espacio métrico completo con respecto a la función de distancia inducida por el producto interno. [4]
Decir que un espacio vectorial complejo H es un espacio de producto interno complejo significa que existe un producto interno que asocia un número complejo a cada par de elementos de H que satisface las siguientes propiedades:
- El producto interno es simétrico conjugado; es decir, el producto interno de un par de elementos es igual al conjugado complejo del producto interno de los elementos intercambiados: Es importante destacar que esto implica que es un número real.
- El producto interno es lineal en su primer argumento [nb 1] . Para todos los números complejos y
- El producto interno de un elemento consigo mismo es definido positivo :
De las propiedades 1 y 2 se deduce que un producto interno complejo es antilineal , también llamado lineal conjugado , en su segundo argumento, lo que significa que
Un espacio de producto interno real se define de la misma manera, excepto que H es un espacio vectorial real y el producto interno toma valores reales. Un producto interno de este tipo será una función bilineal y formará un sistema dual . [5]
La norma es la función de valor real y la distancia entre dos puntos en H se define en términos de la norma por
Que esta función sea una función de distancia significa, en primer lugar, que es simétrica en y, en segundo lugar, que la distancia entre y es cero, y, en caso contrario, la distancia entre y debe ser positiva, y, por último, que se cumple la desigualdad triangular , es decir, que la longitud de un cateto de un triángulo xyz no puede exceder la suma de las longitudes de los otros dos catetos:
Esta última propiedad es, en última instancia, una consecuencia de la desigualdad de Cauchy-Schwarz más fundamental , que se cumple con igualdad si y sólo si y son linealmente dependientes .
Con una función de distancia definida de esta manera, cualquier espacio de producto interno es un espacio métrico , y a veces se lo conoce como espacio pre-Hilbert de Hausdorff . [6] Cualquier espacio pre-Hilbert que además sea un espacio completo es un espacio de Hilbert. [7]
La completitud de H se expresa utilizando una forma del criterio de Cauchy para sucesiones en H : un espacio pre-Hilbert H es completo si cada sucesión de Cauchy converge con respecto a esta norma a un elemento en el espacio. La completitud se puede caracterizar por la siguiente condición equivalente: si una serie de vectores converge absolutamente en el sentido de que entonces la serie converge en H , en el sentido de que las sumas parciales convergen a un elemento de H . [8]
Como espacio normado completo, los espacios de Hilbert son por definición también espacios de Banach . Como tales, son espacios vectoriales topológicos , en los que nociones topológicas como la apertura y el cierre de subconjuntos están bien definidas . De especial importancia es la noción de un subespacio lineal cerrado de un espacio de Hilbert que, con el producto interno inducido por la restricción , también es completo (al ser un conjunto cerrado en un espacio métrico completo) y, por lo tanto, un espacio de Hilbert por derecho propio.
Segundo ejemplo: espacios de secuencia
El espacio de secuencias l 2 consta de todas las secuencias infinitas z = ( z 1 , z 2 , …) de números complejos tales que la siguiente serie converge : [9]
El producto interno en l 2 se define por:
Esta segunda serie converge como consecuencia de la desigualdad de Cauchy-Schwarz y la convergencia de la serie anterior.
La completitud del espacio se cumple siempre que, siempre que una serie de elementos de l 2 converja absolutamente (en norma), entonces converja a un elemento de l 2 . La prueba es básica en el análisis matemático y permite manipular series matemáticas de elementos del espacio con la misma facilidad que series de números complejos (o vectores en un espacio euclidiano de dimensión finita). [10]
Historia

Antes del desarrollo de los espacios de Hilbert, los matemáticos y físicos conocían otras generalizaciones de los espacios euclidianos . En particular, la idea de un espacio lineal abstracto (espacio vectorial) había ganado cierta fuerza hacia finales del siglo XIX: [11] se trata de un espacio cuyos elementos pueden sumarse y multiplicarse por escalares (como números reales o complejos ) sin identificar necesariamente estos elementos con vectores "geométricos" , como los vectores de posición y momento en sistemas físicos. Otros objetos estudiados por los matemáticos a principios del siglo XX, en particular los espacios de sucesiones (incluidas las series ) y los espacios de funciones, [12] pueden considerarse naturalmente como espacios lineales. Las funciones, por ejemplo, pueden sumarse o multiplicarse por escalares constantes, y estas operaciones obedecen a las leyes algebraicas satisfechas por la adición y la multiplicación escalar de vectores espaciales.
En la primera década del siglo XX, se produjeron desarrollos paralelos que condujeron a la introducción de los espacios de Hilbert. El primero de ellos fue la observación, que surgió durante el estudio de las ecuaciones integrales de David Hilbert y Erhard Schmidt [13] , de que dos funciones de valor real integrables al cuadrado f y g en un intervalo [ a , b ] tienen un producto interno
que tiene muchas de las propiedades familiares del producto escalar euclidiano. En particular, la idea de una familia ortogonal de funciones tiene sentido. Schmidt explotó la similitud de este producto interno con el producto escalar habitual para demostrar un análogo de la descomposición espectral para un operador de la forma
donde K es una función continua simétrica en x e y . La expansión de la función propia resultante expresa la función K como una serie de la forma
donde las funciones φ n son ortogonales en el sentido de que ⟨ φ n , φ m ⟩ = 0 para todo n ≠ m . Los términos individuales de esta serie se denominan a veces soluciones de producto elementales. Sin embargo, hay expansiones de funciones propias que no convergen en un sentido adecuado a una función integrable al cuadrado: el ingrediente faltante, que asegura la convergencia, es la completitud. [14]
El segundo desarrollo fue la integral de Lebesgue , una alternativa a la integral de Riemann introducida por Henri Lebesgue en 1904. [15] La integral de Lebesgue hizo posible integrar una clase mucho más amplia de funciones. En 1907, Frigyes Riesz y Ernst Sigismund Fischer demostraron de forma independiente que el espacio L 2 de funciones cuadradas integrables por Lebesgue es un espacio métrico completo . [16] Como consecuencia de la interacción entre geometría y completitud, los resultados del siglo XIX de Joseph Fourier , Friedrich Bessel y Marc-Antoine Parseval sobre series trigonométricas se trasladaron fácilmente a estos espacios más generales, dando como resultado un aparato geométrico y analítico ahora conocido habitualmente como el teorema de Riesz-Fischer . [17]
A principios del siglo XX se demostraron otros resultados básicos. Por ejemplo, el teorema de representación de Riesz fue establecido independientemente por Maurice Fréchet y Frigyes Riesz en 1907. [18] John von Neumann acuñó el término espacio de Hilbert abstracto en su trabajo sobre operadores hermíticos ilimitados . [19] Aunque otros matemáticos como Hermann Weyl y Norbert Wiener ya habían estudiado espacios de Hilbert particulares con gran detalle, a menudo desde un punto de vista motivado físicamente, von Neumann dio el primer tratamiento completo y axiomático de ellos. [20] Von Neumann los utilizó más tarde en su trabajo seminal sobre los fundamentos de la mecánica cuántica, [21] y en su trabajo continuado con Eugene Wigner . El nombre "espacio de Hilbert" fue adoptado pronto por otros, por ejemplo por Hermann Weyl en su libro sobre mecánica cuántica y la teoría de grupos. [22]
La importancia del concepto de espacio de Hilbert se subrayó con la comprensión de que ofrece una de las mejores formulaciones matemáticas de la mecánica cuántica . [23] En resumen, los estados de un sistema mecánico cuántico son vectores en un cierto espacio de Hilbert, los observables son operadores hermíticos en ese espacio, las simetrías del sistema son operadores unitarios y las mediciones son proyecciones ortogonales . La relación entre las simetrías mecánicas cuánticas y los operadores unitarios proporcionó un impulso para el desarrollo de la teoría de representación unitaria de grupos , iniciada en el trabajo de 1928 de Hermann Weyl. [22] Por otro lado, a principios de la década de 1930 quedó claro que la mecánica clásica puede describirse en términos del espacio de Hilbert ( mecánica clásica de Koopman-von Neumann ) y que ciertas propiedades de los sistemas dinámicos clásicos pueden analizarse utilizando técnicas del espacio de Hilbert en el marco de la teoría ergódica . [24]
El álgebra de observables en mecánica cuántica es naturalmente un álgebra de operadores definidos en un espacio de Hilbert, según la formulación de la mecánica matricial de la teoría cuántica de Werner Heisenberg . [25] Von Neumann comenzó a investigar las álgebras de operadores en la década de 1930, como anillos de operadores en un espacio de Hilbert. El tipo de álgebras estudiadas por von Neumann y sus contemporáneos ahora se conocen como álgebras de von Neumann . [26] En la década de 1940, Israel Gelfand , Mark Naimark e Irving Segal dieron una definición de un tipo de álgebras de operadores llamadas C*-álgebras que, por un lado, no hacían referencia a un espacio de Hilbert subyacente y, por otro, extrapolaban muchas de las características útiles de las álgebras de operadores que se habían estudiado previamente. El teorema espectral para operadores autoadjuntos en particular que subyace a gran parte de la teoría del espacio de Hilbert existente se generalizó a las C*-álgebras. [27] Estas técnicas son ahora básicas en el análisis armónico abstracto y la teoría de la representación.
Ejemplos
Espacios de Lebesgue
Los espacios de Lebesgue son espacios de funciones asociados a espacios de medida ( X , M , μ ) , donde X es un conjunto, M es una σ-álgebra de subconjuntos de X , y μ es una medida aditiva contable en M . Sea L 2 ( X , μ ) el espacio de aquellas funciones medibles de valor complejo en X para las cuales la integral de Lebesgue del cuadrado del valor absoluto de la función es finita, es decir, para una función f en L 2 ( X , μ ) , y donde las funciones se identifican si y solo si difieren solo en un conjunto de medida cero .
El producto interno de las funciones f y g en L 2 ( X , μ ) se define entonces como o
donde la segunda forma (conjugación del primer elemento) se encuentra comúnmente en la literatura de física teórica . Para f y g en L 2 , la integral existe debido a la desigualdad de Cauchy-Schwarz, y define un producto interno en el espacio. Equipado con este producto interno, L 2 es de hecho completo. [28] La integral de Lebesgue es esencial para asegurar la completitud: en dominios de números reales, por ejemplo, no hay suficientes funciones que sean integrables según Riemann . [29]
Los espacios de Lebesgue aparecen en muchos entornos naturales. Los espacios L 2 ( R ) y L 2 ([0,1]) de funciones integrables al cuadrado con respecto a la medida de Lebesgue en la línea real y el intervalo unitario, respectivamente, son dominios naturales en los que definir la transformada de Fourier y la serie de Fourier. En otras situaciones, la medida puede ser algo distinto de la medida de Lebesgue ordinaria en la línea real. Por ejemplo, si w es cualquier función medible positiva, el espacio de todas las funciones mesurables f en el intervalo [0, 1] que satisface
se denomina espacio L 2 ponderado L 2
semanas([0, 1]) , y w se denomina función de peso. El producto interno se define por
El espacio ponderado L2
semanas([0, 1]) es idéntico al espacio de Hilbert L 2 ([0, 1], μ ) donde la medida μ de un conjunto A medible según Lebesgue se define por
Los espacios L 2 ponderados como este se utilizan con frecuencia para estudiar polinomios ortogonales , porque diferentes familias de polinomios ortogonales son ortogonales con respecto a diferentes funciones de ponderación. [30]
Espacios de Sobolev
Los espacios de Sobolev , denotados por H s o W s , 2 , son espacios de Hilbert. Se trata de un tipo especial de espacio funcional en el que se puede realizar la diferenciación , pero que (a diferencia de otros espacios de Banach como los espacios de Hölder ) admiten la estructura de un producto interno. Debido a que se permite la diferenciación, los espacios de Sobolev son un entorno conveniente para la teoría de ecuaciones diferenciales parciales . [31] También forman la base de la teoría de métodos directos en el cálculo de variaciones . [32]
Para s un entero no negativo y Ω ⊂ R n , el espacio de Sobolev H s (Ω) contiene L 2 funciones cuyas derivadas débiles de orden hasta s también son L 2 . El producto interno en H s (Ω) es donde el punto indica el producto escalar en el espacio euclidiano de derivadas parciales de cada orden. Los espacios de Sobolev también se pueden definir cuando s no es un entero.
Los espacios de Sobolev también se estudian desde el punto de vista de la teoría espectral, basándose más específicamente en la estructura del espacio de Hilbert. Si Ω es un dominio adecuado, entonces se puede definir el espacio de Sobolev H s (Ω) como el espacio de potenciales de Bessel ; [33] a grandes rasgos,
Aquí Δ es el laplaciano y (1 − Δ) − s / 2 se entiende en términos del teorema de mapeo espectral . Además de proporcionar una definición viable de espacios de Sobolev para s no enteros , esta definición también tiene propiedades particularmente deseables bajo la transformada de Fourier que la hacen ideal para el estudio de operadores pseudodiferenciales . Usando estos métodos en una variedad compacta de Riemann , uno puede obtener por ejemplo la descomposición de Hodge , que es la base de la teoría de Hodge . [34]
Espacios de funciones holomorfas
Espacios resistentes
Los espacios de Hardy son espacios funcionales, que surgen en el análisis complejo y el análisis armónico , cuyos elementos son ciertas funciones holomorfas en un dominio complejo. [35] Sea U el disco unitario en el plano complejo. Entonces el espacio de Hardy H 2 ( U ) se define como el espacio de funciones holomorfas f en U tales que las medias
permanecen acotados para r < 1. La norma en este espacio de Hardy está definida por
Los espacios de Hardy en el disco están relacionados con las series de Fourier. Una función f está en H 2 ( U ) si y solo si donde
Por lo tanto, H 2 ( U ) consiste en aquellas funciones que son L 2 en el círculo y cuyos coeficientes de Fourier de frecuencia negativos se desvanecen.
Espacios de Bergman
Los espacios de Bergman son otra familia de espacios de Hilbert de funciones holomorfas. [36] Sea D un conjunto abierto acotado en el plano complejo (o un espacio complejo de dimensiones superiores) y sea L 2, h ( D ) el espacio de funciones holomorfas f en D que también están en L 2 ( D ) en el sentido de que
donde la integral se toma con respecto a la medida de Lebesgue en D . Claramente L 2, h ( D ) es un subespacio de L 2 ( D ) ; de hecho, es un subespacio cerrado , y por lo tanto un espacio de Hilbert por derecho propio. Esto es una consecuencia de la estimación, válida en subconjuntos compactos K de D , que a su vez se sigue de la fórmula integral de Cauchy . Por lo tanto, la convergencia de una secuencia de funciones holomorfas en L 2 ( D ) implica también convergencia compacta , y por lo tanto la función límite también es holomorfa. Otra consecuencia de esta desigualdad es que el funcional lineal que evalúa una función f en un punto de D es en realidad continuo en L 2, h ( D ) . El teorema de representación de Riesz implica que el funcional de evaluación puede representarse como un elemento de L 2, h ( D ) . Por lo tanto, para cada z ∈ D , existe una función η z ∈ L 2, h ( D ) tal que para todo f ∈ L 2, h ( D ) . El integrando se conoce como núcleo de Bergman de D . Este núcleo integral satisface una propiedad de reproducción
Un espacio de Bergman es un ejemplo de un espacio de Hilbert con núcleo reproductor , que es un espacio de Hilbert de funciones junto con un núcleo K ( ζ , z ) que verifica una propiedad reproductora análoga a esta. El espacio de Hardy H 2 ( D ) también admite un núcleo reproductor, conocido como el núcleo de Szegő . [37] Los núcleos reproductores también son comunes en otras áreas de las matemáticas. Por ejemplo, en el análisis armónico , el núcleo de Poisson es un núcleo reproductor para el espacio de Hilbert de funciones armónicas integrables al cuadrado en la bola unitaria . Que este último sea un espacio de Hilbert es una consecuencia del teorema del valor medio para funciones armónicas.
Aplicaciones
Muchas de las aplicaciones de los espacios de Hilbert aprovechan el hecho de que estos permiten generalizar conceptos geométricos simples, como la proyección y el cambio de base, a partir de su configuración habitual de dimensión finita. En particular, la teoría espectral de operadores lineales autoadjuntos continuos en un espacio de Hilbert generaliza la descomposición espectral habitual de una matriz , y esto suele desempeñar un papel importante en las aplicaciones de la teoría a otras áreas de las matemáticas y la física.
Teoría de Sturm-Liouville

En la teoría de ecuaciones diferenciales ordinarias , se utilizan métodos espectrales en un espacio de Hilbert adecuado para estudiar el comportamiento de los valores propios y las funciones propias de las ecuaciones diferenciales. Por ejemplo, el problema de Sturm-Liouville surge en el estudio de los armónicos de las ondas en una cuerda de violín o un tambor, y es un problema central en las ecuaciones diferenciales ordinarias . [38] El problema es una ecuación diferencial de la forma para una función desconocida y en un intervalo [ a , b ] , que satisface las condiciones de contorno homogéneas generales de Robin Las funciones p , q y w se dan de antemano, y el problema es encontrar la función y y las constantes λ para las que la ecuación tiene una solución. El problema solo tiene soluciones para ciertos valores de λ , llamados valores propios del sistema, y esto es una consecuencia del teorema espectral para operadores compactos aplicado al operador integral definido por la función de Green para el sistema. Además, otra consecuencia de este resultado general es que los valores propios λ del sistema pueden ordenarse en una secuencia creciente que tiende al infinito. [39] [nb 2]
Ecuaciones diferenciales parciales
Los espacios de Hilbert forman una herramienta básica en el estudio de ecuaciones diferenciales parciales . [31] Para muchas clases de ecuaciones diferenciales parciales, como las ecuaciones elípticas lineales , es posible considerar una solución generalizada (conocida como solución débil ) ampliando la clase de funciones. Muchas formulaciones débiles involucran la clase de funciones de Sobolev , que es un espacio de Hilbert. Una formulación débil adecuada se reduce a un problema geométrico, el problema analítico de encontrar una solución o, a menudo lo que es más importante, demostrar que existe una solución y es única para datos de contorno dados. Para ecuaciones elípticas lineales, un resultado geométrico que asegura una solubilidad única para una gran clase de problemas es el teorema de Lax-Milgram . Esta estrategia forma el rudimento del método de Galerkin (un método de elementos finitos ) para la solución numérica de ecuaciones diferenciales parciales. [40]
Un ejemplo típico es la ecuación de Poisson −Δ u = g con condiciones de contorno de Dirichlet en un dominio acotado Ω en R 2 . La formulación débil consiste en hallar una función u tal que, para todas las funciones continuamente diferenciables v en Ω que se anulan en el contorno:
Esto se puede reformular en términos del espacio de Hilbert H1
0(Ω) que consta de funciones u tales que u , junto con sus derivadas parciales débiles, son integrables al cuadrado en Ω y se anulan en el límite. La cuestión se reduce entonces a encontrar u en este espacio tal que para todo v en este espacio
donde a es una forma bilineal continua y b es una funcional lineal continua , dadas respectivamente por
Como la ecuación de Poisson es elíptica , se deduce de la desigualdad de Poincaré que la forma bilineal a es coercitiva . El teorema de Lax-Milgram asegura entonces la existencia y unicidad de las soluciones de esta ecuación. [41]
Los espacios de Hilbert permiten formular de forma similar muchas ecuaciones diferenciales parciales elípticas, y el teorema de Lax-Milgram es entonces una herramienta básica para su análisis. Con modificaciones adecuadas, se pueden aplicar técnicas similares a ecuaciones diferenciales parciales parabólicas y a ciertas ecuaciones diferenciales parciales hiperbólicas . [42]
Teoría ergódica

El campo de la teoría ergódica es el estudio del comportamiento a largo plazo de los sistemas dinámicos caóticos . El caso protípico de un campo al que se aplica la teoría ergódica es la termodinámica , en la que, aunque el estado microscópico de un sistema es extremadamente complicado (es imposible entender el conjunto de colisiones individuales entre partículas de materia), el comportamiento promedio durante intervalos de tiempo suficientemente largos es manejable. Las leyes de la termodinámica son afirmaciones sobre dicho comportamiento promedio. En particular, una formulación de la ley cero de la termodinámica afirma que, en escalas de tiempo suficientemente largas, la única medición funcionalmente independiente que se puede hacer de un sistema termodinámico en equilibrio es su energía total, en forma de temperatura . [43]
Un sistema dinámico ergódico es aquel para el cual, aparte de la energía —medida por el hamiltoniano— no hay otras cantidades conservadas funcionalmente independientes en el espacio de fases . Más explícitamente, supongamos que la energía E es fija, y sea Ω E el subconjunto del espacio de fases que consiste en todos los estados de energía E (una superficie de energía), y sea T t el operador de evolución en el espacio de fases. El sistema dinámico es ergódico si cada función medible invariante en Ω E es constante casi en todas partes . [44] Una función invariante f es aquella para la cual para todo w en Ω E y todo tiempo t . El teorema de Liouville implica que existe una medida μ en la superficie de energía que es invariante bajo la traslación temporal . Como resultado, la traslación temporal es una transformación unitaria del espacio de Hilbert L 2 (Ω E , μ ) que consiste en funciones integrables al cuadrado en la superficie de energía Ω E con respecto al producto interno
El teorema ergódico medio de von Neumann [24] establece lo siguiente:
- Si U t es un semigrupo de un parámetro (fuertemente continuo) de operadores unitarios en un espacio de Hilbert H , y P es la proyección ortogonal sobre el espacio de puntos fijos comunes de U t , { x ∈ H | U t x = x , ∀ t > 0} , entonces
Para un sistema ergódico, el conjunto fijo de la evolución temporal consta únicamente de las funciones constantes, por lo que el teorema ergódico implica lo siguiente: [45] para cualquier función f ∈ L 2 (Ω E , μ ) ,
Es decir, el promedio a largo plazo de un observable f es igual a su valor esperado sobre una superficie de energía.
Análisis de Fourier
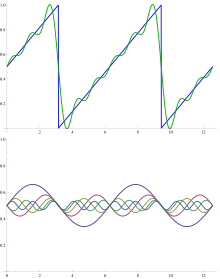

Uno de los objetivos básicos del análisis de Fourier es descomponer una función en una combinación lineal (posiblemente infinita) de funciones base dadas: la serie de Fourier asociada . La serie de Fourier clásica asociada a una función f definida en el intervalo [0, 1] es una serie de la forma donde
En la figura se muestra el ejemplo de la suma de los primeros términos de una serie de Fourier para una función de diente de sierra. Las funciones base son ondas sinusoidales con longitudes de onda la/norte (para un entero n ) más corto que la longitud de onda λ del propio diente de sierra (excepto para n = 1 , laonda fundamental ).
Un problema importante en las series de Fourier clásicas es en qué sentido converge la serie de Fourier, si es que lo hace, a la función f . Los métodos del espacio de Hilbert proporcionan una posible respuesta a esta pregunta. [46] Las funciones e n ( θ ) = e 2π inθ forman una base ortogonal del espacio de Hilbert L 2 ([0, 1]) . En consecuencia, cualquier función integrable al cuadrado puede expresarse como una serie
y, además, esta serie converge en el sentido del espacio de Hilbert (es decir, en la media L 2 ).
El problema también puede estudiarse desde el punto de vista abstracto: cada espacio de Hilbert tiene una base ortonormal , y cada elemento del espacio de Hilbert puede escribirse de forma única como una suma de múltiplos de estos elementos base. Los coeficientes que aparecen en estos elementos base a veces se conocen de forma abstracta como los coeficientes de Fourier del elemento del espacio. [47] La abstracción es especialmente útil cuando es más natural utilizar diferentes funciones base para un espacio como L 2 ([0, 1]) . En muchas circunstancias, es deseable no descomponer una función en funciones trigonométricas, sino más bien en polinomios ortogonales o wavelets , por ejemplo, [48] y en dimensiones superiores en armónicos esféricos . [49]
Por ejemplo, si e n son funciones base ortonormales de L 2 [0, 1] , entonces una función dada en L 2 [0, 1] puede aproximarse como una combinación lineal finita [50].
Los coeficientes { a j } se seleccionan para hacer que la magnitud de la diferencia ‖ f − f n ‖ 2 sea lo más pequeña posible. Geométricamente, la mejor aproximación es la proyección ortogonal de f sobre el subespacio que consiste en todas las combinaciones lineales de { e j } , y se puede calcular mediante [51]
Que esta fórmula minimice la diferencia ‖ f − f n ‖ 2 es una consecuencia de la desigualdad de Bessel y de la fórmula de Parseval.
En varias aplicaciones a problemas físicos, una función puede descomponerse en funciones propias físicamente significativas de un operador diferencial (típicamente el operador de Laplace ): esto forma la base para el estudio espectral de funciones, en referencia al espectro del operador diferencial. [52] Una aplicación física concreta involucra el problema de escuchar la forma de un tambor : dados los modos fundamentales de vibración que un parche de tambor es capaz de producir, ¿se puede inferir la forma del tambor mismo? [53] La formulación matemática de esta pregunta involucra los valores propios de Dirichlet de la ecuación de Laplace en el plano, que representan los modos fundamentales de vibración en analogía directa con los números enteros que representan los modos fundamentales de vibración de la cuerda del violín.
La teoría espectral también subyace a ciertos aspectos de la transformada de Fourier de una función. Mientras que el análisis de Fourier descompone una función definida en un conjunto compacto en el espectro discreto del laplaciano (que corresponde a las vibraciones de una cuerda de violín o un tambor), la transformada de Fourier de una función es la descomposición de una función definida en todo el espacio euclidiano en sus componentes en el espectro continuo del laplaciano. La transformada de Fourier también es geométrica, en un sentido que se precisa mediante el teorema de Plancherel , que afirma que es una isometría de un espacio de Hilbert (el "dominio del tiempo") con otro (el "dominio de la frecuencia"). Esta propiedad de isometría de la transformada de Fourier es un tema recurrente en el análisis armónico abstracto (ya que refleja la conservación de la energía para la transformada de Fourier continua), como lo demuestra, por ejemplo, el teorema de Plancherel para funciones esféricas que ocurren en el análisis armónico no conmutativo .
Mecánica cuántica

En la formulación matemáticamente rigurosa de la mecánica cuántica , desarrollada por John von Neumann , [54] los estados posibles (más precisamente, los estados puros ) de un sistema mecánico cuántico están representados por vectores unitarios (llamados vectores de estado ) que residen en un espacio de Hilbert separable complejo, conocido como el espacio de estados , bien definido hasta un número complejo de norma 1 (el factor de fase ). En otras palabras, los estados posibles son puntos en la proyectivización de un espacio de Hilbert, usualmente llamado espacio proyectivo complejo . La naturaleza exacta de este espacio de Hilbert depende del sistema; por ejemplo, los estados de posición y momento para una sola partícula no relativista de espín cero es el espacio de todas las funciones integrables al cuadrado , mientras que los estados para el espín de un solo protón son elementos unitarios del espacio de Hilbert complejo bidimensional de espinores . Cada observable está representado por un operador lineal autoadjunto que actúa sobre el espacio de estados. Cada estado propio de un observable corresponde a un vector propio del operador, y el valor propio asociado corresponde al valor del observable en ese estado propio. [55]
El producto interno entre dos vectores de estado es un número complejo conocido como amplitud de probabilidad . Durante una medición ideal de un sistema mecánico cuántico, la probabilidad de que un sistema colapse desde un estado inicial dado a un estado propio particular está dada por el cuadrado del valor absoluto de las amplitudes de probabilidad entre los estados inicial y final. [56] Los posibles resultados de una medición son los valores propios del operador, lo que explica la elección de operadores autoadjuntos, ya que todos los valores propios deben ser reales. La distribución de probabilidad de un observable en un estado dado se puede encontrar calculando la descomposición espectral del operador correspondiente. [57]
En un sistema general, los estados no suelen ser puros, sino que se representan como mezclas estadísticas de estados puros o estados mixtos, dadas por matrices de densidad : operadores autoadjuntos de traza uno en un espacio de Hilbert. [58] Además, en el caso de los sistemas mecánicos cuánticos generales, los efectos de una única medición pueden influir en otras partes de un sistema de una manera que se describe en cambio mediante una medida con valor de operador positivo . Por lo tanto, la estructura tanto de los estados como de los observables en la teoría general es considerablemente más complicada que la idealización para los estados puros. [59]
Teoría de la probabilidad
En teoría de probabilidad , los espacios de Hilbert también tienen diversas aplicaciones. Aquí, un espacio de Hilbert fundamental es el espacio de variables aleatorias en un espacio de probabilidad dado , que tiene clase (primer y segundo momentos finitos ). Una operación común en estadística es la de centrar una variable aleatoria restando su esperanza . Por lo tanto, si es una variable aleatoria, entonces es su centrado. En la visión del espacio de Hilbert, esta es la proyección ortogonal de sobre el núcleo del operador de esperanza, que es un funcional lineal continuo en el espacio de Hilbert (de hecho, el producto interno con la variable aleatoria constante 1), y por lo tanto este núcleo es un subespacio cerrado.
La esperanza condicional tiene una interpretación natural en el espacio de Hilbert. [60] Supóngase que se da un espacio de probabilidad, donde es un álgebra sigma en el conjunto , y es una medida de probabilidad en el espacio de medida . Si es un subálgebra sigma de , entonces la esperanza condicional es la proyección ortogonal de sobre el subespacio de que consiste en las funciones -medibles. Si la variable aleatoria en es independiente del álgebra sigma , entonces la esperanza condicional , es decir, su proyección sobre las funciones -medibles es constante. Equivalentemente, la proyección de su centrado es cero.
En particular, si dos variables aleatorias y (en ) son independientes, entonces las variables aleatorias centradas y son ortogonales. (Esto significa que las dos variables tienen covarianza cero: no están correlacionadas ). En ese caso, el teorema de Pitágoras en el núcleo del operador de expectativa implica que las varianzas de y satisfacen la identidad: a veces llamado teorema de Pitágoras de las estadísticas, y es importante en la regresión lineal . [61] Como lo expresa Stapleton (1995), "el análisis de varianza puede verse como la descomposición de la longitud al cuadrado de un vector en la suma de las longitudes al cuadrado de varios vectores, utilizando el Teorema de Pitágoras".
La teoría de las martingalas se puede formular en espacios de Hilbert. Una martingala en un espacio de Hilbert es una secuencia de elementos de un espacio de Hilbert tal que, para cada n , es la proyección ortogonal de sobre la envoltura lineal de . [62] Si son variables aleatorias, esto reproduce la definición habitual de una martingala (discreta): la esperanza de , condicionada a , es igual a .
Los espacios de Hilbert también se utilizan en los fundamentos del cálculo de Itô . [63] A cualquier martingala integrable al cuadrado , es posible asociar una norma de Hilbert en el espacio de clases de equivalencia de procesos progresivamente medibles con respecto a la martingala (usando la variación cuadrática de la martingala como medida). La integral de Itô se puede construir definiéndola primero para procesos simples y luego explotando su densidad en el espacio de Hilbert. Un resultado notable es entonces la isometría de Itô , que atestigua que para cualquier martingala M que tenga una medida de variación cuadrática , y cualquier proceso progresivamente medible H : siempre que la expectativa en el lado derecho sea finita.
Una aplicación más profunda de los espacios de Hilbert que es especialmente importante en la teoría de los procesos gaussianos es un intento, debido a Leonard Gross y otros, de dar sentido a ciertas integrales formales sobre espacios de dimensión infinita como la integral de trayectoria de Feynman de la teoría cuántica de campos . El problema con una integral como esta es que no hay una medida de Lebesgue de dimensión infinita . La noción de un espacio de Wiener abstracto permite construir una medida en un espacio de Banach B que contiene un espacio de Hilbert H , llamado espacio de Cameron-Martin , como un subconjunto denso, a partir de una medida de conjunto cilíndrico finitamente aditiva en H. La medida resultante en B es contablemente aditiva e invariante bajo la traslación de elementos de H , y esto proporciona una forma matemáticamente rigurosa de pensar en la medida de Wiener como una medida gaussiana en el espacio de Sobolev . [64]
Percepción del color
Cualquier color físico verdadero puede representarse mediante una combinación de colores espectrales puros . Como los colores físicos pueden estar compuestos por cualquier número de colores espectrales, el espacio de colores físicos puede representarse adecuadamente mediante un espacio de Hilbert sobre colores espectrales. Los humanos tienen tres tipos de células cónicas para la percepción del color, por lo que los colores perceptibles pueden representarse mediante un espacio euclidiano tridimensional. La correspondencia lineal de muchos a uno del espacio de Hilbert de colores físicos al espacio euclidiano de colores perceptibles por los humanos explica por qué los humanos pueden percibir muchos colores físicos distintos como idénticos (por ejemplo, luz amarilla pura frente a una mezcla de luz roja y verde, véase metamerismo ). [65] [66]
Propiedades
Identidad pitagórica
Dos vectores u y v en un espacio de Hilbert H son ortogonales cuando ⟨ u , v ⟩ = 0 . La notación para esto es u ⊥ v . De manera más general, cuando S es un subconjunto en H , la notación u ⊥ S significa que u es ortogonal a cada elemento de S .
Cuando u y v son ortogonales, se tiene
Por inducción sobre n , esto se extiende a cualquier familia u 1 , ..., u n de n vectores ortogonales,
Mientras que la identidad pitagórica tal como se enuncia es válida en cualquier espacio de producto interno, se requiere completitud para la extensión de la identidad pitagórica a series. [67] Una serie Σ u k de vectores ortogonales converge en H si y solo si la serie de cuadrados de normas converge, y además, la suma de una serie de vectores ortogonales es independiente del orden en el que se toma.
Identidad y polarización del paralelogramo

Por definición, todo espacio de Hilbert es también un espacio de Banach . Además, en todo espacio de Hilbert se cumple la siguiente identidad de paralelogramo : [68]
Por el contrario, cada espacio de Banach en el que se cumple la identidad del paralelogramo es un espacio de Hilbert, y el producto interno está determinado de forma única por la norma por la identidad de polarización . [69] Para espacios de Hilbert reales, la identidad de polarización es
Para espacios de Hilbert complejos, es
La ley del paralelogramo implica que cualquier espacio de Hilbert es un espacio de Banach uniformemente convexo . [70]
Mejor aproximación
En esta subsección se emplea el teorema de proyección de Hilbert . Si C es un subconjunto convexo cerrado no vacío de un espacio de Hilbert H y x es un punto en H , existe un único punto y ∈ C que minimiza la distancia entre x y los puntos en C , [71]
Esto es equivalente a decir que hay un punto con norma mínima en el conjunto convexo trasladado D = C − x . La prueba consiste en mostrar que toda secuencia minimizadora ( d n ) ⊂ D es de Cauchy (usando la identidad del paralelogramo) y por lo tanto converge (usando completitud) a un punto en D que tiene norma mínima. De manera más general, esto se cumple en cualquier espacio de Banach uniformemente convexo. [72]
Cuando este resultado se aplica a un subespacio cerrado F de H , se puede demostrar que el punto y ∈ F más cercano a x se caracteriza por [73]
Este punto y es la proyección ortogonal de x sobre F , y la función P F : x → y es lineal (véase Complementos y proyecciones ortogonales). Este resultado es especialmente significativo en matemáticas aplicadas , especialmente en análisis numérico , donde forma la base de los métodos de mínimos cuadrados . [74]
En particular, cuando F no es igual a H , se puede encontrar un vector v distinto de cero ortogonal a F (seleccionando x ∉ F y v = x − y ). Se obtiene un criterio muy útil al aplicar esta observación al subespacio cerrado F generado por un subconjunto S de H .
- Un subconjunto S de H abarca un subespacio vectorial denso si (y sólo si) el vector 0 es el único vector v ∈ H ortogonal a S .
Dualidad
El espacio dual H * es el espacio de todas las funciones lineales continuas desde el espacio H hasta el cuerpo base. Lleva una norma natural, definida por Esta norma satisface la ley del paralelogramo , y por lo tanto el espacio dual es también un espacio de producto interno donde este producto interno puede definirse en términos de esta norma dual utilizando la identidad de polarización . El espacio dual también es completo, por lo que es un espacio de Hilbert por derecho propio. Si e • = ( e i ) i ∈ I es una base ortonormal completa para H, entonces el producto interno en el espacio dual de cualesquiera dos es donde todos, excepto un número contable, de los términos en esta serie son cero.
El teorema de representación de Riesz proporciona una descripción conveniente del espacio dual. Para cada elemento u de H , existe un elemento único φ u de H * , definido por donde además,
El teorema de representación de Riesz establece que la función de H en H * definida por u ↦ φ u es sobreyectiva , lo que hace que esta función sea un isomorfismo antilineal isométrico . [75] Por lo tanto, para cada elemento φ del dual H * existe uno y solo un u φ en H tal que para todo x ∈ H . El producto interno en el espacio dual H * satisface
La inversión del orden en el lado derecho restablece la linealidad en φ a partir de la antilinealidad de u φ . En el caso real, el isomorfismo antilineal de H a su dual es en realidad un isomorfismo, y por lo tanto los espacios de Hilbert reales son naturalmente isomorfos a sus propios duales.
El vector representativo u φ se obtiene de la siguiente manera. Cuando φ ≠ 0 , el núcleo F = Ker( φ ) es un subespacio vectorial cerrado de H , no igual a H , por lo tanto existe un vector v distinto de cero ortogonal a F . El vector u es un múltiplo escalar adecuado λv de v . El requisito de que φ ( v ) = ⟨ v , u ⟩ produce
Esta correspondencia φ ↔ u se explota mediante la notación bra–ket popular en física . [76] Es común en física asumir que el producto interno, denotado por ⟨ x | y ⟩ , es lineal por la derecha. El resultado ⟨ x | y ⟩ puede verse como la acción de la función lineal ⟨ x | (el bra ) sobre el vector | y ⟩ (el ket ).
El teorema de representación de Riesz se basa fundamentalmente no sólo en la presencia de un producto interno, sino también en la completitud del espacio. De hecho, el teorema implica que el dual topológico de cualquier espacio de producto interno puede identificarse con su completitud. [77] Una consecuencia inmediata del teorema de representación de Riesz es también que un espacio de Hilbert H es reflexivo , lo que significa que la función natural de H en su espacio dual doble es un isomorfismo.
Secuencias débilmente convergentes
En un espacio de Hilbert H , una secuencia { x n } es débilmente convergente a un vector x ∈ H cuando para cada v ∈ H .
Por ejemplo, cualquier secuencia ortonormal { f n } converge débilmente a 0, como consecuencia de la desigualdad de Bessel. Toda secuencia débilmente convergente { x n } está acotada, por el principio de acotación uniforme .
Por el contrario, toda sucesión acotada en un espacio de Hilbert admite subsecuencias débilmente convergentes ( teorema de Alaoglu ). [78] Este hecho puede utilizarse para demostrar resultados de minimización para funcionales convexos continuos , de la misma manera que se utiliza el teorema de Bolzano-Weierstrass para funciones continuas en R d . Entre varias variantes, una afirmación simple es la siguiente: [79]
- Si f : H → R es una función continua convexa tal que f ( x ) tiende a +∞ cuando ‖ x ‖ tiende a ∞ , entonces f admite un mínimo en algún punto x 0 ∈ H .
Este hecho (y sus diversas generalizaciones) son fundamentales para los métodos directos en el cálculo de variaciones . Los resultados de minimización para funcionales convexos también son una consecuencia directa del hecho ligeramente más abstracto de que los subconjuntos convexos cerrados y acotados en un espacio de Hilbert H son débilmente compactos , ya que H es reflexivo. La existencia de subsecuencias débilmente convergentes es un caso especial del teorema de Eberlein-Šmulian .
Propiedades del espacio de Banach
Cualquier propiedad general de los espacios de Banach sigue siendo válida para los espacios de Hilbert. El teorema de aplicación abierta establece que una transformación lineal sobreyectiva continua de un espacio de Banach a otro es una aplicación abierta, lo que significa que envía conjuntos abiertos a conjuntos abiertos. Un corolario es el teorema inverso acotado , que una función lineal continua y biyectiva de un espacio de Banach a otro es un isomorfismo (es decir, una aplicación lineal continua cuya inversa también es continua). Este teorema es considerablemente más simple de demostrar en el caso de los espacios de Hilbert que en los espacios de Banach generales. [80] El teorema de aplicación abierta es equivalente al teorema del grafo cerrado , que afirma que una función lineal de un espacio de Banach a otro es continua si y solo si su grafo es un conjunto cerrado . [81] En el caso de los espacios de Hilbert, esto es básico en el estudio de los operadores no acotados (véase operador cerrado ).
El teorema (geométrico) de Hahn-Banach afirma que un conjunto convexo cerrado puede separarse de cualquier punto exterior a él por medio de un hiperplano del espacio de Hilbert. Esta es una consecuencia inmediata de la propiedad de mejor aproximación: si y es el elemento de un conjunto convexo cerrado F más próximo a x , entonces el hiperplano de separación es el plano perpendicular al segmento xy que pasa por su punto medio. [82]
Operadores en espacios de Hilbert
Operadores acotados
Los operadores lineales continuos A : H 1 → H 2 de un espacio de Hilbert H 1 a un segundo espacio de Hilbert H 2 están acotados en el sentido de que asignan conjuntos acotados a conjuntos acotados. [83] Por el contrario, si un operador está acotado, entonces es continuo. El espacio de tales operadores lineales acotados tiene una norma , la norma del operador dada por
La suma y la composición de dos operadores lineales acotados es nuevamente acotada y lineal. Para y en H 2 , la función que envía x ∈ H 1 a ⟨ Ax , y ⟩ es lineal y continua, y de acuerdo con el teorema de representación de Riesz puede por lo tanto representarse en la forma para algún vector A * y en H 1 . Esto define otro operador lineal acotado A * : H 2 → H 1 , el adjunto de A . El adjunto satisface A ** = A . Cuando se utiliza el teorema de representación de Riesz para identificar cada espacio de Hilbert con su espacio dual continuo, se puede demostrar que el adjunto de A es idéntico a la transpuesta t A : H 2 * → H 1 * de A , que por definición envía al funcional
El conjunto B( H ) de todos los operadores lineales acotados en H (es decir, los operadores H → H ), junto con las operaciones de adición y composición, la norma y la operación adjunta, es un C*-álgebra , que es un tipo de álgebra de operadores .
Un elemento A de B( H ) se llama 'autoadjunto' o 'hermítico' si A * = A . Si A es hermítico y ⟨ Ax , x ⟩ ≥ 0 para cada x , entonces A se llama 'no negativo', escrito A ≥ 0 ; si la igualdad se cumple solo cuando x = 0 , entonces A se llama 'positivo'. El conjunto de operadores autoadjuntos admite un orden parcial , en el que A ≥ B si A − B ≥ 0 . Si A tiene la forma B * B para algún B , entonces A es no negativo; si B es invertible, entonces A es positivo. Una recíproca también es cierta en el sentido de que, para un operador no negativo A , existe una única raíz cuadrada no negativa B tal que
En un sentido precisado por el teorema espectral , los operadores autoadjuntos pueden considerarse de manera útil como operadores que son "reales". Un elemento A de B( H ) se llama normal si A * A = AA * . Los operadores normales se descomponen en la suma de un operador autoadjunto y un múltiplo imaginario de un operador autoadjunto que conmutan entre sí. Los operadores normales también pueden considerarse de manera útil en términos de sus partes reales e imaginarias.
Un elemento U de B( H ) se llama unitario si U es invertible y su inverso está dado por U * . Esto también se puede expresar exigiendo que U sea sobre y ⟨ Ux , Uy ⟩ = ⟨ x , y ⟩ para todo x , y ∈ H . Los operadores unitarios forman un grupo bajo composición, que es el grupo de isometría de H .
Un elemento de B( H ) es compacto si envía conjuntos acotados a conjuntos relativamente compactos . De manera equivalente, un operador acotado T es compacto si, para cualquier secuencia acotada { x k } , la secuencia { Tx k } tiene una subsecuencia convergente. Muchos operadores integrales son compactos y, de hecho, definen una clase especial de operadores conocidos como operadores de Hilbert–Schmidt que son especialmente importantes en el estudio de ecuaciones integrales . Los operadores de Fredholm se diferencian de un operador compacto por un múltiplo de la identidad y se caracterizan de manera equivalente como operadores con un núcleo y conúcleo de dimensión finita . El índice de un operador de Fredholm T se define por
El índice es invariante de homotopía y juega un papel importante en la geometría diferencial a través del teorema del índice de Atiyah-Singer .
Operadores ilimitados
Los operadores no acotados también son manejables en espacios de Hilbert y tienen aplicaciones importantes en la mecánica cuántica . [84] Un operador no acotado T en un espacio de Hilbert H se define como un operador lineal cuyo dominio D ( T ) es un subespacio lineal de H . A menudo, el dominio D ( T ) es un subespacio denso de H , en cuyo caso T se conoce como un operador densamente definido .
El operador adjunto de un operador ilimitado densamente definido se define esencialmente de la misma manera que para los operadores acotados. Los operadores ilimitados autoadjuntos desempeñan el papel de observables en la formulación matemática de la mecánica cuántica. Ejemplos de operadores ilimitados autoadjuntos en el espacio de Hilbert L 2 ( R ) son: [85]
- Una extensión adecuada del operador diferencial donde i es la unidad imaginaria y f es una función diferenciable de soporte compacto.
- El operador de multiplicación por x :
Estos corresponden a los observables de momento y posición , respectivamente. Ni A ni B están definidos en todo H , ya que en el caso de A no es necesario que exista la derivada, y en el caso de B la función producto no necesita ser integrable al cuadrado. En ambos casos, el conjunto de argumentos posibles forma subespacios densos de L 2 ( R ) .
Construcciones
Sumas directas
Dos espacios de Hilbert H 1 y H 2 se pueden combinar en otro espacio de Hilbert, llamado suma directa (ortogonal) , [86] y denotado
que consiste en el conjunto de todos los pares ordenados ( x 1 , x 2 ) donde x i ∈ H i , i = 1, 2 y producto interno definido por
De manera más general, si H i es una familia de espacios de Hilbert indexados por i ∈ I , entonces la suma directa de H i , denotada por consiste en el conjunto de todas las familias indexadas en el producto cartesiano de H i tales que
El producto interno se define por
Cada uno de los H i está incluido como un subespacio cerrado en la suma directa de todos los H i . Además, los H i son ortogonales entre sí. Por el contrario, si hay un sistema de subespacios cerrados, V i , i ∈ I , en un espacio de Hilbert H , que son ortogonales entre sí y cuya unión es densa en H , entonces H es canónicamente isomorfo a la suma directa de V i . En este caso, H se denomina suma directa interna de V i . Una suma directa (interna o externa) también está equipada con una familia de proyecciones ortogonales E i sobre el i ésimo sumando directo H i . Estas proyecciones son operadores acotados, autoadjuntos e idempotentes que satisfacen la condición de ortogonalidad.
El teorema espectral para operadores autoadjuntos compactos en un espacio de Hilbert H establece que H se descompone en una suma directa ortogonal de los espacios propios de un operador, y también da una descomposición explícita del operador como una suma de proyecciones sobre los espacios propios. La suma directa de los espacios de Hilbert también aparece en mecánica cuántica como el espacio de Fock de un sistema que contiene un número variable de partículas, donde cada espacio de Hilbert en la suma directa corresponde a un grado adicional de libertad para el sistema mecánico cuántico. En teoría de la representación , el teorema de Peter-Weyl garantiza que cualquier representación unitaria de un grupo compacto en un espacio de Hilbert se descompone como la suma directa de representaciones de dimensión finita.
Productos tensoriales
Si x 1 , y 1 ∊ H 1 y x 2 , y 2 ∊ H 2 , entonces se define un producto interno sobre el producto tensorial (ordinario) de la siguiente manera. Sobre tensores simples , sea
Esta fórmula se extiende entonces por sesquilinealidad a un producto interno en H 1 ⊗ H 2 . El producto tensorial de Hilbert de H 1 y H 2 , a veces denotado por H 1 H 2 , es el espacio de Hilbert obtenido al completar H 1 ⊗ H 2 para la métrica asociada a este producto interno. [87]
Un ejemplo lo proporciona el espacio de Hilbert L 2 ([0, 1]) . El producto tensorial de Hilbert de dos copias de L 2 ([0, 1]) es isométrico y linealmente isomorfo al espacio L 2 ([0, 1] 2 ) de funciones integrables al cuadrado en el cuadrado [0, 1] 2 . Este isomorfismo envía un tensor simple f 1 ⊗ f 2 a la función en el cuadrado.
Este ejemplo es típico en el siguiente sentido. [88] Asociado a cada producto tensorial simple x 1 ⊗ x 2 está el operador de rango uno de H∗
1a H 2 que mapea un x * ∈ H dado∗
1como
Esta aplicación definida sobre tensores simples se extiende a una identificación lineal entre H 1 ⊗ H 2 y el espacio de operadores de rango finito de H∗
1a H 2 . Esto se extiende a una isometría lineal del producto tensorial de Hilbert H 1 H 2 con el espacio de Hilbert HS ( H∗
1, H 2 ) de operadores de Hilbert–Schmidt de H∗
1a H 2 .
Bases ortonormales
La noción de base ortonormal del álgebra lineal se generaliza al caso de los espacios de Hilbert. [89] En un espacio de Hilbert H , una base ortonormal es una familia { e k } k ∈ B de elementos de H que satisfacen las condiciones:
- Ortogonalidad : Cada dos elementos diferentes de B son ortogonales: ⟨ e k , e j ⟩ = 0 para todo k , j ∈ B con k ≠ j .
- Normalización : Cada elemento de la familia tiene norma 1: ‖ e k ‖ = 1 para todo k ∈ B .
- Completitud : La extensión lineal de la familia e k , k ∈ B , es denso en H .
Un sistema de vectores que satisface las dos primeras condiciones se denomina sistema ortonormal o conjunto ortonormal (o secuencia ortonormal si B es numerable ). Un sistema de este tipo es siempre linealmente independiente .
A pesar del nombre, una base ortonormal no es, en general, una base en el sentido del álgebra lineal ( base de Hamel ). Más precisamente, una base ortonormal es una base de Hamel si y solo si el espacio de Hilbert es un espacio vectorial de dimensión finita. [90]
La completitud de un sistema ortonormal de vectores de un espacio de Hilbert se puede reformular de manera equivalente como:
- para cada v ∈ H , si ⟨ v , e k ⟩ = 0 para todo k ∈ B , entonces v = 0 .
Esto está relacionado con el hecho de que el único vector ortogonal a un subespacio lineal denso es el vector cero, ya que si S es cualquier conjunto ortonormal y v es ortogonal a S , entonces v es ortogonal al cierre del espacio lineal de S , que es todo el espacio.
Algunos ejemplos de bases ortonormales incluyen:
- el conjunto {(1, 0, 0), (0, 1, 0), (0, 0, 1)} forma una base ortonormal de R 3 con el producto escalar ;
- la secuencia { f n | n ∈ Z } con f n ( x ) = exp (2π inx ) forma una base ortonormal del espacio complejo L 2 ([0, 1]) ;
En el caso de dimensión infinita, una base ortonormal no será una base en el sentido del álgebra lineal ; para distinguir las dos, la última base también se denomina base de Hamel . El hecho de que la amplitud de los vectores de la base sea densa implica que cada vector en el espacio puede escribirse como la suma de una serie infinita, y la ortogonalidad implica que esta descomposición es única.
Espacios de secuencia
El espacio de secuencias cuadradas sumables de números complejos es el conjunto de secuencias infinitas [9] de números reales o complejos tales que
Este espacio tiene una base ortonormal:
Este espacio es la generalización de dimensión infinita del espacio de vectores de dimensión finita. Suele ser el primer ejemplo que se utiliza para demostrar que en espacios de dimensión infinita, un conjunto cerrado y acotado no es necesariamente (secuencialmente) compacto (como es el caso en todos los espacios de dimensión finita ). De hecho, el conjunto de vectores ortonormales anterior lo demuestra: es una secuencia infinita de vectores en la bola unitaria (es decir, la bola de puntos con norma menor o igual a uno). Este conjunto está claramente acotado y cerrado; sin embargo, ninguna subsecuencia de estos vectores converge a nada y, en consecuencia, la bola unitaria no es compacta. Intuitivamente, esto se debe a que "siempre hay otra dirección de coordenadas" hacia la que pueden evadirse los siguientes elementos de la secuencia.
Se puede generalizar el espacio de muchas maneras. Por ejemplo, si B es un conjunto cualquiera, entonces se puede formar un espacio de Hilbert de sucesiones con el conjunto índice B , definido por [91]
La suma sobre B se define aquí por el supremo que se toma sobre todos los subconjuntos finitos de B . De ello se deduce que, para que esta suma sea finita, cada elemento de l 2 ( B ) tiene solo un número contable de términos distintos de cero. Este espacio se convierte en un espacio de Hilbert con el producto interno
para todo x , y ∈ l 2 ( B ) . Aquí la suma también tiene solo un número contable de términos distintos de cero, y es incondicionalmente convergente por la desigualdad de Cauchy-Schwarz.
Una base ortonormal de l 2 ( B ) está indexada por el conjunto B , dado por
Desigualdad de Bessel y fórmula de Parseval
Sea f 1 , …, f n un sistema ortonormal finito en H . Para un vector arbitrario x ∈ H , sea
Entonces ⟨ x , f k ⟩ = ⟨ y , f k ⟩ para cada k = 1, …, n . Se deduce que x − y es ortogonal a cada f k , por lo tanto x − y es ortogonal a y . Utilizando la identidad pitagórica dos veces, se deduce que
Sea { f i }, i ∈ I , un sistema ortonormal arbitrario en H . Aplicando la desigualdad anterior a cada subconjunto finito J de I se obtiene la desigualdad de Bessel: [92] (según la definición de la suma de una familia arbitraria de números reales no negativos).
Geométricamente, la desigualdad de Bessel implica que la proyección ortogonal de x sobre el subespacio lineal generado por f i tiene una norma que no excede la de x . En dos dimensiones, esta es la afirmación de que la longitud del cateto de un triángulo rectángulo no puede exceder la longitud de la hipotenusa.
La desigualdad de Bessel es un paso previo al resultado más fuerte llamado identidad de Parseval , que rige el caso en el que la desigualdad de Bessel es en realidad una igualdad. Por definición, si { e k } k ∈ B es una base ortonormal de H , entonces cada elemento x de H puede escribirse como
Incluso si B es incontable, la desigualdad de Bessel garantiza que la expresión está bien definida y consta solo de una cantidad contable de términos distintos de cero. Esta suma se denomina expansión de Fourier de x , y los coeficientes individuales ⟨ x , e k ⟩ son los coeficientes de Fourier de x . La identidad de Parseval afirma entonces que [93]
Por el contrario, [93] si { e k } es un conjunto ortonormal tal que la identidad de Parseval se cumple para cada x , entonces { e k } es una base ortonormal.
Dimensión de Hilbert
Como consecuencia del lema de Zorn , todo espacio de Hilbert admite una base ortonormal; además, dos bases ortonormales cualesquiera del mismo espacio tienen la misma cardinalidad , llamada dimensión de Hilbert del espacio. [94] Por ejemplo, dado que l 2 ( B ) tiene una base ortonormal indexada por B , su dimensión de Hilbert es la cardinalidad de B (que puede ser un entero finito o un número cardinal contable o incontable ).
La dimensión de Hilbert no es mayor que la dimensión de Hamel (la dimensión habitual de un espacio vectorial). Las dos dimensiones son iguales si y solo si una de ellas es finita.
Como consecuencia de la identidad de Parseval, [95] si { e k } k ∈ B es una base ortonormal de H , entonces la función Φ : H → l 2 ( B ) definida por Φ( x ) = ⟨x, e k ⟩ k ∈ B es un isomorfismo isométrico de espacios de Hilbert: es una función lineal biyectiva tal que para todo x , y ∈ H . El número cardinal de B es la dimensión de Hilbert de H . Por lo tanto, todo espacio de Hilbert es isométricamente isomorfo a un espacio de secuencia l 2 ( B ) para algún conjunto B .
Espacios separables
Por definición, un espacio de Hilbert es separable siempre que contenga un subconjunto numerable denso. Junto con el lema de Zorn, esto significa que un espacio de Hilbert es separable si y solo si admite una base ortonormal numerable . Por lo tanto, todos los espacios de Hilbert separables de dimensión infinita son isométricamente isomorfos al espacio de sucesiones sumables al cuadrado.
En el pasado, a menudo se requería que los espacios de Hilbert fueran separables como parte de la definición. [96]
En la teoría cuántica de campos
La mayoría de los espacios utilizados en física son separables, y dado que todos ellos son isomorfos entre sí, a menudo se hace referencia a cualquier espacio de Hilbert separable de dimensión infinita como " el espacio de Hilbert" o simplemente "espacio de Hilbert". [97] Incluso en la teoría cuántica de campos , la mayoría de los espacios de Hilbert son de hecho separables, como lo estipulan los axiomas de Wightman . Sin embargo, a veces se argumenta que los espacios de Hilbert no separables también son importantes en la teoría cuántica de campos, aproximadamente porque los sistemas en la teoría poseen un número infinito de grados de libertad y cualquier producto tensorial de Hilbert infinito (de espacios de dimensión mayor que uno) es no separable. [98] Por ejemplo, un campo bosónico puede considerarse naturalmente como un elemento de un producto tensorial cuyos factores representan osciladores armónicos en cada punto del espacio. Desde esta perspectiva, el espacio de estados natural de un bosón podría parecer un espacio no separable. [98] Sin embargo, es sólo un pequeño subespacio separable del producto tensorial completo el que puede contener campos físicamente significativos (en los que se pueden definir los observables). Otro espacio de Hilbert no separable modela el estado de una colección infinita de partículas en una región ilimitada del espacio. Una base ortonormal del espacio está indexada por la densidad de las partículas, un parámetro continuo, y dado que el conjunto de densidades posibles es incontable, la base no es contable. [98]
Complementos y proyecciones ortogonales
Si S es un subconjunto de un espacio de Hilbert H , el conjunto de vectores ortogonales a S está definido por
El conjunto S ⊥ es un subespacio cerrado de H (se puede demostrar fácilmente usando la linealidad y continuidad del producto interno) y por lo tanto forma un espacio de Hilbert. Si V es un subespacio cerrado de H , entonces V ⊥ se llama complemento ortogonal de V . De hecho, cada x ∈ H puede entonces escribirse de forma única como x = v + w , con v ∈ V y w ∈ V ⊥ . Por lo tanto, H es la suma directa interna de Hilbert de V y V ⊥ .
El operador lineal P V : H → H que mapea x a v se llama proyección ortogonal sobre V . Existe una correspondencia biunívoca natural entre el conjunto de todos los subespacios cerrados de H y el conjunto de todos los operadores autoadjuntos acotados P tales que P 2 = P . Específicamente,
Teorema — La proyección ortogonal P V es un operador lineal autoadjunto en H de norma ≤ 1 con la propiedad P2
voltios= P V . Además, cualquier operador lineal autoadjunto E tal que E 2 = E tiene la forma P V , donde V es el rango de E . Para cada x en H , P V ( x ) es el único elemento v de V que minimiza la distancia ‖ x − v ‖ .
Esto proporciona la interpretación geométrica de P V ( x ) : es la mejor aproximación a x por elementos de V . [99]
Las proyecciones P U y P V se denominan mutuamente ortogonales si P U P V = 0 . Esto es equivalente a que U y V sean ortogonales como subespacios de H . La suma de las dos proyecciones P U y P V es una proyección solo si U y V son ortogonales entre sí, y en ese caso P U + P V = P U + V . [100] La proyección compuesta P U P V generalmente no es una proyección; de hecho, la proyección compuesta es una proyección si y solo si las dos proyecciones conmutan, y en ese caso P U P V = P U ∩ V . [101]
Al restringir el codominio al espacio de Hilbert V , la proyección ortogonal P V da lugar a una aplicación de proyección π : H → V ; es el adjunto de la aplicación de inclusión , lo que significa que para todo x ∈ V e y ∈ H .
La norma del operador de la proyección ortogonal P V sobre un subespacio cerrado distinto de cero V es igual a 1:
Todo subespacio cerrado V de un espacio de Hilbert es por tanto la imagen de un operador P de norma uno tal que P 2 = P . La propiedad de poseer operadores de proyección apropiados caracteriza a los espacios de Hilbert: [102]
- Un espacio de Banach de dimensión mayor que 2 es (isométricamente) un espacio de Hilbert si y solo si, para cada subespacio cerrado V , existe un operador P V de norma uno cuya imagen es V tal que P2
voltios= PV .
Si bien este resultado caracteriza la estructura métrica de un espacio de Hilbert, la estructura de un espacio de Hilbert como espacio vectorial topológico puede caracterizarse en términos de la presencia de subespacios complementarios: [103]
- Un espacio de Banach X es topológica y linealmente isomorfo a un espacio de Hilbert si y solo si, para cada subespacio cerrado V , existe un subespacio cerrado W tal que X es igual a la suma directa interna V ⊕ W .
El complemento ortogonal satisface algunos resultados más elementales. Es una función monótona en el sentido de que si U ⊂ V , entonces V ⊥ ⊆ U ⊥ con igualdad válida si y sólo si V está contenido en la clausura de U . Este resultado es un caso especial del teorema de Hahn-Banach . La clausura de un subespacio puede caracterizarse completamente en términos del complemento ortogonal: si V es un subespacio de H , entonces la clausura de V es igual a V ⊥⊥ . El complemento ortogonal es, por tanto, una conexión de Galois en el orden parcial de subespacios de un espacio de Hilbert. En general, el complemento ortogonal de una suma de subespacios es la intersección de los complementos ortogonales: [104]
Si los V i están además cerrados, entonces
Teoría espectral
Existe una teoría espectral bien desarrollada para operadores autoadjuntos en un espacio de Hilbert, que es aproximadamente análoga al estudio de matrices simétricas sobre los números reales o matrices autoadjuntas sobre los números complejos. [105] En el mismo sentido, se puede obtener una "diagonalización" de un operador autoadjunto como una suma adecuada (en realidad una integral) de operadores de proyección ortogonales.
El espectro de un operador T , denotado σ ( T ) , es el conjunto de números complejos λ tales que T − λ carece de una inversa continua. Si T está acotado, entonces el espectro es siempre un conjunto compacto en el plano complejo, y se encuentra dentro del disco | z | ≤ ‖ T ‖ . Si T es autoadjunto, entonces el espectro es real. De hecho, está contenido en el intervalo [ m , M ] donde
Además, tanto m como M están realmente contenidos dentro del espectro.
Los espacios propios de un operador T están dados por
A diferencia de lo que ocurre con las matrices finitas, no todos los elementos del espectro de T deben ser valores propios: el operador lineal T − λ puede carecer de inverso únicamente porque no es sobreyectivo. Los elementos del espectro de un operador en sentido general se conocen como valores espectrales . Dado que los valores espectrales no necesitan ser valores propios, la descomposición espectral suele ser más sutil que en dimensiones finitas.
Sin embargo, el teorema espectral de un operador autoadjunto T adopta una forma particularmente simple si, además, se supone que T es un operador compacto . El teorema espectral para operadores autoadjuntos compactos establece: [106]
- Un operador autoadjunto compacto T tiene solo una cantidad contable (o finita) de valores espectrales. El espectro de T no tiene ningún punto límite en el plano complejo excepto posiblemente cero. Los espacios propios de T descomponen H en una suma directa ortogonal: Además, si E λ denota la proyección ortogonal sobre el espacio propio H λ , entonces donde la suma converge con respecto a la norma en B( H ) .
Este teorema juega un papel fundamental en la teoría de ecuaciones integrales , ya que muchos operadores integrales son compactos, en particular aquellos que surgen de los operadores de Hilbert-Schmidt .
El teorema espectral general para operadores autoadjuntos implica un tipo de integral de Riemann-Stieltjes con valor de operador , en lugar de una suma infinita. [107] La familia espectral asociada a T asocia a cada número real λ un operador E λ , que es la proyección sobre el espacio nulo del operador ( T − λ ) + , donde la parte positiva de un operador autoadjunto se define por
Los operadores E λ son monótonos crecientes en relación con el orden parcial definido en los operadores autoadjuntos; los valores propios corresponden precisamente a las discontinuidades de salto. Uno de ellos es el teorema espectral, que afirma
La integral se entiende como una integral de Riemann-Stieltjes, convergente respecto de la norma en B( H ) . En particular, se tiene la representación integral escalar ordinaria
Una descomposición espectral algo similar se aplica a los operadores normales, aunque debido a que el espectro ahora puede contener números complejos no reales, la medida de Stieltjes valorada por el operador d E λ debe reemplazarse por una resolución de la identidad .
Una aplicación importante de los métodos espectrales es el teorema de mapeo espectral , que permite aplicar a un operador autoadjunto T cualquier función compleja continua f definida en el espectro de T formando la integral
El cálculo funcional continuo resultante tiene aplicaciones en particular para los operadores pseudodiferenciales . [108]
La teoría espectral de los operadores autoadjuntos no acotados es sólo marginalmente más difícil que la de los operadores acotados. El espectro de un operador no acotado se define exactamente de la misma manera que para los operadores acotados: λ es un valor espectral si el operador resolvente
no es un operador continuo bien definido. La autoadjunción de T todavía garantiza que el espectro sea real. Por lo tanto, la idea esencial de trabajar con operadores no acotados es mirar en cambio el resolvente R λ donde λ no es real. Este es un operador normal acotado , que admite una representación espectral que luego puede transferirse a una representación espectral del propio T. Se utiliza una estrategia similar, por ejemplo, para estudiar el espectro del operador de Laplace: en lugar de abordar el operador directamente, se mira como un resolvente asociado como un potencial de Riesz o un potencial de Bessel .
Una versión precisa del teorema espectral en este caso es: [109]
Teorema — Dado un operador autoadjunto densamente definido T en un espacio de Hilbert H , corresponde una resolución única de la identidad E en los conjuntos de Borel de R , tal que para todo x ∈ D ( T ) e y ∈ H . La medida espectral E se concentra en el espectro de T .
También existe una versión del teorema espectral que se aplica a operadores normales ilimitados.
En la cultura popular
En Gravity's Rainbow (1973), una novela de Thomas Pynchon , uno de los personajes se llama "Sammy Hilbert-Spaess", un juego de palabras con "Hilbert Space". La novela también hace referencia a los teoremas de incompletitud de Gödel . [110]
Véase también
- Espacio de Banach : espacio vectorial normado que es completo
- Espacio de Fock : espacio de estados de múltiples partículas
- Teorema fundamental de los espacios de Hilbert
- Espacio de Hadamard : espacio métrico geodésicamente completo de curvatura no positivaPages displaying wikidata descriptions as a fallback
- Espacio de Hausdorff – Tipo de espacio topológico
- Álgebra de Hilbert
- Módulo C* de Hilbert : objetos matemáticos que generalizan la noción de espacios de Hilbert
- Variedad de Hilbert : Variedad modelada a partir de espacios de Hilbert
- L-semiproducto interno – Generalización de productos internos que se aplica a todos los espacios normados
- Espacio vectorial topológico localmente convexo : un espacio vectorial con una topología definida por conjuntos abiertos convexos
- Teoría de operadores – Campo de estudio matemático
- Topologías de operadores : topologías en el conjunto de operadores en un espacio de Hilbert
- Espacio de estados cuánticos : espacio matemático que representa sistemas cuánticos físicos
- Espacio de Hilbert manipulado : construcción que vincula el estudio de los valores propios "limitados" y continuos en el análisis funcional
- Espacio vectorial topológico – Espacio vectorial con noción de proximidad
Observaciones
- ^ En algunas convenciones, los productos internos son lineales en sus segundos argumentos.
- ^ Los valores propios del núcleo de Fredholm son 1/la , que tienden a cero.
Notas
- ^ Axler 2014, pág. 164 §6.2
- ^ Sin embargo, algunas fuentes llaman a los espacios de dimensión finita con estas propiedades espacios pre-Hilbert, reservando el término "espacio de Hilbert" para los espacios de dimensión infinita; véase, por ejemplo, Levitan 2001.
- ^ Marsden 1974, §2.8
- ^ El material matemático de esta sección se puede encontrar en cualquier buen libro de texto sobre análisis funcional, como Dieudonné (1960), Hewitt y Stromberg (1965), Reed y Simon (1980) o Rudin (1987).
- ^ Schaefer y Wolff 1999, págs. 122-202.
- ^ Dieudonné 1960, §6.2
- ^ Romano 2008, pág. 327
- ^ Roman 2008, pág. 330 Teorema 13.8
- ^ ab Stein y Shakarchi 2005, pág. 163
- ^ Dieudonné 1960
- ^ En gran parte, a partir del trabajo de Hermann Grassmann , a instancias de August Ferdinand Möbius (Boyer y Merzbach 1991, pp. 584-586). La primera explicación axiomática moderna de los espacios vectoriales abstractos apareció en última instancia en la explicación de Giuseppe Peano de 1888 (Grattan-Guinness 2000, §5.2.2; O'Connor y Robertson 1996).
- ^ Una descripción detallada de la historia de los espacios de Hilbert se puede encontrar en Bourbaki 1987.
- ^ Schmidt 1908
- ^ Titchmarsh 1946, §IX.1
- ^ Lebesgue 1904. Se pueden encontrar más detalles sobre la historia de la teoría de la integración en Bourbaki (1987) y Saks (2005).
- ^ Bourbaki 1987.
- ^ Dunford y Schwartz 1958, §IV.16
- ^ En Dunford & Schwartz (1958, §IV.16), el resultado de que cada funcional lineal en L 2 [0,1] está representado por integración se atribuye conjuntamente a Fréchet (1907) y Riesz (1907). El resultado general de que el dual de un espacio de Hilbert se identifica con el espacio de Hilbert mismo se puede encontrar en Riesz (1934).
- ^ por Neumann 1929.
- ^ Kline 1972, pág. 1092
- ^ Hilbert, Nordheim y von Neumann 1927
- ^ desde Weyl 1931.
- ^ Prugovečki 1981, págs. 1-10.
- ^ Por von Neumann 1932
- ^ Peres 1993, págs. 79–99.
- ^ Murphy 1990, pág. 112
- ^ Murphy 1990, pág. 72
- ^ Halmos 1957, Sección 42.
- ^ Hewitt y Stromberg 1965.
- ^ Abramowitz, Milton ; Stegun, Irene Ann , eds. (1983) [junio de 1964]. "Capítulo 22". Manual de funciones matemáticas con fórmulas, gráficos y tablas matemáticas . Serie de Matemáticas Aplicadas. Vol. 55 (Novena reimpresión con correcciones adicionales de la décima impresión original con correcciones (diciembre de 1972); primera ed.). Washington DC; Nueva York: Departamento de Comercio de los Estados Unidos, Oficina Nacional de Normas; Dover Publications. pág. 773. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
- ^ desde Bers, John y Schechter 1981.
- ^ Giusti 2003.
- ^ Stein 1970
- ^ Se pueden encontrar detalles en Warner (1983).
- ^ Una referencia general sobre los espacios de Hardy es el libro Duren (1970).
- ^ Krantz 2002, §1.4
- ^ Krantz 2002, §1.5
- ^ Young 1988, Capítulo 9.
- ^ Pedersen 1995, §4.4
- ^ Se pueden encontrar más detalles sobre los métodos de elementos finitos desde este punto de vista en Brenner y Scott (2005).
- ^ Brezis 2010, sección 9.5
- ^ Evans 1998
- ^ Pathria (1996), Capítulos 2 y 3
- ^ Einsiedler & Ward (2011), Proposición 2.14.
- ^ Reed y Simon 1980
- ^ Un tratamiento de las series de Fourier desde este punto de vista está disponible, por ejemplo, en Rudin (1987) o Folland (2009).
- ^ Halmos 1957, §5
- ^ Bachman, Narici y Beckenstein 2000
- ^ Stein y Weiss 1971, §IV.2.
- ^ Lanczos 1988, págs. 212-213
- ^ Lanczos 1988, Ecuación 4-3.10
- ^ La referencia clásica para los métodos espectrales es Courant y Hilbert 1953. Un relato más actualizado es Reed y Simon 1975.
- ^ Kac 1966
- ^ por Neumann 1955
- ^ Holevo 2001, pág. 17
- ^ Rieffel y Polak 2011, pág. 55
- ^ Peres 1993, pág. 101
- ^ Peres 1993, pág. 73
- ^ Nielsen y Chuang 2000, pág. 90
- ^ Billingsley (1986), pág. 477, ejemplo 34.13}}
- ^ Stapleton 1995
- ^ Hewitt y Stromberg (1965), Ejercicio 16.45.
- ^ Karatzas y Shreve 2019, Capítulo 3
- ^ Stroock (2011), Capítulo 8.
- ^ Hermann Weyl (2009), "Mente y naturaleza", Mente y naturaleza: escritos seleccionados sobre filosofía, matemáticas y física , Princeton University Press.
- ^ Berthier, M. (2020), "Geometría de la percepción del color. Parte 2: colores percibidos a partir de estados cuánticos reales y rebit de Hering", The Journal of Mathematical Neuroscience , 10 (1): 14, doi : 10.1186/s13408-020-00092-x , PMC 7481323 , PMID 32902776 .
- ^ Reed y Simon 1980, Teorema 12.6
- ^ Reed y Simon 1980, pág. 38
- ^ Joven 1988, pág. 23.
- ^ Clarkson 1936.
- ^ Rudin 1987, Teorema 4.10
- ^ Dunford y Schwartz 1958, II.4.29
- ^ Rudin 1987, Teorema 4.11
- ^ Blanchet, Gérard; Charbit, Maurice (2014). Procesamiento de imágenes y señales digitales con MATLAB . Vol. 1 (segunda edición). Nueva Jersey: Wiley. Págs. 349–360. ISBN. 978-1848216402.
- ^ Weidmann 1980, Teorema 4.8
- ^ Peres 1993, págs. 77–78.
- ^ Weidmann (1980), Ejercicio 4.11.
- ^ Weidmann 1980, §4.5
- ^ Buttazzo, Giaquinta y Hildebrandt 1998, Teorema 5.17
- ^ Halmos 1982, Problema 52, 58
- ^ Rudin 1973
- ^ Trèves 1967, Capítulo 18
- ^ Una referencia general para esta sección es Rudin (1973), capítulo 12.
- ^ Véase Prugovečki (1981), Reed y Simon (1980, Capítulo VIII) y Folland (1989).
- ^ Prugovečki 1981, III, §1.4
- ^ Dunford y Schwartz 1958, IV.4.17-18
- ^ Weidmann 1980, §3.4
- ^ Kadison y Ringrose 1983, Teorema 2.6.4
- ^ Dunford y Schwartz 1958, §IV.4.
- ^ Romano 2008, pág. 218
- ^ Rudin 1987, Definición 3.7
- ^ Para el caso de conjuntos de índices finitos, véase, por ejemplo, Halmos 1957, §5. Para conjuntos de índices infinitos, véase Weidmann 1980, Teorema 3.6.
- ^ de Hewitt y Stromberg (1965), Teorema 16.26.
- ^ Levitan 2001. Muchos autores, como Dunford y Schwartz (1958, §IV.4), se refieren a esto simplemente como la dimensión. A menos que el espacio de Hilbert sea de dimensión finita, esto no es lo mismo que su dimensión como espacio lineal (la cardinalidad de una base de Hamel).
- ^ Hewitt y Stromberg (1965), Teorema 16.29.
- ^ Prugovečki 1981, I, §4.2
- ^ von Neumann (1955) define un espacio de Hilbert a través de una base de Hilbert contable, lo que equivale a un isomorfismo isométrico con l 2 . La convención aún persiste en los tratamientos más rigurosos de la mecánica cuántica; véase por ejemplo Sobrino 1996, Apéndice B.
- ^ abc Streater y Wightman 1964, págs. 86-87
- ^ Young 1988, Teorema 15.3
- ^ von Neumann 1955, teorema 16
- ^ von Neumann 1955, teorema 14
- ^ Kakutani 1939
- ^ Lindenstrauss y Tzafriri 1971
- ^ Halmos 1957, §12
- ^ Una explicación general de la teoría espectral en espacios de Hilbert se puede encontrar en Riesz y Sz.-Nagy (1990). Una explicación más sofisticada en el lenguaje de las C*-álgebras se encuentra en Rudin (1973) o Kadison y Ringrose (1997).
- ^ Véase, por ejemplo, Riesz y Sz.-Nagy (1990, Capítulo VI) o Weidmann 1980, Capítulo 7. Este resultado ya era conocido por Schmidt (1908) en el caso de operadores que surgen de núcleos integrales.
- ^ Riesz y Sz.-Nagy 1990, §§107-108
- ^ Shubin 1987
- ^ Rudin 1973, Teorema 13.30.
- ^ Pynchon, Thomas (1973). El arco iris de la gravedad . Viking Press. págs. 217, 275. ISBN. 978-0143039945.
Referencias
- Axler, Sheldon (18 de diciembre de 2014), Linear Algebra Done Right , Undergraduate Texts in Mathematics (3.ª ed.), Springer Publishing (publicado en 2015), pág. 296, ISBN 978-3-319-11079-0
- Bachman, George; Narici, Lorenzo; Beckenstein, Edward (2000), Análisis de Fourier y wavelets , Universitext, Berlín, Nueva York: Springer-Verlag , ISBN 978-0-387-98899-3, Sr. 1729490.
- Bers, Lipman ; John, Fritz ; Schechter, Martin (1981), Ecuaciones diferenciales parciales , American Mathematical Society, ISBN 978-0-8218-0049-2.
- Billingsley, Patrick (1986), Probabilidad y medida , Wiley.
- Bourbaki, Nicolas (1986), Teorías espectrales , Elementos de matemáticas, Berlín: Springer-Verlag, ISBN 978-0-201-00767-1.
- Bourbaki, Nicolas (1987), Espacios vectoriales topológicos , Elementos de matemáticas, Berlín: Springer-Verlag, ISBN 978-3-540-13627-9.
- Boyer, Carl Benjamin ; Merzbach, Uta C (1991), Una historia de las matemáticas (2.ª ed.), John Wiley & Sons, Inc., ISBN 978-0-471-54397-8.
- Brenner, S.; Scott, RL (2005), La teoría matemática de los métodos de elementos finitos (2.ª ed.), Springer, ISBN 978-0-387-95451-6.
- Brezis, Haim (2010), Análisis funcional, espacios de Sobolev y ecuaciones diferenciales parciales , Springer.
- Buttazzo, Giuseppe; Giaquinta, Mariano; Hildebrandt, Stefan (1998), Problemas variacionales unidimensionales , Oxford Lecture Series in Mathematics and its Applications, vol. 15, The Clarendon Press Oxford University Press, ISBN 978-0-19-850465-8, Sr. 1694383.
- Clarkson, JA (1936), "Espacios uniformemente convexos", Trans. Amer. Math. Soc. , 40 (3): 396–414, doi : 10.2307/1989630 , JSTOR 1989630.
- Courant, Richard ; Hilbert, David (1953), Métodos de física matemática, vol. I , Interscience.
- Dieudonné, Jean (1960), Fundamentos del análisis moderno , Academic Press.
- Dirac, PAM (1930), Los principios de la mecánica cuántica , Oxford: Clarendon Press.
- Dunford, N.; Schwartz, JT (1958), Operadores lineales, partes I y II , Wiley-Interscience.
- Duren, P. (1970), Teoría de los espacios H p , Nueva York: Academic Press.
- Einsiedler, Manfred; Ward, Thomas (2011), Teoría ergódica con vistas a la teoría de números , Springer.
- Evans, LC (1998), Ecuaciones diferenciales parciales , Providence: American Mathematical Society, ISBN 0-8218-0772-2.
- Folland, Gerald B. (2009), Análisis de Fourier y su aplicación (reimpresión de Wadsworth y Brooks/Cole 1992 ed.), American Mathematical Society Bookstore, ISBN 978-0-8218-4790-9.
- Folland, Gerald B. (1989), Análisis armónico en el espacio de fases , Annals of Mathematics Studies, vol. 122, Princeton University Press, ISBN 978-0-691-08527-2.
- Fréchet, Maurice (1907), "Sur les ensembles de fonctions et les opérations linéaires", CR Acad. Ciencia. París , 144 : 1414-1416.
- Fréchet, Maurice (1904), "Sur les opérations linéaires", Transacciones de la Sociedad Matemática Estadounidense , 5 (4): 493–499, doi :10.2307/1986278, JSTOR 1986278.
- Giusti, Enrico (2003), Métodos directos en el cálculo de variaciones , World Scientific, ISBN 978-981-238-043-2.
- Grattan-Guinness, Ivor (2000), La búsqueda de raíces matemáticas, 1870-1940 , Princeton Paperbacks, Princeton University Press , ISBN 978-0-691-05858-0, Sr. 1807717.
- Halmos, Paul (1957), Introducción al espacio de Hilbert y la teoría de la multiplicidad espectral , Chelsea Pub. Co
- Halmos, Paul (1982), Un libro de problemas espaciales de Hilbert , Springer-Verlag, ISBN 978-0-387-90685-0.
- Hewitt, Edwin; Stromberg, Karl (1965), Análisis real y abstracto , Nueva York: Springer-Verlag.
- Hilbert, David ; Nordheim, Lothar Wolfgang ; von Neumann, John (1927), "Über die Grundlagen der Quantenmechanik", Mathematische Annalen , 98 : 1–30, doi :10.1007/BF01451579, S2CID 120986758.
- Holevo, Alexander S. (2001), Estructura estadística de la teoría cuántica , Apuntes de clases de física, Springer, ISBN 3-540-42082-7, OCLC 318268606.
- Kac, Mark (1966), "¿Se puede oír la forma de un tambor?", American Mathematical Monthly , 73 (4, parte 2): 1–23, doi :10.2307/2313748, JSTOR 2313748.
- Kadison, Richard V.; Ringrose, John R. (1997), Fundamentos de la teoría de álgebras de operadores. Vol. I , Graduate Studies in Mathematics, vol. 15, Providence, RI: American Mathematical Society , ISBN 978-0-8218-0819-1, Sr. 1468229.
- Kadison, Richard V.; Ringrose, John R. (1983), Fundamentos de la teoría de álgebras de operadores, vol. I: Teoría elemental , Nueva York: Academic Press, Inc.
- Karatzas, Ioannis; Shreve, Steven (2019), Movimiento browniano y cálculo estocástico (2.ª ed.), Springer, ISBN 978-0-387-97655-6
- Kakutani, Shizuo (1939), "Algunas caracterizaciones del espacio euclidiano", Revista japonesa de matemáticas , 16 : 93–97, doi : 10.4099/jjm1924.16.0_93 , MR 0000895.
- Kline, Morris (1972), Pensamiento matemático desde la antigüedad hasta los tiempos modernos, Volumen 3 (3.ª ed.), Oxford University Press (publicado en 1990), ISBN 978-0-19-506137-6.
- Kolmogorov, Andrey ; Fomin, Sergei V. (1970), Introducción al análisis real (edición revisada en inglés, trad. de Richard A. Silverman (1975) ed.), Dover Press, ISBN 978-0-486-61226-3.
- Krantz, Steven G. (2002), Teoría de funciones de varias variables complejas , Providence, RI: American Mathematical Society , ISBN 978-0-8218-2724-6.
- Lanczos, Cornelius (1988), Análisis aplicado (reimpresión de la edición de Prentice-Hall de 1956), Dover Publications, ISBN 978-0-486-65656-4.
- Lebesgue, Henri (1904), Leçons sur l'intégration et la recherche des fonctions primitives, Gauthier-Villars.
- Levitan, BM (2001) [1994], "Espacio de Hilbert", Enciclopedia de Matemáticas , EMS Press.
- Lindenstrauss, J.; Tzafriri, L. (1971), "Sobre el problema de los subespacios complementados", Israel Journal of Mathematics , 9 (2): 263–269, doi :10.1007/BF02771592, ISSN 0021-2172, MR 0276734, S2CID 119575718.
- Marsden, Jerrold E. (1974), Análisis clásico elemental , WH Freeman and Co., MR 0357693.
- Murphy, Gerald J. (1990), C*-álgebras y teoría de operadores , Academic Press, ISBN 0-12-511360-9.
- von Neumann, John (1929), "Allgemeine Eigenwerttheorie Hermitescher Funktionaloperatoren", Mathematische Annalen , 102 : 49–131, doi :10.1007/BF01782338, S2CID 121249803.
- von Neumann, John (1932), "Aplicaciones físicas de la hipótesis ergódica", Proc Natl Acad Sci USA , 18 (3): 263–266, Bibcode :1932PNAS...18..263N, doi : 10.1073/pnas.18.3.263 , JSTOR 86260, PMC 1076204 , PMID 16587674.
- von Neumann, John (1955), Fundamentos matemáticos de la mecánica cuántica , Princeton Landmarks in Mathematics, traducido por Beyer, Robert T., Princeton University Press (publicado en 1996), ISBN 978-0-691-02893-4, Sr. 1435976.
- Nielsen, Michael A. ; Chuang, Isaac L. (2000), Computación cuántica e información cuántica (1.ª ed.), Cambridge: Cambridge University Press , ISBN 978-0-521-63503-5, OCLC 634735192.
- O'Connor, John J.; Robertson, Edmund F. (1996), "Espacios lineales abstractos", Archivo de Historia de las Matemáticas de MacTutor , Universidad de St Andrews
- Pathria, RK (1996), Mecánica estadística (2.ª ed.), Academic Press.
- Pedersen, Gert (1995), Analysis Now , Textos de posgrado en matemáticas, vol. 118, Berlín, Nueva York: Springer-Verlag , ISBN 978-1-4612-6981-6, Sr. 0971256
- Peres, Asher (1993), Teoría cuántica: conceptos y métodos , Kluwer, ISBN 0-7923-2549-4, OCLC 28854083
- Prugovečki, Eduard (1981), Mecánica cuántica en el espacio de Hilbert (2.ª ed.), Dover (publicado en 2006), ISBN 978-0-486-45327-9.
- Reed, Michael ; Simon, Barry (1980), Análisis funcional (vol I de 4 vols) , Métodos de física matemática moderna, Academic Press, ISBN 978-0-12-585050-6.
- Reed, Michael ; Simon, Barry (1975), Análisis de Fourier, autoadjunción (vol II de 4 vols) , Métodos de física matemática moderna, Academic Press, ISBN 9780125850025.
- Rieffel, Eleanor G. ; Polak, Wolfgang H. (4 de marzo de 2011), Computación cuántica: una introducción sencilla , MIT Press, ISBN 978-0-262-01506-6.
- Riesz, Frigyes (1907), "Sur une espèce de Géométrie analytique des systèmes de fonctions sommables", CR Acad. Ciencia. París , 144 : 1409-1411.
- Riesz, Frigyes (1934), "Zur Theorie des Hilbertschen Raumes", Acta Sci. Matemáticas. Szeged , 7 : 34–38.
- Riesz, Frigyes ; Sz.-Nagy, Béla (1990), Análisis funcional , Dover, ISBN 978-0-486-66289-3.
- Roman, Stephen (2008), Álgebra lineal avanzada , Textos de posgrado en matemáticas (tercera edición), Springer, ISBN 978-0-387-72828-5
- Rudin, Walter (1973). Análisis funcional . Serie internacional de matemáticas puras y aplicadas. Vol. 25 (primera edición). Nueva York, NY: McGraw-Hill Science/Engineering/Math . ISBN 9780070542259.
- Rudin, Walter (1987), Análisis real y complejo , McGraw-Hill, ISBN 978-0-07-100276-9.
- Saks, Stanisław (2005), Teoría de la integral (2.ª edición de Dover), Dover, ISBN 978-0-486-44648-6; Monografje Matematyczne , publicado originalmente , vol. 7, Varsovia, 1937.
- Schaefer, Helmut H. ; Wolff, Manfred P. (1999). Espacios vectoriales topológicos . GTM . Vol. 8 (Segunda ed.). Nueva York, NY: Springer New York Imprenta Springer. ISBN 978-1-4612-7155-0.OCLC 840278135 .
- Schmidt, Erhard (1908), "Über die Auflösung linearer Gleichungen mit unendlich vielen Unbekannten", Rend. Circo. Estera. Palermo , 25 : 63–77, doi : 10.1007/BF03029116, S2CID 120666844.
- Shubin, MA (1987), Operadores pseudodiferenciales y teoría espectral , Springer Series in Soviet Mathematics, Berlín, Nueva York: Springer-Verlag , ISBN 978-3-540-13621-7, Sr. 0883081.
- Sobrino, Luis (1996), Elementos de mecánica cuántica no relativista , River Edge, Nueva Jersey: World Scientific Publishing Co. Inc., Bibcode :1996lnrq.book.....S, doi :10.1142/2865, ISBN 978-981-02-2386-1, Sr. 1626401.
- Stapleton, James (1995), Modelos estadísticos lineales , John Wiley and Sons.
- Stewart, James (2006), Cálculo: conceptos y contextos (3.ª ed.), Thomson/Brooks/Cole.
- Stein, E (1970), Integrales singulares y propiedades de diferenciabilidad de funciones , Princeton Univ. Press, ISBN 978-0-691-08079-6.
- Stein, Elias ; Weiss, Guido (1971), Introducción al análisis de Fourier en espacios euclidianos , Princeton, NJ: Princeton University Press, ISBN 978-0-691-08078-9.
- Stein, E; Shakarchi, R (2005), Análisis real, teoría de la medida, integración y espacios de Hilbert , Princeton University Press.
- Streater, Ray ; Wightman, Arthur (1964), PCT, Spin and Statistics and All That , WA Benjamin, Inc.
- Stroock, Daniel (2011), Teoría de la probabilidad: una visión analítica (2.ª ed.), Cambridge University Press.
- Teschl, Gerald (2009). Métodos matemáticos en mecánica cuántica; con aplicaciones a los operadores de Schrödinger. Providence : American Mathematical Society . ISBN 978-0-8218-4660-5..
- Titchmarsh, Edward Charles (1946), Expansiones de funciones propias, parte 1 , Universidad de Oxford: Clarendon Press.
- Trèves, François (1967), Espacios vectoriales topológicos, distribuciones y núcleos , Academic Press.
- Warner, Frank (1983), Fundamentos de variedades diferenciables y grupos de Lie , Berlín, Nueva York: Springer-Verlag , ISBN 978-0-387-90894-6.
- Weidmann, Joachim (1980), Operadores lineales en espacios de Hilbert , Textos de Graduado en Matemáticas, vol. 68, Berlín, Nueva York: Springer-Verlag , ISBN 978-0-387-90427-6, Sr. 0566954.
- Weyl, Hermann (1931), La teoría de grupos y la mecánica cuántica (edición en inglés de 1950), Dover Press, ISBN 978-0-486-60269-1.
- Young, Nicholas (1988), Una introducción al espacio de Hilbert , Cambridge University Press, ISBN 978-0-521-33071-8, Zbl0645.46024 .
Enlaces externos
- "Espacio de Hilbert", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
- El espacio de Hilbert en Mathworld
- 245B, notas 5: Espacios de Hilbert por Terence Tao



























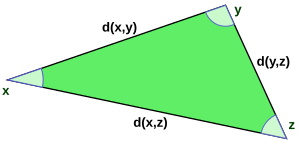

























![{\displaystyle -{\frac {\mathrm {d} }{\mathrm {d} x}}\left[p(x){\frac {\mathrm {d} y}{\mathrm {d} x}}\right]+q(x)y=\lambda w(x)y}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d4e93c4082311667644e8554f78774b963ffb0e)






















![{\displaystyle E[X|{\mathcal {F}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bda70bf9ef6fa0e4a2acbc19572fc775644a4225)












![{\displaystyle E\left[\left(\int _{0}^{t}H_{s}dM_{s}\right)^{2}\right]=E\left[\int _{0}^{t}H_{s}^{2}d\langle M\rangle _{s}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ddc67bd90763bdda507f2bfd375f0106f921894)









































































