Teorema de Ramsey
En combinatoria , el teorema de Ramsey , en una de sus formas de teoría de grafos , establece que se encontrarán camarillas monocromáticas en cualquier etiquetado de aristas (con colores) de un grafo completo suficientemente grande . Para demostrar el teorema para dos colores (por ejemplo, azul y rojo), sean r y s dos enteros positivos cualesquiera . [a] El teorema de Ramsey establece que existe un entero positivo mínimo R ( r , s ) para el cual cada coloración azul-roja de las aristas del grafo completo en R ( r , s ) vértices contiene una camarilla azul en r vértices o una camarilla roja en s vértices. (Aquí R ( r , s ) significa un entero que depende tanto de r como de s ).
El teorema de Ramsey es un resultado fundacional de la combinatoria. La primera versión de este resultado fue demostrada por Frank Ramsey . Con ello se inició la teoría combinatoria hoy llamada teoría de Ramsey , que busca la regularidad en medio del desorden: condiciones generales para la existencia de subestructuras con propiedades regulares. En esta aplicación se trata de la existencia de subconjuntos monocromáticos , es decir, subconjuntos de aristas conexas de un solo color.
Una extensión de este teorema se aplica a cualquier número finito de colores, en lugar de solo dos. Más precisamente, el teorema establece que para cualquier número dado de colores, c , y cualquier entero dado n 1 , …, n c , hay un número, R ( n 1 , …, n c ) , tal que si las aristas de un grafo completo de orden R ( n 1 , …, n c ) están coloreadas con c colores diferentes, entonces para algún i entre 1 y c , debe contener un subgrafo completo de orden n i cuyas aristas sean todas de color i . El caso especial anterior tiene c = 2 (y n 1 = r y n 2 = s ).
Ejemplos
R(3, 3) = 6

Debido al principio del casillero, hay al menos 3 aristas del mismo color (púrpura discontinuo) desde un vértice arbitrario v . Llamando r , s y t a 3 de los vértices que terminan estas aristas , si la arista rs , st o tr (negra sólida) tuviera este color, completaría el triángulo con v . Pero si no, cada una debe ser de color opuesto, completando primero el triángulo rst de ese color.
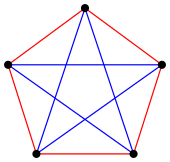
Supongamos que las aristas de un grafo completo en 6 vértices están coloreadas de rojo y azul. Elija un vértice, v . Hay 5 aristas incidentes a v y entonces (por el principio del palomar ) al menos 3 de ellas deben ser del mismo color. Sin pérdida de generalidad podemos suponer que al menos 3 de estas aristas, que conectan el vértice, v , a los vértices, r , s y t , son azules. (Si no, intercambiemos rojo y azul en lo que sigue.) Si alguna de las aristas, ( rs ) , ( rt ) , ( st ) , también es azul, entonces tenemos un triángulo completamente azul. Si no, entonces esas tres aristas son todas rojas y tenemos un triángulo completamente rojo. Dado que este argumento funciona para cualquier coloración, cualquier K 6 contiene un K 3 monocromático y, por lo tanto, R (3, 3) ≤ 6 . La versión popular de esto se llama el teorema de amigos y extraños .
Una prueba alternativa funciona contando dos veces . Es como sigue: Cuenta el número de triples ordenados de vértices, x , y , z , tales que la arista, ( xy ) , es roja y la arista, ( yz ) , es azul. En primer lugar, cualquier vértice dado será el medio de 0 × 5 = 0 (todas las aristas del vértice son del mismo color), 1 × 4 = 4 (cuatro son del mismo color, una es del otro color), o 2 × 3 = 6 (tres son del mismo color, dos son del otro color) de tales triples. Por lo tanto, hay como máximo 6 × 6 = 36 de tales triples. En segundo lugar, para cualquier triángulo no monocromático ( xyz ) , existen precisamente dos de tales triples. Por lo tanto, hay como máximo 18 triángulos no monocromáticos. Por lo tanto, al menos 2 de los 20 triángulos en el K 6 son monocromáticos.
Por el contrario, es posible bicolorizar un K 5 sin crear ningún K 3 monocromático , lo que demuestra que R (3, 3) > 5 . La coloración única [b] se muestra a la derecha. Por lo tanto, R (3, 3) = 6 .
La tarea de demostrar que R (3, 3) ≤ 6 fue uno de los problemas de la Competición Matemática William Lowell Putnam en 1953, así como de la Olimpiada Húngara de Matemáticas en 1947.
Un ejemplo multicolor:R(3, 3, 3) = 17
Un número de Ramsey multicolor es un número de Ramsey que utiliza 3 o más colores. Existen (salvo simetrías) solo dos números de Ramsey multicolor no triviales para los que se conoce el valor exacto, a saber, R (3, 3, 3) = 17 y R (3, 3, 4) = 30. [ 1]
Supongamos que tenemos una coloración de aristas de un grafo completo usando 3 colores, rojo, verde y azul. Supongamos además que la coloración de aristas no tiene triángulos monocromáticos. Seleccione un vértice v . Considere el conjunto de vértices que tienen una arista roja en el vértice v . Esto se llama el vecindario rojo de v . El vecindario rojo de v no puede contener ninguna arista roja, ya que de lo contrario habría un triángulo rojo que constaría de los dos puntos finales de esa arista roja y el vértice v . Por lo tanto, la coloración de aristas inducida en el vecindario rojo de v tiene aristas coloreadas con solo dos colores, a saber, verde y azul. Dado que R (3, 3) = 6 , el vecindario rojo de v puede contener como máximo 5 vértices. De manera similar, los vecindarios verde y azul de v pueden contener como máximo 5 vértices cada uno. Como cada vértice, excepto v , se encuentra en uno de los vecindarios rojo, verde o azul de v , el grafo completo puede tener como máximo 1 + 5 + 5 + 5 = 16 vértices. Por lo tanto, tenemos R (3, 3, 3) ≤ 17 .
Para ver que R (3, 3, 3) = 17 , basta con dibujar una coloración de aristas en el grafo completo sobre 16 vértices con 3 colores que evite los triángulos monocromáticos. Resulta que hay exactamente dos coloraciones de este tipo en K 16 , las llamadas coloraciones no torcidas y torcidas. Ambas coloraciones se muestran en las figuras de la derecha, con la coloración no torcida a la izquierda y la coloración torcida a la derecha.
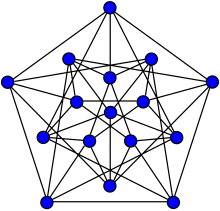
Si seleccionamos cualquier color, ya sea del color sin torcer o torcido, en K 16 y consideramos el gráfico cuyos bordes son precisamente aquellos que tienen el color especificado, obtendremos el gráfico de Clebsch .
Se sabe que hay exactamente dos coloraciones de aristas con 3 colores en K 15 que evitan triángulos monocromáticos, que pueden construirse eliminando cualquier vértice de las coloraciones sin torcer y torcer en K 16 , respectivamente.
También se sabe que hay exactamente 115 coloraciones de aristas con 3 colores en K 14 que evitan los triángulos monocromáticos, siempre que consideremos como iguales las coloraciones de aristas que difieren por una permutación de los colores.
Prueba
Estuche de 2 colores
El teorema para el caso de 2 colores se puede demostrar por inducción en r + s . [2] De la definición se desprende claramente que para todo n , R ( n , 2) = R (2, n ) = n . Esto inicia la inducción. Demostramos que R ( r , s ) existe hallando un límite explícito para él. Por la hipótesis inductiva, R ( r − 1, s ) y R ( r , s − 1) existen.
- Lema 1.
Demostración. Consideremos un grafo completo de R ( r − 1, s ) + R ( r , s − 1) vértices cuyas aristas están coloreadas con dos colores. Elijamos un vértice v del grafo y partamos los vértices restantes en dos conjuntos M y N , de modo que para cada vértice w , w esté en M si la arista ( vw ) es azul, y w esté en N si ( vw ) es rojo. Como el grafo tiene vértices, se sigue que o bien En el primer caso, si M tiene una K s roja , entonces también la tiene el grafo original y hemos terminado. De lo contrario, M tiene una K r − 1 azul y, por lo tanto, tiene una K r azul según la definición de M . El último caso es análogo. Por lo tanto, la afirmación es verdadera y hemos completado la demostración para 2 colores.
En este caso de 2 colores, si R ( r − 1, s ) y R ( r , s − 1) son ambos pares, la desigualdad de inducción se puede fortalecer a: [3]
Demostración . Supóngase que p = R ( r − 1, s ) y q = R ( r , s − 1) son ambos pares. Sea t = p + q − 1 y considérese un grafo bicolor de t vértices. Si d i es el grado del i -ésimo vértice en el subgrafo azul, entonces, por el lema del apretón de manos , es par. Dado que t es impar, debe haber un d i par . Supóngase sin pérdida de generalidad que d 1 es par, y que M y N son los vértices incidentes al vértice 1 en los subgrafos azul y rojo, respectivamente. Entonces, tanto y son pares. Por el principio del Pigeonhole , o bien o bien Como es par y p – 1 es impar, la primera desigualdad se puede fortalecer, por lo que o bien o bien Supongamos Entonces, o bien el subgrafo M tiene un K s rojo y la prueba está completa, o bien tiene un K r – 1 azul que junto con el vértice 1 forma un K r azul . El caso se trata de manera similar.
Estuche de más colores
Lema 2. Si c > 2 , entonces
Prueba. Consideremos un grafo completo de vértices y coloreemos sus aristas con c colores. Ahora 'volvámonos daltónicos' e imaginemos que c − 1 y c son del mismo color. Por lo tanto, el grafo ahora está ( c − 1) -coloreado. Debido a que la definición de tal grafo contiene o bien un K n i coloreado monocromáticamente con el color i para algún 1 ≤ i ≤ c − 2 o un K R ( n c − 1 , n c ) -coloreado en el 'color borroso'. En el primer caso hemos terminado. En el segundo caso, recuperamos la vista de nuevo y vemos que a partir de la definición de R ( n c − 1 , n c ) debemos tener o bien un ( c − 1) -monocromático K n c − 1 o un c -monocromo K n c . En cualquier caso, la prueba está completa.
El lema 1 implica que cualquier R ( r , s ) es finito. El lado derecho de la desigualdad del lema 2 expresa un número de Ramsey para c colores en términos de números de Ramsey para menos colores. Por lo tanto, cualquier R ( n 1 , …, n c ) es finito para cualquier número de colores. Esto demuestra el teorema.
Números de Ramsey
Los números R ( r , s ) en el teorema de Ramsey (y sus extensiones a más de dos colores) se conocen como números de Ramsey. El número de Ramsey R ( m , n ) da la solución al problema de la fiesta, que pregunta el número mínimo de invitados, R ( m , n ) , que deben ser invitados para que al menos m se conozcan entre sí o al menos n no se conozcan entre sí. En el lenguaje de la teoría de grafos, el número de Ramsey es el número mínimo de vértices, v = R ( m , n ) , tales que todos los grafos simples no dirigidos de orden v , contienen una camarilla de orden m , o un conjunto independiente de orden n . El teorema de Ramsey establece que tal número existe para todos los m y n .
Por simetría, es cierto que R ( m , n ) = R ( n , m ) . Se puede extraer un límite superior para R ( r , s ) de la prueba del teorema, y otros argumentos dan límites inferiores. (El primer límite inferior exponencial fue obtenido por Paul Erdős utilizando el método probabilístico .) Sin embargo, hay una gran brecha entre los límites inferiores más estrictos y los límites superiores más estrictos. También hay muy pocos números r y s para los que conocemos el valor exacto de R ( r , s ) .
Calcular un límite inferior L para R ( r , s ) generalmente requiere exhibir una coloración azul/roja del grafo K L −1 sin ningún subgrafo azul K r y ningún subgrafo rojo K s . Un contraejemplo de este tipo se llama grafo de Ramsey . Brendan McKay mantiene una lista de grafos de Ramsey conocidos. [4] Los límites superiores suelen ser considerablemente más difíciles de establecer: uno tiene que verificar todas las coloraciones posibles para confirmar la ausencia de un contraejemplo, o presentar un argumento matemático para su ausencia.
Complejidad computacional
Erdős nos pide que imaginemos una fuerza alienígena, mucho más poderosa que nosotros, que aterriza en la Tierra y exige el valor de R (5, 5) o destruirá nuestro planeta. En ese caso, afirma, deberíamos reunir a todos nuestros ordenadores y a todos nuestros matemáticos e intentar encontrar el valor. Pero supongamos, en cambio, que piden R (6, 6) . En ese caso, cree, deberíamos intentar destruir a los alienígenas. [5]
—Joel Spencer
Un programa informático sofisticado no necesita examinar todos los colores individualmente para eliminarlos todos; sin embargo, es una tarea computacional muy difícil que el software existente solo puede manejar en tamaños pequeños. Cada grafo completo K n tiene1/2n ( n − 1) aristas, por lo que habría un total de c n ( n -1)/2 grafos para buscar (para c colores) si se utiliza la fuerza bruta. [6] Por lo tanto, la complejidad para buscar todos los grafos posibles (mediante fuerza bruta ) es O ( c n 2 ) para c coloraciones y como máximo n nodos.
Es poco probable que la situación mejore con la llegada de las computadoras cuánticas . Uno de los algoritmos de búsqueda más conocidos para conjuntos de datos no estructurados muestra solo una aceleración cuadrática (cf. el algoritmo de Grover ) en relación con las computadoras clásicas, de modo que el tiempo de cálculo sigue siendo exponencial en el número de nodos. [7] [8]
Valores conocidos
Como se describió anteriormente, R (3, 3) = 6 . Es fácil demostrar que R (4, 2) = 4 , y, más generalmente, que R ( s , 2) = s para todo s : un grafo en s − 1 nodos con todas las aristas coloreadas de rojo sirve como contraejemplo y demuestra que R ( s , 2) ≥ s ; entre las coloraciones de un grafo en s nodos, la coloración con todas las aristas coloreadas de rojo contiene un subgrafo rojo de s nodos, y todas las demás coloraciones contienen un subgrafo azul de 2 nodos (es decir, un par de nodos conectados con una arista azul).
Usando desigualdades de inducción y el lema del apretón de manos , se puede concluir que R (4, 3) ≤ R (4, 2) + R (3, 3) − 1 = 9 , y por lo tanto R (4, 4) ≤ R (4, 3) + R (3, 4) ≤ 18 . Solo hay dos grafos (4, 4, 16) (es decir, 2-coloraciones de un grafo completo en 16 nodos sin subgrafos completos rojos o azules de 4 nodos) entre 6,4 × 10 22 2-coloraciones diferentes de grafos de 16 nodos, y solo un grafo (4, 4, 17) (el grafo de Paley de orden 17) entre 2,46 × 10 26 coloraciones. [4] (De ello se deduce que R (4, 4) = 18 .
El hecho de que R (4, 5) = 25 fue establecido por primera vez por Brendan McKay y Stanisław Radziszowski en 1995. [9]
Se desconoce el valor exacto de R (5, 5) , aunque se sabe que está entre 43 (Geoffrey Exoo (1989) [10] ) y 46 (Angeltveit y McKay (2024) [11] ), inclusive.
En 1997, McKay, Radziszowski y Exoo emplearon métodos de generación de grafos asistidos por computadora para conjeturar que R (5, 5) = 43. Pudieron construir exactamente 656 grafos (5, 5, 42) , llegando al mismo conjunto de grafos a través de diferentes rutas. Ninguno de los 656 grafos puede extenderse a un grafo (5, 5, 43) . [12]
Para R ( r , s ) con r , s > 5 , solo hay límites débiles disponibles. Los límites inferiores para R (6, 6) y R (8, 8) no se han mejorado desde 1965 y 1972, respectivamente. [1]
R ( r , s ) con r , s ≤ 10 se muestran en la tabla siguiente. Cuando se desconoce el valor exacto, la tabla enumera los límites más conocidos. R ( r , s ) con r < 3 se dan por R (1, s ) = 1 y R (2, s ) = s para todos los valores de s .
La encuesta estándar sobre el desarrollo de la investigación del número de Ramsey es la Encuesta dinámica 1 del Electronic Journal of Combinatorics , de Stanisław Radziszowski , que se actualiza periódicamente. [1] [13] A menos que se cite lo contrario, las entradas en la tabla siguiente se toman de la edición de junio de 2024. (Tenga en cuenta que hay una simetría trivial en la diagonal ya que R ( r , s ) = R ( s , r ) .)
s a | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 3 | 6 | 9 | 14 | 18 | 23 | 28 | 36 | 40–41 [14] | ||
| 4 | 18 | 25 [9] | 36–40 | 49–58 | 59 [15] –79 | 73–105 | 92–135 | |||
| 5 | 43–46 [11] | 59 [16] –85 | 80–133 | 101–193 | 133–282 | 149 [15] –381 | ||||
| 6 | 102–160 | 115 [15] –270 | 134 [15] –423 | 183–651 | 204–944 | |||||
| 7 | 205–492 | 219–832 | 252–1368 | 292–2119 | ||||||
| 8 | 282–1518 | 329–2662 | 343–4402 | |||||||
| 9 | 565–4956 | 581–8675 | ||||||||
| 10 | 798–16064 |
Asintóticos
La desigualdad R ( r , s ) ≤ R ( r − 1, s ) + R ( r , s − 1) puede aplicarse inductivamente para demostrar que
En particular, este resultado, debido a Erdős y Szekeres , implica que cuando r = s ,
Un límite inferior exponencial,
fue dada por Erdős en 1947 y fue instrumental en su introducción del método probabilístico. Hay una enorme brecha entre estos dos límites: por ejemplo, para s = 10 , esto da 101 ≤ R (10, 10) ≤ 48,620 . Sin embargo, los factores de crecimiento exponencial de cualquiera de los límites no se mejoraron durante mucho tiempo, y para el límite inferior todavía se mantiene en √ 2 . No se conoce ninguna construcción explícita que produzca un límite inferior exponencial. Los límites inferior y superior más conocidos para los números diagonales de Ramsey son
debido a Spencer y Conlon , respectivamente; una preimpresión de 2023 de Campos, Griffiths, Morris y Sahasrabudhe afirma haber logrado un progreso exponencial utilizando una construcción algorítmica basada en una estructura gráfica llamada " libro ", [17] [18] mejorando el límite superior a
con y donde se cree que estos parámetros podrían optimizarse, en particular .
Para los números de Ramsey fuera de la diagonal R (3, t ) , se sabe que son de orden dos/registro t ; esto se puede expresar de manera equivalente a decir que el número de independencia más pequeño posible en un gráfico sin triángulos con n vérticeses
El límite superior para R (3, t ) está dado por Ajtai , Komlós y Szemerédi , [19] el límite inferior fue obtenido originalmente por Kim , [20] y la constante implícita fue mejorada independientemente por Fiz Pontiveros, Griffiths y Morris , [21] y Bohman y Keevash , [22] mediante el análisis del proceso libre de triángulos. Además, el estudio del "proceso libre de H " más general ha establecido los límites inferiores asintóticos más conocidos para los números de Ramsey generales fuera de la diagonal, [23] R ( s , t )
Para los límites se convierte en , pero una preimpresión de 2023 [24] [25] ha mejorado el límite inferior a lo que resuelve una cuestión de Erdős que ofreció 250 dólares por una prueba de que el límite inferior tiene la forma . [26] [27]
Ramsey inducido
Hay un análogo menos conocido pero interesante del teorema de Ramsey para subgrafos inducidos . En términos generales, en lugar de encontrar un subgrafo monocromático, ahora se requiere que encontremos un subgrafo inducido monocromático. En esta variante, ya no es suficiente restringir nuestro enfoque a grafos completos , ya que la existencia de un subgrafo completo no implica la existencia de un subgrafo inducido. El enunciado cualitativo del teorema en la siguiente sección fue demostrado por primera vez de forma independiente por Erdős , Hajnal y Pósa , Deuber y Rödl en la década de 1970. [28] [29] [30] Desde entonces, ha habido mucha investigación para obtener buenos límites para los números de Ramsey inducidos.
Declaración
Sea H un grafo de n vértices. Entonces, existe un grafo G tal que cualquier coloración de las aristas de G con dos colores contiene una copia inducida monocromática de H (es decir, un subgrafo inducido de G tal que es isomorfo a H y sus aristas son monocromáticas). El menor número posible de vértices de G es el número de Ramsey inducido r ind ( H ) .
A veces, también consideramos la versión asimétrica del problema. Definimos r ind ( X , Y ) como el menor número posible de vértices de un grafo G tal que cada coloración de los bordes de G utilizando solo rojo o azul contiene un subgrafo inducido rojo de X o un subgrafo inducido azul de Y .
Historia y límites
De manera similar al teorema de Ramsey, no está claro a priori si existen números de Ramsey inducidos para cada grafo H . A principios de la década de 1970, Erdős , Hajnal y Pósa , Deuber y Rödl demostraron independientemente que este es el caso. [28] [29] [30] Sin embargo, las pruebas originales dieron límites terribles (por ejemplo, torres de dos ) en los números de Ramsey inducidos. Es interesante preguntar si se pueden lograr mejores límites. En 1974, Paul Erdős conjeturó que existe una constante c tal que cada grafo H en k vértices satisface r ind ( H ) ≤ 2 ck . [31] Si esta conjetura es verdadera, sería óptima hasta la constante c porque el grafo completo logra un límite inferior de esta forma (de hecho, es lo mismo que los números de Ramsey). Sin embargo, esta conjetura todavía está abierta a partir de ahora.
En 1984, Erdős y Hajnal afirmaron que habían demostrado el límite [32]
Sin embargo, esto todavía estaba lejos del límite exponencial conjeturado por Erdős. No fue hasta 1998 cuando Kohayakawa , Prömel y Rödl lograron un gran avance , quienes demostraron el primer límite casi exponencial de r ind ( H ) ≤ 2 ck (log k ) 2 para alguna constante c . Su enfoque fue considerar un grafo aleatorio adecuado construido en planos proyectivos y demostrar que tiene las propiedades deseadas con probabilidad distinta de cero. La idea de usar grafos aleatorios en planos proyectivos también se ha utilizado anteriormente en el estudio de las propiedades de Ramsey con respecto a las coloraciones de vértices y el problema de Ramsey inducido en grafos de grado acotado H . [33]
El límite de Kohayakawa, Prömel y Rödl siguió siendo el mejor límite general durante una década. En 2008, Fox y Sudakov proporcionaron una construcción explícita para números de Ramsey inducidos con el mismo límite. [34] De hecho, demostraron que cada ( n , d ,λ) -grafo G con λ pequeño y d adecuado contiene una copia monocromática inducida de cualquier grafo en k vértices en cualquier coloración de aristas de G en dos colores. En particular, para alguna constante c , el grafo de Paley en n ≥ 2 ck log 2 k vértices es tal que todas sus coloraciones de aristas en dos colores contienen una copia monocromática inducida de cada grafo de k vértices.
En 2010, Conlon , Fox y Sudakov pudieron mejorar el límite a r ind ( H ) ≤ 2 ck log k , que sigue siendo el mejor límite superior actual para números de Ramsey inducidos generales. [35] De manera similar al trabajo anterior en 2008, demostraron que cada ( n , d , λ) -grafo G con λ pequeño y densidad de aristas 1 ⁄ 2 contiene una copia monocromática inducida de cada grafo en k vértices en cualquier coloración de aristas en dos colores. Actualmente, la conjetura de Erdős de que r ind ( H ) ≤ 2 ck permanece abierta y es uno de los problemas importantes en la teoría de grafos extremales .
En cuanto a los límites inferiores, no se sabe mucho en general, excepto el hecho de que los números de Ramsey inducidos deben ser al menos los números de Ramsey correspondientes. Se han obtenido algunos límites inferiores para algunos casos especiales (consulte Casos especiales).
Casos especiales
Si bien los límites generales para los números de Ramsey inducidos son exponenciales en el tamaño del gráfico, el comportamiento es muy diferente en clases especiales de gráficos (en particular, los dispersos). Muchas de estas clases tienen números de Ramsey inducidos polinómicos en el número de vértices.
Si H es un ciclo , camino o estrella en k vértices, se sabe que r ind ( H ) es lineal en k . [34]
Si H es un árbol de k vértices, se sabe que r ind ( H ) = O ( k 2 log 2 k ) . [36] También se sabe que r ind ( H ) es superlineal (es decir, r ind ( H ) = ω( k ) ). Nótese que esto contrasta con los números de Ramsey habituales, donde la conjetura de Burr–Erdős (ahora probada) nos dice que r ( H ) es lineal (ya que los árboles son 1- degenerados ).
Para grafos H con número de vértices k y grado acotado Δ , se conjeturó que r ind ( H ) ≤ cn d (Δ) , para alguna constante d que dependa solo de Δ . Este resultado fue demostrado por primera vez por Łuczak y Rödl en 1996, con d (Δ) creciendo como una torre de dos con altura O (Δ 2 ) . [37] Desde entonces se obtuvieron límites más razonables para d (Δ) . En 2013, Conlon, Fox y Zhao demostraron usando un lema de conteo para grafos pseudoaleatorios dispersos que r ind ( H ) ≤ cn 2Δ+8 , donde el exponente es el mejor posible hasta factores constantes. [38]
Generalizaciones
De manera similar a los números de Ramsey, podemos generalizar la noción de números de Ramsey inducidos a hipergrafos y configuraciones multicolores.
Más colores
También podemos generalizar el teorema de Ramsey inducido a un entorno multicolor. Para los grafos H 1 , H 2 , …, H r , definamos r ind ( H 1 , H 2 , …, H r ) como el número mínimo de vértices en un grafo G tal que cualquier coloración de las aristas de G en r colores contenga un subgrafo inducido isomorfo a H i donde todas las aristas están coloreadas en el i -ésimo color para algún 1 ≤ i ≤ r . Sea r ind ( H ; q ) := r ind ( H , H , …, H ) ( q copias de H ).
Es posible derivar un límite en r ind ( H ; q ) que es aproximadamente una torre de dos de altura ~ log q aplicando iterativamente el límite en el caso de dos colores. El límite mejor conocido actualmente se debe a Fox y Sudakov, que logra r ind ( H ; q ) ≤ 2 ck 3 , donde k es el número de vértices de H y c es una constante que depende solo de q . [39]
Hipergrafos
Podemos extender la definición de números de Ramsey inducidos a hipergrafos d -uniformes simplemente cambiando la palabra grafo en el enunciado por hipergrafo . Además, podemos definir la versión multicolor de los números de Ramsey inducidos de la misma manera que en la subsección anterior.
Sea H un hipergrafo d -uniforme con k vértices. Defina la función de torre t r ( x ) haciendo t 1 ( x ) = x y para i ≥ 1 , t i +1 ( x ) = 2 t i ( x ) . Utilizando el método del contenedor de hipergrafos, Conlon, Dellamonica, La Fleur, Rödl y Schacht pudieron demostrar que para d ≥ 3, q ≥ 2 , r ind ( H ; q ) ≤ t d ( ck ) para alguna constante c que depende solo de d y q . En particular, este resultado refleja el límite mejor conocido para el número de Ramsey habitual cuando d = 3 . [40]
Extensiones del teorema
Grafos infinitos
Otro resultado, también llamado comúnmente teorema de Ramsey , se aplica a los grafos infinitos. En un contexto en el que también se discuten grafos finitos, a menudo se lo llama "teorema de Ramsey infinito". Como la intuición proporcionada por la representación gráfica de un grafo disminuye cuando se pasa de grafos finitos a grafos infinitos, los teoremas en esta área suelen expresarse en terminología de teoría de conjuntos . [41]
- Teorema. Sea un conjunto infinito y coloreemos los elementos de (los subconjuntos de de tamaño ) con distintos colores. Entonces existe un subconjunto infinito de tal que los subconjuntos de tamaño de todos tienen el mismo color.
Prueba : La prueba es por inducción sobre n , el tamaño de los subconjuntos. Para n = 1 , la afirmación es equivalente a decir que si divides un conjunto infinito en un número finito de conjuntos, entonces uno de ellos es infinito. Esto es evidente. Suponiendo que el teorema es verdadero para n ≤ r , lo demostramos para n = r + 1 . Dado un c -coloreado de los subconjuntos de ( r + 1) -elementos de X , sea a 0 un elemento de X y sea Y = X \ { a 0 }. Luego inducimos un c -coloreado de los subconjuntos de r -elementos de Y , simplemente añadiendo un 0 a cada subconjunto de r -elementos (para obtener un subconjunto de ( r + 1) -elementos de X ). Por la hipótesis de inducción, existe un subconjunto infinito Y 1 de Y tal que cada subconjunto de r -elementos de Y 1 está coloreado del mismo color en el coloreado inducido. Por lo tanto, existe un elemento a 0 y un subconjunto infinito Y 1 tales que todos los subconjuntos de ( r + 1) elementos de X que consisten en a 0 y r elementos de Y 1 tienen el mismo color. Por el mismo argumento, existe un elemento a 1 en Y 1 y un subconjunto infinito Y 2 de Y 1 con las mismas propiedades. Inductivamente, obtenemos una secuencia { a 0 , a 1 , a 2 , …} tal que el color de cada subconjunto de ( r + 1) elementos ( a i (1) , a i (2) , …, a i ( r + 1) ) con i (1) < i (2) < … < i ( r + 1) depende solo del valor de i (1)Además, hay una cantidad infinita de valores de i(n) que hacen que este color sea el mismo. Tome estos i ( n ) para obtener el conjunto monocromático deseado .
Una forma infinita más fuerte pero desequilibrada del teorema de Ramsey para grafos, el teorema de Erdős–Dushnik–Miller , establece que cada grafo infinito contiene un conjunto independiente numerablemente infinito o una camarilla infinita de la misma cardinalidad que el grafo original. [42]
La versión infinita implica lo finito.
Es posible deducir el teorema finito de Ramsey a partir de la versión infinita mediante una prueba por contradicción . Supóngase que el teorema finito de Ramsey es falso. Entonces existen números enteros c , n , T tales que para cada número entero k , existe una c -coloración de [ k ] ( n ) sin un conjunto monocromático de tamaño T . Sea C k la c -coloración de [ k ] ( n ) sin un conjunto monocromático de tamaño T .
Para cualquier k , la restricción de una coloración en C k +1 a [ k ] ( n ) (ignorando el color de todos los conjuntos que contienen k + 1 ) es una coloración en C k . Defina como las coloraciones en C k que son restricciones de coloraciones en C k +1 . Dado que C k +1 no está vacío, tampoco lo está .
De manera similar, la restricción de cualquier coloración en está en , lo que permite definir como el conjunto de todas esas restricciones, un conjunto no vacío. Continuando así, defina para todos los enteros m , k .
Ahora, para cualquier entero k ,
y cada conjunto no es vacío. Además, C k es finito como
De ello se deduce que la intersección de todos estos conjuntos no es vacía, y sea
Entonces, cada coloración en D k es la restricción de una coloración en D k +1 . Por lo tanto, al no restringir una coloración en D k a una coloración en D k +1 , y continuar haciéndolo, se construye una coloración de sin ningún conjunto monocromático de tamaño T . Esto contradice el teorema de Ramsey infinito.
Si se adopta un punto de vista topológico adecuado, este argumento se convierte en un argumento de compacidad estándar que muestra que la versión infinita del teorema implica la versión finita. [43]
Hipergrafos
El teorema también se puede extender a los hipergrafos . Un m -hipergrafo es un grafo cuyas "aristas" son conjuntos de m vértices – en un grafo normal una arista es un conjunto de 2 vértices. El enunciado completo del teorema de Ramsey para hipergrafos es que para cualesquiera enteros m y c , y cualesquiera enteros n 1 , …, n c , hay un entero R ( n 1 , …, n c ; m) tal que si las hiperaristas de un m -hipergrafo completo de orden R ( n 1 , …, n c ; m ) están coloreadas con c colores diferentes, entonces para algún i entre 1 y c , el hipergrafo debe contener un sub- m -hipergrafo completo de orden n i cuyas hiperaristas sean todas de color i . Este teorema se demuestra usualmente por inducción sobre m , la 'hiper-idad' del grafo. El caso base para la prueba es m = 2 , que es exactamente el teorema anterior.
Para m = 3 conocemos el valor exacto de un número de Ramsey no trivial, a saber, R (4, 4; 3) = 13. Este hecho fue establecido por Brendan McKay y Stanisław Radziszowski en 1991. [44] Además, tenemos: R (4, 5; 3) ≥ 35 , [45] R (4, 6; 3) ≥ 63 y R (5, 5; 3) ≥ 88. [ 45]
Grafos dirigidos
También es posible definir números de Ramsey para grafos dirigidos ; estos fueron introducidos por P. Erdős y L. Moser (1964). Sea R ( n ) el número más pequeño Q tal que cualquier grafo completo con arcos dirigidos simples (también llamado "torneo") y con ≥ Q nodos contenga un subtorneo acíclico (también llamado "transitivo") de n nodos.
Este es el análogo en grafo dirigido de lo que (arriba) se ha llamado R ( n , n ; 2) , el número más pequeño Z tal que cualquier coloración bidimensional de las aristas de un grafo completo no dirigido con ≥ Z nodos, contiene un grafo completo monocromático en n nodos. (El análogo dirigido de los dos colores de arco posibles son las dos direcciones de los arcos, el análogo de "monocromático" es "todas las flechas de arco apuntan en la misma dirección"; es decir, "acíclico").
Tenemos R (0) = 0 , R (1) = 1 , R (2) = 2 , R (3) = 4 , R (4) = 8 , R (5) = 14 , R (6) = 28 y 34 ≤ R (7) ≤ 47. [ 46] [47]
Cardenales incontables
En términos del cálculo de particiones, el teorema de Ramsey puede enunciarse como para todos los n y k finitos . Wacław Sierpiński demostró que el teorema de Ramsey no se extiende a gráficos de tamaño al mostrar que . En particular, la hipótesis del continuo implica que . Stevo Todorčević demostró que, de hecho, en ZFC , , una afirmación mucho más sólida que . Justin T. Moore ha reforzado aún más este resultado. En el lado positivo, un cardinal de Ramsey , , es un cardinal grande definido axiomáticamente para satisfacer la fórmula relacionada: . La existencia de cardinales de Ramsey no se puede demostrar en ZFC.
Relación con el axioma de elección
En matemáticas inversas , hay una diferencia significativa en la fuerza de la prueba entre la versión del teorema de Ramsey para grafos infinitos (el caso n = 2) y para multigrafos infinitos (el caso n ≥ 3). La versión multigrafo del teorema es equivalente en fuerza al axioma de comprensión aritmética , por lo que forma parte del subsistema ACA 0 de la aritmética de segundo orden , uno de los cinco grandes subsistemas en matemáticas inversas. Por el contrario, por un teorema de David Seetapun , la versión gráfica del teorema es más débil que ACA 0 y (combinando el resultado de Seetapun con otros) no cae en uno de los cinco grandes subsistemas. [48] Sin embargo, sobre ZF , la versión gráfica implica el lema clásico de Kőnig , mientras que la implicación inversa no se cumple, [49] ya que el lema de Kőnig es equivalente a la elección contable de conjuntos finitos en este contexto. [50]
Véase también
- Cardenal de Ramsey
- Teorema de París-Harrington
- Sim (juego de lápiz)
- Teoría de Ramsey infinita
- Número de Van der Waerden
- Juego de Ramsey
- Teorema de Erdös-Rado
Notas
- ^ Algunos autores restringen los valores a mayores que uno, por ejemplo (Brualdi 2010) y (Harary 1972), evitando así una discusión sobre la coloración de las aristas de un grafo sin aristas, mientras que otros reformulan el enunciado del teorema para requerir, en un grafo simple , ya sea una r -clique o un conjunto s - independiente , ver (Gross 2008) o (Erdős & Szekeres 1935). De esta forma, la consideración de grafos con un vértice es más natural.
- ^ Hasta automorfismos del grafo.
- ^ abc Radziszowski, Stanisław (2011). "Números pequeños de Ramsey". Encuestas dinámicas. Revista electrónica de combinatoria . 1000 . doi : 10.37236/21 .
- ^ Do, Norman (2006). "Problemas de partidos y teoría de Ramsey" (PDF) . Austr. Math. Soc. Gazette . 33 (5): 306–312.
- ^ "Conocidos de la fiesta".
- ^ ab "Gráficos de Ramsey".
- ^ Joel H. Spencer (1994), Diez conferencias sobre el método probabilístico, SIAM , pág. 4, ISBN 978-0-89871-325-1
- ^ 2.6 Teoría de Ramsey de Matemáticas Iluminadas
- ^ Montanaro, Ashley (2016). "Algoritmos cuánticos: una descripción general". npj Quantum Information . 2 : 15023. arXiv : 1511.04206 . Bibcode :2016npjQI...215023M. doi :10.1038/npjqi.2015.23. S2CID 2992738 – vía Nature.
- ^ Wang, Hefeng (2016). "Determinación de números de Ramsey en una computadora cuántica". Physical Review A . 93 (3): 032301. arXiv : 1510.01884 . Código Bibliográfico :2016PhRvA..93c2301W. doi :10.1103/PhysRevA.93.032301. S2CID 118724989.
- ^ ab McKay, Brendan D.; Radziszowski, Stanislaw P. (mayo de 1995). "R(4,5) = 25" (PDF) . Revista de teoría de grafos . 19 (3): 309–322. doi :10.1002/jgt.3190190304.
- ^ Exoo, Geoffrey (marzo de 1989). "Un límite inferior para R (5, 5) ". Journal of Graph Theory . 13 (1): 97–98. doi :10.1002/jgt.3190130113.
- ^ ab Vigleik Angeltveit; Brendan McKay (septiembre de 2024). " ". arXiv : 2409.15709 [matemáticas.CO].
- ^ Brendan D. McKay, Stanisław P. Radziszowski (1997). "Identidades de conteo de subgrafos y números de Ramsey" (PDF) . Revista de teoría combinatoria . Serie B. 69 (2): 193–209. doi : 10.1006/jctb.1996.1741 .
- ^ Stanisław Radziszowski. "DS1" . Consultado el 17 de agosto de 2023 .
- ^ Angeltveit, Vigleik (31 de diciembre de 2023). " ". arXiv : 2401.00392 [matemáticas.CO].
- ^ abcd Exoo, Geoffrey; Tatarevic, Milos (2015). "Nuevos límites inferiores para 28 números de Ramsey clásicos". Revista electrónica de combinatoria . 22 (3): 3. arXiv : 1504.02403 . Código Bibliográfico :2015arXiv150402403E. doi : 10.37236/5254 .
- ^ Exoo, Geoffrey (26 de octubre de 2023). "Un límite inferior para R(5,6)". arXiv : 2310.17099 [math.CO].
- ^ Campos, Marcelo; Griffiths, Simon; Morris, Robert; Sahasrabudhe, Julian (2023). "Una mejora exponencial para la diagonal de Ramsey". arXiv : 2303.09521 [math.CO].
- ^ Sloman, Leila (2 de mayo de 2023). "Un pequeño gran salto adelante en la teoría de grafos". Revista Quanta .
- ^ Ajtai, Miklós; Komlós, János; Szemerédi, Endre (1 de noviembre de 1980). "Una nota sobre los números de Ramsey". Revista de teoría combinatoria, serie A. 29 (3): 354–360. doi : 10.1016/0097-3165(80)90030-8 . ISSN 0097-3165.
- ^ Kim, Jeong Han (1995), "El número de Ramsey R (3, t ) tiene un orden de magnitud t 2 /log t ", Random Structures and Algorithms , 7 (3): 173–207, CiteSeerX 10.1.1.46.5058 , doi :10.1002/rsa.3240070302
- ^ "El proceso libre de triángulos y el número de Ramsey R(3,k)". bookstore.ams.org . Consultado el 27 de junio de 2023 .
- ^ Bohman, Tom; Keevash, Peter (17 de noviembre de 2020). "Concentración dinámica del proceso sin triángulos". Estructuras y algoritmos aleatorios . 58 (2): 221–293. arXiv : 1302.5963 . doi :10.1002/rsa.20973.
- ^ Bohman, Tom; Keevash, Peter (1 de agosto de 2010). "La evolución temprana del proceso libre de hidrógeno". Inventiones Mathematicae . 181 (2): 291–336. arXiv : 0908.0429 . Código Bibliográfico :2010InMat.181..291B. doi :10.1007/s00222-010-0247-x. ISSN 1432-1297.
- ^ Mattheus, Sam; Verstraete, Jacques (5 de marzo de 2024). "La asintótica de r(4,t)". Anales de Matemáticas . 199 (2). arXiv : 2306.04007 . doi :10.4007/annals.2024.199.2.8.
- ^ Cepelewicz, Jordana (22 de junio de 2023). "Los matemáticos descubren una nueva forma de predecir la estructura en gráficos". Revista Quanta .
- ^ Erdös, Paul (1990), Nešetřil, Jaroslav; Rödl, Vojtěch (eds.), "Problemas y resultados en gráficos e hipergráficos: similitudes y diferencias", Matemáticas de la teoría de Ramsey , Algoritmos y combinatoria, vol. 5, Berlín, Heidelberg: Springer, págs. 12-28, doi :10.1007/978-3-642-72905-8_2, ISBN 978-3-642-72905-8, consultado el 27 de junio de 2023
- ^ "Problemas de Erdős". www.erdosproblems.com . Consultado el 12 de julio de 2023 .
- ^ ab Erdős, P .; Hajnal, A.; Posa, L. (1975). "Fuertes incrustaciones de gráficos en gráficos coloreados". Conjuntos infinitos y finitos, vol. 1 . Coloquios Mathematica Societatis János Bolyai. vol. 10. Holanda Septentrional, Ámsterdam/Londres. págs. 585–595.
- ^ ab Deuber, W. (1975). "Una generalización del teorema de Ramsey". Conjuntos infinitos y finitos, vol. 1 . Coloquios Mathematica Societatis János Bolyai. vol. 10. Holanda Septentrional, Ámsterdam/Londres. págs. 323–332.
- ^ ab Rödl, V. (1973). La dimensión de un grafo y teoremas generalizados de Ramsey (tesis de maestría). Universidad Charles.
- ^ Erdős, P. (1975). "Problemas y resultados sobre grafos finitos e infinitos". Avances recientes en teoría de grafos (Actas del Segundo Simposio Checoslovaco, Praga, 1974) . Academia, Praga. pp. 183–192.
- ^ Erdős, Paul (1984). "Sobre algunos problemas en teoría de grafos, análisis combinatorio y teoría combinatoria de números" (PDF) . Teoría de grafos y combinatoria : 1–17.
- ^ Kohayakawa, Y.; Prömel, HJ; Rodl, V. (1998). "Números de Ramsey inducidos" (PDF) . Combinatoria . 18 (3): 373–404. doi : 10.1007/PL00009828 .
- ^ ab Fox, Jacob ; Sudakov, Benny (2008). "Teoremas de tipo Ramsey inducidos". Avances en Matemáticas . 219 (6): 1771–1800. arXiv : 0706.4112 . doi : 10.1016/j.aim.2008.07.009 .
- ^ Conlon, David ; Fox, Jacob ; Sudakov, Benny (2012). "Sobre dos problemas en la teoría de grafos de Ramsey". Combinatorica . 32 (5): 513–535. arXiv : 1002.0045 . doi : 10.1007/s00493-012-2710-3 .
- ^ Beck, József (1990). "Sobre el tamaño del número de Ramsey de caminos, árboles y circuitos. II". En Nešetřil, J.; Rödl, V. (eds.). Matemáticas de la teoría de Ramsey . Algoritmos y combinatoria. Vol. 5. Springer, Berlín, Heidelberg. págs. 34–45. doi : 10.1007/978-3-642-72905-8_4 . ISBN . 978-3-642-72907-2.
- ^ Łuczak, Tomasz; Rödl, Vojtěch (marzo de 1996). "Sobre números de Ramsey inducidos para grafos con grado máximo acotado". Journal of Combinatorial Theory . Serie B. 66 (2): 324–333. doi : 10.1006/jctb.1996.0025 .
- ^ Conlon, David ; Fox, Jacob ; Zhao, Yufei (mayo de 2014). "Resultados extremos en grafos pseudoaleatorios dispersos". Avances en Matemáticas . 256 : 206–29. arXiv : 1204.6645 . doi : 10.1016/j.aim.2013.12.004 .
- ^ Fox, Jacob ; Sudakov, Benny (2009). "Teoremas de densidad para grafos bipartitos y resultados de tipo Ramsey relacionados". Combinatorica . 29 (2): 153–196. arXiv : 0707.4159v2 . doi : 10.1007/s00493-009-2475-5 .
- ^ Conlón, David ; Dellamonica Jr., Domingos; La Flor, Steven; Rödl, Vojtěch ; Schacht, Mathías (2017). "Una nota sobre los números de Ramsey inducidos". En Loebl, Martín; Nešetřil, Jaroslav ; Thomas, Robin (eds.). Un viaje por las matemáticas discretas . Springer, Cham. págs. 357–366. arXiv : 1601.01493 . doi : 10.1007/978-3-319-44479-6_13 . ISBN 978-3-319-44478-9.
- ^ Gould, Martin. «Teoría de Ramsey» (PDF) . Instituto de Matemáticas, Universidad de Oxford . Archivado desde el original (PDF) el 30 de enero de 2022.
- ^ Dushnik, Ben; Miller, EW (1941). "Conjuntos parcialmente ordenados". Revista Americana de Matemáticas . 63 (3): 600–610. doi :10.2307/2371374. hdl : 10338.dmlcz/100377 . JSTOR 2371374. MR 0004862.. Véanse en particular los teoremas 5.22 y 5.23.
- ^ Diestel, Reinhard (2010). "Capítulo 8, Grafos infinitos". Teoría de grafos (4.ª ed.). Heidelberg: Springer-Verlag. pp. 209–2010. ISBN 978-3-662-53621-6.
- ^ McKay, Brendan D.; Radziszowski, Stanislaw P. (1991). "Se calcula el primer número de Ramsey clásico para hipergrafos". Actas del segundo simposio anual ACM-SIAM sobre algoritmos discretos, SODA'91 : 304–308.
- ^ ab Dybizbański, Janusz (31 de diciembre de 2018). "Un límite inferior para el número de Ramsey del hipergrafo R(4,5;3)". Contribuciones a las matemáticas discretas . 13 (2). doi : 10.11575/cdm.v13i2.62416 . ISSN 1715-0868.
- ^ Smith, Warren D.; Exoo, Geoff, Respuesta parcial al acertijo n.° 27: una cantidad similar a la de Ramsey , consultado el 2 de junio de 2020
- ^ Neiman, David; Mackey, John; Heule, Marijn (1 de noviembre de 2020). "Límites más estrictos en el número de Ramsey dirigido R(7)". arXiv : 2011.00683 [math.CO].
- ^ Hirschfeldt, Denis R. (2014). Slicing the Truth . Serie de notas de conferencias del Instituto de Ciencias Matemáticas, Universidad Nacional de Singapur. Vol. 28. World Scientific.
- ^ Blass, Andreas (septiembre de 1977). "El teorema de Ramsey en la jerarquía de principios de elección". The Journal of Symbolic Logic . 42 (3): 387–390. doi :10.2307/2272866. ISSN 1943-5886. JSTOR 2272866.
- ^ Forster, TE; Truss, JK (enero de 2007). «Teorema de Ramsey y lema de König». Archivo de Lógica Matemática . 46 (1): 37–42. doi :10.1007/s00153-006-0025-z. ISSN 1432-0665.
Referencias
- Ajtai, Miklós ; Komlós, János ; Szemerédi, Endre (1980), "Una nota sobre los números de Ramsey", J. Combin. Teoría Ser. A , 29 (3): 354–360, doi : 10.1016/0097-3165(80)90030-8.
- Bohman, Tom; Keevash, Peter (2010), "La evolución temprana del proceso libre de hidrógeno", Invent. Math. , 181 (2): 291–336, arXiv : 0908.0429 , Bibcode :2010InMat.181..291B, doi :10.1007/s00222-010-0247-x, S2CID 2429894
- Brualdi, Richard A. (2010), Combinatoria introductoria (5.ª ed.), Prentice-Hall, págs. 77–82, ISBN 978-0-13-602040-0
- Conlon, David (2009), "Un nuevo límite superior para los números diagonales de Ramsey", Annals of Mathematics , 170 (2): 941–960, arXiv : math/0607788v1 , doi :10.4007/annals.2009.170.941, MR 2552114, S2CID 9238219.
- Erdős, Paul (1947), "Algunas observaciones sobre la teoría de grafos", Bull. Amer. Math. Soc. , 53 (4): 292–294, doi : 10.1090/S0002-9904-1947-08785-1.
- Erdős, P .; Moser, L. (1964), "Sobre la representación de grafos dirigidos como uniones de ordenamientos" (PDF) , A Magyar Tudományos Akadémia, Matematikai Kutató Intézetének Közleményei , 9 : 125–132, MR 0168494
- Erdős, Paul ; Szekeres, George (1935), "Un problema combinatorio en geometría" (PDF) , Compositio Mathematica , 2 : 463–470, doi :10.1007/978-0-8176-4842-8_3, ISBN 978-0-8176-4841-1.
- Exoo, G. (1989), "Un límite inferior para R(5,5)", Journal of Graph Theory , 13 : 97–98, doi :10.1002/jgt.3190130113.
- Graham, R .; Rothschild, B.; Spencer, JH (1990), Teoría de Ramsey , Nueva York: John Wiley and Sons.
- Gross, Jonathan L. (2008), Métodos combinatorios con aplicaciones informáticas , CRC Press, pág. 458, ISBN 978-1-58488-743-0
- Harary, Frank (1972), Teoría de grafos , Addison-Wesley, págs. 16-17, ISBN 0-201-02787-9
- Ramsey, FP (1930), "Sobre un problema de lógica formal", Actas de la London Mathematical Society , 30 : 264–286, doi :10.1112/plms/s2-30.1.264.
- Spencer, J. (1975), "Teorema de Ramsey: un nuevo límite inferior", J. Combin. Theory Ser. A , 18 : 108–115, doi : 10.1016/0097-3165(75)90071-0.
- Bian, Zhengbing; Chudak, Fabian; Macready, William G.; Clark, Lane; Gaitan, Frank (2013), "Determinación experimental de los números de Ramsey", Physical Review Letters , 111 (13): 130505, arXiv : 1201.1842 , Bibcode :2013PhRvL.111m0505B, doi :10.1103/PhysRevLett.111.130505, PMID 24116761, S2CID 1303361.
Enlaces externos
- "Teorema de Ramsey", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
- Ramsey@Home es un proyecto de computación distribuida diseñado para encontrar nuevos límites inferiores para varios números de Ramsey utilizando una serie de técnicas diferentes.
- Revista Electrónica de Combinatoria: estudio dinámico de números de Ramsey pequeños (por Stanisław Radziszowski)
- Número de Ramsey – de MathWorld (contiene límites inferior y superior hasta R(19, 19))
- Número de Ramsey – Geoffrey Exoo (Contiene R(5, 5) > 42 contraprueba)





















![{\displaystyle [1+o(1)]{\frac {{\sqrt {2}}s}{e}}2^{\frac {s}{2}}\leq R(s,s)\leq s^{-(c\log s)/(\log \log s)}4^{s},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98d3d42edf70185ccfa40a6b0153b034f595e9e1)












![{\displaystyle [X]^{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eba2dbab7c22faa180f674d89ae74d3f2a778337)















![{\displaystyle \aleph _{1}\nrightarrow [\aleph _{1}]_{\aleph _{1}}^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ecac308e6d102699ff81ec9d125bed772486ae6)




