Tetración

En matemáticas , la tetración (o hiper-4 ) es una operación basada en la exponenciación iterada o repetida . No existe una notación estándar para la tetración, aunque la notación de flecha hacia arriba de Knuth y el exponente izquierdo ^x b son comunes. ${\displaystyle \flecha arriba \flecha arriba}$

Según la definición de exponenciación repetida, significa , donde n copias de a se iteran mediante exponenciación, de derecha a izquierda, es decir, la aplicación de tiempos de exponenciación. n se llama la "altura" de la función, mientras que a se llama la "base", análoga a la exponenciación. Se leería como "la n- ésima tetración de a ".${\displaystyle {^{n}a}}$${\displaystyle {a^{a^{\cdot ^{\cdot ^{a}}}}}}$${\estilo de visualización n-1}$

Es la siguiente hiperoperación después de la exponenciación , pero antes de la pentación . La palabra fue acuñada por Reuben Louis Goodstein a partir de tetra- (cuatro) e iteración .

La tetración también se define recursivamente como

${\displaystyle {a\uparrow \uparrow n}:={\begin{cases}1&{\text{si }}n=0,\\a^{a\uparrow \uparrow (n-1)}&{\text{si }}n>0,\end{cases}}}$

permitiendo intentos de extender la tetración a números no naturales como los números reales , complejos y ordinales .

Las dos funciones inversas de la tetración se denominan superraíz y superlogaritmo , análogas a la raíz n y a las funciones logarítmicas. Ninguna de las tres funciones es elemental .

La tetración se utiliza para la notación de números muy grandes .

Aquí se muestran las primeras cuatro hiperoperaciones , siendo la tetración la cuarta de la serie. La operación unaria sucesión , definida como , se considera la operación cero.${\displaystyle a'=a+1}$

1. Adición de n copias de 1 añadidas a una combinada por sucesión.$${\displaystyle a+n=a+\underbrace {1+1+\cdots +1} _{n}}$$
2. Multiplicación de n copias de un combinado por adición.$${\displaystyle a\times n=\underbrace {a+a+\cdots +a} _{n}}$$
3. Exponenciación n copias de una combinada por multiplicación.$${\displaystyle a^{n}=\underbrace {a\times a\times \cdots \times a} _{n}}$$
4. Tetración n copias de a combinadas por exponenciación, de derecha a izquierda.$${\displaystyle {^{n}a}=\underbrace {a^{a^{\cdot ^{\cdot ^{a}}}}} _{n}}$$

Es importante destacar que los exponentes anidados se interpretan de arriba hacia abajo: ⁠ ⁠${\estilo de visualización a^{b^{c}}}$ significa ⁠ ⁠${\displaystyle a^{\izquierda(b^{c}\derecha)}}$ y no ⁠ ⁠${\displaystyle \izquierda(a^{b}\derecha)^{c}.}$

La sucesión, , es la operación más básica; mientras que la adición ( ) es una operación primaria, para la adición de números naturales puede considerarse como una sucesión encadenada de sucesores de ; la multiplicación ( ) también es una operación primaria, aunque para los números naturales puede considerarse análogamente como una adición encadenada que involucra números de . La exponenciación puede considerarse como una multiplicación encadenada que involucra números de y la tetración ( ) como una potencia encadenada que involucra números . Cada una de las operaciones anteriores se define iterando la anterior; ^[1] sin embargo, a diferencia de las operaciones anteriores, la tetración no es una función elemental .$Estilo de visualización a_{n+1}=a_{n}+1$${\estilo de visualización a+n}$${\estilo de visualización n}$${\estilo de visualización a}$${\displaystyle a\veces n}$${\estilo de visualización n}$${\estilo de visualización a}$${\estilo de visualización n}$${\estilo de visualización a}$${\displaystyle ^{n}a}$${\estilo de visualización n}$${\estilo de visualización a}$

El parámetro se denomina base , mientras que el parámetro se puede denominar altura . En la definición original de tetración, el parámetro altura debe ser un número natural; por ejemplo, sería ilógico decir "tres elevado a sí mismo menos cinco veces" o "cuatro elevado a sí mismo la mitad de una vez". Sin embargo, así como la suma, la multiplicación y la exponenciación se pueden definir de formas que permitan extensiones a números reales y complejos, se han hecho varios intentos de generalizar la tetración a números negativos, números reales y números complejos. Una de esas formas de hacerlo es utilizando una definición recursiva para la tetración; para cualquier entero real positivo y no negativo , podemos definir recursivamente como: ^[1]${\estilo de visualización a}$${\estilo de visualización n}$ ${\displaystyle a>0}$ ${\displaystyle n\geq 0}$${\displaystyle \,\!{^{n}a}}$

${\displaystyle {^{n}a}:={\begin{cases}1&{\text{si }}n=0\\a^{\left(^{(n-1)}a\right)}&{\text{si }}n>0\end{cases}}}$

La definición recursiva es equivalente a la exponenciación repetida para alturas naturales ; sin embargo, esta definición permite extensiones a otras alturas como , y también – muchas de estas extensiones son áreas de investigación activa.${\displaystyle ^{0}a}$${\displaystyle ^{-1}a}$${\displaystyle ^{i}a}$

Existen muchos términos para la tetración, cada uno de los cuales tiene cierta lógica detrás, pero algunos no se han vuelto de uso común por una razón u otra. Aquí se presenta una comparación de cada término con su fundamento y contrafundamento.

• El término tetración , introducido por Goodstein en su artículo de 1947 Transfinite Ordinals in Recursive Number Theory ^[2] (generalizando la representación recursiva de la base utilizada en el teorema de Goodstein para utilizar operaciones superiores), ha ganado predominio. También se popularizó en Infinity and the Mind de Rudy Rucker .
• El término superexponenciación fue publicado por Bromer en su artículo Superexponentiation en 1987. ^[3] Fue utilizado anteriormente por Ed Nelson en su libro Predicative Arithmetic, Princeton University Press, 1986.
• El término hiperpotencia ^[4] es una combinación natural de hiper y potencia , que describe acertadamente la tetración. El problema radica en el significado de hiper con respecto a la secuencia de hiperoperaciones . Al considerar las hiperoperaciones, el término hiper se refiere a todos los rangos, y el término súper se refiere al rango 4, o tetración. Por lo tanto, bajo estas consideraciones, hiperpotencia es engañoso, ya que solo se refiere a la tetración.
• El término torre de potencia ^[5] se utiliza ocasionalmente, en la forma "la torre de potencia de orden n " para . La exponenciación se malinterpreta fácilmente: observe que la operación de elevar a una potencia es asociativa por la derecha (ver más abajo). La tetración es exponenciación iterada (llamémosla operación asociativa por la derecha ^), comenzando desde el lado superior derecho de la expresión con una instancia a^a (llamémosla valor c). Exponenciar la siguiente a hacia la izquierda (llamémosla la 'próxima base' b), es trabajar hacia la izquierda después de obtener el nuevo valor b^c. Trabajando hacia la izquierda, use la siguiente a hacia la izquierda, como la base b, y evalúe el nuevo b^c. 'Descienda por la torre' a su vez, con el nuevo valor para c en el siguiente paso descendente.${\displaystyle {\ \encima {\ }}{{\underbrace {a^{a^{\cdot ^{\cdot ^{a}}}}} } \encima n}}$

Debido en parte a cierta terminología compartida y simbolismo de notación similar , la tetración a menudo se confunde con funciones y expresiones estrechamente relacionadas. A continuación, se presentan algunos términos relacionados:

Términos relacionados con la tetración

Terminología	Forma
Tetración	${\displaystyle a^{a^{\cdot ^{\cdot ^{a^{a}}}}}}$
Exponenciales iteradas	${\displaystyle a^{a^{\cdot ^{\cdot ^{a^{x}}}}}}$
Exponenciales anidadas (también torres)	${\displaystyle a_{1}^{a_{2}^{\cdot ^{\cdot ^{a_{n}}}}}}$
Exponentes infinitas (también torres)	${\displaystyle a_{1}^{a_{2}^{a_{3}^{\cdot ^{\cdot ^{\cdot }}}}}}$

En las dos primeras expresiones , a es la base y la cantidad de veces que aparece a es la altura (suma uno para x ). En la tercera expresión, n es la altura , pero cada una de las bases es diferente.

Se debe tener cuidado al hacer referencia a exponenciales iteradas, ya que es común llamar a expresiones de esta forma exponenciación iterada, lo cual es ambiguo, ya que puede significar potencias iteradas o exponenciales iteradas .

Existen muchos estilos de notación diferentes que se pueden utilizar para expresar la tetración. Algunas notaciones también se pueden utilizar para describir otras hiperoperaciones , mientras que otras se limitan a la tetración y no tienen una extensión inmediata.

Estilos de notación para tetración

Nombre	Forma	Descripción
Notación de Rudy Rucker	${\displaystyle \,{}^{n}a}$	Utilizado por Maurer [1901] y Goodstein [1947]; el libro de Rudy Rucker Infinity and the Mind popularizó la notación. [nb 1]
Notación de flecha hacia arriba de Knuth	${\displaystyle {\begin{aligned}a{\uparrow \uparrow }n\\a{\uparrow }^{2}n\end{aligned}}}$	Permite la extensión poniendo más flechas, o, aún más potente, una flecha indexada.
Notación de flecha encadenada de Conway	${\displaystyle a\rightarrow n\rightarrow 2}$	Permite la extensión incrementando el número 2 (equivalente a las extensiones anteriores), pero también, aún más potentemente, alargando la cadena.
Función de Ackermann	${\displaystyle {}^{n}2=\nombre del operador {A} (4,n-3)+3}$	Permite escribir el caso especial en términos de la función de Ackermann.${\estilo de visualización a=2}$
Notación exponencial iterada	$estilo de visualización exp _{a}^{n}(1)}$	Permite una extensión simple a exponenciales iteradas a partir de valores iniciales distintos de 1.
Notaciones de Hooshmand [6]	${\displaystyle {\begin{aligned}&\operatorname {uxp} _{a}n\\[2pt]&a^{\frac {n}{}}\end{aligned}}}$	Utilizado por MH Hooshmand [2006].
Notaciones de hiperoperaciones	${\displaystyle {\begin{aligned}&a[4]n\\[2pt]&H_{4}(a,n)\end{aligned}}}$	Permite la extensión incrementando el número 4; esto da la familia de hiperoperaciones .
Notación de doble cursor	a^^n	Dado que la flecha hacia arriba se utiliza de forma idéntica al símbolo de intercalación ( ^), la tetración puede escribirse como ( ^^); conveniente para ASCII .

La notación anterior utiliza notación exponencial iterada; esta se define en general de la siguiente manera:

${\displaystyle \exp _{a}^{n}(x)=a^{a^{\cdot ^{\cdot ^{a^{x}}}}}}$con n a s.

No hay tantas notaciones para exponenciales iteradas, pero aquí hay algunas:

Estilos de notación para exponenciales iterados

Nombre	Forma	Descripción
Notación estándar	$Estilo de visualización: exp.$	Euler acuñó la notación , y la notación de iteración ha existido durante aproximadamente el mismo tiempo.${\displaystyle \exp _{a}(x)=a^{x}}$${\displaystyle f^{n}(x)}$
Notación de flecha hacia arriba de Knuth	${\displaystyle (a{\uparrow }^{2}(x))}$	Permite superpoderes y funciones superexponenciales al aumentar el número de flechas; utilizado en el artículo sobre números grandes .
Notación de texto	exp_a^n(x)	Basado en notación estándar; conveniente para ASCII .
Notación J	x^^:(n-1)x	Repite la exponenciación. Véase J (lenguaje de programación) [7]
Notación de barrera infinita	${\displaystyle a\uparrow \uparrow n|x}$	Jonathan Bowers acuñó esto, [8] y se puede extender a hiperoperaciones superiores.

Debido al crecimiento extremadamente rápido de la tetración, la mayoría de los valores de la siguiente tabla son demasiado grandes para escribirlos en notación científica. En estos casos, se utiliza la notación exponencial iterada para expresarlos en base 10. Los valores que contienen un punto decimal son aproximados.

Ejemplos de tetración

${\displaystyle x}$	${\displaystyle {}^{2}x}$	${\displaystyle {}^{3}x}$	${\displaystyle {}^{4}x}$	${\displaystyle {}^{5}x}$	${\displaystyle {}^{6}x}$	${\displaystyle {}^{7}x}$
1	1	1	1	1	1	1
2	4 (2 2 )	16 (2 4 )	65.536 (2 16 )	2,00353 × 10 19.728	${\displaystyle \exp _{10}^{3}(4.29508)}$(10 6,03123 × 10 19 727 )	${\displaystyle \exp _{10}^{4}(4.29508)}$(10 10 6,03123 × 10 19 727 )
3	27 (3 3 )	7.625.597.484.987 (3 27 )	${\displaystyle \exp _{10}^{3}(1.09902)}$(1,25801 × 10 3.638.334.640.024 [9] )	${\displaystyle \exp _{10}^{4}(1.09902)}$	${\displaystyle \exp _{10}^{5}(1.09902)}$	${\displaystyle \exp _{10}^{6}(1.09902)}$
4	256 (4 4 )	1.34078 × 10 154 (4 256 )	${\displaystyle \exp _{10}^{3}(2.18726)}$(10 8,0723 × 10 153 )	${\displaystyle \exp _{10}^{4}(2.18726)}$	${\displaystyle \exp _{10}^{5}(2.18726)}$	${\displaystyle \exp _{10}^{6}(2.18726)}$
5	3,125 (5 5 )	1,91101 × 10 2.184 (5 3.125 )	${\displaystyle \exp _{10}^{3}(3.33928)}$(10 1,33574 × 10 2184 )	${\displaystyle \exp _{10}^{4}(3.33928)}$	${\displaystyle \exp _{10}^{5}(3.33928)}$	${\displaystyle \exp _{10}^{6}(3.33928)}$
6	46.656 (6 6 )	2,65912 × 10 36.305 (6 46.656 )	${\displaystyle \exp _{10}^{3}(4.55997)}$(10 2,0692 × 10 36 305 )	${\displaystyle \exp _{10}^{4}(4.55997)}$	${\displaystyle \exp _{10}^{5}(4.55997)}$	${\displaystyle \exp _{10}^{6}(4.55997)}$
7	823,543 (7 7 )	3,75982 × 10 695 974 (7 823 543 )	${\displaystyle \exp _{10}^{3}(5.84259)}$(3,17742 × 10 695.974 dígitos)	${\displaystyle \exp _{10}^{4}(5.84259)}$	${\displaystyle \exp _{10}^{5}(5.84259)}$	${\displaystyle \exp _{10}^{6}(5.84259)}$
8	16.777.216 (8 8 )	6.01452 × 10 15,151,335	${\displaystyle \exp _{10}^{3}(7.18045)}$(5,43165 × 10 15 151 335 dígitos)	${\displaystyle \exp _{10}^{4}(7.18045)}$	${\displaystyle \exp _{10}^{5}(7.18045)}$	${\displaystyle \exp _{10}^{6}(7.18045)}$
9	387.420.489 (9 9 )	4,28125 × 10 369.693.099	${\displaystyle \exp _{10}^{3}(8.56784)}$(4,08535 × 10 369.693.099 dígitos)	${\displaystyle \exp _{10}^{4}(8.56784)}$	${\displaystyle \exp _{10}^{5}(8.56784)}$	${\displaystyle \exp _{10}^{6}(8.56784)}$
10	10.000.000.000 (10 10 )	10 10.000.000.000	${\displaystyle \exp _{10}^{3}(10)}$(10 10.000.000.000 + 1 dígito)	${\displaystyle \exp _{10}^{4}(10)}$	${\displaystyle \exp _{10}^{5}(10)}$	${\displaystyle \exp _{10}^{6}(10)}$

Observación: Si x no difiere de 10 en órdenes de magnitud, entonces para todos los . Por ejemplo, en la tabla anterior, y la diferencia es aún menor para las filas siguientes.${\displaystyle k\geq 3,~^{m}x=\exp _{10}^{k}z,~z>1~\Rightarrow ~^{m+1}x=\exp _{10}^{k+1}z'{\text{ with }}z'\approx z}$${\displaystyle z-z'<1.5\cdot 10^{-15}{\text{ for }}x=3=k,~m=4}$

La tetración se puede extender de dos maneras diferentes; en la ecuación , tanto la base a como la altura n se pueden generalizar utilizando la definición y las propiedades de la tetración. Aunque la base y la altura se pueden extender más allá de los números enteros no negativos a diferentes dominios , incluyendo , funciones complejas como , y alturas de n infinito , las propiedades más limitadas de la tetración reducen la capacidad de extender la tetración.${\displaystyle ^{n}a\!}$${\displaystyle {^{n}0}}$${\displaystyle {}^{n}i}$

La exponencial no está definida de manera consistente. Por lo tanto, las tetraciones no están claramente definidas por la fórmula dada anteriormente. Sin embargo, está bien definida y existe: ^[10]${\displaystyle 0^{0}}$${\displaystyle \,{^{n}0}}$${\displaystyle \lim _{x\rightarrow 0}{}^{n}x}$

${\displaystyle \lim _{x\rightarrow 0}{}^{n}x={\begin{cases}1,&n{\text{ even}}\\0,&n{\text{ odd}}\end{cases}}}$

De esta manera podríamos definir de manera consistente . Esto es análogo a definir .${\displaystyle {}^{n}0=\lim _{x\rightarrow 0}{}^{n}x}$${\displaystyle 0^{0}=1}$

Con esta extensión , por lo que la regla de la definición original sigue siendo válida.${\displaystyle {}^{0}0=1}$${\displaystyle {^{0}a}=1}$

Como los números complejos pueden elevarse a potencias, la tetración se puede aplicar a bases de la forma z = a + bi (donde a y b son reales). Por ejemplo, en ⁿ z con z = i , la tetración se logra utilizando la rama principal del logaritmo natural; utilizando la fórmula de Euler obtenemos la relación:

${\displaystyle i^{a+bi}=e^{{\frac {1}{2}}{\pi i}(a+bi)}=e^{-{\frac {1}{2}}{\pi b}}\left(\cos {\frac {\pi a}{2}}+i\sin {\frac {\pi a}{2}}\right)}$

Esto sugiere una definición recursiva para ^{n +1} i = a′ + b′i dado cualquier ⁿ i = a + bi :

${\displaystyle {\begin{aligned}a'&=e^{-{\frac {1}{2}}{\pi b}}\cos {\frac {\pi a}{2}}\\[2pt]b'&=e^{-{\frac {1}{2}}{\pi b}}\sin {\frac {\pi a}{2}}\end{aligned}}}$

Se pueden derivar los siguientes valores aproximados:

Valores de tetración de bases complejas

${\textstyle {}^{n}i}$	Valor aproximado
${\textstyle {}^{1}i=i}$	i
${\textstyle {}^{2}i=i^{\left({}^{1}i\right)}}$	0,2079
${\textstyle {}^{3}i=i^{\left({}^{2}i\right)}}$	0,9472 + 0,3208 yo
${\textstyle {}^{4}i=i^{\left({}^{3}i\right)}}$	0,0501 + 0,6021 yo
${\textstyle {}^{5}i=i^{\left({}^{4}i\right)}}$	0,3872 + 0,0305 yo
${\textstyle {}^{6}i=i^{\left({}^{5}i\right)}}$	0,7823 + 0,5446 yo
${\textstyle {}^{7}i=i^{\left({}^{6}i\right)}}$	0,1426 + 0,4005 yo
${\textstyle {}^{8}i=i^{\left({}^{7}i\right)}}$	0,5198 + 0,1184 yo
${\textstyle {}^{9}i=i^{\left({}^{8}i\right)}}$	0,5686 + 0,6051 yo

Resolviendo la relación inversa, como en la sección anterior, se obtienen los valores esperados ⁰ i = 1 y ⁻¹ i = 0 , con valores negativos de n que dan resultados infinitos en el eje imaginario. Trazada en el plano complejo , toda la secuencia se desvía en espiral hasta el límite 0,4383 + 0,3606 i , que podría interpretarse como el valor donde n es infinito.

Estas secuencias de tetración se han estudiado desde la época de Euler, pero se comprenden mal debido a su comportamiento caótico. La mayoría de las investigaciones publicadas históricamente se han centrado en la convergencia de la función exponencial infinitamente iterada. La investigación actual se ha beneficiado enormemente de la llegada de potentes ordenadores con software de matemáticas simbólicas y fractales . Gran parte de lo que se sabe sobre la tetración proviene del conocimiento general de la dinámica compleja y de la investigación específica del mapa exponencial. ^{[ cita requerida ]}

La tetración se puede extender a alturas infinitas ; es decir, para ciertos valores de a y n en , existe un resultado bien definido para un n infinito . Esto se debe a que para bases dentro de un cierto intervalo, la tetración converge a un valor finito a medida que la altura tiende a infinito . Por ejemplo, converge a 2 y, por lo tanto, se puede decir que es igual a 2. La tendencia hacia 2 se puede ver evaluando una pequeña torre finita:${\displaystyle {}^{n}a}$${\displaystyle {\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{\cdot ^{\cdot ^{\cdot }}}}}}$

${\displaystyle {\begin{aligned}{\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{1.414}}}}}&\approx {\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{1.63}}}}\\&\approx {\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{1.76}}}\\&\approx {\sqrt {2}}^{{\sqrt {2}}^{1.84}}\\&\approx {\sqrt {2}}^{1.89}\\&\approx 1.93\end{aligned}}}$

En general, la exponencial infinitamente iterada , definida como el límite de cuando n tiende a infinito, converge para e ^{− e} ≤ x ≤ e ^{1/ e} , aproximadamente el intervalo de 0,066 a 1,44, un resultado mostrado por Leonhard Euler . ^[11] El límite, si existe, es una solución real positiva de la ecuación y = x ^y . Por lo tanto, x = y ^{1/ y} . El límite que define la exponencial infinita de x no existe cuando x > e ^{1/ e} porque el máximo de y ^{1/ y} es e ^{1/ e} . El límite tampoco existe cuando 0 < x < e ^{− e} .${\displaystyle x^{x^{\cdot ^{\cdot ^{\cdot }}}}\!\!}$${\displaystyle {}^{n}x}$

Esto puede extenderse a números complejos z con la definición:

${\displaystyle {}^{\infty }z=z^{z^{\cdot ^{\cdot ^{\cdot }}}}={\frac {\mathrm {W} (-\ln {z})}{-\ln {z}}}~,}$

donde W representa la función W de Lambert .

Como el límite y = ^∞ x (si existe en la recta real positiva, es decir para e ^{− e} ≤ x ≤ e ^{1/ e} ) debe satisfacer x ^y = y , vemos que x ↦ y = ^∞ x es (la rama inferior de) la función inversa de y ↦ x = y ^{1/ y} .

Podemos utilizar la regla recursiva para la tetración,

${\displaystyle {^{k+1}a}=a^{\left({^{k}a}\right)},}$

Para probar :${\displaystyle {}^{-1}a}$

${\displaystyle ^{k}a=\log _{a}\left(^{k+1}a\right);}$

Sustituyendo −1 por k obtenemos

${\displaystyle {}^{-1}a=\log _{a}\left({}^{0}a\right)=\log _{a}1=0}$. ^[12]

Los valores negativos más pequeños no se pueden definir bien de esta manera. Sustituyendo −2 por k en la misma ecuación se obtiene

${\displaystyle {}^{-2}a=\log _{a}\left({}^{-1}a\right)=\log _{a}0=-\infty }$

que no están bien definidos. Sin embargo, a veces pueden considerarse conjuntos. ^[12]

Para , cualquier definición de es consistente con la regla porque${\displaystyle n=1}$${\displaystyle \,\!{^{-1}1}}$

${\displaystyle {^{0}1}=1=1^{n}}$Para cualquier .${\displaystyle \,\!n={^{-1}1}}$

This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (July 2019) (Learn how and when to remove this message)

En este momento no existe una solución comúnmente aceptada para el problema general de extender la tetración a los valores reales o complejos de n . Sin embargo, ha habido múltiples enfoques para abordar el tema, y ​​a continuación se describen diferentes enfoques.

En general, el problema es encontrar —para cualquier real a > 0— una función superexponencial sobre real x > −2 que satisfaga${\displaystyle \,f(x)={}^{x}a}$

• ${\displaystyle \,{}^{-1}a=0}$
• ${\displaystyle \,{}^{0}a=1}$
• ${\displaystyle \,{}^{x}a=a^{\left({}^{x-1}a\right)}}$para todos los reales ^[13]${\displaystyle x>-1.}$

Para encontrar una extensión más natural, normalmente se requieren uno o más requisitos adicionales. Por lo general, se trata de una recopilación de los siguientes:

• Un requisito de continuidad (generalmente sólo que sea continuo en ambas variables para ).${\displaystyle {}^{x}a}$${\displaystyle x>0}$
• Un requisito de diferenciabilidad (puede ser una vez, dos veces, k veces o infinitamente diferenciable en x ).
• Un requisito de regularidad (que implica que x es dos veces diferenciable ) que:

  ${\displaystyle \left({\frac {d^{2}}{dx^{2}}}f(x)>0\right)}$a pesar de${\displaystyle x>0}$

El cuarto requisito difiere de un autor a otro y de un enfoque a otro. Hay dos enfoques principales para extender la tetración a alturas reales: uno se basa en el requisito de regularidad y el otro en el requisito de diferenciabilidad . Estos dos enfoques parecen ser tan diferentes que no pueden conciliarse, ya que producen resultados incoherentes entre sí. ^{[ cita requerida ]}

Cuando se define para un intervalo de longitud uno, la función completa se deduce fácilmente para todo x > −2 .${\displaystyle \,{}^{x}a}$

Una aproximación lineal (solución al requisito de continuidad, aproximación al requisito de diferenciabilidad) viene dada por:

${\displaystyle {}^{x}a\approx {\begin{cases}\log _{a}\left(^{x+1}a\right)&x\leq -1\\1+x&-1<x\leq 0\\a^{\left(^{x-1}a\right)}&0<x\end{cases}}}$

por eso:

Valores de aproximación lineal

Aproximación	Dominio
${\textstyle {}^{x}a\approx x+1}$	para −1 < x < 0
${\textstyle {}^{x}a\approx a^{x}}$	para 0 < x < 1
${\textstyle {}^{x}a\approx a^{a^{(x-1)}}}$	para 1 < x < 2

y así sucesivamente. Sin embargo, solo es diferenciable por partes; en valores enteros de x la derivada se multiplica por . Es continuamente diferenciable para si y solo si . Por ejemplo, utilizando estos métodos y${\displaystyle \ln {a}}$${\displaystyle x>-2}$${\displaystyle a=e}$${\displaystyle {}^{\frac {\pi }{2}}e\approx 5.868...}$${\displaystyle {}^{-4.3}0.5\approx 4.03335...}$

Un teorema principal en el artículo de Hooshmand ^[6] establece: Sea . Si es continua y satisface las condiciones:${\displaystyle 0<a\neq 1}$${\displaystyle f:(-2,+\infty )\rightarrow \mathbb {R} }$

• ${\displaystyle f(x)=a^{f(x-1)}\;\;{\text{for all}}\;\;x>-1,\;f(0)=1,}$
• ${\displaystyle f}$es diferenciable en (−1, 0) ,
• ${\displaystyle f^{\prime }}$es una función no decreciente o no creciente en (−1, 0) ,
• ${\displaystyle f^{\prime }\left(0^{+}\right)=(\ln a)f^{\prime }\left(0^{-}\right){\text{ or }}f^{\prime }\left(-1^{+}\right)=f^{\prime }\left(0^{-}\right).}$

entonces se determina de forma única a través de la ecuación${\displaystyle f}$

${\displaystyle f(x)=\exp _{a}^{[x]}\left(a^{(x)}\right)=\exp _{a}^{[x+1]}((x))\quad {\text{for all}}\;\;x>-2,}$

donde denota la parte fraccionaria de x y es la función iterada de la función .${\displaystyle (x)=x-[x]}$${\displaystyle \exp _{a}^{[x]}}$${\displaystyle [x]}$${\displaystyle \exp _{a}}$

La prueba es que las condiciones segunda a cuarta implican trivialmente que f es una función lineal en [−1, 0] .

La aproximación lineal a la función tetratónica natural es continuamente diferenciable, pero su segunda derivada no existe en valores enteros de su argumento. Hooshmand derivó otro teorema de unicidad para ella que establece:${\displaystyle {}^{x}e}$

Si es una función continua que satisface:${\displaystyle f:(-2,+\infty )\rightarrow \mathbb {R} }$

• ${\displaystyle f(x)=e^{f(x-1)}\;\;{\text{for all}}\;\;x>-1,\;f(0)=1,}$
• ${\displaystyle f}$es convexo en (−1, 0) ,
• ${\displaystyle f^{\prime }\left(0^{-}\right)\leq f^{\prime }\left(0^{+}\right).}$

entonces . [Aquí está el nombre de Hooshmand para la aproximación lineal a la función de tetración natural.]${\displaystyle f={\text{uxp}}}$${\displaystyle f={\text{uxp}}}$

La prueba es muy parecida a la anterior; la ecuación de recursión asegura que y luego la condición de convexidad implica que es lineal en (−1, 0) .${\displaystyle f^{\prime }(-1^{+})=f^{\prime }(0^{+}),}$${\displaystyle f}$

Por lo tanto, la aproximación lineal a la tetración natural es la única solución de la ecuación y que es convexa en (−1, +∞) . Todas las demás soluciones suficientemente diferenciables deben tener un punto de inflexión en el intervalo (−1, 0) .${\displaystyle f(x)=e^{f(x-1)}\;\;(x>-1)}$${\displaystyle f(0)=1}$

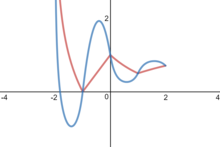
Más allá de las aproximaciones lineales, una aproximación cuadrática (al requisito de diferenciabilidad) viene dada por:

${\displaystyle {}^{x}a\approx {\begin{cases}\log _{a}\left({}^{x+1}a\right)&x\leq -1\\1+{\frac {2\ln(a)}{1\;+\;\ln(a)}}x-{\frac {1\;-\;\ln(a)}{1\;+\;\ln(a)}}x^{2}&-1<x\leq 0\\a^{\left({}^{x-1}a\right)}&x>0\end{cases}}}$

que es diferenciable para todos , pero no dos veces diferenciable. Por ejemplo, Si esto es lo mismo que la aproximación lineal. ^[1]${\displaystyle x>0}$${\displaystyle {}^{\frac {1}{2}}2\approx 1.45933...}$${\displaystyle a=e}$

Por la forma en que se calcula, esta función no se "anula", a diferencia de los exponentes, donde . Es decir,${\displaystyle \left(a^{\frac {1}{n}}\right)^{n}=a}$

${\displaystyle {}^{n}\left({}^{\frac {1}{n}}a\right)=\underbrace {\left({}^{\frac {1}{n}}a\right)^{\left({}^{\frac {1}{n}}a\right)^{\cdot ^{\cdot ^{\cdot ^{\cdot ^{\left({}^{\frac {1}{n}}a\right)}}}}}}} _{n}\neq a}$.

Así como existe una aproximación cuadrática, también existen aproximaciones cúbicas y métodos para generalizar a aproximaciones de grado n , aunque son mucho más difíciles de manejar. ^{[1] [14]}

Aproximación binomial cerca de uno

Utilizando la fórmula de aproximación binomial

${\displaystyle (1+x)^{\alpha }\approx 1+\alpha x.}$

Para valores pequeños de x, podemos anidar exponentes tanto como queramos

${\displaystyle ^{2}(1+x)=(1+x)^{(1+x)}\approx 1+x(1+x)=1+x+x^{2}}$

${\displaystyle ^{3}(1+x)=(1+x)^{((1+x)^{(1+x)})}\approx 1+x(1+x+x^{2})=1+x+x^{2}+x^{3}}$

Significado:

${\displaystyle ^{n}(1+x)\approx \sum _{k=1}^{n}x^{k}}$

Podemos generalizar esta suma para cualquier n, real o complejo.

${\displaystyle (x^{n-1}-1)/(x-1)}$

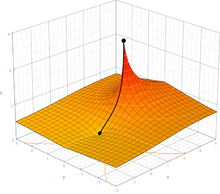
En 2017, se demostró ^[15] que existe una función única F que es una solución de la ecuación F ( z + 1) = exp( F ( z )) y satisface las condiciones adicionales de que F (0) = 1 y F ( z ) se acerca a los puntos fijos del logaritmo (aproximadamente 0,318 ± 1,337 i ) cuando z se acerca a ± i ∞ y que F es holomorfa en todo el plano complejo z , excepto en la parte del eje real en z ≤ −2 . Esta prueba confirma una conjetura previa . ^[16] La construcción de dicha función fue demostrada originalmente por Kneser en 1950. ^[17] El mapa complejo de esta función se muestra en la figura de la derecha. La prueba también funciona para otras bases además de e , siempre que la base sea mayor que . El trabajo posterior extendió la construcción a todas las bases complejas. ^[18]${\displaystyle e^{\frac {1}{e}}\approx 1.445}$

El requisito de que la tetración sea holomorfa es importante para su unicidad. Muchas funciones S pueden construirse como

${\displaystyle S(z)=F\!\left(~z~+\sum _{n=1}^{\infty }\sin(2\pi nz)~\alpha _{n}+\sum _{n=1}^{\infty }{\Big (}1-\cos(2\pi nz){\Big )}~\beta _{n}\right)}$

donde α y β son secuencias reales que decaen lo suficientemente rápido para proporcionar la convergencia de la serie , al menos en valores moderados de Im  z .

La función S satisface las ecuaciones de tetración S ( z + 1) = exp( S ( z )) , S (0) = 1 , y si α _n y β _n se aproximan a 0 lo suficientemente rápido será analítica en un entorno del eje real positivo. Sin embargo, si algunos elementos de { α } o { β } no son cero, entonces la función S tiene multitud de singularidades y líneas de corte adicionales en el plano complejo, debido al crecimiento exponencial de seno y coseno a lo largo del eje imaginario; cuanto menores sean los coeficientes { α } y { β } , más alejadas estarán estas singularidades del eje real.

La extensión de la tetración al plano complejo es, pues, esencial para la unicidad; la tetración real-analítica no es única.

La tetración se puede definir para números ordinales mediante inducción transfinita. Para todos los α y todos los β > 0 :$${\displaystyle {}^{0}\alpha =1}$$$${\displaystyle {}^{\beta }\alpha =\sup(\{\alpha ^{{}^{\gamma }\alpha }:\gamma <\beta \})\,.}$$

La tetración (restringida a ) no es una función recursiva elemental . Se puede demostrar por inducción que para cada función recursiva elemental f , existe una constante c tal que${\displaystyle \mathbb {N} ^{2}}$

${\displaystyle f(x)\leq \underbrace {2^{2^{\cdot ^{\cdot ^{x}}}}} _{c}.}$

Denotamos el lado derecho por . Supongamos, por el contrario, que la tetración es recursiva elemental. también es recursiva elemental. Por la desigualdad anterior, existe una constante c tal que . Al hacer , tenemos que , una contradicción.${\displaystyle g(c,x)}$${\displaystyle g(x,x)+1}$${\displaystyle g(x,x)+1\leq g(c,x)}$${\displaystyle x=c}$${\displaystyle g(c,c)+1\leq g(c,c)}$

La exponenciación tiene dos operaciones inversas: raíces y logaritmos . Análogamente, las inversas de la tetración se denominan a menudo superraíz y superlogaritmo (de hecho, todas las hiperoperaciones mayores o iguales a 3 tienen inversas análogas); por ejemplo, en la función , las dos inversas son la superraíz cúbica de y y el superlogaritmo base  y de x .${\displaystyle {^{3}}y=x}$

La superraíz es la operación inversa de la tetración con respecto a la base: si , entonces y es una n- ésima superraíz de x ( o ).${\displaystyle ^{n}y=x}$${\displaystyle {\sqrt[{n}]{x}}_{s}}$${\displaystyle {\sqrt[{4}]{x}}_{s}}$

Por ejemplo,

${\displaystyle ^{4}2=2^{2^{2^{2}}}=65{,}536}$

Entonces 2 es la cuarta súper raíz de 65,536.

La superraíz de segundo orden , superraíz cuadrada o superraíz cuadrada tiene dos notaciones equivalentes, y . Es la inversa de y se puede representar con la función W de Lambert : ^[19]${\displaystyle \mathrm {ssrt} (x)}$${\displaystyle {\sqrt {x}}_{s}}$${\displaystyle ^{2}x=x^{x}}$

${\displaystyle \mathrm {ssrt} (x)=\exp(W(\ln x))={\frac {\ln x}{W(\ln x)}}}$

La función también ilustra la naturaleza reflexiva de las funciones raíz y logaritmo, ya que la ecuación a continuación solo es verdadera cuando :${\displaystyle y=\mathrm {ssrt} (x)}$

${\displaystyle {\sqrt[{y}]{x}}=\log _{y}x}$

Al igual que las raíces cuadradas , la superraíz cuadrada de x puede no tener una única solución. A diferencia de las raíces cuadradas, determinar el número de superraíces cuadradas de x puede ser difícil. En general, si , entonces x tiene dos superraíces cuadradas positivas entre 0 y 1; y si , entonces x tiene una superraíz cuadrada positiva mayor que 1. Si x es positivo y menor que no tiene ninguna superraíz cuadrada real , pero la fórmula dada anteriormente produce infinitas raíces complejas contables para cualquier x finito distinto de 1. ^[19] La función se ha utilizado para determinar el tamaño de los clústeres de datos . ^[20]${\displaystyle e^{-1/e}<x<1}$${\displaystyle x>1}$${\displaystyle e^{-1/e}}$

En :${\displaystyle x=1}$

$${\displaystyle \mathrm {ssrt} (x)=1+(x-1)-(x-1)^{2}+{\frac {3}{2}}(x-1)^{3}-{\frac {17}{6}}(x-1)^{4}+{\frac {37}{6}}(x-1)^{5}-{\frac {1759}{120}}(x-1)^{6}+{\frac {13279}{360}}(x-1)^{7}+{\mathcal {O}}{\left((x-1)^{8}\right)}}$$

Una de las fórmulas más sencillas y rápidas para obtener una superraíz de tercer grado es la fórmula recursiva. Si se utiliza:${\displaystyle y=x^{x^{x}}}$

• ${\displaystyle x_{0}=1}$
• ${\displaystyle x_{n+1}=\exp(W(W(x_{n}\ln y)))}$

Para cada entero n > 2 , la función ⁿ x está definida y es creciente para x ≥ 1 , y ⁿ 1 = 1 , de modo que la n ésima superraíz de x , , existe para x ≥ 1 .${\displaystyle {\sqrt[{n}]{x}}_{s}}$

Sin embargo, si se utiliza la aproximación lineal anterior, entonces si −1 < y ≤ 0 , entonces no puede existir.${\displaystyle ^{y}x=y+1}$${\displaystyle ^{y}{\sqrt {y+1}}_{s}}$

De la misma manera que la superraíz cuadrada, la terminología para otras superraíces puede basarse en las raíces normales : las "superraíces cúbicas" pueden expresarse como ; la "cuarta superraíz" puede expresarse como ; y la " n -ésima superraíz" es . Nótese que puede no estar definida de manera única, porque puede haber más de una n - ^ésima raíz. Por ejemplo, x tiene una única superraíz (real) si n es impar , y hasta dos si n es par . ^{[ cita requerida ]}${\displaystyle {\sqrt[{3}]{x}}_{s}}$${\displaystyle {\sqrt[{4}]{x}}_{s}}$${\displaystyle {\sqrt[{n}]{x}}_{s}}$${\displaystyle {\sqrt[{n}]{x}}_{s}}$

Al igual que con la extensión de la tetración a alturas infinitas, la superraíz se puede extender a n = ∞ , quedando bien definida si 1/ e ≤ x ≤ e . Nótese que y por lo tanto que . Por lo tanto, cuando está bien definida, y , a diferencia de la tetración normal, es una función elemental . Por ejemplo, .${\displaystyle x={^{\infty }y}=y^{\left[^{\infty }y\right]}=y^{x},}$${\displaystyle y=x^{1/x}}$${\displaystyle {\sqrt[{\infty }]{x}}_{s}=x^{1/x}}$${\displaystyle {\sqrt[{\infty }]{2}}_{s}=2^{1/2}={\sqrt {2}}}$

Del teorema de Gelfond-Schneider se desprende que la superraíz de cualquier entero positivo n es entera o trascendental , y es entera o irracional. ^[21] Todavía es una cuestión abierta si las superraíces irracionales son trascendentales en el último caso.${\displaystyle {\sqrt {n}}_{s}}$${\displaystyle {\sqrt[{3}]{n}}_{s}}$

Una vez que se selecciona una definición de tetración continua creciente (en x ), ^x a , se define el superlogaritmo correspondiente o para todos los números reales x y a > 1 .${\displaystyle \operatorname {slog} _{a}x}$${\displaystyle \log _{a}^{4}x}$

La función slog _a  x satisface:

${\displaystyle {\begin{aligned}\operatorname {slog} _{a}{^{x}a}&=x\\\operatorname {slog} _{a}a^{x}&=1+\operatorname {slog} _{a}x\\\operatorname {slog} _{a}x&=1+\operatorname {slog} _{a}\log _{a}x\\\operatorname {slog} _{a}x&\geq -2\end{aligned}}}$

Además de los problemas con las extensiones de la tetración, hay varias preguntas abiertas respecto de la tetración, particularmente cuando se refieren a las relaciones entre sistemas numéricos como los números enteros y los números irracionales :

• No se sabe si existe un entero positivo n para el cual ⁿ π para , porque no pudimos calcular con suficiente precisión el número de dígitos después de los puntos decimales de . ^{[22] [ cita(s) adicional(es) necesaria(s ) ]} Es similar para ⁿ e para , ya que no conocemos ningún otro método además de algún cálculo directo. De hecho, dado que , entonces . Dados y , entonces para . Se cree que ⁿ e no es un entero para ningún entero positivo n , debido a la independencia algebraica de , dada la conjetura de Schanuel . ^[23]${\displaystyle n\geq 4}$${\displaystyle \pi }$${\displaystyle n\geq 5}$${\displaystyle \log _{10}(e)\cdot {}^{3}e=1656520.36764}$${\displaystyle {}^{4}e>2\cdot 10^{1656520}}$${\displaystyle {}^{3}\pi <1.35\cdot 10^{18}\ll 10^{1656520}}$${\displaystyle \pi <e^{2}}$${\displaystyle {}^{4}\pi <{}^{n}e}$${\displaystyle n\geq 5}$${\displaystyle e,{}^{2}e,{}^{3}e,\dots }$
• No se sabe si ⁿ q es racional para cualquier entero positivo n y racional positivo no entero q . ^[21] Por ejemplo, no se sabe si la raíz positiva de la ecuación ⁴ x = 2 es un número racional. ^{[ cita requerida ]}
• No se sabe si ^e π o ^π e son racionales o no.

Para cada gráfico H en h vértices y cada ε > 0 , defina

${\displaystyle D=2\uparrow \uparrow 5h^{4}\log(1/\varepsilon ).}$

Entonces, cada grafo G en n vértices con como máximo n ^h /D copias de H se puede hacer libre de H eliminando como máximo εn ² aristas. ^[24]

Wikimedia Commons tiene medios relacionados con tetración .

Busque tetración en Wikcionario, el diccionario libre.

• Función de Ackermann
• Notación O grande
• Función exponencial doble
• Hiperoperación
• Logaritmo iterado
• Aritmética de índices de nivel simétricos

• Daniel Geisler, Tetración
• Ioannis Galidakis, On extending hyper4 to nonintegers (sin fecha, 2006 o anterior) (Una revisión más simple y fácil de leer de la siguiente referencia)
• Ioannis Galidakis, Sobre la extensión de hyper4 y la notación de flecha hacia arriba de Knuth a los números reales (sin fecha, 2006 o anterior).
• Robert Munafo, Extensión de la función hiper4 a números reales (Una discusión informal sobre la extensión de la tetración a los números reales).
• Lode Vandevenne, Tetración de la raíz cuadrada de dos . (2004). (Intento de extender la tetración a los números reales.)
• Ioannis Galidakis, Matemáticas , (Lista definitiva de referencias a la investigación sobre tetración. Mucha información sobre la función W de Lambert, superficies de Riemann y continuación analítica).
• Joseph MacDonell, Algunos puntos críticos de la función de hiperpotencia Archivado el 17 de enero de 2010 en Wayback Machine .
• Dave L. Renfro, Páginas web para exponenciales iterados infinitamente
• Knobel, R. (1981). "Exponentials Reiterated". American Mathematical Monthly . 88 (4): 235–252. doi :10.1080/00029890.1981.11995239.
• Hans Maurer, "Über die Funktion für ganzzahliges Argument (Abundanzen)". Mittheilungen der Mathematische Gesellschaft en Hamburgo 4 , (1901), p. 33–50. (Referencia al uso de del artículo de Knobel).${\displaystyle y=x^{[x^{[x(\cdots )]}]}}$ ${\displaystyle \ {^{n}a}}$
• La cuarta operación
• Luca Moroni, Las extrañas propiedades de la torre de poder infinito (https://arxiv.org/abs/1908.05559)

• Galidakis, Ioannis; Weisstein, Eric Wolfgang . "Torre de energía". MathWorld . Consultado el 5 de julio de 2019 .