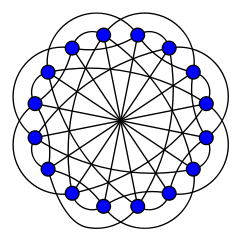
Gráfico de Clebsch

Gráfico de Clebsch
Llamado en honor a	Alfred Clebsch
Vértices	16
Bordes	40
Radio	2
Diámetro	2
Circunferencia	4
Automorfismos	1920
Número cromático	4 [1]
Índice cromático	5
Grosor del libro	4
Número de cola	3
Propiedades	Grafo de Cayley hamiltoniano fuertemente regular Transitorio por vértices Transitorio por aristas Transitorio por distancias .
Tabla de gráficos y parámetros

En el campo matemático de la teoría de grafos , el grafo de Clebsch es uno de dos grafos complementarios en 16 vértices, un grafo regular de 5 con 40 aristas y un grafo regular de 10 con 80 aristas. El grafo de 80 aristas es el grafo cúbico dividido por la mitad de dimensión 5 ; Seidel (1968) lo llamó el nombre de grafo de Clebsch ^[2] debido a su relación con la configuración de 16 líneas en la superficie cuártica descubierta en 1868 por el matemático alemán Alfred Clebsch . La variante de 40 aristas es el grafo cúbico plegado de dimensión 5 ; también se lo conoce como grafo de Greenwood-Gleason después del trabajo de Robert E. Greenwood y Andrew M. Gleason  (1955), quienes lo usaron para evaluar el número de Ramsey R (3,3,3) = 17. ^{[3] [4] [5]}

El grafo cúbico plegado de dimensión 5 (el grafo Clebsch regular de 5) se puede construir añadiendo aristas entre pares opuestos de vértices en un grafo hipercubo de 4 dimensiones. (En un hipercubo de n dimensiones, un par de vértices son opuestos si el camino más corto entre ellos tiene n aristas). Alternativamente, se puede formar a partir de un grafo hipercubo de 5 dimensiones identificando juntos (o contrayendo) cada par opuesto de vértices.

Otra construcción, que conduce al mismo gráfico, es crear un vértice para cada elemento del campo finito GF(16), y conectar dos vértices mediante una arista siempre que la diferencia entre los dos elementos del campo correspondientes sea un cubo perfecto . ^[6]

El grafo cúbico de dimensión 5 dividido por la mitad (el grafo de Clebsch regular de 10) es el complemento del grafo regular de 5. También puede construirse a partir de los vértices de un hipercubo de 5 dimensiones, conectando pares de vértices cuya distancia de Hamming sea exactamente dos. Esta construcción es un ejemplo de la construcción de grafos de Frankl-Rödl . Produce dos subconjuntos de 16 vértices que están desconectados entre sí; ambos medios cuadrados del hipercubo son isomorfos al grafo de Clebsch regular de 10. Se pueden producir dos copias del grafo de Clebsch regular de 5 de la misma manera a partir de un hipercubo de 5 dimensiones, conectando pares de vértices cuya distancia de Hamming sea exactamente cuatro.

El grafo de Clebsch 5-regular es un grafo fuertemente regular de grado 5 con parámetros . ^{[7] [8]} Su complemento, el grafo de Clebsch 10-regular, es por lo tanto también un grafo fuertemente regular, ^{[1] [4]} con parámetros .${\displaystyle (v,k,\lambda,\mu)=(16,5,0,2)}$${\estilo de visualización (16,10,6,6)}$

El grafo de Clebsch regular de 5 elementos es hamiltoniano , no plano y no euleriano . También es conexo por 5 vértices y conexo por 5 aristas . El subgrafo que es inducido por los diez elementos no vecinos de cualquier vértice en este grafo forma una copia isomorfa del grafo de Petersen .

Tiene un grosor de libro de 4 y un número de cola de 3. ^[9]

Las aristas del grafo completo K ₁₆ pueden dividirse en tres copias disjuntas del grafo de Clebsch 5-regular. Como el grafo de Clebsch es un grafo sin triángulos , esto demuestra que existe una tricoloración sin triángulos de las aristas de K ₁₆ ; es decir, que el número de Ramsey R (3,3,3) que describe el número mínimo de vértices en un grafo completo sin una tricoloración sin triángulos es al menos 17. Greenwood y Gleason (1955) utilizaron esta construcción como parte de su prueba de que R (3,3,3) = 17. ^{[5] [10]}

El grafo de Clebsch 5-regular puede colorearse con cuatro colores, pero no con tres: su conjunto independiente más grande tiene cinco vértices, no lo suficiente para dividir el grafo en tres clases de colores independientes. Contiene como subgrafo inducido el grafo de Grötzsch , el grafo cuatricromático sin triángulos más pequeño , y cada subgrafo inducido cuatricromático del grafo de Clebsch es un supergrafo del grafo de Grötzsch. Más fuertemente, cada grafo cuatricromático sin triángulos sin camino inducido de longitud seis o más es un subgrafo inducido del grafo de Clebsch y un supergrafo inducido del grafo de Grötzsch. ^[11]

El gráfico de Clebsch 5-regular es el gráfico de Keller de dimensión dos, parte de una familia de gráficos utilizados para encontrar teselaciones de espacios euclidianos de alta dimensión mediante hipercubos en los que ninguno de los dos se encuentra cara a cara.

El gráfico de Clebsch 5-regular se puede incrustar como una función regular en la variedad orientable de género 5, formando caras pentagonales; y en la superficie no orientable de género 6, formando caras tetragonales.

El polinomio característico del grafo de Clebsch 5-regular es . Debido a que este polinomio se puede factorizar completamente en términos lineales con coeficientes enteros, el grafo de Clebsch es un grafo integral : su espectro consta enteramente de números enteros. ^[4] El grafo de Clebsch es el único grafo con este polinomio característico, lo que lo convierte en un grafo determinado por su espectro.${\displaystyle (x+3)^{5}(x-1)^{10}(x-5)}$

El grafo de Clebsch 5-regular es un grafo de Cayley con un grupo de automorfismos de orden 1920, isomorfo al grupo de Coxeter . Como grafo de Cayley, su grupo de automorfismos actúa transitivamente sobre sus vértices, lo que lo hace transitivo por vértices . De hecho, es transitivo por arcos , por lo tanto transitivo por aristas y transitivo por distancias . También es conexo-homogéneo , lo que significa que cada isomorfismo entre dos subgrafos inducidos conexos se puede extender a un automorfismo de todo el grafo.$Estilo de visualización D_{5}$

• 
  El gráfico de Clebsch es hamiltoniano .
• 
  El número acromático del grafo de Clebsch es 8.
• 
  El número cromático del grafo de Clebsch es 4.
• 
  El índice cromático del grafo de Clebsch es 5.
• 
  Construcción del grafo de Clebsch a partir de un grafo de hipercubo .