Hexadecimal
| Parte de una serie sobre |
| Sistemas de numeración |
|---|
| Lista de sistemas de numeración |
En matemáticas e informática , el sistema de numeración hexadecimal (también base 16 o simplemente hex ) es un sistema de numeración posicional que representa números utilizando una base de dieciséis. A diferencia del sistema decimal que representa números utilizando diez símbolos, el hexadecimal utiliza dieciséis símbolos distintos, más frecuentemente los símbolos "0"–"9" para representar valores del 0 al 9 y "A"–"F" (o "a"–"f") para representar valores del diez al quince.
Los desarrolladores de software y los diseñadores de sistemas utilizan ampliamente los números hexadecimales porque proporcionan una representación conveniente de los valores codificados en binario . Cada dígito hexadecimal representa cuatro bits (dígitos binarios), también conocidos como nibble (o nybble). [1] Por ejemplo, un byte de 6 bits puede tener valores que van desde 000000 hasta 111111 (de 0 a 63 decimal) en formato binario, que se pueden escribir como 00 a 3F en formato hexadecimal.
En matemáticas, normalmente se utiliza un subíndice para especificar la base. Por ejemplo, el valor decimal711 se expresaría en hexadecimal como 2C7 16 . En programación, varias notaciones denotan números hexadecimales, generalmente con un prefijo. El prefijo 0xse usa en C , que denotaría este valor como 0x2C7.
En la codificación de transferencia se utiliza el sistema hexadecimal Base 16 , en el que cada byte del texto sin formato se divide en dos valores de 4 bits y se representa mediante dos dígitos hexadecimales.
Representación
Representación escrita
En la mayoría de los casos de uso actuales, las letras A–F o a–f representan los valores 10–15, mientras que los números 0–9 se utilizan para representar sus valores decimales.
No existe una convención universal para utilizar mayúsculas o minúsculas, por lo que cada una de ellas es predominante o preferida en entornos particulares según los estándares o convenciones de la comunidad; incluso se utiliza una combinación de mayúsculas y minúsculas. Algunas pantallas de siete segmentos utilizan la combinación de mayúsculas y minúsculas "A b C d E F" para distinguir los dígitos A–F entre sí y del 0 al 9.
Existe cierta estandarización en el uso de espacios (en lugar de comas u otros signos de puntuación) para separar valores hexadecimales en una lista larga. Por ejemplo, en el siguiente volcado hexadecimal , cada byte de 8 bits es un número hexadecimal de 2 dígitos, con espacios entre ellos, mientras que el desplazamiento de 32 bits al comienzo es un número hexadecimal de 8 dígitos.
00000000 57 69 6b 69 70 65 64 69 61 2c 20 74 68 65 20 66 00000010 72 65 65 20 65 6e 63 79 63 6c 6f 70 65 64 69 61 20 74 68 61 74 20 61 6e 79 6f 6e 65 20 63 61 6e 00000030 20 65 64 69 74 0a Distinguir del decimal
En contextos en los que la base no está clara, los números hexadecimales pueden ser ambiguos y confundirse con números expresados en otras bases. Existen varias convenciones para expresar valores de forma inequívoca. Un subíndice numérico (escrito en decimal) puede dar la base explícitamente: 159 10 es decimal 159; 159 16 es hexadecimal 159, que equivale a 345 10 . Algunos autores prefieren un subíndice de texto, como 159 decimal y 159 hex , o 159 d y 159 h .
Donald Knuth introdujo el uso de un tipo de letra particular para representar un radio particular en su libro The TeXbook . [2] Las representaciones hexadecimales se escriben allí en un tipo de letra de máquina de escribir : 5A3 , C1F27ED
En los sistemas de texto lineal, como los utilizados en la mayoría de los entornos de programación informática, han surgido diversos métodos:
- Aunque es más conocido por el lenguaje de programación C (y los muchos lenguajes influenciados por C), el prefijo
0xpara indicar una constante hexadecimal puede haber tenido su origen en los sistemas IBM Stretch . Se deriva del0prefijo que ya se utilizaba para las constantes octales . Los valores de bytes se pueden expresar en hexadecimal con el prefijo\xseguido de dos dígitos hexadecimales:'\x1B'representa el carácter de control Esc ;"\x1B[0m\x1B[25;1H"es una cadena que contiene 11 caracteres con dos caracteres Esc incrustados. [3] Para generar un entero como hexadecimal con la familia de funciones printf , se utiliza el código de conversión de formato%Xo .%x - En XML y XHTML , los caracteres se pueden expresar como referencias numéricas hexadecimales mediante la notación , por ejemplo, representa el carácter U+0054 (la letra mayúscula "T"). Si no hay, el número es decimal (por lo tanto, es el mismo carácter). [4]
ode;TxT - En los lenguajes ensambladores derivados de Intel y Modula-2, [5] el hexadecimal se denota con un sufijo H o h : o . Algunas implementaciones requieren un cero inicial cuando el primer carácter del dígito hexadecimal no es un dígito decimal, por lo que se escribiría en lugar de . Algunas otras implementaciones (como NASM) permiten números de estilo C ( ).
FFh05A3H0FFhFFh0x42 - Otros lenguajes ensambladores ( 6502 , Motorola ), Pascal , Delphi , algunas versiones de BASIC ( Commodore ), lenguaje GameMaker , Godot y Forth utilizan
$como prefijo:$5A3,$C1F27ED. - Algunos lenguajes ensambladores (Microchip) utilizan la notación
H'ABCD'(para ABCD 16 ). De manera similar, Fortran 95 utiliza Z'ABCD'. - Ada y VHDL encierran los números hexadecimales entre "comillas numéricas" basadas en:
16#5A3#,16#C1F27ED#. Para las constantes de vector de bits, VHDL utiliza la notaciónx"5A3",x"C1F27ED". [6] - Verilog representa constantes hexadecimales en la forma
8'hFF, donde 8 es el número de bits en el valor y FF es la constante hexadecimal. - Los lenguajes Icon y Smalltalk utilizan el prefijo
16r:16r5A3 - PostScript y Bourne shell y sus derivados denotan hexadecimal con el prefijo
16#:16#5A3,16#C1F27ED. - Common Lisp utiliza los prefijos
#xy#16r. También se puede configurar las variables *read-base* [7] y *print-base* [8] a 16 para cambiar el lector y la impresora de un sistema Common Lisp a la representación de números hexadecimales para leer e imprimir números. Por lo tanto, los números hexadecimales se pueden representar sin el código de prefijo #x o #16r, cuando la base de entrada o salida se ha cambiado a 16. - MSX BASIC , [9] QuickBASIC , FreeBASIC y Visual Basic prefijan números hexadecimales con
&H:&H5A3 - Uso de BBC BASIC y Locomotive BASIC
¶ hexadecimal. [10] - Las series TI-89 y 92 utilizan un
0hprefijo:0h5A3,0hC1F27ED - ALGOL 68 utiliza el prefijo
16rpara indicar números hexadecimales:16r5a3,16rC1F27ED. Los números binarios, cuaternarios (base 4) y octales se pueden especificar de manera similar. - El formato más común para hexadecimal en mainframes IBM ( zSeries ) y computadoras de rango medio ( IBM i ) que ejecutan los sistemas operativos tradicionales ( zOS , zVSE , zVM , TPF , IBM i ) es
X'5A3'oX'C1F27ED', y se usa en ensamblador, PL/I , COBOL , JCL , scripts, comandos y otros lugares. Este formato también era común en otros sistemas IBM (y ahora obsoletos). Ocasionalmente se usaban comillas en lugar de apóstrofos.
Sintaxis que siempre es hexadecimal
A veces se sabe que los números son hexadecimales.
- En las URI (incluidas las URL ), los códigos de caracteres se escriben como pares hexadecimales con el prefijo
%:http://www.example.com/name%20with%20spacesdonde%20es el código para el carácter de espacio (en blanco) , punto de código ASCII 20 en hexadecimal, 32 en decimal. - En el estándar Unicode , un valor de carácter se representa con
U+seguido del valor hexadecimal, por ejemplo,U+00A1el signo de exclamación invertido (¡). - Las referencias de color en HTML, CSS y X Window se pueden expresar con seis dígitos hexadecimales (dos para cada uno de los componentes rojo, verde y azul, en ese orden) prefijados con
#: magenta , por ejemplo, se representa como#FF00FF. [11] CSS también permite abreviaturas de 3 dígitos hexadecimales con un dígito hexadecimal por componente:#FA3abrevia#FFAA33(un naranja dorado: ). - En la codificación entrecomillada e imprimible MIME (extensiones de correo electrónico) , los códigos de caracteres se escriben como pares hexadecimales con el prefijo : es "España" (F1 hex es el código para ñ en el conjunto de caracteres ISO/IEC 8859-1). [12] )
=Espa=F1a - Los datos binarios de PostScript (como los píxeles de una imagen ) se pueden expresar como pares hexadecimales consecutivos sin prefijo:
AA213FD51B3801043FBC... - Cualquier dirección IPv6 se puede escribir como ocho grupos de cuatro dígitos hexadecimales (a veces llamados hextetos ), donde cada grupo está separado por dos puntos (
:). Esta, por ejemplo, es una dirección IPv6 válida:2001:0db8:85a3:0000:0000:8a2e:0370:7334o abreviada eliminando los ceros iniciales como2001:db8:85a3::8a2e:370:7334( Las direcciones IPv4 generalmente se escriben en decimal). - Los identificadores únicos globales se escriben como treinta y dos dígitos hexadecimales, a menudo en agrupaciones desiguales separadas por guiones, por ejemplo
3F2504E0-4F89-41D3-9A0C-0305E82C3301.
Otros símbolos para 10–15 y conjuntos de símbolos en su mayoría diferentes
El uso de las letras A a la F para representar los dígitos superiores al 9 no era universal en la historia temprana de las computadoras.
- Durante la década de 1950, algunas instalaciones, como Bendix-14, favorecieron el uso de los dígitos del 0 al 5 con una raya superior para indicar los valores del 10 al 15 como 0 , 1 , 2 , 3 , 4 y 5 .
- Las computadoras SWAC (1950) [13] y Bendix G-15 (1956) [14] [13] utilizaron las letras minúsculas u , v , w , x , y y z para los valores 10 a 15.
- Las computadoras ORDVAC e ILLIAC I (1952) (y algunos diseños derivados, por ejemplo BRLESC ) usaban las letras mayúsculas K , S , N , J , F y L para los valores 10 a 15. [15] [13]
- El Librascopio LGP-30 (1956) utilizó las letras F , G , J , K , Q y W para los valores 10 a 15. [16] [13]
- En la computadora PERM (1956), los números hexadecimales se escribían como letras O para cero, A a N y P para 1 a 15. Muchas instrucciones de máquina tenían códigos hexadecimales mnemotécnicos ( A = sumar, M = multiplicar, L = cargar, F = punto fijo, etc.); los programas se escribían sin nombres de instrucciones. [17]
- El Honeywell Datamatic D-1000 (1957) utilizó las letras minúsculas b , c , d , e , f y g, mientras que el Elbit 100 (1967) utilizó las letras mayúsculas B , C , D , E , F y G para los valores 10 a 15. [13]
- El Monrobot XI (1960) utilizó las letras S , T , U , V , W y X para los valores 10 a 15. [13]
- El ordenador de parámetros NEC NEAC 1103 (1960) utilizó las letras D , G , H , J , K (y posiblemente V ) para los valores 10-15. [18]
- El Pacific Data Systems 1020 (1964) utilizó las letras L , C , A , S , M y D para los valores 10 a 15. [13]

- Boby Lapointe introdujo nuevos símbolos y nombres numéricos en la notación bibibinaria en 1968.
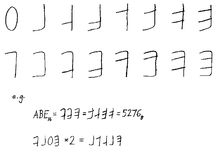
- Bruce Alan Martin, del Laboratorio Nacional de Brookhaven , consideró que la elección de A–F era «ridícula». En una carta de 1968 al editor del CACM , propuso un conjunto de símbolos completamente nuevo basado en las posiciones de los bits. [19]

- En 1972, Ronald O. Whitaker de Rowco Engineering Co. propuso una fuente triangular que permite la "lectura binaria directa" para "permitir tanto la entrada como la salida de las computadoras sin tener en cuenta las matrices de codificación". [20] [21]
- Algunos chips decodificadores de pantalla de siete segmentos (por ejemplo, 74LS47) muestran una salida inesperada debido a la lógica diseñada solo para producir 0-9 correctamente. [22]
Representaciones verbales y digitales
Como no había números tradicionales para representar las cantidades del diez al quince, se volvieron a emplear letras alfabéticas como sustituto. La mayoría de los idiomas europeos carecen de palabras no decimales para algunos de los números del once al quince. Algunas personas leen números hexadecimales dígito por dígito, como un número de teléfono, o utilizando el alfabeto fonético de la OTAN , el Alfabeto Fonético Conjunto del Ejército y la Marina o un sistema ad hoc similar . A raíz de la adopción del hexadecimal entre los programadores del IBM System/360 , Magnuson (1968) [23] sugirió una guía de pronunciación que daba nombres cortos a las letras del hexadecimal; por ejemplo, "A" se pronunciaba "ann", B "bet", C "chris", etc. [23] Rogers (2007) [24] publicó en línea otro sistema de nombres que intenta hacer que la representación verbal sea distinguible en cualquier caso, incluso cuando el número real no contiene los números A–F. En las tablas siguientes se enumeran ejemplos. Babb (2015) elaboró otro sistema de nombres, basándose en un chiste de Silicon Valley . [25]
Otros han propuesto utilizar las convenciones verbales del Código Morse para expresar dígitos hexadecimales de cuatro bits, donde "dit" y "dah" representan cero y uno, respectivamente, de modo que "0000" se expresa como "dit-dit-dit-dit" (....), dah-dit-dit-dah (-..-) expresa el dígito con un valor de nueve, y "dah-dah-dah-dah" (----) expresa el dígito hexadecimal para el decimal 15.

Se han ideado sistemas de conteo de dígitos tanto para sistemas binarios como hexadecimales. Arthur C. Clarke sugirió utilizar cada dedo como un bit de encendido/apagado, lo que permite contar con los dedos desde cero hasta 1023 10 con diez dedos. [26] Otro sistema para contar hasta FF 16 (255 10 ) se ilustra a la derecha.
| Número | Pronunciación |
|---|---|
| A | Ana |
| B | apuesta |
| do | Cristóbal |
| D | punto |
| mi | Ernesto |
| F | helada |
| 1A | Antena |
| A0 | annty |
| 5B | apuesta cincuenta |
| A01C | annty cristiana |
| 1AD0 | Anteen Doty |
| 3A7D | treinta y setenta y un puntos |
| Número | Pronunciación |
|---|---|
| A | diez |
| B | once |
| do | doce |
| D | draco |
| mi | gemelo electrónico |
| F | bueno |
| 10 | Texas |
| 11 | Una teek |
| 1º grado | primer plano |
| 50 | Quinto |
| C0 | doceavo día |
| 100 | cien |
| 1000 | Miles |
| 3E | 3er ciclo-eptwin |
| E1 | Eptek-uno |
| C4A | mil doscientos cuatrocientos diez |
| 1743 | un-mil-setecientos -cuatro-tres |
Señales
El sistema hexadecimal puede expresar números negativos de la misma manera que el decimal: −2A para representar −42 10 , −B01D9 para representar −721369 10 y así sucesivamente.
El hexadecimal también se puede utilizar para expresar los patrones de bits exactos utilizados en el procesador , por lo que una secuencia de dígitos hexadecimales puede representar un valor con signo o incluso un valor de punto flotante . De esta manera, el número negativo −42 10 se puede escribir como FFFF FFD6 en un registro de CPU de 32 bits (en complemento a dos ), como C228 0000 en un registro FPU de 32 bits o C045 0000 0000 0000 en un registro FPU de 64 bits (en el estándar IEEE de punto flotante ).
Notación exponencial hexadecimal
Así como los números decimales se pueden representar en notación exponencial , también lo pueden hacer los números hexadecimales. La notación P utiliza la letra P (o p , por "potencia"), mientras que E (o e ) cumple una función similar en la notación decimal E. El número después de la P es decimal y representa el exponente binario . Aumentar el exponente en 1 multiplica por 2, no por 16: 20p0 = 10p1 = 8p2 = 4p3 = 2p4 = 1p5 . Por lo general, el número se normaliza de modo que los dígitos hexadecimales comiencen con 1. (cero suele ser 0 sin P ).
Ejemplo: 1.3DEp42 representa 1.3DE 16 × 2 42 10 .
La notación P es requerida por el estándar de punto flotante binario IEEE 754-2008 y puede usarse para literales de punto flotante en la edición C99 del lenguaje de programación C. [ 27] Usando los especificadores de conversión %a o %A , esta notación puede ser producida por implementaciones de la familia de funciones printf siguiendo la especificación C99 [28] y el estándar POSIX Single Unix Specification (IEEE Std 1003.1) . [29]
Conversión
Conversión binaria
.jpg/440px-Hewlett-Packard_Model_HP-16C_Programmable_RPN_Calculator,_HP's_First_and_Only_Calculator_esp._for_Programmers,_built_1982-1989_(edited_to_rectangular,_V2).jpg)
La mayoría de las computadoras manipulan datos binarios, pero es difícil para los humanos trabajar con una gran cantidad de dígitos incluso para un número binario relativamente pequeño. Aunque la mayoría de los humanos están familiarizados con el sistema de base 10, es mucho más fácil convertir el binario en hexadecimal que en decimal porque cada dígito hexadecimal se corresponde con un número entero de bits (4 10 ). Este ejemplo convierte 1111 2 en base diez. Dado que cada posición en un numeral binario puede contener un 1 o un 0, su valor se puede determinar fácilmente por su posición desde la derecha:
- 0001 2 = 1 10
- 0010 2 = 2 10
- 0100 2 = 4 10
- 1000 2 = 8 10
Por lo tanto:
| 1111 2 | = 8 10 + 4 10 + 2 10 + 1 10 |
| = 15 10 |
Con un poco de práctica, convertir 1111 2 en F 16 en un solo paso se vuelve fácil (ver la tabla en la representación escrita). La ventaja de usar hexadecimal en lugar de decimal aumenta rápidamente con el tamaño del número. Cuando el número se vuelve grande, la conversión a decimal es muy tediosa. Sin embargo, cuando se convierte en hexadecimal, es trivial considerar la cadena binaria como grupos de 4 dígitos y convertir cada uno en un solo dígito hexadecimal. [30]
Este ejemplo muestra la conversión de un número binario a decimal, asignando cada dígito al valor decimal y sumando los resultados.
| (1001011100) 2 | = 512 10 + 64 10 + 16 10 + 8 10 + 4 10 |
| = 604 10 |
Compare esto con la conversión a hexadecimal, donde cada grupo de cuatro dígitos puede considerarse independientemente y convertirse directamente:
| (1001011100) 2 | = | 0010 | 0101 | 1100 2 | ||
| = | 2 | 5 | C 16 | |||
| = | 25C 16 | |||||
La conversión de hexadecimal a binario es igualmente directa. [30]
Otras conversiones sencillas
Aunque el sistema cuaternario (base 4) se utiliza poco, se puede convertir fácilmente de y hacia hexadecimal o binario. Cada dígito hexadecimal corresponde a un par de dígitos cuaternarios, y cada dígito cuaternario corresponde a un par de dígitos binarios. En el ejemplo anterior 2 5 C 16 = 02 11 30 4 .
El sistema octal (base 8) también se puede convertir con relativa facilidad, aunque no de forma tan trivial como con las bases 2 y 4. Cada dígito octal corresponde a tres dígitos binarios, en lugar de cuatro. Por lo tanto, podemos convertir entre octal y hexadecimal mediante una conversión intermedia a binario seguida de la reagrupación de los dígitos binarios en grupos de tres o cuatro.
Resto de división en la base de origen
Como ocurre con todas las bases, existe un algoritmo sencillo para convertir la representación de un número en hexadecimal realizando operaciones de división de números enteros y resto en la base de origen. En teoría, esto es posible desde cualquier base, pero para la mayoría de los humanos, solo el decimal y para la mayoría de las computadoras, solo el binario (que se puede convertir con métodos mucho más eficientes) se pueden manejar fácilmente con este método.
Sea d el número a representar en hexadecimal, y la serie h i h i−1 ...h 2 h 1 los dígitos hexadecimales que representan el número.
- yo ← 1
- h yo ← d mod 16
- d ← (d − h i ) / 16
- Si d = 0 (devuelve la serie h i ) de lo contrario incrementa i y pasa al paso 2
"16" puede ser reemplazado por cualquier otra base que se desee.
A continuación se muestra una implementación en JavaScript del algoritmo anterior para convertir cualquier número en hexadecimal en una representación de cadena. Su propósito es ilustrar el algoritmo anterior. Sin embargo, para trabajar con datos en serio, es mucho más recomendable trabajar con operadores bit a bit .
función toHex ( d ) { var r = d % 16 ; if ( d - r == 0 ) { volver a Char ( r ); } volver a Hex (( d - r ) / 16 ) + toChar ( r ); } función toChar ( n ) { const alpha = "0123456789ABCDEF" ; devolver alfa . charAt ( n ); } Conversión mediante suma y multiplicación

También es posible realizar la conversión asignando a cada lugar de la base de origen la representación hexadecimal de su valor posicional, antes de realizar la multiplicación y la suma para obtener la representación final. Por ejemplo, para convertir el número B3AD a decimal, se puede dividir el número hexadecimal en sus dígitos: B (11 10 ), 3 (3 10 ), A (10 10 ) y D (13 10 ), y luego obtener el resultado final multiplicando cada representación decimal por 16 p ( siendo p la posición del dígito hexadecimal correspondiente, contando de derecha a izquierda, comenzando con 0). En este caso, tenemos que:
B3AD = (11 × 16 3 ) + (3 × 16 2 ) + (10 × 16 1 ) + (13 × 16 0 )
que es 45997 en base 10.
Herramientas para la conversión
Muchos sistemas informáticos proporcionan una utilidad de calculadora capaz de realizar conversiones entre varios sistemas numéricos, frecuentemente incluidos los hexadecimales.
En Microsoft Windows , la utilidad Calculadora se puede configurar en modo Programador, que permite realizar conversiones entre bases de datos de 16 (hexadecimal), 10 (decimal), 8 ( octal ) y 2 ( binario ), las bases más utilizadas por los programadores. En el modo Programador, el teclado numérico en pantalla incluye los dígitos hexadecimales de la A a la F, que están activos cuando se selecciona "Hex". Sin embargo, en el modo hexadecimal, la Calculadora de Windows solo admite números enteros.
Aritmética elemental
Las operaciones elementales como la división se pueden realizar indirectamente a través de la conversión a un sistema numérico alternativo , como el sistema decimal comúnmente utilizado o el sistema binario donde cada dígito hexadecimal corresponde a cuatro dígitos binarios.
Alternativamente, también se pueden realizar operaciones elementales directamente dentro del propio sistema hexadecimal, basándose en sus tablas de suma y multiplicación y sus algoritmos estándar correspondientes, como la división larga y el algoritmo de resta tradicional.
Números reales
Números racionales
Al igual que con otros sistemas numéricos, el sistema hexadecimal se puede utilizar para representar números racionales , aunque las expansiones repetidas son comunes ya que dieciséis (10 16 ) tiene un solo factor primo: dos.
Para cualquier base, 0,1 (o "1/10") siempre es equivalente a uno dividido por la representación de ese valor base en su propio sistema numérico. Por lo tanto, ya sea dividiendo uno por dos para binario o dividiendo uno por dieciséis para hexadecimal, ambas fracciones se escriben como 0.1. Debido a que la base 16 es un cuadrado perfecto (4 2 ), las fracciones expresadas en hexadecimal tienen un período impar con mucha más frecuencia que las decimales, y no hay números cíclicos (excepto dígitos simples triviales). Los dígitos recurrentes se exhiben cuando el denominador en términos más bajos tiene un factor primo que no se encuentra en la base; por lo tanto, cuando se usa la notación hexadecimal, todas las fracciones con denominadores que no son una potencia de dos dan como resultado una cadena infinita de dígitos recurrentes (como tercios y quintos). Esto hace que el hexadecimal (y el binario) sean menos convenientes que el decimal para representar números racionales, ya que una proporción mayor se encuentra fuera de su rango de representación finita.
Todos los números racionales finitamente representables en hexadecimal son también finitamente representables en decimal, duodecimal y sexagesimal : es decir, cualquier número hexadecimal con un número finito de dígitos también tiene un número finito de dígitos cuando se expresa en esas otras bases. Por el contrario, sólo una fracción de aquellos finitamente representables en las últimas bases son finitamente representables en hexadecimal. Por ejemplo, el decimal 0,1 corresponde a la representación recurrente infinita 0,1 9 en hexadecimal. Sin embargo, el hexadecimal es más eficiente que el duodecimal y el sexagesimal para representar fracciones con potencias de dos en el denominador. Por ejemplo, 0,0625 10 (un dieciseisavo) es equivalente a 0,1 16 , 0,09 12 y 0;3,45 60 .
| norte | Factores primos decimales de: base, b = 10: 2 , 5 ; b − 1 = 9: 3 ; b + 1 = 11: 11 | Factores primos hexadecimales de: base, b = 16 10 = 10: 2 ; b − 1 = 15 10 = F: 3, 5 ; b + 1 = 17 10 = 11: 11 | ||||
|---|---|---|---|---|---|---|
| Recíproca | Factores primos | Representación posicional (decimal) | Representación posicional (hexadecimal) | Factores primos | Recíproca | |
| 2 | 1/2 | 2 | 0,5 | 0,8 | 2 | 1/2 |
| 3 | 1/3 | 3 | 0,3333 ... = 0,3 | 0,5555 ... = 0,5 | 3 | 1/3 |
| 4 | 1/4 | 2 | 0,25 | 0,4 | 2 | 1/4 |
| 5 | 1/5 | 5 | 0,2 | 0.3 | 5 | 1/5 |
| 6 | 1/6 | 2 , 3 | 0,1 6 | 0,2 A | 2 , 3 | 1/6 |
| 7 | 1/7 | 7 | 0.142857 | 0.249 | 7 | 1/7 |
| 8 | 1/8 | 2 | 0,125 | 0,2 | 2 | 1/8 |
| 9 | 1/9 | 3 | 0.1 | 0.1C7 | 3 | 1/9 |
| 10 | 1/10 | 2 , 5 | 0,1 | 0,1 9 | 2 , 5 | 1/A |
| 11 | 1/11 | 11 | 0.09 | 0.1745D | B | 1/B |
| 12 | 1/12 | 2 , 3 | 0,08 3 | 0,1 5 | 2 , 3 | 1/C |
| 13 | 1/13 | 13 | 0.076923 | 0.13B | D | 1/D |
| 14 | 1/14 | 2 , 7 | 0.0 714285 | 0,1 249 | 2 , 7 | 1/E |
| 15 | 1/15 | 3 , 5 | 0.0 6 | 0.1 | 3 , 5 | 1/F |
| 16 | 1/16 | 2 | 0,0625 | 0,1 | 2 | 1/10 |
| 17 | 1/17 | 17 | 0.0588235294117647 | 0.0F | 11 | 1/11 |
| 18 | 1/18 | 2 , 3 | 0.0 5 | 0.0 E38 | 2 , 3 | 1/12 |
| 19 | 1/19 | 19 | 0.052631578947368421 | 0.0D79435E5 | 13 | 1/13 |
| 20 | 1/20 | 2 , 5 | 0,05 | 0,0 °C | 2 , 5 | 1/14 |
| 21 | 1/21 | 3 , 7 | 0.047619 | 0.0C3 | 3 , 7 | 1/15 |
| 22 | 1/22 | 2 , 11 | 0,0 45 | 0,0 BA2E8 | 2 , B | 1/16 |
| 23 | 1/23 | 23 | 0.0434782608695652173913 | 0.0B21642C859 | 17 | 1/17 |
| 24 | 1/24 | 2 , 3 | 0,041 6 | 0,0 A | 2 , 3 | 1/18 |
| 25 | 1/25 | 5 | 0,04 | 0.0A3D7 | 5 | 1/19 |
| 26 | 1/26 | 2 , 13 | 0.0 384615 | 0.0 9D8 | 2 , D | 1/1A |
| 27 | 1/27 | 3 | 0.037 | 0.097B425ED | 3 | 1/1B |
| 28 | 1/28 | 2 , 7 | 0,03 571428 | 0.0 924 | 2 , 7 | 1/1 taza |
| 29 | 1/29 | 29 | 0. 0344827586206896551724137931 | 0.08D3DCB | 1D | 1/1D |
| 30 | 1/30 | 2 , 3 , 5 | 0.03 | 0.08 | 2 , 3 , 5 | 1/1E |
| 31 | 1/31 | 31 | 0.032258064516129 | 0.08421 | 1º grado | 1/1F |
| 32 | 1/32 | 2 | 0,03125 | 0,08 | 2 | 1/20 |
| 33 | 1/33 | 3 , 11 | 0.03 | 0.07C1F | 3 , B | 1/21 |
| 34 | 1/34 | 2 , 17 | 0.0 2941176470588235 | 0.0 78 | 2 , 11 | 1/22 |
| 35 | 1/35 | 5 , 7 | 0.0 285714 | 0.075 | 5 , 7 | 1/23 |
| 36 | 1/36 | 2 , 3 | 0,02 7 | 0,0 71 °C | 2 , 3 | 1/24 |
| 37 | 1/37 | 37 | 0.027 | 0.06EB3E453 | 25 | 1/25 |
Números irracionales
La siguiente tabla muestra las expansiones de algunos números irracionales comunes en decimal y hexadecimal.
| Número | Representación posicional | |
|---|---|---|
| Decimal | Hexadecimal | |
| √ 2 (la longitud de la diagonal de un cuadrado unitario) | 1.414 213 562 373 095 048 ... | 1.6A09E667F3BCD... |
| √ 3 (la longitud de la diagonal de un cubo unitario ) | 1.732 050 807 568 877 293 ... | 1.BB67AE8584CAA... |
| √ 5 (la longitud de la diagonal de un rectángulo de 1×2) | 2.236 067 977 499 789 696 ... | 2.3C6EF372FE95... |
| φ (phi, la proporción áurea = (1+ √ 5 )/2 ) | 1.618 033 988 749 894 848 ... | 1.9E3779B97F4A... |
| π (pi, la relación entre la circunferencia y el diámetro de un círculo) | 3.141 592 653 589 793 238 462 643 383 279 502 884 197 169 399 375 105 ... | 3.243F6A8885A308D313198A2E0 3707344A4093822299F31D008... |
| e (la base del logaritmo natural ) | 2.718 281 828 459 045 235 ... | 2.B7E151628AED2A6B... |
| τ (la constante de Thue-Morse ) | 0,412 454 033 640 107 597 ... | 0,6996 9669 9669 6996... |
| γ (la diferencia límite entre la serie armónica y el logaritmo natural) | 0,577 215 664 901 532 860 ... | 0.93C467E37DB0C7A4D1B... |
Potestades
Las potencias de dos tienen expansiones muy simples en hexadecimal. Las primeras dieciséis potencias de dos se muestran a continuación.
| 2x | Valor | Valor (Decimal) |
|---|---|---|
| 2 0 | 1 | 1 |
| 2 1 | 2 | 2 |
| 2 2 | 4 | 4 |
| 2 3 | 8 | 8 |
| 2 4 | 10 hex | 16 de diciembre |
| 2 5 | 20 hex | 32 dic |
| 2 6 | 40 hex | 64 dic |
| 2 7 | 80 hex | 128 dic |
| 2 8 | 100 hex | 256 dic |
| 2 9 | 200 hex | 512 dic |
| 2 A (2 10 dic ) | 400 hex | 1024 dic |
| 2 B (2 11 dic ) | 800 hex | 2048 diciembre |
| 2 C (2 12 dic ) | 1000 hex | 4096 dic |
| 2 D (2 13 dic ) | 2000 hex | 8192 dic |
| 2 E (2 14 dic ) | 4000 hex | 16.384 dic |
| 2 F (2 15 dic ) | 8000 hex | 32.768 dic |
| 2 10 (2 16 dic ) | 10000 hex | 65.536 dic |
Historia cultural
Las unidades de medida tradicionales chinas eran de base 16. Por ejemplo, un jīn (斤) en el antiguo sistema equivale a dieciséis taeles . El suanpan ( ábaco chino ) se puede utilizar para realizar cálculos hexadecimales como sumas y restas. [31]
Al igual que con el sistema duodecimal , ha habido intentos ocasionales de promover el hexadecimal como el sistema numérico preferido. Estos intentos a menudo proponen una pronunciación y símbolos específicos para los numerales individuales. [32] Algunas propuestas unifican las medidas estándar para que sean múltiplos de 16. [33] [34] Una de esas primeras propuestas fue presentada por John W. Nystrom en Project of a New System of Arithmetic, Weight, Measure and Coins: Proposed to be called the Tonal System, with Sixteen to the Base , publicado en 1862. [35] Nystrom, entre otras cosas, sugirió el tiempo hexadecimal , que subdivide un día por 16, de modo que hay 16 "horas" (o "10 tims ", pronunciado tontim ) en un día. [36]
La palabra hexadecimal se registró por primera vez en 1952. [37] Es macarrónica en el sentido de que combina el griego ἕξ (hex) "seis" con el latín -decimal . La alternativa totalmente latina sexadecimal (compárese la palabra sexagesimal para la base 60) es más antigua y se usa al menos ocasionalmente desde fines del siglo XIX. [38] Todavía se usa en la década de 1950 en la documentación de Bendix . Schwartzman (1994) sostiene que el uso de sexadecimal puede haberse evitado debido a su sugerente abreviatura de sexo . [39] Muchos idiomas occidentales desde la década de 1960 han adoptado términos equivalentes en formación al hexadecimal (por ejemplo, el francés hexadécimal , el italiano esadecimale , el rumano hexazecimal , el serbio хексадецимални , etc.) pero otros han introducido términos que sustituyen palabras nativas para "dieciséis" (por ejemplo, el griego δεκαεξαδικός, el islandés sextándakerfi , el ruso шестнадцатеричной , etc.)
La terminología y la notación no se establecieron hasta finales de la década de 1960. En 1969, Donald Knuth argumentó que el término etimológicamente correcto sería senidenario , o posiblemente sedenario , un término latino que pretendía transmitir "agrupado por 16" modelado sobre binario , ternario , cuaternario , etc. Según el argumento de Knuth, los términos correctos para la aritmética decimal y octal serían denario y octonario , respectivamente. [40] Alfred B. Taylor utilizó senidenario en su trabajo de mediados del siglo XIX sobre bases numéricas alternativas, aunque rechazó la base 16 debido a su "número incómoda de dígitos". [41] [42]
La notación actual que utiliza las letras A a F se establece como el estándar de facto a partir de 1966, a raíz de la publicación del manual Fortran IV para IBM System/360 , que (a diferencia de las variantes anteriores de Fortran) reconoce un estándar para ingresar constantes hexadecimales. [43] Como se señaló anteriormente, NEC (1960) y The Pacific Data Systems 1020 (1964) utilizaron notaciones alternativas . El estándar adoptado por IBM parece haber sido ampliamente adoptado en 1968, cuando Bruce Alan Martin en su carta al editor del CACM se queja de que
Con la ridícula elección de las letras A, B, C, D, E, F como símbolos numéricos hexadecimales, que se suma a los ya problemáticos problemas de distinguir los números octales (o hexadecimales) de los números decimales (o nombres de variables), ha llegado el momento de reconsiderar nuestros símbolos numéricos. ¡Esto debería haberse hecho antes de que las malas decisiones se convirtieran en un estándar de facto!
El argumento de Martin era que el uso de los numerales del 0 al 9 en números no decimales "nos implica un esquema de valor posicional de base diez": "¿Por qué no utilizar símbolos (y nombres) completamente nuevos para los siete o quince dígitos distintos de cero necesarios en octal o hexadecimal? Incluso el uso de las letras A a P sería una mejora, pero símbolos completamente nuevos podrían reflejar la naturaleza binaria del sistema". [19] También argumentó que "reutilizar letras alfabéticas para dígitos numéricos representa un gigantesco paso atrás respecto de la invención de glifos distintos y no alfabéticos para numerales hace dieciséis siglos" (como los numerales Brahmi , y más tarde en un sistema de numeración hindú-arábigo ), y que los estándares ASCII recientes (ASA X3.4-1963 y USAS X3.4-1968) "deberían haber preservado seis posiciones de tabla de códigos después de los diez dígitos decimales, en lugar de llenarlas innecesariamente con caracteres de puntuación" (":;<=>?") que podrían haberse colocado en otro lugar entre las 128 posiciones disponibles.
Base16 (codificación de transferencia)
Base16 (como nombre propio sin espacio) también puede referirse a una codificación de binario a texto que pertenece a la misma familia que Base32 , Base58 y Base64 .
En este caso, los datos se dividen en secuencias de 4 bits y cada valor (entre 0 y 15 inclusive) se codifica utilizando uno de los 16 símbolos del conjunto de caracteres ASCII . Aunque se pueden utilizar 16 símbolos cualesquiera del conjunto de caracteres ASCII, en la práctica, siempre se eligen los dígitos ASCII "0" a "9" y las letras "A" a "F" (o las minúsculas "a" a "f") para alinearlos con la notación escrita estándar para números hexadecimales.
La codificación Base16 tiene varias ventajas:
- La mayoría de los lenguajes de programación ya tienen funciones para analizar códigos hexadecimales codificados en ASCII.
- Al ser exactamente medio byte, 4 bits son más fáciles de procesar que los 5 o 6 bits de Base32 y Base64 respectivamente.
- Los símbolos 0–9 y A–F son universales en notación hexadecimal, por lo que se entienden fácilmente a simple vista sin necesidad de recurrir a una tabla de búsqueda de símbolos.
- Muchas arquitecturas de CPU tienen instrucciones dedicadas que permiten el acceso a medio byte (también conocido como " nibble "), lo que lo hace más eficiente en hardware que Base32 y Base64.
Las principales desventajas de la codificación Base16 son:
- La eficiencia espacial es de solo el 50%, ya que cada valor de 4 bits de los datos originales se codificará como un byte de 8 bits. En cambio, las codificaciones Base32 y Base64 tienen una eficiencia espacial del 63% y el 75% respectivamente.
- Posible complejidad añadida al tener que aceptar tanto letras mayúsculas como minúsculas
La compatibilidad con la codificación Base16 es omnipresente en la informática moderna. Es la base del estándar W3C para la codificación de porcentajes de URL , donde un carácter se reemplaza por un signo de porcentaje "%" y su forma codificada en Base16. La mayoría de los lenguajes de programación modernos incluyen directamente compatibilidad con el formato y el análisis de números codificados en Base16.
Véase también
- Base32 , Base64 (esquemas de codificación de contenido)
- Hora hexadecimal
- Punto flotante hexadecimal de IBM
- Editor hexadecimal
- Volcado hexadecimal
- Fórmula Bailey-Borwein-Plouffe (BBP)
- Lenguaje hexadecimal
- Notación P
Referencias
- ^ "El sistema hexadecimal". Guía digital de Ionos . Archivado desde el original el 2022-08-26 . Consultado el 2022-08-26 .
- ^ Knuth, Donald Ervin (1986). El TeXbook. Duane Bibby. Reading, Mass. ISBN 0-201-13447-0. OCLC 12973034. Archivado desde el original el 16 de enero de 2022. Consultado el 15 de marzo de 2022 .
{{cite book}}: CS1 maint: location missing publisher (link) - ^ La cadena
"\x1B[0m\x1B[25;1H"especifica la secuencia de caracteres Esc [ 0 m Esc [ 2 5; 1 H . Estas son las secuencias de escape utilizadas en un terminal ANSI que restablecen el conjunto de caracteres y el color, y luego mueven el cursor a la línea 25. - ^ "El estándar Unicode, versión 7" (PDF) . Unicode . Archivado (PDF) del original el 2016-03-03 . Consultado el 2018-10-28 .
- ^ "Modula-2 – Vocabulario y representación". Modula −2 . Archivado desde el original el 2015-12-13 . Consultado el 2015-11-01 .
- ^ "Introducción a los tipos de datos VHDL". Tutorial de FPGA . 2020-05-10. Archivado desde el original el 2020-08-23 . Consultado el 2020-08-21 .
- ^ "Variable *read-base* en Common Lisp". CLHS . Archivado desde el original el 2016-02-03 . Consultado el 2015-01-10 .
- ^ "Variable *print-base* en Common Lisp". CLHS . Archivado desde el original el 26 de diciembre de 2014 . Consultado el 10 de enero de 2015 .
- ^ MSX is Coming — Parte 2: MSX por dentro Archivado el 24 de noviembre de 2010 en Wayback Machine Compute! , número 56, enero de 1985, pág. 52
- ^ Los programas BBC BASIC no son totalmente portables a Microsoft BASIC (sin modificaciones) ya que este último utiliza
&como prefijo valores octales&O. (Microsoft BASIC utiliza principalmente como prefijo octal y&Hcomo prefijo hexadecimal, pero el ampersand por sí solo produce una interpretación predeterminada como prefijo octal. - ^ "Explicación de los colores web hexadecimales". Archivado desde el original el 22 de abril de 2006. Consultado el 11 de enero de 2006 .
- ^ "Codificación de caracteres ISO-8859-1 (ISO Latin 1)". www.ic.unicamp.br . Archivado desde el original el 2019-06-29 . Consultado el 2019-06-26 .
- ^ abcdefg Savard, John JG (2018) [2005]. "Aritmética informática". quadibloc . Los primeros días del hexadecimal. Archivado desde el original el 2018-07-16 . Consultado el 2018-07-16 .
- ^ "2.1.3 Notación sexadecimal". Manual de referencia del programador G15D (PDF) . Los Ángeles, CA, EE. UU.: Bendix Computer , División de Bendix Aviation Corporation . p. 4. Archivado (PDF) desde el original el 2017-06-01 . Consultado el 2017-06-01 .
Esta base se utiliza porque un grupo de cuatro bits puede representar cualquiera de los dieciséis números diferentes (de cero a quince). Al asignar un símbolo a cada una de estas combinaciones, llegamos a una notación llamada sexadecimal (generalmente "hex" en la conversación porque nadie quiere abreviar "sexo"). Los símbolos en el lenguaje sexadecimal son los diez dígitos decimales y en la máquina de escribir G-15, las letras "u", "v", "w", "x", "y" y "z". Estas son marcas arbitrarias; otras computadoras pueden usar caracteres alfabéticos diferentes para estos últimos seis dígitos.
- ^ Gill, S.; Neagher, RE; Muller, DE; Nash, JP; Robertson, JE; Shapin, T.; Whesler, DJ (1956-09-01). Nash, JP (ed.). "ILLIAC Programming – A Guide to the Preparation of Problems For Solution by the University of Illinois Digital Computer" (PDF) . bitsavers.org (Cuarta impresión. Edición revisada y corregida). Urbana, Illinois, EE. UU.: Digital Computer Laboratory, Graduate College, University of Illinois . págs. 3–2. Archivado (PDF) desde el original el 2017-05-31 . Consultado el 2014-12-18 .
- ^ Manual de programación de la computadora electrónica Royal Precision LGP – 30. Port Chester, Nueva York: Royal McBee Corporation . Abril de 1957. Archivado desde el original el 2017-05-31 . Consultado el 2017-05-31 .(NB. Esta secuencia un tanto extraña era de los siguientes seis códigos numéricos secuenciales del teclado del código de caracteres de 6 bits del LGP-30 ).
- ^ Manthey, Steffen; Leibrandt, Klaus (2 de julio de 2002). "Die PERM und ALGOL" (PDF) (en alemán). Archivado (PDF) desde el original el 3 de octubre de 2018 . Consultado el 19 de mayo de 2018 .
- ^ Computadora digital NEC Parametron tipo NEAC-1103 (PDF) . Tokio, Japón: Nippon Electric Company Ltd. 1960. Cat. No. 3405-C. Archivado (PDF) desde el original el 2017-05-31 . Consultado el 2017-05-31 .
- ^ abc Martin, Bruce Alan (octubre de 1968). "Cartas al editor: sobre notación binaria". Comunicaciones de la ACM . 11 (10). Associated Universities Inc. : 658. doi : 10.1145/364096.364107 . S2CID 28248410.
- ^ ab Whitaker, Ronald O. (enero de 1972). Escrito en Indianápolis, Indiana, EE. UU. "Más sobre el hombre y la máquina" (PDF) . Cartas. Datamation . Vol. 18, núm. 1. Barrington, Illinois, EE. UU.: Technical Publishing Company . pág. 103. Archivado (PDF) desde el original el 5 de diciembre de 2022 . Consultado el 24 de diciembre de 2022 .(1 página)
- ^ ab Whitaker, Ronald O. (1976-08-10) [1975-02-24]. "Selector de rango y pantalla combinados para uso con instrumentos digitales que emplean el sistema de numeración binario" (PDF) . Indianápolis, Indiana, EE. UU. Patente estadounidense 3974444A. Archivado (PDF) desde el original el 24 de diciembre de 2022. Consultado el 24 de diciembre de 2022 .(7 páginas)
- ^ "SN5446A, '47A, '48, SN54LS47, 'LS48, 'LS49, SN7446A, '47A, '48, SN74LS47, 'LS48, 'LS49 Decodificadores/controladores de BCD a siete segmentos". Dallas, Texas, EE. UU.: Texas Instruments Incorporated . Marzo de 1988 [1974]. SDLS111. Archivado (PDF) desde el original el 20 de octubre de 2021. Consultado el 15 de septiembre de 2021 .(29 páginas)
- ^ abc Magnuson, Robert A. (enero de 1968). "Una guía de pronunciación hexadecimal". Datamation . Vol. 14, núm. 1. pág. 45.
- ^ ab Rogers, SR (2007). «Palabras con números hexadecimales». Intuitor . Archivado desde el original el 17 de septiembre de 2019. Consultado el 26 de agosto de 2019 .
- ^ Babb, Tim (2015). «Cómo pronunciar el sistema hexadecimal». Bzarg . Archivado desde el original el 2020-11-11 . Consultado el 2021-01-01 .
- ^ Clarke, Arthur; Pohl, Frederik (2008). El último teorema . Ballantine. pág. 91. ISBN 978-0007289981.
- ^ "ISO/IEC 9899:1999 – Lenguajes de programación – C". ISO . Iso.org. 2011-12-08. Archivado desde el original el 2016-10-10 . Consultado el 2014-04-08 .
- ^ "Fundamento de la Norma Internacional – Lenguajes de Programación – C" (PDF) . Open Standards . 5.10. Abril de 2003. págs. 52, 153–154, 159. Archivado (PDF) desde el original el 2016-06-06 . Consultado el 2010-10-17 .
- ^ IEEE y The Open Group (2013) [2001]. «dprintf, fprintf, printf, snprintf, sprintf: salida con formato de impresión». Especificaciones básicas de The Open Group (número 7, IEEE Std 1003.1, edición de 2013). Archivado desde el original el 21 de junio de 2016. Consultado el 21 de junio de 2016 .
- ^ ab Mano, M. Morris; Ciletti, Michael D. (2013). Diseño digital: con una introducción a Verilog HDL (quinta edición). Pearson Education . págs. 6, 8–10. ISBN 978-0-13-277420-8.
- ^ "算盤 Suma y resta hexadecimal en un ábaco chino". totton.idirect.com . Archivado desde el original el 2019-07-06 . Consultado el 2019-06-26 .
- ^ "Propuesta de símbolo hexadecimal de base 4^2". Hauptmech . Archivado desde el original el 20 de octubre de 2021 . Consultado el 4 de septiembre de 2008 .
- ^ "Cuartel general de Intuitor Hex". Intuitor . Archivado desde el original el 4 de septiembre de 2010 . Consultado el 28 de octubre de 2018 .
- ^ Niemietz, Ricardo Cancho (21 de octubre de 2003). "Una propuesta para la adición de los seis dígitos hexadecimales (AF) a Unicode" (PDF) . ISO/IEC JTC1/SC2/WG2 . Consultado el 25 de junio de 2024 .
- ^ Nystrom, John William (1862). Proyecto de un nuevo sistema de aritmética, peso, medida y monedas: Se propone que se denomine Sistema Tonal, con dieciséis como base. Filadelfia: Lippincott.
- ^ Nystrom (1862), p. 33: "Al expresar el tiempo, el ángulo de un círculo o los puntos de la brújula, la unidad tim debe indicarse como un número entero y sus partes como fracciones tonales , ya que 5·86 tims es cinco veces y metonby [*"sutim y metonby" John Nystrom da accidentalmente parte del número en nombres decimales; en el esquema de pronunciación de Nystrom, 5=su, 8=me, 6=by, cf unifoundry.com Archivado el 19 de mayo de 2021 en Wayback Machine ].
- ^ CE Fröberg, Tablas de conversión hexadecimales , Lund (1952).
- ^ El Century Dictionary de 1895 utiliza sexadecimal en el sentido más general de "relativo a dieciséis". Un uso explícito temprano de sexadecimal en el sentido de "utilizar la base 16" se encuentra también en 1895, en el Journal of the American Geographical Society of New York , vols. 27-28, p. 197.
- ^ Schwartzman, Steven (1994). Las palabras de las matemáticas: un diccionario etimológico de términos matemáticos utilizados en inglés . Asociación Matemática de Estados Unidos. pág. 105. ISBN 0-88385-511-9.sv hexadecimal
- ^ Knuth, Donald. (1969). El arte de la programación informática , volumen 2. ISBN 0-201-03802-1 . (Capítulo 17.)
- ^ Alfred B. Taylor, Informe sobre pesos y medidas, Asociación farmacéutica, octava sesión anual, Boston, 15 de septiembre de 1859. Véanse las páginas 33 y 41.
- ^ Alfred B. Taylor, "Numeración octonaria y su aplicación a un sistema de pesos y medidas", Proc Amer. Phil. Soc. Vol XXIV Archivado el 24 de junio de 2016 en Wayback Machine , Filadelfia, 1887; páginas 296–366. Véanse las páginas 317 y 322.
- ^ IBM System/360 Lenguaje FORTRAN IV Archivado el 19 de mayo de 2021 en Wayback Machine (1966), pág. 13.
