Nudo toroidal

En teoría de nudos , un nudo toroidal es un tipo especial de nudo que se encuentra en la superficie de un toro no anudado en R ³ . De manera similar, un enlace toroidal es un enlace que se encuentra en la superficie de un toro de la misma manera. Cada nudo toroidal se especifica mediante un par de números enteros coprimos p y q . Un enlace toroidal surge si p y q no son coprimos (en cuyo caso el número de componentes es mcd ( p , q )). Un nudo toroidal es trivial (equivalente al nudo no anudado) si y solo si p o q es igual a 1 o −1. El ejemplo no trivial más simple es el nudo (2,3)-toroidal, también conocido como nudo de trébol .

Un nudo toroidal se puede representar geométricamente de múltiples maneras que son topológicamente equivalentes (ver Propiedades a continuación) pero geométricamente distintas. La convención utilizada en este artículo y sus figuras es la siguiente.

El nudo toroidal ( p , q ) gira q veces alrededor de un círculo en el interior del toro, y p veces alrededor de su eje de simetría rotacional . ^{[nota 1]} . Si p y q no son primos entre sí, entonces tenemos un vínculo toroidal con más de un componente.

La dirección en la que las hebras del nudo se enrollan alrededor del toro también está sujeta a diferentes convenciones . La más común es que las hebras formen un tornillo dextrógiro para pq > 0. ^{[3] [4] [5]}

El nudo toroide ( p , q ) se puede dar mediante la parametrización

${\displaystyle {\begin{aligned}x&=r\cos(p\phi )\\y&=r\sin(p\phi )\\z&=-\sin(q\phi )\end{aligned}}}$

donde y . Esto se encuentra en la superficie del toro dado por (en coordenadas cilíndricas ).${\displaystyle r=\cos(q\phi )+2}$${\displaystyle 0<\phi <2\pi}$${\displaystyle (r-2)^{2}+z^{2}=1}$

También son posibles otras parametrizaciones, ya que los nudos se definen hasta la deformación continua. Las ilustraciones para los nudos toroidales (2,3) y (3,8) se pueden obtener tomando , y en el caso del nudo toroidal (2,3) restando además respectivamente y de las parametrizaciones anteriores de x e y . Esta última se generaliza sin problemas a cualquier coprimo p,q que satisfaga .${\displaystyle r=\cos(q\phi )+4}$${\displaystyle 3\cos((pq)\phi )}$${\displaystyle 3\sin((pq)\phi )}$${\estilo de visualización p<q<2p}$

Un nudo toroidal es trivial si y solo si p o q son iguales a 1 o −1. ^{[4] [5]}

Cada nudo toroidal no trivial es primo ^[6] y quiral . ^[4]

El nudo toro ( p , q ) es equivalente al nudo toro ( q , p ). ^{[3] [5]} Esto se puede demostrar moviendo las hebras en la superficie del toro. ^[7] El nudo toro ( p , − q ) es el anverso (imagen especular) del nudo toro ( p , q ). ^[5] El nudo toro ( − p , − q ) es equivalente al nudo toro ( p , q ) excepto por la orientación invertida.

Cualquier nudo toroidal ( p , q ) se puede realizar a partir de una trenza cerrada con p hebras. La palabra trenza adecuada es ^[8]

${\displaystyle (\sigma _{1}\sigma _{2}\cdots \sigma _{p-1})^{q}.}$

(Esta fórmula asume la convención común de que los generadores de trenzas son giros rectos, ^{[4] [8] [9] [10]} lo que no se sigue en la página de Wikipedia sobre trenzas).

El número de cruce de un nudo toroidal ( p , q ) con p , q > 0 viene dado por

c = mín(( p −1) q , ( q −1) p ).

El género de un nudo toroidal con p , q > 0 es

${\displaystyle g={\frac {1}{2}}(p-1)(q-1).}$

El polinomio de Alexander de un nudo toroidal es ^{[3] [8]}

${\displaystyle t^{k}{\frac {(t^{pq}-1)(t-1)}{(t^{p}-1)(t^{q}-1)}},}$dónde${\displaystyle k=-{\frac {(p-1)(q-1)}{2}}.}$

El polinomio de Jones de un nudo toroidal (diestro) está dado por

${\displaystyle t^{(p-1)(q-1)/2}{\frac {1-t^{p+1}-t^{q+1}+t^{p+q}}{1-t^{2}}}.}$

El complemento de un nudo toral en la 3-esfera es una variedad fibrosa de Seifert , fibrosa sobre el disco con dos fibras singulares.

Sea Y el gorro de burro p -plegable con un disco retirado de su interior, Z el gorro de burro q -plegable con un disco retirado de su interior, y X el espacio cociente obtenido al identificar Y y Z a lo largo de su círculo límite. El complemento de nudo de la deformación del nudo toroidal ( p , q ) se retrae al espacio X . Por lo tanto, el grupo de nudos de un nudo toroidal tiene la presentación

${\displaystyle \langle x,y\mid x^{p}=y^{q}\rangle .}$

Los nudos de toro son los únicos nudos cuyos grupos de nudos tienen un centro no trivial (que es cíclico infinito, generado por el elemento en la presentación anterior).${\displaystyle x^{p}=y^{q}}$

El factor de estiramiento del nudo toroidal ( p , q ), como una curva en el espacio euclidiano , es Ω(min( p , q )), por lo que los nudos toroidales tienen factores de estiramiento ilimitados. El investigador universitario John Pardon ganó el Premio Morgan 2012 por su investigación que demostró este resultado, que resolvió un problema originalmente planteado por Mikhail Gromov . ^{[11] [12]}

Los nudos toroidales ( p , q )− surgen al considerar el vínculo de una singularidad hipersuperficial compleja aislada. Se interseca la hipersuperficie compleja con una hiperesfera , centrada en el punto singular aislado, y con un radio suficientemente pequeño para que no encierre, ni se encuentre con, ningún otro punto singular. La intersección da una subvariedad de la hiperesfera.

Sean p y q números enteros coprimos, mayores o iguales a dos. Considérese la función holomorfa dada por Sea el conjunto de tales que Dado un número real definimos la triesfera real como dada por La función tiene un punto crítico aislado en ya que si y solo si Por lo tanto, consideramos la estructura de cerca de Para hacer esto, consideramos la intersección Esta intersección es el llamado enlace de la singularidad El enlace de , donde p y q son coprimos, y ambos mayores o iguales a dos, es exactamente el nudo ( p , q )−toro. ^[13]${\displaystyle f:\mathbb {C} ^{2}\to \mathbb {C} }$${\displaystyle f(w,z):=w^{p}+z^{q}.}$${\displaystyle V_{f}\subset \mathbb {C} ^{2}}$${\displaystyle (w,z)\in \mathbb {C} ^{2}}$${\displaystyle f(w,z)=0.}$${\displaystyle 0<\varepsilon \ll 1,}$${\displaystyle \mathbb {S} _{\varepsilon }^{3}\subset \mathbb {R} ^{4}\hookrightarrow \mathbb {C} ^{2}}$${\displaystyle |w|^{2}+|z|^{2}=\varepsilon ^{2}.}$${\displaystyle f}$${\displaystyle (0,0)\in \mathbb {C} ^{2}}$${\displaystyle \partial f/\partial w=\partial f/\partial z=0}$${\displaystyle w=z=0.}$${\displaystyle V_{f}}$${\displaystyle (0,0)\in \mathbb {C} ^{2}.}$${\displaystyle V_{f}\cap \mathbb {S} _{\varepsilon }^{3}\subset \mathbb {S} _{\varepsilon }^{3}.}$${\displaystyle f(w,z)=w^{p}+z^{q}.}$${\displaystyle f(w,z)=w^{p}+z^{q}}$

• Desanudar , 3 ₁ nudo (3,2), 5 ₁ nudo (5,2), 7 ₁ nudo (7,2), 8 ₁₉ nudo (4,3), 9 ₁ nudo (9,2), 10 ₁₂₄ nudo (5,3)

Mesa #	De	Imagen	PAG	Q	Cruz #
0	0 1				0
3a1	3 1		2	3	3
5a2	5 1		2	5	5
7a7	7 1		2	7	7
8n3	8 19		3	4	8
9a41	9 1		2	9	9
10n21	10 124		3	5	10
11a367			2	11	11
13a4878			2	13	13
14n21881			3	7	14
15n41185		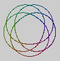	4	5	15
15a85263			2	15	15
16n783154			3	8	16
			2	17	17
			2	19	19
			3	10	20
			4	7	21
			2	21	21
			3	11	22
			2	23	23
			5	6	24
			2	25	25
			3	13	26
			4	9	27
			2	27	27
			5	7	28
			3	14	28
			2	29	29
			2	31	31
			5	8	32
			3	16	32
			4	11	33
			2	33	33
			3	17	34
			6	7	35
			2	35	35
			5	9	36
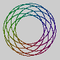			7	8	48
			7	9	54
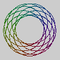			8	9	63

Un nudo g-toro es una curva cerrada dibujada sobre un g-toro . Más técnicamente, es la imagen homeomórfica de un círculo en S³ que se puede realizar como un subconjunto de un cuerpo de manija de género g en S³ (cuyo complemento es también un cuerpo de manija de género g ). Si un enlace es un subconjunto de un cuerpo de manija de género dos, es un enlace de doble toro . ^[14]

Para el género dos, el ejemplo más simple de un nudo de doble toro que no es un nudo de toro es el nudo en forma de ocho . ^{[15] [16]}

• Nudo alterno
• Nudo satelital
• Nudo hiperbólico
• Bobinado irracional de un toro
• Topópolis

• "36 nudos toroidales", Atlas de nudos .
• Weisstein, Eric W. "Nudo toroidal". MathWorld .
• Renderizador de nudos toroidales en Actionscript
• Diversión con el nudo PQ-Torus