Grupo de trenzas

En matemáticas , el grupo trenzado de n hebras (denominado ), también conocido como el grupo trenzado de Artin , ^[1] es el grupo cuyos elementos son clases de equivalencia de n -trenzas (por ejemplo, bajo isotopía ambiental ), y cuya operación de grupo es la composición de trenzas (véase § Introducción). Ejemplos de aplicaciones de los grupos trenzados incluyen la teoría de nudos , donde cualquier nudo puede representarse como el cierre de ciertas trenzas (un resultado conocido como teorema de Alexander ); en física matemática donde la presentación canónica de Artin del grupo trenzado corresponde a la ecuación de Yang-Baxter (véase § Propiedades básicas); y en invariantes monodromía de geometría algebraica . ^[2]$Estilo de visualización B_{n}$

En esta introducción, supongamos que n = 4 ; la generalización a otros valores de n será sencilla. Consideremos dos conjuntos de cuatro elementos que se encuentran sobre una mesa, con los elementos de cada conjunto dispuestos en una línea vertical, y de tal manera que un conjunto se encuentra al lado del otro. (En las ilustraciones siguientes, estos son los puntos negros). Utilizando cuatro hebras, cada elemento del primer conjunto se conecta con un elemento del segundo conjunto de modo que se produce una correspondencia uno a uno. Este tipo de conexión se denomina trenza . A menudo, algunas hebras tendrán que pasar por encima o por debajo de otras, y esto es crucial: las dos conexiones siguientes son trenzas diferentes :

es diferente de

Por otra parte, dos conexiones que pueden hacerse parecer iguales "tirando de los hilos" se consideran la misma trenza:

es lo mismo que

Es necesario que todas las hebras se muevan de izquierda a derecha; nudos como los siguientes no se consideran trenzas:

no es una trenza

Se pueden componer dos trenzas cualesquiera dibujando la primera al lado de la segunda, identificando los cuatro elementos en el medio y conectando las hebras correspondientes:

compuesto con

rendimientos

Otro ejemplo:

compuesto con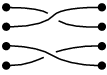

rendimientos

La composición de las trenzas σ y τ se escribe como στ .

El conjunto de todas las trenzas de cuatro hebras se denota por . La composición de trenzas anterior es, de hecho, una operación de grupo . El elemento de identidad es la trenza que consta de cuatro hebras horizontales paralelas, y el inverso de una trenza consiste en aquella trenza que "deshace" lo que hizo la primera trenza, lo que se obtiene al invertir un diagrama como los anteriores a lo largo de una línea vertical que pasa por su centro. (Las dos primeras trenzas de ejemplo anteriores son inversas entre sí).$Estilo de visualización B_{4}$

La teoría de trenzado se ha aplicado recientemente a la mecánica de fluidos , específicamente al campo de la mezcla caótica en flujos de fluidos. El trenzado de trayectorias espacio-temporales (2 + 1)-dimensionales formadas por el movimiento de barras físicas, órbitas periódicas o "barras fantasma" y conjuntos casi invariantes se ha utilizado para estimar la entropía topológica de varios sistemas de fluidos naturales y diseñados mediante el uso de la clasificación de Nielsen-Thurston . ^{[3] [4] [5]}

Otro campo de intensa investigación que involucra grupos trenzados y conceptos topológicos relacionados en el contexto de la física cuántica es la teoría y la implementación experimental (conjeturada) de las partículas propuestas, los aniones . Estos pueden muy bien terminar formando la base para la computación cuántica con corrección de errores , por lo que su estudio abstracto es actualmente de importancia fundamental en la información cuántica .

Para fundamentar la discusión informal anterior sobre los grupos trenzados, es necesario utilizar el concepto de homotopía de la topología algebraica , definiendo los grupos trenzados como grupos fundamentales de un espacio de configuración . Alternativamente, se puede definir el grupo trenzado de manera puramente algebraica a través de las relaciones trenzadas, teniendo en cuenta las imágenes solo para guiar la intuición.

Para explicar cómo reducir un grupo trenzado en el sentido de Artin a un grupo fundamental, consideramos una variedad conexa de dimensión al menos 2. El producto simétrico de copias de significa el cociente de , el producto cartesiano de -tupla de por la acción de permutación del grupo simétrico sobre hebras que operan sobre los índices de coordenadas. Es decir, una -tupla ordenada está en la misma órbita que cualquier otra que sea una versión reordenada de ella.${\estilo de visualización X}$${\estilo de visualización n}$${\estilo de visualización X}$$Estilo de visualización X^{n}}$${\estilo de visualización n}$${\estilo de visualización X}$${\estilo de visualización n}$${\estilo de visualización n}$

Un camino en el producto simétrico de pliegues es la forma abstracta de discutir puntos de , considerados como una -tupla desordenada, trazando independientemente cadenas. Como debemos exigir que las cadenas nunca pasen una por la otra, es necesario que pasemos al subespacio del producto simétrico, de órbitas de -tuplas de puntos distintos . Es decir, eliminamos todos los subespacios de definidos por condiciones para todos los . Este es invariante bajo el grupo simétrico, y es el cociente por el grupo simétrico de las -tuplas no excluidas . Bajo la condición de dimensión serán conexos.${\estilo de visualización n}$${\estilo de visualización n}$${\estilo de visualización X}$${\estilo de visualización n}$${\estilo de visualización n}$${\estilo de visualización Y}$${\estilo de visualización n}$$Estilo de visualización X^{n}}$${\displaystyle x_{i}=x_{j}}$${\displaystyle 1\leq i<j\leq n}$${\estilo de visualización Y}$${\estilo de visualización n}$${\estilo de visualización Y}$

Con esta definición, entonces, podemos llamar al grupo trenzado de con cuerdas${\estilo de visualización X}$${\estilo de visualización n}$ el grupo fundamental de (para cualquier elección de punto base – esto está bien definido hasta el isomorfismo). El caso donde es el plano euclidiano es el original de Artin. En algunos casos se puede demostrar que los grupos de homotopía superiores de son triviales.${\estilo de visualización Y}$${\estilo de visualización X}$${\estilo de visualización Y}$

Cuando X es el plano, la trenza puede cerrarse , es decir, los extremos correspondientes pueden conectarse en pares, para formar un enlace , es decir, una unión posiblemente entrelazada de bucles posiblemente anudados en tres dimensiones. El número de componentes del enlace puede ser cualquiera de 1 a n , dependiendo de la permutación de hebras determinada por el enlace. Un teorema de J. W. Alexander demuestra que cada enlace puede obtenerse de esta manera como el "cierre" de una trenza. Compárese con los enlaces de cuerdas .

Diferentes trenzas pueden dar lugar al mismo enlace, de la misma manera que diferentes diagramas de cruce pueden dar lugar al mismo nudo . En 1935, Andrey Markov Jr. describió dos movimientos en diagramas de trenzas que producen equivalencia en las trenzas cerradas correspondientes. ^[6] Una versión de un solo movimiento del teorema de Markov fue publicada por en 1997. ^[7]

Vaughan Jones definió originalmente su polinomio como un invariante de trenza y luego demostró que dependía únicamente de la clase de la trenza cerrada.

El teorema de Markov da condiciones necesarias y suficientes bajo las cuales los cierres de dos trenzas son enlaces equivalentes. ^[8]

El "índice de trenzado" es el número mínimo de cuerdas necesarias para hacer una representación de trenzado cerrada de un enlace. Es igual al número mínimo de círculos de Seifert en cualquier proyección de un nudo. ^[9]

Los grupos de trenza fueron introducidos explícitamente por Emil Artin en 1925, aunque (como señaló Wilhelm Magnus en 1974 ^[10] ) ya estaban implícitos en el trabajo de Adolf Hurwitz sobre monodromía de 1891.

Los grupos de trenzas pueden describirse mediante presentaciones explícitas , como lo demostró Emil Artin en 1947. ^[11] Los grupos de trenzas también se entienden mediante una interpretación matemática más profunda: como el grupo fundamental de ciertos espacios de configuración . ^[11]

Como dice Magnus, Hurwitz dio la interpretación de un grupo trenzado como el grupo fundamental de un espacio de configuración (cf. teoría de trenzado ), una interpretación que se perdió de vista hasta que fue redescubierta por Ralph Fox y Lee Neuwirth en 1962. ^[12]

Considere las siguientes tres trenzas:

$estilo de visualización {\displaystyle \sigma _{1}}$	$Estilo de visualización: sigma _{2}$	$estilo de visualización {\displaystyle \sigma _{3}}$

Cada trenza de se puede escribir como una composición de varias de estas trenzas y sus inversas. En otras palabras, estas tres trenzas generan el grupo . Para ver esto, se escanea una trenza arbitraria de izquierda a derecha en busca de cruces; comenzando por la parte superior, siempre que se encuentre un cruce de hebras y , o se escribe hacia abajo, dependiendo de si la hebra se mueve debajo o sobre la hebra . Al llegar al extremo derecho, la trenza se ha escrito como un producto de las y sus inversas.$Estilo de visualización B_{4}$$Estilo de visualización B_{4}$${\estilo de visualización i}$${\estilo de visualización i+1}$${\displaystyle \sigma _{i}}$$Estilo de visualización: sigma-1$${\estilo de visualización i}$${\estilo de visualización i+1}$${\estilo de visualización \sigma}$

Está claro que

(i) ,${\displaystyle \sigma _{1}\sigma _{3}=\sigma _{3}\sigma _{1}}$

Aunque las dos relaciones siguientes no son tan obvias:

(iia) ,${\displaystyle \sigma _{1}\sigma _{2}\sigma _{1}=\sigma _{2}\sigma _{1}\sigma _{2}}$

(iib)${\displaystyle \sigma _{2}\sigma _{3}\sigma _{2}=\sigma _{3}\sigma _{2}\sigma _{3}}$

(Estas relaciones se pueden apreciar mejor dibujando la trenza en una hoja de papel). Se puede demostrar que todas las demás relaciones entre las trenzas , y ya se derivan de estas relaciones y de los axiomas de grupo.$estilo de visualización {\displaystyle \sigma _{1}}$$Estilo de visualización: sigma _{2}$$estilo de visualización {\displaystyle \sigma _{3}}$

Generalizando este ejemplo a los hilos, el grupo puede definirse de forma abstracta mediante la siguiente presentación :${\estilo de visualización n}$$Estilo de visualización B_{n}$

${\displaystyle B_{n}=\left\langle \sigma _{1},\ldots ,\sigma _{n-1}\mid \sigma _{i}\sigma _{i+1}\sigma _{i}=\sigma _{i+1}\sigma _{i}\sigma _{i+1},\sigma _{i}\sigma _{j}=\sigma _{j}\sigma _{i}\right\rangle ,}$

donde en el primer grupo de relaciones y en el segundo grupo de relaciones, . Esta presentación conduce a generalizaciones de los grupos trenzados llamados grupos de Artin . Las relaciones cúbicas, conocidas como relaciones trenzadas , desempeñan un papel importante en la teoría de las ecuaciones de Yang-Baxter .${\displaystyle 1\leq i\leq n-2}$${\displaystyle |ij|\geq 2}$

• El grupo trenzado es trivial , es el grupo cíclico infinito y es isomorfo al grupo de nudos del nudo trilobulado ; en particular, es un grupo no abeliano infinito .${\displaystyle B_{1}}$${\displaystyle B_{2}}$ ${\displaystyle \mathbb {Z} }$${\displaystyle B_{3}}$
• El grupo trenzado de n hebras se incorpora como subgrupo en el grupo trenzado de n hebras añadiendo una hebra extra que no cruza ninguna de las primeras n hebras. La unión creciente de los grupos trenzados con todos es el grupo trenzado infinito .${\displaystyle B_{n}}$${\displaystyle (n+1)}$${\displaystyle B_{n+1}}$${\displaystyle n\geq 1}$ ${\displaystyle B_{\infty }}$
• Todos los elementos no idénticos de tienen orden infinito , es decir, no tienen torsión .${\displaystyle B_{n}}$${\displaystyle B_{n}}$
• Existe un orden lineal invariante por la izquierda llamado orden de Dehornoy .${\displaystyle B_{n}}$
• Para , contiene un subgrupo isomorfo al grupo libre en dos generadores.${\displaystyle n\geq 3}$${\displaystyle B_{n}}$
• Existe un homomorfismo definido por σ _i ↦ 1 . Por ejemplo, la trenza σ ₂ σ ₃ σ ₁ ⁻¹ σ ₂ σ ₃ se mapea a 1 + 1 − 1 + 1 + 1 = 3 . Esta función corresponde a la abelianización del grupo de trenzas. Como σ _i ^k ↦ k , entonces σ _i ^k es la identidad si y solo si . Esto prueba que los generadores tienen orden infinito.${\displaystyle B_{n}\to \mathbb {Z} }$${\displaystyle k=0}$

Al olvidar cómo se retuercen y se cruzan las hebras, cada trenza en n hebras determina una permutación en n elementos. Esta asignación es sobreyectiva y compatible con la composición, y por lo tanto se convierte en un homomorfismo de grupo sobreyectivo B _n → S _n del grupo de trenzas al grupo simétrico . La imagen de la trenza σ _i ∈ B _n es la transposición s _i = ( i , i +1) ∈ S _n . Estas transposiciones generan el grupo simétrico, satisfacen las relaciones del grupo de trenzas y tienen orden 2. Esto transforma la presentación de Artin del grupo de trenzas en la presentación de Coxeter del grupo simétrico:

${\displaystyle S_{n}=\left\langle s_{1},\ldots ,s_{n-1}|s_{i}s_{i+1}s_{i}=s_{i+1}s_{i}s_{i+1},s_{i}s_{j}=s_{j}s_{i}{\text{ for }}|i-j|\geq 2,s_{i}^{2}=1\right\rangle .}$

El núcleo del homomorfismo B _n → S _n es el subgrupo de B _n llamado grupo trenzado puro sobre n hebras y denotado como P _n . Este puede verse como el grupo fundamental del espacio de n -tuplas de puntos distintos del plano euclidiano. En un trenzado puro, el principio y el final de cada hebra están en la misma posición. Los grupos trenzados puros encajan en una secuencia corta y exacta.

${\displaystyle 1\to F_{n-1}\to P_{n}\to P_{n-1}\to 1.}$

Esta secuencia se divide y, por lo tanto, los grupos trenzados puros se realizan como productos semidirectos iterados de grupos libres.

El grupo trenzado es la extensión central universal del grupo modular , y estos se ubican como redes dentro del grupo de cobertura universal (topológico).${\displaystyle B_{3}}$ ${\displaystyle \mathrm {PSL} (2,\mathbb {Z} )}$

${\displaystyle {\overline {\mathrm {SL} (2,\mathbb {R} )}}\to \mathrm {PSL} (2,\mathbb {R} )}$.

Además, el grupo modular tiene centro trivial, y por lo tanto el grupo modular es isomorfo al grupo cociente de módulo su centro , y equivalentemente, al grupo de automorfismos internos de .${\displaystyle B_{3}}$${\displaystyle Z(B_{3}),}$${\displaystyle B_{3}}$

A continuación se muestra una construcción de este isomorfismo . Definir

${\displaystyle a=\sigma _{1}\sigma _{2}\sigma _{1},\quad b=\sigma _{1}\sigma _{2}}$.

De las relaciones de trenzado se deduce que . Denotando este último producto como , se puede verificar a partir de las relaciones de trenzado que${\displaystyle a^{2}=b^{3}}$${\displaystyle c}$

${\displaystyle \sigma _{1}c\sigma _{1}^{-1}=\sigma _{2}c\sigma _{2}^{-1}=c}$

lo que implica que está en el centro de . Sea el subgrupo de generado por c , ya que C  ⊂  Z ( B ₃ ) , es un subgrupo normal y se puede tomar el grupo cociente B ₃ / C . Afirmamos que B ₃ / C ≅ PSL(2, Z ) ; este isomorfismo puede tener una forma explícita. Las clases laterales σ ₁ C y σ ₂ C se asignan a${\displaystyle c}$${\displaystyle B_{3}}$${\displaystyle C}$${\displaystyle B_{3}}$

${\displaystyle \sigma _{1}C\mapsto R={\begin{bmatrix}1&1\\0&1\end{bmatrix}}\qquad \sigma _{2}C\mapsto L^{-1}={\begin{bmatrix}1&0\\-1&1\end{bmatrix}}}$

donde L y R son los movimientos estándar de izquierda y derecha en el árbol de Stern-Brocot ; es bien sabido que estos movimientos generan el grupo modular.

Alternativamente, una presentación común para el grupo modular es

${\displaystyle \langle v,p\,|\,v^{2}=p^{3}=1\rangle }$

dónde

${\displaystyle v={\begin{bmatrix}0&1\\-1&0\end{bmatrix}},\qquad p={\begin{bmatrix}0&1\\-1&1\end{bmatrix}}.}$

Al mapear a a v y b a p se obtiene un homomorfismo de grupo sobreyectivo B ₃ → PSL(2, Z ) .

El centro de B ₃ es igual a C , una consecuencia de los hechos de que c está en el centro, el grupo modular tiene centro trivial y el homomorfismo sobreyectivo anterior tiene núcleo C .

Se puede demostrar que el grupo trenzado B _n es isomorfo al grupo de clases de mapeo de un disco perforado con n perforaciones. Esto se visualiza más fácilmente imaginando que cada perforación está conectada por una cuerda al límite del disco; cada homomorfismo de mapeo que permuta dos de las perforaciones puede verse entonces como una homotopía de las cuerdas, es decir, un trenzado de estas cuerdas.

A través de esta interpretación grupal de clases de mapeo de trenzas, cada trenza puede clasificarse como periódica, reducible o pseudo-Anosov .

Si se da una trenza y se conecta el primer elemento de la izquierda con el primer elemento de la derecha utilizando una nueva cuerda, el segundo elemento de la izquierda con el segundo elemento de la derecha, etc. (sin crear ninguna trenza en las nuevas cuerdas), se obtiene un enlace y, a veces, un nudo . El teorema de Alexander en la teoría de trenzas establece que lo inverso también es cierto: cada nudo y cada enlace surge de esta manera a partir de al menos una trenza; dicha trenza se puede obtener cortando el enlace. Dado que las trenzas se pueden dar concretamente como palabras en los generadores σ _i , este es a menudo el método preferido para ingresar nudos en programas de computadora.

El problema verbal para las relaciones de trenzado se puede resolver de manera eficiente y existe una forma normal para los elementos de B _n en términos de los generadores σ ₁ , ..., σ _{n −1} . (En esencia, calcular la forma normal de un trenzado es el análogo algebraico de "tirar de las hebras", como se ilustra en nuestro segundo conjunto de imágenes anterior). El sistema de álgebra computacional GAP gratuito puede realizar cálculos en B _n si los elementos se dan en términos de estos generadores. También existe un paquete llamado CHEVIE para GAP3 con soporte especial para grupos de trenzados. El problema verbal también se resuelve de manera eficiente a través de la representación de Lawrence-Krammer .

Además del problema de palabras, existen varios problemas computacionales difíciles conocidos que podrían implementar grupos trenzados y se han sugerido aplicaciones en criptografía . ^[13]

En analogía con la acción del grupo simétrico por permutaciones, en varios contextos matemáticos existe una acción natural del grupo trenzado sobre n -tuplas de objetos o sobre el producto tensorial n -plegado que involucra algunos "giros". Considérese un grupo arbitrario G y sea X el conjunto de todas las n -tuplas de elementos de G cuyo producto es el elemento identidad de G . Entonces B _n actúa sobre X de la siguiente manera:

${\displaystyle \sigma _{i}\left(x_{1},\ldots ,x_{i-1},x_{i},x_{i+1},\ldots ,x_{n}\right)=\left(x_{1},\ldots ,x_{i-1},x_{i+1},x_{i+1}^{-1}x_{i}x_{i+1},x_{i+2},\ldots ,x_{n}\right).}$

De este modo, los elementos x _i y x _{i +1} intercambian sus lugares y, además, x _i se tuerce por el automorfismo interno correspondiente a x _{i +1} – esto asegura que el producto de los componentes de x siga siendo el elemento identidad. Se puede comprobar que se satisfacen las relaciones de grupo trenzado y que esta fórmula define de hecho una acción de grupo de B _n sobre X . Como otro ejemplo, una categoría monoidal trenzada es una categoría monoidal con una acción de grupo trenzado. Tales estructuras desempeñan un papel importante en la física matemática moderna y conducen a invariantes de nudos cuánticos .

Los elementos del grupo trenzado B _n se pueden representar de forma más concreta mediante matrices. Una representación clásica de este tipo es la representación de Burau , donde las entradas de la matriz son polinomios de Laurent de una sola variable . Había sido una pregunta de larga data si la representación de Burau era fiel , pero la respuesta resultó ser negativa para n  ≥ 5. De manera más general, era un importante problema abierto si los grupos trenzados eran lineales . En 1990, Ruth Lawrence describió una familia de "representaciones de Lawrence" más generales que dependen de varios parámetros. En 1996, Chetan Nayak y Frank Wilczek postularon que en analogía con las representaciones proyectivas de SO(3) , las representaciones proyectivas del grupo trenzado tienen un significado físico para ciertas cuasipartículas en el efecto Hall cuántico fraccionario . ^[14] Alrededor de 2001, Stephen Bigelow y Daan Krammer demostraron de forma independiente que todos los grupos trenzados son lineales. Su trabajo utilizó la representación de Lawrence-Krammer de dimensión que depende de las variables q y t . Al especializar adecuadamente estas variables, el grupo trenzado puede realizarse como un subgrupo del grupo lineal general sobre los números complejos .${\displaystyle n(n-1)/2}$${\displaystyle B_{n}}$

Existen muchas maneras de generalizar esta noción a un número infinito de hebras. La manera más sencilla es tomar el límite directo de los grupos de trenzas, donde las funciones de unión envían los generadores de a los primeros generadores de (es decir, mediante la unión de una hebra trivial). Este grupo, sin embargo, no admite ninguna topología metrizable mientras permanezca continuo.${\displaystyle f\colon B_{n}\to B_{n+1}}$${\displaystyle n-1}$${\displaystyle B_{n}}$${\displaystyle n-1}$${\displaystyle B_{n+1}}$

Paul Fabel ha demostrado que hay dos topologías que pueden imponerse al grupo resultante, cada una de las cuales, al completarse, produce un grupo diferente. ^[15] La primera es un grupo muy dócil y es isomorfo al grupo de clases de mapeo del disco infinitamente perforado, un conjunto discreto de perforaciones que limitan el límite del disco .

El segundo grupo puede considerarse igual que los grupos trenzados finitos. Si se coloca una hebra en cada uno de los puntos , el conjunto de todas las trenzas (donde una trenza se define como una colección de caminos desde los puntos a los puntos de modo que la función produce una permutación en los puntos finales) es isomorfo a este grupo más salvaje. Un hecho interesante es que el grupo trenzado puro en este grupo es isomorfo tanto al límite inverso de los grupos trenzados puros finitos como al grupo fundamental del cubo de Hilbert menos el conjunto${\displaystyle (0,1/n)}$${\displaystyle (0,1/n,0)}$${\displaystyle (0,1/n,1)}$${\displaystyle P_{n}}$

${\displaystyle \{(x_{i})_{i\in \mathbb {N} }\mid x_{i}=x_{j}{\text{ for some }}i\neq j\}.}$

La cohomología de un grupo se define como la cohomología del espacio de clasificación de Eilenberg–MacLane correspondiente , , que es un complejo CW determinado únicamente por hasta homotopía. Un espacio de clasificación para el grupo trenzado es el n- ^ésimo espacio de configuración desordenada de , es decir, el espacio de todos los conjuntos de puntos desordenados distintos en el plano: ^[16]${\displaystyle G}$ ${\displaystyle K(G,1)}$${\displaystyle G}$${\displaystyle B_{n}}$${\displaystyle \mathbb {R} ^{2}}$${\displaystyle n}$

${\displaystyle \operatorname {UConf} _{n}(\mathbb {R} ^{2})=\{\{u_{1},...,u_{n}\}:u_{i}\in \mathbb {R} ^{2},u_{i}\neq u_{j}{\text{ for }}i\neq j\}}$.

Así que por definición

Los cálculos de los coeficientes en se pueden encontrar en Fuks (1970). ^[17]${\displaystyle \mathbb {Z} /2\mathbb {Z} }$

De manera similar, un espacio de clasificación para el grupo trenzado puro es , el n- ^ésimo espacio de configuración ordenado de . En 1968, Vladimir Arnold demostró que la cohomología integral del grupo trenzado puro es el cociente del álgebra exterior generada por la colección de clases de grado uno , sujetas a las relaciones ^[18]${\displaystyle P_{n}}$${\displaystyle \operatorname {Conf} _{n}(\mathbb {R} ^{2})}$ ${\displaystyle \mathbb {R} ^{2}}$${\displaystyle P_{n}}$${\displaystyle \omega _{ij}\;\;1\leq i<j\leq n}$

${\displaystyle \omega _{k,\ell }\omega _{\ell ,m}+\omega _{\ell ,m}\omega _{m,k}+\omega _{m,k}\omega _{k,\ell }=0.}$

• Grupo Artin-Tetas
• Categoría monooidal trenzada
• Espacio vectorial trenzado
• Álgebra de Hopf trenzada
• Teoría de nudos
• Criptografía no conmutativa
• Grupo de trenzas esféricas

• "Grupo de trenzas". PlanetMath .
• CRAG: Biblioteca de computación de criptografía y grupos del Centro de criptografía algebraica de la Universidad Stevens
• Macauley, M. Clase 1.3: Grupos en ciencia, arte y matemáticas. Teoría de grupos visuales . Universidad de Clemson.
• Bigelow, Stephen . «Exploración del subprograma Java B5». Archivado desde el original el 4 de junio de 2013. Consultado el 1 de noviembre de 2007 .
• Página de Lipmaa, Helger, Criptografía y Grupos Braid, archivada desde el original el 3 de agosto de 2009
• Dalvit, Ester (2015). Trenzas – la película.
• Scherich, Nancy. Representaciones de los grupos de trenzas. Dance Your PhD .ampliado más en Detrás de las matemáticas de "Baila tu doctorado", Parte 1: Los grupos de trenzas.